Introduction

China is the largest coal consumer in the world1. Abundant coal reserves2,3 will ensure that coal remains its primary energy source for the foreseeable future. With the depletion of shallow coal resources, deep mining has increasingly become the industry standard. This transition accentuates the inherent characteristics of coal beds, namely strong adsorption and low permeability, which become more pronounced with the advancement of deep mining techniques4,5. These factors contribute to increased difficulties in gas drainage. Consequently, the frequency of severe coal and gas outburst accidents, which pose significant threats to mining safety, is rising6,7. Among the various safety incidents in coal mines, coal and gas outbursts are particularly dangerous8,9,10. Such events represent a highly complex dynamic phenomenon in underground mining11,12,13. The shock waves generated during these outbursts not only have the potential to cause casualties and damage mine infrastructure but may also trigger gas and coal dust explosions, resulting in extensive secondary disasters14,15,16.

Currently, the complete elimination of protruding accidents in coal mines remains unachievable. Given their sudden and unpredictable nature, it is essential to develop effective devices to attenuate shock wave energy for ensuring safety. Numerous scholars have employed theoretical analysis, experimental verification, and numerical simulations to investigate such devices. Many studies have demonstrated that fillers with good dispersion in the polymer matrix exhibit better shock wave mitigation performance17,18,19,20,21,22. Wei, C et al.23 utilized flexible composites composed of an SR matrix and STF microdroplets; experimental results showed that these composites significantly attenuate shock waves.

However, the addition of fillers increases costs and necessitates complex comparisons, thereby complicating operations. Currently, devices for reducing shock wave energy primarily consist of flexible materials, rigid materials, or a combination of both24,25,26,27,28,29. Pang et al.30 validated a numerical method against experimental results from methane/air explosions in steel pipes and concluded that roadway support can inhibit shock wave propagation. Gao Huan et al.31 found that flexible pipelines effectively suppress shock wave propagation. Li et al.32 demonstrated using a round tube gas explosion test system that internally installed rigid and flexible cavity devices can effectively attenuate and absorb shock wave overpressure. Gui et al.33 established a calculation model for gas explosions through numerical analysis and experimentation and proposed that metallic foams effectively reduce explosion flames and shock waves. The flexible composite materials utilized by Jia, sy et al.34 and Liyi et al.35 exhibited favorable shock wave energy absorption capabilities in experiments. Lastly, Ren et al.36, drawing on principles of flexible buffering combined with traditional mining safety equipment, advocated for the use of elastic buffer devices to attenuate shock wave impacts. Numerical simulations demonstrated that elastic devices with different effective cross-sections can significantly accelerate the attenuation of shock wave energy, offering an extremely consistent mitigating effect.

In summary, flexible materials have shown considerable ability to inhibit shock-wave propagation and absorb shock waves. Moreover, elastic devices based on the flexible buffering principle have very limited applications in coal mines. With increasing mining depth, outburst accidents occur more frequently, and there is an urgent demand for safety protection equipment capable of repeatedly absorbing the energy of outburst shock waves. Previous studies have established that elastic devices can effectively reduce shock wave energy, indicating their potential for further exploration. However, the theoretical models of elastic buffer devices have rarely been transformed into practical implementations, and empirical investigations using physical simulation experiments remain scarce. This research pioneers the physical realization of an elastic buffer device. Building on earlier theoretical work36, the study combines theoretical analysis with experimental research to further evaluate the capacity of elastic devices to attenuate shock wave energy in mines.

Theoretical research

Principle of elastic energy absorption

Hooke’s Law states that, within the elastic limit, the stress applied to an elastic object is directly proportional to the strain produced. During deformation, the mechanical energy stored from the interplay between elastic forces and potential energy in various regions of the object is defined as elastic potential energy. This energy remains stored within the structure of the elastic material or physical system as potential mechanical energy. Both Hooke’s Law and the expression for elastic potential energy were formulated by British physicist Robert Hooke. The details are as follows:

$$\:F=k{\Delta\:}x=PS\:$$
(1)
$$\:U=\frac{1}{2}k{{\Delta\:}x}^{2}$$
(2)

where F represents the pressure applied to the spring (N), Δx denotes the spring deformation (mm), k indicates the spring constant (N/mm), S represents the compressed area (m²), P is the pressure, and U is the elastic potential energy (J). The calculation of elastic potential energy is outlined below. The spring constant k depends solely on the spring’s manufacturing materials and structural parameters. This concept was originally proposed by the British physicist Robert Hooke.

The formula for calculating k is as follows:

$$\:k=\frac{G{d}^{4}}{8N{D}^{3}}$$
(3)

where d is the spring wire diameter, mm; D is the spring center diameter, mm; N is the number of spring coils; G is the spring material shear modulus.

From Eq. (1) to (3) can be obtained:

$$\:k=\frac{F}{{\Delta\:}x}=\frac{G{d}^{4}}{8N{D}^{3}}=\frac{PS}{\varDelta\:x}=\frac{2U}{{{\Delta\:}x}^{2}}$$
(4)

where l is the length of the spring (mm) and D₀ is the outer diameter (mm). The spring center diameter is given by D = D0 − d (mm). The maximum compression of the spring is l − Nd, meaning the spring deformation Δx < l − Nd. Since the material and specifications of the spring are known, G, d, and D are also known. Under the condition that the pressure P is determined, and with both ends of the spring fixed to rigid baffles, the force-bearing area S of the spring can be considered as the area corresponding to its outer diameter, which is πD₀². Finally, the relationship between the number of spring coils N and the spring deformation Δx can be derived. Based on this relationship, a spring with appropriate parameters can be selected and the spring constant k calculated. A 304 stainless-steel compression spring, customized according to the above formula (4), has the following specifications: d = 6 mm, D0 = 60 mm, l = 180 mm, N = 10, and G = 80,000 MPa.

Let the length and width of the frontal baffle of the elastic device be L and W respectively (area \(\:S=LW\)), and the internal height of the cavity (the length of the spring in its natural state) be H, then \(\:{{\Delta\:}x}_{max}=(H-Nd)\). Within a single elastic device, the count of springs is denoted as i. The number of such elastic devices sharing an identical cross-sectional area in the roadway is n. Additionally, the protruding pressure is represented by \(\:{P}_{0}{(P}_{0}\in\:[{P}_{min},{P}_{max}])\). For effective energy absorption, the elastic devices within the same cross-sectional area of the roadway must meet the following conditions:

$$\:{P}_{max}LW\le\:\frac{in{{\Delta\:}x}_{max}G{d}^{4}}{8N{D}^{3}}.$$
(5)

Further derivation leads to:

$$\:G\ge\:\frac{8N{D}^{3}{P}_{max}LW}{in{{\Delta\:}x}_{max}{d}^{4}}.$$
(6)

Combined with Eqs. (2), (3), the expression for the elastic potential energy stored by an elastic device of the same cross-section of the lane is given by:

$$\:{U}_{max}=\frac{inG{d}^{4}{{\Delta\:}x}^{2}}{16N{D}^{3}}.$$
(7)

Derived theoretically, the shear modulus of the spring material used in the elastic device and the range of elastic potential energy accumulated per cycle are respectively given by \(\:G\in\:[\frac{8N{D}^{3}{P}_{max}LW}{in{{\Delta\:}x}_{max}{d}^{4}},+{\infty\:})\) and \(\:U\in\:[0,\frac{inG{d}^{4}{{{\Delta\:}x}_{max}}^{2}}{16N{D}^{3}}]\).

From an energy perspective, coal and gas protrusions can be understood as a process where gas expansion energy and the elastic energy of the coal body jointly convert into the kinetic energy of the coal and rock mass. The initial energy sources for this process predominantly include two components: the elastic potential energy and gas expansion energy of the coal body37,38. These components can be quantified as follows:

$$\:{W}_{1}=\frac{1}{2E}\frac{\left[{\sigma\:}_{1}^{2}+{\sigma\:}_{2}^{2}+{\sigma\:}_{3}^{2}-2\mu\:\left({\sigma\:}_{1}{\sigma\:}_{2}+{\sigma\:}_{1}{\sigma\:}_{3}+{\sigma\:}_{2}{\sigma\:}_{3}\right)\right]}{\gamma\:}$$
(8)
$$\:{W}_{2}=\sum\:_{i=1}^{n}{k}_{i}{V}_{i}\rho\:(X-\int\:{q}_{i}dt){E}_{i}$$
(9)

where \(\:{W}_{1}\) represents the elastic potential energy, \(\:{\sigma\:}_{1}{,{\sigma\:}_{2},\sigma\:}_{3}\) are the principal stresses in three perpendicular directions (MPa); E is the modulus of elasticity of the coal body (MPa); µ is the Poisson’s ratio of the coal body; γ is the density of the coal body (t/m3); \(\:{W}_{2}\) is the expansion energy of gas (MJ/t); ρ is the average density of the coal seam (kg/m3); X is the average gas content of the coal seam (m3); \(\:{q}_{i}\) is the coal wall gas outflow function (m3); ki is the residual coefficient of the ith part of protruding gas flow; \(\:{V}_{i}\) is the volume of the coal body corresponding to the ith part of protruding gas flow (m3); and \(\:{E}_{i}\) is the unit mass gas expansion energy of the ith part of the protruding gas flow.

Assuming λ represents the number of segments of the elastic device installed simultaneously in the roadway, and by integrating Eqs. (8), (9) and (10), the ratio η, which indicates the maximum theoretical energy absorption of the elastic device relative to the total energy of the incident shock wave, can be calculated as follows:

$$\:\eta\:=\frac{U}{{W}_{1}+{W}_{2}}$$
(10)
$$\:\eta\:=\frac{\lambda\:E\gamma\:}{8N{D}^{3}}\frac{inG{d}^{4}{\varDelta\:x}^{2}}{[{\sigma\:}_{1}^{2}+{\sigma\:}_{2}^{2}+{\sigma\:}_{3}^{2}-2\mu\:\left({\sigma\:}_{1}{\sigma\:}_{2}+{\sigma\:}_{1}{\sigma\:}_{3}+{\sigma\:}_{2}{\sigma\:}_{3}\right)+2E\gamma\:\sum\:_{i=1}^{n}{k}_{i}{V}_{i}\rho\:(X-\int\:{q}_{i}dt\left){E}_{i}\right]}.$$
(11)

Basic structure of elastic cushioning device

The basic structure of elastic cushioning device is introduced from four aspects: the overall structure of the elastic device, the external cavity, the airbag cushion, and the spring assembly.

(1) Overall structure.

In this study, three elastic devices with different effective cross-sectional areas were developed: 300 mm × 300 mm, 300 mm × 250 mm, and 300 mm × 200 mm. These devices with varying cross-sectional areas provide a material basis for different layout configurations in the subsequent sections. This paper focuses on the device with a 300 mm × 300 mm cross-sectional area. The detailed structural specifications are shown in Figs. 1 and 2.

Fig. 1
figure 1

Diagram of the elastic device. (a) Model figure {created using SolidWorks software (Using SolidWorks 2023 SP5.0, Dassault Systèmes; Official website: https://www.3ds.com/products-services/solidworks/)}. (b) Concrete figure.

Full size image
Fig. 2
figure 2

Dimensional drawing of the elastic device.

Full size image

(2) External cavity.

The external cavity, comprising the side and bottom plates, forms the structural framework of the elastic device. This configuration not only stabilizes the device’s form but also directs the trajectory of the front baffle plate, ensuring that the compression of the spring assembly remains perpendicular to the bottom plate. Such an orientation maximizes energy conversion and enhances the device’s energy absorption capabilities. In this experiment, the baffle was fabricated from 304 stainless-steel plates with a thickness of 6 mm, and the connection was achieved via welding. The detailed structure is shown in Figs. 3 and 4.

Fig. 3
figure 3

External chamber of the elastic device. (a) Model figure {created using SolidWorks software (Using SolidWorks 2023 SP5.0, Dassault Systèmes; Official website: https://www.3ds.com/products-services/solidworks/)}. (b) Concrete figure.

Full size image
Fig. 4
figure 4

External cavity dimension drawing.

Full size image

(3) Airbag cushion.

The airbag cushion is essential to the functionality of the elastic device, serving two primary functions: first, to counteract significant frontal shock waves by working in conjunction with the spring assembly to attenuate these shocks; and second, to maintain the integrity of the external cavity’s structure. It effectively absorbs impact energy and reduces collision forces between the elastic device and the pipeline wall, thereby protecting both the device and the pipeline structure. High-density sponge and rubber are the preferred materials for the airbag cushion. Detailed illustrations are presented in Fig. 5.

Fig. 5
figure 5

Device airbag cushion. (a) Elastic device with airbag cushion. (b) Physical drawing of elastic device - front

Full size image

(4) Spring assembly.

The spring assembly, a critical component of the elastic device, consists of an internal chamber spring, a rotating shaft spring, and a compressible airbag pad. Its performance plays a key role in determining the energy absorption capacity of the device. The assembly stores impact energy and uses elastic deformation to attenuate shock wave transmission in tunnel environments. The internal chamber spring, the primary energy-absorbing and energy-releasing element, has a wire diameter of 6 mm, an outer diameter of 60 mm, 12 coils, a shear modulus of 80,000 MPa, and a total length of 180 mm. It stores energy by converting the kinetic energy of shock waves impacting the front baffle into elastic potential energy. Once a predefined threshold is reached, the stored energy is released, generating a counterforce that reduces the shock wave’s impact. The device is connected to the pipe wall via a rotating shaft, with the shaft spring providing an initial rebound force. However, due to the significant impact of shock waves, the shaft spring alone is inadequate for effective rebound. Therefore, an additional mechanism is employed, which, when attached to one side of the specimen and the pipe wall, maintains tension throughout, thereby enhancing the rebound effect. The details are shown in Fig. 6.

Fig. 6
figure 6

Spring assembly diagram. (a) Elastic device without airbag cushion. (b) Physical drawing of elastic device – back.

Full size image

Elastic device response mechanism

(1) In the absence of protrusions, to ensure uninterrupted underground operations, the elastic device is positioned at an approximate 30-degree angle to both the rotary axis and the roadway wall. When a protrusion occurs, the device pivots around the rotary axis to a 90-degree angle relative to the pipeline wall under the impact force, providing frontal protection against shock waves. Initially, the protruding shock wave impacts the front baffle of the elastic device, which is mounted on an airbag pad. The pad compresses and deforms under the applied pressure. If the airbag pad is unable to withstand the increasing pressure and deformation, the impact force is transmitted to the internal spring components within the chamber. These components elastically compress to absorb the energy of the shock wave, converting it into elastic potential energy and temporarily storing it. The stored energy is then used to counteract the shock wave, enhancing the device’s response in subsequent phases.

(2) To mitigate the risk of excessive energy concentration due to the elastic device’s obstructive properties, the device is engineered to rotate under pressure toward the pipe wall when the shock wave energy reaches a critical threshold of the rotating shaft spring. This rotation continues until the device is positioned parallel to both walls of the pipe. As the direction of energy release is opposite to that of shock wave propagation, this configuration effectively reduces the shock wave energy. Concurrently, the rotation of the elastic device causes a sudden increase in the pipe cross-section, facilitating the transition of shock wave propagation from a smaller to a larger cross-section and thereby achieving overpressure attenuation. The details are shown in Fig. 7.

Fig. 7
figure 7

Diagram of the conceptual simulation device {created using Blender software (Using Blender 3.6.1, Blender Foundation; Official website: https://www.blender.org/download/)}.

Full size image

(3) Once the energy of the protruding shock wave is reduced to a specific level, the elastic device, under the diminished impact force, rotates back to its original position, effectively counteracting the shock wave.

The rotation of the elastic device leads to a sudden reduction in the pipeline cross-section, resulting in a surge of shock wave energy at the front of the device. The elastic device then cyclically repeats the processes outlined in Sect. (2) and (3), thereby ensuring continuous attenuation and absorption of the protruding shock wave’s energy.

Experiments

Experimental system

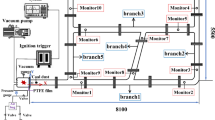
This study employs the coal and gas protrusion simulation system developed by China Coal Technology and Engineering Group for experimental research. The system consists of a tunnel simulation system, a protrusion power system, and a data acquisition system. The experimental pipeline has a total length of 60,159 mm, a diameter of 1,000 mm, and a wall thickness of 50 mm. A rupture disc, located 12 m from the pipe’s sealed end, initiates the experiments. Five pressure sensors are strategically positioned along the inner center of the pipe for hierarchical measurement, at distances of 24 m, 27 m, 30 m, 33 m, and 42 m from the rupture disc. In addition, a high-speed camera is installed at the pipe’s opening end. The pipeline is also equipped with three groups of elastic devices, each comprising four devices, installed at distances of 25.5 m, 28.5 m, and 31.5 m from the rupture disc.

To visually observe the attenuation effect of the elastic device on the shock wave, an iron door of 6 mm thickness made of 304 stainless steel was installed at the open end of the pipeline. In this experimental study, a custom-crafted DN1000 flat-circular flameless explosion-venting rupture disc is employed. Fabricated from 304 stainless steel, it is engineered with designed burst pressures of 600 kPa, 800 kPa, and 1000 kPa, respectively. The high-pressure methane storage tank, provided by Shanghai Shenjiang Pressure Vessel Co., Ltd., is filled with high-purity methane gas at a concentration of 99.99%. The SK-20 water-ring vacuum pump and compressor, produced by Zibo Zhongren Machinery Co., Ltd., is selected; it operates at a rotational speed of 740 r/min, achieves an ultimate pressure of 8300 Pa, offers a maximum gas flow rate of 30 m3/min, and is powered by a 37-KW motor. In this experiment, the CY400 high-frequency pressure sensor manufactured by Chengdu Keda Shengying Technology Co., Ltd. is used. It has a measuring range of 0–1.0 MPa and a measurement accuracy of ± 0.25% FS. Equipped with a sensitive sensing diaphragm, the sensor demonstrates excellent isolation capabilities, stability, vibration resistance, and shock resistance in complex environments. The data acquisition device is the TST6260 transient signal tester produced by Chengdu Test Electronic Information Co., Ltd. It features a maximum sampling rate of 20 Msps, a measurement accuracy of ± 0.25% FS, parallel channel options of 8CH/16CH, a 14-bit A/D converter, and a bandwidth of 1 MHz. The high-speed camera, with a maximum frame rate of 240 fps, is capable of outputting clear color videos at 240 fps to meet the experimental requirements. Details of the experimental system are shown in Fig. 8.

Fig. 8
figure 8

Schematic diagram of the experimental system.

Full size image

Elastic device arrangement

This paper investigates the attenuation effects of elastic devices on the energy of protruding shock waves in a mine tunnel under different configurations, aiming to identify the optimal installation and arrangement strategy. Three configurations of elastic devices are proposed, classified based on the effective cross-sectional area relative to the shock wave propagation direction: unchanged, reduced, and increased (hereinafter referred to as unchanged, smaller, and larger, respectively, as illustrated in Fig. 9). Let A denote the cross-sectional area of the roadway, Ai represent the effective cross-sectional area of the i-th elastic device, and Ai indicate the net effective cross-sectional area of the roadway at the i-th elastic device ___location, calculated as A*i = A-Ai (i = 1,2,3). Additionally, for unchanged effective sections, the condition A*1 = A*2 = A*3 is required; for reduced sections, A*1 < A*2 < A*3; and for enlarged sections, A*1 > A*2 > A*3.

Fig. 9
figure 9

Schematic diagrams of the 3 types of arrangement of the elastic device.

Full size image

Experimental scheme

This paper investigates the energy attenuation law of shock wave propagation in mines under three distinct protruding pressures and three configurations of elastic buffer devices. The high-pressure gas storage tank and rupture disc system used in the experiment require precise control of the pressure triggering conditions. Integer or half-integer kPa values (e.g., 800 kPa) are easier to calibrate and reproduce in engineering practice. Focusing on a gas pressure of 740 kPa, which is considered the lowest critical value for outburst occurrence, three outburst pressures were set: 600 kPa, 800 kPa, and 1000 kPa. The experimental schemes are listed in Table 1.

Table 1 Experimental schemes.
Full size table

Experimental step

This paper examines the propagation of shock waves along a “linear” pipeline following a coal and gas protrusion, with pressure release from the port leading to shock waves measured at five sequential points: P1, P2, P3, P4, and P5. The specific experimental steps, organized chronologically, are divided as follows:

(1) As per the experimental design, set varying protruding pressures and arrange the installation of devices sequentially; configure and calibrate each component of the testing system to ensure all devices are in a ready state.

(2) Pressurize the pipeline and commence the experiment. Once the gas pressure within the pipeline reaches a critical level, the rupture disc at the center is automatically breached to facilitate pressure relief and initiate the protrusion, thereby generating the shock wave.

(3) Post-protrusion, promptly close the high-pressure gas storage tank, verify the effective data capture by the data acquisition system, ensure the high-speed camera system functions correctly, and promptly save and export the data for subsequent analysis and research.

Methods of analysis

(1) Qualitative analysis.

This study estimates the energy magnitude at the pipe’s end by comparing the intensity of the impact airflow and the degree of opening of the iron gate at the pipe’s terminus.

(2) Quantitative analysis.

Research indicates that shock wave overpressures below 20 kPa are unlikely to cause significant harm to underground personnel, suggesting that these overpressure levels are safe. The safety threshold for shock wave-induced injury to the human body is influenced by various factors; thus, the value of 20 kPa is not absolute. This threshold has been reported in numerous studies The magnitude of the overpressure and the duration of its action are closely related to the impact on human fatalities. The smaller the overpressure and the shorter the duration of its action, the significantly higher the survival rate of people will be, and the underground equipment will also suffer less damage39,40,41,42,43. The shock wave injury rating scale is provided in Table 2.

Table 2 Shock wave injury rating scale.
Full size table

The relationship between the damage degree of some ventilation equipment and facilities and the overpressure of the shock wave is shown in Table 344. According to the impulse criterion of shock wave damage mechanisms, the damage force exerted on personnel is directly proportional to the overpressure and the duration of exposure. Therefore, if an elastic device can substantially reduce the overpressure at the pipeline’s end and the time required to reach a safe level, it can be inferred that the device attenuates shock wave energy effectively.

Table 3 Classification of shockwave - induced underground equipment damage.
Full size table

In order to facilitate the subsequent analysis and research, the following provisions: P1max represents the peak overpressure measured at measuring point P1 in the pipeline under different experimental programs; P5max represents the peak overpressure measured at measuring point P5 in the pipeline under different experimental programs. T1 represents the time when P5 reaches the peak overpressure; T2 represents the time when P5 reaches the safety level, the time when the measuring point P5 is reduced from the peak overpressure to less than 20 kPa.

Results

Qualitative analysis

In accordance with the experimental protocol, twelve experiments were conducted to investigate the propagation of protruding shock waves under the buffering effect of elastic devices. The experimental observations captured at the moment the peak pressure reached the open end of the pipeline are illustrated in Figs. 10, 11 and 12.

Fig. 10
figure 10

Experimental group I pipe end experimental phenomenon.

Full size image
Fig. 11
figure 11

Experimental group II pipe end experimental phenomenon.

Full size image
Fig. 12
figure 12

Experimental group III pipe end experimental phenomenon.

Full size image

It can be seen from Figs. 10, 11 and 12:

(1) After the protrusion event, the iron door at the pipeline’s end is forced open to either side by the shock wave, carrying dust and fine debris within the pipeline to create a shock airflow that propagates to the pipeline’s terminus.

(2) Under identical protruding pressures, the impact airflow at the pipeline’s end is more intense in the absence of an elastic device. The installation of an elastic device results in a lighter color of the impact airflow and a reduced opening amplitude of the iron door at the pipeline’s end. This suggests that the presence of elastic devices in the pipeline attenuates the energy of the shock wave.

Quantitative analysis

To further quantify the experimental results, overpressure changes at each measurement point were collected via pressure sensors during the experimental process. After data smoothing, the overpressure change curves for each measurement point are displayed in Figs. 13, 14 and 15. Concurrently, a summary table of relevant experimental data from Experimental Group I, II and III has been compiled based on the monitored data, as presented in Tables 4, 5 and 6.

Fig. 13
figure 13

Experimental group I overpressure-time curve of each measurement point.

Full size image
Table 4 Summary table of relevant experimental data.
Full size table
Table 5 Table of time reduction rate.
Full size table
Table 6 Table of reduction rate of P5 peak overpressure.
Full size table
Fig. 14
figure 14

Experimental group II overpressure-time curve of each measurement point.

Full size image
Fig. 15
figure 15

Experimental group III overpressure-time curve of each measurement point.

Full size image

From Figs. 13, 14 and 15; Tables 4, 5 and 6, it can be seen:

(1) Following the protrusion, overpressure at each measurement point rapidly peaked and exhibited alternating phases of positive and negative pressure, which then progressively decayed and stabilized over time. When equipped with elastic devices, the front end of the pipeline (from P1 to P3) displayed more pronounced alternations between positive and negative pressure phases in the shock wave overpressure, suggesting localized overpressure increases. This is attributed to pressure concentration areas forming in front of the elastic device, leading to energy concentration. Concurrently, the buffer effect of the elastic device moderated the fluctuations in overpressure at measurement points P4 and P5, demonstrating a suppression effect. Consequently, a significant decrease in overpressure was observed at the end of the pipeline (P4, P5), indicating that the elastic device substantially diminishes the energy of the shock wave.

(2) At measurement point P5, the reduction in shock wave overpressure compared with scenarios without elastic devices installed is significant across three different device arrangements. When the arrangement remains unchanged, the peak overpressure reduction ranges from 53.5 to 68.4%. In setups where the device size is smaller or larger, the reductions are 49.4–64.9% and 33.7–53.8%, respectively.

(3) Under the influence of the elastic device, the time required to reach the safety level at the end of the pipeline is significantly reduced. Specifically, with an unchanged arrangement, the time reduction at measurement point P5 ranges from 65.0 to 82.8%. When the device size is smaller, this reduction spans from 40.6 to 61.1%, and when the size is larger, from 33.7 to 79.6%. Notably, with an unchanged installation method, the rate of reduction increases as the protrusion pressure escalates.

(4) Under consistent protrusion pressures, the attenuation effect of the elastic device on shock wave energy varies with its arrangement. Among the experimental groups, the most effective attenuation occurs when the effective section remains unchanged, followed by the smallest change, and the least effective when the change is large.

(5) Regardless of the variation in protrusion pressure, the attenuation pattern of the elastic device on the energy of the shock wave remains constant across the same effective section changes. However, the attenuation effect intensifies with increasing protrusion pressure.

Discussion

Results interpretation

(1) Analysis in Sect. 4.1 shows that when no elastic device is installed in the pipeline, an increase in outburst pressure results in a progressively stronger impact airflow, and the gas color gradually deepens. When an elastic device is installed in an “unchanged” arrangement (Figs. 10b, 11b and 12b), the color of the impact airflow at the pipeline end is the lightest, presenting a faint grayish-white, indicating the most significant attenuation of shock wave energy. The dust-carrying capacity of the airflow is minimal, and the opening amplitude of the iron door is the smallest. When an elastic device is installed in “Smaller” arrangement (Figs. 10c, 11c and 12c), the airflow color is slightly darker than that in the unchanged arrangement, showing a medium gray tone. Although the energy attenuation effect is noticeable, the dust concentration in the airflow is higher than that in the unchanged arrangement, and the iron door opens slightly wider. When an elastic device is installed in “Larger” arrangement (Figs. 10d, 11d and 12d), the impact airflow exhibits the darkest color, appearing as a deep gray. Compared with the other two arrangements, it carries more dust and debris, and the iron door opening amplitude is the largest, indicating the weakest energy attenuation effect among the three configurations.

It can be concluded that the arrangement with a reduced effective cross-sectional area is superior to that with an enlarged one, and the arrangement with an unchanged effective cross-sectional area is superior to that with a reduced one.

(2) The result analysis in Sect. 4.2 demonstrates that when the arrangement of the elastic devices remains unchanged, they can partition the roadway into more independent and uniformly distributed sections. This division fills more of the intermediate voids in the roadway, enhancing the elastic devices’ ability to attenuate the energy of the outburst shock wave and accelerating its decay. Meanwhile, the analysis also verifies that the shock wave energy is stronger in the middle and weaker near the two side walls.

Comparison with previous studies

Referring to the numerical simulation data of the elastic device in Ref36. , the data in the first column is denoted as Pre-P5max, with values ranging from 41 to 96, while the data in the second column is denoted as P5max, with values ranging from 32.3 to 93.6. Detailed data are presented in Table 7. An analysis of variance (ANOVA) was conducted on these two groups. At a significance level of α = 0.05 and by referring to the F-distribution table, the critical value Fcrit was found to be approximately 4.49 when the degrees of freedom were (1, 16). Since the calculated F-value is 0.098, which is less than Fcrit, the null hypothesis was not rejected. In other words, there is no significant difference between the means of the two groups. This indicates that no significant difference exists between the experimental data and the numerical simulation results. Detailed data are presented in Table 8.

Table 7 Data comparison.
Full size table
Table 8 Variance data.
Full size table

Limitations and future perspectives

(1) Based on this study, systematic tests on impact loads, such as specific impulse and positive-pressure time, can be performed in future research. In a high-strain-rate response environment, these characteristic coefficients are crucial for understanding the structural dynamic response. Furthermore, in the follow - up, it is necessary to add the quantitative correlation between spring parameters (such as shear modulus, number of turns) and energy attenuation. Additionally, a strength check of the elastic device structure is necessary. Through multiple experimental tests, it can be determined whether its structural strength remains within the safe range under critical working conditions. Finally, the current elastic device does not account for the influence of environmental factors, such as coal dust and humidity, on the durability of the elastic components. Subsequent studies could include additional experiments considering these factors.

(2) In this experiment, the elastic devices were installed with a spacing of 3 m. In actual coal mine roadways, the same spacing can be adopted. Additionally, based on the length of the roadway and the areas where gas outbursts are likely to occur, the elastic devices should be installed at key positions that may be affected by outburst shock waves, such as near the excavation and mining working faces and at the key nodes of ventilation roadways. Preferably, the layout method maintains the effective cross-sectional area of the elastic devices unchanged. During actual installation, it is necessary to design the size and installation angle of the elastic devices rationally according to the actual dimensions and shapes of the roadways, and to appropriately increase the number of devices or the installation density.

(3) Future research should increase the number of experiments, incorporate multiple variables such as roadway curvature, and consider various environmental factors including coal dust and humidity. Strength tests and durability analyses of the actual device should be performed, the limit value of energy absorption quantified, and the attenuation mechanism revealed. Furthermore, experimental tests in real-world environments should be conducted to promote the transformation of this device into practical applications.

Conclusion

Experimental research was conducted to evaluate the energy attenuation of prominent shock waves in mines facilitated by the buffer-absorption capabilities of an elastic device. The conclusions are summarized as follows:

(1) The principle of elastic energy absorption was analyzed, and the elastic device was designed and manufactured. The study revealed the mechanism by which the elastic device attenuates the energy of prominent shock waves in mines, as well as the device’s response principle. Experimentally, the mitigating effect of the elastic device on the energy generated by the outburst shock wave was verified, demonstrating its high practicability and feasibility.

(2) According to the experimental program, 12 experiments were conducted. Analysis of shock overpressure changes over time at five measurement points yielded significant findings. When the elastic device was installed with an unchanged effective cross-sectional area, it proved most effective in attenuating the energy of the protruding shock wave. The peak overpressure at the end of the pipeline was significantly reduced, with decreases at measurement point P5 ranging from 53.5 to 68.4%. Additionally, the time required for the peak overpressure at P5 to drop below 20 kPa was markedly shortened, with reductions ranging from 65.0 to 82.8%. Notably, the reduction rate increased with the escalation of protrusion pressure. When the effective cross-sectional area of the device remains unchanged, the attenuation effect is optimal. Moreover, as the outburst pressure increases, the attenuation effect becomes better.

(3) Owing to its flexible buffer design, the elastic device in the pipeline effectively attenuates shock wave energy. This capability enhances the alternation between positive and negative overpressure changes at the front end of the pipeline (P1 to P3) and enables gradual, staged energy release. Consequently, the impact energy at the pipeline’s end (P4, P5) is significantly reduced, thereby lowering losses from protruding disasters and improving personnel safety.