Introduction

In recent years, there has been a growing interest among researchers and scientists in solving nonlinear partial differential equations (NLPDEs) and deriving their exact solutions1,2,3. Among these equations, the nonlinear Schrödinger equation (NLSE) stands out as one of the most extensively studied, particularly in the realms of nonlinear optics and optical fiber systems4,5,6,7. Optical fibers play a crucial role in enabling the efficient transmission of data over long distances with minimal loss and signal degradation. To maintain stability and ensure reliable communication, it is essential to analyze critical factors such as dispersion, nonlinearity, and attenuation, as these directly impact signal quality and limit achievable data rates8,9,10. The NLSE serves as a fundamental model in fiber optics, describing wave systems and capturing the intricate interactions between dispersion and nonlinear effects. Researchers have utilized the NLSE to investigate various phenomena, including soliton dynamics, microtubule motion in optical fiber systems, novel soliton structures, peakon and cuspon excitations, and modifications of the Schrödinger equation11,12,13. Studies have also focused on the NLSE under different types of nonlinearities, such as dual-power law, Kerr law, quadratic-cubic, and parabolic law nonlinearities14,15. Understanding these propagation mechanisms enables advancements in fiber design, the development of enhanced modulation techniques, and the implementation of effective signal processing strategies16,17,18.

Stochastic partial differential equations (SPDEs) play a vital role in modeling physical, biological, and chemical systems influenced by randomness19,20. Their applications span diverse fields, including finance, engineering, biophysics, climate science, and materials science, reflecting the importance of incorporating stochastic effects into complex system analyses21,22. One notable example is the use of SPDEs in studying optical solitons, self-sustaining wave packets in nonlinear fiber optics described by the nonlinear Schrödinger equation. The NLSE captures the effects of an optical fiber’s nonlinear refractive index, often modeled by Kerr nonlinearity. When multiplicative white noise is introduced, it significantly alters soliton behavior, stabilizing solutions around zero and influencing their long-term dynamics. This has led researchers to develop innovative methods to analyze such noise effects, offering insights that could enhance signal processing and transmission in optical communication systems. For a better understanding of these nonlinear phenomena, it is important to study the analytic solutions of the NPDEs. Thus, different techniques have been previously discovered and improved to construct soliton solutions for NPDEs. These techniques include the enhanced modified tanh expansion method23, the simple equation method24, the enhanced algebraic method25, the Jacobi elliptic function expansion technique26, the modified F-expansion method27, the generalized Kudryashov method28,29, the Sardar sub-equation technique30,31, the trial equation method32, the \(\phi ^6 -\) model expansion method33, the modified Kudryashov method34, the generalized exponential rational function technique35, and the Lie symmetry analysis method36.

Numerous mathematical models have been refined to describe wave propagation in optical fibers, revealing fascinating phenomena driven by the complex interplay between dispersion and nonlinearity. These insights have found applications across various fields, including plasma physics, fluid dynamics, and optical systems, broadening the scope of research and technological innovation in these areas37,38,39. In this paper, we investigate the dynamical behavior of various novel optical solutions to the newly proposed generalized derivative NLSE model, which includes perturbation terms with multiplicative white noise, as follows:

$$\begin{aligned} i\left( q^m\right) _t+\alpha \left( q^m\right) _{xx}^{2\mu }+i \beta \left( |q|^{2n} q^m\right) _x^{\mu }+m\sigma q^m \frac{d W(t)}{dt}=i \gamma |q|^{2n}\left( q^m\right) _x^{\mu }+\delta |q|^{4n} q^m, 0<\mu \le 1, \end{aligned}$$
(1)

where q(x, t) represents a complex valued function, and i is defined as \(\sqrt{-1}\). The initial term outlines the generalized linear progression over time. Interestingly, the constant \(\alpha , \sigma ,\beta ,\gamma\) and \(\delta\) are all real values, and m and n are positive integer values. The parameter \(\alpha\) represents the coefficient linked to generalized chromatic dispersion (CD), whereas \(\beta\) serves as the coefficient for the generalized nonlinear effects. Additionally, \(\sigma\) denotes the coefficient of the noise strength, and W(t) defines the standard Wiener process, characterized by derivative \(\frac{dW}{dt}\), which acts as white noise. The perturbative components on the right-hand side of the Eq. (1) represent the dissipative term and the higher-order nonlinearity, respectively. The parameter \(\sigma\) modulates the influence of the external stochastic or random effects through the fractional Brownian motion W(t), while \(\delta\) is a real parameter that contributes to the higher-order nonlinear interaction. By selecting these parameters carefully, the proposed model remains both physically interpretable and mathematically tractable, enabling the construction of exact solutions and facilitating bifurcation or stability analyses relevant to nonlinear optics and related fields.

Equation (1) is reduced to the generalized NLSE form in the case where \(\gamma =\delta =0\). Specifically, with conditions \(m=n=\beta =\alpha =1\), Eq. (1) transforms into the derivative NLSE. Interestingly, the scenario where \(\sigma =0\) for Eq. (1) has been examined previously in the context described in40. The present type of nonlinear Schrödinger equation was very recently studied by Elsayed et al. in41,42,43,44. The main purpose of this paper is to derive various optical soliton solutions to the generalized derivative NLSE model with multiplicative white noise using the new direct mapping method and the Kudryashov method. Furthermore, the dynamical behavior of the novel optical solutions under the influence of multiplicative white noise is analyzed.

Definition 1.1

$$\begin{aligned} {{L}_{\beta }}\left( q \right) (z)=\underset{d\rightarrow 0}{\mathop {\lim }}\,\frac{q(z+d{{z}^{1-\beta }})-q(z)}{d}, \beta \in (0,1]. \end{aligned}$$
(2)

Suppose that \({{q}_{1}}\) and \({{q}_{2}}\) are conformable differentiable of order \(\beta\), and \({{s}_{1}},{{s}_{2}}\in \mathbb {R}\). The followings are hold45:

  1. i.

    \({{L}_{\beta }}({{s}_{1}}{{q}_{1}}+{{s}_{2}}{{q}_{2}})={{s}_{1}}{{L}_{\beta }}({{q}_{1}})+{{s}_{2}}{{L}_{\beta }}({{q}_{2}}).\)

  2. ii.

    \({{L}_{\beta }}({{x}^{l}})=l{{x}^{l-\beta }}\) for all \(l\in \mathbb {R}\).

  3. iii.

    \({{L}_{\beta }}({{q}_{1}}{{q}_{2}})={{q}_{2}}{{L}_{\beta }}({{q}_{1}})+{{q}_{1}}{{L}_{\beta }}({{q}_{2}})\).

  4. iv.

    \({{L}_{\beta }}\left( \frac{{{q}_{1}}}{{{q}_{2}}} \right) =\frac{{{q}_{2}}{{L}_{\beta }}({{q}_{1}})-{{q}_{1}}{{L}_{\beta }}({{q}_{2}})}{{{q}_{2}}^{2}}\).

Fractional calculus has become a powerful framework for accurately modeling a wide range of physical phenomena. Modern fractional-order models offer greater flexibility and adaptability than traditional integer-order models, making them well-suited for complex systems. This study explores the fundamental principles of the conformable derivative, which plays a crucial role in understanding the behavior and dynamics of various physical processes46,47. With broad applications in physics, engineering, economics, and biology, the conformable derivative serves as an effective analytical tool for addressing complex challenges across multiple disciplines48,49.

Standard Wiener process

The Standard Wiener process, commonly known as Brownian motion, plays a fundamental role in both physics and mathematics. It describes the erratic movement of a particle suspended in a fluid, caused by continuous collisions with the fluid’s molecules. This motion is characterized by randomness, continuity, and certain statistical properties, making it a vital concept in various scientific fields. From this point, let us define the SWP W(t) as follows:

Definition 2.1

The stochastic process W(t), \(t\ge 0\) is called SWP if it fulfills :

  1. 1.

    W(t) is continuous,

  2. 2.

    \(W(0)=0\),

  3. 3.

    W(t) is has independent increments,

  4. 4.

    \(W(t)-W(s)\) has normal distribution.

Formulation of problem

In this section, we apply the new Kudryashov method to analyze the generalized derivative NLSE model, which is influenced by multiplicative white noise and conformable derivatives. The goal is to derive several closed-form optical solutions in various forms. We begin by employing the following transformations:

$$\begin{aligned} \begin{aligned}&q(x,t)=U(\xi ){e}^{i[-k\frac{x^\mu }{\mu }+wt+\sigma W(t)-\sigma ^2 t]},\, \\&\xi =\frac{x^\mu }{\mu }-Ct. \\ \end{aligned} \end{aligned}$$
(3)

The constants k, w, , and C are real numbers to be determined, representing the soliton’s frequency, wave number, and velocity, respectively. By substituting the transformations from (3) into Eq. (3), we derive the following real part:

$$\begin{aligned}&k m \left( \beta -\gamma \right) U\! \left( \xi \right) ^{2n+2}-\delta U\! \left( \xi \right) ^{4n+2}-m \Big (\left( \alpha k^{2} m-\sigma ^{2}+w\right) U\! \left( \xi \right) ^{2}\nonumber \\ &\quad -\alpha U(\xi )U''(\xi )-\alpha \left( m-1\right) U'(\xi )^2\Big )=0, \end{aligned}$$
(4)

and the following imaginary part:

$$\begin{aligned} U(\xi )^{m-1} U'(\xi ) \left( U\! \left( \xi \right) ^{2 n} m \beta +2 U\! \left( \xi \right) ^{2 n} n \beta -U\! \left( \xi \right) ^{2 n} m \gamma -2 m^{2} \alpha k-mC\right) =0, \end{aligned}$$
(5)

From Eq. (5), we obtain

$$\begin{aligned} \begin{aligned}&C=-2\alpha k,\\&\beta =\frac{m\gamma }{2n+m}. \end{aligned} \end{aligned}$$
(6)

To obtain an integer value for N, hence, we need the following relation:

$$\begin{aligned} U(\xi )=(G(\xi ))^\frac{1}{2n}. \end{aligned}$$
(7)

Inserting the above relation into Eq. (4), we obtain:

$$\begin{aligned} mkG(\xi )^{3}(\beta -\gamma ) -\left( k^{2} m^{2} \alpha +\left( w-\sigma ^{2}\right) m+\delta G\left( \xi \right) ^{2}\right) G\left( \xi \right) ^{2}+\frac{m \alpha }{2n}G(\xi )G''(\xi )+\frac{m \alpha }{4 n^{2}}(m-2 n)G'(\xi )^2=0. \end{aligned}$$
(8)
Table 1 Comparison of analytical methods for solving nonlinear differential equations.
Full size table

Application of the new Kudryashov method

In this section, we derive a range of innovative optical soliton solutions for the studied model, obtained using the new Kudryashov method, which was first introduced by N. Kudryashov in 202250. Although it works well for producing exact solutions to nonlinear partial differential equations, the new Kudryashov approach has certain drawbacks. Its usefulness to more complicated or highly non-polynomial systems is limited, primarily because it works best with equations that have polynomial or rational nonlinearities. The method’s effectiveness in addressing large-scale or extended models is further diminished by the symbolic computing it requires, which can become laborious for higher-dimensional or highly nonlinear systems. Here, we posit that the solution to Eq. (8) can be represented as the following series:

$$\begin{aligned} G(\xi )={{f}_{0}}+\sum \limits _{i=1}^{N}{{{f}_{i}}}B {{(\xi )}^{i}}, \end{aligned}$$
(9)

where \({{f}_{0}},{{f}_{1}},...,{{f}_{N}}\) are real constants, and N denotes a balancing parameter. By balancing principle for \(G(\xi )G''(\xi )\) and \(G(\xi )^4\) in Eq. (8), we obtain \(N=1\). Thus, Eq. (9) reduced to the following series:

$$\begin{aligned} G(\xi )={{f}_{0}}+{{f}_{1}}B(\xi ), \end{aligned}$$
(10)

where \(B(\xi )\) satisfies the following relation:

$$\begin{aligned} {{\left( \frac{dB(\xi )}{d\xi } \right) }^{2}}=\eta ^2{B}^{2}(\xi )(1\pm \chi {B}^{2}(\xi )). \end{aligned}$$
(11)

Here, the solutions of the above equation are defined as follows:

$$\begin{aligned} B_{1}(\xi )=\frac{2\varepsilon H}{H^{2} {\mathrm e}^{\varepsilon \eta \xi }\mp \chi {\mathrm e}^{-\varepsilon \eta \xi }}, \end{aligned}$$
(12)

and the hyperbolic function is

$$\begin{aligned} B_{2}(\xi )=\frac{2 \varepsilon H}{\left( H^{2}\mp \chi \right) \cosh \left( \eta \xi \right) +\left( H^{2}\pm \chi \right) \sinh \left( \eta \xi \right) }, \end{aligned}$$
(13)

where \(\varepsilon =\mp 1\) and \(\chi , H,\eta ,\) and m are constants.

By substituting Eqs. (10) and (11) into Eq. (8), we obtain a polynomial in terms of the powers of \(B(\xi )\). Next, we organize the terms according to their respective powers and equate each corresponding coefficient to zero. This procedure results in a system of algebraic equations and solving the system, one can have the following results:

$$\begin{aligned} \begin{aligned} \text{[ }-45pt][r]{(B(\xi ))^{0}: -f_{1}^{4} \delta -\frac{f_{1}^{2} m \alpha \chi \,\eta ^{2}}{n}-\frac{f_{1}^{2} m \alpha \chi \,\eta ^{2} \left( m-2 n\right) }{4 n^{2}}=0,}\\ \end{aligned} \end{aligned}$$
$$\begin{aligned} \begin{aligned} \text{[ }-39.25pt][r]{ (B(\xi ))^{1}:k f_{1}^{3} m \left( \beta -\gamma \right) -4 f_{0} f_{1}^{3} \delta -\frac{f_{0} m \alpha f_{1} \chi \,\eta ^{2}}{n}= 0,}\\ \end{aligned} \end{aligned}$$
$$\begin{aligned} \begin{aligned} \text{[ }381.25pt][r]{(B(\xi ))^{2}:3 k f_{0} f_{1}^{2} m \left( \beta -\gamma \right) -\left( k^{2} m^{2} \alpha +\left( w-\sigma ^{2}\right) m+f_{0}^{2} \delta \right) f_{1}^{2}-5 f_{0}^{2} f_{1}^{2} \delta +\frac{f_{1}^{2} m \alpha \,\eta ^{2}}{2 n}+\frac{f_{1}^{2} m \alpha \,\eta ^{2} \left( m-2 n\right) }{4 n^{2}}= 0,}\\ \end{aligned} \end{aligned}$$
$$\begin{aligned} \begin{aligned} \text{[ }273.25pt][r]{(B(\xi ))^{3}:3 k f_{0}^{2} f_{1} m \left( \beta -\gamma \right) -2 \left( k^{2} m^{2} \alpha +\left( w-\sigma ^{2}\right) m+f_{0}^{2} \delta \right) f_{0} f_{1}-2 f_{0}^{3} f_{1} \delta +\frac{f_{0} m \alpha f_{1} \eta ^{2}}{2 n}= 0,}\\ \end{aligned} \end{aligned}$$
$$\begin{aligned} \begin{aligned} \text{[ }29.25pt][r]{(B(\xi ))^{4}: k f_{0}^{3} m \left( \beta -\gamma \right) -\left( k^{2} m^{2} \alpha +\left( w-\sigma ^{2}\right) m+f_{0}^{2} \delta \right) f_{0}^{2}= 0.}\\ \end{aligned} \end{aligned}$$
Figure 1
figure 1

The bright plots of \({{\left| {{q}_{1}}(x,t) \right| }^{2}}\), where \(H=\eta =1,k=2,\gamma =0.1,\delta =-0.3,\chi =4\), and \(n=3\).

Full size image

Result 1.

$$\begin{aligned} \begin{aligned}&f_{0}=-\frac{2 k n \left( \gamma -\beta \right) }{3 \delta },f_{1}=-\frac{2 \sqrt{2\chi }\, \left( \gamma -\beta \right) n k}{3 \delta },\alpha =-\frac{4 k^{2} n^{2} \left( \beta -\gamma \right) ^{2}}{9 \eta ^{2} \delta },\\&m=2n,w=\frac{8 n^{3} \left( \beta -\gamma \right) ^{2} k^{4}+4 n \eta ^{2} \left( \beta -\gamma \right) ^{2} k^{2}+9 \delta \,\eta ^{2} \sigma ^{2}}{9 \eta ^{2} \delta }. \\ \end{aligned} \end{aligned}$$
(14)

Utilizing Eqs. (3), (6), (7), (10), (12)-(13), and (14), we can have the following optical solutions:

$$\begin{aligned} {{q}_{1}}(x,t)&={\left( -\frac{k n \gamma }{3 \delta }-\frac{2 \sqrt{2\chi }\, \gamma n k H}{3 \delta \left( H^{2} {\mathrm e}^{\eta \left( \frac{x^\mu }{\mu }+\Gamma _1\right) }+\chi {\mathrm e}^{-\eta \left( \frac{x^\mu }{\mu }+\Gamma _1\right) }\right) }\right) }^{\frac{1}{2 n}} {\mathrm e}^{i \left( \sigma W\left( t\right) -k \frac{x^\mu }{\mu }+\frac{\Gamma _2 t}{9 \eta ^{2} \delta }-\sigma ^{2} t\right) }, \end{aligned}$$
(15)
$$\begin{aligned} {{q}_{2}}(x,t)&={\left( -\frac{k n \gamma }{3 \delta }-\frac{2 \sqrt{2\chi }\, \gamma n k H}{3 \delta \left( \left( H^{2}+\chi \right) \cosh \! \left( \eta \left( \frac{x^\mu }{\mu }+\Gamma _1\right) \right) +\left( H^{2}-\chi \right) \sinh \! \left( \eta \left( \frac{x^\mu }{\mu }+\Gamma _1\right) \right) \right) }\right) }^{\frac{1}{2 n}}\nonumber \\ &\quad \times {\mathrm e}^{i \left( \sigma W\left( t\right) -k \frac{x^\mu }{\mu }+\frac{\Gamma _2 t}{9 \eta ^{2} \delta }-\sigma ^{2} t\right) }, \end{aligned}$$
(16)

where \(\chi >0\).

Suppose that \(\chi =-H^2\). By inserting the value of \(\chi\) into Eq. (16), we acquired the following soliton solutions:

$$\begin{aligned}&{{q}_{3}}(x,t)={\left( -\frac{k n \gamma }{3 \delta }-\frac{ \sqrt{-2H^{2}}\, \gamma n k}{3 \delta H}\textrm{csch}\left( \eta \left( \frac{x^\mu }{\mu }+\Gamma _1\right) \right) \right) }^{\frac{1}{2 n}} {\mathrm e}^{i\left( \sigma W\left( t\right) -k \frac{x^\mu }{\mu }+\frac{\Gamma _2 t}{9 \eta ^{2} \delta }-\sigma ^{2} t\right) }.&\end{aligned}$$
(17)

Suppose that \(\chi =H^2\). By inserting the value of \(\chi\) into Eq. (16), we acquired the following soliton solutions:

$$\begin{aligned}&{{q}_{4}}(x,t)={\left( -\frac{k n \gamma }{3 \delta }-\frac{ \sqrt{2H^{2}}\, \gamma n k}{3 \delta H}\textrm{sech}\left( \eta \left( \frac{x^\mu }{\mu }+\Gamma _1\right) \right) \right) }^{\frac{1}{2 n}} {\mathrm e}^{i\left( \sigma W\left( t\right) -k \frac{x^\mu }{\mu }+\frac{\Gamma _2 t}{9 \eta ^{2} \delta }-\sigma ^{2} t\right) },&\end{aligned}$$
(18)

where \(\Gamma _1=\frac{4 k^{3} n^{3} \gamma ^{2} t}{9 \eta ^{2} \delta }\) and \(\Gamma _2=2 \gamma ^{2} k^{4} n^{3}+\eta ^{2} \gamma ^{2} k^{2} n+9 \delta \,\eta ^{2} \sigma ^{2}\).

Figure 2
figure 2

The bright plots of \({{\left| {{q}_{1}}(x,t) \right| }^{2}}\),where \(H=\eta =1,k=2,\gamma =0.1,\delta =-0.3,\chi =4\), and \(n=3\).

Full size image

Result 2.

$$\begin{aligned}&f_{0}=f_0,f_{1}= -\sqrt{\chi }\, f_{0},\alpha = -\frac{4 f_{0}^{2} \delta }{3 \eta ^{2}},k=-\frac{8 \delta f_{0}}{3 n \left( -\beta +\gamma \right) },\nonumber \\&\quad m= n,w= \frac{27 \left( n \sigma ^{2}+\frac{5}{3} f_{0}^{2} \delta \right) \left( \beta -\gamma \right) ^{2} \eta ^{2}+256 f_{0}^{4} \delta ^{3}}{27 n \eta ^{2} \left( \beta -\gamma \right) ^{2}}. \end{aligned}$$
(19)

Utilizing Eqs. (3), (6), (7), (10), (12)-(13), and (19), we can have the following optical solutions:

$$\begin{aligned}&{{q}_{5}}(x,t)=\left( f_{0}-\frac{2 \sqrt{\chi }\, f_{0} H}{H^{2} {\mathrm e}^{\eta \left( \frac{x^\mu }{\mu }-\frac{32 f_{0}^{3} \delta ^{2} t}{3 \eta ^{2} \gamma }\right) }+\chi {\mathrm e}^{-\eta \left( \frac{x^\mu }{\mu }-\frac{32 f_{0}^{3} \delta ^{2} t}{3 \eta ^{2} \gamma }\right) }}\right) ^{\frac{1}{2 n}} {\mathrm e}^{i \left( \frac{4 \delta f_{0} x^\mu }{n \gamma \mu }+\Gamma _3+\sigma W\left( t\right) -\sigma ^{2} t\right) },&\end{aligned}$$
(20)
$$\begin{aligned} {{q}_{6}}(x,t)&={\left( f_{0}-\frac{2 \sqrt{\chi }\, f_{0} H}{\left( H^{2}+\chi \right) \cosh \! \left( \eta \left( \frac{x^\mu }{\mu }-\frac{32 f_{0}^{3} \delta ^{2} t}{3 \eta ^{2} \gamma }\right) \right) +\left( H^{2}-\chi \right) \sinh \! \left( \eta \left( \frac{x^\mu }{\mu }-\frac{32 f_{0}^{3} \delta ^{2} t}{3 \eta ^{2} \gamma }\right) \right) }\right) }^{\frac{1}{2 n}}\nonumber \\ &\quad \times {\mathrm e}^{i \left( \frac{4 \delta f_{0} x^\mu }{n \gamma \mu }+\Gamma _3+\sigma W\left( t\right) -\sigma ^{2} t\right) }, \end{aligned}$$
(21)

where \(\chi >0\).

Suppose that \(\chi =-H^2\). By inserting the value of \(\chi\) into Eq. (21), we acquired the following soliton solutions:

$$\begin{aligned}&{{q}_{7}}(x,t)={\left( f_{0}-\frac{\sqrt{-H^{2}}\, f_{0} }{H}\textrm{csch}\! \left( \eta \left( \frac{x^\mu }{\mu }-\frac{32 f_{0}^{3} \delta ^{2} t}{3 \eta ^{2} \gamma }\right) \right) \right) }^{\frac{1}{2 n}} {\mathrm e}^{i \left( \frac{4 \delta f_{0} x^\mu }{n \gamma \mu }+\Gamma _3+\sigma W\left( t\right) -\sigma ^{2} t\right) }.&\end{aligned}$$
(22)

Suppose that \(\chi =H^2\). By inserting the value of \(\chi\) into Eq. (21), we acquired the following soliton solutions:

$$\begin{aligned}&{{q}_{8}}(x,t)={\left( f_{0}-\frac{\sqrt{H^{2}}\, f_{0}}{H}\textrm{sech}\left( \eta \left( \frac{x^\mu }{\mu }-\frac{32 f_{0}^{3} \delta ^{2} t}{3 \eta ^{2} \gamma }\right) \right) \right) }^{\frac{1}{2 n}} {\mathrm e}^{i \left( \frac{4 \delta f_{0} x^\mu }{n \gamma \mu }+\Gamma _3+\sigma W\left( t\right) -\sigma ^{2} t\right) },&\end{aligned}$$
(23)

where \(\Gamma _3=\frac{\left( \gamma ^{2} \left( n \sigma ^{2}+\frac{5}{3} f_{0}^{2} \delta \right) \eta ^{2}+\frac{64}{3} f_{0}^{4} \delta ^{3}\right) t}{n \eta ^{2} \gamma ^{2}}\).

Figure 3
figure 3

The wave plots of \(Re(q_1(x,t))\), where \(H=\eta =1,k=2,\gamma =0.1,\delta =-0.3,\chi =4\), and \(n=3\).

Full size image

Result 3.

$$\begin{aligned} \begin{aligned}&f_{0}=\frac{\sqrt{2}\, f_{1}}{2 \sqrt{\chi }},f_{1}=f_1,w=\frac{2 \sqrt{2}\, \left( \frac{3}{4} \sqrt{2\chi }\, \eta ^{2} \sigma ^{2}+\left( k^{2} n^{2}+\frac{1}{2}\eta ^{2}\right) k \left( \beta -\gamma \right) f_{1}\right) }{3 \sqrt{\chi }\, \eta ^{2}},\\&m=2n,\alpha =\frac{f_{1} \sqrt{2}\, \left( -\beta +\gamma \right) n k}{3 \sqrt{\chi }\, \eta ^{2}},\delta =-\frac{2 \sqrt{2\chi }\, \left( -\beta +\gamma \right) n k}{3 f_{1}}\\ \end{aligned} \end{aligned}$$
(24)

Utilizing Eqs. (3), (6), (7), (10), (12)-(13), and (24), we can have the following optical solutions:

$$\begin{aligned} {{q}_{9}}(x,t)&=\left( \frac{\sqrt{2}\, f_{1}}{2 \sqrt{\chi }}+\frac{2 f_{1} H}{H^{2} {\mathrm e}^{\eta \left( \frac{x^\mu }{\mu }-\Gamma _4\right) }+\chi {\mathrm e}^{-\eta \left( \frac{x^\mu }{\mu }-\Gamma _4\right) }}\right) ^{\frac{1}{2 n}} {\mathrm e}^{i \left( \sigma W\left( t\right) -k \frac{x^\mu }{\mu }+\frac{\Gamma _5 t}{6 \sqrt{\chi }\, \eta ^{2}}-\sigma ^{2} t\right) }, \end{aligned}$$
(25)
$$\begin{aligned} {{q}_{10}}(x,t)&={\left( \frac{\sqrt{2}\, f_{1}}{2 \sqrt{\chi }}+\frac{2 f_{1} H}{\left( H^{2}+\chi \right) \cosh \! \left( \eta \left( \frac{x^\mu }{\mu }-\Gamma _4\right) \right) +\left( H^{2}-\chi \right) \sinh \! \left( \eta \left( \frac{x^\mu }{\mu }-\Gamma _4\right) \right) }\right) }^{\frac{1}{2 n}} \nonumber \\ &\quad \times {\mathrm e}^{i \left( \sigma W\left( t\right) -k \frac{x^\mu }{\mu }+\frac{\Gamma _5 t}{6 \sqrt{\chi }\, \eta ^{2}}-\sigma ^{2} t\right) }. \end{aligned}$$
(26)

where \(\chi >0\).

Suppose that \(\chi =-H^2\). By inserting the value of \(\chi\) into Eq. (26), we acquired the following soliton solutions:

$$\begin{aligned} {{q}_{11}}(x,t)&={\left( \frac{\sqrt{2}\, f_{1}}{2 \sqrt{-H^{2}}}+\frac{f_{1}}{H}\textrm{csch}\left( \eta \left( \frac{x^\mu }{\mu }-\frac{2 \sqrt{2}\, \gamma n^{2} k^{2} f_{1} t}{3 \sqrt{-H^{2}}\, \eta ^{2}}\right) \right) \right) }^{\frac{1}{2 n}}\nonumber \\ &\quad \times {\mathrm e}^{i \left( \sigma W\left( t\right) -k \frac{x^\mu }{\mu }+\frac{\sqrt{2}\left( 3 \sqrt{-2H^{2}}\, \eta ^{2} \sigma ^{2}-2 k^{3} f_{1} \gamma n^{2}-k f_{1} \gamma \,\eta ^{2}\right) t}{6 \sqrt{-H^{2}}\, \eta ^{2} }-\sigma ^{2} t\right) }. \end{aligned}$$
(27)

Suppose that \(\chi =H^2\). By inserting the value of \(\chi\) into Eq. (26), we acquired the following soliton solutions:

$$\begin{aligned} {{q}_{12}}(x,t)&={\left( \frac{\sqrt{2}\, f_{1}}{2 \sqrt{H^{2}}}+\frac{f_{1}}{H}\textrm{sech}\left( \eta \left( \frac{x^\mu }{\mu }-\frac{2 \sqrt{2}\, \gamma n^{2} k^{2} f_{1} t}{3 \sqrt{H^{2}}\, \eta ^{2} }\right) \right) \right) }^{\frac{1}{2 n}} \nonumber \\ &\quad \times {\mathrm e}^{i \left( \sigma W\left( t\right) -k \frac{x^\mu }{\mu }+\frac{\sqrt{2}\left( 3 \sqrt{2H^{2}}\, \eta ^{2} \sigma ^{2}-2 k^{3} f_{1} \gamma n^{2}-k f_{1} \gamma \,\eta ^{2}\right) t}{6 \sqrt{H^{2}}\, \eta ^{2} }-\sigma ^{2} t\right) }, \end{aligned}$$
(28)

where \(\Gamma _4=\frac{2 f_{1} \sqrt{2}\, \gamma n^{2} k^{2} t}{3 \sqrt{\chi }\, \eta ^{2}}\) and \(\Gamma _5=\sqrt{2}\,\left( 3 \sqrt{2\chi }\, \eta ^{2} \sigma ^{2}-2 \gamma k^{3} f_{1} n^{2}-\gamma k f_{1} \eta ^{2}\right)\).

Figure 4
figure 4

The dark plots of \({{\left| {{q}_{5}}(x,t) \right| }^{2}}\), where \(f_0=4,n=\eta =3,\delta =0.3,\gamma =5,\chi =0.2,H=2\), and \(\mu =1\).

Full size image
Figure 5
figure 5

The dark plots of \({{\left| {{q}_{5}}(x,t) \right| }^{2}}\), where \(f_0=4,n=\eta =3,\delta =0.3,\gamma =5,\chi =0.2\), and \(H=2\).

Full size image

Result 4.

$$\begin{aligned} \begin{aligned}&f_{0}=\frac{8 \eta ^{2} \left( \sigma ^{2}-w\right) }{\left( 4 n^{2} k^{2}+5 \eta ^{2}\right) k \left( \gamma -\beta \right) },f_{1}=\frac{8 \sqrt{\chi }\, \left( \sigma ^{2}-w\right) \eta ^{2}}{\left( 4 n^{2} k^{2}+5 \eta ^{2}\right) \left( \gamma -\beta \right) k},\\&\alpha =\frac{4 n \left( \sigma ^{2}-w\right) }{4 n^{2} k^{2}+5 \eta ^{2}},\delta = \frac{3 \left( n^{2} k^{2}+\frac{5}{4} \eta ^{2}\right) k^{2} n \left( \beta -\gamma \right) ^{2}}{16 \eta ^{2} \left( w-\sigma ^{2}\right) },m= n.\\ \end{aligned} \end{aligned}$$
(29)

Utilizing Eqs. (3), (6), (7), (10), (12)-(13), and (29), we can have the following optical solutions:

$$\begin{aligned}&{{q}_{13}}(x,t)=\left( \frac{12 \eta ^{2} \left( \sigma ^{2}-w\right) }{\Gamma _6}+\frac{24 \sqrt{\chi }\, \left( \sigma ^{2}-w\right) \eta ^{2} H}{\Gamma _6\left( H^{2} {\mathrm e}^{\eta \left( \frac{x^\mu }{\mu }-\Gamma _7\right) }+\chi {\mathrm e}^{-\eta \left( \frac{x^\mu }{\mu }-\Gamma _7\right) }\right) }\right) ^{\frac{1}{2 n}} {\mathrm e}^{i \left( \sigma W\left( t\right) -k \frac{x^\mu }{\mu }+wt-\sigma ^{2} t\right) },&\end{aligned}$$
(30)
$$\begin{aligned}&{{q}_{14}}(x,t)\nonumber \\&=\left( \frac{12 \eta ^{2} \left( \sigma ^{2}-w\right) }{ \Gamma _6}+\frac{24 \sqrt{\chi }\, \left( \sigma ^{2}-w\right) \eta ^{2} H}{\Gamma _6 \left( \left( H^{2}+\chi \right) \cosh \! \left( \eta \left( \frac{x^\mu }{\mu }-\Gamma _7\right) \right) +\left( H^{2}-\chi \right) \sinh \! \left( \eta \left( \frac{x^\mu }{\mu }-\Gamma _7\right) \right) \right) }\right) ^{\frac{1}{2 n}}\nonumber \\&{\mathrm e}^{i \left( \sigma W\left( t\right) -k \frac{x^\mu }{\mu }+wt-\sigma ^{2} t\right) }, \end{aligned}$$
(31)

where \(\chi >0\).

Suppose that \(\chi =-H^2\). By inserting the value of \(\chi\) into Eq. (31), we acquired the following soliton solutions:

$$\begin{aligned} {{q}_{15}}(x,t)&=\left( \frac{12 \eta ^{2} \left( \sigma ^{2}-w\right) }{\Gamma _6}+\frac{12 \sqrt{-H^{2}}\, \left( \sigma ^{2}-w\right) \eta ^{2}}{\Gamma _6 H}\textrm{csch}\left( \eta \left( \frac{x^\mu }{\mu }-\Gamma _7\right) \right) \right) ^{\frac{1}{2 n}}\nonumber \\ &\quad \times {\mathrm e}^{i\left( \sigma W\left( t\right) -k \frac{x^\mu }{\mu }+wt-\sigma ^{2} t\right) }. \end{aligned}$$
(32)

Suppose that \(\chi =H^2\). By inserting the value of \(\chi\) into Eq. (31), we acquired the following soliton solutions:

$$\begin{aligned} {{q}_{16}}(x,t)&=\left( \frac{12 \eta ^{2} \left( \sigma ^{2}-w\right) }{\Gamma _6}+\frac{12 \sqrt{H^{2}}\, \left( \sigma ^{2}-w\right) \eta ^{2}}{\Gamma _6 H}\textrm{sech}\left( \eta \left( \frac{x^\mu }{\mu }-\Gamma _7\right) \right) \right) ^{\frac{1}{2 n}}\nonumber \\ &\quad \times {\mathrm e}^{i\left( \sigma W\left( t\right) -k \frac{x^\mu }{\mu }+wt-\sigma ^{2} t\right) }, \end{aligned}$$
(33)

where \(\Gamma _6=\gamma k \left( 4 n^{2} k^{2}+5 \eta ^{2}\right)\) and \(\Gamma _7=\frac{8 n^{2} \left( \sigma ^{2}-w\right) k \,t}{\left( 4 n^{2} k^{2}+5 \eta ^{2}\right) }\).

Figure 6
figure 6

The wave plots of \(Im({q}_{5}(x,t))\), where \(f_0=4,n=\eta =3,\delta =0.3,\gamma =5,\chi =0.2,H=2\), and \(\sigma =0\).

Full size image

Result 5.

$$\begin{aligned}&f_{0}=f_0,f_{1}=-\sqrt{2\chi }\, f_{0},\delta =-\frac{2 k n \left( \gamma -\beta \right) }{3 f_{0}},\eta =\frac{ \sqrt{6\alpha k n f_{0} \left( \gamma -\beta \right) }}{3 \alpha },\nonumber \\ &\quad m= 2n,w= -2\alpha k^{2} n+\frac{2 f_{0} \left( \beta -\gamma \right) k}{3}+\sigma ^{2}. \end{aligned}$$
(34)

Utilizing Eqs. (3), (6), (7), (10), (12)-(13), and (34), we can have the following optical solutions:

$$\begin{aligned} {{q}_{17}}(x,t)&=\left( f_{0}-\frac{2 \sqrt{2\chi }\, f_{0} H}{H^{2} {\mathrm e}^{\Gamma _8}+\chi {\mathrm e}^{-\Gamma _8}}\right) ^{\frac{1}{2 n}} {\mathrm e}^{i \left( \sigma W\left( t\right) -k \frac{x^\mu }{\mu }+\left( \sigma ^{2}-2 \alpha k^{2} n-\frac{1}{3} f_{0} k \gamma \right) t-\sigma ^{2} t\right) }, \end{aligned}$$
(35)
$$\begin{aligned} {{q}_{18}}(x,t)&={\left( f_{0}-\frac{2 \sqrt{2\chi }\, f_{0} H}{\left( H^{2}+\chi \right) \cosh \! \left( \Gamma _8\right) +\left( H^{2}-\chi \right) \sinh \! \left( \Gamma _8\right) }\right) }^{\frac{1}{2 n}} \nonumber \\ &\quad \times {\mathrm e}^{i \left( \sigma W\left( t\right) -k \frac{x^\mu }{\mu }+\left( \sigma ^{2}-2 \alpha k^{2} n-\frac{1}{3} f_{0} k \gamma \right) t-\sigma ^{2} t\right) }, \end{aligned}$$
(36)

where \(\chi >0\).

Suppose that \(\chi =-H^2\). By inserting the value of \(\chi\) into Eq. (36), we acquired the following soliton solutions:

$$\begin{aligned}&{{q}_{19}}(x,t)={\left( f_{0}-\frac{\sqrt{-2H^{2}}\, f_{0}}{H}\textrm{csch}\left( \Gamma _8\right) \right) }^{\frac{1}{2 n}} {\mathrm e}^{i \left( \sigma W\left( t\right) -k \frac{x^\mu }{\mu }+\left( \sigma ^{2}-2 \alpha k^{2} n-\frac{1}{3} f_{0} k \gamma \right) t-\sigma ^{2} t\right) }.&\end{aligned}$$
(37)

Suppose that \(\chi =H^2\). By inserting the value of \(\chi\) into Eq. (36), we acquired the following soliton solutions:

$$\begin{aligned}&{{q}_{20}}(x,t)={\left( f_{0}-\frac{\sqrt{2H^{2}}\, f_{0}}{H}\textrm{sech}\left( \Gamma _8\right) \right) }^{\frac{1}{2 n}} {\mathrm e}^{i \left( \sigma W\left( t\right) -k \frac{x^\mu }{\mu }+\left( \sigma ^{2}-2 \alpha k^{2} n-\frac{1}{3} f_{0} k \gamma \right) t-\sigma ^{2} t\right) },&\end{aligned}$$
(38)

where \(\Gamma _8=\frac{ \sqrt{12\alpha k n f_{0} \gamma }}{6 \alpha } \left( \frac{x^\mu }{\mu }-4 \alpha k n \,t\right)\).

Figure 7
figure 7

The W-shaped solutions of \(|{q}_{9}(x,t)|^2\), where \(k=n=\mu =1,f_1=H=-4,\gamma =-0.2,\chi =0.1\), and \(\eta =1.1\).

Full size image

Result 6.

$$\begin{aligned} \begin{aligned}&f_{0}= -\frac{\sqrt{\delta n \left( \sigma ^{2}-w\right) }}{\delta },f_{1}= -\frac{\sqrt{\delta \chi n \left( \sigma ^{2}-w\right) }}{\delta },\alpha = \frac{3 \left( \beta -\gamma \right) ^{2}}{8 \delta },\\&\eta =\frac{4 \sqrt{-2 \delta n( \sigma ^{2}-w)}}{3 \left( \gamma -\beta \right) },k= \frac{8\delta \left( w-\sigma ^{2}\right) }{3 \left( \beta -\gamma \right) \sqrt{\delta n \left( \sigma ^{2}-w\right) }},m=n. \end{aligned} \end{aligned}$$
(39)

Utilizing Eqs. (3), (6), (7), (10), (12)-(13), and (39), we can have the following optical solutions:

$$\begin{aligned} {{q}_{21}}(x,t)&={\left( -\frac{\sqrt{\delta n \left( \sigma ^{2}-w\right) }}{\delta }-\frac{2 \sqrt{\delta \chi n \left( \sigma ^{2}-w\right) }\, H}{\delta \left( H^{2} {\mathrm e}^{\Gamma _9}+\chi {\mathrm e}^{-\Gamma _9}\right) }\right) }^{\frac{1}{2 n}} {\mathrm e}^{i \left( \frac{ \left( w-\sigma ^{2}\right) 4\delta x^\mu }{\sqrt{\delta n \left( \sigma ^{2}-w\right) }\gamma \mu }+wt+\sigma W\left( t\right) -\sigma ^{2}t\right) }, \end{aligned}$$
(40)
$$\begin{aligned} {{q}_{22}}(x,t)&={\left( -\frac{\sqrt{\delta n \left( \sigma ^{2}-w\right) }}{\delta }-\frac{2 \sqrt{\delta \chi n \left( \sigma ^{2}-w\right) }\, H}{\delta \left( \left( H^{2}+\chi \right) \cosh \! \left( \Gamma _9\right) +\left( H^{2}-\chi \right) \sinh \! \left( \Gamma _9\right) \right) }\right) }^{\frac{1}{2 n}}\nonumber \\ &\quad \times {\mathrm e}^{i \left( \frac{ \left( w-\sigma ^{2}\right) 4\delta x^\mu }{\sqrt{\delta n \left( \sigma ^{2}-w\right) }\gamma \mu }+wt+\sigma W\left( t\right) -\sigma ^{2}t\right) }, \end{aligned}$$
(41)

where \(\delta n \left( \sigma ^{2}-w\right) >0\) and \(\delta \chi n \left( \sigma ^{2}-w\right) >0\).

Suppose that \(\chi =-H^2\). By inserting the value of \(\chi\) into Eq. (41), we acquired the following soliton solutions:

$$\begin{aligned}&{{q}_{23}}(x,t)={\left( -\frac{\sqrt{\delta n \left( \sigma ^{2}-w\right) }}{\delta }-\frac{\sqrt{-\delta H^{2} n \left( \sigma ^{2}-w\right) }}{\delta H}\textrm{csch}\left( \Gamma _9\right) \right) }^{\frac{1}{2 n}} {\mathrm e}^{i \left( \frac{ \left( w-\sigma ^{2}\right) 4\delta x^\mu }{\sqrt{\delta n \left( \sigma ^{2}-w\right) }\gamma \mu }+wt+\sigma W\left( t\right) -\sigma ^{2}t\right) }.&\end{aligned}$$
(42)

Suppose that \(\chi =H^2\). By inserting the value of \(\chi\) into Eq. (41), we acquired the following soliton solutions:

$$\begin{aligned}&{{q}_{24}}(x,t)={\left( -\frac{\sqrt{\delta n \left( \sigma ^{2}-w\right) }}{\delta }-\frac{\sqrt{\delta H^{2} n \left( \sigma ^{2}-w\right) }}{\delta H}\textrm{sech}\left( \Gamma _9\right) \right) }^{\frac{1}{2 n}} {\mathrm e}^{i \left( \frac{ \left( w-\sigma ^{2}\right) 4\delta x^\mu }{\sqrt{\delta n \left( \sigma ^{2}-w\right) }\gamma \mu }+wt+\sigma W\left( t\right) -\sigma ^{2}t\right) },&\end{aligned}$$
(43)

where \(\Gamma _9=\frac{2 \sqrt{2 \delta n \left( w-\sigma ^{2}\right) }}{\gamma } \left( \frac{x^\mu }{\mu }+\frac{4 \gamma n \left( w-\sigma ^{2}\right) t}{3 \sqrt{\delta n \left( \sigma ^{2}-w\right) }}\right)\), \(\delta n \left( \sigma ^{2}-w\right) >0\), and \(\delta H^{2} n \left( \sigma ^{2}-w\right) >0,\).

Figure 8
figure 8

The W-shaped solution of \(|{q}_{9}(x,t)|^2\), where \(k=n=\mu =1,f_1=H=-4,\gamma =-0.2,\chi =0.1\), and \(\eta =1.1\).

Full size image
Figure 9
figure 9

The W-shaped solution of \(|{q}_{9}(x,t)|^2\), where \(k=n=\mu =1,f_1=H=-4,\gamma =-0.2,\chi =0.1\), and \(\eta =1.1\).

Full size image
Figure 10
figure 10

The wave plot of \(Re({q}_{9}(x,t))\), where \(k=n=\mu =1,f_1=H=-4,\gamma =-0.2,\chi =0.1\), and \(\eta =1.1\).

Full size image

Results and discussion

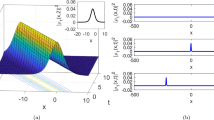
As depicted in Figs. 1 and 9, graphs (a), (b), and (c), the bright solution surfaces exhibit a smooth appearance in the absence of noise \(\sigma =0\). However, with the introduction of noise and an increase in its intensity \(\sigma >0\), the surface patterns progressively deteriorate. Notably, higher levels of noise result in surfaces that tend to become increasingly planar. To supplement the three-dimensional visualizations

As depicted in Figs. 1 and 2, graphs (a), (b), and (c), the bright solution surfaces exhibit a smooth appearance in the absence of noise (\(\sigma =0\)). As the white noise parameter \(\sigma\) increases (e.g., moving from \(\sigma =0\) in subplots (a) and (d) to \(\sigma =0.05\) and 0.1 in subplots (b, c) and (e, f)), the solutions demonstrate greater fluctuations and instability. The noise introduces perturbations to the soliton profiles, causing broader and less sharp peaks in the soliton amplitude. The presence of white noise models real-world scenarios where random fluctuations, such as thermal or environmental noise, affect the stability of solitons during propagation. Higher noise levels can destabilize solitons, potentially leading to energy dissipation or chaotic behaviors. In optical fiber communication, understanding the noise impact helps design systems with improved robustness to stochastic disturbances. Varying the conformable derivative parameter \(\mu\) (\(\mu = 1, 0.7,\) and 0.4) influences the soliton’s sharpness and energy distribution. Smaller \(\mu\) values result in broader solitons with smoother profiles, while higher \(\mu\) values preserve sharper peaks and more localized energy. The interaction between \(\sigma\) (white noise) and \(\mu\) (conformable derivative) dictates the overall stability and dynamics of the soliton. Larger noise levels combined with lower \(\mu\) values lead to more unstable and diffused solitons. These results highlight the importance of balancing noise and system parameters to achieve desired outcomes in practical applications.

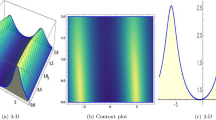
From Fig. 3, the behavior of the wave function \(\operatorname {Re}({{q}_{1}}(x,t))\) under varying values of white noise \(\sigma\) and conformable derivative parameter \(\mu\) is analyzed. In subplots (a), (b), and (d), increasing \(\sigma\) introduces noticeable fluctuations in the wave pattern. The wave profile becomes less smooth as \(\sigma\) increases, suggesting a more stochastic influence on the system. White noise simulates external random disturbances in physical systems, such as thermal noise in optical fibers or environmental perturbations in wave propagation. Comparing subplots (a) and (b) (where \(\mu = 1\) and \(\mu = 0.7\), respectively), the reduction in \(\mu\) leads to changes in wave localization and amplitude. Lower \(\mu\) values result in broader and less steep wave patterns, indicating reduced system nonlinearity and larger \(\mu\) values maintain sharper and more localized waveforms, reflecting stronger nonlinear effects. The interplay between \(\sigma\) and \(\mu\) determines the wave’s stability and profile. High \(\sigma\) and low \(\mu\) amplify instability and broaden wave patterns, whereas low \(\sigma\) and high \(\mu\) preserve soliton integrity. Subgraph (c) displays an oscillatory behavior of \(\operatorname {Re}({{q}_{1}}(x,t))\) for \(\mu\), highlighting periodic wave patterns over time at a specific spatial position \(x=1\). Stable oscillations represent reliable signal propagation with minimal distortion, which is crucial for high-speed communication systems. Subgraph (f) also exhibits oscillatory behavior of \(\operatorname {Re}({{q}_{1}}(x,t))\) but for a lower conformable derivative value \(\mu = 0.7\) and at a fixed spatial position \(x=1\). The wave amplitude appears more irregular compared to subgraph (c), with smaller oscillation peaks indicating a reduction in soliton strength. Reducing \(\mu\) weakens the nonlinearity, making the soliton less robust to the influence of noise. This results in more irregularities and smaller amplitudes in the oscillatory pattern. Figure 4 illustrates the comparison of three-dimensional and contour plots of dark soliton to \({{\left| {{q}_{5}}(x,t) \right| }^{2}}\). The profile displays a clean, undisturbed shape. This indicates the absence of noise (\(\sigma =0\)), where the soliton solution is stable and retains its characteristic form. The energy density remains concentrated and localized, consistent with soliton propagation in noise-free environments. Noise starts to influence the solution, introducing visible disturbances in the soliton’s shape. The structure begins to lose its coherence, and irregularities emerge, suggesting the destabilizing effect of moderate noise \(\sigma =0.25\). With higher noise intensity (\(\sigma =0.5\)), the soliton becomes significantly distorted. The surface demonstrates larger deviations, indicating that the noise disrupts the energy concentration and leads to more chaotic propagation.

Figure 5, graph (a) for \(\mu =1\), the plot displays a clear periodic pattern, where \({{\left| {{q}_{5}}(x,t) \right| }^{2}}\) oscillates with consistent peaks and valleys. The amplitude decreases slightly as time progresses. Figure 5, graphs (b) and (c), reducing \(\mu\) introduces more irregularities and reduces the peak amplitude. The oscillatory pattern becomes less uniform over time. The same behavior can be observed in Fig. 5, graphs (d), (e), and (f). Besides, in Fig. 5, \(\sigma\) represents the strength of white noise in the system. The plots clearly indicate how varying \(\sigma\) influences the behavior of \({{\left| {{q}_{5}}(x,t) \right| }^{2}}\)for different values of \(\mu\) the conformable derivative and positions x. Figure 6 illustrates the effect of different values of \(\mu\) on the wave soliton solution \(\operatorname {Im}({{q}_{5}}(x,t))\). Here, the dynamical behaviuor of the soliton under the influence of the conformable derivative is depicted.

Figures 7 and 8 depicts the comparison of the W-shaped solutions of \({{\left| {{q}_{9}}(x,t) \right| }^{2}}\)under varying noise strengths (\(\sigma =0,0.4,\) and 0.7) and conformable derivative parameter \(\mu\) (\(\mu =1\) and \(\mu =0.7\) in 3D and contour visualizations. In the absence of noise, the W-shaped structure remains intact and well-defined. This indicates stability in the solution and reflects an undisturbed propagation of the optical pulse. Moderate noise introduces distortions in the W-shaped structure when (\(\sigma =0.25\) and \(\sigma =0.5\)). The central peaks of the soliton begin to broaden, and the edges display irregularities. These effects indicate that the presence of noise starts to interfere with the stability of the solution, leading to partial energy dispersion. Further, under strong noise conditions when (\(\sigma =1\)), the W-shaped soliton becomes highly distorted, with the pattern showing significant irregularities. This indicates that the system is dominated by noise, causing the soliton’s energy to spread and leading to a loss of coherence.

Figures 8 and 9 present the W-shaped profiles of the soliton solution \({{\left| {{q}_{9}}(x,t) \right| }^{2}}\) and wave soliton \(\operatorname {Re}({{q}_{9}}(x,t))\) for different values of the temporal parameter. The figures provide a detailed view of how the soliton intensity evolves over spatial direction. The soliton exhibits the highest energy concentration at the core (\(x=0\)). W-shaped solitons can be employed in optical communication systems to transmit signals over long distances with minimal distortion. However, Figs. 8 and 9 depict the evolution of the W-shaped solution \({{\left| {{q}_{9}}(x,t) \right| }^{2}}\)and wave soliton \(\operatorname {Re}({{q}_{9}}(x,t))\) under varying noise strengths (\(\sigma =0,0.25,0.5,1\)) in 2D visualizations. In the absence of noise, the structures of the soliton solutions remain intact and well-defined. This demonstrates the stability of the solution and indicates undisturbed propagation of the optical pulse. Moderate noise introduces distortions in the structure of soliton solutions in the presence of white noise. The central peaks of the soliton begin to broaden, and the edges display irregularities. These effects indicate that the presence of noise starts to interfere with the stability of the solution, leading to partial energy dispersion. Further, under strong noise conditions, the soliton becomes highly distorted, with the pattern showing significant irregularities. This indicates that the system is dominated by noise, causing the soliton’s energy to spread and leading to a loss of coherence. From Fig. 10, the soliton behavior is analyzed under the influence of the temporal parameter and white noise parameter. Higher white noise levels introduce irregularities in the soliton shape. The soliton becomes less stable, showing more fluctuations and distortions in amplitude over time.

These findings emphasize the relationship between environmental noise and the performance of fiber optic networks, demonstrating that when noise levels exceed a certain threshold, the functionality of soliton-based systems may be significantly impaired. Smaller values ensure strong energy localization and stability, while larger values lead to broader soliton profiles due to dispersion. These insights are vital for designing and optimizing soliton-based communication systems. The results emphasize the need to minimize noise in optical fiber systems to preserve soliton integrity. Techniques like dispersion management and noise filtering are crucial for maintaining stable soliton propagation.

Conclusion

In this paper, we successfully constructed various novel optical soliton solutions and analyzed the dynamical behavior of these solutions under the influence of multiplicative white noise and conformable derivative. Using the new Kudryashov method, we obtained various optical soliton solutions, including solitary wave solutions, bright solitons, dark solitons, singular solitons, and W-shaped solitons. The influence of the white noise parameter, the conformable order derivative, and the temporal parameter on the present soliton solutions is discussed through three-dimensions, two-dimensions, and contour plots. These findings have the potential to significantly impact a variety of scientific fields, pushing the boundaries of knowledge and opening up new possibilities in the study of nonlinear phenomena. Understanding the dynamics of nonlinear systems under stochastic effects can enhance the design of optical signal processing systems, leading to improved noise management and clearer signals in telecommunications. Moreover, the modulation instability and perturbation analysis of the obtained solutions under varying physical conditions remain open for exploration. Extending the model to include variable coefficients or higher-order dispersion terms would also enhance its relevance to real-world optical systems.