Introduction

With to the progress of information technology and widespread internet availability, unauthorized and unlawful activities such as accessing, modifying, and spreading digital material have grown more convenient and widespread. The integrity of the information and content as well as copyright security are at risk when there is no security system in place for digital information accessibility. Numerous methods, including steganography1 and digital watermarking2,3, have been designed to overcome this problem. The practice of embedding and extracting information from a cover image without the naked eye is known as digital image watermarking. When a watermark—which is essentially data—is included into a cover image, it creates a marked image that is ready for transmission. In fact, the marked image doesn’t plainly disclose whether a watermark has been applied to the image; it is solely amiable to the authorized receiver for whom the watermark information can be obtained precisely. Applications of watermarking techniques in images can be manifold. The watermark information will be used for a variety of purposes, including image protection and verification, as well as clandestine communication with hidden messages. Furthermore, the watermark itself can be encoded to serve other functions, such as providing additional protection through encryption methods or restoring information integrity via error correction codes in the event of a cyber-attack4.

Protection of digital content has been one of the vast areas for research. With the development of techniques in internet technologies, more and more problems of copying, verifying, and distributing arise among unauthorized users. As a result, numerous watermarking techniques have been thoroughly investigated for uses such content authentication, copyright protection, broadcast monitoring, and copyright control2. A single bit or a multi-bit watermark can be used, and both are essentially produced using a pseudo-random sequence that is obtained from a pseudo-random number generation model. Moreover, it may appear as a grayscale or binary image5. Conventional image watermarking studies6 only takes into account single-bit extractions for copyright protection, where the output shows whether or not a picture has a watermark. Recent image watermarking studies focuses mostly on multi-bit situations which recovers the entire communicative watermark data, to enable a vast array of applications2,7. The majority of image watermarking techniques take into account a wide range of variables, including watermark undetectability and fidelity of the marked-image. In addition to meeting all the requirements listed above, the suggested image watermarking system also accomplishes one of its top goals: the watermark will remain visible even if the tagged image is damaged or deteriorated. A strong picture watermarking approach should ideally maintain the watermark under a specific class of distortion without the need for any further techniques. Nevertheless, under numerous attack circumstances, the watermark is correctly extracted, and its restoration can be accomplished via a variety of encoding techniques8.

Despite the progress achieved by prior watermarking methods, they are not free from problems in the aspects of security, robustness, and capacity. Some of the methods face challenges of achieving high confidentiality levels while at the same time having high image quality. Also, the problem of the model’s vulnerability to various image distortion attacks still persists.

This research aims at proposing a new model on image watermarking to overcome the mentioned limitations. In this paper, we propose to combine honey encryption (HE) and reversible cellular automata in order to develop a highly effective watermarking system. This research seeks to answer crucial questions: How effectively can these techniques be combined to achieve a high level of security while maintaining image quality? And how does the performance of this novel approach compare to existing watermarking methods in terms of imperceptibility, robustness against attacks, and the amount of data that can be embedded? Our innovation is the use of a combination of neural cryptography and reversible cellular automata for hashing information and maintaining the security of confidential information in the watermarking process. This process can expand the application of our proposed method to other issues such as steganography. The paper’s contributions are listed as follows:

  • Proposing a novel and secure method for digital watermarking based on the combination of HE and reversible cellular automata.

  • Improving the robustness of the proposed method against image distortion attacks in watermarking applications using the reversible cellular automata strategy.

  • Presenting a method with the capability of storing a high volume of information for watermarking applications.

The paper follows this progression: In “Related works” section examines similar works. In “Proposed method” section describes the proposed method, followed by in “Research findings”’s section research finding and “Conclusion”’s section conclusions.

Related works

A review of the studies that have been completed is presented in this section. Mellimi et al.9 presented a robust image watermarking method using lifting wavelet transform (LWT) and deep neural network (DNN) that ensures high imperceptibility and high robustness; therefore, it achieved an average peak signal-to-noise ratio (PSNR) of 44.1148 dB when tested on 600 images, which makes it suitable for real-time applications with better performance compared to its contemporaries. Ding et al.10 proposed a watermarking technique based on DNNs. The approach was trained on a dataset of images and shown the ability to protect test images in a generic manner. Assessments verified its usefulness, while certain learned characteristics were discovered to be susceptible to JPEG compression attacks.

Fang et al.11 developed a robust watermarking framework, where an invertible neural block was used for both embedding and extraction, enabling high-quality visual content and high accuracy, with accuracy higher than 95% in the case of black-box distortions. Dhaya12 applied the light weight convolution neural network (LW-CNN) method to digital watermarking. With the introduction of an integrated watermark, the necessary embedding was done, which indicates that prompt work occurred when a watermark from any database was required for tiring to the database. Li et al.13 suggested a concealed attack methodology using generative adversarial networks, perceptual losses, targeting on the original image, utilizing low and high-level information for imperceptibility in robust watermarking.

Wu et al.14 contributed a digital watermarking framework for DNNs that allowed the watermarking of output images for a number of image processing tasks, including colorization, super-resolution, editing, and semantic segmentation. Sharma and Mir15 proposed an optimization technique that was time efficient for image watermarking by using machine learning algorithms such as Discrete Cosine Transform, Ant Colony Optimization, and Light Gradient Boosting algorithm, which had optimized the time enhancement and reduced the evaluation time. Cao et al.16 contributed a screen-shooting resistant watermarking scheme with DNNs to improve imperceptibility and robustness against real-scene attacks on digital mobile devices, improving computational efficiency.

Jamali et al.17 presented an end-to-end network for watermarking, based on a CNN, by using dynamic embedding and blind watermarking that minimizes the impact on visual quality, thus beating most of the algorithms available in imperceptibility and robustness. Hao et al.18 presented an efficient image watermark algorithm that comprises a generative adversarial network with a generator, an adversary module, a high-pass filter for mid-frequency embedding, superior visual performance, and a higher weight for the image center region. Ge et al.19 proposed a document image watermarking scheme based on DNNs, which has very impressive performance compared to existing approaches in terms of robustness and image quality. Their approach incorporated an encoder, a decoder, a noise layer, a text-sensitive loss function, and an embedding strength adjustment strategy.

Mahapatra et al.20 had developed a CNN-based watermarking algorithm, enhancing robustness and invisibility, outperforming state-of-the-art schemes through high invisibility and robustness against multiple attacks. The majority of image watermarking techniques take into account a wide range of variables, including watermark undetectability and fidelity of the An innovative picture watermarking solution utilizing singular value decomposition (SVD) and discrete wavelet transform (DWT) has been presented by Naffouti et al.21. It was evaluated for security, robustness against assaults, and visual imperceptibility and compared to state-of-the-art techniques. An integrated watermarking system that makes use of deep learning and attention processes named DARI-Mark, was introduced by Zhao et al.22. An attention network, a watermark extraction network, a watermark insertion network, and an attack layer were the primary four elements of the framework. The implementation of this approach has enhanced the resilience of DARI-Mark against prevalent image attacks, such as JPEG compression and noise addition.

Zear and Singh23 had presented a watermarking method using SVD, discrete cosine transform (DCT), and lifting wavelet transform, enhancing the security of data and increasing information watermark robustness. Khudhair et al.24 proposed a new method of secure reversible data hiding that enhances a histogram shifting approach. Their approach applies block-wise histogram shifting and least significant bits (LSB) embedding to obtain high embedding capacity with acceptable image distortion. To increase security, the method also uses encryption. A watermarking system for medical images that provides patient identification and data integrity was designed by Khaldi et al.25. Their method is to encode patient information into the watermark using redundant DWT and Schur decomposition. The system shows high levels of image quality preservation and resilience to most of the attacks.

To overcome the low embedding capacity limitation that occurs in the existing integer wavelet transform (IWT) based watermarking techniques, Sayah et al.26 proposed a solution. Thus, they proposed a blind and high-capacity data hiding scheme for medical images using IWT and SVD. The proposed method is capable of maintaining the quality of images and its resilience against various attacks is also proved. Hemalatha et al.27 emphasized on enhancing the performance of the blind image steganalysis. Their approach involves curvelet denoising of the images, third order SPAM (subtractive pixel adjacency matrix) features and an ensemble classifier for clean and stego image classification. The method yielded high detection accuracy on a range of stego images that were produced by various embedding techniques. Table 1 provides a summary of the studied works.

Table 1 Summary of the studied works.
Full size table

The analyzed literature shows a wide range of approaches for image watermarking, and different techniques are used, such as DNNs, wavelets (LWT, DWT), SVD, and basic methods, including histogram shifting. However, despite the fact that many studies reach high levels of imperceptibility, robustness, and capacity; several research gaps can be identified. Most of the existing methods are application based (medical images, document images), or are based on a specific type of attack. Furthermore, some methods can be vulnerable to some attacks, require high time consumption, or have low capacity of embedded information. Our model to fill these gaps is to integrate the benefits of honey encryption and reversible cellular automata. Honey encryption makes the attacks difficult by adding ambiguity to the system and therefore improves security. Reversible cellular automata offer a strong and fast method of inserting and reading the watermark and at the same time reducing the interferences on the image. Such a novel approach may provide a mix of techniques that may enhance security, robustness and invisibility in comparison with the existing methods.

Proposed method

In this section, a new algorithm for image watermarking is introduced using a combination of HE and reversible cellular automata. In the proposed method, HE and reversible cellular automata are used for pixel scrambling and permutation of the image. In the following section, first the tools used for steganography in the proposed method will be described, and then the steps of digital watermarking in the proposed method will be presented.

Honey encryption algorithm in the proposed method

In the proposed method, a HE-based algorithm28 is used to improve the security of image steganography. In this algorithm, the message space is considered as the set M = {0, 1, …, 255}. The set M can include all the intensity values of the pixels in the image. The input of the proposed HE algorithm is the pixels of the watermarked image. Initially, all the values of the set M are mapped to a space S. The space S consists of the set of all binary permutations of n bits, such that more than one value in the space S can be assigned to each member of the set M. In other words, each member of M is assigned to a range of the S space. For this purpose, the number of bits in the set S must be large enough. In the proposed method, n = 16 is considered, so for each member of M, we will have at least one member in the space S and at most \(\log_{2} \left| M \right|\) members. To determine the number of members that should be assigned to each member of M in S, the probability of the presence of the members of M in the image is used. Therefore, if the value mi is present in the image with a probability of \(p_{i} = \frac{n}{\left| M \right|}\; (\)n is the number of occurrences of the value mi in the image), \(\left\lceil n \times \frac{\left| S \right|}{{\left| M \right|}} \right\rceil\) members of S can be assigned to the value mi. This condition is shown in Fig. 1.

Fig. 1
figure 1

Assigning the S space to the members of M in HE.

Full size image

According to Fig. 1, a number of members of the set S are assigned to each member of the set M. For encrypting each pixel of the image, first the pixel value is searched in the M space, and then one of the members of S that is assigned to the current pixel is randomly selected. Next, the value extracted in S is subjected to an XOR operation with the primary key. The resultant value will be the altered pixel value employing HE. It is important to mention that the key utilized in the HE technique has the same size as the elements of the S space, which is (equal to n).

Reversible cellular automata model in the proposed algorithm

A dynamic system made up of individual cells with a finite state and state space is known as a cellular automaton. The definition of a cellular automation is as follows: CA is equal to \(\left\{ {C, S, V, F} \right\}\), wherein C is the cell space; S represents a collection of discrete cell states; V stands the set of cell neighbors used to identify the cell’s next state; and F represents the cell state transitions, which defines the rules used to decide the cell’s next state. \(S = \left\{ {0, 1} \right\}\) is the simplest way to specify the set of cell states. There are four types of cellular automata: two-dimensional, three-dimensional, linear, and higher-dimensional. Because it can adapt to a greater number of issues under investigation than the other examples, the two-dimensional cellular automata offers the greatest number of applications. The suggested approach makes use of two-dimensional cellular automata in accordance with the two-dimensional nature of pictures. Several models have been proposed for modeling the neighborhood principles in cellular automata, including the von Neumann, Moore, and expanded Moore models. The neighborhood principles in the cellular automata are modeled using the von Neumann model, which is the simplest case in the proposed method to decrease computing complexity. This decision has no bearing on how broadly the suggested algorithm may be used. Only the cells to the left, right, above, and below are regarded as neighbors for each cell in this model. The state transition function in cellular automata can be generally expressed as:

$$F:C^{t} \to C^{t + 1}$$
(1)

whereas \(C^{t}\) represents the cell’s current state; \(F\) is the transition function; and \(C^{t + 1}\) is the cell’s next state in the equation above. Specifically, we will have the following for every cell at coordinates \(\left( {i,j} \right)\):

$$F: S_{i,j}^{t + 1} = f\left( {S_{i - r,j - r}^{t} , \ldots ,S_{i,j}^{t} , \ldots ,S_{i + r,j + r}^{t} } \right)$$
(2)

where f is the collection of rules for altering the state of the cellular automata; Si,j is the state of the cell at ___location \(\left( {i,j} \right)\); and \(r\) is the neighborhood radius in the equation above.

According to the suggested approach, each cell’s prior state serves as a useful input for figuring out the cell’s future state. Thus, the following modification is made to Eq. (2) for the suggested method:

$$F: S_{i,j}^{t + 1} = f\left( {S_{i - r,j - r}^{t} , \ldots ,S_{i,j}^{t} , \ldots ,S_{i + r,j + r}^{t} ,S_{i,j}^{t - 1} } \right)$$
(3)

The reversibility of the suggested cellular automata is guaranteed by Eq. (3). Reversible cellular automata are the name given to this kind of automata29. By returning each cell to its initial state, maintaining the prior state of each cell speeds up the decoding of the encoded pictures. The reversible cellular automata is employed in the suggested approach to propagate and alter the values associated with each pixel’s bits.

Proposed algorithm

The proposed algorithm consists of two main operations: disturbance and embedding. In the disturbance stage, using HE and reversible cellular automata, different points of the watermark image are modified. Then, in the embedding stage, the LSB algorithm will be used to store the watermark image in the cover image. After performing these two stages, the steganographic image will be obtained. The flowchart of the steganography stages in the proposed method is shown in Fig. 2.

Fig. 2
figure 2

Flowchart of the embedding steps using the proposed method.

Full size image

Assuming 256 by 256 pixel dimensions for the picture to be watermarked, we can still be broad. The stages required to watermark the provided image into a cover image employing the suggested approach are outlined in the following steps:

Step 1 We convert the watermark image matrix \(X_{256 \times 256}\) into a 1-dimensional array M = \(\left\{ m_{1} ,m_{2} , \right.\) …, \(\left. m_{65536} \right\}\).

Step 2 Using Eq. (4), we perform the initial propagation in the vectorized watermark data:

$$\left\{ {\begin{array}{*{20}l} {m_{1}^{\prime} = m_{1} \oplus m_{65536} } \hfill & {} \hfill \\ {m_{j + 1}^{\prime} = m_{j} \oplus m_{j}^{\prime} , } \hfill & {\quad j = 1,2, \ldots ,65536} \hfill \\ \end{array} } \right.$$
(4)

The bitwise XOR operator is represented by ⊕ in the equation above. The set \(M^{\prime}\) in a structure of \(M^{\prime}\) = \(\left\{ m^{\prime}_{1} ,m^{\prime}_{2} , \right.\) …, \(\left. m^{\prime}_{65536} \right\}\) will be the outcome of this operation. Figure 3 displays the outcome of the first propagation on the cameraman image.

Fig. 3
figure 3

Result of performing the propagation operation on the cameraman image (source: USC-SIPI30).

Full size image

Step 3 In this step, the initial key for HE is generated based in the diffused watermark data. To do this, sum of values of the \(M\) is calculated first. Then, divide the obtained value by \(2^{n}\) (where \(n\) is the length of the binary strings in the HE algorithm). The remainder of the division will be within the range of \(\left[ {0,2^{n} } \right)\). Convert the obined number to a binary sequence and use it as the initial HE’s key. The calculation of the HE algorithm’s initial key is as follows:

$$HE_{key} = \left( {\left( {\mathop \sum \limits_{\forall p \in M} p} \right) mod \, 2^{n} } \right)$$
(5)

where \(p\) represents each value in vector \(M\); and \(n\) refers to the length of the binary strings in the HE algorithm.

Step 4 In the next step, using the HE algorithm, we transform the \(M^{\prime}\) matrix obtained from the second step and obtain the matrix \(F\) according to the process described in “Honey encryption algorithm in the proposed method” section. Figure 4 shows the output resulting from the application of this step on the cameraman image.

Fig. 4
figure 4

The output of applying HE on the image of the cameraman.

Full size image

Step 5 The bit properties of each pixel in the image will be altered using a reversible cellular automaton in the next stage. Since most of the meaningful data in pixels are contained in their 4 significant bits, we will only take into account these bits in pixels as the diffusible data in order to conserve memory and execution time. This stage generates a 2D reversible cellular automata with 256 × 256 dimensions by creating a cell in the automaton for each pixel in the picture. Every cellular automaton cell holds the four most important bits after first converting the value found in its matching pixel to base two. Additionally, the initial cell states are obtained from the zi,n matrix as follows:

$$C_{i,j}^{t0} = z_{{N_{s} + i,N_{s} + j}}$$
(6)

Table 2 displays the local rules governing each cellular automaton cell’s subsequent state. The descriptions of each bit in this table are as follows:

  • \(S_{i,j - 1}^{t}\): The present value of the bit in the current cell’s neighbor on the left.

  • \(S_{i - 1,j}^{t}\): The present value of the bit in the current cell’s neighbor located above.

  • \(S_{i,j}^{t}\): The present value of the bit in the current cell.

  • \(S_{i + 1,j}^{t}\): The present value of the bit in the current cell’s located below.

  • \(S_{i,j + 1}^{t}\): The present value of the bit in the current cell’s neighbor on the right.

  • \(S_{i,j}^{t - 1}\): The previous value of the bit in the current cell.

  • \(S_{i,j}^{t + 1}\): The future value of the bit in the current cell.

Table 2 Instructions for transformation of each automata cell.
Full size table

The cellular automata state change operation is carried out by each cellular automaton cell according to the guidelines provided in Table 2 for each of its 4 bits. This process is carried out \(L\) rounds. After \(L\) repetitions, the 4 changed bits in every cell of \(C^{{t_{L} }}\) are considered as the result of this step.

To clarify the operation of the reversible cellular automata model, we describe the changes made by this model on a pixel. Let’s consider an image matrix shown in Fig. 5a. In the following, the operations made by reversible cellular automata to modify the most significant bit in the second row and column of the matrix. The desired pixel has a value of 27 which has the binary value of 00011011. As mentioned, in cellular automata we consider the four most valuable bits. Therefore, 0001 will be the initial value of the cell located in the second row and column of the automata. Also, the previous value of the cell in the first iteration is extracted using the sequence zi,n and will have the value of 1100. Now, using Table 2, we determine the next state of each automata cell. For example, in the desired pixel, the value of the cell is equal to 0001. For each bit in the cell, use the rules in Table 2 to obtain the next states. In the mentioned example, we check the most valuable bit in the target cell. Figure 5b shows the state of the cell in the second row and column, as well as the neighbors of the cell in the reversible cellular automata.

Fig. 5
figure 5

The operations made by reversible cellular automata for diffusing images.

Full size image

In Fig. 5b, we consider the state change rules for the most significant bit of the cell shown. In this cell, the most significant bit is 0. The left neighbor in the corresponding bit has the value 0, the right neighbor has the value 1, the upper neighbor has the value 1, and the lower neighbor has the value 1. Therefore, the resulting sequence to determine the next state of the desired bit in automata is as (\(S_{i,j - 1}^{t} S_{i - 1,j}^{t} S_{i,j}^{t} S_{i + 1,j}^{t} S_{i,j + 1}^{t} = 0 1 0 1 1\), \(S_{i,j}^{t - 1} = 1\)). Therefore, based on Table 2, we will have (\(S_{i,j}^{t + 1} = 1\)).

Step 6 In the final step, two-dimensional discrete wavelet decomposition is used to store the confidential information in the cover image. We will describe this method in more detail. To store the confidential information in the cover image, we first convert the information from the previous step to binary format. In this way, each confidential pixel is described as 8 bits. Then, we will decompose the cover image using two-dimensional discrete wavelet decomposition and the Haar function. The wavelet components resulting from the decomposition of a hypothetical image are shown in Fig. 6.

Fig. 6
figure 6

Wavelet components resulting from the decomposition of cameraman image (source: USC-SIPI30) using the Haar function.

Full size image

According to Fig. 6, the approximation band contains low-frequency information in the image and contains a significant portion of the spatial ___domain information of the image. This band will have a higher priority for storing confidential information. The other detail bands (horizontal, vertical, and diagonal) contain high-frequency information and mainly contain the edge details of the cover image. These bands will only be used to store confidential information if the approximation band does not have enough space to store the confidential information. This is because changing the detail bands may cause changes in the edges of the image and may have observable effects.

If we consider the cover image as \(c\) and the encrypted binary confidential data (the result of step 5) as \(b\), then the steps of hiding the confidential data bytes \(b\) in the image \(c\) will be as follows:

  1. (6-1)

    We convert the image \(c\) using two-dimensional discrete wavelet decomposition into the bands \(d\).

  2. (6-2)

    We encrypt the confidential data and convert it into a binary vector b (in the form of bytes).

  3. (6-3)

    We extract the approximation band \(a\) om the wavelet components \(d\).

  4. (6-4)

    We sequentially store the encrypted byte values \(b\) in \(a\).

  5. (6-5)

    We repeat step 4 until all bytes of \(b\) are stored in \(a\) or the capacity of \(a\) is full.

  6. (6-6)

    If all bytes of \(b\) have been stored in \(a\), we go to step 11, and if the capacity of \(a\) is full, we go to the next step.

  7. (6-7)

    We extract the next high-frequency detail band \(f\) from the wavelet components \(d\).

  8. (6-8)

    We sequentially store the remaining erypted byte values \(b\) in the detail band \(f\).

  9. (6-9)

    We repeat step 8 until all bytes of \(b\) are stored in \(f\) or the capacity of \(f\) is full.

  10. (6-10)

    If all bytes of \(b\) have been stored in \(f\), we go to step 11, and if the capacity of \(f\) is full, we repeat steps 7–10.

  11. (6-11)

    We apply the inverse discrete wavelet decomposition to the approximation band and the resulting detail bands.

  12. (6-12)

    We perform the inverse normalization operation by multiplying each pixel by 255 and remapping the pixel space of the cover image back to the range [0,255].

We return the resulting image as the watermark output. The steps of encrypting a 4 × 4 image using the proposed method are shown in Fig. 7.

Fig. 7
figure 7

Steps of encrypting a 4 × 4 matrix by the introduced approach.

Full size image

The initial input, a 4 × 4 matrix, is seen in Fig. 7a. Image (b) is obtained by first executing the initial procedure of diffusion using Eq. (4) and then transforming the image matrix to a vector. Each output is shown in matrix form for improved visibility. The total of the values in the resulting picture matrix is determined in the next step. The computed sum for this image equals 6. This number can be divided by \(2^{8} = 256\) to find the remainder 6. This number serves as the HE algorithm’s starting encryption key. After applying the HE technique on image 7b, image 7c displays the encrypted image that was produced. The last step is the use of a reversible cellular automaton to create the encrypted image, which results in image 7d.

It should be noted that by doing the reverse of the described watermarking operation, it is possible to extract the watermark image. Therefore, with the watermarked image W, the operations of extracting watermark information from the image are:

  1. 1.

    The reverse of the steps described in step 6 is applied to the image to extract the coded confidential data from the watermark image in the form of a matrix like \(B\).

  2. 2.

    By using reversible cellular automata, and the rules mentioned in Table 2, the bits of matrix \(B\) will be converted to the state before the values change. We display this matrix as \(B^{\prime}\).

  3. 3.

    We convert the matrix \(B^{\prime}\) into a vector like \(V\).

  4. 4.

    Convert all the values of the vector \(V\) with the HE key that was created in the HE process, using the XOR operator to obtain the decoded vector \(V^{\prime}\).

  5. 5.

    By using Eq. (4), the reverse of the initial propagation operation will be done on the values of the vector \(V^{\prime}\).

  6. 6.

    Convert the vector obtained from the previous step into a matrix form (the same size as the watermark image) to obtain the initial image.

Research findings

The proposed approach was implemented using MATLAB 2020a. In addition, we used AE-CNN20 and DWT-SVD21 papers to compare the effectiveness of the proposed method. In these experiments, we used a dataset of 20 images including 256 × 256 to 512 × 512 grayscale images. However, in this section, we have presented results based on only three samples from this data set. Finally, we have reported the average values obtained from these three samples in the final results.

The following performance evaluation metrics for watermarking models are presented:

The mean square error (MSE) is a measuring metric used to determine the significance of changes after embedding the watermark data in the cover image. The MSE is calculate Eq. (7)31:

$$MSE = \left( \frac{1}{n} \right)*\mathop \sum \limits_{i = 1}^{n} (Y_{i} - \widehat{{Y_{i} }})^{2}$$
(7)

where \(Y_{i}\) represents the initial pixel values; \(\widehat{{Y_{i} }}\) represents the pixel values for the same position in the resulting image.

The PSNR equation is used in image and video processing to assess the quality of multimedia files. This equation determines the ratio of the signal energy to the noise in a signal and is defined as31:

$$PSNR = 20 \times \log_{10} \frac{{\left( {255} \right)}}{{\sqrt {MSE} }}$$
(8)

where 255 is the maximum allowable value for the signal; and MSE is the difference between the initial and result image which is calculated by Eq. (7).

The mean absolute error (MAE) is a commonly utilized performance evaluation measure for measuring differences. It computes the mean of the absolute disparities between the initial and the result image.

$$MAE = \frac{1}{N }\mathop \sum \limits_{i = 1}^{N} \left| {Y_{i} - \hat{Y}_{l} } \right|$$
(9)

where \(Y_{i}\) represents the initial pixel values; \(\widehat{{Y_{i} }}\) represents the pixel values for the same position in the resulting image.

In Fig. 8, we have three images: the mandrill, boat, and home images, which are our cover images. The secret image is also shown in Fig. 8d. Our goal is to be able to embed the secret image in Fig. 8d within the images 8a–c, and other watermarked images.

Fig. 8
figure 8

Some examples of images used in the experiments (a) mandrill30, (b) boat30 (c) house30 and (d) secret image.

Full size image

In Figs. 9, 10, and 11, we have performed the watermarking operation based on the proposed method and other methods, and we have shown the result of the watermarking, i.e., the changes that have occurred in the image compared to the original image, in the bottom row of the figure. This shows that the proposed method has been able to reduce the changes appropriately. Here, the changes in the bits are displayed as white, which shows that the proposed method has significantly reduced the amount of changes compared to the compared methods.

Fig. 9
figure 9

The watermark images generated by the proposed method for the Mandrill image (source: USC-SIPI30) compared to other methods.

Full size image
Fig. 10
figure 10

The watermark images generated by the proposed method for the boat image (source: USC-SIPI30) compared to other methods.

Full size image
Fig. 11
figure 11

The watermark images generated by the proposed method for the home image (source: USC-SIPI30) compared to other methods.

Full size image

Table 3 shows the values of MSE, MAE, and PSNR of three images, Mandrill, Boat, and Home, computed for the proposed method and the other two methods called AE-CNN and DWT-SVD. The proposed method has very low values of MSE and MAE compared to the other two, and a high value of PSNR. These results return the lowest values of MSE and MAE and the highest PSNR value, proving that the proposed method has introduced fewer changes into the images and increased the quality of the watermarked images. While the AE-CNN method has given high values of MSE and MAE and a low value of PSNR, which reflects that this method has introduced more changes in the images. The DWT-SVD method outperformed the AE-CNN method in both metrics but still showed lower performance compared to the proposed method.

Table 3 Comparison of mean squared error, mean absolute error, and signal-to-noise ratio for image steganography.
Full size table

In Fig. 12, histogram analysis was performed on the watermarked images. In this figure, on the left side, the original image and its histogram are shown, and on the right side, the resulting watermarked image and its histogram are shown. This shows that the resulting image has the minimum histogram difference compared to other methods. The standard deviation resulting from storing watermark information in the image using the proposed method, for all images on average, is equal to 4.15, which represents a 12.53% reduction compared to the compared methods.

Fig. 12
figure 12

Histogram analysis for the boat image: (a) Original image (source: USC-SIPI30), (b) Image after watermarking (c) Histogram plot of the original image (d) Histogram plot of the image after watermarking.

Full size image

In Fig. 13, histogram analysis was also performed on the secret image. On the left side, the watermarked secret image is shown along with its histogram plot. On the right side, the result of the fifth step, which is the reversible cellular automata-based distorted image, is shown along with its histogram plot. It is evident here that our proposed method has been able to perform hashing of the information in such a way that the texture information of the image is not visible through the histogram plot. In other words, the distribution of the light intensity values or the intensity values in the image is distributed in the range of 0–255, in a way that the original image information cannot be accessed through the histogram analysis of the resulting image. This indicates that the proposed method has been able to provide a strategy that effectively counters analysis attacks.

Fig. 13
figure 13

Histogram analysis for the confidential image: (a) Original image (b) Hashing image (c) Histogram plot of the original image (d) Histogram plot of the hashing image.

Full size image

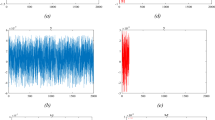
Figure 14 demonstrates the results obtained from polar histogram analysis32. The analysis shows different gradient distributions for original (Fig. 14a,c) and permuted (Fig. 14b,d) Boat and Mandrill images through polar histograms. Figure 14a and c show non-uniform patterns which represent the original image structures yet Fig. 14b and d display uniform radial patterns. The permutation process along with HE and RCA demonstrates strong diffusion properties which make intensity gradient directions random. The security enhancement of the proposed watermarking scheme depends on this diffusion method which both conceals the watermark while making statistical attacks less effective and protects confidentiality through gradient pattern disruption.

Fig. 14
figure 14

Polar histogram analysis of Boat and Mandrill images: (a) polar histogram of the initial Boat image, (b) result of permuting Boat image, (c) polar histogram of the initial Mandrill image, and (d) result of permuting Mandrill image.

Full size image

In Table 4, the correlation coefficient values before and after the hashing process for images are shown. For calculating the correlation coefficient, a thousand random pixels were selected from each image, and the correlation coefficients of each pixel with its horizontal and vertical neighbors were calculated. Then, the mean of these values was obtained. The results show that the correlation coefficient for our proposed method in images hashed by this method (i.e., the fifth step of the proposed method) has significantly decreased compared to the correlation values before hashing. This indicates that our method has succeeded in reducing the pixel correlation information or the texture uniformity of images as much as possible, so that texture analysis cannot reconstruct the original confidential image. This feature can be effective in the resistance of the proposed method against statistical attacks.

Table 4 Correlation coefficients in neighboring pixels before and after hashing the images.
Full size table

To examine the randomness of the hashing process, we carried out the entropy test, and the results are presented in Table 5. This table shows the entropy values of the cover image, the result image, and the entropy of the hashing and perturbation result (the fifth step). The results indicate that the entropy of the cover image and the result image is very low, meaning that the chance of random information in these images is minimal. However, the entropy result of the hashing is nearly 8, which, for images stored in 8 bits, represents complete randomness of information. This demonstrates that the proposed method for cover images, after hashing, was able to achieve a value close to 8.

Table 5 Information entropy test results.
Full size table

Figures 15, 16, 17 and 18 show the normalized correlation values for the changes applied to the result image and then the information extraction. In this way, the images were distorted with different intensities, based on noise or data compression, and then the extraction operation was performed on these distorted images, and the correlation of the information was calculated for the image before and after the distortion.

Fig. 15
figure 15

Normalized correlation values for pepper and salt noise attacks with different intensities.

Full size image
Fig. 16
figure 16

Normalized correlation values for Speckle noise attacks with different noise variances.

Full size image
Fig. 17
figure 17

Normalized correlation values for Gaussian noise attacks with different noise variances.

Full size image
Fig. 18
figure 18

Normalized correlation values for JPEG compression attacks with different compression ratios.

Full size image

The NC values of the proposed watermarking method and two comparison methods (AE-CNN and DWT-SVD) are shown in Fig. 15 for different levels of Salt & Pepper noise. The NC metric quantifies a level of similarity between extracted and original watermark to estimate the stability of the watermarking approach. One can identify a general tendency in the figure—as the intensity of the salt and pepper noise increases, the NC values for all three methods decrease. This is expected because higher noise level increases the level of distortion of the image and thus make it more difficult for the extractor to obtain a good estimate of the watermark. Nevertheless, the proposed method is observed to provide better accuracy than both AE-CNN and DWT-SVD in all the cases with different noise levels. This means that the proposed method is less sensitive to the degradation due to salt and pepper noise than the other methods. The higher NC values retained by the proposed method indicate that this method is more effective at protecting the inserted watermark from being affected by noise.

Additionally, the figure indicates that the decline in NC for the proposed method is not as steep as that of the other two methods as the noise intensity rises. This implies that the proposed method is more resilient to the levels of noise distortion as is illustrated in the following figures. Therefore, the figure clearly supports the hypothesis that the proposed watermarking method has higher robustness against salt and pepper noise than AE-CNN and DWT-SVD. These superior performances can be seen from the fact that the proposed method achieves higher NC values than the other method at various levels of noise intensity showing that the proposed method is able to preserve the watermarked image better in the presence of noise.

From Fig. 16, which shows the performance under different Speckle noise variances, the proposed method is superior to AE-CNN and DWT-SVD in terms of higher NC values at all noise levels. This shows excellent ability to perform under Speckle noise degradation which is better as compared to the other image watermarking methods. Moreover, the decrease rate of NC with the increase of noise variance in the proposed method is slower, indicating that it has better capability to preserve the watermark under more serious Speckle noise environment.

Figures 17, which show the performance under Gaussian noise also prove the effectiveness of the proposed method. As was the case with Speckle noise, the suggested approach demonstrates higher NC values compared to the two other methods when the Gaussian noise variances are varied. The ability to achieve such performance on all the test images shows that the proposed watermarking scheme is effective in dealing with different types of noise.

In conclusion, it can be seen from Figs. 15, 16 and 17 that the suggested watermarking method has better robustness to various noise attacks than the AE-CNN and DWT-SVD. This consistent performance of the proposed method for different types and level of noise further signifies the superiority and efficiency of the method in maintaining the robustness of the water mark.

Figure 18 shows the resistance of the proposed watermarking method along with AE-CNN20 and DWT-SVD21 against JPEG compression attacks. The NC values are plotted against different JPEG quality factors, with smaller quality factors indicating higher compression rates and, therefore, larger image distortions. As anticipated, the NC values for all three methods reduce as the JPEG quality factor reduces. This is because at higher compression ratios even more distortions and artefacts are injected into the picture and therefore the watermark extraction becomes even more difficult. But it is observed that the proposed method has always higher NC values than AE-CNN and DWT-SVD at all the JPEG quality factors. This shows that the proposed method has a better tolerance toward the degradation generated by the JPEG compression artifacts.

In addition, it was observed that the performance difference between the proposed method and the other two methods increases as the value of the quality factor reduces. From this it can be concluded that the proposed method is less sensitive to distortions and that the advantage grows with increasing compression level. Further, the rate of NC decrease for the proposed method is observed to be comparatively lower than AE-CNN and DWT-SVD. This suggests that the proposed method is less sensitive to JPEG compression, in the sense that the watermark is less distorted even when the compression is high. Thus, Fig. 18 gives a clear indication that the proposed watermarking method is more robust against JPEG compression than AE-CNN and DWT-SVD. The improvement in performance of the proposed method is consistent even when the quality factor is varied, which proves the reliability of the method in the presence of JPEG compression artifacts.

These graphs show that the proposed method has greater resistance to various distortions. This resistance is seen both against noise changes (salt and pepper noise, Speckle noise, and Gaussian noise) and against compression attacks. So that the performance of the proposed method against compression changes is significantly better than other methods and has a lower error rate. Also, the normalized correlation of information extraction in the proposed method is higher than other methods.

Analysis of computational cost

The proposed watermarking algorithm requires analytical evaluation through its sequential steps’ computational complexities which are defined by N (total watermark pixels) and M (total cover pixels).

  • Step 1 (Vectorization): Converting the watermark image (with N pixels) to a 1D vector has a time complexity of \(O\left( N \right)\).

  • Step 2 (Initial Propagation): The initial diffusion using XOR operations on the N elements takes \(O\left( N \right)\) time.

  • Step 3 (HE Key Generation): Calculating the sum of N elements and performing the modulo operation takes \(O\left( N \right)\) time. The subsequent conversion to a binary key of fixed length k is considered \(O\left( 1 \right)\) or \(O\left( k \right)\) if k is significant but constant. Thus, the overall complexity is \(O\left( N \right)\).

  • Step 4 (HE Transformation): For each of the N pixels, the Honey Encryption process involves a constant-time search in the message space M, a constant-time random selection from the assigned range in S, and a constant-time XOR operation with the n-bit key (\(n = 16\)). Therefore, the time complexity of the HE transformation is \(O\left( N \right)\).

  • Step 5 (Reversible Cellular Automata): Applying the RCA for L iterations on the watermark image (with N pixels) with a constant neighborhood size takes \(O\left( {L \cdot N} \right)\) time.

  • Step 6 (Discrete Wavelet Transform and Embedding): Performing a limited-level (d) Haar DWT on the cover image (with M pixels) takes \(O\left( M \right)\) time. Embedding the \(O\left( N \right)\) bits (assuming each pixel contributes a fixed number of bits after processing) of the watermarked data into the wavelet coefficients takes time proportional to the number of bits, which is \(O\left( N \right)\). The inverse DWT also takes \(O\left( M \right)\) time. Therefore, the overall time complexity of the embedding process is roughly \(O\left( {max\left( {N,M} \right) \cdot \left( {1 + L} \right)} \right)\). Considering that cover image is larger than the watermark (\(M \ge N\)), the time complexity of this step would be \(O\left( {M \cdot \left( {1 + L} \right)} \right)\).

In contrast, the training process for AE-CNN20 requires significantly higher computational resources than the proposed method because it performs orders of magnitude more operations especially when working with complex architectures and large datasets.

With respect to DWT-SVD21, both methods involve DWT which is \(O\left( M \right)\). The SVD operation on an M × M matrix has a complexity of \(O( {M^{\frac{3}{2}} } )\), which is generally higher than the HE and RCA steps in our proposed method, especially if \(L\) is kept relatively low. Our method demonstrates comparable or better computational efficiency than DWT-SVD especially for bigger image dimensions when the \(O( {M^{\frac{3}{2}} } )\) term of SVD starts to dominate.

Conclusion

In this paper, a novel image watermarking technique is proposed that combines the use of HE and reversible cellular automata. The proposed method had two main phases:

  • In the first phase, the initial image matrix was converted to a vector, diffused using XOR, and then transformed using HE and reversible cellular automata.

  • In the second phase, the transformed matrix was embedded into the cover image using discrete wavelet transform, without significantly changing the visual information of the image.

Using this approach, the researchers were able to increase the amount of confidentiality of the information while at the same time reducing the number of changes that had been made to the cover image information. It was realized from the findings that this strategy had been successful in terms of maintaining the confidentiality of the information and defending against attacks that used image distortion. The following are the limitations of the paper.

The main limitation is the high computational complexity of this method. This complexity is due to the use of reversible cellular automata in the proposed method. To increase the security level of the watermark information, the number of cellular automata transformations must be increased so that the information can be changed in more cycles. However, each repetition of this reversible cellular automata requires a greater number of computational operations. This causes the algorithm to spend more time on image watermarking. Therefore, for the use of this method in real-time applications and real-world conditions, it is necessary to use more efficient computational techniques in future research.