Introduction

Lightweight porous structures have become crucial components in structural lightweight design across aerospace, automotive, marine, biomedical implant, and construction industries. Their widespread adoption stems from their unique combination of physical and mechanical properties, including high strength-to-weight ratios, exceptional stiffness, thermal insulation capabilities, and superior energy absorption performance1,2. In recent years, nature-inspired metamaterials research has received increasing attention. By observing the complex and efficient structures and functions in nature, researchers have designed new metamaterials with special properties. Compared with materials prepared by traditional manufacturing processes, these metamaterials show significant differences and advantages in performance and function realisation mechanisms. Not only do they exhibit excellent properties in terms of mechanical properties, energy absorption, and modulability, but they also show great potential for sustainability and multifunctional integration. Through sophisticated structural configurations, researchers have demonstrated enhanced energy absorption capabilities3, optimized thermal management properties4, and tailored biocompatibility features5 that meet specific engineering requirements. This design philosophy aims to transcend conventional material limitations by strategically engineering micro- and macro-scale architectures while maintaining synergy with biological design principles emerging in contemporary materials research.

Traditional manufacturing techniques, such as investment casting6, melt gas injection7, and powder dense melting8, are limited to simple lattice structures. The high cost and inherent limitations of these traditional manufacturing techniques are inapplicable in fabricating metamaterials with complex structures. Selective Laser Melting (SLM) is one of the major techniques in Additive Manufacturing (AM)9 for metallic materials. The SLM overcomes the limitations of traditional manufacturing techniques, and reduces the difficulty of manufacturing metal parts with complex structures, and reduces the associated material waste and production time by minimizing the component size.

Previous studies on BCC lattice structures10 mainly focused on their mechanical performance. Based on the node connectivity of rods, Maxwell’s laws determine the bending or tensile behavior of the truss structures. That is why the truss structures have high strength and stiffness11,12. However, stress concentration at nodes in low-density truss-based lattice structures significantly compromises their practical performance.

Recently, researches on the configuration of BCC lattice structures have been carried. In order to explore a specific kind of lattice structure with light-weight and good mechanical properties, Bai et al.13 proposed a Body-Centered Tetragonal (BCT) lattice structure by removing the constraint of isotropy size in BCC lattice structure. A multi-objective optimization model for the configuration size of the BCT lattice structure was developed by taking the size of BCT cell configuration as the design variables, the size of lattice material and manufacturing process as the constraints, and the relative density, the initial stiffness and the strength of plastic collapse as the multi-objective evaluation functions. Based on the optimization model, the optimal configuration dimension of BCT lattice cell was obtained by using the ideal point method. Sami et al.14 designed a simple cubic lattice structure using the topology optimization method and compared it with BCC by experiments and simulations. The optimized structure exhibited two mixed deformation modes of tension and bending and showed better mechanical properties. Zhao et al.15 used a parametric method to design a BCC lattice structure with tapered support plates, which improved the problem of stress concentration at the nodes. Li et al.16,17 investigated the deformation modes and strain–stress evolution of the BCC lattice structure, and found that plastic hinges were formed at the nodes. An eccentric body cubic lattice structure was proposed based on BCC, and the influence of the eccentricity position on its mechanical properties was discussed.

On the other hand, Alomar et al.18 investigated the mechanical properties and deformation mechanisms of a novel circular-based lattice structure and BCC with a more uniform stress distribution using both numerical and experimental methods. Bai et al.19 proposed a curved rod design method to obtain a novel lattice structure that exhibits excellent energy absorption capacity and less stress concentration. Li et al.20 proposed a three-dimensional (3D) lattice structure with curved rods instead of conventional straight rods. Those studies showed that the curved rod cell-based design is more likely to alleviate the stress concentration phenomenon at the nodes of the structure. Fu et al.21 investigated the theoretical model of cell stiffness for curved rod lattice structure and its structure with different fractal degrees, which can effectively realize the stiffness modulation. Similarly, Mukherjee et al.22 proposed a curved hexagonal lattice structure composed of a mixture of straight and curved rods. Theoretical model of equivalent modulus of elasticity was also build up, which can evaluate the elastic properties of lattice structures with special curvature angles. Those studies provide a theoretical basis for further exploration of the mechanical behavior of lattice structures.

The investigation into optimized design methodologies for lattice metamaterials holds substantial academic significance and serves as a pivotal driver for technological advancement. Nevertheless, current lightweight-oriented lattice metamaterial designs face critical challenges: (1) Structural abruptness at unit cell junctions hinders smooth geometric transitions, adversely affecting manufacturing precision; (2) Stress concentration at nodal regions frequently induces shear fractures, forcing conventional optimization strategies targeting enhanced energy absorption to compromise mechanical performance through unavoidable trade-offs. To address these challenges, this study pioneers a trigonometric function-based design strategy that revolutionizes lattice architecture through three key innovations: First, we develop curved-strut configurations governed by trigonometric equations to precisely control unit cell morphology and spatial distribution. Second, arc-shaped nodal transitions with zero curvature (κ = 0) replace traditional rectilinear connections in lightweight metallic lattice metamaterials, eliminating stress-concentrating sharp junctions. Third, a multidisciplinary framework integrating FEM simulations and mechanical testing systematically optimizes quasi-static/dynamic mechanical properties, energy absorption efficiency, stress distribution uniformity, and failure mechanism refinement. This paradigm shift from conventional rectilinear designs to curvature-engineered architectures demonstrates how geometric innovation can simultaneously enhance multiple performance metrics while resolving intrinsic limitations of existing lattice metamaterials.

In this paper, three novel trigonometric function curved rod cell-based lattice structures were proposed and their fillet-node-optimized configurations were investigated. The effects of different trigonometric function curved rods on the mechanical properties and energy absorption capacity of truss-based metamaterials fabricated by SLM were investigated. The relationships between different structural features and their corresponding compression behaviors and damage mechanisms were discussed. The optimization strategy of the nodes of the trigonometric function curved rod cell-based lattice structures was also validated. Compared with the trigonometric function-based lattice structures, the fillet-node-optimized strategy have higher stiffness, strength, energy absorption capacity and stable mechanical properties, and are less sensitive to the overall failure.

Materials and methods

Trigonometric function-based lattice metamaterials design

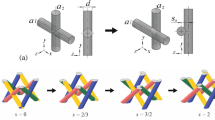
In this study, we established a benchmark using the BCC lattice as the baseline configuration. Through mathematically-driven topological substitution, three novel trigonometric function-based lattice metamaterials were developed by strategically replacing original straight rods with parametric trigonometric-curved rod units. These advanced architectures are systematically designated as: Tangent Function Curved Rod Cell-based (TCRC), Sine Function Curved Rod Cell-based (SCRC) and Cosine Function Curved Rod Cell-based (CCRC), as illustrated in Fig. 1, where d is rod diameter, L is unit cell size and a is trigonometric coefficient. These parameters collectively ensure constant volume fraction (\(V_{f}\)) across all configurations through constrained geometric relationships (Table 1).

Fig. 1
figure 1

(a) Trigonometric function-based lattice structure design strategy; (b) TCRC, (c) SCRC, (d) CCRC.

Full size image
Table 1 Geometric parameters of trigonometric function-based unit cells.
Full size table

Traditional BCC straight rod nodes only meet the positional continuity (\(x_{i}^{(1)} = x_{i}^{(2)}\)), the first-order derivative discontinuity (\(\frac{dy}{{dx}}\left| {_{left} } \right. \ne \frac{dy}{{dx}}\left| {_{right} } \right.\)), resulting in curvature \(\kappa\) dispersion; the second-order continuity of trigonometric curves can ensure smooth transition of the rod curvature, ensure the continuity of the curvature at the nodes (\(\kappa_{left} = \kappa_{right}\) ), and eliminate the geometrical singularity, thus reducing the 3D printing defect rate. In addition, the curved rod design enables quantitative optimisation of the stress concentration factor:

Original BCC:

$$K_{t} = 1 + 2\sqrt {\frac{D}{\rho }} (\rho \to 0divergence$$
(1)

Optimized curved-node achieve finite stress concentration by curvature control:

$$K_{t} = 1 + \frac{2R}{{\sqrt {\left( {R + d} \right)^{2} - R^{2} } }}\left( {{\text{curvature radius}}\;R > 0\;convergence} \right)$$
(2)

Hence, building upon the conventional BCC lattice framework, we pioneered the innovative development of trigonometric function-based lattice metamaterials through mathematical modulation of nodal curvature continuity.

Volume fraction quantification:

$$V_{f} = \frac{{V_{solid} }}{{V_{unit} }}$$
(3)

where \(V_{f}\) is volume fraction (dimensionless), \(V_{solid}\) is solid material volume within unit cell (mm3) and \(V_{unit}\) is unit cell volume (mm3).

Actual density computation:

$$\rho_{lattice} = V_{f} \rho_{TC4}$$
(4)

where \(\rho_{lattice}\) is designed lattice density (g/cm3), \(\rho_{TC4}\) is bulk material density.

Theoretical relative density:

$$\rho_{r} = \frac{{\rho_{lattice} }}{{\rho_{TC4} }}$$
(5)

where \(\rho_{r}\) is dimensionless relative density (\(0 < \rho_{r} < 1\)).

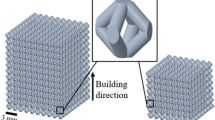
Each structure contains 4 × 4 × 4 cell units, the overall size is 15 × 15 × 15 mm3. Under the condition of keeping the length unchanged, the rod is controlled by adjusting the coefficients of trigonometric function so that the relative density of each structure is kept the same. This controlled geometric architecture guarantees homogeneous mechanical coupling between adjacent unit cells while establishing a computationally tractable framework for subsequent finite element analysis of deformation mechanisms and energy dissipation characteristics.

SLM was performed using a near-spherical gas atomized Ti-6Al-4V23 powder with a narrow particle size distribution between 15 and 45 \({\mu m}\). The chemical composition of Ti-6AL-4V is shown in (Table 2). Using a commercially available metal rapid prototyping machine named Renishaw AM250, make sure that the substrate was flat and tidy before the SLM process started.

Table 2 Chemical composition of Ti-6Al-4V powder (mass fraction, wt%).
Full size table

Figure 2 shows the schematic design and built structures of BCC, TCRC, SCRC, and CCRC lattices. To systematically investigate the mechanical behavior divergence between trigonometric function-based cellular lattice architectures and traditional lattice configurations, a BCC lattice structure was selected as the control group. Through quantitative characterization and multidimensional performance evaluation, this study establishes a comprehensive evaluation framework to discern critical differences in load-bearing capacity, energy absorption efficiency, and failure modes between the two architectures. The findings aim to reveal potential advantages and limitations of trigonometric function-based cellular lattice structures in structural mechanics, serving as a theoretical foundation for topology-optimized lattice design.

Fig. 2
figure 2

Comparative schematics of 3D modelled and SLM fabricated metamaterials: (a,e) BCC; (b,f) TCRC; (c,g) SCRC; (d,h) CCRC.

Full size image

Lattice metamaterials fabricated via additive manufacturing exhibit systematic geometric deviations between 3D modelled and SLM fabricated metamaterials (Fig. 2 and Table 3). This discrepancy originates from three principal mechanisms: First, process parameters govern melt pool thermodynamics, where improper parameter selection induces layer-wise error accumulation. Second, volumetric shrinkage during powder melting-solidification phase transitions generates heterogeneous deformation, creating residual stress-induced macroscopic distortion. Third, post-processing inaccuracies in wire cutting coupled with heat-affected zone effects amplify dimensional variances. Despite these multiscale manufacturing challenges, the measured specimens demonstrate controlled relative errors below 3%, falling within acceptable thresholds for uniaxial compression testing requirements.

Table 3 Dimensional comparison between trigonometric function-based lattice designs and SLM-fabricated specimens.
Full size table

The multiscale size effect is the change in mechanical properties of a structure or sample as its geometric scale changes. In lattice metamaterials, the size effect is usually manifested as a decreasing trend in the overall strength of the structure as the overall size increases, whereas smaller-sized lattice structures may exhibit strength and ductility characteristics better than predicted values. A nonlinear finite element analysis was performed on dot-matrix metamaterials with edge lengths of 7.5 mm, 15 mm and 22.5 mm, respectively, as shown in (Fig. 3). The existence of the multiscale size effect, i.e., the maximum load carrying capacity of the structure gradually decreases as the size increases, is further verified. Therefore, in order to ensure the consistency of the experimental conditions and avoid the interference of the size effect on the mechanical property analysis, all the structural simulation models of dot matrix metamaterials in this paper uniformly adopt the external size of 15 mm × 15 mm × 15 mm to ensure the comparability and reliability of the simulation test results.

Fig. 3
figure 3

Numerical investigation of size effects.

Full size image

Microstructure

The surface morphology was analyzed using an electron microscope. For each type of lattice structure, ultrasonic bath cleaning and drying was performed to remove the scattered metal powders attached to the samples. Electron microscopy was used to observe and characterize the micro-morphology of the Ti-6AL-4V samples to identify internal pores and defects. The results are showed in (Fig. 4). No large defects or obvious cracks were found in the samples, and the rods did not show any large deformation or fracture. Therefore, these lattice samples are suitable for quasi-static compression testing.

Fig. 4
figure 4

SEM micrographs illustrating the as-fabricated surface morphology of representative lattice configurations: (a,e) BCC; (b,f) TCRC; (c,g) SCRC; (d,h) CCRC, with low and high-magnification views of strut junction regions.

Full size image

Numerical simulation with FEM

To mitigate the influence of grid resolution on \(\sigma \sim \varepsilon\) curve predictions, a grid independence study was performed as illustrated in (Fig. 5). Four distinct grid sizes (0.1 mm, 0.15 mm, 0.2 mm and 0.5 mm) were systematically evaluated. Notably, the finite element model with the coarsest 0.5 mm mesh exhibited significant deviations from other configurations, while simulations employing meshes of 0.1 mm, 0.15 mm, and 0.2 mm demonstrated remarkable consistency. Based on this sensitivity analysis, the 0.2 mm grid configuration was ultimately adopted for subsequent simulations, striking an optimal balance between computational accuracy and efficiency.

Fig. 5
figure 5

Lattice convergence analysis.

Full size image

According to the method of obtaining \(\sigma \sim \varepsilon\) curve shown in Fig. 6a of the Ti-6AL-4V metamaterial, we carried out simulation and compression tests for the three new materials fabricated using SLM to obtain their properties.The compression platens were simulated as rigid shells with kinematic coupling to reference points. Boundary conditions included: full constraint on the lower platen and quasi-static displacement loading (8 mm amplitude, 0.01 mm/s rate) on the upper platen (Fig. 6b). For Ti-6AL-4V-stainless steel contact nonlinearity, a penalty contact algorithm (normal stiffness factor: 0.1, friction coefficient μ = 0.2) was implemented to ensure convergence (residual force ratio < 5%). Material properties of Ti-6AL-4V23 (Table 4) were incorporated into an explicit dynamic step (time increment: 1 × 10⁻⁶ s, mass scaling factor: 500) maintaining quasi-static conditions (kinetic/internal energy ratio < 5%).

Fig. 6
figure 6

(a) \(\sigma \sim \varepsilon\) curve of the Ti-6AL-4V metamaterial. (b) FEM model of lattice structure with constrains.

Full size image
Table 4 Material properties of the quasi-static finite element model.
Full size table

The Johnson–Cook (J-C) constitutive model is employed to characterize the thermo-viscoplastic behavior of metallic materials under dynamic loading conditions. The flow stress is expressed as a multiplicative function of strain hardening, strain rate sensitivity, and thermal softening effects24.

$$\sigma_{VM} = (A + B\left( {\varepsilon_{eq}^{pl} } \right)^{n} )[1 + Cln(\frac{{\dot{\varepsilon }_{eq}^{pl} }}{{\dot{\varepsilon }_{ref} }})][1 - (\frac{{T - T_{r} }}{{T_{m} - T_{r} }})^{m} ]$$
(6)

where \(\sigma_{VM}\) is von Mises equivalent stress (MPa), \(\varepsilon_{eq}^{pl}\) is accumulated equivalent plastic strain, \(\dot{\varepsilon }_{eq}^{pl}\): equivalent plastic strain rate (s−1), \(\dot{\varepsilon }_{ref}\) is reference strain rate (\(1.0 \times 10^{{{ - }3}} {\text{s}}^{ - 1}\)), \(T\),\(T_{m}\) and \(T_{r}\) are test temperature (K), melting temperature (K) and reference temperature (298 K) respectively. Material constants A is quasi-static yield strength (MPa), B is strain hardening coefficient (MPa), n is strain hardening exponent, C is strain rate sensitivity coefficient, m is thermal softening exponent (Table 5).

Table 5 Parameters of J-C intrinsic and fracture models42.
Full size table

The J-C fracture criterion defines the equivalent plastic strain at damage initiation as25:

$$\varepsilon_{f} = [D_{1} + D_{2} exp(D_{3} \eta )](1 + D_{4} ln(\frac{{\dot{\varepsilon }_{eq}^{pl} }}{{\dot{\varepsilon }_{ref} }})(1{ + }D_{5} \frac{{T - T_{r} }}{{T_{m} - T_{r} }})$$
(7)

where \(\eta { = }\sigma_{hyd} /\sigma_{VM}\) represents the stress triaxiality, with \(\sigma_{hyd}\)  denoting the hydrostatic stress. \(D_{1} \sim D_{5}\) are the material constants related to the damage strain and stress triaxiality, where \(D_{1} \sim D_{3}\) can be obtained by combining the FEM simulation results with different stresses at the reference strain rate and the reference temperature, \(D_{4}\) and \(D_{5}\) are the constants obtained from tensile tests with different strain rates at the reference temperature, and tensile tests with different temperatures at the reference strain rate.

The damage accumulation variable is computed incrementally:

$$\omega = \sum {\frac{{\vartriangle \varepsilon_{eq}^{pl} }}{{\varepsilon_{f} }}}$$
(8)

Element removal occurs when \(\omega > 1.0\), ensuring energy-conserved fracture propagation while avoiding numerical instability26.

Compression test

Quasi-static axial compression testing was conducted on a 100 kN universal testing machine (CMT5105, MTS Systems) following ISO 13314:2011 guidelines27, with experimental configuration details illustrated in (Fig. 7). The displacement-controlled protocol maintained a constant crosshead velocity of 2 mm/min, employing triplicate testing for statistical verification. Termination criteria were set at either 95 kN load threshold or 8 mm displacement.

Fig. 7
figure 7

Compression test platform.

Full size image

Results and discussion

Geometric and structural features

The surface morphology and cross-sectional images of the SLM lattice structure were characterized by electron microscopy, as shown in (Fig. 4). Continuous geometrical structure with obvious defects or broken grain cells can be found. Spherical air holes are mostly formed during the SLM curing process, and the air holes are prone to act as crack initiation points during the loading process28. During the SLM machining, the CAD model was decomposed into a number of polyhedral layers. The laminar build-up brought inevitable stepping effect, resulting in a relatively rough surface. Due to the inevitable machining heat-affected zone and cooling process, an inhomogeneous micro-grain organization was formed29. The machining temperature difference leads to a significant thermal diffusion phenomenon. A slight degree of suspension buildup occurs due to convergence at the bottom of the rod junction, resulting in some variation in shape and position between two neighboring stubs30. Internal stresses, i.e., thermal expansion, generated during the SLM process also contribute to dimensional errors. Despite these shortcomings, the SLM has the advantage of high machining accuracy. No large defects or obvious cracks were found in the samples, and the rods did not show any large deformation or fracture. Therefore, these lattice samples are suitable for quasi-static compression testing.

Deformation behavior and mechanical properties

The multi-physics compression response of BCC and trigonometric function-modulated lattice metamaterials was systematically investigated through integrated computational-experimental methodology. As demonstrated in (Figs. 8, 9), the complete deformation sequence spanning elastic buckling, plastic collapse propagation, and densification stages was captured. The compressive mechanical properties of these four metamaterials under the same conditions of relative density depend on their rod cell geometry. An in-depth study of them can provide an important basis for analyzing the structural deformation and fracture mechanisms. Figure 9 shows the deformation process of these four metamaterials with a relative density of 0.2.

Fig. 8
figure 8

FEM of compressive behavior in BCC and trigonometric function-based lattice metamaterials.

Full size image
Fig. 9
figure 9

Multi-stage compressive deformation mechanisms of lattice metamaterials at normalized relative density.

Full size image

The BCC had severe stress concentration, and the failure mechanism is complete fracture at the rod nodes. In BCC, some nodes fractured at 20% strain, some struts fractured and fall off at 30% strain. The compressed BCC bend along the diagonal direction to form 45°shear damage31,32, which lead to structural failure and a significant reduction in strength.

The TCRC lattice structure demonstrates a progressive layer-wise collapse mechanism coupled with shear-driven failure modes under compressive loading. During the initial stage (0% strain), the structure maintains pristine geometric integrity without detectable deformation. At 20% strain, global structural distortion emerges while preserving macroscopic stability and load-bearing capacity. As strain reaches 30%, localized failure initiates through top-layer unit cell crushing, triggering sequential collapse propagation along the loading axis accompanied by buckling instability, though no material detachment occurs. Upon achieving 40% strain, the upper layers undergo complete crushing, marking the transition to the catastrophic failure phase characterized by abrupt stability degradation and irreversible structural disintegration. This staged failure progression highlights the interplay between geometric hierarchy and shear-dominated deformation in governing the energy absorption behavior of lattice architectures.

The failure mechanism of SCRC samples was shear damage. Obvious shear slip phenomenon occurred at 20% strain. And the arcs cannot continue to maintain the original shape, but do not detach. Shear damage appeared at 30% strain.

The failure mechanism of CCRC samples was shear damage. The CCRC samples was subjected to shear stresses forming a 45°shear band in the opposite direction. The significant difference between the flexural and axial compression states leaded to a significant reduction in the load-bearing capacity of the homogeneous deformation in the elastic phase and the overall shear deformation in the fracture plateau phase.

During the nonlinear damage phase, multiple peak stresses were present in all structures and were usually associated with progressive damage in different layers. In addition, the structural damage of the truss-based BCC occurred at about 24% strain. The collapse strain of SCRC and CCRC was about 21%. The TCRC was similar to BCC, did not start to collapse until the compressive strain reaches 24%, indicating that the TCRC has the same stability and superior load-bearing capacity of the BCC structure.

In summary, the failure mechanisms of BCC, SCRC, and CCRC lattice structures all manifest as 45° diagonal shear failure, exerting substantial impacts on their mechanical performance: First, this failure mode causes remarkable reductions in both maximum load-bearing capacity and structural stiffness, leading to abrupt loss of structural support post-failure. Second, the formation of shear bands induces damage localization, compromising the inherent uniform deformation characteristics and energy absorption capabilities of lattice structures, thereby diminishing overall toughness and energy dissipation efficiency. This prevalent 45° shear failure has emerged as a critical determinant affecting structural stability and mechanical behavior, necessitating special consideration during structural design optimization processes. In distinct contrast, the TCRC lattice architecture successfully mitigates diagonal shear failure through its redesigned topology. Instead, its failure mechanism transitions to localized compressive collapse confined to the upper layers. This modified failure pattern enables more progressive structural deformation and controlled damage progression, consequently enhancing key mechanical properties including peak load capacity, toughness indices, and energy absorption efficiency compared to conventional lattice designs. These performance enhancements demonstrate the TCRC structure’s superior mechanical advantages over traditional lattice configurations, highlighting its potential for energy-absorbing applications.

Figure 10a shows the compressive \(\sigma \sim \varepsilon\) curves obtained by quasi-static FEM simulation of BCC and three new lattice structures. Figure 10b demonstrates the compressive \(\sigma \sim \varepsilon\) curves obtained from experimental tests of BCC and three new lattice structures. The \(\sigma \sim \varepsilon\) curves of the three new lattice structures are generally higher than those of the BCC structure, indicating that they are subjected to higher maximum compressive stress than the BCC structure. This indicates that the lattice structures of TCRC, SCRC, and CCRC exhibit good static load-bearing potential during the plastic yielding stage. However, it is worth noting that the activation of the failure mechanism of SCRC and CCRC structures, except TCRC, is earlier than that of BCC structures.

Fig. 10
figure 10

(a) The compressive \(\sigma \sim \varepsilon\) curves obtained by quasi-static FEM simulation of BCC and three new lattice structures. (b) The compressive \(\sigma \sim \varepsilon\) curves obtained from experimental tests of BCC and three new lattice structures.

Full size image

Their mechanical responses can be divided into 4 states: elastic phase, plastic yielding phase, platform fracture phase, and densification phase. The main functions of a metamaterial are usually lost at the end of the elastic and plastic yielding phases. Therefore, the mechanical properties of these two phases are usually studied33. Figure 11 provides comparative data for compressive strength, yield strength, and modulus of elasticity for these four metamaterials in compression simulations and experiments. All these metamaterials experienced a rapid increase in stress during the elastic phase. The compressive strength value of BCC is about 53 MPa. The compressive strength values of the three new designed trigonometric function curved rod unit cell-based lattice structures are higher than that of BCC. SCRC has the highest compressive strength, which is about 68 MPa. The elastic modulus value of BCC is about 772 MPa. The elastic modulus of the new designed 3 trigonometric function curved rod unit cell-based lattice structures are also higher than that of BCC. TCRC has the highest elastic modulus, which is about 918 MPa. In addition, BCC stops elastic deformation at 9% strain, while all the new designed 3 trigonometric function curved rod unit cell-based lattice structures stop elastic deformation at about 15% strain. The remarkable synergy between high stiffness and excellent elastic strain enables the clear observation of the maximum peak stress attained in the lattice structure constructed based on trigonometric function unit cells. In the supermaterial system built on the truss principle, as the tensile action dominates the entire structure, once the unit cell reaches the peak of its compressive strength, it will immediately exhibit an extremely significant stress drop trend. Tracing back to the origin, this phenomenon is mainly caused by the structural bending fracture induced by axial compression buckling. This fracture mechanism not only contributes to the formation of 45° shear bands but also causes the detachment of massive debris from the main structure. As the degree of strain continues to rise, new shear bands and cracks emerge continuously like mushrooms after rain, thus triggering a subsequent series of stress fluctuations.

Fig. 11
figure 11

Comparative data from simulations and experiments: (a) Elastic modulus, (b) Plateau strength, (c) Peak compressive strength for different lattice structures at the same relative density.

Full size image

Based on the previous research, the mechanical properties and energy absorption capacities of the trigonometric cell-based lattice structures have been improved. But there still exists a serious stress concentration phenomenon. In order to reduce the stress concentration, we considered the strengthening of the nodes of the trigonometric function curved rod cell-based lattice structures. Specifically, the structural transition enhancement is adopted for the lattice center node and the rod unit articulation node. The fillet-node-optimized trigonometric function curved rod cell-based lattice structures are named as TCRC-ipv, SCRC-ipv, and CCRC-ipv, respectively. The experimental compressive strain–stress curves of these structures are shown in (Fig. 12).

Fig. 12
figure 12

Morphological and mechanical characterization of fillet-node-optimized lattice metamaterials: (a,b) TCRC-ipv lattice. (c,d) SCRC-ipv lattice. (e,f) CCRC-ipv lattice. (g ~ i) Comparison of \(\sigma \sim \varepsilon\) curves of fillet-node-optimized lattice compression tests with different lattice structures at the same relative density.

Full size image

In Fig. 12, it is observed that the curve changes are basically the same. The first phase is linear elastic state, followed by a sudden and significant decrease in the stress associated with brittle fracture, and finally a densification phase. In contrast, the fillet-node-optimized trigonometric function curved rod cell-based lattice structures improve in both the elastic and plastic phases of the curve. Thus, the fillet-node-optimized lattice structures exhibit a better static load-bearing potential than its counterparts. In TCRC, structural failure occurs at around 24% strain. However, TCRC-ipv does not start collapsing until compressive strains reach 27%, structural failure delayed by about 3%. Besides, the first peak strength loss is much lower. These means that the TCRC-ipv has more excellent structural stability and load-bearing capacity than TCRC. SCRC and SCRC-ipv have nearly identical compressive strain, both collapse at around 21% strain. CCRC-ipv has a compressive strain of around 24%, and its structural failure is delayed by about 3%.

There are differences in the failure modes between the trigonometric-based lattice structures(TCRC,SCRC,CCRC) and the fillet-node-optimized trigonometric function curved rod cell-based lattice structures(TCRC-ipv,SCRC-ipv,CCRC-ipv). Figure 13 shows the main compressive deformation behavior under 30% strain from both quasi-static compression tests and simulations. The trigonometric-based lattice structures are more prone to stress concentration at the junctions between struts and nodes, leading to brittle fracture. For the fillet-node-optimized lattice structures, the TCRC-ipv and CCRC-ipv designs experience more pronounced bending or overall buckling before failure, exhibiting more dispersed and progressive failure modes. For the SCRC-ipv structure, the failure mode under 30% compressive strain is similar to that of the SCRC structure, mainly dominated by strut buckling and fracture.

Fig. 13
figure 13

Comparative analysis of 30% strain deformation patterns: experimental-simulation correlation for trigonometric-based vs. fillet-node-optimized lattice structures.

Full size image

Figure 14 shows in detail the compression test and simulation mechanical properties of the three new designed lattice structures and the fillet-node-optimized lattice structures. It can be found that the properties such as peak compressive strength, stiffness in linear state and platform strength show a significant improvement trend after the node-reinforcement. As can be seen from Table 6, the stiffness of the lattice structure calculated from the linear elastic region of the curve under nearly the same conditions of relative density indicates that the TCRC-ipv structure has the highest compressive strength (84 MPa), yield strength (51 MPa), and elastic modulus (1071 MPa). The SCRC structure has a similar modulus of elasticity (1062MPa), but the compressive strength, yield strength were significantly lower than those of the TCRC-ipv structure.

Fig. 14
figure 14

Comparative data from simulations and experiments: (a) Elastic modulus, (b) Plateau strength, (c) Peak compressive strength for the trigonometric-modulated variants and the fillet-node-optimized configurations at the same relative density.

Full size image
Table 6 Comparison of mechanical properties of Ti-6Al-4V lattice structure.
Full size table

Fillet-node-optimized configurations affected the mechanical properties of TCRC, SCRC and CCRC structures. Among them, the TCRC-ipv structure has the best mechanical properties with the most significant mechanical property enhancement; while the SCRC-ipv structure has relatively small performance enhancement.

Gibson and Ashby established analytical formulations for predicting elastic modulus (E) and yield strength (\(\sigma_{y}\)) of lattice materials under varying test parameters. This study employs their constitutive equations for curved-strut lattice analysis:

$$\frac{{E_{latt} }}{{E_{{\text{m}}} }} = C_{1} \left( {\frac{{\rho_{latt} }}{{\rho_{m} }}} \right)^{n}$$
(9)
$$\frac{{\sigma_{latt} }}{{\sigma_{m} }} = C_{2} \left( {\frac{{\rho_{latt} }}{{\rho_{m} }}} \right)^{n}$$
(10)

For SLM-fabricated lattices, the Gibson-Ashby coefficients C₁ (0.1–4.0) and C₂ (0.1–1.0) were experimentally calibrated. Power-law exponents n and m are typically material constants, for straight-strut configurations n = 234, m = 1.535. Table 7 presents Gibson-Ashby performance coefficients derived from experimental means, demonstrating excellent agreement with theoretical ranges, key observations show that TCRC variants exhibit 15–23% higher C₂ values than BCC baseline, indicating enhanced strength scaling. All predicted coefficients reside within Gibson-Ashby validity bounds (C₁: 0.1–4.0; C₂: 0.1–1.0). Curvature effects reduce n values by 18–22% relative to straight-strut references.

Table 7 Gibson-Ashby performance coefficients determined from experimental averages.
Full size table

Energy absorption

In porous materials, the onset of densification strain typically marks the transition from the plateau phase to the densification stage, accompanied by a sharp stress increase with strain. However, lattice structures often exhibit no distinct densification characteristics in their \(\sigma \sim \varepsilon\) responses. This phenomenon can be attributed to their unique failure mechanisms: under compressive loading, lattice structures tend to develop penetrating shear failure bands along the maximum shear stress direction (~ 45°). Once these shear bands form, the structure undergoes continuous failure, leading to rapid degradation or stabilization of load-bearing capacity, which hinders further compaction. Unlike foam materials, where collapsed cellular fragments can accumulate and enhance overall stiffness, localized yielding in lattice structures post-shear failure does not translate into macroscopic stiffness improvement but instead causes global softening. Consequently, due to the lack of robust secondary load-bearing mechanisms, lattice structures rarely enter a typical densification phase during compression, and their \(\sigma \sim \varepsilon\) curves lack the characteristic steep stress rise associated with densification. To accurately evaluate energy absorption performance and define densification behavior in lattice structures, the Energy Absorption Efficiency (EAE) method is employed36,37. The critical strain, termed the initial densification strain (\(\varepsilon_{cd}\)), is defined as the practical limit for energy absorption applications in lattice structures38. Beyond this strain threshold, lattice structures lose their capacity for sustained energy absorption. The \(\varepsilon_{cd}\) is determined using the energy absorption efficiency method (EAEM)39, where the energy absorption efficiency (η) is calculated as:

$$\eta = \frac{EA}{\sigma } = \frac{{\int_{0}^{\varepsilon } {\varepsilon d\varepsilon } }}{\sigma \left( \varepsilon \right)}$$
(11)

The point corresponding to the maximum value of the energy absorption efficiency curve is the strain value at the end of the plastic deformation phase of the lattice structure, which is determined as the termination point of the integral of the energy absorption calculation. It is given by:

$$\frac{{{\text{d}}\eta }}{{{\text{d}}\varepsilon }}|_{{\varepsilon = \varepsilon_{{{\text{cd}}}} }} = 0$$
(12)

From Eq. (12), the energy absorption capacity of a given lattice structure is the area bounded by the X-axis at the onset of reaching the densification strain \(\varepsilon_{{{\text{cd}}}}\) under the \(\sigma \sim \varepsilon\) curve:

$$W = \int_{0}^{\varepsilon } {\sigma \left( \varepsilon \right)} {\text{d}}\varepsilon$$
(13)

The energy absorption efficiency curves for different lattice structures are shown in Fig. 15 and the total energy absorption is shown in (Fig. 15c). From Fig. 15a, it can be seen that the energy absorption efficiency curves of the lattice structures show significant fluctuations with the increase of compressive strain. This fluctuation is related to the stability of the structure. During compression, the lattice structure undergoes localized structural fractures. With higher stress fluctuations and higher energy absorption, leads to peaks in the energy absorption efficiency curves at these localized structural fractures locations.

Fig. 15
figure 15

Energy absorption efficiency versus normalized relative density for lattice structures: (a) Baseline BCC vs. trigonometric-modulated variants (TCRC/SCRC/CCRC); (b) Fillet-node-optimized configurations (TCRC-ipv/SCRC-ipv/CCRC-ipv); (c) Total energy absorption.

Full size image

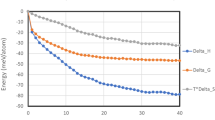
The initial densification strain εcd shown in Fig. 16 is defined as the strain at which the energy absorption efficiency reaches its maximum value on the efficiency-strain curve. The BCC lattice structure with a relative density of 0.2 has an energy absorption capacity of 9.89 MJ/m3. The SCRC has an energy absorption capacity of 9.72 MJ/m3. The CCRC has the lowest energy absorption capacity (W of 9.43 MJ/m3). It is worth mentioning that the TCRC lattice structure has the highest energy absorption capacity (W = 12.35 MJ/m3), which is 1.25 times higher than that of the BCC.

Fig. 16
figure 16

Energy absorption performance benchmarking of lattice structures under normalized relative density: (a) Baseline BCC versus trigonometric-modulated architectures (TCRC/SCRC/CCRC); (b) Fillet-node-optimized configurations (TCRC-ipv/SCRC-ipv/CCRC-ipv).

Full size image

At the same relative density, the energy absorption capacity depends on the geometry of the structure. As can be seen from Fig. 16, \(W_{TCRC - ipv}\) increases to 18.38 MJ/m3, which is 48.82% higher than \(W_{TCRC}\). The \(W_{SCRC - ipv}\) increases to 12.29 MJ/m3, which is only 2.57 MJ/m3 higher than \(W_{SCRC}\). The \(W_{SCRC - ipv}\) increases by 26.44% with respect to \(W_{SCRC}\), which is an insignificant advantage. The \(W_{CCRC - ipv}\) increased to 14.59 MJ/m3, which is 54.71% higher than \(W_{CCRC}\). The energy absorption capacity of CCRC-ipv is close to that of TCRC-ipv.

In order to evaluate and compare the energy absorption capacities of metamaterials, Fig. 17 shows the normalized energy absorption per unit volume of the lattice structure \(W/E_{{\text{m}}}\) versus the corresponding normalized stress \(\sigma_{{\text{b}}} /E_{{\text{m}}}\). Maiti et al.40 and Ashbyl41 used this form of energy absorption diagram when discussing large-size nodes matrix monolithic cells. This comparison can be used as a guiding factor in the selection of energy absorbing materials. In Fig. 17, (I) represents the elastic phase, in which the material undergoes mainly elastic deformation and energy absorption is relatively low. (II) denotes the plastic yielding phase, in which the material starts to deform plastically and the energy absorption gradually increases. (III) represents the plateau stress phase, where the material absorbs a large amount of energy .

Fig. 17
figure 17

Normalized energy absorbed per unit volume versus normalized peak stress for lattice structures with different relative densities: (a) Baseline BCC versus trigonometric-modulated architectures (TCRC/SCRC/CCRC); (b) Fillet-node-optimized configurations (TCRC-ipv/SCRC-ipv/CCRC-ipv).

Full size image

In Fig. 17a, compare the energy absorption properties of BCC with three new lattice structures. The normalized energy curves of TCRC, SCRC, and CCRC in phase (I) and phase (II) are located on the right side of BCC. Their energy absorption properties are mainly shown in the elastic phase and plastic phase, which can absorb more energy in a larger range of stress thresholds. The curves of TCRC are slightly higher than the other lattices in phase (III), indicating a better energy absorption capability in the plateau stress phase, which can absorb energy more efficiently. In Fig. 17b, compare the energy absorption properties of the node-reinforced lattice structure, the SCRC-ipv curves are located on the right side in phase (I) and phase (II), and are significantly higher than the other node-reinforced lattices in phase (III), which indicates that the SCRC-ipv structure has a higher energy absorption capacity at high stresses.

The energy normalization curve of the node-reinforced lattice structure extends upward to a greater extent, and it can absorb more energy in the high stress region, showing a significant advantage on energy absorption capability. Overall, TCRC-ipv is more affected and significantly outperforms other node-reinforced lattice structures in energy absorption capability.

Conclusion

This study presents an innovative approach to enhance the mechanical performance and energy absorption capabilities of lattice metamaterials by addressing the dual challenges of stress concentration in nodal regions and the trade-off between lightweight design and load-bearing capacity. Through computational modeling and experimental validation, we developed trigonometric function-based lattice structures with optimized nodal transitions. The principal findings can be summarized as follows:

  1. (1)

    Novel structural design methodology: We established a theoretical framework for BCC lattice structures and developed trigonometric equations for constructing crank rod axial morphology. Three innovative cellular architectures (TCRC, SCRC, and CCRC) were designed, complemented by nodal rounding transition strategies to mitigate stress concentration effects. This optimization process yielded enhanced models (TCRC-ipv, SCRC- ipv, CCRC- ipv) demonstrating improved mechanical performance.

  2. (2)

    Enhanced mechanical performance: the trigonometric function-based topology optimization strategy combined with nodal fillet design significantly enhances overall structural performance. The TCRC-ipv configuration exhibits optimal comprehensive mechanical properties: compared with the reference BCC structure, it achieves 39.2% enhancement in elastic modulus, 59.4% increase in peak compressive strength, and 46.1% improvement in yield strength. Additionally, the energy absorption stress plateau elevates by 10.3%, with specific energy absorption capacity remarkably augmented by 86.1%.

  3. (3)

    These findings demonstrate that trigonometric function-based design combined with nodal transition optimization effectively addresses the inherent limitations of conventional lattice structures. The TCRC-ipv architecture shows particular promise for engineering applications requiring optimal mass-specific strength and energy absorption capabilities, such as impact-resistant structures and energy dissipation systems. This work provides both theoretical insights and practical guidelines for developing advanced multifunctional metamaterials with tunable mechanical properties.

While this study demonstrates significant advancements in lattice metamaterials, several limitations warrant consideration. The current analysis primarily focuses on quasi-static loading conditions, leaving dynamic impact responses and long-term fatigue behavior unexplored. Additionally, manufacturing constraints for complex trigonometric geometries and scalability to large-scale structures remain to be addressed. Future research should investigate multi-material hybridization, anisotropic design adaptations, and environmental factor integration to broaden applicability. Machine learning-driven optimization frameworks could further refine topology-performance relationships, while experimental validation under real-world operational scenarios would strengthen practical relevance.aterials with tunable mechanical properties.