Deep learning-based single-shot computational spectrometer using multilayer thin films

Spectrometers are powerful tools used in scientific research and industrial settings for chemical analysis¹, remote sensing², and other applications. Although spectrometers are used in various applications, they are typically confined to static environments, such as laboratories and factories, due to their bulky size, long operational times, and high costs. Due to these restrictions and practical application requirements, optical filter-based spectroscopy is emerging as a promising technique. A configuration of a filter-based spectrometer could be realized by attaching a filter array to a complementary metal-oxide-semiconductor (CMOS) image sensor. Unlike grating-based spectrometers, which require diffractive optics and motorized components, a low-cost and compact design can be realized. However, numerous narrow-bandpass filters are required to cover a wide wavelength range with high resolution. Fabricating such delicate filters is challenging, as it is complicated to integrate them into small CMOS sensor areas in an array form.

Instead of enhancing the resolution of spectrometers through the elaboration of optical filters, computational approaches have been employed in conventional spectrometers to improve resolution^3,4. Additionally, advanced computational spectrometers that employ compressed sensing (CS) theory^5,6,7 have been proposed to increase resolution further, while reducing the number of filters required^8,9. To reconstruct the unknown spectrum of incident light, these spectrometers primarily adopt iterative numerical optimization methods^10,11,12, leveraging the sparsity of light sources or their sparse representation on a particular basis. Owing to the sparse nature of signals and filter design technique under CS theory, these computational spectrometers have achieved a 7-fold improvement in spectral resolution⁹. To realize these improvements, various spectral encoders, such as quantum dot filters^13,14, etalon filters^15,16, photonic crystal slabs^17,18, van der Waals junctions^19,20,21, nanowires²², and multilayer thin films (MTFs)^23,24 have been proposed. Unlike conventional spectrometers that selectively measure specific light wavelengths, these advanced photonic structures are designed with unique transmission functions, enabling the measurement of a broad wavelength range. By adopting these photonic structures, it is possible to cover a broad wavelength spectrum with a minimal number of measurements, thereby achieving a compact device size.

Recent advances in signal reconstruction algorithms based on DL²⁵ have significantly impacted the field of CS. By adopting CS theory, sensing systems achieve faster measurements and reduced costs. Traditionally, these advantages were hindered by slow reconstruction speeds due to the reliance on complex numerical optimization algorithms. However, DL has successfully addressed these issues by replacing traditional reconstruction methods with neural networks that can efficiently reconstruct original signals^26,27,28. The integration of the CS and DL frameworks has led to improved performance and reduced computational complexity.

In this study, we propose a DL-based single-shot computational spectrometer for recovering both narrow and broad spectral ranges. As a hardware configuration of the spectrometer, we employed an MTF filter array consisting of 36 filters and a CMOS camera. To train, validate, and test our DL architecture, we collected 3,223 spectra with abundant spectral features, including both narrow and broad spectra, using combinations of color filters and a monochromator. After training, we evaluated the performance using the data that was not used in the training or validation process. The average root mean squared error (RMSE) for the test set was 0.0288. The experimental results demonstrate that the proposed DL architecture effectively reconstructs both narrowband quasi-monochromatic and broadband mixed spectra, simultaneously reconstructing them without introducing biases. The proposed spectrometer is compact, single-shot, and suitable for mass production. Furthermore, applying the DL technique can offer a high resolution, a wide working range, and fast measurement. Therefore, the proposed spectrometer can serve as a new form factor for on-site detection, such as in drink inspection, counterfeit document detection, and self-diagnosis.

The main contributions of this paper are outlined as follows:

1. 1.

   A DL-based computational spectrometer utilizing an MTF filter array in a single-shot structure is presented, offering a compact size, high resolution, wide working range, and fast reconstruction, leveraging a mass-producible MTF filter array.

2. 2.

   A diverse spectral dataset is developed to train and evaluate the DL architecture, demonstrating effective performance for reconstructing both narrow and broad spectra simultaneously.

3. 3.

   This study extends the previous work presented by Kim et al.²⁴ for spectral reconstruction.

The rest of the article is organized into multiple sections such as, “Problem restatement” , “Related work” , “Methods” , “Experimentation”, “Results and discussions”, “Comparison with conventional and modern spectrometers”, “Open research challenges”, “Conclusion”.

This study addresses the challenge of reconstructing spectral information from the intensities measured using an MTF filter array attached to a CMOS image sensor. The problem at hand is classified as an underdetermined system represented by \({y} = {A} {x} + {n}\), where the number of wavelengths exceeds the number of filters used, making it challenging to reconstruct the incident spectrum \({\bf{x}}\) from the measured intensities \({\bf{y}}\). Traditional methods²⁹ may struggle to provide unique solutions due to this limitation. To address this challenge, we consider various techniques, including regularization (L1 and L2 regularization, Tikhonov regularization, and total variation regularization)^30,31, optimization algorithms (gradient descent, the Adam optimizer, proximal gradient methods, alternating least squares, and coordinate descent)^24,32, and advanced DL-based reconstruction methods. Regularization guides solutions toward plausible outcomes, while optimization algorithms minimize a cost function to approximate unknown quantities. We focus on DL for its strong capacity to model complex data relationships. Convolutional neural networks (CNNs) excel in capturing patterns across wavelengths, enabling full-spectrum reconstruction from limited data. We propose a dense layer and U-Net architecture with residual connections to address this underdetermined problem, aiming for high accuracy, compact size, and fast operation, which is suitable for mobile and on-site spectrometry.

In this section, recent advances in computational spectrometers are introduced by focusing on their photonic structures, reconstruction methods, and demonstrations.

Zhang et al.³³ introduced a promising approach to computational spectroscopy by integrating a metasurface-based spectrometer with DL algorithms. Their snapshot computational spectroscopy tool demonstrated significant advancements in terms of size, speed, and versatility, with a compact design (100 \(\times\) 50 \(\times\) 50 mm³) and sub-nanometer resolution. The study reported spectral reconstruction accuracy of 99.4%, spectral resolution of 0.4 nm, and measurement error of 0.32 nm, which is less than its spectral resolution. In this context, this method is a competitive alternative to traditional spectrometers. However, the reliance on extensive experimental spectral data for DNN training, combined with the limited operational range from 400 to 900 nm, poses challenges to its broader applicability. Despite these constraints, the framework provides a solid foundation for developing portable and efficient spectroscopic tools, particularly when extended to ultraviolet (UV) and infrared (IR) applications and optimized for encoder designs. Overall, this study represents a critical step toward the development of miniaturized, rapid, and accurate spectroscopic technologies. However, its scalability and applicability in diverse real-world scenarios remain areas for further exploration.

Bian et al.³⁴ proposed an advanced on-chip computational hyperspectral imaging solution, which combines a broadband multispectral filter array with a spectral reconstruction network. The broadband multispectral filter array enhances light throughput by modulating incident light across a broad spectral range, thereby improving performance in low-light and long-distance imaging applications. The spectral reconstruction network efficiently reconstructs hyperspectral data cubes from compressed measurements, offering high-resolution in real-time hyperspectral imaging. The proposed sensors cover spectral ranges from 400 to 1000 nm or from 400 to 1700 nm, and achieve excellent spectral resolution and high light throughput. These sensors outperform traditional systems, especially in low-light conditions. Practical applications, including agriculture, health monitoring, and industrial automation, showcase the sensor’s high signal-to-noise ratio and broadband capabilities. Despite the promising performance, challenges such as the complex fabrication process and the need for computational resources remained unaddressed by the authors. Still, the sensors provide a compact and efficient solution for next-generation hyperspectral imaging, with applications in diverse fields.

Chen et al.³⁵ proposed an ultra-simplified computational spectrometer in their study, which employs a one-to-broadband diffraction mapping strategy using an arbitrarily shaped pinhole as the partial disperser. Their design eliminates the need for complex pre-encoding, calibration, and high-precision fabrication. It achieved spectral peak ___location accuracy better than 1 nm over a 200 nm bandwidth and a resolution of 3 nm for a bimodal spectrum. The compact spectrometer provides single-shot spectrum measurements across a broad wavelength range, making it ideal for mobile applications. It also addressed a breakthrough in broadband coherent diffractive imaging, overcoming challenges like unknown illumination spectra and detector quantum efficiency corrections. The authors’ proposed solution offers a low-cost, robust solution with great potential for broadband spectrum metrology and computational imaging.

Yako et al.³⁶ proposed a video-rate hyperspectral camera that combines CS with CMOS-compatible Fabry–Pérot filters to overcome the limitations of traditional HS imaging systems, such as low sensitivity and resolution. The proposed system achieves a sensitivity of 45% for visible (VIS) light, a spatial resolution of 3 pixels at a 3 dB contrast, and a frame rate of 32.3 frames per second (fps) at VGA resolution, comparable to standard RGB cameras. AI-based image reconstruction further accelerates the frame rate to 34.4 fps at full HD resolution. This innovation offers a compact, efficient, and high-performance solution for real-world high-speed (HS) imaging, with potential applications in consumer devices, including smartphones and drones. The system’s reliance on iterative reconstruction may pose computational challenges, necessitating further optimization for widespread adoption. Compressive sensing method for hyperspectral image reconstruction, leveraging a fast iterative shrinkage-thresholding algorithm (FISTA) for efficient recovery is observed in literature³⁷. FISTA enables improved reconstruction quality over conventional wavelet methods, especially when combined with patch-based encoding and randomized matrices¹².

Tan et al.³⁸ proposed utilizing smartphones as speckle spectrometers to achieve good results with minimal hardware. The authors’ proposed model reconstructs VIS-wavelength spectra from 470 to 670 nm within a second using a mobile computing app by injecting light into an optical fiber and capturing the resulting speckle patterns with a smartphone camera, utilizing a concept of a reversed lens. Their technique can resolve single and multi-peaked spectra, including metameric pairs. The smartphone-based spectrometer, though smaller in magnification compared to traditional microscope objectives, offers broadband operation and a resolution of 2 nm. The setup requires several components, including a fiber coupler, optical fiber, and a reversed lens, which allows it to fit within a compact module. While the technique does not surpass current grating spectrometers in performance, it introduces an alternative sensing method with the potential for further development and portability. The initial calibration may be labor-intensive, but the system shows significant hope for overcoming traditional spectrometer size limitations.

Bielczynski et al.³⁹ presented a novel, portable, handheld Vis–NIR spectrometer capable of non-invasive plant pigment quantification, showing promise for advanced precision agriculture. The device demonstrated impressive accuracy in estimating anthocyanin and chlorophyll contents, achieving correlation coefficients of 0.84 and 0.77, respectively, with conventional gold-standard methods. The authors’ proposed design integrates wireless data transfer and dual preprogrammed methods for pigment quantification, offering cost-effectiveness and ease of use. Their results validate the spectrometer’s reliability for indoor applications and its potential for routine plant health monitoring. But, the performance under outdoor conditions remains to be validated. Moreover, the limited spectral range restricts its utility to specific vegetation indices, leaving room for further improvements to broaden its capabilities. This work represents a significant step toward developing affordable and portable plant monitoring tools, but highlights the need for expanded applications and rigorous field testing to facilitate widespread adoption.

Huang et al.¹⁵ introduced a computational spectrometer using etalon filters. They combined a 10 \(\times\) 10 array of etalon filters with a CCD array as the hardware configuration. By varying the thickness of the cavity layer, each etalon filter achieved a unique transmittance pattern. The L1-norm minimization method¹⁰ was employed to reconstruct the input spectra from measurements of the etalon array. The results were demonstrated by reconstructing the transmitted light from bandpass filters and the spectra from the laser source.

Wang et al.¹⁷ utilized a photonic crystal slab to configure spectral encoders. Unique transmittance patterns were obtained by varying structural parameters, including slab size, lattice shape, and the distance between holes. The input spectra were reconstructed by minimizing regularized squared error with non-negativity constraints. They demonstrated the efficacy of their method by reconstructing monochromatic lights such as LEDs, HeNe lasers, and the outputs of a monochromator.

Li et al.¹³ employed quantum dot filters, varying the ratio of oleic acid to precursor, to achieve unique transmittance patterns. The Total Variation (TV) algorithm was used to reconstruct the input spectra. They demonstrated their results by reconstructing the reflected light from objects such as a watermelon, grape, and spinach. Similarly, Li et al.⁴⁰ improved the CASSI system with a dual-camera design, utilizing structural information from a grayscale camera along with TwIST¹¹ and TV regularization to enhance hyperspectral image reconstruction. This approach significantly improved image quality and reduced runtime, achieving a PSNR gain of 8.99 dB, a structural similarity (SSIM) increase of 0.0757, and a spectral angular mapper (SAM) reduction of 0.1987.

Kim et al.^23,24 designed MTFs with unique transmittance patterns by randomly omitting the intermediate layers from a reference MTF with 19 layers. The L1-norm minimization method¹⁰ was utilized to recover input signals. Their demonstrations included reconstructing monochromatic lights from LEDs and outputs of a monochromator. Additionally, in²⁴, they showed hyperspectral imaging of an LED matrix using a pinhole camera model. Despite these advancements, demonstrations of computational spectrometers have been limited to a narrow range of examples and types, including monochromatic lights, LEDs, and laser sources. Still, the proposed MTF filter array, with a compact footprint of 4.5 \(\times\) 4.5 mm² and operating in the 500–850 nm wavelength range, enables hyperspectral imaging (HSI) in miniaturized devices, such as Magnetic-Assisted Capsule Endoscopy (MACE). Integrated with a CMOS sensor, this MTF filter array allows selective spectral filtering for tissue differentiation. It supports computational algorithms like SAVE (Spectrum-Aided Visual Enhancer) to convert White Light Images (WLI) into enhanced images similar to Narrow Band Imaging (NBI), enabling improved mucosal visualization and early cancer detection in resource-constrained systems^41,42.

The numerical optimization methods^10,11,12 used for spectra reconstruction assume that all signals in nature are sparse or can be sparsely represented in a specific ___domain. However, not all spectra can be sparsely represented using a fixed sparsifying basis, resulting in limitations to their representation capability. Moreover, these approaches perform well for precisely measured signals and handcrafted parameters predetermined through prior information, such as spectral sensitivities, sparsifying bases, line shapes, and full widths at half maximums (FWHMs) of spectra. Thus, the reconstruction performance of a spectrum could be biased depending on the variations in noise levels and predetermined parameters. These limitations hinder the use of computational spectrometers for accurately recovering various waveforms of spectra.

To mitigate these issues, researchers have employed DL methods as alternatives to numerical optimization methods for computational spectrometers. Kim et al.⁴³ utilized a convolutional neural network (CNN) to recover input spectra from measurements taken by a proposed MTFs-based spectrometer. They trained their network using a synthetic dataset created by combining multiple Gaussian distribution functions with varying FWHMs, peak locations, and amplitudes. Their simulation demonstrated that the reconstruction results of the proposed method outperformed conventional numerical optimization methods¹⁰. In a subsequent study⁴⁴, they introduced ResCNN to improve the reconstruction results further. They trained and evaluated the network using synthetic datasets with Gaussian and Lorentzian distribution functions, as well as spectral datasets such as the US Geological Survey (USGS) spectral library version 7⁴⁵ and the Munsell colors glossy spectral dataset⁴⁶. Performance was validated through simulation experiments. Wen et al.⁴⁷ proposed a DL-based spectrometer using dielectric films. They trained the reconstruction network with a synthetic dataset featuring Gaussian distribution functions and spectral datasets^48,49. Their reconstruction performance was demonstrated with simulated spectra and monochromatic lights. Brown et al.⁵⁰ proposed a DL-based spectrometer using plasmonic encoders. Unlike the methods proposed by Kim et al.^43,44, they did not use prior knowledge of filter functions to initialize the first layer of the reconstruction network. To train and evaluate their spectrometer, they collected an experimental dataset using a programmable supercontinuum laser, comprising 60,644 pairs of spectra with varying numbers of spectral peaks and CS measurements from the proposed spectrometer. Initially, the spectrometer performed well for 15 hours of continuous experimentation; however, its performance degraded over time due to environmental variations. To address this issue, they captured additional data pairs and applied transfer learning techniques. For DL-based computational spectrometers, demonstrating the reconstruction results of raw measurements can be hindered by ___domain shift, which occurs when the distribution of simulated measurements differs from that of real measurements. This discrepancy arises because the datasets used to train reconstruction networks do not include the actual measurement noise of sensors when measuring input lights. Thus, the difference between training datasets and real measurements has a significant impact on the generalizability of the reconstruction network.

Zhang et al.^51,52 combined DL and CS techniques to enhance the performance of quantum dot spectrometers. In⁵¹, instead of directly applying a neural network to recover the input signal, they first used numerical optimization algorithms to recover the signals. Then they applied their neural network to refine the results. Conversely, in⁵², a neural network was used to denoise the CS measurements before applying numerical optimization to recover the input signals. They trained and evaluated the neural network using a spectral dataset⁴⁶ and an experimental dataset comprising 704 pairs of measurements from the proposed spectrometer and spectra obtained using various combinations of colored plastics. By integrating DL into the CS framework, they improved the results of CS recovery algorithms. However, the inherent limitations of numerical optimization methods remain.

In this work, to address the issues mentioned above, we propose a DL-based single-shot computational spectrometer using MTFs. Our DL architecture is trained on a dataset of 3223 spectra and raw measurements obtained through various combinations of color filters and a monochromator, resulting in an abundance of spectral features. Our experiments demonstrate that the proposed DL architecture effectively reconstructs both narrow and broad spectra, benefiting from the richness of our dataset. Additionally, we showcase the reconstruction of transmitted spectra through commercial drinks, highlighting the spectrometer’s suitability for on-site detection applications such as drink inspection, counterfeit document detection, and self-diagnosis.

The proposed method comprises three main components: fabrication of the MTF filter, image acquisition, signature reconstruction, and identification using DL.

Fabrication of the MTF filter array

Unlike the etalon filters (see “Related work”), which are fabricated by varying the thickness of interspacing dielectric layers, MTF filters are fabricated by modifying both the number of layers and their thicknesses. MTF filters with unique transmission functions are achieved by alternately depositing two materials with varying thicknesses. A total of 36 MTF filters with distinct transmission characteristics were fabricated by selectively omitting specific layers using shadow masks during the deposition process. The omission of an intermediate layer causes the upper and lower layers to merge, forming a single layer with a modified thickness. The designed layer thicknesses for the MTF filters are provided in Table 1. The filter array was fabricated using wafer-level stencil lithography with shadow masks, which allows for the stacking of alternating layers of titanium dioxide (TiO₂) and silicon dioxide (SiO₂), enabling scalable, reproducible, and mass-produced fabrication. TiO₂ and SiO₂ act as the low and high refractive index materials, respectively. The refractive indices for TiO₂ and SiO₂ are approximately 2.6 and 1.45 at 600 nm, respectively. As a result, 169 identical filter arrays were fabricated on a single wafer²⁴.

These films were deposited onto a borosilicate glass wafer, which has a refractive index of approximately 1.472 at 588 nm, using shadow masks to define specific areas for deposition. The TiO₂ layers were deposited using direct current (DC) magnetron sputtering, a technique for depositing thin films onto a substrate by bombarding a target material with high-energy ions, causing atoms to be ejected and deposited as a thin layer on the substrate^53,54,55,56. A Ti target was sputtered in a mixed gas flow of 188 sccm (standard cubic centimeters per minute) argon (Ar) and 12 sccm oxygen (O₂), with the DC power set to 700 W. Shadow masks ensured that TiO₂ was deposited only on designated regions of the wafer. For the SiO₂ layers, radiofrequency (RF) magnetron sputtering was used. A Si target was sputtered in a gas flow of 185 sccm Ar and 15 sccm O₂, with RF power at 300 W. Different shadow masks were used to control the deposition patterns and thicknesses of the SiO₂ layers. The alternating deposition of TiO₂ and SiO₂ layers was repeated 17 times, with shadow masks changed accordingly to achieve the desired multilayer structure.

Individual depositions of TiO₂ were performed ten times, while SiO₂ was deposited nine times. Following the completion of thin film deposition, the surface of the thin films was coated with a photoresist. Germanium (Ge) was then deposited across the entire wafer area using an e-beam evaporator. The lift-off process was carried out by soaking the deposited wafer in acetone, allowing the photoresist to dissolve. As the photoresist was removed, the Ge layer deposited on top of it was lifted off and washed away. This process resulted in the formation of a square Ge grid with a size of 400 \(\upmu\)m and a spacing of 300 \(\upmu\)m. The Ge grid was designed to separate the MTF filters and prevent incident light from interfering with them. Finally, the wafer underwent a cleaning process before being diced to produce the MTF filter arrays.

After fabrication, the filters with unique transmission functions were obtained by stacking multiple layers of thin films with varying numbers and thicknesses. These carefully designed MTF filters enable the capture of broad-spectrum light across a wide range of wavelengths. Integrated with a complementary metal-oxide-semiconductor (CMOS) sensor, the MTF filter array serves as a fundamental component in the proposed computational spectroscopy system^57,58,59.

It is worth mentioning that using TiO₂ as a high-refractive-index material instead of SiNx, which was used in previous work²³, could reduce the number of layers required to achieve the unique transmission functions. Moreover, by utilizing stencil lithography, the MTF filter can be fabricated through a simplified process that eliminates the need for an etching step.

SEM analysis of the MTF filter

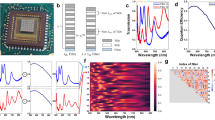
The Ultra-High-Resolution Field Emission Scanning Electron Microscope (UHR-FE-SEM, model Verios 5 UC) image in Fig. 1a provides detailed elemental information. Energy Dispersive X-ray Spectroscopy (EDX) analysis of the fabricated Ge/SiO₂/TiO₂ multilayer thin films on borosilicate glass substrates revealed trace amounts of Na and C. The presence of Na is attributed to possible ion diffusion from the borosilicate substrate, which inherently contains alkali metals. The detected carbon is likely due to surface contamination from ambient exposure or handling, a common occurrence in surface-sensitive characterization techniques.

SEM analysis of the fabricated MTF filter array (a) elemental view under UHR-FE-SEM, (b) surface view, (c) cross-sectional SEM image of MTF filter 36.

Full size image

Figure 1b, also captured using the UHR-FE-SEM (Verios 5 UC), shows the surface morphology of the MTF filter array. Minimal measurement deviations are observed, ranging from 0.0032 to 0.0075 \(\upmu\)m. The SEM image displays each filter unit as approximately 392.5 \(\times\) 392.5 \(\upmu\)m², while the designed dimensions are 400 \(\times\) 400 \(\upmu\)m². Similarly, the inter-filter spacing is measured as 296.8 \(\upmu\)m against the intended 300 \(\upmu\)m. The deposited Ge layer is designed to cover an area of 500 \(\times\) 500 \(\upmu\)m, whereas the measured dimension from the SEM image is approximately 493.3 \(\times\) 493.3 \(\upmu\)m.

Figure 1c shows a uniform deposition of SiO₂/TiO₂ layers both within a single filter and consistently across multiple filters. This cross-sectional image was obtained using the Hitachi Focused Ion Beam (FIB) system, model NX5000, which also integrates SEM imaging functionality. Although attempts were made to image the cross-section with the UHR-FE-SEM (Verios 5 UC), the NX5000 FIB system yielded superior cross-sectional contrast and clarity for our sample. Figure 1c specifically corresponds to Filter 36 and confirms both uniformity in deposition and consistency in filter width.

The fourth layer in this cross-section appears to be the thickest, as it combines Layer 4 (SiO₂), Layer 5 (omitted TiO₂), and Layer 6 (SiO₂). According to Table 1, the individual thicknesses are 188 nm (SiO₂), 0 nm (TiO₂), and 109 nm (SiO₂), summing to a theoretical total of 297 nm. Due to the omission of TiO₂ (Layer 5), this segment represents a merged SiO₂ region. The SEM-measured thickness for this combined region is 249 nm, indicating a negligible difference of 48 nm within the acceptable measurement tolerance. The SEM system’s correction error is noted to be 0.0791 \(\mu\)m, supporting the validity of the measured thickness values.

A total of eleven distinguishable layers were observed instead of the expected 19 layers. This is due to the apparent merging of layers 4 and 6, 8 and 10, and 13 and 15, along with the omission of layers 5, 9, 14, 16, and 17, possibly during deposition or imaging. The analysis excluded regions above and below the yellow rectangle in the SEM image. The top region corresponds to the filter surface, while the bottom includes the base layer of Ge and borosilicate wafer, which exhibit electron charging effects typical of insulating substrates during SEM imaging, and this is observed as a deflected bright region. Additional thickness measurements presented in Fig. 1c further confirm the precision and consistency of the multilayer deposition across the filter structure.

Problem formulation: a system model

The proposed study focuses on reconstructing spectral information from single-shot intensity measurements obtained through an MTF filter array on a CMOS sensor, a key function of the proposed DL-based computational spectrometer. So, for problem formulation, let, \({y}\) represents the vector of intensities measured by the CMOS sensor, \({x}\) denotes the vector of unknown incident spectrum values at different wavelengths, \({T}\) be the transmission matrix of the MTF filters, \({Q}\) be the diagonal matrix representing the quantum efficiency of the CMOS sensor, and \({n}\) be the measurement noise of system. The relationship between the measured intensities \({y}\) and the incident spectrum \({x}\) is given by Equation 1.

where:

represents the spectrum at different wavelengths \(\lambda _j\) (with \(j = 1, 2, \dots , N\)).

where \(T_i(\lambda _j)\) is the transmission function of the \(i\)-th MTF filter at wavelength \(\lambda _j\), and there are \(M\) filters.

where \(Q(\lambda _j)\) is the spectral response (quantum efficiency) of the CMOS sensor at wavelength \(\lambda _j\). If the sensor had interference between wavelengths (e.g., if detecting light at \(\lambda _1\) affected the response at \(\lambda _2\)), then \(Q\) would contain nonzero off-diagonal elements. However, in a CMOS sensor, each wavelength \(\lambda _j\) has an independent response, so only the diagonal elements are nonzero; this is why \(Q\) is taken to be a diagonal matrix. It simplifies computation in spectral reconstruction. Since \(Q\) is diagonal, multiplying it with \(x\) (the incident spectrum) is straightforward.

This means that each wavelength’s intensity is simply scaled by its respective quantum efficiency, making calculations more efficient.

Each element \(A_i(\lambda _j)\) is given as \(A_i(\lambda _j) = T_i(\lambda _j) Q(\lambda _j)\). This represents the combined transmission of the \(i\)-th MTF filter and the spectral response of the CMOS sensor at wavelength \(\lambda _j\). So, by combining the transmission matrix \({T}\) and the spectral response matrix \({Q}\) into a sensing matrix \({A}\), the system Equation 1) simplifies to Equation 2.

Here, \({y}\) represents the intensities recorded by the CMOS sensor for each of the \({M}\) filters.

The following section discusses how a DL algorithm, U-Net, based on convolutional neural networks (CNN), is integrated into the system. The DL-based architecture processes the captured intensities to reconstruct the whole spectrum with high accuracy, leveraging the tailored properties of the MTF filter array to enhance resolution and minimize errors.

DL-based computational spectroscopy

The DL-based computational spectroscopy leverages neural networks to reconstruct spectra from compressed or indirect measurements, facilitating the design of compact, low-cost spectrometers. Unlike traditional spectrometers that rely on precise optical components to directly measure specific wavelengths, DL-based systems utilize broad-spectrum data captured through photonic structures such as multilayer thin films or filter arrays. The relationship between the measured intensities \({y}\) and the true spectrum \({x}\) is already derived as \({y} = {A} {x} + {n}\) (Eq. 2), where \({A}\) denotes the system’s response matrix, and \({n}\) represents noise. In this context, a U-Net architecture is employed to approximate the mapping between the captured intensities \({y}\) and the reconstructed spectrum \(\hat{{x}}\) as Eq. (3):

where \(\theta\) comprises the trainable parameters (weights and biases) of the U-Net model.

To evaluate the reconstruction performance, the RMSE is considered over Mean Squared Error \(MSE = \frac{1}{n} \sum _{i=1}^{n} ( x_i - {\hat{x}}_i )^2\) because is in the same units as the target variable, making it easier to interpret. Additionally, RMSE penalizes larger errors more due to the squaring of differences, making it more sensitive to outliers. Because of these characteristics, it is utilized as the loss function given by Eq. (4), which quantifies the difference between the ground truth (GT) spectra \({x}\) and the reconstructed spectra \(\hat{{x}}\):

The optimization of the U-Net parameters is performed using the Adam optimizer⁶⁰, which updates the parameters based on the gradient of the RMSE loss function:

The first moment \(m_t\) and the second moment \(v_t\) of the gradients are updated as follows:

where \(\beta _1\) and \(\beta _2\) are decay rates for the first and second moments, respectively. The bias-corrected moment estimates are given by:

Finally, the model parameters are updated as follows:

where \(\eta\) is the learning rate, and \(\epsilon\) is a small constant used to prevent division by zero. This DL-based approach not only enhances spectral resolution but also accelerates measurement processes, resulting in smaller, mobile-friendly devices that are suitable for on-site applications.

Experimental setup

Figure 2a depicts a schematic of our experimental setup. A collimating beam is divided into two beams after passing through a color filter and a long pass filter. A spectrum of a single split beam was measured using a commercial spectrometer (Black-Comet, StellarNet), which served as the GT. The other beam was fed into the MTF filter array and modulated by the transmission functions of the filters. The modulated intensities of the beam were captured with a CMOS camera (EO-1312M, Edmund optics) as a monochrome image with a single exposure. By connecting the spectrometer and CMOS camera to a laptop using universal serial bus (USB) cables, we simultaneously collected a monochrome image of the GT spectrum. We collected a dataset comprising 3223 pairs of GT spectra and corresponding monochrome images. The dataset comprised 350 narrow spectra with an FWHM of 4 nm and 2873 broad spectra. To collect narrow spectra, we used a halogen lamp (KLS-150H-LS-150D, Kwangwoo) and a monochromator (MMAC-200, Mi Optics). A beam from the halogen lamp was fed into the monochromator, generating a narrow spectrum. By changing the peak locations of narrow spectra from 500 to 849 nm with 1 nm spacing, we measured 350 spectra. To collect broad spectra, we generated various shapes of spectra using color filters (Color filter booklet, Edmund optics) as shown in Fig. 2a. A beam from the halogen lamp was modulated by color filters, generating a broad spectrum. By changing combinations of color filters, we measured 2873 broad spectra of various waveforms.

The captured monochrome image had a size of 1280 \(\times\) 1024 pixels, and the GT spectrum comprised a signal of 350 elements measured over the wavelength range, \(\lambda\), of 500–850 nm with a 1 nm spacing. As shown in Fig. 2b, we extracted 36 intensities from the filter array in the monochrome image. These intensities were fed into the DL architecture to reconstruct the spectra. Figure 2c shows examples of reconstructed test spectra using the trained DL architecture. The RMSE between the GT spectra (dashed black lines) and reconstructed spectra (solid blue lines) was used to evaluate the reconstruction performance. The reconstructed spectra were consistent, as indicated by the RMSE values listed in the upper left corner of each plot in this figure.

DL-based single-shot computational spectrometer. (a) Schematic of the experimental setup. A collimated beam from a light source is split into two beams by a beam splitter (BS) after passing through a color filter and a long pass filter (LPF). The spectrum of a beam is measured using a commercial spectrometer. The other beam is modulated by the MTF filter array and captured as an image by a CMOS camera. (b) DL architecture comprises a dense layer and a U-Net backbone architecture with residual connections. (c) Examples of recovered test spectra using the trained DL architecture. Dashed black lines represent GT spectra measured using a commercial spectrometer. Solid blue lines represent reconstructed spectra using the proposed spectrometer.

Full size image

Figure 3a shows a photograph and an optical microscope image of the fabricated MTF filter array. The MTF filter array had a 6 \(\times\) 6 square grid shape. Each MTF filter had a size of 400 \(\times\) 400 \(\upmu\)m², and the filters were 300 \(\mu\)m apart. The entire size of the filter array was 4.5 \(\times\) 4.5 mm². Each MTF filter had its own color due to its unique transmission function, T, and the color was uniform across each filter. Figure 3b shows examples of spectral sensitivities of the fabricated filters with the CMOS camera. Unlike bandpass optical filter-based spectrometers, the MTF filter-based computational spectrometer modulates the spectrum of incident light in a wide wavelength range with broad spectral sensitivities. Therefore, a few filters are sufficient to measure the spectral information of the incident light uniquely. Figure 3c shows the measured data. The CMOS camera and halogen lamp were calibrated to extract intensities from monochrome images in the range of 0–255, and the CMOS camera’s auto contrast function was turned off. The spectra were measured with a fixed integration time. A single pixel of the CMOS camera had a size of 5.2 \(\times\) 5.2 \(\upmu\)m². Underneath each filter, there were approximately 70 \(\times\) 70 pixels. From the monochrome image of the MTF filter array illuminated by the incident light (left), 36 measured intensities were extracted by taking the average value of central 40 \(\times\) 40 pixels of each filter as one measured intensity. For pixels at the filter boundary, there might have been a misalignment during fabrication, and a beam passing through a filter could overlap another beam in experiments. Therefore, we excluded pixels on the filter boundaries. Three examples of measured intensities are plotted in the center of Fig. 3c, corresponding to the GT spectra on the right of Figure 3c.

Fabricated MTF filter array for single-shot computational spectroscopy. (a) Photograph (left) and optical microscope image (right) of the fabricated MTF filter array. (b) Examples of spectral sensitivities of MTF filters with the CMOS camera. (c) Examples of measured data include a monochrome image of the MTF filter array (left), some extracted intensities from monochrome images (center), and the GT spectra of incident lights corresponding to the extracted intensities (right).

Full size image

DL-architecture

The proposed DL architecture consists of a dense layer and a U-Net backbone⁶¹ with residual connections. Before entering the U-Net backbone, 36 measured intensities were extended to a size of 350 by applying a linear transformation using the dense layer. This extension enabled the U-Net backbone to become deeper, which could be beneficial for feature extraction and reconstruction. The U-Net backbone comprises a contracting path and an expansive path. In the first stage of the contracting path, extended intensities go through the main branch that comprises a one-dimensional (1D) convolution (Conv), 1D batch normalization (BaN), rectified linear unit (ReLU), and Conv. As a shortcut branch, the extended intensities go through a Conv. The two branches are added to form a residual connection. The output of the residual connection becomes the input of the next stage of the contracting path. Like the first stage, the input of the second stage of the contracting path goes through the main and residual branches and becomes a residual connection. In the main branch, we reduce input size by a factor of 2 and double the number of feature maps using two sets of BaN, ReLU, and Conv. We used Conv with stride 2 to reduce the size. In the residual branch, the input goes through Conv with stride 2 and BaN. The output of the contracting path is upsampled by applying a 1D transposed convolution (ConvTrans). It is concatenated with the corresponding feature maps from the contracting path to serve as the input to the first stage of the expansive path. The input is routed through the main and residual branches and then summed. These upsampling, concatenation, and summation were repeated four times. The output of the expanding path passes through a convolutional layer to become a signal with 350 elements. Finally, the output signal and extended intensities were added to become a reconstructed spectrum.

By leveraging the summation between the extended intensities and the output signal of the U-Net backbone, the U-Net backbone learns the residue between the extended intensities and ground truth spectra. The learning residue is more effective than directly learning target spectra⁶². Residual connections in the U-Net backbone prevent the gradient vanishing problem, which can stop the update of learnable parameters in a deep learning (DL) architecture during the training process⁶³. Additionally, it is possible to enhance the depth of the DL architecture.

Training and testing

The proposed DL architecture was trained on our dataset, minimizing a mean squared error between the reconstructed and GT spectra. We randomly divided the dataset into training, validation, and test sets, each containing 2576, 324, and 323 pairs, respectively. Before training the DL architecture, we performed data preprocessing. The measured intensities from a monochrome image were divided by the maximum value of intensities, and the corresponding GT spectrum was min-max normalized. Therefore, we trained the DL architecture to reconstruct the unknown spectra in the normalized intensity form.

Using the validation set, we monitored the performance of the DL architecture for every epoch during the training process. As such, we can select the number of epochs before overfitting occurs. The selected number of epochs was 400. The batch size and learning rates were 8 and 0.0005, respectively. The training process was completed within \(\sim\)1.4 hours, and reconstruction results on the test set were obtained within \(\sim\)2 seconds. The DL architecture was built on the PyTorch framework⁶⁴. The training and testing were performed on a computer equipped with an Intel Core i7-5820K CPU and an NVIDIA GeForce RTX 2060 graphics processing unit.

Reconstruction of test spectra

Figure 4 shows the reconstruction results of the proposed computational spectrometer. The RMSE distribution of 323 test spectra is as shown in the histogram in Fig. 4a. Blue and orange boxes represent the RMSE distribution of 33 narrow and 290 broad spectra, respectively.

Three examples of the best and worst spectral reconstructions are shown in Fig. 4b, c, respectively. Dashed black lines represent GT spectra and solid-colored lines represent the reconstructed spectra. The RMSE value is written in the upper left corner of each graph. The error, defined as \(\hat{{x}}-{x}\), is plotted at the bottom of each graph.

The average RMSE of all test spectra was 0.0288. The average RMSEs of the narrow and broad spectra were 0.0158 and 0.0303, respectively, indicating better results in the reconstruction of the narrow spectra. As shown in Fig. 4b, the reconstructed spectra of the best examples were almost the same as the GT spectra. The reconstructed spectra exhibited abrupt changes in narrow peaks, with peak positions matching well. Moreover, the reconstructed spectra of the worst examples did not accurately reflect the waveform changes of the GT spectra. Excluding the best and worst cases, the DL architecture accurately recovered the test spectra, as shown in the RMSE distribution in Fig. 4a.

Result of spectral reconstructions. (a) Histogram of the RMSE distribution for the test set; the average RMSE is 0.0288. Blue and orange boxes represent the RMSE distribution of narrow and broad spectra, respectively. (b) Three examples of the best spectral reconstructions. (c) Three examples of the worst spectral reconstructions. Dashed black lines represent GT spectra. Solid blue and orange lines represent the reconstructed spectra. Solid light gray lines at the bottom of each graph represent the error.

Full size image

Figure 5 shows spectral reconstructions of narrow spectra with an FWHM of 4 nm in the test dataset. We evenly present the reconstruction results from the test set according to peak locations. The peak locations of GT spectra in Fig. 5a–f are 520, 588, 655, 707, 768, and 834 nm, respectively. Solid colored lines represent the reconstructed spectra, and dashed black lines represent GT spectra. The RMSE values of the reconstructions are 0.0124, 0.0133, 0.0149, 0.0177, 0.0144, and 0.0198, respectively. The reconstructed spectrum exhibits spectral features characterized by narrow peaks with significant intensity changes near the peak locations and no intensity changes elsewhere, except at the peak locations. The reconstructed spectra matched the steep increment of narrow peaks from the enlarged inset graphs. The peak ___location differences between the reconstructed and GT spectra are within 1 nm, and the FWHMs of the reconstructed spectra are within 5 nm. The DL model was able to accurately reconstruct the narrow spectral peaks from the test dataset, regardless of their ___location within the spectrum.

Spectral reconstructions of narrow spectra in the test set. Solid colored lines represent recovered spectra. Dashed black lines represent GT spectra. (a) 520 nm. (b) 588 nm. (c) 655 nm. (d) 707 nm. (e) 768 nm. (f) 834 nm. The RMSE between the reconstructed and GT spectrum is written in the upper left corner of each graph. Solid light gray lines at the bottom of each graph represent the error.

Full size image

Spectral reconstructions of continuous spectra in the test set. Solid orange lines represent the reconstructed spectra. Dashed black lines represent the GT spectra. (a)–(f) An example of the spectrum at the second, third, fourth, fifth, and sixth intervals of the RMSE histogram, respectively. Solid light gray lines at the bottom of each graph represent the error.

Full size image

Figure 6 shows spectral reconstructions of broad spectra in the test set. According to the interval of the histogram (Fig. 4a), we present the reconstruction results of broad spectra. Solid orange lines represent reconstructed spectra, and dashed black lines represent GT spectra. The RMSE values of the reconstructions in Fig. 6a–f are 0.0164, 0.0231, 0.0324, 0.0412, 0.0469, and 0.0523, respectively. The reconstructed spectra matched well with the spectral features of the GT spectra. For example, a broad background band with multiple peaks is well-expressed in Fig. 6a–c, and spectral valleys are well-represented in Fig. 6d, e. The reconstruction of the flat-top shape in Fig. 6f matches well with the GT spectrum. In addition, from the error, the differences between the reconstructed and GT spectra are within 0.1. Overall, the proposed DL architecture represents various spectra features of the broad spectra.

From Fig. 4, 5 and 6, we demonstrate the spectral reconstruction performances of the proposed DL architecture. The DL architecture can recover narrow and broad spectra in fine detail. In particular, it could be overfitted to broad spectra due to the different proportions of narrow and broad spectra. However, narrow spectra can be well represented through the depth of layers and the numerous learnable parameters of the DL architecture. Unlike numerical optimization methods that require spectral sensitivities, such as transmission functions and sparsifying bases, the proposed DL architecture does not require prior information to recover unknown spectra. The DL architecture requires a dataset for training, but it provides the reconstruction result end-to-end after training is complete. In addition, the proposed DL architecture reconstructed 323 test spectra within \(\sim\)2 s, which is not possible using numerical optimization methods. This is a significant advantage over numerical optimization methods, which require human intervention for precise parameter tuning in spectral reconstruction.

Reconstructions of the transmission spectra of five drinks. (a) Photograph of drink samples of five colors: pink, yellow, light yellow, blue, and purple. (b)–(f) Reconstructed transmission spectra of drinks. Dashed black lines represent GT spectra, and solid lines, except for light gray, represent the reconstructed transmission spectra using the DL architecture. Solid light gray lines represent the reconstructed transmission spectra using the numerical optimization method, sparse recovery (SR).

Full size image

Reconstruction of drink spectra

We further explored the spectral resolving ability of the proposed computational spectrometer with commercial drinks. Reconstructions of transmission spectra for five drinks were performed using the trained DL architecture. The samples of five drinks were prepared using disposable polystyrene cuvettes with a capacity of 4 ml (Fig. 7a). The monochrome images and transmission spectra of drinks were measured using the experimental setup depicted in Figure 2a by replacing color filters with drink samples. From the monochrome image, we extracted 36 intensities and fed them into the trained DL architecture, obtaining the reconstruction result. The reconstructed transmission spectra of five drinks are illustrated in Fig. 7b–f. Dashed black lines represent GT spectra, and solid lines represent the reconstructed spectra except for light gray. Solid light gray lines represent the reconstructed transmission spectra obtained using the numerical optimization method of sparse recovery. We only used the trained DL architecture without human intervention to reconstruct the transmission spectra. On the other hand, we required prior information on spectral sensitivities, the optimal sparsifying basis, and numerous interventions to determine the best parameters for sparse recovery. The RMSE for each drink is written in the upper left corner of the graph. The average RMSE of the reconstructed transmission spectra using the DL architecture is 0.0554. The average RMSE using sparse recovery is 0.1648. As shown in Fig. 7, the reconstruction results of the DL architecture match well with the GT spectra. However, the reconstructed spectra from sparse recovery differed significantly from the GT spectra. The difference in reconstruction performance between the DL architecture and sparse recovery appears to be due to background noise. Because the DL architecture is trained using data with background noise, it shows stable reconstruction performance over the noise. However, sparse recovery is sensitive to noise and works well for precisely measured intensities.

Key considerations in practical scenarios

Environmental factors

In the current experimental setup (see “Experimental setup”), our computational spectrometer is deployed in controlled laboratory conditions, whereas deploying such a spectrommeter outside the controlled environment in real scenarios may introduce challenges related to temperature fluctuations, humidity, optical scattering, and external noise, all of which can affect the optical response of the multilayer thin film (MTF) filters and consequently the measured spectral signal. In our proposed system, the MTF filter array is fabricated using alternating layers of TiO₂ and SiO₂, deposited via DC and RF magnetron sputtering under tightly controlled gas flows and power settings. The resulting dielectric multilayers exhibit robust and stable interference-based transmission spectra. Moreover, both TiO₂ and SiO₂ are chemically inert and thermally stable upto 400 °C^65,66, mainly when deposited on borosilicate glass, which further enhances resistance to environmental stress⁶⁷. Argon was used as the inert carrier gas during sputtering to prevent unwanted chemical reactions, while oxygen was added precisely to control stoichiometry, ensuring reproducibility across filter batches. However, despite these fabrication advantages, it is believed that environmental variables may still cause slight shifts in the filters’ transmittance due to humidity-induced changes in refractive index or thermal expansion, which can be modeled as a perturbation. To capture the influence of environmental factors, the transmission matrix of the proposed model Equation 1 can be modeled as:

where \(T_0\) is the nominal filter transmission matrix under standard conditions, and \(\Delta T \in {\mathbb {R}}^{M \times N}\): is an environment-dependent perturbation. Specifically, \(\Delta T\) is modeled as a function of key physical variables: temperature (\(T_{\text {env}}\)), relative humidity (\(H\)), optical scattering or misalignment (\(S\)), and ambient reflectance or stray light (\(R\)). These variables can affect the refractive indices and physical thicknesses of the dielectric layers, thereby altering the spectral characteristics of the filters. As a result, the effective sensing matrix becomes:

Substituting into the forward model yields:

The perturbation term \(\Delta A x\) represents an environment-induced distortion in the measurement, which varies depending on both the external conditions and the input spectrum. To mitigate the impact of such variations, we can adopt two complementary strategies. First, we can simulate perturbations \(\Delta A\) during the training phase of our DL-based reconstruction model, enabling the network to learn robust representations of a wide range of environmental conditions. These synthetic perturbations are intended to be derived from empirical measurements and physics-based models of thin-film behavior under varying temperature and humidity conditions. Second, we plan to integrate environmental sensors, such as miniature temperature and humidity sensors, into the spectrometer housing. These sensors allow for real-time estimation of the environmental state, which can be used to approximate \(\Delta A\) and perform a compensation step before reconstruction:

This correction pipeline an enhance the reliability of spectral reconstruction under fluctuating conditions, providing a foundation for adapting the system to uncontrolled outdoor or industrial environments. By modeling and addressing the effects of environmental perturbations on the MTF filter array, an extended version of the proposed model may improve the spectrometer’s applicability beyond laboratory settings, ensuring robust and accurate operation in real-world scenarios. For the proposed MTF-filter-based spectrometer, incorporating the known system matrix \({\bf{A}}\) into the loss function or embedding it as a layer within the network architecture (e.g., \(\hat{{\bf{x}}} = f_{\theta }({\bf{A}}, {\bf{y}})\)) can help directly enforce the physical measurement model during training. This hybrid strategy ensures that the reconstructed spectra remain consistent with both the learned representations and the known optical characteristics of the TiO₂/SiO₂ multilayer thin-film filter stack. Even if our MTF filter arrays are only tested in a laboratory environment, which is very mild, the robustness of TiO₂ and SiO₂ films deposited by PECVD (Plasma-Enhanced Chemical Vapor Deposition) may adapt to the complex application environment under various environments (temperature, humidity, light illumination conditions, etc.)⁶⁸.

Spectra out of learning distribution and overfitting

If the DL model is not well-trained with diverse data, it may underperform when faced with spectra that fall outside the training distribution, meaning. When a trained model encounters spectra outside its training distribution, its reconstruction accuracy may drop due to poor generalization. To address this, uncertainty estimation methods like Monte Carlo Dropout can help identify unreliable predictions^69,70. Monte Carlo Dropout is highly effective for DL models, especially in scenarios involving uncertainty, limited training data, or out-of-distribution inputs. By enabling dropout during inference, it provides not just predictions but also confidence estimates, helping detect when the model is unsure. This is crucial in applications such as spectroscopy, where unseen spectral patterns may emerge. Unlike traditional deterministic models, MC Dropout provides a scalable Bayesian approximation without requiring modifications to the network architecture. Similarly, to improve robustness against spectra outside the training distribution, a Spectral Information Divergence (SID)-based sparse representation classifier can be employed. Unlike traditional L2-norm measures, SID evaluates the probabilistic divergence between spectral signatures, preserving spectral characteristics more effectively and enhancing generalization to unseen spectral patterns.⁷¹. Out-of-distribution (OOD) detection is crucial for identifying spectra from unknown classes that were not seen during training, thereby improving model robustness in real-world settings. Techniques like OpenPCS-Class leverage intermediate network features to distinguish in-distribution data from OOD, enabling reliable multi-class classification beyond the training ___domain⁷². Additionally, hybrid approaches that incorporate physical priors can constrain predictions, thereby improving reliability. These strategies collectively improve model robustness in real-world spectral sensing scenarios, a few of them are reviewed in Table 2. It is important to note that while these benefits are significant, they come at the cost of increased computational complexity at the DL model level. This complexity can lead to slower reconstruction and decision-making processes, which we believe are unsuited for battery-powered devices such as smartphones and other mobile platforms.

During the training of the DL model, overfitting was carefully considered, and regularization techniques were employed, including a dropout rate of 50% (i.e., randomly dropping out 50% of neurons). In addition to the aforementioned techniques, such as OOD validation and Monte Carlo methods, overfitting can be further mitigated using data augmentation strategies, such as noise injection and synthetic data generation, which expose the model to a broader range of spectral patterns^80,81,82. Additionally, L2 regularization can help control model complexity and prevent overfitting⁸³.

Reproducibility and scalability

To validate reproducibility, we fabricated 169 identical multilayer thin-film (MTF) filter arrays on a single wafer, as shown in Fig. 2a. Each filter array follows a 6 \(\times\) 6 square grid pattern with precise dimensions (400 \(\times\) 400 \(\mu\)m², 300 \(\mu\)m spacing), yielding a total array size of 4.5 \(\times\) 4.5 \(\mu\)m². The high degree of uniformity in filter fabrication was achieved through precise control over the deposition process. For mass production, our method utilizes direct current (DC) and radio frequency (RF) magnetron sputtering with precisely controlled deposition parameters. The use of TiO₂ (high refractive index) and SiO₂ (low refractive index) ensures stable optical properties, with deposition thicknesses carefully regulated via shadow masks. By omitting specific layers in a controlled manner, we achieved 36 unique MTF filters while maintaining high reproducibility across batches. The exact thickness values of each deposited layer are provided in Table 1, demonstrating the controlled variation in layer configurations while maintaining deposition accuracy.

Stencil lithography provides a simplified and scalable alternative to conventional etching-based processes, thereby reducing fabrication complexity and the potential inconsistencies introduced by additional processing steps. Moreover, the lift-off process, which utilizes photoresist and Ge deposition, further enhances the structural consistency of the filter arrays. To assess the feasibility of large-scale production, we analyzed the thickness variations across different filters. The provided thickness table confirms that the designed layer configurations were accurately achieved, with controlled variations where required (e.g., selective omission of intermediate layers). Future work will further explore batch-to-batch variations by fabricating multiple wafers and analyzing spectral deviations to gain a deeper understanding of these variations. However, the results from our current fabrication indicate that the technique is promising for reproducible, high-throughput production of MTF filter arrays with consistent spectral characteristics.

Furthermore, to mitigate reproducibility and scalability issues in wafer-level stencil lithography of multilayer thin-film filters, advanced optical monitoring techniques during the deposition process are crucial. One practical approach is polychromatic optical monitoring, which uses multiple monitoring wavelengths instead of a single one, as in conventional monochromatic monitoring⁸⁴. This method enables real-time tracking of layer thicknesses and spectral performance, allowing for partial compensation of accumulated thickness errors in previously deposited layers. By comparing real-time transmittance measurements with theoretical models, the monitoring system can dynamically adjust deposition parameters, thereby enhancing uniformity across large batches and improving the precision of spectral reconstruction. Simulation-driven algorithms can further optimize the choice of monitoring wavelengths, tailored to the filter design and material dispersion properties.

Critical analysis on extension of the proposed MTF filter

We recognize the significance of UV and IR spectrometers in their various applications. We evaluated the applicability of our spectrometer for broader spectral domains. However, it is clearly stated that we intentionally designed our MTF filter array for the range from 500 to 850 nm, which strikes a practical balance between spectral performance, material feasibility, and economic viability, particularly for compact and low-power applications. We do not advocate extending the present filter design to UV and IR from its current spectrum range, as this would necessitate significant modifications at multiple levels. In terms of filter design, UV compatibility often requires materials such as HfO₂ and SiO₂ layers⁸⁵, new materials such as GaN (Gallium Nitride), InGaAs (Indium Gallium Arsenide), and InP (Indium Phosphide) that are excellent for cutting-edge semiconductor industry procedures for 200 to 700 nm (the UV-VIS range)⁸⁶, MgF₂ or Al₂O₃ to ensure adequate transmission from the UV region of 230 nm to the beginning of VIS region of 400 nm⁸⁷, whereas IR filters rely on substrates like Ge or ZnSe, which are not only cost-intensive but also present fabrication challenges due to higher absorption losses and thermal sensitivity in multilayer stacks^88,89,90. Additionally, achieving uniform and reproducible deposition of these materials on a wafer scale further complicates scalability. From a DL perspective, broadening the spectral range introduces new complexities. Training models for UV or IR demands large volumes of representative spectral data, which are often scarce or expensive to acquire.

Note that filter reconfiguration would necessitate recalibration and retraining of the model to match new spectral response profiles, incurring additional computational and labor overhead. Such demands compromise the low-cost, lightweight nature of our current solution. Sensor limitations also play a pivotal role: while our system is optimized for CMOS sensors readily available for the VIS-NIR range, extending to UV would require GaN or SiC-based sensors, and IR detection would necessitate InGaAs or HgCdTe sensors, which would significantly increase the overall system cost and power consumption. In contrast, our current design maintains a 1 nm wavelength resolution (ability to reconstruct a narrow peak without distortion) within a carefully chosen range from 500 to 850 nm, which is suitable for many real-world applications, such as biomedical imaging, agriculture, and environmental monitoring, where UV or far-IR data are typically non-critical. By focusing on this specific band, we retain advantages in manufacturing simplicity, system compactness, energy efficiency, and cost-effectiveness, making the spectrometer highly suited for battery-powered or mobile deployments. Since the spectral bandwidth can be further extended to the UV and IR range by engineering the filter design of the MTF filter. Furthermore, our deep learning model relies on spectral variability in our filter design, so we believe that spectral reconstruction performance becomes more robust by increasing spectral variability through the adoption of nanoarchitectures, such as plasmonic nanoantennas and photonic nanocavities, which is one of our ongoing projects.

Conventional spectrometers primarily include grating-based, prism-based, Fabry-Pérot, and Fourier Transform Infrared (FTIR) spectrometers. Grating and prism spectrometers operate on the principles of spatial dispersion and have long been used due to their simplicity and reliability⁹¹. Fabry-Pérot interferometers, renowned for their tunability and compact form, are frequently utilized in high-resolution, narrowband applications^92,93. FTIR spectrometers, particularly using Michelson interferometers, are standard in infrared spectroscopy due to their broad spectral coverage and high resolution⁹⁴. While newer approaches, such as computational and metasurface spectrometers, are emerging, conventional types remain dominant in both commercial and laboratory settings⁹⁵. These spectrometers and their operating principles are well discussed in surveys such as^96,97. The trade-offs between conventional and filter-based computational spectrometers primarily revolve around balancing spectral resolution, hardware complexity, and system integration. Conventional spectrometers, such as grating-based or Fourier-transform systems, offer exceptional spectral precision and broad wavelength coverage, making them the gold standard for laboratory-based applications requiring detailed spectral analysis. These include material characterization, remote sensing, and advanced biomedical diagnostics, where high resolution and broad spectral range are critical. Several state-of-the-art computational spectrometers have recently been introduced, each with its advantages and disadvantages. For example, Yang et al. presented a computational spectrometer with the world’s smallest footprint using a single band-graded nanowire²². Yoon et al. reported single-pixel implantable computational spectrometer designs based on a single van der Waals junction, offering considerable advantages in footprint, spectral resolution, and bandwidth^19,20,21. Still, their approaches require further engineering for commercialization, as the large-scale integration of nanowires and two-dimensional materials is not yet compatible with CMOS image sensors, resulting in high-cost and complex fabrication processes.

In contrast, the proposed spectrometer, based on an MTF filter array with a wavelength resolution of 1 nm, a spectral range of 500 to 850 nm, and a compact footprint of 4.5 \(\times\) 4.5 mm², is optimized for rapid, single-shot spectral reconstruction using DL. A comparison with conventional, semi-conventional, and modern spectrometers is presented in Table 3. While a direct apple-to-apple comparison is not feasible, the provided comparison sufficiently demonstrates the effectiveness of the proposed spectrometer. The resolution of the proposed spectrometer is adequate for capturing narrow spectral features relevant to applications such as noninvasive health monitoring, food quality inspection, vegetation assessment, and industrial material classification. Although it may not achieve the ultra-high spectral fidelity or broad wavelength coverage of traditional systems, particularly in the UV or IR regions, it offers a practical solution where speed, portability, and cost efficiency are prioritized. Its miniature size enables seamless integration into handheld, wearable, and mobile platforms, facilitating real-time diagnostics and monitoring in the field and point-of-care settings. Furthermore, the simplified optical architecture, combined with scalable thin-film fabrication and data-driven reconstruction, supports high-throughput, low-cost manufacturing, making it well-suited for deployment in resource-constrained environments and consumer electronics.

The proposed system demonstrated effective reconstruction over the range from 500 to 850 nm with a 1 nm spacing. Still, the spectra within our dataset were measured under the assumption that the angle of the incident light is normal to the MTF filter array. The measured intensities vary according to the angle of incident light, which can reduce the performance of the proposed model when it is under various angles of incident light. Furthermore, DL models, including the proposed U-Net architecture, may overfit to a smaller training dataset. This could reduce robustness when the model is subjected to spectra with new features or noise characteristics. Several research challenges have been identified that require attention from the research community to enhance the potential of HSI applications.

1. 1.

   The DL architecture requires substantial computational power for training, especially with large datasets and high-resolution applications, which restricts accessibility for those without advanced computational hardware.

2. 2.

   Achieving uniform layer thicknesses and precise transmission functions across the MTF filter array remains challenging with scalable wafer-level stencil lithography. Larger array sizes increase the likelihood of thickness variability, potentially impacting filter behavior and reconstruction accuracy.

3. 3.

   Changes in temperature, lighting, and possible contamination on sensors or filters may influence spectral measurement accuracy, so these factors for consistent performance in various real-world conditions may require additional preprocessing or adaptive modeling.

4. 4.

   Leveraging the MTF filters’ spatial information for real-time hyperspectral imaging demands additional hardware and careful calibration, making it challenging to maintain speed and resolution for practical use in hyperspectral applications.

This study presents a DL-based, single-shot computational spectrometer that combines a 6 \(\times\) 6 MTF filter array with a CMOS camera, achieving a compact and cost-effective design suitable for mobile applications. The MTF filter array, fabricated using wafer-level stencil lithography, enables high-throughput production and confirms its uniformity with analysis through SEM and FIB, making it an affordable option for on-site detection and simple diagnostic tests. With the ability to reconstruct high-resolution spectra across a broad wavelength range (500–850 nm, 1 nm spacing) in approximately 0.006 seconds per spectrum, the spectrometer demonstrates efficient performance, achieving an average RMSE of 0.0288 for test spectra, including reliable transmission spectrum reconstructions for commercial beverages. The DL architecture, trained on 2576 data pairs, achieves rapid and accurate spectral reconstruction that is typically infeasible with traditional numerical optimization methods, highlighting the advantages of DL for real-time applications. The compact size, minimal optical complexity, and fast measurement capabilities make this spectrometer a promising tool for various applications, such as drink inspection, counterfeit document detection, and self-diagnosis. Moreover, due to the MTF filters’ capacity for spatial data acquisition, this setup could be expanded into a snapshot hyperspectral imaging system, maximizing its versatility in capturing spectral information efficiently. We believe that the proposed spectrometer is commercially viable and is one of the strongest promising solutions for miniaturized computational spectrometry. We are looking ahead toward fabrication for commercialization, provided the funding is made available.

1. 1.

   Stoichiometry, in chemistry, the determination of the proportions in which elements or compounds react with one another. The rules followed in the determination of stoichiometric relationships are based on the laws of conservation of mass and energy and the law of combining weights or volumes.

2. 2.

   Perturbation mean small disturbance. When some external factors affect the system and the exact solution is not available, then the external factor affecting the system, is considered as a small perturbation to the system to find out the solution to explain its behavior and energy.

3. 3.

   Sputtering is a technique for depositing thin films onto a substrate by bombarding a target material with high-energy ions, causing atoms to be ejected and deposited as a thin layer on the substrate.

4. 4.

   A shadow mask is a template or mask with specific patterns or openings designed to allow certain materials to pass through while blocking others. It is used in techniques like physical vapor deposition (PVD) or chemical vapor deposition (CVD) to precisely deposit thin films onto substrates.

5. 5.

   Quantum efficiency (QE) of the detector is the ratio of the number of carriers that is collected by the detector to the number of photons incident on the detector.

6. 6.

   PECVD stands for Plasma-Enhanced Chemical Vapor Deposition, a technique used to deposit thin films from a gas state to a solid state on a substrate, utilizing plasma to enhance the chemical reactions and enable deposition at lower temperatures.