Introduction

Hydroxyl-terminated polybutadiene (HTPB) propellants are widely recognized as high-performance solid propellants. They are composed of metallic fuel, inorganic oxidizers, HTPB binder, curing agents, and plasticizers1,2. Functioning as a polymeric binder, HTPB integrates heterogeneous raw materials into a homogeneous matrix. It exhibits exceptional high energy density, stable structure, chemical stability, and good processability3. These attributes have made HTPB propellants indispensable in aerospace and defense applications, driving advancements in propulsion technologies4. Among the critical stages in propellant manufacturing, the curing process significantly determines the final mechanical and thermochemical properties of the product5. Therefore, the study of the curing process is crucial for the wider application of HTPB propellants in aerospace and defense fields.

In order to investigate the impact of the curing process on propellant properties, numerous scholars have utilized simulation and DSC experimental methods to explore the optimization of curing parameters. For example, Moghimi Rad et al.6 developed a computational solver (CureFOAM) based on OpenFOAM to analyze the temperature-dependent curing kinetics of HTPB resin. The results showed a maximum relative error of 5% compared to experimental data. Similarly, Chen et al.7 studied the multi-physical field effects during the curing of nitrate ester plasticized polyether (NEPE) propellants, correlating residual stress distributions with thermal and chemical gradients. Liu et al.8 investigated the mechanisms of residual stress and strain formation in nitrate ester plasticized polyether (NEPE) propellant grains through numerical simulations. Using the ABAQUS finite element (FE) platform, they systematically examined the temperature evolution, curing degree, and stress/strain distributions during the curing and cooling phases.

Abraham Varghese et al.9 discovered that the reaction levels differed between the pre-gel and post-gel stages. By measuring the viscosity and torque changes during the reaction between HTPB and TDI, they found that the reaction rate of the system was influenced by the mole fraction of trifunctional hydroxyl groups and the amount of small-molecule alcohols added. This finding is crucial for controlling the curing process and determining the applicability period of HTPB propellant. Sangmook Lee et al.10 employed DSC and a rheometer to study the curing reaction of HTPB with IPDI. They determined the activation energy of the reaction and constructed the master curve, providing a basis for predicting key information in the manufacturing process of polymer-bonded explosives and HTPB propellants.

Ma Hui et al.11 compared the effects of different catalysts on the curing reaction of the HTPB-IPDI system using DSC and viscosity tests. They concluded that DBTDL has high catalytic activity but a short application period, while TECH has low toxicity and a long application period. This research provides a reference for choosing a suitable curing catalyst for HTPB propellant. L.T. DeLuca et al.12 characterized HTPB-based solid fuels in terms of performance, mechanical properties, and pollution through the design of burner experiments, etc. They found that HTPB has issues such as a low regression rate and explored strategies to enhance the performance of HTPB propellant by adding high-energy metal additives, which is of great significance for improving the performance of HTPB propellant.

Jiahu Guo et al.13 used FT-IR spectroscopy to study the curing reaction between HTPB and IPDI and determined the kinetic parameters and the two-step reaction mechanism, which aids in understanding the curing process of polyurethane in HTPB propellant. Hui Ma et al.14 investigated the curing reaction of HTPB and HDI-trimer with different catalyst mass fractions through rheological dynamics and obtained the relationship between the applicable period of the system and the catalyst mass fraction. This provides theoretical guidance for controlling the applicable period of the curing system of HTPB propellant. They also15 investigated the effect of different curing agents on the curing reaction of HTPB-based adhesive systems using the viscosity testing method. They determined the rheological reaction rate constants and the applicable period of different systems and found that the viscosity of the HDI-trimer-cured HTPB system increased rapidly in the later stage, which is beneficial for improving the final performance of the product in the manufacturing process of HTPB propellant.

Xing Zhang et al.16 investigated the curing reaction and performance of EHTPB-IPDI and HTPB-IPDI systems using DSC, viscosity tests, and a universal testing machine. They found that the EHTPB-IPDI system is more reactive during curing, and its cured product has better thermal stability and mechanical properties, which is more advantageous in the application of HTPB propellant. Also, DBTDL has a better catalytic effect on this system than TECH. Jie Zhou et al.17 investigated the polyurethane moisture-curing reaction using in-situ FTIR spectroscopy and DFT calculations. The results showed that the reaction initially followed one-stage reaction kinetics. The increase in humidity and temperature accelerated the reaction process, and additional water molecules acted as catalysts for the reaction, providing theoretical references for understanding the polyurethane curing process in HTPB propellants.

Ehtasimul Hoque et al.18 explored the curing kinetics of 4 - (dimethylsilyl) butylferrocene - grafted HTPB with the aid of DSC, viscosity tests, etc. They found that although the activation energy of this system was higher, the curing reaction rate was faster, and the catalytic effect of Fe(AA)3 was better than that of DBTDL. This can help optimize the formulation design and the curing process of HTPB propellant. C. Korah Bina et al.19 examined the curing reaction of HTPB with different isocyanates using DSC, viscosity tests, and FTIR spectroscopy. They found that the catalytic effect of FeAA on the curing reaction of HTPB was better, and the results of the viscosity tests were consistent with the DSC analysis, which is of great significance for the curing research and practical production of HTPB propellant. Despite these advancements, detailed investigations into HTPB propellant curing mechanisms remain limited.

This paper presents an analysis of the curing process using differential scanning calorimetry (DSC), combining experimental and theoretical approaches. Curing behavior was characterized at various heating rates, and the influence of heating rate on reaction kinetics was investigated. Kinetic parameters for the curing reaction were determined using the Kissinger and Ozawa methods. Furthermore, thermochemical and finite element (FE) models were developed to simulate the curing process, revealing the evolution of temperature and degree of cure. Validated by isothermal and adiabatic experiments based on thermally activated Arrhenius-type kinetics, the model explains the enhancement of rheological properties. This effectively bridges the gap between laboratory-scale observations and FE implementation requirements20,21,22,23.

The paper is structured as follows: Sect. 2 details the experimental setup, including materials such as HTPB, ammonium perchlorate, and aluminum powder. The preparation of propellant slurries using a 5 L vertical planetary mixer is comprehensively described. Section 3 develops two theoretical models: (1) A thermochemical model that precisely defines the degree of cure and reaction rate, incorporating Arrhenius-type thermally activated kinetics and heat release during curing; and (2) A finite element (FE) modeling framework detailing the application of an FE solver for curing process simulation, covering software implementation, model geometry, and material thermophysical properties. Section 4 presents results and corresponding discussions. Based on non-isothermal DSC data, it analyzes the influence of heating rate on curing reaction kinetics. Activation energies and other kinetic parameters were calculated using the Kissinger and Ozawa methods. Simulation results are compared with experimental data, with temperature and degree of cure evolution investigated at different nodal positions during curing. Section 5 summarizes the study, confirming that heating rate significantly affects curing reaction kinetics, thereby validating the model. Future work may extend the model by incorporating additional practical factors to enhance process control.

Experiment setup

Material

The investigated propellant material consists of HTPB as the polymeric binder, along with ammonium perchlorate (AP) and aluminum powder (Al) as solid fillers. The basic formulation of the NEPE propellant is presented in Table 1. The molecular structures of HTPB, Dioctyl sebacate (DOS), and Toluene Diisocyanate (TDI) are shown in Fig. 1.

Table 1 The propellant composition.
Full size table
Fig. 1
figure 1

Molecular structure of HTPB DOS and TDI.

Full size image

Propellant slurry preparation

The propellant slurry was synthesized in a 5 - L vertical planetary mixer equipped with dual counter - rotating blades that operated at 30 rpm. The formulation used a bimodal solid - loading system consisting of 78 wt% particulate components, namely aluminum fuel (with a particle size of 5 μm) and ammonium perchlorate oxidizer (the ratio of coarse - to - fine AP was 2:1, with D50 values of 120 μm and 7 μm respectively). The liquid phase, accounting for 22 wt%, was a polyurethane prepolymer system composed of HTPB, DOS plasticizer, and TDI curing agent. The mixer was configured with a thermal - management jacket, which maintained the slurry temperature at 323.15–333.15 K through regulated hot - water circulation.

Curing experiment

The prepared slurry was transferred into pillar-shaped molds and underwent thermal curing in a precision-controlled oven kept at a constant temperature of 323.15 K. As depicted in Fig. 2 (positions A–C), a triaxial thermal monitoring setup was adopted. T-type thermocouples were strategically placed at different geometric locations within the specimen. The thermopotential signals from the measuring end of the thermocouples were amplified by an amplifier, and the temperature at the reference end was detected by an integrated temperature sensor. The overall schematic of the isothermal curing system is illustrated in Fig. 3.

Thermal analysis was carried out using a DT-40 Differential Scanning Calorimeter (DSC). Specimens, weighing between 5.0 and 6.0 mg, were subjected to non-isothermal scanning from 293.15 K to 483.15 K at four heating rates, namely 5, 10, 15, and 20 K·min⁻¹. This process helped in establishing a comprehensive thermal database for the optimization of the HTPB propellant formulation.

Fig. 2
figure 2

T-Type thermocouple ___location distribution.

Full size image
Fig. 3
figure 3

Overall diagram of constant temperature curing system.

Full size image

Non-isothermal DSC method

Thermal analysis of the samples was conducted using differential scanning calorimetry (DSC)24. The experiment was carried out in a high-pressure crucible with nitrogen as the ambient gas. To study the curing reaction kinetics of the samples, four different heating rates were set: 2.5 K/min, 5 K/min, 10 K/min, and 15 K/min. Throughout the experiment, the peak exothermic temperature of the sample at these four heating rates was recorded in real time by a precisely controlled temperature control system.

Theoretical models

Thermo-chemical model

The chemical processes that take place during the aging of polymers after they are cast are accompanied by substantial temperature variations. Consequently, the curing process is an exothermic and thermally activated reaction25.

Since the kinetics of the reaction is determined by the curing agent concentration, χ, for more convenient handling and interpretation, the degree of curing, \(\:0\le\:\zeta\:\le\:1\), is defined in the normalized format as:

$$\:\zeta\:=\frac{\chi\:}{{\chi\:}_{\infty\:}},$$
(1)

where \(\:{\chi\:}_{\infty\:}\) is the final value of \(\:\chi\:\) (attained under perfect conditions). Thus, it can be hypothesized that the curing degree serves as the internal variable of the system, thereby indicating how far the kinetic reaction has progressed.

The reaction rate, denoted as \(\:\dot{\zeta\:}=A\left(\zeta\:\right)\) is a characteristic feature of the kinetic reaction. Typically, it is a function of the curing degree \(\:\zeta\:\) itself.

$$\:A\left(\zeta\:\right)={K}_{0}\left(1-\zeta\:\right)\left(\zeta\:+{\zeta\:}_{0}\right),$$
(2)

where \(\:{K}_{0}\) represents the chemical affinity, and \(\:{\zeta\:}_{0}\) corresponds to the value of the curing degree associated with the initial curing agent concentration \(\:{\chi\:}_{0}\), This correspondence ensures that the reaction initiates with an initial reaction rate \(\:A\left({\zeta\:}_{0}\right)\ne\:0\). The proposed evolution law can be further refined by incorporating an exponential term, as illustrated in the following expression:

$$\:A\left(\zeta\:\right)={K}_{0}\left(1-\zeta\:\right)\left(\zeta\:+{\zeta\:}_{0}\right)\cdot exp\left(-\delta\:\zeta\:\right),$$
(3)

where \(\:\delta\:\) is a novel parameter of the model, which has the ability to predict the peak that corresponds to the maximum transformation rate. Consequently, the transformation process proceeds more rapidly at the onset of the curing process and slows down towards the end.

Kamal-Sourour proposed alternative models of the general form26.

$$\:A\left(\zeta\:\right)=\left({K}_{1}+{K}_{2}\:{\zeta\:}^{m}\right){\left(1-\zeta\:\right)}^{n}.$$
(4)

The curing process is also governed by thermally activated reactions. An Arrhenius-type law will be taken into account as well to explain its acceleration caused by the temperature field27,28,29. Therefore, the following formula is proposed for calculating the curing rate:

$$\:\dot{\zeta\:}=A\left(\zeta\:\right)\:exp\left(-\frac{{E}_{a}}{RT}\right),$$
(5)

where the Arrhenius exponential term includes the temperature T, the universal gas constant R for ideal gases, and the activation energy of the reaction \(\:{E}_{a}\).

Upon examining this rate equation, it becomes clear that the thermal activation represented by the Arrhenius factor plays a crucial role at the initiation of the reaction. As the reaction progresses, significant attenuation is brought about by both the permeability exponential term and the factor \(\:\left(1-\zeta\:\right)\), This results in the suppression of the reaction evolution as the curing degree approaches its final value \(\:\left(\zeta\:=1\right)\). Therefore, the kinetic equations, which must have positive values, incorporate the essential elements necessary for a realistic simulation of the kinetic reaction.

The curing reaction is typically characterized by the release of energy (\(\:{\dot{Q}}_{reac}\)) in the form of heat, which can be expressed as follows:

$$\:{\dot{Q}}_{reac}=L\dot{\zeta\:}.$$
(6)

The heat release during the curing reaction depends on the progression of the curing process, denoted as L, which represents the total heat released throughout the entire kinetic reaction. When the released heat is measured under adiabatic conditions, the proposed curing model can be readily calibrated by fitting the curve of the heat release evolution, as described below:

$$\:\zeta\:\left(t\right)\:=\frac{\varDelta\:{Q}_{reac}\left(t\right)\:}{L}.$$
(7)

Finite element modeling

The curing process of HTPB propellant was simulated using a finite element solver. First, after integrating the curing interface, 3D modeling was carried out using the GID software tool or other CAD-supported software for propellant modeling, and an appropriate rendering mode was selected for the simulation.

The presented curing model has been tested with several geometries of interest, and the relevant data are presented in Table 2. The thermos-physical material properties are showed in Table 3. The 3D geometry model of the HTPB propellant depicted in Fig. 4a was ultimately chosen for this paper. The geometry of the HTPB propellant was discretized into 128,040 tetrahedral solid elements, as illustrated in Fig. 4b.

The solver type was set as DIRECT, the Time Increment was set to 60, the Number of Time Steps was set to 100, and the boundary function was defined as linear.

Table 2 Geometric model No.1.
Full size table

The thermos-physical material properties used for the simulation of all test cases are reported below:

Table 3 The thermos-physical material properties.
Full size table
Fig. 4
figure 4

3D propellant model.

Full size image

Results and discussion

Curing reaction kinetics based on non-thermal DSC method

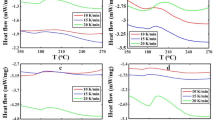
As shown in Fig. 5, the DSC curing reaction exhibits a smooth exothermic profile. It has been observed that the time needed for the curing reaction is remarkably shortened as the heating rate increases. Moreover, an upward trend in the onset, peak, and end temperatures of the curing process has been noted with the rise in the heating rate. This phenomenon can be attributed to the fact that a higher heating rate causes the molecular chains during the curing process to be unable to arrange themselves rapidly enough according to the rules. Consequently, higher temperatures are required for the transition to the elastomeric state.

Fig. 5
figure 5

The Y-axis offset stacked plot of the exothermic curve of DSC for the curing reaction.

Full size image

The curing reaction temperatures of the experimentally used patterns at different heating rates are depicted in Table 4.

Table 4 Kinetic parameters of curing reaction.
Full size table

In the table: β is the rate of temperature increase (K·min− 1); Ti is the starting temperature of the curing reaction during the test (K); Tp is the peak temperature of the curing reaction during the test (K); Tf is the ending temperature of the curing reaction during the test (K).

The principal approaches for ascertaining the activation energy of the curing reaction are the Kissinger method and the Ozawa method28,29,30. The Kissinger equation can be formulated as follows:

$$\:{ln}\frac{\beta\:}{{T}_{p}^{2}}=ln\frac{AR}{\varDelta\:E}-\frac{\varDelta\:E}{R{T}_{p}},$$
(8)

where A is the curing finger front factor, (s− 1); ∆E is the reaction activation energy, (kJ·mol− 1); R is the molar gas constant, J/(mol·K).

Kissinger’s method determines the activation energy of the curing reaction. It conducts a linear fitting with 1000/\(\:{T}_{p}\:\:\text{a}\text{s}\:\text{t}\text{h}\text{e}\:\text{a}\text{b}\text{s}\text{c}\text{i}\text{s}\text{s}\text{a}\:\text{a}\text{n}\text{d}\:\text{ln}\frac{\beta\:}{{T}_{p}^{2}}\) as the ordinate. The activation energy of the curing reaction process is then derived from the slope of the resulting straight line obtained by the fit. Additionally, based on the value of the intercept, an estimate of the pre-exponential factor A can be obtained. Likewise, with the aid of Crane’s equation31, the number of reaction stages n in the curing reaction process can be determined. This is achieved by performing a linear fitting with 1000/\(\:{T}_{p}\:\)as the abscissa and ln\(\:\beta\:\) as the ordinate. The Crane equation is expressed as follows:

$$\:\frac{d\left(ln\beta\:\right)}{d(1/{T}_{p})}\approx\:-\left(\frac{\varDelta\:E}{nR}\right).$$
(9)
Fig. 6
figure 6

Kissinger method for solving kinetic parameters.

Full size image

The fitting results are presented in Fig. 6. Based on the content of the figure, the calculated values are \(\:\varDelta\:E=\) 22.439 KJ·mol−1, A = 33.779s−1 and n = 0.8527.

The Ozawa equation can be expressed as

$$\:log\beta\:=log\frac{A\varDelta\:E}{Rf\left(\alpha\:\right)}-2.315-0.4567\frac{\varDelta\:E}{RT},$$
(10)

where \(\:f\left(\alpha\:\right)\:\)is the mechanism function of the inhomogeneous phase system.

According to the above equation, Ozawa’s method is used to calculate the activation energy of the curing reaction by performing a linear fit. The activation energy of the curing reaction process is derived from the slope of the line obtained through the fit. The kinetic equations fitted by Ozawa’s method are shown in Fig. 7. Similarly, with the aid of Crane’s equation, the number of reaction stages n in the curing reaction process can be determined.

Fig. 7
figure 7

Ozawa method for solving kinetic parameters.

Full size image

The kinetic parameters of the curing reaction process are shown in Table 5 below.

Table 5 Kinetic parameters of the curing reaction process.
Full size table

Temperature and curing degree during curing process

The curing temperature-time curves at various nodes of the experimental test conducted in an oven maintained at 323.15 K are illustrated in Fig. 8. Evidently, as indicated by the data, the temperature of the outermost layer is higher than that of the inner part, and the final temperature approaches the preset oven temperature. The curing process can be elaborated upon in three distinct stages.

In the initial stage, the temperature of the propellant samples rises rapidly during the curing process. This is predominantly attributed to the heat transfer from the interior of the oven and the exothermic characteristic of the propellant curing reaction. Specifically, the temperature reaches approximately 320.15 K at around the 4000-second mark.

During the second stage, the temperature within the solid propellant undergoes a gradual increase until it reaches a peak, followed by a slight decline. This phenomenon can be ascribed to the exothermic nature of the curing reaction. The rapid release of heat during the reaction, which is relatively low in comparison to the rate of heat transfer with the ambient environment, causes a slight decrease in temperature once the crosslinking reaction is completed.

In the final stage, owing to the stabilization of the ambient temperature, the internal temperature of the solid propellant gradually converges towards the external ambient temperature.

Figure 9 presents a comparison of the curing temperature - time profiles at different nodes during the curing experiments and the simulation process. It can be observed that the temperature - change experimental process at points A, B, and C is essentially similar to the simulation process. The maximum error in the comparison between the experimental and simulation data for the three measurement points, as derived from the figures, is less than 5%. The 50 °C simulation is carried out based on the simulations at 333.15 K and 348.15 K, in line with the experimental results.

Fig. 8
figure 8

Experimental testing of curing temperature-time curves at different nodes.

Full size image
Fig. 9
figure 9

Comparison of experimental and simulated temperature change curves.

Full size image

Analysis of simulation results

It is hypothesized that the experimental results under the 323.15 K condition are essentially consistent with the simulation outcomes. As a result, curing simulation experiments were carried out at 333.15 K and 348.15 K. As shown in Fig. 10, during the 323.15 K curing process, the temperature profile initially rises rapidly at the start of curing and then increases gradually due to a small amount of heat release until the curing is complete. Eventually, the temperature reaches 323 K, and the final temperature is identical at all measurement points. This is because, in the early stages of curing, the heat from the oven is rapidly transferred to the propellant sample, and the exothermic nature of the propellant curing reaction also contributes to the rapid temperature increase. As the reaction progresses, the exothermic rate of the reaction reaches an equilibrium with the ambient heat transfer rate, and the rate of temperature rise slows down until, at the end of curing, the temperature stabilizes around the set ambient temperature.

As depicted in Fig. 11, the curability curve commences to rise steadily and decelerates as it approaches the completion of curing. In the initial phase of curing, the curing agent reacts comprehensively with HTPB and other components. The curing reaction rate is high, leading to a rapid increase in the degree of cure. As the reaction progresses, the curing agent is gradually depleted, the number of unreacted active sites diminishes, the reaction rate declines, and the growth of the degree of cure slows down until curing is complete. At this point, the degree of cure attains its maximum value. The cloud diagram of the curing simulation process is shown in Fig. 12.

Fig. 10
figure 10

Temperature curve at 323.15 K.

Full size image
Fig. 11
figure 11

Curing degree curve at 323.15 K.

Full size image
Fig. 12
figure 12

Simulation of curing process at 323.15 K.

Full size image

Figures 13 and 14 illustrate the temperature profile and cure degree change profile at 333.15 K. When curing at 333.15 K, the temperature trend is similar to that at 323.15 K. However, the maximum temperature after curing reaches 333 K, which is higher than that at 323.15 K. This is because, at higher temperatures, the molecular thermal motion intensifies and the reactivity increases. As a result, the curing reaction rate accelerates. With a higher reaction rate, more heat is released within the same time interval. Consequently, the final temperature is higher.

According to the simulated cloud diagram in Fig. 15, it can be seen that the curing time at 333.15 K is shortened from 3618 min at 323.15 K to 1243 min. In accordance with the Arrhenius equation, higher temperatures lead to an increase in the reaction rate constant. As a result, the curing reaction is expedited, thereby decreasing the time needed for curing.

Fig. 13
figure 13

Temperature curve at 333.15 K.

Full size image
Fig. 14
figure 14

Curing degree curve at 333.15 K.

Full size image
Fig. 15
figure 15

Simulation of curing process at 333.15 K.

Full size image

Curing occurs more rapidly at 348.15 K, with the process being completed in 473 min at a temperature of 348 K. The results are shown in Figs. 16 and 17. Higher temperatures further enhance molecular mobility and reaction rates. This enables the curing reaction to release a greater amount of heat and reach higher temperatures within a shorter time frame.

When the temperature was elevated, the discrepancies in temperature and degree of curing at various measurement points grew more substantial. This is because an increase in temperature accentuates the disparities in reaction rates at different positions, and it also intensifies the heat transfer and the lack of uniformity in the reaction process between the inner and outer parts of the samples.

During the later stage of the curing process, the shortening of the stage during which the temperature rises gradually is the principal factor contributing to the decrease in the curing time. This can be attributed to the rapid reaction rate at high temperatures. The heat accumulated in the initial stage of the swift reaction allows the system to attain higher temperatures more rapidly and enter the later curing stage. Additionally, in the later stage, the reaction rate becomes less sensitive to the influence of temperature, resulting in the shortening of this stage and, consequently, a reduction in the overall curing time. It can be clearly observed from Fig. 18 that under the condition of 348.15 K, the total curing time is only 473 min, which is a significant reduction compared to that under the other two temperature conditions in the experimental setup.

Fig. 16
figure 16

Temperature curve at 348.15 K.

Full size image
Fig. 17
figure 17

Curing degree curve at 348.15 K.

Full size image
Fig. 18
figure 18

Simulation of curing process at 348.15 K.

Full size image

Conclusions

This study comprehensively investigated the curing kinetics and process of HTPB propellant through integrated experimental and theoretical approaches. Materials were carefully prepared, and systematic DSC experiments at varying heating rates captured reaction data. Theoretically, thermochemical and finite element models were developed, successfully revealing temperature and cure degree evolution patterns.

  1. (1)

    Non-isothermal DSC analysis demonstrates that increased heating rates significantly shorten reaction time while raising initial, peak, and end temperatures. This occurs as accelerated heating disrupts molecular chain ordering, requiring higher transition temperatures to the elastomeric state. Kinetic parameters calculated via Kissinger and Ozawa methods further elucidate heating rate effects.

  2. (2)

    Curing experiments show higher temperatures at the sample surface than core, with both ultimately reaching oven temperature. The three-stage curing process was accurately simulated, with < 5% maximum error versus experimental data. This validates the model’s reliability in predicting temperature and cure degree profiles.

Building on validated curing kinetics models, this work paves the way for: (1) Rocket motor manufacturing through real-time cure monitoring during large-scale propellant casting to eliminate defects; (2) Next-generation propellants via model adaptation for AP/Al nanocomposites and sustainable HTPB alternatives; (3) Polymer-matrix armor systems by extending temperature-control protocols to impact-resistant flexible composites.