Introduction

Ocean waves are inherently dispersive, since they propagate at speeds dependent on their wavelength. This dispersion is quantified by the phase speed \(c_p(k)=\omega (k)/k\), where the frequency \(\omega (k)\) depends on the wavelength L through the magnitude \(k=|\textbf{k}|=2 \pi /L\) of the wavenumber vector \(\textbf{k}\). For instance, in deep water, the linear dispersion relation \(\omega (k)=\sqrt{g k}\) applies, leading to a phase speed \(c_p(k)=\sqrt{g/k}\), where g is the gravitational acceleration. Consequently, longer waves (large L and small k) travel faster than shorter waves (small L and large k). Although waves generally have a predominant direction, in the open ocean, they can arrive from multiple directions at different speeds and wavelengths. In rare conditions, waves arrive in an organized manner, nearly in phase, leading to constructive interference, or linear dispersive focusing, and potentially resulting in unexpectedly large individual waves.

Such linear mechanism is insufficient for fully describing the formation of real extreme or rogue waves. Ocean waves exhibit characteristics beyond the pure sinusoidal shapes of linear waves, featuring rounded troughs and sharper crests1. These nonlinear effects can increase larger wave heights by 15 to 20 percent, further amplifying the effects of constructive interference2,3. To explain second-order effects in simple terms, consider two elementary waves of the same amplitude a and traveling along the main direction of propagation x. Their frequencies are \(\omega _1\) and \(\omega _2\), and wavenumbers \(k_1\) and \(k_2\). They can non-resonantly interact to generate second-order waves of amplitude \(a^2\), frequency \(\omega _1\pm \omega _2\) and wavenumber \(k_1\pm k_2\). Second-order waves do not satisfy the dispersion relation and they are said to be non-resonant, since \(\omega _1\pm \omega _2\ne \omega (k_1\pm k_2)\). They are bound, or phase-locked, to the linear waves that generate them. For example, if \(k_1=k_2=k\) and we define the wave phase \(\theta =k x-\omega t\), the surface displacement \(\eta\) of a Stokes wave in deep water is given by the sum of a linear sinusoidal wave and a phase-locked (bound) quadratic component with doubled frequency and wavenumber:

$$\begin{aligned} \eta (x,t)=a\cos (\theta ) + \frac{1}{2}k a^2 \cos (2\theta )\,. \end{aligned}$$
(1)

It is the bound wave that renders the surface displacements vertically skewed, sharpening the crests and rounding the troughs. Third-order bound waves \(\sim a^3\cos (3\theta )\) can be also generated by the non-resonant interaction of three waves, but their magnitude is typically smaller than that of the second-order wave components (see right panels of Fig. 4). Similarly, elementary waves traveling in different directions, defined by vector wavenumbers \((\textbf{k}_1,\textbf{k}_2)\), generate second-order waves with wavenumbers \((\textbf{k}_1\pm \textbf{k}_2)\)(see, e.g1,2,4.,). Clearly, second-order effects are primarily contributed by the elementary waves traveling along the main direction of a wave field.

Another mechanism to explain the formation of rogue waves is nonlinear focusing, resulting from third-order quasi-resonant wave-wave interactions triggered by modulational instability5, hereafter referred as MI. This mechanism is typical of waves confined within a unidirectional channel, where energy becomes trapped between the channel’s walls, unlike in the open ocean. Under these unique conditions, the largest crests of wave groups traveling along the channel can grow at the expense of neighboring waves. Energy exchange among neighboring waves occurs through resonant and quasi-resonant four-wave interactions of \(O(a^3)\) in wave amplitude6. In unidirectional fields, resonances occur when four elementary waves \(A_j\textrm{exp}(i\theta _j)\), where \(\theta _j=k_j x - \omega _j t\) and \(j=1,\dots 4\), form a Fourier quartet that satisfies the quasi-resonant conditions \(k_1+k_2-k_3-k_4=0\) and \(\omega _1+\omega _2 -\omega _3-\omega _4\le \omega _m\epsilon ^2\), where \(\epsilon\) is a small parameter, \(\omega _m\) is the mean frequency, and \(k_j\) and \(\omega _j=\omega (k_j)\) as the respective wavenumbers and frequencies. In such conditions, energy is unevenly exchanged among the four waves and spread to other quartets sharing the same harmonic wave. This energy transfer is triggered by MI, as unidirectional wave surface fields destabilize to long-wave perturbations5. MI is a non-stationary phenomenon that triggers the amplification of the wave envelope symmetrically over a well defined modulation time scale7; it can surpass the effects of second-order bound wave interactions in unidirectional wave systems. The energy transfer due to MI is explained by the one-dimensional (1D) Nonlinear Schrödinger (NLS) equation and has been observed in wave flumes8,9,10,11.

Typical oceanic wind seas are characterized by short-crested, multidirectional wave fields. Energy can propagate and spread along any direction, since waves are not confined as in a long channel, reducing the NLS-type energy exchange mechanisms between neighboring waves3,7,12. Therefore, MI is likely to have a negligible impact on the growth and shaping of large realistic oceanic waves, particularly in finite water depth, where its effects are further weakened3. As a result, surface displacements are expected to be predominantly skewed vertically by second-order bound modes, characterized by sharper crests and shallower troughs. This crest-trough, or bound-wave, asymmetry is measured by the third-order statistical moment of surface skewness.

This concept offers an alternative rationale to investigate the potential activity of third-order modulational instabilities in wave records. These instabilities could symmetrically amplify wave envelopes, thereby enhancing the dynamic component of fourth-order cumulants, or kurtosis, of wave surface elevations6. Thus, if we render a wave record non-skewed or vertically symmetric, any observed statistical deviations from Gaussianity should essentially reflect the effects of third-order quasi-resonant instabilities. In this work, we use this approach to investigate the nature of rogue wave formation in the central North Sea. We examine a new dataset of high-frequency laser altimeter wave measurements collected over 18 years (\(2003-2020\)) at the offshore ‘Ekofisk’ platform13 (see Fig. 1). The dataset comprises approximately 27, 500 surface elevation time series, each 30 minutes long. Our analysis also considers metocean parameters estimated by the Norwegian Reanalysis Archive (NORA3) wave model hindcast, produced by the Norwegian Meteorological Institute14. Drawing on Fedele15, we introduce the NLS model for crest heights to examine statistical deviations of extreme waves from Gaussianity. This crest model accounts for both second-order nonlinearities and third-order modulational instability effects.

This paper is structured as follows. The Results section presents an analysis of the wave properties of the measured sea states at Ekofisk and the associated extreme wave statistics. We conclude by summarizing our key findings in the Conclusions section. We refer to the Methods section for the definitions of the wave parameters, data analytical methods and probabilistic wave models adopted in our study.

Fig. 1
figure 1

Ekofisk B oil and gas platform operated by ConocoPhillips Norway in the central North Sea. Lasers are located in the middle of the footbridge (photo by Mika P. Malila).

Full size image
Fig. 2
figure 2

NORA3 sea state parameters of the 27505 half-hourly sea states estimated for the period 2003-2018. (Left) Half-hourly significant wave height \(H_s\) as a function of the ratio \(r=H_{\textrm{swell}}/H_{\textrm{windwaves}}\) measuring the swell and windwave components to the total wave energy; (middle-left) the difference between the dominant swell direction \(\theta _{\textrm{swell}}\) and windwaves direction \(\theta _{\textrm{windwaves}}\) versus r; (middle-right) directional spread \(\sigma _{\theta }\) versus r; surface skewness \(\lambda _3\) versus r. Blue squares denote all sea states with significant wave height \(H_s>2\) m. Black dots mark the associated storms observed during the analyzed period, and red filled circles mark those storms whose peak significant wave heights were above 8 meters.

Full size image
Fig. 3
figure 3

Ekofisk dataset: summary of the metocean characteristics of the 27505 half-hourly sea states recorded during 2003-2020. Left panels: (top) wind intensity \(U_{10}\) as a function of wave age \(c_p/U_{10}\), and the other three plots depict the spectral bandwidth \(\nu\), directional spread \(\sigma _{\theta }\) and water depth factor \(k_m\,d\) as a function of the maximum significant wave height \(H_s\) of the sea state. The threshold \(k_m d=1.363\) below which modulational instability vanishes is also shown. Red marks denote extreme sea states with normalized maximum crest height \(h/H_s>1.4\). Right panels depict the statistical cumulants of the measured sea states. In particular, the first three top panels depict the surface skewness \(\lambda _3\), bound excess kurtosis \(\lambda _{40}^b\) and dynamic excess kurtosis \(\lambda _{40}^d\) as a function of the directional spread \(\sigma _{\theta }\) of the sea state. The bottom panel depicts the dynamic excess kurtosis as a function of the modulational time scale \(t_{mod}/T_m=0.13/(\nu \sigma _{\theta })\), where \(T_m\) is the mean wave period associated to the mean frequency \(\omega _m=2\pi /T_m\). Red markers indicate sea states exceeding the threshold values specified in the red legend of each respective panel.

Full size image

Results

In this section we first discuss the meteorological and wave characteristics of the measured sea states. Next, we examine the metocean parameters describing the two most intense storms measured at Ekofisk: Borgny in 2006 and Andrea in 200716,17. We then conduct a novel composite statistical analysis of the most severe sea states, accounting for data heterogeneity. The composite probability distribution of crest heights is then estimated from the entire dataset and the most extreme sea states. Hereafter, when a model or method is used, we reference the corresponding Methods subsection.

Table 1 Wave parameters and various statistics of Andrea and Borgny at the storm peak in comparison to El Faro, Draupner and Gaia rogue sea states21. We refer to the Methods subsection “Wave parameters” for definitions.
Full size table

Metocean characteristics

The Ekofisk platform is located in the central North Sea, at approximately 56.55 degrees North and 3.21 degrees East. The surrounding landmasses - continental Europe to the east and south, Scandinavia to the northeast, and the British Islands to the west - are responsible for the predominance of relatively young, fetch-limited sea states under many meteorological conditions. Well-developed sea states and, correspondingly, the largest wave heights, are typically associated with winter storms approaching from the large fetch to the north and northwest of the platform22. Relevant wave parameters are defined in the Methods subsection ”Wave parameters”.

We examine the metocean characteristics of the sea state ensemble relying on the NORA3 wave model hindcast14,23 at the Ekofisk platform for the period \(2003-2020\). To guarantee the stationarity assumption of sea states, drawing on Fedele et al.24, we determined that the optimal sea state duration, \(T_\textrm{sea}\), of 30 minutes minimizes the variation between waves in consecutive sea states during storms. However, in such shorter sea states, estimates of higher-order statistical moments, such as kurtosis, are unreliable, whereas longer sea states violate stationarity. This caveat is further discussed in the Methods subsection “Statistical Unreliability of Kurtosis Estimates.”

The overall statistics of NORA3 hindcast parameters are depicted in Fig. 2. The wave ensemble includes 27505 half-hourly sea states observed from 2003 to 2020. The left panel displays the half-hourly significant wave height \(H_s\) as a function of the ratio \(r=H_\textrm{swell}/H_\textrm{windwaves}\), while the middle panel displays the misalignment between swells and windwaves, i.e., the difference between the dominant swell direction \(\theta _\textrm{swell}\) and the direction \(\theta _\textrm{windwaves}\) of wind waves. Here, \(H_\textrm{swell}\) and \(H_\textrm{windwaves}\) are the hindcast swell and windwave significant wave heights, respectively. The most intense storms (\(H_\textrm{s}>8\) m) exhibit negligible swells, which are also not aligned with wind waves, ruling out the mechanism of rogue wave formation due to wave-current interactions. Furthermore, tidal current data from an Acoustic Doppler Current Profiler (ADCP) at a depth of 10 meters at one of the Ekofisk platforms indicate that 10-minute average current speeds range between 0 and 0.25 m/s, too low to significantly enhance waves. In contrast, along the southeast coast of Africa, the Agulhas Current creates an area of intense wave focusing due to adverse currents, with mean speeds around 1.6 m/s and peaks exceeding 2.5 m/s (see, e.g.25, and references therein).

Additionally, we note that the observed sea states tend to reduce their directional, or angular, spread as they intensify during storms, as clearly depicted in the third panel from the left of Fig. 2. This generic trend can be explained as follows: when the prevailing westerly wind associated with low pressure systems approaching the North Sea from the west, veers towards the northwest as the low pressure dips southward, the broad-banded westerly wind sea may be blocked by the British Islands. This leads to narrow-banded (in both frequency and direction) yet mature sea states in the central North Sea.

Skewness and kurtosis

We consider integral statistics such as the Tayfun steepness \(\mu =\lambda _3/3\) and the excess kurtosis \(\lambda _{40}\) of the zero-mean surface elevation \(\eta (t)\). Wave skewness \(\lambda _3\) describes asymmetric second-order bound nonlinearities, which alter the sea surface with higher, sharper crests and shallower, more rounded troughs1,2,26,27,28. The excess kurtosis measures symmetric nonlinearities due to free-wave resonances, causing more frequent symmetric amplifications of the wave envelope compared to Gaussian sea states. The excess kurtosis comprises a dynamic component7,18 \(\lambda _{40}^{d}\), which measures third-order resonant wave-wave interactions, and a bound contribution \(\lambda _{40}^{b}\), induced by both second-order and higher bound nonlinearities1,2,20,26.

Figure 3 summarizes various estimated wave parameters and statistics of the 27505 sea state records of the Ekofisk dataset. In particular, extreme wind velocities \(U_{10}\) reach values up to 30 m/s and occur in young, undeveloped sea states with a small wave age \(c_p/U_{10}\) (see top-left panel of Fig. 3). Notably, during intense storms (\(H_s>8\) m), rogue waves with crest height \(h>1.4H_s\) occurred in sea states with a small directional spread \(\sigma _{\theta }\approx 30\) [deg], a large frequency spread \(\nu \approx 0.5\) and in intermediate waters, where \(k_m d\approx 1.8-10\). This implies a relatively moderate interaction of large waves with the seabed (for reference, waves are considered in deep waters when \(k_m d>\pi\)24). This is just slightly above the critical threshold 1.363, below which third-order modulational instabilities disappear. Both directional and frequency spread reduce as the sea states become more energetic during the growing phase of the storms (see left column of Fig. 3, second and third panels from the top).

The right panels of Fig. 3 depict statistical cumulants of the measured sea states. In particular, the first three top panels show the surface skewness \(\lambda _3\), bound excess kurtosis \(\lambda _{40}^b\), and dynamic excess kurtosis \(\lambda _{40}^d\) as a function of the directional spread \(\sigma _{\theta }\) of the sea state. The bottom panel depicts the dynamic excess kurtosis \(\lambda _{40}^d\) as a function of the modulational time scale \(t_{mod}/T_m=0.13/(\nu \sigma _{\theta })\), where \(T_m\) is the mean wave period associated with the mean frequency \(\omega _m=2\pi /T_m\). The time scale \(t_{mod}\), introduced by Fedele (2015)7, is the intrinsic time it takes for the dynamic kurtosis of a modulationally unstable sea state to reach its maximum value before decaying to a Gaussian state. Shorter (longer) modulation times imply smaller (larger) dynamic kurtosis.

Skewness is estimated directly from the time series of sea states, whereas the bound and dynamic excess kurtosis are estimated using the theoretical models described in the Methods subsection ”Wave Parameters”. We note that the dynamic excess kurtosis \(\lambda _{40}^d\) is negligible with a very short modulational time scale \(t_{mod}\) less than the mean wave period \(T_m\). Longer times \(t_{mod}\gg T_m\) would have implied enhanced growth of the central waves of ocean groups at the expense of neighboring waves. On the contrary, both skewness \(\lambda _3\) and bound excess kurtosis \(\lambda _{40}^b\) are large during intense sea states implying the dominance of second-order asymmetric bound nonlinearities over the third-order resonance interactions, which are practically insignificant. Finally, we also observe negative values of surface skewness in small-energy sea states where swells are dominant over windwaves (see right panel of Fig. 2).

Fig. 4
figure 4

Borgny and Andrea storms: time history of (left column) surface skewness \(\lambda _{3}\) (left axis) and significant wave height \(H_s\) (right axis), (central column) excess kurtosis \(\lambda _{40}\). Here, the blue line denotes the observed moments estimated from data, whereas the red bold line denotes their moving average. The colored strip denotes the \(95\%\) confidence bands of the moment estimates. The right column depicts the time history of the surface displacement \(\eta =\eta _1+\eta _2+\eta _3\) (black) of the largest wave of the storm and the respective non-skewed free component \(\eta _1\) (red) and the bound second- and third-order components \(\eta _2\) (blue) and \(\eta _3\) (green), respectively.

Full size image

The Borgny and Andrea storms

In this section, we discuss the metocean characteristics of the sea states generated by the two strongest storms observed as they passed through the North Sea: specifically, Borgny in October-November 2006 and Andrea in November 2007. Following Boccotti29 we define a storm as a sequence of 30-min sea states with the significant wave height \(H_s\) that remains above a given threshold, which in our study is set to 4 meters. The metocean parameters of the two storms are compared to those of the simulated El Faro12, Draupner3, and Gaia24 rogue sea states, and are summarized in Table 1. Note that the five sea states all have similar metocean characteristics.

The statistical parameters history for the two analyzed storms is depicted in Fig. (4). For Borgny, in the top row, the first two panels display, from left to right, the hourly variations of the observed skewness \(\lambda _3\) (blue), estimated from data, and significant wave height \(H_s\) (bold black), as well as the observed excess kurtosis \(\lambda _{40}\) (blue). Red bold lines denote their moving average. The same comparisons for Andrea are shown in the bottom panels. The observed values of both skewness and excess kurtosis are erratic due to the short record duration set to respect the sea state stationarity. The large spike in moment estimates for the Andrea storm is due to the famous rogue wave observed in the sample; this spike disappears if the outlier wave is removed from the sample. The colored strip denotes the \(95\%\) confidence intervals of the moment estimates as derived in the Methods subsection ”Statistical Unreliability of Kurtosis Estimates”. The relative error in skewness is roughly \(10-15\%\) and that in excess kurtosis is nearly \(100\%\), or higher. This indicates that excess kurtosis estimates are particularly sensitive to sample size, making them unreliable, whereas skewness estimates remain less affected. Additionally, the nonstationarity of the storm contributes to the variability of these estimates. The assumption that ocean waves remain stationary during a 30-minute sea state is an approximation, as waves continue to receive energy from the growing wind. Quantifying this influence from probabilistic principles remains a challenging problem.

The right panels of Fig. 4 display the time history of the surface displacement \(\eta =\eta _1+\eta _2+\eta _3\) (bold line) for the largest wave of the Borgny and Andrea storms, along with the respective non-skewed free component \(\eta _1\) (red line) and the second-and third-order bound components \(\eta _2\) and \(\eta _3\) (blue and green lines). The methodology used to decompose \(\eta\) into its free and bound wave components27 is described in the Methods subsection ”Non-skewed surface displacements”. Note that \(\eta _3\) is negligible and large waves display sharper crests and rounded troughs due to the asymmetric second-order bound nonlinearities.

Both Borgny and Andrea rogue sea states are short-crested, characterized by small directional spreading and negligible maximum dynamic excess kurtosis of \(O(10^{-3})\), as reported in Table 1. In the open ocean, wave energy is not confined to a long channel and can spread directionally. Third-order quasi-resonant nonlinearities are essentially insignificant3,7,30,31,32,33 in such realistic oceanic conditions3,34,35 and further attenuated by the finite depth24 of the seabed at Ekofisk. In summary, our analysis indicates that NLS-type modulational instabilities play an insignificant role in the formation of large waves3,7, in agreement with recent analysis of available oceanic observations21,36,37,38,39,40,41,42,43,44,45.

In the following statistical analysis, to compare the empirical wave statistics with probabilistic models, which functionally depend on Tayfun steepness \(\mu =\lambda _3/3\) and kurtosis, we estimate \(\mu\) using the observed skewness, while the dynamic and bound kurtosis are estimated from the respective theoretical models (see Methods subsection Wave Parameters). This aligns with previous statistical analyses2,21,24 showing good agreement between theory and measurements when using observed skewness \(\lambda _3<0.6\) to estimate Tayfun steepness as proven in46. The values of excess kurtosis \(\lambda _{40}\approx 18\mu ^2\) are primarily due to bound nonlinearities and depend quadratically on the Tayfun stepness \(\mu\) (see Methods subsection ”Wave Parameters”). Clearly, if wave statistics are based solely on the sample of waves within the 30-minute sea state of the Andrea rogue wave, which contains \(O(10^2)\) waves, the rogue wave would appear as an outlier in the small sample. However, we propose a composite statistical approach that accounts for the heterogeneity of the 27, 500 sea states analyzed in this study. This is achieved through a weighted average of the statistical properties of each sea state, ensuring that the Andrea wave is not an outlier within a larger sample of \(O(10^6)\) waves.

Fig. 5
figure 5

Ekofisk dataset: composite crest and trough exceedance probabilities of (top row) the ensemble of sea states whose \(H_s>4\) m (\(1.5\cdot 10^6\) waves) and (bottom row) same statistics of the the ensemble of the severest sea states with Tayfun steepness \(\mu =\lambda _3/3>0.07\) and \(\sigma _{\theta }<30\) [deg] (\(3.2\cdot 10^4\) waves). Left plots: the contribution of each sea state to the wave statistics is weighted by the values of the Tayfun steepness \(\mu\) and directional spread \(\sigma _{\theta }\). Middle plots depict the statistics of crest and trough heights of the nonlinear \(\eta\), and the same statistics for the non-skewed free component \(\eta _1\) is depicted in the right plots. Marks denote empirical distributions from data of crest heights (square) and trough heights (circle), R=Rayleigh (dash line), F=3D Forristall (black), TF=\(3^{\textrm{rd}}\) Tayfun-Fedele (red), MNB=Modified-Narrow-Band (green) and NLS15 (blue) models.

Full size image
Fig. 6
figure 6

Composite wave statistics based on wave age of sea states. Top row panels: skewness \(\lambda _3\), excess bound and dynamic kurtosis \(\lambda _{40}^b\) and \(\lambda _{40}^d\) and maximum crest height \(h/H_s\) as a function of wave age \(c_p/U_{10}\) for the Ekofisk ensemble of sea states (squares). Red circles denote sea states whose maximum crest height \(h/H_s>1.4\). Middle and bottom row panels: composite crest and trough exceedance probabilities of the ensembles of developed sea states whose wave age \(c_p/U_{10}>1\) (\(7.0\cdot 10^5\) waves) and that of the youngest sea states whose wave age \(c_p/U_{10}<1\) (\(7.4\cdot 10^5\) waves). Left plot: the contribution of each sea state to the wave statistics is weighted by the values of the Tayfun steepness and wave age. Middle plot depicts the statistics of crest and trough heights of the nonlinear \(\eta\), and the same statistics for the non-skewed free component \(\eta _1\) is depicted in the right plot. Marks denote empirical distributions from data of crest heights (square) and trough heights (circle), R=Rayleigh (dash line), F=3D Forristall (black), TF=\(3^{\textrm{rd}}\) Tayfun-Fedele (red), MNB=Modified-Narrow-Band (green) and NLS15 (blue) models.

Full size image
Fig. 7
figure 7

Ekofisk dataset: joint probability density function of the normalized crest height \(h_C/\sigma\) and trough heights \(h_T/\sigma\) of the non-skewed free surface displacements \(\eta _1\) and nonlinear \(\eta\) of the ensemble of sea states with \(H_s>4\) m.

Full size image

Composite wave statistics

We now describe the statistics of rogue waves encountered by a fixed observer at the Ekofisk platform. Following Dysthe et al.47, a wave is defined as rogue if its crest height \(h>1.25 H_s\) and the crest-to-trough (wave) height \(H>2 H_s\), where \(H_s\) is the significant wave height of the sea state in which the rogue wave occurred. Drawing on Fedele15, the statistical deviations of extreme waves from Gaussianity are examined by a new probabilistic distribution of crest heights that accounts for both second-order and third-order modulational instability effects, hereafter referred to as the NLS model (see Methods subsection ”The NLS model for crest heights” for derivation). Comparisons against well-known second-order models are also presented.

Wave statistics is typically analyzed for stationary sea states. However, when considering the 18-year ensemble of sea states measured at Ekofisk with varying and diverse metocean parameters, the statistical models need to be adapted for non-stationary data. Estimating the statistics using overall averages of wave parameters may yield an underestimation of exceedance probabilities, as stronger and weaker sea states are weighted with the same importance. In such cases, composite wave statistics provide a framework to analyze waves in diverse metocean conditions. To achieve this, we draw on Fedele48,49 to define a composite probability structure of a heterogeneous ensemble of sea states, as described in the Methods subsection ”Composite wave statistics”.

The variability of the standard deviation \(\sigma\), or significant wave height \(H_s=4\sigma\), is taken into account by normalizing the surface height measurements of each 30-minute sea state by the respective observed \(\sigma\). For the data set at hand, we choose the Tayfun steepness \(\mu =\lambda _3/3\) and the directional spread \(\sigma _{\theta }\) as the wave parameters to classify and bin the sea states of the Ekofisk ensemble. Adding a third, or fourth parameter in the classification of sea states yields practically the same results. The parameter values are collected in bins of size \((\Delta \mu ,\Delta \sigma _{\theta })\) centered at \(\mu _i,\sigma _{\theta _j}\), with \(i=1,\dots N_{\mu },j=1,\dots N_{\sigma _{\theta }}\), where \(N_{\mu }\) and \(N_{\sigma _{\theta }}\) are the number of bins. The weight \(W_{i,j}\) is the fraction of number of sea states whose \(\mu\) and \(\sigma _{\theta }\) values are within the ranges \([\mu _i\pm \Delta \mu ]\) and \([\sigma _{\theta _j}\pm \Delta {\sigma _{\theta }}]\) relative to the total number of sea states (see left panel on the top of Fig. 5). We aim to estimate the probability of randomly picking a wave from the ensemble whose crest or trough height exceeds the normalized threshold \(\xi H_s\). This is the probability, or occurrence frequency \(P^{(C)}_\mathrm{{ex}}(\xi )\), of wave crest and trough heights exceeding a given threshold \(\xi H_s\) as encountered by a fixed observer. The composite probability of exceedance for crest or trough heigths

$$\begin{aligned} P^{(C)}_\mathrm{{ex}}(\xi )=\sum _{i,j} W_{i,j} P(\xi |\mu _i,\sigma _{\theta _j}) \, \end{aligned}$$

is determined by the weighted sum of the stationary conditional probabilities \(P_\mathrm{{ex}}(\xi |\mu _i,\sigma _{\theta _j})\), with the sum running over the number of bins. Hereafter, the conditional crest exceedance probability is described by the NLS15 model. For comparisons, we also consider the third-order Tayfun-Fedele26 (TF), modified narrow-band46 (MNB), Tayfun1,2 (T), 3D-Forristall28 (F) and the linear Rayleigh (R) distributions (see respective Methods subsections for model definitions). For trough heights, we consider the MNB model.

The top panels of Fig. 5 describe the composite crest and trough exceedance probabilities of the ensemble of approximately 14300 sea states with \(H_s>4\) m. The ensemble includes approximately 1.5 million waves. For such large samples, the confidence bands15 are tightly aligned with the predicted probabilities, and have been omitted for clarity in the plots. The top-middle panel depicts the composite probabilities of exceedance of crest and trough heights of the nonlinear \(\eta\). Deviations from the Rayleigh distribution are observed. Specifically, the asymmetry of crest and trough heights is evident, and the observed crest exceedance probabilities are well explained by the second-order F (black), TF (red) and MNB (green) models. The TF model is practically the same as the MNB model, indicating that second-order effects dominate in shaping the sea surface. The NLS model also describes the statistics reasonably well as a tight upper bound, implying that third-order modulational instabilities are essentially insignificant. This is further confirmed by the same statistics for the non-skewed free component \(\eta _1\), depicted in the right panel of the top row. The procedure to de-skew the time series relies on the narrowband approximation, and it is able to reduce about \(95-97\%\) of the bound-wave, or crest-trough, asymmetry. This is because large waves are narrowband2,36. This implies that crest and trough distributions are nearly identical and close to Gaussian, indicating negligible effects of both dynamic and bound kurtosis. This is also corroborated by the very small value of the parameter \(\chi =\Lambda /16\approx \lambda _{40}/6~\sim ~[0.017-0.033]\) of the NLS model, which is proportional to the excess kurtosis \(\lambda _{40}\). This just accounts for the bound excess kurtosis \(\lambda ^{b}_{40}\) since the dynamic component is insignificant as shown in the top panels of Fig. 6. An exact reduction of the bound-wave asymmetry is practically unfeasible as it would require estimating the complex Fourier components (amplitudes and phases), or complex directional spectrum, of the non-skew wave field using the multidirectional Stokes expansion2 from short time series to guarantee stationarity. However, as discussed above, this would lead to unreliable estimates of higher order correlators involved in the inversion procedure.

Similar conclusions apply for the composite statistics of crest and trough heights of the ensemble of the severest sea states with Tayfun steepness \(\mu =\lambda _3/3>0.07\) and \(\sigma _{\theta }<30\) [deg] displayed in the bottom row of Fig. 5. This ensemble includes approximately \(3.2\cdot 10^4\) waves. Here, the crest and trough exceedance probabilities of the non-skewed free component \(\eta _1\) are nearly identical, further indicating that second-order bound nonlinearities shape large waves of the severest sea states, in agreement with recent statistical analyses of ocean measurements21,37,38,39,40,41,42,43,45,50.

We also carried out composite wave statistics based on the wave age of sea states. The top panels of Fig. 6 display skewness \(\lambda _3\), excess bound and dynamic kurtosis \(\lambda _{40}^b\) and \(\lambda _{40}^d\), and maximum crest height \(h/H_s\) as a function of the wave age \(c_p/U_{10}\) for the ensemble of all sea states. Rogue waves with crest heights \(h/H_s>1.4\) occurred in younger sea states with \(c_p/U_{10}<1\), characterized by larger skewness and bound kurtosis but negligible dynamic kurtosis. The composite crest and trough exceedance probabilities for the ensemble of these youngest sea states (\(7.4\cdot 10^5\) waves) are shown in the middle panels of Fig. 6. For these observed young seas, kurtosis is primarily dominated by the bound component, which exceeds that of more developed old seas (\(c_p/U_{10}>1\)), as shown in the top panels of Fig. 6. The negligible dynamic kurtosis suggests that the bound kurtosis reflects the steepening of wave crests in energetic young seas.

In summary, third-order MI is absent in the observed young seas, and the statistics are well described by second-order nonlinearities affecting skewness and bound kurtosis. Similar conclusions hold for the ensemble of the most developed sea states with \(c_p/U_{10}>1\) (approximately \(7.6\cdot 10^5\) waves), which exhibit a less pronounced bound kurtosis, as shown in Fig. 6. Finally, the crest-trough asymmetry is clearly evident in Fig. 7, which displays the unconditional joint probability density function of the normalized crest height \(X=h_C/\sigma\) and trough heights \(Y=h_T/\sigma\) of the non-skewed free surface displacements \(\eta _1\) and nonlinear \(\eta\) of the Ekofisk ensemble of sea states with \(H_s>4\) m. Note that the ensemble is not ordered: in the binning process, the crests and troughs are not picked from the same wave. On average, the non-skewed crest and trough amplitudes are symmetric (\(X\sim Y)\), whereas those of the nonlinear \(\eta\) are not, since \(X\sim 2Y\).

Fig. 8
figure 8

Comparison of models for dynamic excess kurtosis as a function of the directional spreading parameter R. The left panel shows the Fedele (2015)7, Mori et al. (2011)51, and Janssen and Bidlot (2009)18 models. The right panel illustrates the ratio r between the two models by Mori et al. and Fedele.

Full size image

Our results differ from the recent conclusions of Toffoli et al. (2024)52, who reported field measurements suggesting that resonant interactions are evident in young sea states in the Southern Ocean. We note that their wave analysis does not account for skewness and relies solely on the observed kurtosis, which is estimated from short stereo video wave measurements. Such estimates may have limitations in statistical reliability, as explained in the Methods subsection ”Statistical Unreliability of Kurtosis Estimates”.

Moreover, in their study, the estimation of dynamic kurtosis for multidirectional seas is essential for determining the dominance of MI relative to bound nonlinearities. However, their predictions of dynamic kurtosis rely on an inadequate approximation by Mori et al. (2011)51 of an incorrect model originally derived by Janssen and Bidlot (2009)18. The correct model was derived by Fedele (2015)7 and later reconfirmed by Janssen and Janssen (2019)53. We note that Toffoli et al52. reported an incorrect form of Mori et al. approximation51 in their paper, which may have been a typographical error. It remains unclear whether the authors actually used the original approximation in their study or the altered version reported in their paper. Regardless, Mori et al.51 approximation consistently overestimates the correct dynamic kurtosis for all values of the directional spreading parameter R, as demonstrated below.

The correct dynamic excess kurtosis was derived by Fedele (2015)7 by solving a six-fold integral and is given by the practical formula

$$\begin{aligned} \lambda _{40}^{d,\text {Fedele}}= 3 BFI^2 \frac{b}{(2\pi )^2}\frac{1-R}{R + b R_0}, \quad 0 \le R \le 1\,, \end{aligned}$$

where BFI is the Benjamin-Feir index, and the coefficients \(R_0 = 3\sqrt{3}/(4\pi ^3)\) and \(b = 2.48\) (see Methods subsection ”Wave parameters” for definitions). The incorrect model by Janssen and Bidlot (2009)18 is given when \(b = 1\). The dynamic kurtosis vanishes at \(R = 1\), denoting the transition between focusing (\(R<1\)) and defocusing (\(R>1\)) regimes. Indeed, for broader directional seas (\(R> 1\)), the wave dynamics is of the defocusing type, modulational instability is absent, and the dynamic excess kurtosis is always negative6,7, that is \(\lambda _{40}^{d}(R) = -\lambda _{40}^{d}(1/R)/R\). In contrast, the approximation by Mori et al. (see Eq. 40 given in their paper51)

$$\begin{aligned} \lambda _{40}^{d,\text {Mori et al.}} = BFI^2 \frac{\pi }{\sqrt{3}} \frac{1}{1 + 7 R}, \quad 0 \le R \le 1\,, \end{aligned}$$

does not vanish at \(R=1\) as it should, leading to a discontinuity. Moreover, Toffoli et al.52 reported a modified form in their paper that replaces the factor \(1/(1 + 7 R)\) with its square \(1/(1+7R)^2\) instead (see their Eqs. 1 and 3). While this may have been an inadvertent typographical error, it nevertheless violates the theoretical limits for both small and large R-values7,18.

For comparison, the left panel of Fig. 8 displays the various dynamic kurtosis models referenced in this study, and the right panel shows the ratio r between the two models by Mori et al. and Fedele, plotted as a function of the directional spreading parameter R. From this, it is evident that the approximation by Mori et al. consistently overestimates the correct dynamic kurtosis for all values of R. It also exhibits a nonphysical discontinuity across \(R=1\).

In the directional spreading range \(0.5< R < 18\), which corresponds to the young sea states where Toffoli et al.52 claim MI is significant (see Figure 2 in their paper), the Mori et al. model significantly overestimates dynamic excess kurtosis by more than a factor 3. Notably, for the directionally broader young seas (\(R>1\)), dynamic excess kurtosis is always negative, suggesting that MI was likely ineffective in most of their analyzed young sea states. Our analysis indicates that steepening effects increase the bound component of kurtosis and may be misinterpreted as due to MI if kurtosis and its bound and dynamic components are improperly estimated.

Conclusions

We have analyzed a dataset of high-frequency laser altimeter wave measurements at the offshore Ekofisk platform in the central North Sea. Our findings show that kurtosis estimates from 30-minute records are unreliable due to the short duration, making them highly sensitive to outliers, or large waves. Longer records would stabilize these estimates, but stationarity is violated. In contrast, estimates of third-order moments, or wave skewness, are less affected by sample variability.

The measurements indicate that wave surface displacements are primarily skewed by second-order bound nonlinearities, resulting in a crest-trough, or bound-wave, asymmetry reflected in the wave statistics. An analysis of a composite dataset of severe sea states implies that third-order MI has no discernible effect on large-wave statistics, with the dominant second-order bound-wave asymmetry mainly enhancing the linear dispersive focusing of extreme waves. A new probabilistic NLS model for crest heights is introduced to examine statistical deviations of extreme waves from Gaussianity due to both second-order nonlinearities and MI effects. The new model describes the wave statistics reasonably well implying that MI is insignificant. In energetic younger seas, steeper wave crests exhibited larger skewness and bound kurtosis compared to older seas. Across all analyzed sea states, dynamic kurtosis was negligible, indicating that MI played no significant role in shaping large waves.

Methods

Ekofisk measurements

The wave surface elevation measurements were made on the ConocoPhillips Norway-operated Ekofisk oil and gas platform complex in the central North Sea. The water depth in the area of the wave measurements is approximately 70 m. The measurements consist of 5-Hz range measurements by four Optech infrared laser altimeters located on a footbridge oriented approximately southwest-northeast that connects two neighboring platforms, Ekofisk 2/4 K to the east and 2/4 B to the west. The 5-Hz dataset covers the period 2003-2020, and the quality control, including the despiking algorithm and criteria for discarding corrupted data, is described by Malila et al.54. As in the preliminary data analysis presented by Malila et al.13, the four co-located laser altimeter signals are combined such that the highest quality signal is prioritized. In cases where a full 20-minute sea state measurement from the primary laser signal is corrupted, the dataset is patched by one of the remaining three laser signals, if available. As reported by Malila et al.13, the quality control effectively discards the majority of all available data from sea states with \(H_\textrm{s} < 3 \textrm{m}\). Directional sea state parameters were obtained from the NORA3 wave hindcast14, produced using the WAM cycle 4.7.0 wave model with wind forcing from the NORA3 atmospheric hindcast23. The wave model hindcast has a horizontal spatial resolution of 3 km and outputs hourly integrated parameters.

Wave parameters

The significant wave height \(H_s\) is defined as the mean value \(H_{1/3}\) of the highest one-third of wave heights. It can be estimated from a zero-crossing analysis or approximately as \(H_s \approx 4\sigma\), from the wave omnidirectional spectrum \(S_o(f)=\int _{0}^{2\pi } S(f,\theta )\textrm{d}{\theta }\), where \(\sigma =\sqrt{m_0}\) is the standard deviation of surface elevations, and \(m_j=\int S_o(f) f^j\textrm{d}f\) are spectral moments. Here, \(S(f,\theta )\) is the directional wave spectrum, \(\theta\) is the direction of waves at frequency f, and the cyclic frequency is \(\omega =2\pi f\). In this work, we use the spectral-based estimate, which is \(5\%-10\%\) larger than \(H_{1/3}\) estimated from the measured time series.

The cyclic frequency \(\omega _p\) of the spectral peak defines the dominant wave period \(T_{p}=2\pi /\omega _p\). The mean zero-crossing wave period \(T_{0}\) is equal to \(2\pi /\omega _0\), with \(\omega _0=2\pi \sqrt{m_2/m_0}\). The associated wavelength \(L_{0}=2\pi /k_0\) follows from the linear dispersion relation \(\omega _0 = \sqrt{gk_0 \tanh (k_0 d)}\), with d the water depth. The mean spectral frequency is defined as \(\omega _{m}=2\pi m_{1}/m_{0}\)1 and the associated mean period \(T_m\) is equal to \(2\pi /\omega _m\). A characteristic wave steepness is defined as \(\mu _m=k_m\sigma\), where \(k_{m}\) is the wavenumber corresponding to the mean spectral frequency \(\omega _{m}\)1. We also define the following parameters: \(q_m = k_m d, Q_m = \tanh q_m\), the phase velocity \(c_m = \omega _m/k_m\), and the group velocity \(c_g=c_m\left[ 1+2q_{m}/\mathrm {sinh(2}q_{m})\right] /2\).

The wave age \(c/U_{10}\) is defined as the ratio of the characteristic phase speed of surface waves to the wind speed measured at \(10-m\) height. The wave age is an indicator of the wind’s impact and wave growth. We choose \(c_{p}=\omega _p/k_p\) as the phase speed at the spectral peak. Young seas have small wave age and the wave field experiences strong wind forcing, leading to high wave growth rates. In contrast, as the wave age approaches unity, wave growth decreases significantly55.

Frequency spreading is measured by the spectral bandwidth \(\nu =(m_0 m_2/m_1^2-1)^{1/2}\), and the angular spreading \(\sigma _{\theta }=\sqrt{\int _0^{2\pi }D(\theta )(\theta -\theta _m)^2 \textrm{d}\theta }\), where \(D(\theta )=\int _0^{\infty }S(\omega ,\theta )\textrm{d}\omega /\sigma ^2\), and \(\theta _m=\int _0^{2\pi }D(\theta )\theta \textrm{d}\theta\) is the mean direction. Note that \(\omega _0=\omega _m\sqrt{1+\nu ^2}\). An alternative measure of spectral bandwidth is given by the Boccotti parameter \(\psi ^{*}=\psi (\tau ^{*})\). This is given by the absolute value of the first minimum of the normalized covariance function \(\psi (\tau )=\overline{\eta (t)\eta (t+\tau )}/\sigma ^{2}\) at \(\tau =\tau ^{*}\)29, and \(\eta (t)\) is the zero-mean surface wave displacements.

The wave skewness \(\lambda _3\) and the excess kurtosis \(\lambda _{40}\) of the zero-mean surface elevation \(\eta (t)\) are given by

$$\begin{aligned} \lambda _3=\overline{\eta ^3}/\sigma ^3,\qquad \lambda _{40}=\overline{\eta ^4}/\sigma ^4-3 \,. \end{aligned}$$
(2)

Here, overbars denote statistical averages and \(\sigma\) is the standard deviation of surface wave elevations. The excess kurtosis of weakly nonlinear random seas

$$\begin{aligned} \lambda _{40}=\lambda _{40}^{d}+\lambda _{40}^{b} \end{aligned}$$
(3)

comprises a dynamic component \(\lambda _{40}^{d}\) due to nonlinear quasi-resonant wave-wave interactions6,18 and a Stokes bound harmonic contribution \(\lambda _{40}^{b}\)20. In deep water it reduces to the simple form \(\lambda _{40,NB}^{b}=18\mu _m^{2}=2\lambda _{3,NB}^2\)6,20,56 where \(\lambda _{3,NB}\) is the skewness of narrowband waves1. In deep water, the dynamic component \(\lambda _{40}^{d}\) is given in terms of a six-fold integral7

$$\begin{aligned} \lambda _{40}^{d}(t)=6\, BFI^2 \textrm{Im} \int _0^{\nu ^2 \omega _m t} \frac{1}{\sqrt{1-2 i\alpha + 3\alpha ^2}} \frac{1}{\sqrt{1-2 i R \alpha + 3 R\alpha ^2}}\,\textrm{d}\alpha \,. \end{aligned}$$
(4)

Here, \(i=\sqrt{-1}\), \(\textrm{Im}(x)\) denotes the imaginary part of x, the Benjamin-Feir index \(BFI=\sqrt{2}\mu _m/\nu\) and the directional spreading parameter \(R=\sigma _{\theta }^{2}/2\nu ^{2}\) is a dimensionless measure of the multidirectionality of dominant waves6,7,51. In the focusing regime (\(0<R<1\)) the maximum dynamic kurtosis attains at the modulation time scale \(\omega _m\,t_{mod}=(\nu ^2 \sqrt{3\,R})^{-1}\), or \(t_{mod}/T_m\approx \,0.13/(\nu \sigma _{\theta })\). The dynamic excess kurtosis maximum is well approximated by7

$$\begin{aligned} \lambda _{40}^{d,\textsf{max}}=3 BFI^2 \frac{b}{(2\pi )^2}\frac{1-R}{R + b R_0}\,\quad 0\le R\le 1\,, \end{aligned}$$
(5)

where \(R_0=3\sqrt{3}/(4\pi ^3)\) and \(b=2.48\). In contrast, in the defocusing regime (\(R>1\)) the dynamic excess kurtosis is always negative and \(\lambda _{40}^{d}(R)=-1/R\,\lambda _{40}^{d}(1/R)\)6,7. The extension to intermediate water depth d readily follows by redefining the Benjamin-Feir Index as \(BFI_d=\alpha _S\, BFI\)18,57, where the depth factor \(\alpha _S\) depends on the dimensionless depth \(k_m\,d\) (see, for example24). In the deep-water limit, \(\alpha _S\) becomes 1. As the dimensionless depth \(k_m\,d\) decreases, \(\alpha _S\) decreases and becomes negative for \(k_m\,d<1.363\) and so does the dynamic excess kurtosis as an indication that modulation instability is not active (defocusing regime).

Fig. 9
figure 9

Estimates of skewness and excess kurtosis (right) as functions of the sample size: (right) the 30-minute sea state during the Andrea rogue wave event (\(H_s = 10\) m, 9000 samples at 5 Hz) and (right) stereo measurements of a 20-minute sea state with \(H_s = 7.5\) m over a trapezoidal imaged area that extends over a field of \(140 \times 150\) m\(^2\) (\(N_s\approx 56^3\) spatial points at 0.5 m resolution, with 6000 temporal samples at each point at 5 Hz). Both datasets were recorded at the Ekofisk ___location. The top panels display time series of surface elevations, while the bottom panels show estimates of skewness and excess kurtosis as functions of sample size, along with \(95\%\) confidence bands. Here, N is the sample size, while \(N_s\) is the number of stereo-imaged spatial points.

Full size image

Statistical unreliability of kurtosis estimates

Probabilistic wave models functionally depend on skewness \(\lambda _3\) and excess kurtosis \(\lambda _{40}\), rather than on the full kurtosis \(3+\lambda _{40}\). As a result, we are concerned about the reliability of these estimates from wave measurements. The nonstationarity of ocean waves limits the use of long records for estimating such high-order statistical moments. Shorter sea states yield unstable kurtosis estimates, whereas longer sea states violate stationarity. Excess kurtosis is highly sensitive to outliers; the presence or absence of a single large wave in small samples can significantly alter the estimate. In contrast, larger samples provide more stable estimates by averaging out extreme values over numerous observations. The sample endpoints also influence estimates in small sea states. If a large wave occurs near the beginning or end of a sample, it can artificially inflate excess kurtosis, whereas if the sample excludes extreme waves, kurtosis may be underestimated.

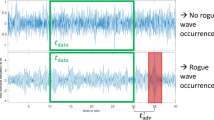
As an example, consider Figure 9, where we present estimates of wave skewness and excess kurtosis from time records of surface elevations analyzed in this study, as well as from stereo measurements13, as a function of the sample size. Specifically, the left panels of the figure display (top) the 30-minute sea state time series of the Andrea rogue wave with a significant wave height of \(H_s = 10\) m and (bottom plots) estimates of skewness and excess kurtosis as functions of sample size, where the sea state duration of \(30\text { min}\) corresponds to the maximum size of \(30~\text {min} \times 60~\text {s} \times 5~\text {Hz} = 9000\) samples. The \(95\%\) confidence bands derived below are also displayed. Kurtosis estimates remain highly sensitive to the presence of large waves in the sample, causing abrupt jumps in value, whereas skewness estimates are less affected by large waves as the sample size increases. Similar conclusions hold for the stereo measurements shown in the right panels (\(H_s = 7.5\) m), where the kurtosis is estimated from space-time stereo data blocks that grow in size with the duration time of the sample. Although jumps in the kurtosis are still observed, they appear less abrupt. This smoothing effect is attributed to the broader spatial coverage and the spatial correlation of the wave field where several wave packets are captured within the stereo-imaged ___domain (maximum temporal size of \(20~\text {min} \times 60~\text {s} \times 5~\text {Hz} = 6000\) samples and \(N_s\approx 56^3\) stereo-imaged spatial points at 0.5-m resolution). In contrast, when a single-point time series is extracted from the stereo data, the kurtosis shows abrupt jumps similar to those seen in the point measurements in the left panel.

We can derive the theoretical expected value and variance of the skewness and excess kurtosis estimators:

$$\begin{aligned} \hat{\lambda }_3 = \frac{\sum _{n=1}^N X_n^3}{N}, \quad \hat{\lambda }_{40} = \frac{\sum _{n=1}^N X_n^4}{N} - 3, \end{aligned}$$

where the measurements \(X_1, \dots , X_N\) are assumed stochastically independent and sampled from a zero-mean, non-Gaussian variable X with unit variance. Correct to first order \(O(\lambda _3,\lambda _{40})\), the probability density function of X is given by the truncated third-order Gram-Charlier series:

$$\begin{aligned} p_X(x) = \frac{\exp \left( -\frac{x^2}{2}\right) }{\sqrt{2 \pi }}\left[ 1+\frac{\lambda _3}{3!} H_3(x) + \frac{\lambda _4}{4!} H_4(x)\right] , \end{aligned}$$

where the Hermite polynomials are \(H_3(x) = x^3-3x\) and \(H_4(x) = x^4-6x^2+3\). From this expansion, the third and fourth moments follow as \(E[X^3] = \lambda _3\) and \(E[X^4] = 3+\lambda _{40}\), where E[X] is the statistical average, or expected value, of X.

The mean and variance of the skewness estimator \(\hat{\lambda }_3\) are derived as follows:

$$\begin{aligned} E[\hat{\lambda }_3] = \frac{\sum _{n=1}^N E[X_n^3]}{N} = \lambda _3, \quad \text {Var}[\hat{\lambda }_3] = \text {Var}\left[ \frac{\sum _{n=1}^N X_n^3}{N}\right] = \frac{\text {Var}[X^3]}{N}\,, \end{aligned}$$

where \(\text {Var}[X]\) is the variance of X. Since

$$\begin{aligned} \text {Var}[X^3] = E[X^6] - (E[X^3])^2 \approx 15(1+\lambda _{40}) - \lambda _3^2, \end{aligned}$$

we obtain, to first order,

$$\begin{aligned} E[\hat{\lambda }_3] = \lambda _3, \quad \text {Var}[\hat{\lambda }_3] = \frac{15(1+\lambda _4)}{N}+O(\lambda _3^2/N)\,, \end{aligned}$$

where quadratic terms are neglected, as the Gram-Charlier series is truncated at first order in skewness and excess kurtosis. Similarly, for the excess kurtosis estimator, to first order, we find:

$$\begin{aligned} E[\hat{\lambda }_{40}] = \lambda _{40}, \quad \text {Var}[\hat{\lambda }_{40}] = \frac{96 + 204\lambda _{40}}{N}+O(\lambda _{40}^2/N)\,. \end{aligned}$$

Both estimators are unbiased, as their statistical expectations match the theoretical values. For a sample size of \(N = 9000\) corresponding to a 30-min sea state (sampling frequency 5 Hz), skewness \(\lambda _3\) in the range \([0-0.6]\) and excess kurtosis \(\lambda _{40}\) in \([0-0.3]\), the \(95\%\) confidence semi-interval, or error, depends primarily on the sample size:

$$\begin{aligned} e_{\lambda _3} = 1.96\sqrt{\text {Var}[\lambda _3]}\sim 0.08-0.10\,, \end{aligned}$$

for skewness, and

$$\begin{aligned} e_{\lambda _{40}} = 1.96 \sqrt{\text {Var}[\lambda _{40}]} \sim 0.20-0.26\,, \end{aligned}$$

for excess kurtosis. The relative error in skewness is \(10-16\%\), whereas that in excess kurtosis is \(80-100\%\), indicating that kurtosis estimates are highly unreliable due to their strong dependence on sample size. In contrast, skewness estimates are much less affected and remain relatively stable. The errors are mildly dependent on skewness and kurtosis within the characteristic range of oceanic seas, so that \(e_{\lambda _3}\approx 1.96 \sqrt{15/N}\) and \(e_{\lambda _{40}}\approx 1.96\sqrt{96/N}\) with good approximation.

We conclude that both skewness and kurtosis estimates from field data are influenced by the limited duration and small sample sizes. However, kurtosis estimates are particularly sensitive to sample size, whereas skewness estimates remain less affected by it. To compare the observed wave statistics with probabilistic models, which functionally depend on Tayfun steepness \(\mu =\lambda _3/3\) and kurtosis, we estimate \(\mu\) using the observed skewness, while the dynamic and bound kurtosis are estimated from the respective theoretical models (see Methods subsection Wave Parameters). This is consistent with previous statistical analyses2,21,24, which demonstrate a good agreement between theoretical predictions and measurements when estimating Tayfun steepness using observed skewness \(\lambda _3<0.6\), as established in46.

Composite wave statistics

Drawing on Fedele49, the statistics of waves of an ensemble of heterogeneous sea states with different metocean parameters is formalized as follows. For example, consider the wave crest height h of a wave in the ensemble. The associated probability density function (pdf) is defined as

$$\begin{aligned} p^{(C)}_h(x)=\int \cdots \int p_h(x|b_1,b_2,\cdots ,b_M)\,p(b_1,b_2,\cdots ,b_M)\,\text {d}\,b_1\text {d}\,b_2\cdots \text {d}\,b_M\,, \end{aligned}$$
(6)

where \(\{b_j\}_{j=1,M}\) are M wave parameters of the sea state, e.g., the Tayfun steepness \(\mu\), directional spread \(\sigma _{\theta }\), among others. In the preceding expression \(p_h(x|b_1,b_2,\cdots ,b_M)\) is the conditional pdf of a wave crest in a sea state with given parameters \(b_j\) whose height h is in the interval \([x,x+\textrm{d}\,x]\) and \(p(b_1,b_2,\cdots ,b_M)\) is the joint pdf of the parameters whose values are in the intervals \([b_1,b_1+\textrm{d}\,b_1,\cdots b_M,b_M+\textrm{d}\,b_M]\), which encodes the heterogeneity of the sea state ensemble. Eq. (6) can be interpreted as the average value of \(p_h(x|b_1,b_2,\cdots ,b_M)\) with respect to the random variables \(b_j\), that is,

$$\begin{aligned} p^{(C)}_h(x)=\overline{p_h(x|\textbf{b})}^{\textbf{b}}\,, \end{aligned}$$
(7)

where the random vector \(\textbf{b}=(b_1,b_2,\cdots ,b_M)\) and the labeled overline denotes the statistical average with respect to \(\textbf{b}\) only. Taylor expanding around the mean \(\overline{\textbf{b}}\), up to the second order, yields

$$\begin{aligned} p^{(C)}_h(x)=p_h(x|\overline{\textbf{b}})+\textbf{g}^{\textsf{T}}(\overline{\textbf{b}})(\textbf{b}-\overline{\textbf{b}})+\frac{1}{2}(\textbf{b}-\overline{\textbf{b}})^{\textsf{T}}\textbf{H}(\overline{\textbf{b}})(\textbf{b}-\overline{\textbf{b}})\,, \end{aligned}$$
(8)

where \(\textsf{T}\) denotes matrix transposition, the vector \(\textsf{g}\) and the Hessian matrix have entries

$$\begin{aligned} \left[ \textsf{g}(\overline{\textbf{b}})\right] _j=\frac{\partial p_h(x|b_1,b_2,\cdots ,b_M)}{\partial _{b_j}}\Bigg |_{\textbf{b}=\overline{\textbf{b}}}\,,\quad \left[ \textsf{H}(\overline{\textbf{b}})\right] _{ij}=\frac{\partial ^2 p_h(x|b_1,b_2,\cdots ,b_M)}{\partial _{b_i}\partial _{b_j}}\Bigg |_{\textbf{b}=\overline{\textbf{b}}}\,. \end{aligned}$$
(9)

From Eq. 7, taking the stochastic average yields

$$\begin{aligned} p^{(C)}_h(x)=p_h(x \big |\overline{b}_1,\overline{b}_2,\cdots ,\overline{b}_M)+\sum _{i j} \left[ \frac{\partial ^2 p_h(x|b_1,b_2,\cdots ,b_M)}{\partial _{b_i}\partial _{b_j}}\right] _{\textbf{b}=\overline{\textbf{b}}} B_{i j}\,, \end{aligned}$$
(10)

where

$$\begin{aligned} \textbf{B}=[B_{ij}]=(\textbf{b}-\overline{\textbf{b}})^{\textsf{T}}(\textbf{b}-\overline{\textbf{b}})\, \end{aligned}$$
(11)

is the correlation matrix of the M parameters, in particular \(B_{jj}\) is the variance of \(b_j\). The correlation coefficients \(B_{ij}\) can be easily estimated from the nonstationary time series of the surface elevation. As a result, the composite pdf in Eq. 10 is the sum of (i) the conditional pdf \(p_h(x|\overline{\textbf{b}})\) on the average parameters, and (ii) additional terms that account for the spreading of the parameters from their mean values. This implies that in a heterogeneous ensemble, the first term \(p_h(x|\overline{\textbf{b}})\) alone may yield misleading results as the intrinsic variance of the parameters and their correlations are neglected.

In practice, the composite \(p^{(C)}_h(x)\) is estimated by approximating the integration in Eq. 6 as the weighted average24

$$\begin{aligned} p^{(C)}_h(x)=\frac{\sum p_h(x|b_{j_1},b_{j_1},\dots ,b_{j_M}) W_{j_1,j_2,\dots j_M}}{\sum W_{j_1,j_2,\dots j_M}}\,, \end{aligned}$$
(12)

where the weight \(W{j_1,j_2,\cdots j_M}\) is the number of sea states of the heterogeneous ensemble whose parameters \(b_j\) have values in the range

$$\begin{aligned} |b_m-b_{j_m}|\le \Delta _{m}\,,\quad m=1,\dots M\,, \end{aligned}$$
(13)

where the parameter values are collected in bins of size \((\Delta _{1},\dots \Delta _{M})\) centered at \(b_{j_1},b_{j_1},\cdots ,b_{j_M}\), with \(j_m=1,\dots Q_m\). The sum runs over the number of bins \(Q_{m}\) for each index \(j_m\).

Consider now the probability, or occurrence frequency \(P^{(C)}_\mathrm{{ex}}(\xi )\) of a wave crest, or trough height exceeding a given threshold \(\xi H_s\) as encountered by a fixed observer, where \(H_s=4\sigma\). That is the probability of randomly picking from the collection of waves observed at a fixed point, a wave whose crest or trough height exceeds the threshold \(\xi H_s\). This follows from Eq. (12) as

$$\begin{aligned} P^{(C)}_\mathrm{{ex}}(\xi )=\frac{\sum P(\xi |b_{j_1},b_{j_1},\dots ,b_{j_M}) W_{j_1,j_2,\dots j_M}}{\sum W_{j_1,j_2,\dots j_M}}\,, \end{aligned}$$
(14)

where \(P_\mathrm{{ex}}(\xi |b_{j_1},b_{j_2},\cdots ,b_{j_M})\) is the stationary probability of exceedance of crest or trough heights of a sea state with wave parameters \(b_{j_1},b_{j_2},\cdots ,b_{j_M}\).

Non-skewed surface displacements

Here, we follow a statistical procedure outlined in Fedele et al.27. Consider a time series of the nonlinear surface displacements \(\eta\) measured at a given point in space. Relying on the narrowband approximation1,2, we approximate \(\eta\) as the narrowband sum of

$$\begin{aligned} \eta =\eta _1+\frac{\beta }{2}\left( \eta _1^2 - \hat{\eta }_1^2 \right) +\frac{3 \beta ^2}{8}\left( \eta _1^3 - 3\eta _1\hat{\eta }_1^2 \right) \,, \end{aligned}$$
(15)

where \(\eta _1\) is the first-order non-skewed harmonic component and the other two terms are the second and third-order bound harmonic components, respectively. Here, \(\hat{\eta }_1\) is the Hilbert transform of \(\eta _1\) and \(\beta\) is a steepness parameter determined by imposing \(\eta _1\) to be unskewed, that its skewness \(\langle \eta _1^3\rangle =0\), where \(\langle \cdot \rangle =0\) denotes time average. From an inversion of Eq. (15) we obtain

$$\begin{aligned} \eta _1=\eta - \frac{\beta }{2}\left( \eta ^2- \hat{\eta }^2 \right) + \frac{\beta ^2}{8} \left( \eta ^3- 3\eta \hat{\eta }^2 \right) +O(\beta ^3)\,. \end{aligned}$$
(16)

Imposing \(\langle \eta _1^3\rangle =0\) yields, correct to \(O(\beta ^2)\), the quadratic equation \(A_2 \beta ^2 - A_1 \beta + A_0 =0\), where

$$\begin{aligned} A_0=\langle \eta ^3\rangle \,,\quad A_1=3\frac{\langle \eta ^4\rangle \langle \eta ^2\hat{\eta }^2\rangle }{2}\,, \quad A_2=\frac{9\langle \eta ^5\rangle -21\langle \eta ^3\hat{\eta }^2\rangle +6\langle \eta \hat{\eta }^4\rangle }{8}\,. \end{aligned}$$
(17)

The physically meaningful solution of \(\beta\) is given by \(\beta =\left( A_1-\sqrt{A_1^2-4 A_0\, A_2}\right) /(2 A_2)\), which is an estimate of the Tayfun steepness \(\mu\). Then, the unskewed time series \(\eta _1\) is estimated from Eq. (16).

The NLS model for crest heights

Drawing on Fedele15, consider the spatial Nonlinear Schrodinger (NLS) equation that models weakly unidirectional nonlinear waves in deep waters. To \(O(\epsilon ^2)\), the surface displacement \(\eta\) from the mean water level, observed at a fixed point x in time t, is given by

$$\begin{aligned} \eta =\textrm{Re}\{a\textrm{e}^{i\phi }+\frac{k_m a^2}{2} \textrm{e}^{2 i\phi }+\frac{3 k_m^2 a^3}{8} \textrm{e}^{3 i\phi }\}\,, \end{aligned}$$
(18)

where \(\eta =\eta (x,t)\), \(B(\xi ,\tau )\) is the dimensionless complex envelope and \(\phi =k_m x - \omega _m t+\theta\). Here, \(\theta\) is the wave phase uniformly distributed in \([0,2\pi ]\), initially at \(x = 0\). The wave steepness \(\epsilon =k_m a_0\), \(a_0\) is the characteristic amplitude, and \(a=a_0 B\). \(\textrm{Re}(z)\) is the real part of z and \(c_g\) is the group velocity corresponding to the spectral mean frequency \(\omega _m\), and wavenumber \(k_m = \omega _m^2 / g\). The complex envelope satisfies the NLS equation

$$\begin{aligned} \partial _{\xi } B + i\partial ^2_{\tau } B + i|B|^2 B=0\,, \end{aligned}$$
(19)

where the slow time scale \(\tau =\epsilon \omega _m (t-x/c_g)\) and slow space \(\xi =\epsilon ^2 k_m x\). The complex envelope can be expressed in the form \(a_0 B \textrm{e}^{i\phi } = \eta _1 + \hat{\eta }_1\), where the linear non-skewed component \(\eta _1\) of the surface displacement and its Hilbert transform \(\hat{\eta }_1\) are given by

$$\begin{aligned} \eta _1=a_0 |B| \cos (\alpha +\phi )\,, \quad \hat{\eta }_1=a_0 |B| \sin (\alpha +\phi )\,, \end{aligned}$$
(20)

where \(a_0 |B| = \sqrt{\eta _1^2 + \hat{\eta }_1^2}\) and \(\alpha =\tan ^{-1}(\hat{\eta }_1/\eta _1) -\phi\). As a result, the surface displacement (18) can be written as the sum of

$$\begin{aligned} \eta =\eta _1+\eta _2+\eta _3\,, \end{aligned}$$
(21)

where the second and third order bound harmonic components are given by

$$\begin{aligned} \eta _2=\frac{k_m}{2}\left( \eta _1^2 - \hat{\eta }_1^2 \right) \,,\quad \eta _3=\frac{3 k_m^2}{8}\left( \eta _1^3 - 3\eta _1\hat{\eta }_1^2 \right) \,. \end{aligned}$$
(22)

Hereafter, we set \(a_0 = \textrm{max}(\eta _1)\), and also let \(S_{\eta _1}\) and \(S_{\eta }\) denote the frequency spectra of \(\eta _1\) and \(\eta\), respectively. The ordinary moments of \(S_{\eta _1}\) are \(m_j=\int S_{\eta _1}\omega ^j d\omega\) so that \(\sigma ^2=m_0\) is the variance of \(\eta\), the mean frequency \(\omega _m=m_1/m_0\) and the spectral bandwidth \(\nu =\sqrt{m_0 m_2/m_1^2 -1}\). The NLS equation is integrable with infinite conservative quantities: in ideal conditions with no dissipation, such invariants are constant along the channel. Three important invariants are the Action, Momentum and Hamiltonian

$$\begin{aligned} \textsf{A}=\langle |B|^2 \rangle \,,\quad \textsf{M}=i\langle B\partial _{\tau }B^*-B^*\partial _{\tau }B\rangle /2\,,\quad \textsf{H}=\langle |\partial _{\tau }B|^2 -|B|^4/2\rangle \,, \end{aligned}$$
(23)

where the angle brackets represent averages with respect to the slow time \(\tau\). To describe the spectral variability of waves, Fedele et al.27 define a convenient measure for the spectral bandwidth of the envelope B as

$$\begin{aligned} \Delta _{\omega }^2=\epsilon ^2 \frac{\langle |\partial _{\tau }B|^2\rangle }{\langle |B|^2 \rangle }=\epsilon ^2 \left( \frac{\textsf{H}}{\textsf{A}} + \frac{\langle |B|^4\rangle }{2\langle |B|^2\rangle }\right) \,, \end{aligned}$$
(24)

where the second term within brackets is proportional to the kurtosis, or fourth-order moment of the wave envelope. This implies that the spectral bandwidth increases with kurtosis, in agreement with wave tank measurements27,58,59.

Assume that at \(x=0\) near the wavemaker, the initial wave envelope field is a Gaussian process of time. The associated dimensionless crest amplitude \(\xi _0=h_0/\sigma _0\) is normalized by the standard deviation of the surface displacements. As the wave field propagates away from the wavemaker, it becomes a non-Gaussian process of time at \(x\gg x_0\) due to quasi-resonant interactions triggered by modulational instability, which causes energy exchange among the harmonic components. Let \(\xi =h/\sigma\) represent the dimensionless nonlinear wave crest amplitude at x, also normalized by the standard deviation of the surface displacements. The associated crest height \(\xi _s\), which is free of second-order bound harmonic components, satisfies the Tayfun quadratic equation \(\xi =\xi _s + \mu /2 \xi _s^2\), where \(\mu\) is the Tayfun steepness1,2. The bound-free crest amplitudes at the wavemaker (\(x=0\)) and away from it at x are related by the conservation of the Hamiltonian, \(\textsf{H}(x)=\textsf{H}(0)\):

$$\begin{aligned} \langle |\partial _{\tau }B(x)|^2 -|B(x)|^4/2\rangle =\langle |\partial _{\tau }B(0)|^2\rangle \,, \end{aligned}$$
(25)

where at \(x=0\), the nonlinear component is neglected as the field is assumed to be linear and Gaussian. Using Eq. (24):

$$\begin{aligned} \Delta ^2_{\omega }(x)=\Delta ^2_{\omega }(0)+\epsilon ^2\frac{\langle |B(x)|^4\rangle }{2\langle |B(x)|^2\rangle }\,, \end{aligned}$$
(26)

where \(\Delta _{\omega }(x)\) is the spectral bandwidth at x. From the invariance of the action \(\textsf{A}\), the ratio of the crest amplitudes follows as

$$\begin{aligned} \frac{\xi _s}{\xi _0}=\sqrt{\frac{\Delta _{\omega }(x)}{\Delta _{\omega }(0)}}\,. \end{aligned}$$
(27)

Using Eq. (26) yields

$$\begin{aligned} \frac{\xi _s^4}{\xi ^4_0}=\frac{\Delta ^2_{\omega }(x)}{\Delta ^2_{\omega }(0)}=1+BFI_0^2\frac{\langle |B(x)|^4\rangle }{4 \langle |B(x)|^2\rangle }\,, \end{aligned}$$
(28)

where the Benjamin-Feir index near the wavemaker is defined as \(BFI_0=\sqrt{2}\,\epsilon /\Delta _{\omega }(0)\). This index measures the dominance of nonlinearities over linear wave dispersion, as measured by the spectral bandwidth. The far-field amplitude B(x) depends on that of the near-field at the wavemaker (\(x=0\)). Thus, we set \(B(x)=\alpha (x) \xi _0\), where \(\alpha\) is a parameter to be determined. This parameter encodes the spatial variability of waves along the tank through the statistical fourth-order moments of surface elevations at x, as demonstrated in the following. Eq. (28) can be written as

$$\begin{aligned} \frac{\xi _s^4}{\xi _0^4}=1+\chi \xi _0^2\,, \end{aligned}$$
(29)

where the parameter \(\chi =\alpha BFI_0^2/4\) measures the competition between nonlinearities and linear dispersion along x. Thus, the Gaussian crest height \(\xi _0\) at the wavemaker and the nonlinear crest height \(\xi _s\) away from it are related by the sixth-order algebraic equation:

$$\begin{aligned} \xi _0^4+\chi \xi _0^6= \xi _s^4\,. \end{aligned}$$
(30)

The probability that the crest amplitude at x exceeds the threshold \(\xi \sigma\) is then defined as

$$\begin{aligned} P(h>\xi \sigma )=\exp \left( -\xi _0^2/2\right) \,. \end{aligned}$$
(31)

Alternatively,

$$\begin{aligned} P(h>\xi H_s)=\exp \left( -8\xi _0^2\right) \,, \end{aligned}$$
(32)

where now \(\xi _0\) satisfies \(\xi _0^4+16\chi \xi _0^6= \xi _s^4\), and \(\xi =\xi _s + 2\mu \,\xi _s^2\). For small values of \(\chi \ll 1\),

$$\begin{aligned} P(h>\xi H_s)=\exp \left( -8\xi _0^2\right) (1 + 64\chi \xi ^4)+O(\chi ^2)\,, \end{aligned}$$
(33)

and comparing with the third-order Tayfun-Fedele model \(P_{TF}(\xi )\) in Eq. (34) gives \(\chi\) in terms of statistical cumulants as \(\chi =\Lambda /16\). Thus, the fourth-order cumulant \(\Lambda \sim 4 BFI_0^2\) is proportional to the squared Benjamin-Feir index. The model is easily generalized for waves in water depth d by redefining the Benjamin-Feir Index as \(BFI_d=\alpha _S\, BFI\)18,57, where the depth factor \(\alpha _S\) depends on the dimensionless depth \(k_m\,d\)(see, e.g24.,). In the deep-water limit, \(\alpha _S\) becomes 1.

The Tayfun-Fedele model for crest heights

The probability \(P(\xi )\) that a wave crest observed at a fixed point of the ocean in time exceeds the threshold \(\xi H_s\) can be described by the third-order Tayfun-Fedele model26,

$$\begin{aligned} P_{TF}(\xi )=\textrm{Pr}\left[ h>\xi \,H_s\right] =\textrm{exp}\left( -8\,\xi _{0}^{2}\right) \left[ 1+\varLambda \xi _{0}^{2}\left( 4\,\xi _{0}^{2}-1\right) \right] \,, \end{aligned}$$
(34)

where \(\xi _{0}\) follows from the quadratic equation \(\xi =\xi _{0}+2\mu \,\xi _{0}^{2}\)1. Here, the Tayfun wave steepness \(\mu =\lambda _{3}/3\) is of \(O(\mu _m)\) and it is a measure of second-order bound nonlinearities as it relates to the skewness \(\lambda _{3}\) of surface elevations2. The parameter \(\varLambda =\lambda _{40}+2\lambda _{22}+\lambda _{04}\) is a measure of third-order nonlinearities and is a function of the fourth order cumulants \(\lambda _{nm}\) of the water surface elevation \(\eta\) and its Hilbert transform \(\hat{\eta }\)26. In particular, \(\lambda _{22}=\overline{\eta ^2\hat{\eta }^2}/\sigma ^4-1\) and \(\lambda _{04}=\overline{\hat{\eta }^4}/\sigma ^4-3\).

In this study, we assume the relations between cumulants60 \(\lambda _{22}=\lambda _{40}/3\) and \(\lambda _{04}=\lambda _{40}\), and \(\varLambda\) is approximated solely in terms of the excess kurtosis as \(\varLambda _{\textrm{appr}}={8\lambda _{40}}/{3}\). The abovementioned cumulant relations have been proven to hold for linear and second-order narrowband waves only61. For third-order nonlinear seas, our numerical studies indicate that \(\varLambda \approx \varLambda _{\textrm{appr}}\) within a \(3\%\) relative error in agreement with observations27,62.

Second-order seas, referred to as Tayfun sea states63, have \(\varLambda =0\) and \(P_{TF}\) reduces to the Tayfun (T) distribution1

$$\begin{aligned} P_{T}(\xi )=\textrm{exp}\left( -8{\xi _{0}^2}\right) . \end{aligned}$$
(35)

Gaussian seas have both \(\mu =0\) and \(\varLambda =0\), and \(P_{TF}\) reduces to the Rayleigh (R) distribution

$$\begin{aligned} P_{R}(\xi )=\textrm{exp}\left( -8{\xi ^{2}}\right) \,. \end{aligned}$$
(36)

The Tayfun distribution represents an exact result for large second order wave crest heights and it depends solely on the steepness parameter defined as \(\mu =\lambda _{3}/3\)2.

The Modified Narrowband (MNB) model

Tayfun and Alkhalidi46 introduced the MNB model as an improved version of the conventional second-order narrowband model, addressing unrealistic model features in shallow waters and extending its applicability to highly nonlinear waves from deep water to the shoaling and surf zones (see also the crest model developed by Karmpadakis and Swan64, which accounts for breaking effects dominant in shallow waters). The MNB exceedance probability for crest heights is given by

$$\begin{aligned} P_{MNB}(\xi )=\textrm{Pr}\left[ h>\xi \,H_s\right] =\textrm{exp}\left( -8{\xi _{0}^2}\right) \,, \end{aligned}$$
(37)

where \(\xi _{0}\) follows from the quadratic equation43,46

$$\begin{aligned} \xi =\left( \xi _{0}+2\varepsilon \xi _{0}^{2}\right) /\alpha _1\,. \end{aligned}$$
(38)

Here,

$$\begin{aligned} \varepsilon =0.3571\lambda _{3}-0.0227\lambda _{3}^{2}+0.0444\lambda _{3}^{3}\,,\quad \alpha _1=1+0.0146\lambda _3+0.0147\lambda _3^2+0.0219\lambda _3^3\,. \end{aligned}$$
(39)

The associated excess kurtosis is given by

$$\begin{aligned} \lambda _{40,MNB}=0.0276\lambda _{3}+1.4275\lambda _{3}^{2}-0.0063\lambda _{3}^{3}\,. \end{aligned}$$
(40)

The MNB model is valid over the range of skewness values \(0\le \lambda _3\le 2\).

The Forristall model

The exceedance probability is given by28

$$\begin{aligned} P_{F}(\xi )=\textrm{exp}\left( -{(\xi /\alpha )^{\beta }}\right) \,, \end{aligned}$$
(41)

where \(\alpha _2=0.3536+ 0.2892 S_1 + 0.1060 U_r\), \(\beta _2=2-2.1597 S_1+ 0.0968 U_r.^2\) for unidirectional (long-crested) seas and \(\alpha _3=0.3536+0.2561 S_1+0.0800 U_r\), \(\beta _3=2-1.7912 S_1-0.5302 U_r+0.284 U_r^2\) for multi-directional (short-crested) seas. Here, \(S_1=2\pi H_s/(g T_m^2)\) is a characteristic wave steepness and the Ursell number \(U_r=H_s/(k_m^2 d^3)\), where \(k_m\) is the wavenumber associated with the mean period \(T_m=m_0/m_1\) and d is the water depth.