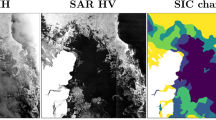
Abstract
The Surface Wave Investigation and Monitoring (SWIM) instrument is the first to adopt a rotation detection mode at multiple small incidence angles (0°–10°), which is mainly used for wave detection. SWIM is able to cover the north and south latitudes to 83°, and detect sea ice. However, the SWIM spatial resolution is relatively low (18 km), which limits its application in sea ice detection. Therefore, this study proposes, for the first time, a sea ice image reconstruction method at small incidence angles, which can improve the spatial resolution and extend the incidence angle range of image reconstruction methods. First, several image reconstruction methods are investigated and compared using SWIM data. Second, the optimal method (Scatterometer Image Reconstruction, SIR) with more sea ice detail and stronger noise suppression is selected. Third, the parameter settings of SIR are investigated and its reconstruction quality improves with increasing iteration number. Finally, based on the 6°–10° SWIM data in the Severnaya Zemlya and northeastern Kara Sea, the image reconstruction is carried out using the SIR method. The results are evaluated using the normalized standard deviation that can reach 0.55, and discussed based on sea ice charts and Sentinel-1 SAR images with good agreement.
Similar content being viewed by others
Introduction
Arctic sea ice is a crucial component of the global climate system and significantly influences the detection of some important ocean phenomena. Additionally, its gradual melting may accelerate the opening of the “Arctic Passage”1. Therefore, sea ice monitoring helps track global climate change, ensures maritime safety, and protects polar interests2,3.
Microwave remote sensing technology, known for its wide coverage, long time series, and rapid data acquisition, has become the primary method for sea ice monitoring in the Arctic; these methods utilize scatterometers, altimeters, and synthetic aperture radar (SAR). These sensors operate mainly at medium incidence (scatterometers and SARs) and normal incidence (altimeters) modes. SWIM is a novel microwave sensor that employs a multiple-small-incidence-angle detection mode for the first time. Research on SWIM for sea ice detection is scarce. In addition, existing studies are solely based on SWIM footprint data4,5,6, which was carried out in our previous study5,6. Additionally, the low spatial resolution (18 km) of SWIM limits the resolution of its detection results, so sea ice types may not be recognized clearly and accurately in detail. Image reconstruction methods can improve the spatial resolution of remote sensing data through the spatial overlap of observations at different times7,8. This method is especially suitable for regions with stable or slowly changes in surface characteristics of objects, which is applicable to sea ice distribution in the Arctic in the winter9,10. However, image reconstruction methods have only been applied to scatterometers at medium incidence angles and have not yet been applied to remote sensing data at small incidence angles. Therefore, considering the new characteristics of the small-incidence-angle mode and on the basis of our previous study, the motivation in this research focuses on SWIM image reconstruction and several key problems should be explored as follows.
-
(1)
The potential of image reconstruction using SWIM data.
-
(2)
The ability of image reconstruction at different incidence angles.
-
(3)
The selection of the optimal image reconstruction method.
-
(4)
The evaluation of the image reconstruction method.
In this study, the image reconstruction method using small-incidence-angle data is proposed for the first time. SWIM data and their preprocessing are described. Then, image reconstruction methods are introduced. An optimal image reconstruction method is selected through a quantitative comparison of the reconstructed results of different methods. Finally, the optimal method is applied to reconstruct images of different incidence angles at 6°–10°, and then their reconstruction effects are evaluated by the normalized standard deviation and discussed with the AARI ice charts and Sentinel-1 SAR images. Our study will not only improve the resolution and applicability of SWIM, but also fill the research gap in image reconstruction methods for small incidence angles.
Data and region
Research data
-
(1)
SWIM
SWIM is loaded on the China–France Oceanography Satellite (CFOSAT) operating in a polar orbit whose orbit parameters are shown in Table 111,12. SWIM aims to observe ocean surface waves and can detect regions of northern and southern latitudes up to 83°, covering the polar sea ice region. SWIM is the first spaceborne real aperture radar system operating in the Ku Band with six beams (0° to 10°) and the entire azimuth angle range (0°–360°)13,14. The projection geometries and footprint distributions in the Arctic are shown in Fig. 1, and the swath is nearly 90 km from the nadir to the outer edge of the footprint at an incidence angle of 10°, with a footprint of approximately 18 km15,16. SWIM nominal macrocycle parameters and associated real-time processing parameters are shown in Table 2. The SWIM data are processed into three levels (https://www.aviso.altimetry.fr/en/home.html): L1A, L1B and L2. The L1A level data, including echo waveforms with geographic information of each bin, can be used for image reconstruction. SWIM data are provided in the file format of the network Common Data Form.
-
(2)
Sea Ice Chart
The sea ice charts used in this study are from the Arctic and Antarctic Research Institute (AARI, http://www.aari.ru/), which supports marine navigation and assists other commercial and scientific purposes17. Sea ice conditions are mapped manually on the basis of observations from air reconnaissance flights, ship reports, polar meteorological stations, drift buoys, ground stations, and satellite data (GPS, infrared radiometers, radiometers, SAR, SLAR, visible spectrometer)18,19. The AARI issues one chart every seven days and provides sea ice charts using vector files and thematic maps, as shown in Fig. 2. In the Arctic ice year from October to April, sea ice charts include nilas, young ice (YI), first-year ice (FYI), multiyear ice (MYI), fast ice (FI), and open water (OW). According to our previous work, nilas and YI stabilize to a very small extent from January to March and exhibit similar growth properties. Therefore, these two types of sea ice are considered to be one type of thin ice (TI)5.
-
(3)
Sentinel-1 SAR
Sentinel-1 is the first of the five missions as part of the Copernicus Initiative of the European Commission (EC) and the European Space Agency (ESA). The Sentinel-1 mission, as a two-satellite constellation (A/B) in the C-band, obtains all-weather, all-day images (https://asf.alaska.edu/), including four exclusive modes (stripmap, SM; interferometric wide swath, IW; extrawide swath, EW; wave, WV) and four products (Level-0; Level-1 single look complex SLC; Level-1 ground range detected, GRD; Level-2 ocean, OCN).
Sentinel-1A/B can support high-resolution ice charting services, such as sea ice extent and sea ice types in the Arctic20,21. Moreover, beyond supporting operational services, Sentinel-1A/B data exhibit enhanced capabilities for short- and long-term variables of ice sheets22,23.
-
(4)
2 m Air Temperature
The 2 m air temperature in the research region is provided by the European Centre for Medium-Range Weather Forecasts (ECMWF), that is, ECMWF Reanalysis v5 (ERA5, https://cds.climate.copernicus.eu/datasets). ERA5 is the fifth generation ECMWF atmospheric reanalysis of the global climate covering the period from January 1940 to the present24. ERA5 is produced by the Copernicus Climate Change Service (C3S) at ECMWF. At present, ERA5 can provide hourly 2 m air temperature data. The daily 2 m air temperature is obtained from the 24-h average value.
Research region
The Kara Sea is an important passage of the Northern Sea Route and is generally divided into the southwestern and northeastern parts due to different oceanographic and meteorological conditions25. In winter the Kara Sea is in a transition zone between a large and stable high-pressure cell over central Siberia and low-pressure ridges over the Barents and Norwegian seas26. Severnaya Zemlya and the northeastern Kara Sea are the research region for image reconstruction, as shown in Fig. 3. The sea depth in this region is shallow (less than 50 m). Meanwhile, this region is not significantly influenced by the relatively warm extension of the North Atlantic Current. The air temperature is very low with monthly temperatures ranging from − 30 to − 20 °C in February27,28. The dominant sea ice types in this region are FYI, FI and TI, and are characterized by FI along the coasts26,29. During the middle of the freezing period (September–May), the sea ice distribution in this region exhibits minimal changes over short periods, and sea ice changes depend mainly on the 2 m air temperature30. This situation is suitable for sea ice image reconstruction experiments.
The sea ice distribution was relatively stable in the research region from 1–10 February 2021, according to the AARI charts and 2 m air temperature of ERA5. The AARI provides two ice charts, as shown in Fig. 4. One is from 31 January to 2 February (Chart I), and the other is from 7–9 February (Chart II). Figure 4 shows a relatively stable distribution of sea ice types (TI, FYI and FI). ERA5 provides daily air temperatures from 28 January to 13 February 2021, including the research time, as shown in Fig. 5. The air temperature changed by about 6 °C and did not change significantly, resulting in a small increase in TI extent, which ensured the stability of the sea ice distribution in accordance with Fig. 4.
SWIM L1A level data at each incidence angle provide echo waveforms of each footprint. The waveforms of sea ice types and sea water at different small incidence angles are shown in Fig. 6, which reveals significant differences in waveform characteristics among the incidence angles. Consequently, the small incidence angles can be divided into three sets: 0°–2°, 4°, and 6°–10°. The waveforms at 0°–2° are similar to those in nadir detection mode and cannot be used for image reconstruction. The SWIM data at angles of 6°–10° belong to oblique incidence and are available for image reconstruction. However, 4° could be regarded as a transition from 0°–2° to 6°–10°, and the accuracies of sea ice recognition and classification based on SWIM footprints are the worst according to our previous research5,6, so 4° is not very suitable for image reconstruction. Therefore, SWIM L1A data at angles of 6°–10° are used for image reconstruction in this study.
In the research region from 1–10 February 2021, the CFOSAT tracks are shown in Fig. 7a, and SWIM footprints of 6°–10° are shown in Fig. 7b–d. The distributions of SWIM footprints at 8° and 10° are more uniform and more suitable for image reconstruction. And the orbit numbers of these footprints include ten sets of 12468–12474, 12483–12489, 12498−12504, 12513−12519, 12529−12533, 12544 − 12549, 12559−12565, 12574−12580, 12589−12595, 12604−12610.
The Sentinel-1 SAR images used for evaluating the reconstructed images are listed in Table 3. Considering the spatial resolution (kilometer) of the reconstructed images, we use the wide swath (approximately 400 km) and low-resolution (approximately 90 m) SAR images of the Level-1 GRD products.
Method
Principles of image reconstruction using remote sensing data
The image reconstruction algorithm is essentially realized through the overlapping of multiple measurements across the ground coverage area7,8,31. In the coordinate system of the reconstruction model, the resolution of the reconstructed image is defined as \({S}_{c}\times {S}_{a}\) (where “c” represents the scanning direction and “a” represents the flight direction), and the reconstructed image includes \({N}_{c}\times {N}_{a}\) units; then, the remote sensing data are projected onto this coordinate grid, as shown in Fig. 8.
Assuming noiseless measurements, the remote sensing measurements \({z}_{j}\) and the pixel values σ0 of the reconstructed image are related by the matrix equation:
where Z is the N-dimensional vector of measurements \({z}_{j}\) and j (\(\in \left[1,N\right]\)) represents the j-th measurement. H is the weighting function matrix \(h\left( {c,a,j} \right) \in \left[ {0,1} \right]\) for the reconstructed image pixels; S is the M-dimensional vector (\(M={N}_{\text{c}}\times {N}_{\text{a}})\) of pixel values \({\sigma }^{0}\left(c,a,j\right)\), with the i-th pixel value \({s}_{i}={\sigma }^{0}\left(c,a,j\right)\) and \(i=c+a{N}_{c}\); this equation also requires the input of the boundary information of the j-th measurement.
To solve the matrix S, the boundaries of each remote sensing measurement are calculated. Then, \(h(c,a,j)\) is built, and the reconstruction matrix equation is constructed. Finally, \({\sigma }^{0}(c,a,j)\) is solved.
Construction of the SWIM image reconstruction model
Calculation of SWIM measurement boundaries
The SWIM footprint contains many range bins (Table 2). To fully utilize this feature, each footprint can be divided into 9 measurement units. The mean backscattering coefficient of the range bins within each measurement unit is used as its measured value zj. The coordinates of the four corner points of each measurement unit are then calculated in the coordinate system of the reconstructed image to serve as the measurement boundaries.
Building the SWIM weighting function
The accuracy of the reconstructed image depends on the weighting function \(h(c,a,j)\). Weighting functions are typical functions of the azimuth angle and track position, and standard calculation methods can be very time-consuming. Considering that the impact range of each SWIM bin is usually highly concentrated, \(h(c,a,j)\) within the measurement unit can be simplified to 1, otherwise 0. This approach significantly reduces the computational complexity while causing minimal image quality loss32,33.
Construction of the SWIM reconstruction matrix equation
The image reconstruction methods include the additive algebraic reconstruction method (AART), the multiplicative algebraic reconstruction method (MART), and the scatterometer image reconstruction method (SIR)34. AART assigns an initial value to each pixel of a reconstructed image and then updates it through additive update terms, making the value continuously approximate the true value.
MART is similar to AART but uses multiplicative update terms for its iterations.
SIR improves the multiplicative update terms of MART for iterative updating.
where \({s}_{i}^{k+1}\) represents the i-th pixel value at the k + 1-th iteration. hji is the weighting function of the j-th measurement. N is the number of measurements. \({u}_{ij}^{k}\) denotes the updated item, and \({f}_{j}^{k}\) is the forward mapping; then, \({d}_{j}^{k}\) is the scale factor. \({z}_{j}\) is the j-th measurement. M is the number of pixels in the reconstructed image. w represents the adjustable factor with a typical value of 1/2.
Compared with the AART, MART, and SIR algorithms, the optimal algorithm is chosen for image reconstruction using SWIM data; then, the matrix equation is constructed. To solve this equation, it is also necessary to first assign initial iteration values of the reconstructed image. Although initial values can be given randomly in theory, it has been shown that the initial values of the reconstructed image can be improved through the interpolation method. In this paper, the inverse distance weighting (IDW) interpolation method is used to compute initial values, which is simple in principle, easy to compute, in accordance with the first law of geography, and widely used35.
Evaluation of the SWIM reconstruction model
To assess the reconstruction accuracy, a normalized standard deviation (Kp) is introduced36,37:
where \(var\left({\sigma }^{0}\right)\) is the variance of \({\sigma }^{0}\) and \(E\left({\sigma }^{0}\right)\) is the mean value of \({\sigma }^{0}\).
Results
The optimal image reconstruction method based on SWIM data
On the basis of the unique characteristics of SWIM data and the resolution standards of existing sea ice products, 10-day SWIM data with a 2.5 km resolution are used for image reconstruction. Based on SWIM data at the 10° incidence angle, the reconstructed images are obtained using the three methods respectively, as shown in Fig. 9. Then, these images are compared and analyzed by visual interpretation and Kp. Figure 9 shows that the distributions of backscattering coefficients in the AARI and MART reconstructed images are discontinuous, whereas, the backscattering coefficients in the SIR reconstructed image change relatively smoothly.
When the initial values are set, AART updates more than 80 percent of the pixels to negative values after the first iteration, which is not reasonable and violates physical laws. Thus, its Kp value cannot be calculated. The Kp values of the MART and SIR algorithms are shown in Fig. 10.
For the SIR algorithm, the reconstruction quality improves with increasing iteration number k, whereas for the MART algorithm, k has little effect on the reconstruction quality, and the Kp values of the SIR are much lower than those of the MART. Thus, SIR performs better than AART and MART, which agrees with the performance analysis results using scatterometer data in medium incidence angles38,39,40. The SIR provides more details and exhibits stronger noise suppression capability. Consequently, the SIR algorithm is selected for SWIM image reconstruction research in the following sections.
SWIM reconstructed images at different incidence angles
SWIM reconstructed images at 6°–10° incidence angles are shown in Fig. 11. The reconstructed image at the 6° incidence angle contains many erroneously reconstructed bright points and relatively obvious traces of the orbit; these situations are significantly reduced at 8°–10° incidence angles.
Evaluation of the SWIM reconstruction model
Kp is used to evaluate the SWIM image reconstruction qualities at 6°–10° incidence angles, as shown in Fig. 12a. At each incidence angle, Kp decreases as the iteration number k increases. Then, the changing rates are very low after k up to 20, and are about zero for k > 20, as shown in Fig. 12b. After 30 iterations, the \({K}_{p}\) values stabilize at 0.6, 0.56, and 0.55 for the incidence angles of 6°, 8° and 10°, respectively. This indicates that \({K}_{p}\) decreases as the incidence angle increases, i.e. the reconstructed image quality is higher at 8° and 10° than 6°, which is consistent with the previous analysis (Figs. 7 and 11). Moreover, the Kp values of 6°–10° incidence angles after 30 iterations exhibit small differences, which means that all three angles are suitable for image reconstruction.
Discussion
As mentioned above, the resolution of SWIM data is low. Image reconstruction methods can enhance spatial resolution, but it is carried out in medium incidence angles. This study reveals the feasibility of image reconstruction using SWIM data at small incidence angles and the selection of the optimal image reconstruction method (SIR). The SIR method also performs better than other methods in sea ice mapping using scatterometer data with medium incidence angles38,39,40. The SIR method is applied to SWIM data, and the image reconstruction capability at each incidence angle is assessed. The results show the enhanced spatial resolution and better interpretability of SWIM data. However, the temporal resolution of the reconstructed images is low. The increase in temporal resolution can be achieved by reducing the spatial resolution (2.5 km) to 4.45 km (the reconstructed image resolution of scatterometers). Existing research results and operational sea ice products show that resolutions of 2.5 km to 4.45 km have little effect on sea ice classification accuracy. The resolutions of existing operational sea ice type identification products are generally 10 km41,42, 12.5 km43,44, and 25 km45,46. Thus, the reduced spatial resolution also meets the existing requirements of sea ice operational monitoring and services. Moreover, if the influence of incidence angles in SWIM data can be eliminated, the data at incidence angles of 6°–10° can be merged to reconstruct images, and improve the temporal resolution of reconstructed images. How to eliminate the influence of the incident angle will be focus of future work. For example, at different incidence angles, the weighting function is set to 0 or 1, as in this study. However, in fact, the weighting function is related to the incidence angles. Therefore, when fusing data at different incidence angles, the weighting function should be constructed according to SWIM footprint parameters (the incidence angle, azimuth, track position and size). Note that, the proposed method is developed using limited data and spatiotemporal region. Its applicability in larger regions and time periods will be investigated in our further research.
AARI ice charts provide sea ice conditions by combining field observations, remote sensing data, and manual interpretation. Moreover, ERA5 air temperatures show only small changes, which ensures the stability of the sea ice distribution (Fig. 5). Compared with the reconstructed images and charts, the sea ice type distributions and variations are shown in Fig. 13. The FYI was stable during this period, resulting in similar and clear FYI distribution in the reconstructed images of all three incidence angles. The FI had small changes except those in the upper region (grey solid rectangle). In this upper region (grey solid rectangle), the FI extent decreased from Chart I to Chart II. In the reconstructed images at 6° and 8°, this variation was shown as a transformation from FI to TI, whereas it did not exist at 10°. This may be due to the different distributions of the footprints at the three incidence angles (Fig. 7). Furthermore, the detection areas of SWIM footprints at different incidence angles do not completely overlap, and the information at three incidence angles is somewhat distinct. It means that the reconstructed image reflects the fusion information in the multiple days of the coverage at its incidence angle. Thus, the reconstructed images at different incidence angles sometimes show some differences in the sea ice distribution. This is one of the motivations for further research on image reconstruction by fusing multi-incidence-angle data in the future work, so that the reconstructed image can contain more comprehensive sea ice information in the study area. The TI adjacent to the FI around Severnaya Zemlya drifted (grey dotted rectangle) and expanded (grey dashed rectangle) in two charts. The reconstructed images clearly combined the changes. The TI in other regions also exhibited this situation but was relatively chaotic. This may be due to both the AARI ice charts and the reconstructed images extracted from the multi-day data.
To further consider the time-varying effect, Sentinel-1 SAR images are introduced to analyze the situation, as shown in Fig. 14. The FYI was still stable. The TI not adjacent to the FI exhibited relatively obvious changes in the SAR images only one day apart, resulting in some chaos mentioned in the paragraph above. This situation occurred in all the reconstructed images at 6°–10°. Consequently, the varying distributions could affect the reconstructed images when combining multi-day data. However, this situation has small influences on the overall distribution of sea ice types on a large scale, as shown in the reconstructed images.
Therefore, the proposed method can reconstruct images using small incidence angle data for the first time. The reconstructed images actually show the combination of sea ice type distributions from 1 to 10 February. Although sea ice changes affect the reconstructed results, the reconstructed images can still effectively map sea ice types on a large scale for sea ice monitoring. It can not only improve the spatial resolution of SWIM, but also extend the incidence angle range of image reconstruction methods.
Conclusions
For the first time, an image reconstruction method is proposed on the basis of remote sensing data at multiple small incidence angles. By comparing the AART, MART, and SIR methods using SWIM data, SIR is the optimal method with stronger noise suppression capability and more details. The SIR algorithm setting is investigated with w = 1/2 and k = 30. On the basis of SWIM data at 6°–10° incidence angles in the research region, the images are reconstructed using the SIR method. The reconstructed images are subsequently evaluated on the basis of the Kp, AARI ice charts and Sentinel-1 SAR images. Although the highest reconstruction accuracy is obtained at the 10° incidence angle, the values of Kp do not show obvious differences at the three incidence angles. Therefore, all the data at 6°–10° can be used for image reconstruction. This research not only improves the sea ice detection capability of SWIM and provides sea ice distributions on a large scale but also extends the incidence angle range of image reconstruction methods.
In this research, ten-day SWIM data at angles of 6°–10° in the sea ice region with a stable distribution are used for the proposed SIR method. In future work, more data from different regions and durations will be used to verify the validity and robustness of our method and improve its performance. In addition, SWIM data at three incidence angles may be merged to reconstruct images to improve temporal resolution and completeness of sea ice information. Machine learning and data fusion techniques will also be introduced to promote both temporal and spatial resolution without significant trade-offs by fusing SWIM, scatterometer and passive microwave data. Furthermore, SWIM data in the apparently variable region of sea ice pose a challenge for image recognition, which will be investigated. Finally, the proposed method will be applied to sea ice recognition and classification.
Data availability
Sentinel-1A/B SAR images are provided by https://asf.alaska.edu/. AARI sea ice charts are from https://www.aari.ru/. ERA5 air temperature is obtained from https://cds.climate.copernicus.eu/datasets. The SWIM data are available from the institutions at https://aviso-data-center.cnes.fr and https://osdds.nsoas.org.cn, but there are restrictions on the availability of these data, which has been used under license for the current study, and are therefore not publicly available. However, the data are available from the authors (Meijie Liu, [email protected]) upon reasonable request and with the permission of the institutions.
References
Ricker, R. et al. Evidence for an increasing role of ocean heat in Arctic winter sea ice growth. J. Clim. 34(13), 5215–5227. https://doi.org/10.1175/JCLI-D-20-0848.1 (2021).
Wang, A. et al. Analysis of sea ice parameters for the design of an offshore wind farm in the Bohai Sea. Ocean Eng. 239, 109902. https://doi.org/10.1016/j.oceaneng.2021.109902 (2021).
Sumata, H., de Steur, L., Divine, D. V., Granskog, M. A. & Gerland, S. Regime shift in Arctic Ocean sea ice thickness. Nature 615(7952), 443–449. https://doi.org/10.1038/s41586-022-05686-x (2023).
Peureux, C. et al. Sea-ice detection from near-nadir Ku-band echoes from CFOSAT/SWIM scatterometer. Earth Space Sci. 9, e2021EA002046. https://doi.org/10.1029/2021EA002046 (2022).
Liu, M. et al. Arctic sea ice classification based on CFOSAT SWIM data at multiple small incidence angles. Remote Sens. 14(1), 91. https://doi.org/10.3390/rs14010091 (2021).
Liu, M. et al. Sea ice recognition for CFOSAT SWIM at multiple small incidence angles in the Arctic. Front. Mar. Sci. 9, 1–19. https://doi.org/10.3389/fmars.2022.986228 (2022).
Long, D. G., Hardin, P. J. & Whiting, P. T. Resolution enhancement of spaceborne scatterometer data. IEEE Trans. Geosci. Remote Sens. 31(3), 700–715. https://doi.org/10.1109/36.225536 (1993).
Lindsley, R. D. & Long, D. G. Enhanced-resolution reconstruction of ASCAT backscatter measurements. IEEE Trans. Geosci. Remote Sens. 54(5), 2589–2601. https://doi.org/10.1109/TGRS.2015.2503762 (2016).
Long, D. G. NSCAT views land and ice. In Proceedings of the IGARSS '98 Sensing and Managing the Environment 1998 IEEE International Geoscience and Remote Sensing Symposium Proceedings (Cat No98CH36174), F 6–10 July 1998. 4: 1973–1985, https://doi.org/10.1109/IGARSS.1998.703712 (1998).
Meier, W. N. & Stroeve, J. Comparison of sea-ice extent and ice-edge ___location estimates from passive microwave and enhanced-resolution scatterometer data. Ann. Glaciol. 48, 65–70. https://doi.org/10.3189/172756408784700743 (2017).
Hauser, D., Tourain, C., Hermozo, L., Alraddawi, D. & Tran, N. T. New observations from the SWIM radar on-board CFOSAT: Instrument validation and ocean wave measurement assessment. IEEE Trans. Geosci. Remote Sens. 59(1), 1–22. https://doi.org/10.1109/TGRS.2020.2994372 (2020).
Hauser, D., Xiaolong, D., Aouf, L., Tison, C. & Castillan, P. Overview of the CFOSAT mission. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), F 10–15 July 2016. 5789–5792, https://doi.org/10.1109/IGARSS.2016.7730512 (2016).
Hauser, D. et al. CFOSAT: A new Chinese–French satellite for joint observations of ocean wind vector and directional spectra of ocean waves. Remote. Sens. Ocean. Inland Waters Tech. Appl. Chall. 9878T, 1–20. https://doi.org/10.1117/12.2225619 (2016).
Grelier, T., Amiot, T., Tison, C., Delaye, L., Hauser, D. & Castillan, P. The SWIM instrument, a wave scatterometer on CFOSAT mission. In 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS): 5793–5796. https://doi.org/10.1109/igarss.2016.7730513 (2016).
Hauser, D. et al. SWIM: The first spaceborne wave scatterometer. IEEE Trans. Geosci. Remote Sens. 55(5), 3000–3014. https://doi.org/10.1109/TGRS.2017.2658672 (2017).
Xu, Y. et al. China–France Oceanography Satellite (CFOSAT) simultaneously observes the typhoon-induced wind and wave fields. Acta Oceanol. Sin 38(11), 158–161. https://doi.org/10.1007/s13131-019-1506-3 (2019).
Arctic and Antarctic Research Institute. Compiled by V. Smolyanitsky, V. Borodachev, A. Mahoney, F. Fetterer, and R. G. Barry. 2007. Sea Ice Charts of the Russian Arctic in Gridded Format, 1933–2006, Version 1. [Indicate subset used]. Boulder, Colorado USA. NSIDC: National Snow and Ice Data Center. https://doi.org/10.7265/N5D21VHJ. [Date Accessed].
Mahoney, A. R., Barry, R. G., Smolyanitsky, V. & Fetterer, F. Observed sea ice extent in the Russian Arctic, 1933–2006. J. Geophys. Res. 113, 11005. https://doi.org/10.1029/2008JC004830 (2008).
Selyuzhenok, V., Krumpen, T., Mahoney, A., Janout, M. & Gerdes, R. Seasonal and interannual variability of fast ice extent in the southeastern Laptev Sea between 1999 and 2013. J. Geophys. Res. Oceans 120(12), 7791–7806. https://doi.org/10.1002/2015JC011135 (2015).
Tan, W., Li, J., Xu, L. & Chapman, A. M. Semiautomated segmentation of Sentinel-1 SAR imagery for mapping sea ice in labrador coast. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 11(5), 1419–1432. https://doi.org/10.1109/JSTARS.2018.2806640 (2018).
Scharien, R. K. & Nasonova, S. Incidence angle dependence of texture statistics from sentinel-1 HH-Polarization images of winter Arctic sea ice. IEEE Geosci. Remote Sens. Lett. 19, 1–5. https://doi.org/10.1109/LGRS.2020.3039739 (2022).
Nagler, T., Rott, H., Hetzenecker, M., Wuite, J. & Potin, P. The sentinel-1 mission: New opportunities for ice sheet observations. Remote Sens. 7(7), 9371–9389. https://doi.org/10.3390/rs70709371 (2015).
De Gélis, I., Colin, A. & Longepe, N. Prediction of categorized sea ice concentration from Sentinel-1 SAR images based on a fully convolutional network. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 14, 5831–5841. https://doi.org/10.1109/JSTARS.2021.3074068 (2021).
Hersbach, H., Bell, B., Berrisford, P., Biavati, G., Horányi, A., Muñoz Sabater, J., Nicolas, J., Peubey, C., Radu, R., Rozum, I., Schepers, D., Simmons, A., Soci, C., Dee, D. & Thépaut, J. N. ERA5 hourly data on single levels from 1940 to present. Copernicus Climate Change Service (C3S) Climate Data Store (CDS), https://doi.org/10.24381/cds.adbb2d47 (2023).
Duan, C., Dong, S. & Wang, Z. Estimates of sea ice mechanical properties in the Kara Sea. Pure Appl. Geophys. 177, 5101–5116. https://doi.org/10.1007/s00024-020-02543-8 (2020).
Lundhaug, M. ERS SAR studies of sea ice signatures in the Pechora Sea and Kara Sea region. Can. J. Remote. Sens. 28(2), 114–127. https://doi.org/10.5589/m02-022 (2002).
Wytiahlowsky, H. E. Recent glacier change (1965–2021) and identification of surge-type glaciers on Severnaya Zemlya, Russian High Arctic. In Durham theses, Durham University. Available at Durham E-Theses Online: http://etheses.dur.ac.uk/14855/ (2023).
Chernova1, N. V ., Spiridonov, V. A., Syomin, V. L. & Gavrilo, M. V. Notes on the fishes of the Severnaya Zemlya archipelago and the spawning area of polar cod Boreogadus saida (Gadidae). In Proceedings of the Zoological Institute RAS, 325(2): 248–268, https://doi.org/10.31610/trudyzin/2021.325.2.248 (2021).
Lundhaug, M., Johannessen, O. M. & Esbensen, K. H. Seasonal ERS SAR studies of sea ice in the Pechora and Kara Sea region. In ERS-ENVISAT Symposium Looking Down To Earth in the New Millennium: 1–7, https://doi.org/10.5589/m02-022 (2007).
Duan, C., Dong, S., Xie, Z. & Wang, Z. Temporal variability and trends of sea ice in the Kara Sea and their relationship with atmospheric factors. Polar Sci. 20, 136–147. https://doi.org/10.1016/j.polar.2019.03.002 (2019).
Long, D. G., Early, D. S. & Drinkwater, M. R. Enhanced resolution ERS-1 scatterometer imaging of Southern Hemisphere polar ice. In Proceedings of the Proceedings of IGARSS '94 - 1994 IEEE International Geoscience and Remote Sensing Symposium: 156–158. https://doi.org/10.1109/igarss.1994.399066 (1994).
Ivan, S. A. & David, G. L. The spatial response function of SeaWinds backscatter measurements [C]. Proceedings of SPIE, Earth Observing Systems VIII, edited by William L. Barnes, 5151: 609–618, https://doi.org/10.1117/12.506255 (2003).
Williams, B. A. & Long, D. G. Reconstruction from aperture-filtered samples with application to scatterometer image reconstruction. IEEE Trans. Geosci. Remote Sens. 49(5), 1663–1676. https://doi.org/10.1109/tgrs.2010.2086063 (2011).
Early, D. S. & Long, D. G. Image reconstruction and enhanced resolution imaging from irregular samples. IEEE Trans. Geosci. Remote Sens. 39(2), 291–302. https://doi.org/10.1109/36.905237 (2001).
Yan, J. B. et al. Adaptive IDW interpolation algorithm considering spatial heterogeneity. J. Wuhan Univ. Inf. Sci. Ed. 45(1), 97–104. https://doi.org/10.13203/j.whugis20180213 (2020).
Long, D. G. & Spencer, M. W. Radar backscatter measurement accuracy for a spaceborne pencil-beam wind scatterometer with transmit modulation. IEEE Trans. Geosci. Remote Sens. 35(1), 102–114. https://doi.org/10.1109/36.551939 (1997).
Long, D. G. & Oliphant, T. Wind measurement accuracy for the NASA scatterometer. Proc. SPIE Earth Obs. Syst. 3117, 98–106. https://doi.org/10.1117/12.278915 (1997).
Remund, Q. P. & Long, D. G. Sea ice extent mapping using Ku band scatterometer data. J. Geophys. Res. Ocean 104(C5), 11515–11527. https://doi.org/10.1029/98jc02373 (1999).
Remund, Q. P. & Long, D. G. A decade of QuikSCAT scatterometer sea ice extent data. IEEE Trans. Geosci. Remote Sens. 52(7), 4281–4290. https://doi.org/10.1109/tgrs.2013.2281056 (2014).
Remund, Q. P. & Long, D. G. Iterative estimation of Antarctic sea ice extent using SeaWinds data. In Proceedings of the IGARSS 2000 IEEE 2000 International Geoscience and Remote Sensing Symposium F24–28 July 2000, 2000. 491–493, https://doi.org/10.1109/igarss.2000.861606 (2000).
OSI SAF. Global Sea Ice Type (netCDF) - Multimission, EUMETSAT SAF on Ocean and Sea Ice [Data Set]. https://doi.org/10.15770/EUM_SAF_OSI_NRT_2006 (2017).
U.S. National Ice Center. U.S. National Ice Center Arctic and Antarctic Sea Ice Concentration and Climatologies in Gridded Format. (G10033, Version 1). Fetterer, F. & Stewart, J. S. (Comps.) [Data Set]. Boulder, Colorado USA. National Snow and Ice Data Center. https://doi.org/10.7265/46cc-3952. [describe subset used if applicable]. Date Accessed 05 June 2025 (2020).
U.S. National Ice Center, Fetterer, F., Savoie, M., Helfrich, S. & Clemente-Colón, P. Multisensor Analyzed Sea Ice Extent - Northern Hemisphere (MASIE-NH). (G02186, Version 1). [Data Set]. Boulder, Colorado USA. National Snow and Ice Data Center. https://doi.org/10.7265/N5GT5K3K. [describe subset used if applicable]. Date Accessed 05 June 2025 (2010).
Meier, W. N., Fetterer, F., Windnagel, A. K., Stewart, J. S. & Stafford, T. NOAA/NSIDC Climate Data Record of Passive Microwave Sea Ice Concentration. (G02202, Version 5). [Data Set]. Boulder, Colorado USA. National Snow and Ice Data Center. https://doi.org/10.7265/rjzb-pf78. [describe subset used if applicable]. Date Accessed 05 June 2025 (2024).
Comiso, J. C. Bootstrap Sea Ice Concentrations from Nimbus-7 SMMR and DMSP SSM/I-SSMIS. (NSIDC-0079, Version 4). [Data Set]. Boulder, Colorado USA. NASA National Snow and Ice Data Center Distributed Active Archive Center. DOI: https://doi.org/10.5067/X5LG68MH013O. [describe subset used if applicable]. Date Accessed 05 June 2025 (2023).
OSI SAF. Global Sea Ice Concentration Climate Data Record v3.0 (AMSR)—Multimission, EUMETSAT SAF on Ocean and Sea Ice [Data Set]. https://doi.org/10.15770/EUM_SAF_OSI_0015 (2022)
Acknowledgements
We are deeply grateful for the invaluable data provided by the CFOSAT SWIM, Sentinel-1A/B SAR, AARI ice charts and ERA5. These data played a crucial role in supporting key information for this study. This research was funded in part by the Key Laboratory of Space Ocean Remote Sensing and Application, MNR, 2023CFO015; the National Natural Science Foundation of China under grant 41976173, 61971455, and 41976168; the Shandong Provincial Natural Science Foundation, China under grant ZR2019MD016, ZR2020MD095, ZR201910290171; the Shandong Joint Fund of National Natural Science Foundation of China under grant U2006207.
Author information
Authors and Affiliations
Contributions
M. L. and W. B. wrote the main manuscript text; M. L., X. Z., R. Y., and W. B. constructed the model; Y. X., M. G. and N. W. processed the SWIM data; H. Y., M. L., and W. B. evaluated the results; Y. L., Y. Z., Y. L., and X. B. downloaded the SWIM data. All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Bi, W., Yu, H., Zhang, X. et al. Image reconstruction of Arctic sea ice using SWIM data at small incidence angles. Sci Rep 15, 23386 (2025). https://doi.org/10.1038/s41598-025-07244-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-025-07244-7