Introduction

In light of the robust advancement of multi-agent system theory, substantial achievements have been realized in investigating cooperative control within MAS1,2,3. Among the myriad intriguing topics in the practical application of motion coordination, formation control4,5,6,7 emerges as particularly compelling, as it primarily seeks to synthesize essential multi-agent activities, including surrounding detection, data collection, task allocation, and target tracking to achieve the establishment and sustained maintenance of a designated high-dimensional spatial configuration. The preceding discussion pertains exclusively to isomorphic MAS, in which all agents possess identical model parameters. However, in practical scenarios, variations in environmental conditions and functional requirements may result in systems comprising individual agents that diverge in model parameters, dimensions, and functionalities. For instance, a HMAS composed of UAVs and UGVs can effectively capitalize on the strengths of UAVs while offsetting the shortcomings of UGVs, thereby facilitating the collaborative execution of more intricate tasks. HMAS in air-ground collaboration exhibits a broad spectrum of application domains8,9, encompassing fire monitoring10, as well as reconnaissance and search-and-rescue operations11,12.

Major military powers worldwide emphasize the collaborative capabilities and robust performance of air-ground combat systems composed of UAVs and UGVs. In recent years, heterogeneous uncrewed combat systems formed by UAVs and UGVs have garnered favor among military powers due to their rapid response times, formidable communication capabilities, inconspicuous sizes, and precise target reconnaissance accuracy13,14,15,16,17,18,19. The increasing diversity of application domains for UAVs and UGVs has led to a surge in the demand for enhanced reliability and safety of complex control systems within contemporary industrial frameworks. This is particularly pertinent for MAS, where the failure of a single agent may bring about functioning loss, and the propagation of such failures through inter-agent communication links can amplify their impact, potentially leading to the collapse of the entire system. Consequently, FTC technology is an indispensable component, as fault-tolerant mechanisms can provide technical assurances for individual stability, global stability of MAS, task accomplishment, and performance maintenance. Research on fault-tolerant technology for MAS has sparked considerable enthusiasm among scholars. Reference20 proposes a fault detection and FTC strategy for fixed-wing UAVs under actuator faults, sensor malfunctions, and environmental disturbances. An unknown input observer has been developed to estimate system faults, disturbances, and state information. By integrating the estimates from the observer, an FTFC based on the backstepping method has been engineered. Reference21 investigates the collision avoidance capabilities of leader-follower multi-UAV systems under actuator failures and saturation conditions. The developed fault-tolerant mechanism effectively compensates for the effects induced by actuator failures.

Additionally, a collision avoidance mechanism has been designed to replan feasible and safe trajectories, ensuring the performance of trajectory tracking. Reference22 investigates the UAV formation control problem involving multiple vertical takeoff and landing (VTOL) drones while accounting for actuator failures, parameter variations, and external disturbances, proposing a corresponding adaptive distributed FTC algorithm. This algorithm is proficient in precisely achieving formation objectives and demonstrates excellent fault tolerance against actuator failures and robustness to external disturbances. Reference23 introduces a fixed-time FTC method and proposes a fuzzy adaptive FTC to address the problem of rapid time-constrained tracking for hypersonic vehicles. Reference24 investigates the fixed-time fault-tolerant consensus problem within directed topologies of higher-order nonlinear multi-agent models. A fixed-time observer based on power technology has been designed to monitor unpredictable actuator failures effectively. The fixed-time tracking protocol, developed in conjunction with observational information, effectively compensates for the impact of failures. It is evident that the research focus of MAS is not limited to conventional aerial vehicles; spacecraft also represent one of the prominent areas of study25,26,27. While a substantial body of research exists on fault-tolerant control for isomorphic MAS, the fault-tolerant methods specifically designed for heterogeneous systems comprising UAVs and UGVs remain relatively scarce. This represents one of the motivations for the present study. Reference28 examines the FTFC problem for heterogeneous UAV-UGV systems with finite sequence failures, proposing a formation tactic deriving from backstepping and adaptive FTC that enables UAVs and UGVs to achieve the desired formation in the XOY plane while ensuring convergence of the UAVs along the Z-axis. Reference29 investigates the air-ground coordination problem between UAVs with actuator faults, external disturbances, model uncertainties, and healthy UGVs. A neuro-adaptive nonsingular fast terminal sliding mode control(SMC) has been created by integrating adaptive neural network control(NNC) laws. The proposed controller’s effectiveness was confirmed through experiments involving three designed UAVs and UGVs. The methods mentioned earlier are primarily robust-based strategies, focusing on observers, SMC, adaptive control, and NNC, with the primary objective of addressing system reliability. However, extensive research has been lacking in addressing the optimization and FTFC problem to conserve system resource costs.

Reference30 introduces a control allocation strategy for leader-follower MAS governed by general dynamic equations that can handle actuator failures. By leveraging local information and optimization theory, a distributed fault-tolerant consensus algorithm for MAS has been proposed, and its effectiveness has been validated. The proposed control allocation strategy effectively addresses actuator shutdown failures and partial failure issues, ensuring the consensus error converges to zero. It focuses solely on the design for homogeneous agents, and the designed allocation control strategy is applied to leader-following MAS. Reference31 investigates the fixed-time optimal FTFC output problem for heterogeneous MAS. A hierarchical FTFC framework is proposed to isolate the faults’ effects, thereby preventing cascading failures. A new adaptive fixed-time FTFC has been constructed for each agent, which can rapidly converge the formation error of faulty agents to a vicinity near the origin, incorporating optimization theory; the formulated formation control strategy is a fixed-time FTC output tracking method. Both methods are fault-tolerant-based, but their emphases are different.

Thus, this paper introduces a leader-following-based fault-tolerant formation control method for heterogeneous UAV-UGV systems, combining optimal control theory to propose an optimal fault-tolerant controller with optimized performance. It solves the FTFC problem of heterogeneous UAVs-UGV systems with actuator the partial loss of effectiveness(PLOE) and interruption faults. The contributions of this study are as follows:

  1. 1.

    First, the state equations of UAVs and UGVs are introduced, utilizing the Kronecker product to formulate a state space representation that integrates both UAVs and UGVs into a heterogeneous system. An actuator fault model is established, and the fault model is incorporated into the heterogeneous state space, resulting in the heterogeneous MAS fault model.

  2. 2.

    An optimal fault-tolerant controller is designed, constructing a performance index function comprising error vectors and control variables for each agent in the UAVs-UGVs heterogeneous system. Based on optimal control theory, a Hamiltonian function incorporating actuator fault information is formulated, yielding the solution that minimizes the Hamiltonian, which serves as the optimal FTC law. A new Lyapunov function is developed to demonstrate its stability.

  3. 3.

    Finally, a control allocation algorithm combined with optimization theory is introduced, resulting in an optimal FTFC method that can handle leaders with unknown inputs and external environmental disturbances. The feasibility of the control law is proven using the Lyapunov stability theory. The optimal FTC effectively compensates for the impacts caused by actuator faults, overcoming PLOE and interruption faults under conditions where the leader has unknown inputs and external environmental disturbances.

The balance of this paper is listed as follows. Section “Preliminaries and problem formulation” presents several foundational principles and preparatory knowledge, including establishing models for UAVs and UGVs and problem descriptions. Section “Fault-tolerant formation controller design and analysis” details the principle of the control allocation algorithm and the design of the optimal fault-tolerant controller, along with its proof. Section “Simulations” provides the experimental and designed simulation results of the control laws. Section “Conclusions” concludes this study and outlines the focus of future work.

Preliminaries and problem formulation

A. Graph theory

The weighted undirected graph \(G=(V,E,A)\) is utilized to Symbolize the communication network for \(\text {n}\) agents within MAS, where \(V=\begin{pmatrix}v_1,v_2,\ldots v_n\end{pmatrix}\) indicate the nodes set in the graph \(\text {G}\). \(E=\left\{ e_{ij}=\left( v_{i},v_{j}\right) \right\} \subseteq v\times v\) signifies the communication between the \(\text {n}\) nodes, and \({e}_{ij}=\begin{pmatrix}v_i,v_j\end{pmatrix}\) refers to the graph G ’s edge set. If the information exchange occurs bidirectionally, G is classified as an undirected graph; conversely, that is classified as a directed graph. \(A=\begin{bmatrix}a_{ij}\end{bmatrix}_{n\times n}\) represents the graph G ’s adjacency matrix, where \(a_{ij}\) indicates the data transfer between nodes \(\nu _{i}\) and \(\nu _{j}\), specifically, \({a}_{ij}>0\) indicates communication, while \(a_{ij}=0\) denotes a lack of communication. We then define the Laplacian matrix \(L=[l_{ij}]\in R^{n\times n}\) between the follower agents as follows.

$$l_{ij}={\left\{ \begin{array}{ll}\sum _{k=1}^Na_{ik},& i=j\\ \\ -a_{ij},& i\ne j\end{array}\right. }$$

The leader is denoted by \(V_0\) , and the matrix \(D=diag(d_{01},d_{02},\ldots ,d_{0n})\) represents the communication relationship between the leader and followers. The overall matrix of the leader-following MAS network topology is defined by \(\mathscr {G}=L+D\) .

B. Second-order dynamic model of the UGV

Informed by reference32, the dynamic equation for the UGV is obtained as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll}\dot{p}_{gi}=v_{gi}\\ \dot{v}_{gi}=u_{gi}\end{array}\right. } \end{aligned}$$
(1)

where \(p_{gi}=\begin{bmatrix}p_{gi}^x,p_{gi}^y\end{bmatrix}^T\) embodies the formation of the ground position for UGV. \(v_{gi}=\left[ v_{gi}^{x},v_{gi}^{y}\right] ^{T}\) corresponds to the formation of their speeds and \(u_{gi}=\left[ u_{gi}^{x},u_{gi}^{y}\right] ^{T}\) represents the input in the systems.

We assume that there are \(\text {m}\) UGV in the system. The multi-vehicle system can be expressed as:

$$\begin{aligned} \dot{x}_{Gi}=A_{g}x_{Gi}+B_{g}u_{Gi}+f(t,x_{Gi}) \end{aligned}$$
(2)

where \(x_{Gi}=\left( p_{i}^{x} ,p_{i}^{y} ,v_{i}^{x} ,v_{i}^{y} \right) ^{T},u_{Gi}=\left( u_{i}^{x} ,u_{i}^{y} \right) ,i=1,2,...,m\),\(f(t,x_{Gi})\)represents the external environmental disturbance acting on the UGV.

$$A_g=\begin{bmatrix}0& 1\\ 0& 0\end{bmatrix}\otimes I_2,B_g=\begin{bmatrix}0\\ 1\end{bmatrix}\otimes I_2.$$

Here, \(\otimes\) designates the Kronecker product. \(A_{g},B_{g}\) represent the state matrix and output matrix of the UGV, respectively.

Let the expected formation of the formation be denoted as \(h_{g}=\begin{pmatrix}h_{g}^{x},h_{g}^{y}\end{pmatrix}^{T}\). Based on this \(h_{g}\) , the formation error can be represented as \(\delta _{G}=\left( \delta _{G}^{x},\delta _{G}^{y}\right) ^{T}=\left( p_{gi}^{x}-h_{g}^{x},p_{gi}^{y}-h_{g}^{y}\right) ^{T}\). Therefore, when the UGVs system experiences actuator failures, the following conditions must be met for the formation to be considered complete:

$$\begin{aligned} lim_{t\rightarrow \infty }\parallel \delta _{gi}-\delta _{gj}\parallel =0,lim_{t\rightarrow \infty }=\parallel v_{gi}\parallel =0. \end{aligned}$$
(3)

C. Second-order dynamic model of the UAV

Informed by reference33, the dynamic equation for the UAV is obtained as follows:

$$\begin{aligned} \begin{aligned}&\ddot{p}^{x}=g\theta \\&\ddot{p}^{y}=-g\phi \\&\ddot{p}^{z}=f_{z}/m-g \\&g\ddot{\phi }=M_{\phi }/I_{x} \\&g\ddot{\theta }=M_{\theta }/I_{y} \\&\ddot{\psi }=M_{\psi }/I_{z} \end{aligned} \end{aligned}$$
(4)

where \(p^{x},p^{y},p^{z}\) manifests the positions of the drone along the X, Y, and Z axes in the global coordinate system; \(\phi ,\theta ,\psi\) denote the drone’s three turning angles are in 3D; \(f_{z}\) illustrates the total lift generated by the four propellers; \(I_{_x},I_{_y},I_{_z}\) refer to the moments of inertia about the X, Y, and Z axes, respectively; \(g\ddot{\phi },g\theta ,\dot{\psi }\) represents the control inputs required to maneuver the drone’s rotation about the three coordinate axes.

We assume that there are l UAVs in the system. The multi-vehicle system can be expressed as:

$$\begin{aligned} \dot{x}_{Ai}=A_{a}x_{Ai}+B_{a}u_{Ai}+f(t,x_{Ai}) \end{aligned}$$
(5)

where \(x_{Ai}=(p_{i},v_{i},\Omega _{i},\Omega _{i})^{T},\) \(p_{i}=\left( p_{i}^{x},p_{i}^{y},p_{i}^{z}\right) ^{T},\) \(v_{i}=\left( v_{i}^{x},v_{i}^{y},v_{i}^{z}\right) ^{T},\) \(u_{Ai}=\left( u_{i}^{x},u_{i}^{y},u_{i}^{z}\right) ^{T}\), \(\Omega _{i}=\left( g\theta _{i},-g \phi _{i},\psi \right) ^{T},\)\(\dot{\Omega }_{i}=\left( g\dot{\theta }_{i},-g \dot{\phi }_{i},\ddot{\psi } \right) ^{T},i=1,2,\ldots ,l\), \(f(t,x_{Ai})\)stands for the external environmental disturbance acting on the UAV.

$$A_a=\begin{bmatrix}0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\\ 0& 0& 0& 0\end{bmatrix}\otimes I_3,B_a=\begin{bmatrix}0\\ 0\\ 0\\ 0\\ 1\end{bmatrix}\otimes I_3$$

Here, \(\otimes\) designates the Kronecker product. \(A_{a},B_{a}\) represent the state matrix and output matrix of the UAV, respectively.

Let the expected formation of the formation be denoted as \(h_a=\left( h_a^x,h_a^y,h_a^z\right) ^T\) . Based on this \(h_{a}\) , the formation error can be represented as \(\delta _{A}=\left( \delta _{A}^{x},\delta _{A}^{y},\delta _{A}^{z}\right) ^{T}=\left( p_{ai}^{x}-h_{a}^{x},p_{ai}^{y}-h_{a}^{\nu },p_{ai}^{z}-h_{a}^{z}\right) ^{T}\) . Therefore, when the UGVs system experiences actuator failures, the following conditions must be met for the formation to be considered complete:

$$\begin{aligned} \begin{aligned}&lim_{t\rightarrow \infty }\parallel \delta _{ai}-\delta _{aj}\parallel =0,\\ &lim_{t\rightarrow \infty }\parallel v_{ai}\parallel =0,\\ &lim_{t\rightarrow \infty }\parallel \Omega _{i}\parallel =0,\\ &lim_{t\rightarrow \infty }\parallel \dot{\Omega }_{i}\parallel =0\end{aligned} \end{aligned}$$
(6)

D. Heterogeneous multi-agent systems

By establishing models (2) and (5) for UAVs and UGVs in the preceding chapters and introducing the actuator failure model (9), we can construct the state space expression for the actuator failure in the heterogeneous MAS by merging state variables. The formal definition of the heterogeneous MAS state space model is as follows:

$$\begin{aligned} \begin{aligned}&\begin{bmatrix}\dot{\mathbf {X_G}}\\ \\ \dot{\mathbf {X_A}}\end{bmatrix}=\begin{bmatrix}A_g& & 0\\ 0& & A_a\end{bmatrix}\begin{bmatrix}\mathbf {X_G}\\ \mathbf {X_A}\end{bmatrix}+\begin{bmatrix}B_g& & 0\\ 0& & B_a\end{bmatrix}\begin{bmatrix}\mathbf {U_G}\\ \mathbf {U_A}\end{bmatrix}+\begin{bmatrix}f(x_G)\\ f(x_A)\end{bmatrix}\\&\dot{X}=AX+BU+F\end{aligned} \end{aligned}$$
(7)

where

$$\begin{aligned}&\mathrm {X=[P_A^T,V_A^T,\Omega _A^T,\Omega _A^T,P_{G}^T,V_{G}^T]^T\left( X_A^T,X_G^T\right) ^T,A=\left( \begin{matrix}A_a& 0\\ 0& A_g\end{matrix}\right) ,B=\left( \begin{matrix}B_a& 0\\ 0& B_g\end{matrix}\right) ,}\\&\mathrm {U=[U_{A},U_{G}]^{T},}\\&\mathrm {P_{A}=[p_{i}^{x},p_{i}^{y},p_{i}^{z}]^{T},i=0,1,2,\ldots l,}\\&\mathrm {V_{A}=[v_{i}^{x},v_{i}^{y},v_{i}^{z}]^{T},i=0,1,2,\ldots l,}\\ &\Omega _{\textrm{A}}=[\Omega _{1},\Omega _{2},\ldots ,\Omega _{l}]^{\textrm{T}},\Omega _{\textrm{i}}=[g\theta _{i},-g\phi _{i},\dot{\psi }_{i}]^{\textrm{T}},i=0,1,2,\ldots l,\\ &\dot{\Omega }_{\textrm{A}}=[\dot{\Omega }_{1},\dot{\Omega }_{2},\ldots ,\dot{\Omega }_{l}]^{\textrm{T}},\dot{\Omega }_{\textrm{i}}=[g\dot{\theta }_{i},-g\dot{\phi }_{i},\ddot{\psi }_{i}]^{\textrm{T}},i=0,1,2,\ldots l,\\&\textrm{P}_{G} =[p_{l+1},p_{l+2},\ldots ,p_{l+m}]^{T},p_{i}=[p_{gi}^{x},p_{gi}^{y}]^{T},i=l+1,\ldots l+m, \\&\textrm{V}_{\textrm{G}} =[v_{l+1},v_{l+2},\ldots ,v_{l+m}]^{T},v_{i}=[v_{gi}^{x},v_{gi}^{y}]^{T},i=l+1,\ldots l+m, \\ \\&\textrm{A}_{\textrm{a}} =\begin{bmatrix}0_{3\times 3}& I_{3}& 0_{3\times 3}& 0_{3\times 3}\\ 0_{3\times 3}& 0_{3\times 3}& I_{3}& 0_{3\times 3}\\ 0_{3\times 3}& 0_{3\times 3}& 0_{3\times 3}& I_{3}\\ 0_{3\times 3}& 0_{3\times 3}& 0_{3\times 3}& 0_{3\times 3}\end{bmatrix}\otimes \textrm{I}_{l},\textrm{B}_{\textrm{a}}=\begin{bmatrix}0_{3\times 3}\\ 0_{3\times 3}\\ 0_{3\times 3}\\ 1_{3}\end{bmatrix}\otimes \textrm{I}_{l},\textrm{A}_{\textrm{g}}=\begin{bmatrix}0_{2\times 2}& I_{2}\\ 0_{2\times 2}& 0_{2\times 2}\end{bmatrix}\otimes \textrm{I}_{m},\textrm{B}_{\textrm{g}}=\begin{bmatrix}0_{2\times 2}\\ I_{2}\end{bmatrix}\otimes \textrm{I}_{m} \end{aligned}$$

To more effectively illustrate the communication relationships among heterogeneous MAS, a basic linear transformation of the system’s Laplacian matrix is required. When there are \(\text {m}\) UGV and \(\text {l}\) UAV in the system, the corresponding Laplacian matrix is as follows:

$$L=\begin{bmatrix}L_{AA}& L_{AG}\\ L_{GA}& L_{GG}\end{bmatrix}$$

where \(L_{AG},L_{GA}\) represents information between heterogeneous agents. The expected formation for the heterogeneous MAS is denoted as \(h=\left( h_a^T,h_g^T\right) ^T\) , and the corresponding formation error is represented as

$$\delta =\left( \delta _{A}^{x},\delta _{A}^{y},\delta _{A}^{Z},\delta _{G}^{x},\delta _{G}^{y}\right) ^{T}=\left( p_{ai}^{x}-h_{a}^{x},p_{ai}^{y}-h_{a}^{y},p_{ai}^{z}-h_{a}^{z},p_{gi}^{x}-h_{g}^{x},p_{gi}^{y}-h_{g}^{y}\right) ^{T}.$$

Therefore, when the UGV and UAV systems experience actuator failures, the following conditions must be fulfilled for the formation to be deemed complete:

$$\begin{aligned} \begin{aligned}&\mathop {\textrm{lim}}\limits _{t\rightarrow \infty }\parallel p_{i}(t)-p_{0}(t)\parallel =0,\mathop {\textrm{lim}}\limits _{t\rightarrow \infty }\parallel v_{i}(t)-v_{0}(t)\parallel =0,\\ &\mathop {\textrm{lim}}\limits _{t\rightarrow \infty }\parallel \Omega _{i}(t)-\Omega _{0}(t)\parallel =0,\\ &\lim _{t\rightarrow \infty }\parallel \dot{\Omega }_{i}-\dot{\Omega }_{0}\parallel =0,i=1,2,\ldots ,m+l\end{aligned} \end{aligned}$$
(8)

E. Actator fault model

Due to the variability of the operational environment, actuator failures in UAV and UGV systems are inevitable; for instance, a propeller of the UAV may become jammed, or a drive wheel of the UGV may experience insufficient power. This study primarily focuses on actuator failure faults, collectively representing the failure model as follows:

$$\begin{aligned} u_{i}^{f}=(I-\mathscr {P}_{i})u_{i},i=1,\ldots ,m,\ldots ,m+l \end{aligned}$$
(9)

where \(\mathscr {P}_{i}\) designates the actuator failure coefficient. The actuator failure for the UGV can be expressed as \(\mathscr {P}_{Gi}=diag(\rho _{ix},\rho _{iy})\in R^{2}\), while for the UAV it can also be represented as \(\mathscr {P}_{Ai}=diag(\rho _{ix},\rho _{iy},\rho _{iz})\in R^{3}\) , with the constraint \(\mathscr {P}_{Gi},\mathscr {P}_{Ai}\in [0,1]\). Based on Eq. (9), we can derive the system state model after actuator failure as follows:

$$\begin{aligned} \dot{x}_{i}=Ax_{i}+Bu_{i}^{f}+f(x_i) \end{aligned}$$
(10)

Fault-tolerant formation controller design and analysis

Currently, most fault-tolerant consistency control methods for MAS focus on addressing PLOE and external environmental disturbance faults, while research on handling actuator interruption faults in HMAS is still relatively limited. This chapter primarily investigates how to achieve system consistency in a leader-following HMAS under partial actuator failure and actuator interruption faults and how to complete formation tasks based on consistency.

A. Control allocation algorithm

Based on Ref.34, we can derive the principle of the control allocation algorithm, and its application can solve the stability problem when actuator saturation faults occur. The dynamic model of the leader-following heterogeneous MAS after introducing the control allocation algorithm is:

$$\begin{aligned} {\left\{ \begin{array}{ll}\dot{x}_i=Ax_i+B_vv_i\\ v_i=Cu_{iv},& \end{array}\right. },i=1,2,...,N, \end{aligned}$$
(11)

where \(v_{i}\in R^{k}\) represents the virtual control input of the i -th agent and represents the consistency fault-tolerant controller obtained by the control allocation algorithm. When the system experiences actuator faults, we have the following mathematical equations to describe the situation.

Based on the concept of the virtual controller in the control allocation algorithm, we can derive the following optimization equation:

$$\begin{aligned} \begin{aligned}&\min _{u_{i\nu }}u_{i\nu }^{T}W_{i}^{-1}(t)u_{i\nu }\\ &\text {subject to }Cu_{i\nu }=v_{i}\end{aligned} \end{aligned}$$
(12)

where \(W_{i}^{-1}(t)=\left( W_{i}^{-1}(t)\right) ^{T}\in R^{m\times m},i=1,2,...,N\) is a positive definite matrix. Generally, \(W_{i}(t)\) represents the optimization objective function, and in the absence of actuator faults, \(W_{i}(t)=I\) . When actuator faults occur in the system, \(W_{i}(t)\) can be expressed as: \(W_{i}(t)=(1+\varepsilon )I-\mathscr {P}_{i}(t)\) , \(\varepsilon \rightarrow 0^{+}\) is a nonzero normal constant that ensures \(W_{i}(t)\) remains an invertible matrix after an actuator interruption fault occurs.

Next, we present some basic assumptions used in the analysis.

Assumption 1

The communication graph among the followers is strongly connected, with at least one follower being directly linked to the leader.

Assumption 2

The matrix B is of deficient rank, \(rank(B)<\min (m,n)\) .

Note 1

The validity of Assumption 1 indicates that the matrix B has a nontrivial full-rank decomposition. That is, there exist matrices \(B_{\nu }\in R^{n\times k}\) and \(C\in R^{k\times m}\) such that \(B=B_{_v}C\) , and \(rank(B)=rank(B_{_v})=rank(C)\) .

Assumption 3

35In the leader-follower MAS, even if \(m-k\) actuator faults occur, the remaining actuators can still function properly and ensure the completion of the specified task.

Note 2

Assumption 3 is the fundamental condition for ensuring system controllability. The i -th agent’s stability depends on the number of actuator interruption faults l. If \((m-k)<l\) , then, the system can achieve stability; otherwise, the system will approach collapse.

B. Optimal FTC derived from the control allocation algorithm

All control objective problems have been transformed into a consensus problem aimed at driving the error vector of the controlled objects toward zero. For a single UAV and UGV, we first define the state vector as follows:

$$\tilde{x}_{Ai}=\left( \delta _{ai}^{x},\delta _{ai}^{y},\delta _{ai}^{z},\dot{p}_{ai}^{x},\dot{p}_{ai}^{y},\dot{p}_{ai}^{z},g\theta ,-g\phi ,\psi ,g\dot{\theta },-g\dot{\phi },\psi \right) ^{T},\tilde{x}_{Gi}=\left( \delta _{gi}^{x},\delta _{gi}^{y},\dot{p}_{gi}^{x},\dot{p}_{gi}^{y}\right) ^{T},$$

the design and analysis of the fault-tolerant controller after introducing the control allocation algorithm are presented. Then, the theoretical results are extended to scenarios where the leader has unknown control inputs and the follower agents’ actuators are affected by external environmental disturbances. The effectiveness and stability of the proposed algorithm are verified through theoretical analysis. The consensus error for the i -th follower is defined as,

$$e_{i}(t)=\sum _{j\in N_i}a_{ij}(\tilde{x}_{i}-\tilde{x}_{j})+d_{0i}(\tilde{x}_{i}-x_{0}),i=1,2,...,N.$$
$$\begin{aligned} \begin{aligned}&J_{i}=\int _{0}^{\infty }\Bigl [\tilde{x}_{Ai}^{T}Q\tilde{x}_{Ai}+(u_{Ai}^{f})^{T}Ru_{Ai}^{f}\Bigr ]dt\\&\omega _{i}=\int _{0}^{\infty }\Bigl [\tilde{x}_{Gi}^{T}T\tilde{x}_{Gi}^{T}+(u_{Gi}^{f})^{T}\gamma u_{Gi}^{f}\Bigr ]dt\end{aligned} \end{aligned}$$
(13)

Since the dimensionality of the UAV state vector differs from that of the UGV state vector, the weight coefficient for the UAV is set as \(Q=q^{*}I_{12},R=r*I_{3}\), where \(q>0,r>0\). The weight coefficient for the UGV is set as \(T=\lambda *I_{6},\gamma =\mu *I_{3}\), where \(\lambda>0,\mu >0.\)

When actuator faults occur in the system, the performance index function (13), after introducing the control allocation algorithm, will change as follows:

$$\begin{aligned} \begin{aligned}&J_{\dot{n}}=\int _{0}^{\infty }\left\lfloor e_{Ai}^{T}Qe_{Ai}+\left( v_{Ai}\right) ^{T}R_{i\nu }(t)v_{Ai}\right\rfloor dt\\ &\omega _{\textrm{iv}}=\int _{0}^{\infty }\left[ e_{Gi}^{T}Te_{Gi}+(v_{Gi})^{T}\gamma _{iv}(t)v_{Gi}\right] dt \end{aligned} \end{aligned}$$
(14)

where \(R_{\textrm{iv}}(t)\in R^{k\times k}\) is a positive definite symmetric matrix. The virtual controller \(v_i\) that minimizes it can be obtained by solving the performance index function represented by Eq. (14). Then, using Eq. (12), the optimal consensus FTC can be derived.

Next, we present some lemmas required to obtain the optimal fault-tolerant controller.

Lemma 1

36Consider the performance index function represented by Eqs. (13) and (14). If the matrices in these equations satisfy the following relationship:

$$\begin{aligned} CR_{iu}^{-1}(t)C^{T}=R_{iv}^{-1}(t) \end{aligned}$$
(15)

Then, it can be concluded that the optimal virtual controller \(v_i\) obtained from Eq. (13) and the optimal control obtained from Eq. (14) satisfy: \(Cu_{iu}^*=v_i^*\) . Meanwhile, the state trajectories of the agents obtained by the two different methods are identical.

Lemma 2

36If the matrices in the performance index function \(J_{iv}\) and \(J_{iu}\) satisfy the following conditions:

$$\begin{aligned} R_{iu}(t)=W_{i}^{-1}(t)+C^{T}[R_{iv}(t)-(CW_{i}(t)C^{T})^{-1}]C \end{aligned}$$
(16)

Then, the two optimal FTC obtained from Eqs. (12–14) are identical.

Theorem 1

For a leader-follower MAS, the dynamics equation of the leader with unknown control input is given by:

$$\begin{aligned} \dot{x}_{0}=Ax_{0}+Bu_{0} \end{aligned}$$
(17)

The dynamics equation of the follower affected by external environmental disturbances can be expressed as:

$$\begin{aligned} \dot{x}_{i}=Ax_{i}+Bu_{i}+f(t,x_{i}),i=1,2,...,N. \end{aligned}$$
(18)

Meanwhile, the performance index functions (12), (13) and Eq. (14) are defined for the follower agent. Furthermore, Assumptions 1, 2, and 3 are all satisfied. For the given matrices \(R_{\textrm{iv}}(t)\) and \(W_{i}(t),R_{iu}(t)\) satisfies the equation \(R_{iu}(t)=W_{i}^{-1}(t)+C^{T}[R_{iv}(t)-(CW_{i}(t)C^{T})^{-1}]C\).Meanwhile, \(u_0\) and \(f(t,x_i)\) are both independent of the controller \(u_i\) . At this point, the optimal fault-tolerant consensus controller for the i -th follower is:

$$\begin{aligned} {\left\{ \begin{array}{ll}u_{iv}^{*}(t)=-0.5(d_{0i}+\sum _{j=1}^{N}a_{ij})W_{i}(t)C^{T}(CW_{i}(t)C^{T})^{-1}CR_{iu}^{-1}(t)B^{T}\lambda _{i}^{*},\\ \dot{\lambda }_{i}^{*}=-(2Qe_{i}(t)+A^{T}\lambda _{i}^{*}),& \end{array}\right. } \end{aligned}$$
(19)

where \(\lambda _{i}^{*}\in R^{n}\) represents an auxiliary variable. Meanwhile, under the effect of this optimal consensus FTC, the consensus error of the leader-follower MAS can achieve asymptotic stability despite actuator PLOE and interruption faults. Proof: First, solve for the optimal consensus FTC \(u_{iv}^*(t)\) under actuator PLOE and interruption faults. According to the system dynamics model (18), the derivative of the consensus error for the i -th follower can be calculated as:

$$\begin{aligned} \dot{e}_{i}(t)=Ae_{i}(t)+\sum _{j\in N_{i}}a_{ij}B(u_{iu}(t)-u_{ju}(t))+d_{0i}B(u_{iu}(t)-u_{0})+f(t,x_{i}) \end{aligned}$$
(20)

Here, we let matric \(f(t,x_i)=f(t,x_j)\), defined a Hamiltonian function as follows:

$$\begin{aligned} \begin{aligned}H_{i}(t,e_{i},u_{iu},\lambda _{i})&=e_{i}^{T}(t)Qe_{i}(t)+u_{iu}^{T}(t)R_{iu}(t)u_{iu}(t)\\ &\quad+\lambda _{i}^{T}\left( Ae_{i}(t)+\sum _{j=1}^{N}a_{ij}B(u_{iu}(t)-u_{ju}(t))+d_{0t}B(u_{iu}(t)-u_{0})+f(t,x_{i})\right).\end{aligned} \end{aligned}$$
(21)

where \(\lambda\) is the co-state vector. Since \(u_{iu}^{*}\) are unconstrained, the minimum condition is that the Hamiltonian function (21) takes an unconditional minimum to the control input \(u_{iu}\) . Compute t the function’s derivative for the input:

$$\begin{aligned} \frac{\partial H_{i}(t,e_{i},u_{iu},\lambda _{i})}{\partial u_{iu}}=2R_{iu}(t)u_{iu}(t)+(d_{0i}+\sum _{j=1}^{N}a_{ij})B^{\textrm{T}}\lambda _{i} \end{aligned}$$
(22)

Since

$$\begin{aligned} \frac{\partial ^2H_i(t,e_i,u_{iu},\lambda _i)}{\partial (u_{iu})^2}=2R_{iu}(t)>0 \end{aligned}$$
(23)

Therefore, let \(\frac{\partial H_{i}(t,e_{i},u_{iu},\lambda _{i})}{\partial u_{iu}}=0\),we obtain the following:

$$\begin{aligned} u_{iu}^{*}(t)=-0.5(d_{0i}+\sum _{i=1}^{N}a_{ij})R_{iu}^{-1}(t)B^{T}\lambda _{i}^{*} \end{aligned}$$
(24)

Equation (24) is the control that minimizes the Hamiltonian function (21), i.e., the optimal control. According to the canonical equation, we obtain:

$$\begin{aligned} \begin{aligned}&\dot{e}_{i}(t)=\frac{\partial H_{i}(t,e_{i},u_{iu},\lambda _{i})}{\partial \lambda _{i}}=Ae_{i}(t)+\sum _{j=1}^{N}a_{ij}B(u_{iu}(t)-u_{ju}(t))+d_{0i}B(u_{iu}(t)-u_{0})+f(t,x_{i})\\ &\dot{\lambda }^{*}=-\frac{\partial H_{i}(t,e_{i},u_{iu},\lambda _{i})}{\partial e_{i}}=-2Qe_{i}(t)-A^{T}\lambda _{i}\end{aligned} \end{aligned}$$
(25)

Therefore, we obtain the optimal consensus controller in the absence of faults as:

$$\begin{aligned} {\left\{ \begin{array}{ll}u_{iu}^{*}(t)=-0.5(d_{0i}+\sum _{j=1}^{N}a_{ij})R_{iu}^{-1}(t)B^{T}\lambda _{i}^{*}\\ \dot{\lambda }_{i}^{*}=-(2Qe_{i}(t)+A^{T}\lambda _{i}^{*})& \end{array}\right. }\quad ,\quad i=1,2,...,N. \end{aligned}$$
(26)

We can obtain the optimal consensus controller according to Lemma 1 and the conclusions in36. At the same time, the leader has an unknown input, and the followers handle actuator PLOE, interruption faults, and external environmental disturbances. The controller is expressed as:

$$\begin{aligned} {\left\{ \begin{array}{ll}u_{iv}^{*}(t)=-0.5(d_{0i}+\sum _{j=1}^{N}a_{ij})W_{i}(t)C^{T}(CW_{i}(t)C^{T})^{-1}CR_{ii}^{-1}(t)B^{T}\lambda _{i}^{*}\\ \dot{\lambda }_{i}^{*}=-(2Qe_{i}(t)+A^{T}\lambda _{i}^{*}).& \end{array}\right. } \end{aligned}$$
(27)

Next, we analyze whether the leader-follower system with unknown inputs and external disturbances can achieve consensus under the effect of equation (27) and examine the stability of the leader-follower MAS.

First, we perform the following transformation on the variables:

$$\begin{aligned}&e_{\nu }=\left[ e_{1\nu }^{*T}(t),e_{2\nu }^{*T}(t),...,e_{N\nu }^{*T}(t)\right] ^{T},\\ &e_{u}=\left[ e_{1u}^{*T}(t),e_{2u}^{*T}(t),...,e_{Nu}^{*T}(t)\right] ^{T},\\ &u_{\nu }=[u_{1\nu }^{*T}(t),u_{2\nu }^{*T}(t),...,u_{N\nu }^{*T}(t)]^{T},\\ &u_{u}=\left[ u_{1u}^{*T}(t),u_{2u}^{*T}(t),...,u_{Nu}^{*T}(t)\right] ^{T},\\ &\lambda =[\lambda _{1}^{*T},\lambda _{2}^{*T},...,\lambda _{N}^{*T}]^{T},\\ &\nu =[\nu _{1}^{*T},\nu _{2}^{*T},...,\nu _{N}^{*T}]^{T}\end{aligned}.$$

The Kronecker product form of equation (20) can be written as:

$$\begin{aligned} \dot{e}_{\nu }=(I\otimes A)e_{\nu }+(G\otimes B_{\nu })\nu , \end{aligned}$$
(28)
$$\begin{aligned} \dot{e}_{u}=(I\otimes A)e_{u}+(G\otimes B)u_{u}. \end{aligned}$$
(29)

Built on the Lyapunov stability theory, we define the Lyapunov function for the error system represented by Eqs. (28) and (29) as follows:

$$\begin{aligned} V_{v}(e_{v}(t))=\int _{t}^{\infty }[e_{v}^{T}(t)(I\otimes Q)e_{v}(t)+\nu ^{T}R_{v}(t)\nu ]dt, \end{aligned}$$
(30)
$$\begin{aligned} V_{u}(e_{u}(t))=\int _{t}^{\infty }[e_{u}^{T}(t)(I\otimes Q)e_{u}(t)+u^{T}R_{u}(t)u]dt, \end{aligned}$$
(31)

where \(R_{\nu }(t)=diag(R_{1\nu }(t),R_{2\nu }(t),...,R_{N\nu }(t))\in R^{Nk\times Nk},R_{u}(t)=diag(R_{1u}(t),R_{2u}(t),...,R_{Nu}(t))\in R^{Nm\times Nm}\) represents the matrix composed of positive definite matrices in the function (13). The optimal controller can make the Hamiltonian function equal to 0.

$$\begin{aligned} H_{i}(t,e_{iu}^{*},u_{iu}^{*},\lambda _{i}^{*})=0. \end{aligned}$$
(32)

Based on37, Eq. (32) can be rewritten as:

$$\begin{aligned} \begin{aligned}H_{i}&(t,e_{iu}^{*},u_{iu}^{*},\frac{\partial V_{iu}(e_{iu}^{*}(t))}{\partial e_{iu}^{*}(t)})\\ &=e_{iu}^{*T}(t)Qe_{iu}^{*}(t)+u_{iu}^{*T}R_{iu}(t)u_{iu}^{*}\\ &\quad+\frac{\partial V_{iu}^{T}(e_{iu}^{*}(t))}{\partial e_{iu}^{*}(t)}\left( Ae_{iu}^{*}\left( t\right) +\sum _{j=1}^{N}a_{ij}B\left( u_{iu}^{*}-u_{ju}^{*}\right) +d_{0i}B(u_{iu}^{*}(t)-u_{0})+f(t,x_{i})\right) \\ &=0.\end{aligned} \end{aligned}$$
(33)

where \(V_{iu}(e_{iu}^{*}(t))>0\) and \(V_{iu}(0)=0\), Eq. (33) can be rewritten as:

$$\begin{aligned} \begin{aligned}&\frac{\partial V_{iu}^{T}(t)}{\partial e_{iu}^{*}(t)}\left( Ae_{iu}^{*}(t)+\sum _{j=1}^{N}a_{ij}B(u_{iu}^{*}-u_{ju}^{*})+d_{0i}B(u_{iu}^{*}(t)-u_{0})+f(t,x_{i})\right) \\ &=-(e_{iu}^{*T}(t)Qe_{iu}^{*}(t)+u_{iu}^{*T}R_{iu}(t)u_{iu}^{*}).\end{aligned} \end{aligned}$$
(34)

By computing the time derivative of the Lyapunov function \(V_{iu}(e_{iu}^{*}(t))\) , we obtain:

$$\begin{aligned} \begin{aligned}\dot{V}_{iu}(e_{iu}^{*})&=\frac{\partial V_{iu}^{T}\left( e_{iu}^{*}(t)\right) }{\partial e_{iu}^{*}\left( t\right) }\dot{e}_{iu}^{*}\left( t\right) \\ &=\frac{\partial V_{iu}^{T}(e_{iu}^{*}(t))}{\partial e_{iu}^{*}(t)}\left( Ae_{iu}^{*}(t)+\sum _{j=1}^{N}a_{ij}B(u_{iu}^{*}-u_{ju}^{*})+d_{0i}B(u_{iu}^{*}(t)-u_{0})+f(t,x_{i})\right) \\ &=-(e_{iu}^{*T}(t)Qe_{iu}^{*}(t)+u_{iu}^{*T}R_{iu}(t)u_{iu}^{*}).\end{aligned} \end{aligned}$$
(35)

Since the matrices Q and R are both positive definite, the following inequality can be obtained:

$$\begin{aligned} \dot{V}_{iu}(e_{iu}^{*}(t))<0. \end{aligned}$$
(36)

For the error system represented by Eq. (29) and the corresponding Lyapunov function in Eq. (31), its derivative can be expressed as:

$$\begin{aligned} \dot{V}_{u}\left( e_{u}\left( t\right) \right) =\sum _{i=1}^{N}\dot{V}_{iu}\left( e_{iu}^{*}\left( t\right) \right) =-\sum _{i=1}^{N}e_{iu}^{*T}\left( t\right) Qe_{iu}^{*}\left( t\right) +u_{iu}^{*T}R_{iu}\left( t\right) u_{iu}^{*}<0. \end{aligned}$$
(37)

\(V_{_u}(e_{_u}(t))>0\) is positive definite, and \(\dot{V}_u(e_u(t))<0\) . According to the Lyapunov stability theory, this error system can achieve asymptotic stability. From Eq. (12), the obtained virtual controller \(v_{i}\in R^{k}\) ensures that the leader-follower MAS achieves consensus without faults. The optimal consensus FTC \(u_{iv}^{*}(t)\) obtained through the control allocation algorithm enables the leader-follower MAS with actuator faults and complete the formation task effectively.

Next, we apply the control allocation algorithm to the leader-follower UAV-UGV system to obtain the optimal FTC law for UAVs and UGVs.

For each UAV, the control input is:

$$\begin{aligned} u_{Ai}=-0.5(d_{0i}+\sum _{j=1}^{N}a_{\ddot{y}})W_{i}(t)C^{T}(CW_{i}(t)C^{T})^{-1}CR_{iu}^{-1}(t)B_{a}^{T}P_{Ai}\tilde{x}_{Ai} \end{aligned}$$
(38)

For each UGV, the control input is:

$$\begin{aligned} u_{Gi}=-0.5(d_{0i}+\sum _{j=1}^{N}a_{ji})W_{i}(t)C^{T}(CW_{i}(t)C^{T})^{-1}C\gamma _{iu}^{-1}(t)B_{g}^{T}P_{Gi}\tilde{x}_{Gi} \end{aligned}$$
(39)

Simulations

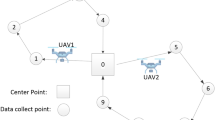
This section designs experiments for the optimal FTFC of the HMAS presented in Chapter 3, verifying the feasibility of the FTFC algorithm through these experiments. This study considers an experimental setup with a heterogeneous MAS composed of 3 UAVs and 3 UGVs. The leader is UAV node 0, 1, 2, and 3 represent UAVs, while 4, 5, and 6 represent UGVs, and the communication relationships among follower agents are shown in Fig. 1.

Fig. 1
figure 1

Communication topology of the follower HMAS.

Full size image

Based on the communication topology in Fig. 1, we can obtain the corresponding Laplacian matrix and overall matrix as follows:

$$\begin{aligned}&L=\begin{pmatrix}2& -1& -1& |& 0& 0& 0\\ -1& 1& 0& |& 0& 0& 0\\ 0& -1& 1& |& 0& 0& 0\\ 0& 0& -1& |& 1& 0& 0\\ 0& 0& 0& |& -1& 1& 0\\ 0& 0& 0& |& 0& -1& 1\end{pmatrix}=\begin{pmatrix}L_{AA}& L_{AG}\\ L_{GA}& L_{GG}\end{pmatrix},\end{aligned} \mathscr {G}=L+D=\begin{pmatrix}3& -1& -1& 0& 0& 0\\ -1& 2& 0& 0& 0& 0\\ 0& -1& 1& 0& 0& 0\\ 0& 0& -1& 1& 0& 0\\ 0& 0& 0& -1& 0& 0\\ 0& 0& 0& 0& -1& 1\end{pmatrix}$$

Suppose UAV2 and UGV2 do not experience any failures while the remaining agents undergo actuator faults to varying degrees, with the specific fault levels given by:

$$\mathscr {P}_{A1}=\begin{bmatrix}1& 0& 0\\ 0& \sin (t\pi /15)& 0\\ 0& 0& 1\end{bmatrix},\mathscr {P}_{A3}=\begin{bmatrix}e^{-t/30}& 0& 0\\ 0& 0& 0\\ 0& 0& 0.1\end{bmatrix},\mathscr {P}_{G1}=\begin{bmatrix}1& 0\\ 0& 0.5\sin t\end{bmatrix},\mathscr {P}_{G3}=\begin{bmatrix}1& 0\\ 0& (t/15)^2\end{bmatrix}$$

The UAV system’s initial states are presented in Table 1, while the UGV system’s initial states are given in Table 2, as shown below.

Table 1 Initial states of the UGV system
Full size table
Table 2 Initial states of the UAV system
Full size table

The experimental platform used in this section is Matlab 2017a, and the states of UAVs and UGVs are defined as \(\tilde{x}_{Ai}=\left( \delta _{ai}^{x},\delta _{ai}^{y},\delta _{ai}^{z},\nu _{ai}^{x},\nu _{ai}^{y},\nu _{ai}^{z},g\theta ,-g\phi ,\dot{\psi },g\dot{\theta },-g\dot{\phi },\ddot{\psi }\right) ^{T},\tilde{x}_{Gi}=\left( \delta _{gi}^{x},\delta _{gi}^{y},\nu _{gi}^{x},\nu _{gi}^{y}\right) ^{T},i=1,2,3\) in section “B. Optimal FTC derived from the control allocation algorithm”. The value of \(\varepsilon\) is set to 0.0001, \(Q=60^{*}I_{12},R_{,}=40^{*}I_{6},T=60^{*}I_{4},\gamma _{,}=40^{*}I_{4}\) , formation information is set to \(h_{a1}=[0,0,0]^T,h_{a2}=[-10,15,0]^T,h_{a3}=[0,30,0]^T;h_{g1}=[0,0]^T,h_{g2}=[-10,15]^T,h_{g3}=[0,30]^T\), the environmental disturbance is set to \(f(t,x_{i})=-0.33\sin x_{i}\) , and the correlation coefficient matrices of UAVs and UGVs are set as follows:

$$B_{av}=\begin{bmatrix}0_{3\times 3}& 0_{3\times 3}\\ 0_{3\times 3}& 0_{3\times 3}\\ 0_{3\times 3}& 0_{3\times 3}\\ I_{3}& 0_{3\times 3}\end{bmatrix},C_{a}=\begin{bmatrix}I_{3}\\ 0_{3\times 3}\end{bmatrix},B_{gv}=\begin{bmatrix}0_{2\times 2}& 0_{2\times 2}\\ I_{2}& 0_{2\times 2}\end{bmatrix},C_{g}=\begin{bmatrix}I_{2}\\ 0_{2\times 2}\end{bmatrix}$$

Based on the aforementioned formation equations of the leader-follower heterogeneous MAS, the topology Fig. 1, and the corresponding parameter matrix design, the following section conducts simulation experiments on three types of agent faults. It provides the corresponding simulation results and analysis.

A. Simulation results without control input

First, we conduct simulation experiments under the condition that the leader has no control input, with the actuator failures of the follower agents present from the beginning of the system operation. The total runtime of the experimental design is as described above, and the actuator failure coefficient matrix of the followers is as well.

Figures 2, 3, 4, 5, 6, 7, 8 and 9 show the simulation results of the optimal FTFC law. Figures 2 and 3 illustrate the state changes of the UAV and UGV heterogeneous MAS under the optimal fault-tolerant formation control protocol. From Figure 2, it can be observed that UAV’s position states and UGV’s position states eventually tend towards stable values. The position states of the X-axis achieve consensus at \(t=20s\) . The X-axis stabilizes at two values. Figure 3 shows that UAV’s position states and UGV’s position states approach stable values at \(t=20s\) . The Y-axis stabilizes at three values, forming a triangular formation.

Fig. 2
figure 2

The position status of UAV and UGV in the X-axis without input from the leader and external environmental interference.

Full size image
Fig. 3
figure 3

The position status of UAV and UGV in the Y-axis without input from the leader and external environmental interference.

Full size image
Fig. 4
figure 4

The position status of UAV in the Z-axis without input from the leader and external environmental interference

Full size image
Fig. 5
figure 5

The velocity status of UAV and UGV in the X-axis without input from the leader and external environmental interference.

Full size image
Fig. 6
figure 6

The velocity status of UAV and UGV in the Y-axis without input from the leader and external environmental interference.

Full size image
Fig. 7
figure 7

The velocity status of UAV in the Z-axis without input from the leader and external environmental interference.

Full size image
Fig. 8
figure 8

The attitude and angular velocity states of UAV without input from the leader and external environmental interference.

Full size image

From Fig. 4, we can see that the UAVs’ Z-axis position states converge at \(t=15s\). As a result of Figs. 2 and 3, the leader-follower heterogeneous MAS completes the formation task at \(t = 20s.\)

Figures 5 and 6 show the velocity states of UAVs and UGVs along the X and Y axes under external environmental disturbances using the control allocation algorithm. Figure 5 shows that the X-axis velocity state of the leader in the heterogeneous MAS stabilizes over \(t=20s\) under the condition of no input from the leader and external environmental disturbances. Figure 6 shows that the Y-axis velocity states of UAVs and UGVs converge to 0 m/s over \(t=20s\) , completing the formation task. The three UAVs and three UGVs converge to the same position. The Y-axis velocity error of the UAVs stabilizes at 0 m/s.

Figures 7 and 8 show the simulation results under the optimal FTFC protocol. Figure 7 shows the velocity state along the Z-axis of UAVs under the condition of actuator partial failure. From the figure, it is evident that the UAV’s velocity state of the Z-axis stabilizes at \(t=20s\). Figure 8 shows the UAV’s attitude angles and angular velocity states during the formation process with actuator failure. It can be observed that the attitude angle of the UAVs approaches zero rad at \(t=15s\) , and the pitch angle, yaw angle, and steering angle, along with their angular velocities, eventually approach 0 rad and 0 rad/s . That is, the UAVs ultimately reach stability.

Figure 8 shows the formation state of UAVs and UGVs in a three-dimensional coordinate system using the optimal FTFC. Figure 8 shows that the UAVs and UGVs system completes the formation at \(t=30s\), even under actuator failures and external disturbances. The three UAVs and three UGVs converge to the same corresponding position.

Fig. 9
figure 9

Formation trajectory of HMAS without input from the leader and external environmental interference.

Full size image

Figure 9 shows the positions of UAVs and UGVs at \(t=30s\) and \(t=45s\) are marked with circles and stars , respectively, and their corresponding positions are connected using line segments to visually display the dynamic relationship. Through comparative analysis, it can be concluded that both UAVs and UGVs successfully constructed triangular formations at the time points of \(t=30s\) and \(t=45s\), and the formation structure remained strictly consistent. Specifically, each UAV’s position formed a one-to-one mapping relationship with the UAV’s position, verifying the accuracy and synchronization of the formation control strategy. Further observation reveals that despite the passage of time, the two can still maintain a stable relative distance and angle during the movement process, fully demonstrating the robustness of the formation algorithm. This result not only confirms the collaborative feasibility of HMAS (UAVs and UGVs) in complex environments, but also provides important experimental support for MAS formation optimization and FTC.

B. Simulation results with control input from the leader

We provide the simulation results with the leader having control input. In this simulation, the experiment is designed with one leader and six follower HMAS, with a system runtime of 50 seconds. The actuator failures in the follower agents do not occur initially but appear during the simulation, with different actuator failure coefficient matrices applied at various time intervals.

At \(t\in (0,20]\), no actuator faults occur for all UAVs and UGVs, and the actuator failure coefficient matrix is:

$$W_{A1}(t)=W_{A2}(t)=W_{A3}(t)=W_{G1}(t)=W_{G2}(t)=W_{G3}(t)=\begin{bmatrix}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{bmatrix}$$

At \(t\in [20,50]\), all UAVs and UGVs experience actuator failures, with the failure coefficient matrix being the same as in Experiment A. The leader’s control input is \(u_{0}=[0,0,1]^{T}\) ,let \(f(t,x_{i})=-10\sin x_{i}\) , the external interference of UAVs and UGVs is set to \([-10 sin(x_i), -10 sin(x_i), 0,0,0,0], [-10 sin(x_i), -10 sin(x_i), 0,0].\)

Figures 10, 11, 12, 13 and 14 show the simulation results with the leader having control input and external environmental disturbances. Figures 10 and 11 display the state changes of the UAVs and UGVs heterogeneous MAS under the optimal FTFC. From Figure 10 , it can be observed that the UAV and UGV position states eventually converge to a stable value. The X-axis position state reaches consensus at \(t=20s\). The X-axis stabilizes at two values. Figure 11 shows that the UAV and UGV position states stabilize at \(t=20s\) . The Y-axis stabilizes at three values, completing the triangular formation.

Figure 11 portrays the formation trajectory of UAVs and UGVs in three-dimensional space using the optimal FTFC protocol. From the figure, that can be observed the UAVs and UGVs converge to the desired positions and achieve a triangular formation under conditions of partial actuator failure. Three UAVs and three UGVs converge to the corresponding identical positions, with the UAVs ultimately stabilizing at a height of 80 m.

Fig. 10
figure 10

The position status of UAV and UGV in the X-axis with unknown input from the leader and external environmental interference.

Full size image
Fig. 11
figure 11

The position status of UAV and UGV in the Y-axis with unknown input from the leader and external environmental interference.

Full size image
Fig. 12
figure 12

The position status of UAV in the Z-axis with unknown input from the leader and external environmental interference.

Full size image
Fig. 13
figure 13

The attitude and angular velocity states of UAV with unknown input from the leader and external environmental interference.

Full size image
Fig. 14
figure 14

Formation trajectory of HMAS with unknown input from the leader and external environmental interference.

Full size image

From Fig. 12, it is clear that the UAV’s Z-axis position state converges at \(t=15s\). Figures 10 and 11 show that the leader-following heterogeneous MAS completes the formation task at \(t=20s\) .

Figure 13 shows the UAV’s attitude angles and angular velocity states during the formation process with actuator failure. One can observe that the UAVs’ attitude angle approaches zero rad at \(t=15s\). After the faults occur at \(t=20s\) , the angle states and angular velocities converge to 0 rad and 0 rad/s , meaning the UAVs eventually reach stability.

Figure 14 shows the positions of UAVs and UGVs at \(t = 30s\) and \(t =45s\) are marked with circles and stars , respectively, and their corresponding positions are connected using line segments to visually display the dynamic relationship. Under the coupling effect of unknown input from the leader and external environmental interference from followers, the drone and unmanned vehicle successfully achieved a triangular formation, and the formation strictly remained consistent. Despite the local shaking of the drone trajectory caused by environmental interference, based on the optimal FTFC under the control allocation algorithm, all agents converge to the preset position within a finite time. This result indicates that the proposed FTC strategy can effectively coordinate the collaborative motion of heterogeneous agents in dynamic disturbance environments, providing a solution that combines accuracy and FTC for MAS formation control in complex scenarios.

Conclusions

This paper investigates the FTFC problem for a heterogeneous MAS composed of quadrotor UAVs and Mecanum wheeled UGVs under actuator faults. Firstly, a control system model for UAVs and UGVs with actuator faults is established, utilizing the Kronecker product to incorporate UAVs and UGVs of differing dimensions into the state equations, thereby forming a heterogeneous system, solving the formation problem caused by the mismatch in state-space dimensions of UAVs and UGVs. We defined performance indices for each UAV and UGV, considering the leader’s unknown inputs, external disturbances, and actuator faults. Using optimal control theory, we obtained the optimal fault-tolerant controllers. By combining control allocation with optimal control, we designed the optimal FTFC for HMAS, proving its effectiveness in addressing actuator PLOE and interruptions faults. Finally, simulation experiments validate the designed optimal FTC’s effectiveness. In subsequent research, we will concentrate on the FTCC under conditions of unknown actuator faults, fixed time, and switching topologies, ensuring the system possesses both strong robustness and rapid responsiveness.