Introduction

Renewable energy is getting important these days due to the rise in energy demand all over the world and the depletion of fossil fuels. Particularly wind and solar energy systems are more attractive to share 10–20% of the total load fed by conventional energy resources1,2. Both wind and solar energy are getting much attention these days for grid-tied renewable energy resources3. However, wind energy has certain advantages over solar energy like the capability of producing electricity both during day and night, less space requirement and low cost4. In India, China and USA the average available wind potential per annum is 102,778 MW, 2380 GW and 10,459 GW respectively. But the installed capacity in these countries at the end of 2020 is 45.887 GW, 441 GW and 150.429 GW respectively5. India is in the fourth position in the total installed capacity of wind generators in the world. However, the installed capacity is very less when compared to the available potential and hence it is understood the growth potential available for wind energy.

Earlier, wind generators are equipped with fixed-speed wind energy conversion systems. In spite of the cheaper cost, they need separate excitation controllers and will be subjected to high mechanical stress. A variable speed wind energy conversion system can overcome the above limitations. Both Doubly Fed Induction Generators (DFIG) and Permanent Magnet Synchronous Generators (PMSG) can be used for variable speed wind energy conversion systems6,7. Most of the variable speed systems utilize induction generators. But they require a separate excitation and hence there will be considerable excitation losses. Also, a multi-pole structure will increase the size of the machine, and hence the construction will become complicated8,9. The drastic reduction in the price of magnetic materials and technical up-gradation has made permanent magnet generators (PMG) more attractive to overcome the limitations of DFIG. GE has incorporated 150 tons, 7.6 m diameter permanent magnet generator in its 6 MW direct- drive units which is the high-capacity generator10. Siemens had also made a change in regards to the generator. In the past, direct-drive machine rotors have been located inside the system. Siemens is now inverting the machine so that, the rotor is on the outside. Siemens has released its 6.6 MW direct-drive prototype11. The aforementioned development carried out at the world-leading wind generator manufacturers reveals that the permanent magnet generator technology continuously evolving in the field of wind energy conversion systems and its adoption rate becomes so high in the near future.

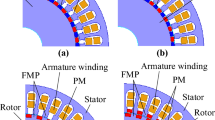
In general, the PMGs have the two kinds of structural topology based on the flux flow between the stator and rotor part of the generators. The Radial Flux Permanent Magnet Generators (RFPMGs) and the axial flux permanent magnet generators (AFPMGs) are the two kinds. The internal rotor RFPMG provides high torque and power12,13. Apart from the installation of the RFPMG with internal rotor structure is simple and has minimum time requirement14,15,16. Nevertheless, it offers more weight due to the consumption of more materials and minimum power density. On the other hand, the RFPMG with the outer rotor module has a good agreement with the lower material consumption and high-power density than the inner rotor RFPMG17,18,19. Another version of the PMGs is axial flux PMGs. Generally, this kind of PMGs has less volumetric consumption than the radial flux PMGs. Also, it delivers less distorted output torque which ensures the smooth rotations of the wind turbine-generator set20. Though the core-less structure of AFPMG offers less weight and negligible core loss the slotted AFPMG develops high magnetic flux than the coreless AFPMG due to the presence of its laminated core in the stator21,22. Also, it provides a stable flux distribution over the rotor part23. Hence the parameters associated with the flux distribution will support in improving the overall performance of the machine. The coreless structure of stator cannot be incorporated in single sided AFPMG. Whereas in double sided AFPMG can accommodate the coreless stator configuration. Good dynamic stability, high effective length of air-gap, and improved natural cooling are found to be the features of double rotor AFPMG24,25. Even though multi-rotor configurations provide good performance, the limitation on the total cost of the machine resist the usage of multi-rotor configuration especially the usage of rotors with more than two26. Hence the AFPMG which has two outer rotor configuration and a slotted stator structure is considered in this article32. provides insights into modular AFPMSG optimization for efficiency and manufacturability, while33 offers a comparative analysis of PMVG and PMSG designs, highlighting efficiency trade-offs. These additions enhance the study’s context and justify the need for the proposed double-sided slotted AFPMG design.

The outer rotor RFPMG and the DSAFPMG are designed and modelled through the Finite Element Analysis (FEA) technique. The Ansys Maxwell software has been used to modelled the machines and their performance has been evaluated in the aspects like flux distribution, the output generated voltage and current, moving and cogging torque, weight, losses, efficiency and power quality. The 300 W prototype of double-sided slotted AFPMG were developed and the hardware results are presented to validate the performance of the proposed DSAFPMG.

The article is structured as, Sect. 2 describes the design and modelling of RFPMG and AFPMG, Sect. 3 deals with Finite Element Analysis (FEA) of the permanent magnet generators, Sect. 4 reveals the experimental verifications of DSAFPMG and the conclusion given in Sect. 5.

Design and modelling of radial flux and axial flux PMGs

The Rotor and stator design of both radial and axial flux PMG has been accomplished in this section. The main dimensions like outer rotor diameter (D0), axial length (L), and dimensions of permanent magnets are calculated in the rotor design. Whereas, in the stator design, core, slot, and stator coil dimensions are identified.

The design parameters can be calculated based on the specific required rating and other electrical quantities such as power rating, output frequency and supply voltage. A 300 W, 220 V, 3 phase, star connection generator with the speed range of 150 to 200 rpm has been taken as the specification selected for the both generators. These parameters are taken to be an input parameter to identify the design parameters values. A 300 W generator are considered here since it is sufficient to generate the power to charge the battery which will suitable to domestic applications. The charger circuit needs to be incorporated between the wind generators and the load/battery to convert the generated voltage to the required voltage level. The rated speed of the generator has been selected from the range 150 to 200 rpm. This speed of the generator can be easily attained through the average wind velocity available during day and night time.

Design and modelling of RFPMG

The 2-dimensional view of radial flux PMG with outer rotor configuration and its corresponding magnetic equivalent circuit is shown in below Fig. 1.

Fig. 1
figure 1

(a) 2-dimensional view and (b) Magnetic Equivalent circuit of RFPMG.

Full size image

In determining the key parameters such as outer diameter, axial length, and permanent magnet dimensions, the basic power equation based on classical electromagnetic design principles and empirical optimizations from prior studies is presented in Eq. (1).

$$\:P=\frac{{B}_{g}{A}_{e}{L}_{s}f\eta\:}{{k}_{w}}$$
(1)

where, \(\:{B}_{g}\) is the air-gap flux density, \(\:{A}_{e}\) is the electrical loading, \(\:{L}_{s}\) is the stack length, \(\:f\) is the frequency, \(\:\eta\:\) is the efficiency, \(\:{k}_{w}\) is the winding factor.

Each term in these equations has been selected based on optimized values from prior research studies, including Kamper et al.27, which provided empirical data on winding factor selection, electrical loading constraints, and air-gap flux density optimization. The Eq. (2) shows the detailed rated output power of the RFPMG.

$$\:{P}_{R}=\frac{1}{1+{k}_{{\varnothing}}}\frac{m}{{m}_{1}}\frac{\pi\:}{2}{k}_{e}{k}_{i}{k}_{p}\eta {B}_{g\:}A\:\frac{f}{p}\:{\lambda\:}_{D}^{2}{D}_{0}^{2}{L}_{e}$$
(2)

The diameter of outer periphery of the radial flux generator is given in (3),

$$\:{D}_{0}\:=\sqrt{\frac{{P}_{R}}{\frac{1}{1+{k}_{\varnothing\:}}\frac{m}{{m}_{1}}\frac{\pi\:}{2}{k}_{e}{k}_{i}{k}_{p}\eta {B}_{g\:}A\:\frac{f}{p}\:{\lambda\:}_{D}^{2}{L}_{e}}}$$
(3)

where \(\:{\lambda\:}_{D}=\frac{{D}_{i}}{{D}_{0}}\) is the diameter ratio, A is the total electrical loading of the machine \(\:{k}_{e}\)Emf factor, \(\:{k}_{i}\) is the current waveform factor,\(\eta\) is the efficiency, \(\:{B}_{g\:}\:is\:the\:\)Airgap flux density and f is the frequency of the machine. The below L/D ratio is used to identify the axial length of the machine27.

$$\:\frac{L}{D}=\frac{\pi\:\sqrt{P}}{4P}$$
(4)

The expression (5) gives the outer diameter of stator of the machine,

$$D\,=\,{D_{arc}} - 2\left( {{l_m}} \right) - 2\delta$$
(5)

The various parameters associated with the stator’s slot are given in Eqs. (6)–(10).

$$\:{h}_{sy}=\:\frac{1}{2}\:(D-{D}_{i}-2{h}_{ss}$$
(6)
$$\:{b}_{ss1}=\:\pi\:\:\frac{D-2{h}_{sw}}{{Q}_{s}}-{b}_{ts}$$
(7)
$$\:{h}_{ry}=\:\frac{1}{2}\:({D}_{0}-{D}_{arc}$$
(8)
$$\:{b}_{ss2}=\:\pi\:\:\frac{D-2{h}_{ss}}{{Q}_{s}}-{b}_{ts}$$
(9)
$$\:{k}_{open}=\frac{{b}_{s0}}{{b}_{ss1}}$$
(10)

hsy, bss1, hry, bss2, kopen are the height of stator yoke, opening slot width, thickness of the rotor back iron, slot width and opening factor respectively.

Where Darc -arc diameter, lm – Permanent magnet’s thickness and δ – Length of air-gap.

Through the Eq. (11) the total required slots of the stator can be identified,

$${\text{Required slots}},~{N_s}={\text{ }}2 \times m \times p \times q$$
(11)

The emf generated at the machine is calculated through Eqs. (12),

$$\:{\text{E}}_{a}=\frac{2{\uppi\:}}{\sqrt{2}}\:f{N}_{ph}{K}_{w1}{{\varnothing}}_{p}$$
(12)

where Nph –turns/ phase, \(\:{\varnothing\:}_{p}\) – pole flux resulted from spatial flux density’s harmonic components and f – supply frequency. Further, flux beneath the poles (\(\:{\varnothing\:}_{p})\) can be determined as,

$$\:{\varnothing\:}_{p}=B{L}_{max}\frac{LD}{2P}$$
(13)

where D and L are the diameter of the air-gap and axial length of stator core respectively.

BLmax -Maximum value of a fundamental component in flux density distribution.

The torque generated at RFPMG is given in (14),

$$\:{T}_{re}=\sqrt{2}\:\pi\:{R}^{2}{L}_{e}{B}_{g1}{K}_{s}$$
(14)

where R- radius of outer rotor, Le- effective length of the machine, Bg1- maximum flux density, ks- open slot space factor respectively.

Design and modelling of AFPMG

The 2-dimensional view of axial flux configuration of the DSAFPMG and its magnetic equivalent circuit is shown in Fig. 2.

Fig. 2
figure 2

(a) 2-Dimensional view and (b) Magnetic Equivalent circuit of AFPMG.

Full size image

Similarly, for AFPMG, the rated power in simple form is given in Eq. (15),

$$\:P=\frac{{\pi\:{D}_{0}^{2}B}_{g}{A}_{e}f\eta\:}{4}$$
(15)

where \(\:{D}_{0}\) is the outer diameter. The outer diameter \(\:{D}_{0}\) was optimized to minimize core loss while ensuring adequate flux linkage, referencing empirical optimizations for axial flux machine topologies, as presented by Ashrafzadeh et al.32.

The air-gap flux density B_g is determined using the relationship|

$$\:{B}_{g}={B}_{r}\times\:\frac{{g}_{eff}}{{g}_{eff}+{\mu\:}_{r}\times\:{t}_{m}}$$
(16)

where, \(\:{B}_{r}\) is the remanent flux density of the permanent magnet, \(\:{t}_{m}\) is the magnet thickness, \(\:{\mu\:}_{r}\) is the relative permeability of the magnet material, \(\:{g}_{eff}\) is the effective air gap, including mechanical tolerances.

The selection of magnet thickness \(\:{t}_{m}\) was optimized by balancing the required flux density and cost constraints. A thicker magnet increases flux density but also raises material costs, whereas a thinner magnet reduces performance. The final optimization ensured efficient magnetic loading while minimizing unnecessary weight and cost27.

The empirical design data from literature and finite element analysis (FEA) results confirm that the derived equations align with previous optimization studies in PMG topologies, including Ashrafzadeh et al.‘s multi-objective GA-based optimization study for AFPMSG32. These derivations provide the necessary foundation for the design and optimization of AFPMG and RFPMG, ensuring high efficiency and robust performance in low-speed wind energy applications. The Eq. (17) shows the detailed rated output power of the AFPMG considering all the contributed parameter in design.

$$\:{P}_{R}=\:\frac{1}{1+{k}_{{\varnothing}}}\frac{m}{{m}_{1}}\frac{\pi\:}{2}{k}_{e}{k}_{i}{k}_{p}{k}_{L}\eta {B}_{g\:}A\:\frac{f}{p}\:(1-{\lambda\:}^{2})\frac{1+\lambda\:}{2}{D}_{0}^{3}$$
(17)

The outer surface diameter of the machine is given by28,

$$\:{D}_{0}={{(P}_{R\:}/\:\frac{1}{1+{k}_{\varnothing\:}}\frac{m}{{m}_{1}}\frac{\pi\:}{2}{k}_{e}{k}_{i}{k}_{p}{k}_{L}\eta {B}_{g\:}A\:\frac{f}{p}\:(1-{\lambda\:}^{2})\frac{1+\lambda\:}{2})}^{\frac{1}{3}}$$
(18)

The total outer diameter (Dt) of the AFPMG,

$$\:{D}_{t}=\:{D}_{0}+2{W}_{cu}$$
(19)
$$\:{W}_{cu}=\:\frac{{D}_{i}-\sqrt{({D}_{i}^{2}-2{A}_{s}{D}_{g})/{\alpha\:}_{s}{K}_{cu}{J}_{s}\:}}{2}$$
(20)

where \(\:{W}_{cu}\)is the end winding overhang, Dg is the average diameter of the generator. The axial length of the machine is determined using the Eqs. (21),

$$\:{L}_{e}=\:{L}_{s}+2{L}_{r}+2g$$
(21)

where \(\:{L}_{s}\) is axial length of the stator, \(\:{L}_{r}\) is axial length of the rotor and g is the air gap length. Where the axial length of the stator Ls is

$$\:{L}_{s}=\:{L}_{cs}+2{W}_{cu}$$
(22)

Since the proposed generator is the slotted topology machine, the axial length of the stator slot (Ls) will be equal to end winding overhang (Wcu). The axial length of the stator core \(\:{L}_{cs}\) is identified by29,

$$\:{L}_{cs}=\frac{{B}_{g}{\alpha\:}_{p}\pi\:{D}_{0}(1+\lambda\:)}{{B}_{cs}\:4\:p}$$
(23)

where\(\:{\:B}_{cs}\) - stator core flux density and \(\:{\alpha\:}_{p}\) - pole pitch ratio. The axial length of the rotor and the rotor core are given in Eqs. (24) & (25),

$$\:{L}_{r}=\:{L}_{cr}+\:{L}_{PM}$$
(24)
$$\:{L}_{cr}=\frac{{B}_{u}\pi\:{D}_{0}(1+\lambda\:)}{{B}_{cr}\:8\:p}$$
(25)

\(\:{B}_{cr}\)- Flux density of the rotor core, Bu - surface flux density of the permanent magnet. The number of slots per pole per phase of AFPMG is calculated using the Eq. (26)

$$\:{q}_{1}=\raisebox{1ex}{${Z}_{1}$}\!\left/\:\!\raisebox{-1ex}{$2pm$}\right.$$
(26)

where Z1- total number of conductors, p- number of pole pairs and m- number of phases.

The machine’s inner diameter is determined through the Eqs. (27),

$$\:{\text{D}}_{\text{i}\text{n}}={\text{D}}_{\text{o}\text{u}\text{t}}\times\:{\uplambda\:}$$
(27)

The emf generated at the machine terminals is given by,

$$\:{E}_{pk}=\:{k}_{e}{N}_{ph}{B}_{g}\frac{f}{p}\:(1-{\lambda\:}^{2})\:{D}_{0}^{2}$$
(28)

where Ke - EMF factor, Nph - number of turns per phase, Bg - air gap flux density, f - frequency, p - machine pole pairs, λ – ratio of outer surface diameter and the inner surface diameter of the AFPMG.

The required minimum average torque developed by the machine is,

$$\:{T}_{r}=\:\frac{{m}_{1}}{\sqrt{2}}p{N}_{1}{K}_{w1}{{\Phi\:}}_{f}{I}_{a}$$
(29)
$$\:{T}_{r}={K}_{T\:}{I}_{a}$$
(30)

where, KT is the torque constant and the same can be calculated as,

$$\:{K}_{T}=\frac{{m}_{1}}{\sqrt{2}}p{N}_{1}{K}_{w1}{{\Phi\:}}_{f}$$
(31)

where p - number of poles, N1 - number of turns per phase, kw1 - winding factor, ɸf - magnetic flux, Ia - armature current. Table 1 shows the various specification of the machines. The choice of 300 W, 220 V, 3-phase, star-connected generator with a speed range of 150–200 rpm was driven by practical considerations for small-scale wind energy conversion, where efficiency and compactness are paramount. The rated speed was chosen to match the typical wind velocity profile in small-scale applications, ensuring reliable operation.

Table 1 Design specifications of the generators.
Full size table

Finite element analysis (FEA) of the permanent magnet generators

The Finite Element Analysis (FEA) is the tool to analyse the machines with complex geometry. It gives the accurate results thereby the further analysis on the machine can be done effectively. Apart, the factors which influence the performance of the machine can be determined and the same shall be optimized. The generators have been modelled through the software platform i.e., Ansys Maxwell Electromagnetic suite version 17.234. The parameters given in Table 1 have been given as inputs for the modelling. This is used for electromagnetic field simulations due to its high accuracy in solving complex nonlinear magnetostatic problems using the Finite Element Method (FEM) through Altair Flux 202235. The Magnetic Flux Distribution Analysis enabled precise visualization of flux paths and potential saturation regions. The torque pulsations and ripples were studied in torque computation and cogging torque estimations. Additionally, Ansys Maxwell provides high-resolution meshing capabilities, which were essential for evaluating field variations at critical regions such as air-gaps and permanent magnets. The simulation results of the various parameters like magnetic flux density and distribution, induced voltage, current and torque production at the generators are given in detail.

Electromagnetic analysis of RFPMG

The cross-section view of RFPMG is shown in Fig. 3 which modelled through Ansys Maxwell Electromagnetic suite version 17.2. The finite element analysis (FEA) carried out through Altair Flux for the RFPMG model. FEA using Altair Flux 2022 was employed primarily for thermal and core loss analysis due to its superior capabilities in modeling heat dissipation, eddy current losses, and iron losses within electrical machines. The Thermal Conductivity Modeling has given the temperature rise due to core and copper losses. It has assisted in refining the design for minimal losses and improved efficiency. The flux distributions and vector direction over the various parts of the Radial Flux PM are obtained from the FEA are shown in Figs. 4 and 5.

Fig. 3
figure 3

Cross section view of RFPMG.

Full size image
Fig. 4
figure 4

Magnetic Flux Distribution of RFPMG.

Full size image

The magnetic flux produced from the permanent magnets are distributed and gets linked with the stator coils well as shown in Fig. 4. It is noticed that the flux density at the permanent magnets, air-gap and the stator coils are 1 Tesla, 0.8 Tesla and 0.73 Tesla respectively. Hence the flux produced by the permanent magnets linked with the stator coils with some leakage flux. Figure 5 shows the alignment of flux at the different segment of the generator.

Fig. 5
figure 5

Vector Direction of Magnetic Flux Distribution.

Full size image

From the direction of flux as given in Fig. 5, it is implicit that the flux distributed radially at the air-gap. Figure 6 shows the induced emf waveforms of RFPMG at rated load conditions with the rated speed of 150 rpm.

Fig. 6
figure 6

The induced emf at rated load and rated speed condition.

Full size image

From Fig. 6, it is observed that, the emf induced at the stator coil of the RFPMG is 105 V at rated load condition. The generated stator current during rated load condition is shown in Fig. 7.

Fig. 7
figure 7

3ɸ current waveform at Stator Coil during Rated Load Condition.

Full size image

From this, it is understood that RFPMG has the capability of generating 0.95 A rms current at its stator coils. The Fig. 8 shows the machine’s moving torque.

Fig. 8
figure 8

Moving torque of RFPMG.

Full size image

From Fig. 8, it is understood that the average moving torque of the radial flux PMG is 18.08 Nm.

It is essential to examine the solid losses in the machines since it is the most influencing parameter when compared to the copper loss of the machine30. The solid loss of the generator is 8.44 W shown in Fig. 9.

Fig. 9
figure 9

Solid Loss at rated load condition at RFPMG.

Full size image

Electromagnetic analysis of DSAFPMG

The dimensions determined during the design stage as presented in Table 1 are used to model the double-side slotted axial flux PMG in Ansys Maxwell Electromagnetic Suite (version 17.2) and the corresponding model is shown in Fig. 10.

Fig. 10
figure 10

Model of DSAFPMG.

Full size image

The finite element analysis (FEA) is performed using Altair Flux for the DSAFPMG model and its flux linkage and vector direction of various parts of the DSAFPMG are obtained in simulation studies are shown in Figs. 11 and 12.

Fig. 11
figure 11

Flux linkage of DSAFPMG.

Full size image

From Fig. 11, it is noticed that the flux density at the permanent magnets, air-gap and the stator coils are 1.28 Tesla, 0.963 Tesla and 0.85 Tesla respectively. It is also observed that the slotted AFPMG produces more flux density than RFPMG. The magnetic field vector direction of the machine has been shown in Fig. 12.

Fig. 12
figure 12

Vector Direction of Magnetic Flux of DSAFPMG.

Full size image

The emf generation from the double side slotted AFPMG at rated load conditions is shown in Fig. 13. The generated emf of the AFPMG is observed as 119.59 V as shown in Fig. 13 which is higher than the generated emf at RFPMG. This higher value of induced emf is achieved due to the double-sided rotor structure in AFPMG. Also, it is observed that the waveform quality of the induced emf has been significantly improved due to the nonappearance of the coil overhang in AFPMG.

Fig. 13
figure 13

The emf generation of DSAFPMG.

Full size image

The generated current at the stator part of the DSAFPMG at rated load conditions is given in Fig. 14.

Fig. 14
figure 14

Generated Current of DSAFPMG During Rated Load Condition.

Full size image
Fig. 15
figure 15

Generated Moving torque of DSAFPMG.

Full size image

It is noticed that the current generation of DSAFPMG is 1.02 A as shown in Fig. 14. The moving torque is shown in Fig. 15. The average moving torque of the generator observed as 24.59 Nm as shown in Fig. 15. The Fig. 16 shows the solid losses of the generator.

Fig. 16
figure 16

Solid Loss of the DSAFPMG.

Full size image

The solid loss of DSAFPMG is 4.98 W. This minimum value of solid loss is attained since the number of turns per coil is minimum than RFPMG. The various performance parameters of the outer rotor RFPMG and DSAFPMG are listed in Table 2. By integrating both software tools, a comprehensive FEA study was conducted to ensure optimal performance of the proposed DSAFPMG compared to RFPMG, leading to a validated prototype with 97.85% efficiency. This comparison has been made with rated load and rated speed condition of 150 RPM.

Table 2 Performance parameters of the Generators.
Full size table

Form the Table 2, it is understood that the proposed DSAFPMG with double rotor configuration provides higher value of generated emf 119.5 V, Output torque 24.59 Nm and Magnetic flux density of 0.963 Web than RFPMG and existing AFPMG. Its copper loss is slightly higher than the existing machine and due to less core loss, magnetic loss and friction losses, it records the better efficiency of 97.85%. The weight of the proposed machine is reduced by 60% than the existing AFPMG. Hence the proposed generator offers better performance than RFPMG and the existing AFPMG. The said performance parameters make the DSAFPMG becomes more appropriate for the low-speed range wind turbine applications.

Experimental verifications of Double-sided slotted AFPMG

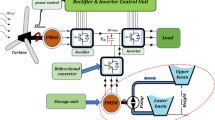
This section gives the details of the experimental validation through various results. The experimental setup of three-phase 300 W double-sided slotted double AFPMG is shown in Fig. 17. The generator is coupled with the prime mover i.e., single phase induction motor with Variable Speed Drive (VSD). This VSD is used to vary the speed of the generator and its associated hardware results are measured through the instrument FLUKE 434 power quality analyser. The below prototype testing setup represents all the components.

Fig. 17
figure 17

Experimental Setup of the Double-sided Slotted AFPMG.

Full size image

The generated voltage at the output terminal of the generator is shown in Fig. 18 for the speed range of 50 rpm, 100 rpm and 150 rpm at rated load condition. It also shows the output voltage at no-load condition.

Fig. 18
figure 18

Output voltage of the generator at the speed of (a) 50 rpm (b) 100 rpm and (c) 150 rpm at rated load condition (d) 150 rpm at no load condition.

Full size image

It is observed from Fig. 18 the generated voltage is increasing while the speed of the generator increases. It is also observed that the no load voltage (125.6 V) as shown in Fig. 18 (d) is greater than the voltage at rated load (118.2 V) as shown in Fig. 18 (c) since the loading factor is less during the no load case.

The current waveform for different loading conditions is given in Fig. 19. From this, it is understood that the load current is directly proportional to the generator loading. The load current at 1/4th, ½, 3/4th and full load is 0.2 A, 0.5 A, 0.7 A and 1 A respectively.

Fig. 19
figure 19

Load Current at (a) 1/4th load (b) ½ load (c) 3/4th load (d) full load conditions.

Full size image

From Fig. 19, The below Figure.20 gives the Total current Distortion (THD) of the current produced at the generator for the different loading conditions.

Fig. 20
figure 20

Current THD of AFPMG at (a) 1/4th load (b) ½ load (c) 3/4th load (d) full load conditions.

Full size image

From Fig. 20, it is understood that the current THD is keeps on decreasing with the increase in current. The current THD at 1/4th, ½, 3/4th and full load is 6.4%, 5.9%, 4.7% and 4% respectively. This continuous decrement of THD with respect to the loading is due to the distortion level of the current waveform. The rated load and the rated speed 150 rpm are fixed and the measurement have been taken for the various electrical parameters such as real, reactive, apparent power and power factor is given Fig. 21.

Fig. 21
figure 21

Electrical Parameters of proposed double-sided slotted AFPMG at rated load condition.

Full size image

It is observed from Fig. 21, the real and reactive power is almost same i.e., 0.34 kW and the apparent power is only 0.06 kW. Since the resistive load is connected at the generator the power factor is only about 0.98. It indicates that the current is in-phase with the generated voltage.

In Table 3 the deviation of the machine performance indices with respect to the simulation environment is presented. It is observed that the machine reaches the simulated efficiency at lower loads than the rated condition. However, at the rated load, we observe a small deviation, as mentioned. These results confirm the reliability of the simulated model, with deviations remaining within an acceptable range. The minor differences can be attributed to practical factors such as material imperfections, temperature variations, and measurement tolerances.

Table 3 Comparison of simulated with experimental readings.
Full size table

While the proposed DSAFPMG demonstrates significant efficiency gains, the limitations at very low speeds, less than 50 RPM, the back-EMF and power output drop significantly. The core heating is observed at higher loads greater than 300 W for few minutes, which needs improved cooling solutions. The double-sided rotor structure increases manufacturing effort compared to simpler RFPMG designs.

Cost analysis of the design

The cost breakdown considers material costs, manufacturing expenses, and operational savings compared to conventional designs. The Table 4 provides the cost of the major components purchased for fabrication of the proposed machine as per the design specifications.

Material cost breakdown

Manufacturing and assembly costs

The fabrication and assembling of DSAFPMG is carried out, the labour and process cost is given in Table 5.

Table 4 Material cost for DSAFPMG.
Full size table
Table 5 Fabrication and process.
Full size table

Operational cost savings & ROI

Compared to conventional RFPMGs and commercial small wind generators, the proposed DSAFPMG provides: Higher efficiency (97.85%), reducing energy losses. Lower core loss (4.98 W), leading to improved thermal performance and longer lifespan. Reduced material costs due to optimized magnet thickness and efficient copper utilization. The total cost of the unit is presented in Table 6.

Table 6 Total cost of double-sided slotted AFPMG.
Full size table

The proposed DSAFPMG, with an estimated total cost of $204.05, offers a cost-effective alternative to traditional RFPMGs while delivering superior efficiency and performance.

Conclusion

The design methodology of RFPMG and DSAFPMG has been proposed and modelled through ANSYS Maxwell Electromagnetic suite 17.2 software. The finite element analysis gives evidence for the betterment of proposed AFPMG for low-speed wind energy conversion system. The proposed double-sided slotted Axial Flux Permanent Magnet Generator (AFPMG) was designed and optimized to achieve high efficiency and low losses, making it a suitable candidate for small-scale, low-speed wind energy conversion systems. The finite element analysis (FEA) using Ansys Maxwell and thermal, core loss analysis using Altair Flux confirmed the accuracy of the electromagnetic and thermal modeling, validating the design for real-world implementation.

The optimized DSAFPMG achieves 97.85% efficiency, with a torque output of 24.59 Nm and 119.5 V output voltage at an operational speed of 150–200 rpm. The magnetic flux density of 0.963 Wb ensures optimal utilization of the NdFeB (N35/N38) permanent magnets, balancing performance and cost.

A key highlight of the proposed design is the reduction in core losses (4.98 W) compared to conventional radial flux designs, ensuring improved thermal performance. Additionally, the optimized magnet thickness (6.17 mm) was chosen to achieve the required flux linkage while minimizing material costs.

A comparative analysis with other designs, demonstrated that the proposed DSAFPMG achieves a better balance of efficiency, flux density, and applicability for low-speed wind applications. While Ashrafzadeh’s32 design focuses on high-power applications and Zhu’s8 model explores coreless configurations, the proposed DSAFPMG is tailored for lightweight, small-scale renewable energy systems. Arish et al.’s33 study highlights the trade-offs between PMVG and PMSG designs, showing that the proposed DSAFPMG surpasses these alternatives in efficiency while maintaining cost-effectiveness.

In future the optimization of coil winding configurations, and exploration of multi-phase excitation techniques to enhance power density and reliability can be studied. Additional improvements in cooling techniques and material selection could further enhance the generator’s long-term performance in real-world wind energy applications.

This study demonstrates that axial flux topologies can provide high-efficiency solutions for distributed renewable energy, particularly in low-speed wind turbine applications. The results confirm that DSAFPMGs can outperform conventional radial flux machines in weight, efficiency, and core loss reduction, making them a promising alternative for future energy solutions.