Introduction

The characteristic of “coal-rich, oil-poor and gas-poor” energy resources has determined that China’s energy structure, which is mainly based on coal, will not change in the short term1. According to statistics, the amount of coal resources suitable for open-pit mining in China only accounts for about 15% of the national coal resources, so the main way of coal mining in China is to mine it from wells2,3. With the development and exploitation of deep resources, the deep rock mass has been in the complex geomechanical environment of “three highs and one disturbance” for a long time, which makes the structural characteristics and mechanical behaviour of the deep rock mass become more complex. The deep tunnel rock shows a series of engineering response problems, such as discontinuous, uncoordinated large-scale deformation, large-scale instability damage and so on. In addition, the main manifestation of the deep tunnel rock damage is the formation and development of the plastic zone of the surrounding rock, and the different geometric distribution pattern and range of the plastic zone determines the damage mode and degree of the surrounding rock.

Regarding the deformation morphology of the plastic zone of the surrounding rock in the deep tunnel, scholars at home and abroad have conducted relevant researches by using theoretical analysis, numerical simulation and similar tests. Some of the scholars believe that the plastic zone of the surrounding rock belongs to round, oval or similar regular shape4. Other scholars pointed out that in the mining of close coal seam group, the surrounding rock of the roadway of the lower coal seam is under the condition of non-uniform stress field, and after the roadway is affected by the stress field of mining, the surrounding rock will show irregular shape plastic zone, such as “butterfly-type” and “saddle-type” plastic zone.

Research on the morphology of “butterfly” and “saddle” plastic zone of the surrounding rock under the environment of complex stress field. Yao et al.5 used the combination of theoretical analysis, numerical simulation and field test to study the change rule of the morphology of the plastic zone in the roadway, and pointed out that under the influence of mining, the “butterfly” plastic zone formed by roadway excavation is always relatively consistent with the direction of the main stress. Yuan et al.6 Based on the Mohr–Coulomb criterion, established a mechanical model of a circular roadway under a deep dynamic pressure environment, derived the implicit equation of the boundary of the surrounding rock plastic zone, and studied the mechanical conditions for the formation of Type I and Type II “butterfly” plastic zones. The definition of malignant expansion of the plastic zone and its criticality were defined, and the deformation and damage mechanism of the deep dynamic pressure mining roadway was revealed. Aiming at the problem that it is difficult to predict the roof plate deformation when the roadway crosses the fault, Liu et al.7 accurately determine the ___location of the maximum deformation while taking into account the changes in the width of the upper and lower roof plates. A method is proposed to calculate the maximum deformation position of the roof plate when the roadway crosses a normal fault. Yun et al.8 investigated the deformation and damage characteristics of the roadway perimeter rock at different stages of the roof mining process of the isolated island face.Taking a coal mine in Yangquan City, Shanxi Province as the background of the project, the laser interferometer (FLASH) and FLAC numerical simulation were used to investigate the deformation and damage characteristics of the roadway perimeter rock of the roof mining roadway at different stages of the mining process. Shan et al.9 established a mechanical model of the rectangular roadway rock by applying the complex function and elasticity theory, and obtained an analytical solution of the stress distribution of the rectangular roadway rock under the non-uniform stress field, and then mapped the spatial stress distribution model of the rectangular roadway rock. Liang et al.10 used Matlab software to establish the mechanical model of trapezoidal quarry elastic thin plate, and based on Kantorovich approximate variational method, the stress characteristics inside the trapezoidal thin plate were obtained, and the numerical calculation method for the damage of the overlying rock layers was given. The numerical calculation shows that 14,210 working face due to the existence of water-conducting fissure zone roadway occurred “left-deflected saddle”, “saddle” and “right-deflected saddle” transformed each other peripheral rock deformation and damage characteristics. Based on the theory of elastic–plastic mechanics, Li et al.11 and Wanget al.12 used numerical simulation to study the distribution law of the plastic zone of the surrounding rock in the roadway with non-uniform stress field, and obtained the different shapes of the surrounding rock plastic zone and different expansion trends, and put forward the theory of “butterfly-type” plastic zone of the surrounding rock in the roadway. The theory of “butterfly-type” plastic zone was proposed, and by constructing the boundary equation of the surrounding rock plastic zone under the condition of non-uniform stress field, the formation mechanism of the distribution pattern of the surrounding rock plastic zone in the roadway was revealed, and the influence of each parameter of the surrounding rock “butterfly-type” plastic zone on the deformation and destruction of the surrounding rock in the roadway, the collapse, and the region-typical dynamic disaster of the mine was elaborated, which provided a new direction for the prevention and control of the disaster of the coal mine.

With regard to the theoretical assumptions and the derivation of the plastic zone of the surrounding rock of deep roadways in complex environments: Zhao et al.13 derived the boundary line equation of the plastic zone of the surrounding rock of roadways with non-uniform stress field based on the unified strength theory, and successfully predicted the development pattern of the plastic zone of deep roadways. Ma et al.14 and others studied the distribution law of the partial stress field of the surrounding rock and the plastic zone by using the Mohr–Coulomb strength criterion, and obtained the partial stress formula of the surrounding rock of circular roadway under non-uniform stress field and the calculation method of the plastic zone radius.

In summary, the theoretical derivation of the “butterfly-type” plastic zone of the surrounding rock in the deep roadway under the complex stress environment doesn’t take into account the influence of the intermediate principal stress of the rock body and the nature of the rock body or the degree of damage on the elastic–plastic zone of the surrounding rock, or it is based on the assumption of a uniform stress field, which can’t meet the needs of engineering practice very well. Therefore, the deformation and damage characteristics of the surrounding rock and the influencing factors of its plastic zone on the dynamic pressure of the roadway under the residual coal pillar in the process of coal seam group mining still need to be studied in depth.

The article takes the research background of −850m roadway in Qujiang Coal Mine, −850m roadway is located in the western second mining area of Qujiang Coal Mine, which is longitudinally laid flat under the 805 working face and coal pillar, affected by the mining movement of the upper working face and the pre-stressing pressure of the coal pillar, the periphery of the roadway is no longer a pure non-uniform stress field, but a non-uniform stress field with both vertical and horizontal dynamic pressures exists. Firstly, by constructing a mechanical model of the non-uniform stress field under mining and modifying the unified strength theory based on the Hoek–Brown strength criterion, a non-linear unified strength theory of rock is established, which comprehensively considers the intermediate principal stresses, the rock properties and the structure of the rock body. Secondly, the plastic zone boundary equations of the surrounding rock with non-uniform stress field under mining were proposed by using the solved non-linear unified strength theory of rock; the effects of lateral pressure coefficient, Hoek–Brown parameter and intermediate principal stress as well as dynamic pressure coefficient on the morphology of the plastic zone were investigated. Finally, the numerical software FLAC3D is used for simulation to verify the validity of the theoretically derived boundary equation of the plastic zone of the confining rock with non-uniform stress field under mining. The study also reveals the deformation and damage characteristics and the morphology of the plastic zone of the deep dynamic pressure reverse mining roadway, and provides a theoretical guidance basis for the deformation control of the peripheral rock in this type of roadway.

Project overview

Overview of the Qujiang Coal Mine

Qujiang Coal Mine is known as “the first well in Jiangnan”, and the reasonable exploitation of its coal resources is related to the power and industrial upgrading projects in the whole Jiangxi area. The well field of Qujiang Coal Mine extends from the east to the Jurassic stripping limit of the B4 coal seam, from the west to the exploration and mining limit of the B4 coal seam, from the south to the Tertiary stripping limit of the B4 coal seam and from the north to the neighbouring Jianxin Coal Mine. The Qujiang Coal Mine is 5.5 km wide from north to south and 9 km long from east to west, covering an area of approximately 50 km2. Figure 1 shows the geographical ___location of the Qujiang Coal Mine and the coal mine site.

Fig. 1
figure 1

Geographical ___location and site conditions of Qujiang Coal Mine: (a) Geographical ___location; (b) Qujiang Coal Mine.

Full size image

The mine adopts vertical shaft single level zoned up and downhill development, longwall backward coal mining method and longwall backward full fall roof management method, the mine ventilation adopts two-wing diagonal type, the mining level elevation is −850m, and the mining coal seam is B4 coal seam, which has a thickness of 2.5–3.0m and a dip angle of 10°–12°. The west mining area is located in the west wing of the mine at the −850m level, bounded by the west 20m of the 1001 cut-eye and 1002 cut-eye in the west, the downhill of the haulage machine in the east, the boundary of the protected coal pillar of the 010A drilling hole in the north, and the south to the 15m below the 1002 and 809 workings down the tunnels. The average strike length of the mining area is 1863m, the inclined length is 797m, the inclined area is 1485170m2 and it is designed for double-wing mining.B4 coal seam basic situation, the coal seam structure is simple, the coal seam is partially bifurcated, and the thickness of the coal seam is getting thinner from the northeast to the southwest, as shown in Table 1.

Table 1 Comprehensive histogram of the top and bottom plates of the B4 seam
Full size table

Roadway space ___location

The proposed mining 805 working face is located in the west two mining area, the working face adopts a single strike long wall arrangement, with a mineable strike length of 490m and an inclined length of 140m; of which the 805 working face is the unmined area in the north, the 806 hollow area in the south, the west two track downhill lane, the west two transporter downhill lane, and the east is the cut eye of the 805 east face. According to 805 working face trench, wind tunnel, cutting eye excavation exposure, 805 working face geological structure is relatively complex, wind tunnel, trench, respectively exposed several faults, fault nature for the positive fault, fall 0.5–1.9m, faults are extended to the working face, the working face back to the mining brought some impact.

The −850m roadway is located in the west second mining area, below the rock layer 30–45m away from the bottom plate of B4 coal seam, shouldering the transportation of materials, rocks and people in the whole west second mining area, with the relative ground elevation of + 15.1m ~  + 37.8m, and the elevation of the underground elevation of -845.064 to -837.874 m (belonging to the deep high-stress roadway). The rock strata of the roadway strike NW, incline SE, strike about 40°–60°, and dip angle 10°–12°. The lithology of the roadway excavation is mainly dominated by siltstone and mudstone, and the rock hardness testing firmness coefficient f = 4–6. From the neighboring roadway revelation, the geological structure is more complicated, the fault is more developed, and the mining pressure is larger; its ground is mainly dominated by paddy field and dry land, and there are a small number of buildings, as shown in Fig. 2.

Fig. 2
figure 2

Schematic diagram of the spatial ___location of the −850m roadway: (a) Structural style; (b) Anchoring interface. Note: ①—upper roof (siltstone); ②—direct top (fine siltstone); ③—false roof (gray shale); ④—B4 coal seam; ⑤—pseudo-bottom (gray mudstone); ⑥—direct bottom (mudstone); ⑦-Old Bottom (siltstone and mudstone).

Full size image

Roadway section and support form

The design section of −850m roadway is straight wall semi-circular arch, with section of 4.7m × 3.7m and net section of 4.5m × 3.6 m. Since the design of −850m roadway started to be dug at the beginning of the establishment of the mine, the support structure adopts the more traditional anchor mesh rope + spray layer flexible support.

The two gangs support is designed as: ladder beam + anchor + metal mesh joint support, the roof support is designed as: ladder beam + anchor (cable) + metal mesh joint support (in the roadway over the fault or encounter special geological conditions, if necessary, using 29U-type shed to strengthen the support, row spacing 0.6m). No sprayed concrete in the first stage for the time being, and sprayed concrete at one time in the later stage according to the requirements, as shown in Fig. 3.

Fig. 3
figure 3

Original support structure and site condition of −850m roadway: (a) Form of original support for the roadway; (b) Situation on the ground.

Full size image
  1. (1)

    Anchor rod and mesh

    Anchor rods are made of MG335, with right-handed T-type external threads throughout, rod diameter of not less than 22mm, length of 2.4m. Anchor row spacing is 700mm × 600mm, with a piece of steel tray with specifications of 120mm × 120mm × 8mm, and exposed length of the anchor rods is 50–100mm, and each of which is anchored by a roll of MSK2360 resin anchoring agent. The anchors must be tightened with a torque wrench after installation, the preload force shall not be less than 300N·m, and the design anchoring force shall not be less than 90kN.The mesh adopts 12# iron wire machine-woven rhombic mesh, and the specification (length × width) is 3.6m × 1.9m.

  2. (2)

    Anchor cable and channel steel

    Anchor cable is applied at the symmetrical top plate of the roadway, and the anchor cable adopts ￠17.8mm 1860 grade steel strand, with specifications of 1 × 7 × 17.8 (7 strands) and a length of 7.3m, and when it meets with crushed zone or crosses the faults, it adopts lengthened anchor cable, and three rolls of MSK2360 resin medicinal rolls are used for each anchor cable, and the exposed length of the anchor cable is 150–250mm. The anchor cable is anchored into the stable rock layer with a length of not less than 1.5m and a pull-out resistance of more than 224kN. 18# channel steel is used for the channel, with a length of 1.8m, and three holes are centered to arrange the anchor cable eyes evenly, the diameter of the anchor cable eye openings is 20mm, and the spacing is 0.7m, with five groups in each row, and each group of three roots is uniformly and symmetrically distributed on the arch baseline (one group is centered, two groups are at 45° to the center line, and the other two are arranged in the arch shoulder of the roadway). The joists are of 1.8m length. The joists are made of channel steel with a length of 1.8m, arranged parallel to the center line of the roadway, with a row spacing of 2.1m between each group of anchor cables, and the material of the joists and specifications of the anchor cable eyes are the same as those of the joists in the coal roadway.

  3. (3)

    Ladder beam and slurry

    The main and secondary steel bars of the ladder beam are welded with round steel bars of 10mm in diameter, the spacing of the main bars is not more than 80mm, the spacing of the reinforcement bars is not more than 300mm, and the spacing of the reinforcement bars is not more than 100mm, and the material used is A3 round steel, and the top of the rocky alley and the two gangs are all in the shape of a well arrangement. Spray slurry using shotcrete, a shotcrete thickness of 50–70mm, concrete weight ratio cement: sand: stone = 1:2:2. which the relative position of the original support structure of the roadway, as shown in Fig. 4.

Fig. 4
figure 4

Original support structure and site condition of −850m roadway: (a) Ladder beams and anchor locations; (b) Anchor rod and anchor cable position.

Full size image

Theoretical analysis of the plastic zone of surrounding rocks

Nonlinear uniform strength criterion for rocks

At present, the theoretical calculations about the plastic zone of the surrounding rock of the roadway mainly include the two-dimensional stress distribution solution around the circular hole derived by Kirsch, and the modified Fenner’s equation for the radius and stress of the plastic zone of the circular roadway derived and modified by Fenner and Kastner15. However, the above theoretical derivation about plastic zone does not consider the influence of factors such as the main stress in the middle of the rock mass and the nature of the rock mass or the degree of damage on the plastic zone of the surrounding rock, or it is based on the assumption of a uniform stress field, and it does not satisfy the needs of practice very well. Moreover, the stress field in the tunnel in the actual project is not a uniform stress field, at this time, the lateral pressure coefficient λ ≠ 1 peripheral rock plastic zone is often butterfly-type or tongue-shaped. Therefore, the study of the characteristics of the surrounding rock plastic zone under the non-uniform stress field is a prerequisite for discerning the deformation mechanism of the surrounding rock.

The Hoek–Brown strength criterion16,17 is the relationship between ultimate principal stresses during rock failure given by Hoek and Brown by trial-and-error method through rock triaxial test data. Although this criterion does not consider the effect of intermediate principal stresses on the damage of the rock mass, it takes into account the joints of the rock mass and thus is closer to the engineering reality.

According to scholars, it is found that when the influence of intermediate principal stresses is considered, the strength of the rock mass will increase by about 30% compared with that when it is not considered, so the strength of the rock mass is closely related to the intermediate principal stresses.

In order to consider the influence of intermediate principal stresses, Nomikos et al.18 proposed the unified strength theory. This theory is applicable to geotechnical materials with unequal tensile and compressive strengths. However, the unified strength theory does not consider the internal joints and damage of the rock mass during the stress process, the nonlinear relationship when the rock mass is damaged.

Based on the theoretical hypothesis proposed by Jiu et al.19 the article modified and improved on the basis of integrating the advantages of the unified strength theory and Hoek–Brown strength criterion, and obtained a nonlinear unified strength criterion for rock that integrates the intermediate principal stresses, the rock properties, and the structure of the rock mass, which better overcomes the deficiencies of the above single theoretical criterion. The expression of the yield function F of the nonlinear unified strength criterion for rock is as follows:

When σ2 ≤ (σ1 + ασ3)/(1 + α):

$$F = \left[ {\sigma_{1} - \frac{1}{1 + b}\left( {b\sigma_{2} + \sigma_{3} } \right)} \right]^{2} - \frac{{m\sigma_{c} }}{1 + b}\left( {b\sigma_{2} + \sigma_{3} } \right) - s\sigma_{c}^{2} = 0$$
(1)

When σ2 > (σ1 + ασ3)/(1 + α):

$$F{\prime} { = }\left[ {\frac{1}{{1{ + }b}}\left( {b\sigma_{2} + \sigma_{1} } \right) - \sigma_{3} } \right]^{2} - m\sigma_{{\text{c}}} \sigma_{3} - s\sigma_{{\text{c}}}^{2} = 0$$
(2)

where: σc is the uniaxial compressive strength of the rock; α is the ratio of the uniaxial compressive strength of the rock to the uniaxial tensile strength; m and s are constants and empirical parameters of the Hoek–Brown criterion, m reflects the degree of softness and hardness of the rock and is taken as 1 × 10–7 ~ 25, 1 × 10–7 for the severely perturbed rock mass and 25 for the intact one; s reflects the degree of fragmentation of the rock mass and is taken as 0–1. σ3, σ2 and σ1 refer to the minimum, intermediate and maximum principal stresses of rock damage, respectively; b is a unified strength theory parameter (0 ≤ b ≤ 1), reflecting the effect of intermediate principal stresses on the damage of materials.

When b = 0, the intermediate principal stresses do not play a role. At this point the modified nonlinear unified strength theory of rock will degenerate into Hoek–Brown strength theory:

$$F{ = }\left( {\sigma_{1} - \sigma_{3} } \right)^{2} - m\sigma_{{\text{c}}} \sigma_{3} - s\sigma_{{\text{c}}}^{2} = 0$$
(3)

When b = 1, the effect of intermediate principal stress is the largest, that is, the effect of intermediate principal stress is fully considered. At this time, the modified nonlinear unified strength theory of rock degenerates into nonlinear twin shear strength theory :

$$\left. \begin{gathered} F{ = }\left[ {\sigma_{1} - \frac{1}{2}\left( {\sigma_{2} + \sigma_{3} } \right)} \right]^{2} - \frac{{m\sigma_{{\text{c}}} }}{2}\left( {\sigma_{2} + \sigma_{3} } \right) - s\sigma_{{\text{c}}}^{2} = 0 \ldots \ldots \ldots \sigma_{2} \le \frac{{\sigma_{1} { + }\alpha \sigma_{3} }}{{1{ + }\alpha }} \hfill \\ F{\prime} { = }\left[ {\frac{1}{2}\left( {\sigma_{2} + \sigma_{1} } \right) - \sigma_{3} } \right]^{2} - m\sigma_{{\text{c}}} \sigma_{3} - s\sigma_{{\text{c}}}^{2} = 0 \ldots \ldots \ldots \ldots \ldots \ldots \sigma_{2} > \frac{{\sigma_{1} { + }\alpha \sigma_{3} }}{{1{ + }\alpha }} \hfill \\ \end{gathered} \right\}$$
(4)

In Eqs. (1) and (2), when σ2 = σ3 = 0, that is, b = 0, the uniaxial compressive strength of rock mass can be obtained :

$$\sigma_{cm} = \sigma_{{\text{c}}} \sqrt s$$
(5)

In Eqs. (1) and (2), when σ1 = σ2 = 0, that is, b = 0, the uniaxial tensile strength of rock mass can be obtained :

$$\sigma_{tm} = \frac{1}{2}\sigma_{{\text{c}}} \left[ {m - \sqrt {m^{2} + 4s} } \right]$$
(6)

For intact rock mass, s = 1, according to Eqs. (5) and (6), the ratio of uniaxial tensile strength to uniaxial compressive strength of intact rock mass is :

$$\alpha = \frac{{\sigma_{tm} }}{{\sigma_{{{\text{c}}m}} }} = \frac{1}{2}\left[ {m - \sqrt {m^{2} + 4} } \right]$$
(7)

Mechanical model and basic assumptions

During the whole service period, the 850m roadway will not only bear the disturbance generated during the initial excavation, but also bear the influence of the upper 806 working face and 805 working face as well as other nearby working faces, and at this time, the stress field of the peripheral rock area of the roadway has become an extremely complicated non-uniform stress field of the dynamic pressure of the back-mining.

During the working life, the deep roadway will be subjected to many times of back-mining disturbance from the upper working face, resulting in the peripheral rock around the roadway experiencing the complete mechanical process of increased vertical and horizontal stresses caused by mining and then gradually decreasing. the role of mining dynamic pressure cycle, as shown in Fig. 5.

Fig. 5
figure 5

Stress distribution of −850m roadway.

Full size image

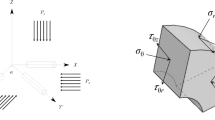
In order to facilitate the analysis of the stress state of the surrounding rock of the straight-wall semi-circular arch tunnel under mining, the mechanical model of the surrounding rock of the straight-wall semi-circular arch tunnel is simplified, and the tunnel environment is regarded as a bi-directionally distributed isobaric stress field, the ground stress is equal in the vertical direction, and the lateral pressure is equal in the horizontal direction. Accordingly, the mechanical model of the surrounding rock of the straight-wall semi-circular arch roadway with non-uniform stress field under mining is established as shown in Fig. 6, and the following basic assumptions are made20.

Fig. 6
figure 6

Mechanical model of surrounding rock of deep high stress roadway under mining.

Full size image
  1. (1)

    The irregular section of the roadway can be replaced by a circle by equivalent substitution, noting that the average burial depth of the roadway H ≥ 20r0, the radius of the circular roadway r0, and the infinite length of the flat roadway;

  2. (2)

    The rock mass around the roadway is an ideal elastic–plastic body, isotropic and homogeneous medium;

  3. (3)

    The external boundary conditions are vertical principal stress P0 and horizontal principal stress λP0;

  4. (4)

    Dynamic pressure coefficients are introduced, vertical dynamic pressure D1 and horizontal dynamic pressure coefficient D2;

Analytical solution for stresses in the tunnel enclosure

In the actual theory, for the non-circular roadway generally through the iso-substitution circle to replace the characteristic equations of the distribution of the surrounding rock stress and plastic zone of the non-circular cross-section roadway, and at present the commonly used iso-substitution circle such as:

$$r_{0} { = }{{\left[ {\left( \frac{B}{2} \right)^{2} { + }H^{2} } \right]} \mathord{\left/ {\vphantom {{\left[ {\left( \frac{B}{2} \right)^{2} { + }H^{2} } \right]} {2H}}} \right. \kern-0pt} {2H}}$$
(8)

where: r0 is the radius of the isosurrogate circle, and H and B are the height and span of the straight-walled semicircular archway, respectively.

The perimeter load of the roadway can be decomposed into:

$$\left\{ \begin{gathered} D_{1} P_{0} = p + q \hfill \\ \lambda D_{2} P_{0} = p - q \hfill \\ \end{gathered} \right.$$
(9)

Solving Eq. (9) yields:

$$\left\{ \begin{gathered} p = \frac{1}{2}\left( {D_{1} + D_{2} \lambda } \right)P_{0} \hfill \\ q = \frac{1}{2}\left( {D_{1} - D_{2} \lambda } \right)P_{0} \hfill \\ \end{gathered} \right.$$
(10)

For case (A), the analytical solution of stress for case (A) is obtained based on the results of rock mechanics theory:

$$\left. \begin{gathered} \sigma_{\theta } \hfill \\ \sigma_{r} \hfill \\ \end{gathered} \right\} = p\left( {1 \pm \frac{{r_{0}^{2} }}{{r^{2} }}} \right) = \frac{1}{2}\left( {D_{1} + D_{2} \lambda } \right)P_{0} \left( {1 \pm \frac{{r_{0}^{2} }}{{r^{2} }}} \right)$$
(11)

where: σr, σe are the radial and circumferential stresses at any point of the roadway enclosure in polar coordinates, respectively.

For case (B), the stress field in the surrounding rock is: by the internal boundary conditions:

$$r = r_{0} ,\sigma_{r} = \tau_{r\theta } = 0$$
(12)

by the outer boundary conditions and the Mohr’s circle stresses:

$$\left\{ \begin{gathered} \sigma_{r} = \frac{{\sigma_{1} + \sigma_{3} }}{2} + \frac{{\sigma_{1} - \sigma_{3} }}{2}\cos 2\alpha \hfill \\ \tau_{r\theta } = \frac{{\sigma_{1} - \sigma_{3} }}{2}\sin 2\alpha \hfill \\ \end{gathered} \right.$$
(13)

σ1 = p, σ3 = -q, α = 90°- θ, and substitution gives the external boundary stress condition at r → ∞:

$$\left\{ \begin{gathered} \sigma_{r} = - q\cos 2\theta \hfill \\ \tau_{r\theta } = q\sin 2\theta \hfill \\ \end{gathered} \right.$$
(14)

From the stress boundary conditions in Eqs. (12) and (14), the stress solution for case (B) is clearly related to r, 2θ. The associated stress function is established:

$$F\left( {r,\theta } \right) = f\left( r \right)\cos 2\theta$$
(15)

Substituting F(r,θ) into the biharmonic sum equation:

$$\left( {\frac{{\partial^{2} f}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial f}{{\partial r}} + \frac{1}{{r^{2} }}\frac{{\partial^{2} f}}{{\partial \theta^{2} }}} \right)\left( {\frac{{\partial^{2} f}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial f}{{\partial r}} + \frac{1}{{r^{2} }}\frac{{\partial^{2} f}}{{\partial \theta^{2} }}} \right)\cos \theta = 0$$
(16)

Solved:

$$\frac{{d^{4} f}}{{dr^{4} }} + \frac{2}{r}\frac{{d^{3} f}}{{dr^{3} }} - \frac{9}{{r^{2} }}\frac{{d^{3} f}}{{dr^{2} }} + \frac{9}{{r^{3} }}\frac{df}{{dr}} = 0$$
(17)

The generalized solution of Eq. (17) is.

$$f\left( r \right) = Ar^{4} + Br^{3} + C + Dr^{ - 2}$$
(18)

Solved:

$$\left\{ \begin{gathered} \sigma_{r} = - \left( {2B + \frac{4C}{{r^{2} }} + \frac{6D}{{r^{4} }}} \right)\cos 2\theta \hfill \\ \sigma_{\theta } = \left( {12Ar^{2} + 2B + \frac{6D}{{r^{2} }}} \right)\cos 2\theta \hfill \\ \tau_{r\theta } = \left( {6Ar^{2} + 2B - \frac{4C}{{r^{2} }} - \frac{6D}{{r^{4} }}} \right) = 0 \hfill \\ \end{gathered} \right.$$
(19)

Solving for the constant of integration according to the boundary conditions gives:

$$A = 0,B = q/2,C = qr_{0}^{2} ,D = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}\left( {qr_{0}^{4} } \right)$$
(20)

The stress solution for case (B) is obtained by substituting Eq. (20) into Eq. (19):

$$\left\{ \begin{gathered} \sigma_{r} = \frac{1}{2}P_{0} \left( {D_{1} - D_{2} \lambda } \right)\left( {1 - 4\frac{{r_{0}^{2} }}{{r^{2} }} + 3\frac{{r_{0}^{4} }}{{r^{4} }}} \right)\cos 2\theta \hfill \\ \sigma_{\theta } = \frac{1}{2}P_{0} \left( {D_{1} - D_{2} \lambda } \right)\left( {1 + 3\frac{{r_{0}^{4} }}{{r^{4} }}} \right)\cos 2\theta \hfill \\ \tau_{r\theta } = \frac{1}{2}P_{0} \left( {D_{1} - D_{2} \lambda } \right)\left( {1 + 2\frac{{r_{0}^{2} }}{{r^{2} }} - 3\frac{{r_{0}^{4} }}{{r^{4} }}} \right)\sin 2\theta \hfill \\ \end{gathered} \right.$$
(21)

The two cases of internal stresses in the circular tunnel enclosure are obtained by the above solution, and they are superimposed to obtain the analytical solution of elastic stresses in the tunnel enclosure under the condition of non-uniform stress field. The analytical solution of total stress is obtained by superposing case (A) and case (B):

$$\left\{ \begin{gathered} \sigma_{r} = \frac{{D_{1} + D_{2} \lambda }}{2}P_{0} \left( {1 - \frac{{r_{0}^{2} }}{{r^{2} }}} \right) - \frac{{D_{1} - D_{2} \lambda }}{2}P_{0} \left( {1 - 4\frac{{r_{0}^{2} }}{{r^{2} }} + 3\frac{{r_{0}^{4} }}{{r^{4} }}} \right)\cos 2\theta \hfill \\ \sigma_{\theta } = \frac{{D_{1} + D_{2} \lambda }}{2}P_{0} \left( {1 + \frac{{r_{0}^{2} }}{{r^{2} }}} \right) + \frac{{D_{1} - D_{2} \lambda }}{2}P_{0} \left( {1 + 3\frac{{r_{0}^{4} }}{{r^{4} }}} \right)\cos 2\theta \hfill \\ \tau_{r\theta } = \frac{{D_{1} - D_{2} \lambda }}{2}P_{0} \left( {1 + 2\frac{{r_{0}^{2} }}{{r^{2} }} - 3\frac{{r_{0}^{4} }}{{r^{4} }}} \right)\sin 2\theta \hfill \\ \end{gathered} \right.$$
(22)

where: θ is the polar angle of the center of the iso-surrogate circle, and τrθ is the shear stress at a point of the surrounding rock in polar coordinates in the roadway.

Boundary equation of the plastic zone of the tunnel enclosure

At present, when scholars at home and abroad study the boundary equation of the plastic zone of the surrounding rock, they usually solve the stress of the surrounding rock according to the elasticity theory, and then substitute this stress into the plasticity condition, which is called the invisible equation of the plastic zone if it can satisfy the boundary condition of the plastic zone21,22. Although this method is an approximate solution, it is important for analyzing the state of the tunnel surrounding rock.

Let σ2 = n(σ1 + σ3)/2, n be the intermediate principal stress parameters. For the plane strain problem n ≤ 1; when n tends to 1, the rock mass is in plastic state, when n < 1 the rock mass is in elastic state. So when solving the boundary equation of plastic zone, take n = 1:

$$\sigma_{2} { = }\frac{{\sigma_{1} { + }\sigma_{3} }}{2}$$
(23)

From the analysis of the stress state at a point in elastoplastic mechanics, the maximum and minimum principal stresses at a point are calculated as:

$$\left. \begin{gathered} \sigma_{1} \hfill \\ \sigma_{3} \hfill \\ \end{gathered} \right\} = \frac{{\sigma_{\theta } { + }\sigma_{r} }}{2} \pm \sqrt {\frac{1}{4}\left( {\sigma_{\theta } - \sigma_{r} } \right)^{2} - \tau_{r\theta }^{2} }$$
(24)

The analysis substitutes Eqs. (23) and (24) into Eq. (1) to obtain the equation of the boundary line of the plastic zone of a deep, highly stressed roadway in a nonuniform stress field under mining:

$$f\left( {r,\theta } \right) = \left( {\frac{{2{ + }b}}{2 + 2b}} \right)^{2} \left[ {\left( {\sigma_{\theta } - \sigma_{r} } \right)^{2} + 4\tau_{r\theta }^{2} } \right] - \frac{{m\sigma_{{\text{c}}} }}{2 + 2b}\left[ {\left( {b + 1} \right)\left( {\sigma_{\theta } + \sigma_{r} } \right) - \sqrt {\left( {\sigma_{\theta } - \sigma_{r} } \right) + 4\tau_{r\theta }^{2} } } \right] - s\sigma_{{\text{c}}}^{2} = 0$$
(25)

When λ = 1, the boundary equation of the plastic zone of the surrounding rock of the dynamic pressure uniform stress field roadway is obtained:

$$f_{{\lambda { = }1}} \left( {r,\theta } \right) = \left( {\frac{{2{ + }b}}{1 + b}} \right)^{2} P_{0}^{2} \left( {\frac{{r_{0} }}{r}} \right)^{4} { + }\frac{{m\sigma_{c} }}{1 + b}\left[ {P_{0} \left( {\frac{{r_{0} }}{r}} \right)^{2} - \left( {b + 1} \right)P_{0} } \right] - s\sigma_{{\text{c}}}^{2} = 0$$
(26)

When b = 0, the boundary line equation of the surrounding rock in the plastic zone under Hoek–Brown strength theory is obtained:

$$f_{{\lambda { = }1}} \left( {r,\theta } \right) = 4P_{0}^{2} \left( {\frac{{r_{0} }}{r}} \right)^{4} { + }m\sigma_{{\text{c}}} P_{0} \left( {\frac{{r_{0} }}{r}} \right)^{2} - m\sigma_{{\text{c}}} P_{0} - s\sigma_{{\text{c}}}^{2} = 0$$
(27)

When b = 1, the boundary line equation of the plastic zone under the nonlinear double shear strength theory is obtained for the tunnel enclosure:

$$f_{{\lambda { = }1}} \left( {r,\theta } \right) = 9P_{0}^{2} \left( {\frac{{r_{0} }}{r}} \right)^{4} { + 2}m\sigma_{{\text{c}}} P_{0} \left( {\frac{{r_{0} }}{r}} \right)^{2} - 4m\sigma_{{\text{c}}} P_{0} - 4s\sigma_{{\text{c}}}^{2} = 0$$
(28)

Boundary analysis of the plastic zone of the roadway enclosure

Since the −850m roadway is surrounded by several mining faces during the whole service period, the disturbance of the mining faces will inevitably cause the change of the lateral pressure coefficient, rock mass parameter, the size of the principal stresses in the rock mass, and the dynamic pressure coefficient in the rock mass around the roadway. Exploring the effects of different lateral pressure coefficients and rock mass, intermediate principal stresses, and dynamic pressure coefficients on the deformation and damage of the tunnel peripheral rock with the development of plastic zones and the distribution of morphology is an intrinsic mechanism to solve the large deformation of the tunnel peripheral rock23.

Based on the deduced invisible boundary equation of the plastic zone of the surrounding rock with non-uniform stress field under mining, the calculation program of the invisible boundary equation of the plastic zone was compiled by Matlab, and the plastic distribution data of the roadway under different conditions were solved, and then the Origin plotting software was used to draw a schematic diagram of the range of the plastic zone.

Effect of lateral pressure coefficient and rock mass on the plastic zone

For the influence of rock mass and lateral pressure coefficient on the distribution characteristics of the plastic zone of the surrounding rock of the roadway, the mudstone with lower strength around the roadway is selected as the research object. From the −850m roadway investigation report, the discounted rock mechanical parameters of mudstone uniaxial compressive strength σc = 35MPa, initial ground stress P0 = 850 × 2400 × 10 = 20.0MPa, roadway radius r0 = 2.5m, mudstone cohesion c = 4.2MPa, and internal friction angle φ = 25°. The dynamic pressure coefficient is taken as D1 = D2 = 1.0. The influence of dynamic pressure is not considered at this time. Combined with the actual situation of the ground stress distribution, the lateral pressure coefficient λ was selected as 0.25, 0.5, 0.75, 1.0, 1.5, 2.0 and 2.5, respectively, to observe the distribution of the plastic zone of the surrounding rock of the roadway. According to the modified m and s estimation table given by Hoek–Brown24, two sets of Hoek–Brown empirical parameters were selected as in Table 2.

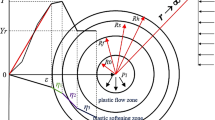
Table 2 Hoek–Brown empirical parameters.
Full size table

By analyzing several sets of true triaxial tests of rocks, Jiu et al.19 gave the value of intermediate principal stress of mudstone, b = 0.5. According to the above results, the rock parameters were substituted into the invisible boundary equation of the plastic zone (25) and Matlab software was used to get the distribution data of the plastic zone of the surrounding rocks with different lateral pressure coefficients, and then Origin software was used to draw the boundary of the plastic zone as shown in Fig. 7.

Fig. 7
figure 7

Boundary of plastic zone of surrounding rock with different lateral pressure coefficients: (a) m = 0.639, s = 0.00019; (b) m = 0.313, s = 0.00002.

Full size image

From Fig. 7, it can be seen that the geometric distribution of the plastic zone of the surrounding rock in the roadway is closely related to the quality of the rock mass and the lateral pressure coefficient λ. (1) When the lateral pressure coefficient λ ≠ 1.0, the plastic zone of the surrounding rock mainly develops towards the corners of the roadway and has certain inclination, but the overall shape is similar to the “butterfly-type”, and the more the value of the lateral pressure coefficient λ deviates from l, the more the shape of the plastic zone is close to the “butterfly-type”. The more the value of lateral pressure coefficient λ deviates from l, the more the shape of the plastic zone is similar to the “butterfly-type”. (2) When the lateral pressure coefficient λ < 1.0, it can be seen that the radius of the plastic zone in the horizontal direction is slightly smaller than that in the vertical direction, and the centerline of the butterfly lobe is biased toward the vertical stress P0, about 3°–5°. (3) When λ > 1.0, the radius of the plastic zone in the horizontal direction is slightly larger than that in the vertical direction, and the centerline of the butterfly lobe is biased toward the horizontal stress λP0, about 3°–5°.

Comparing Fig. 7a,b, it can be seen that when the lateral pressure coefficient λ is a certain value, the range of the plastic zone is affected by the rock mass parameter m and s. The larger the values of m and s are, the better the rock mass is, the better the resistance to deformation and damage is, and the smaller the range of the plastic zone is, and vice versa the larger the range of the plastic zone is.

In summary, the overall rock mass parameter only changes the size of the radius of the plastic zone, while the lateral pressure coefficient not only affects the radius of the plastic zone but also determines the distribution characteristics of the plastic zone.

Effect of intermediate principal stresses on the plastic zone

For the influence of the intermediate principal stress σ2 of the rock mass on the distribution characteristics of the plastic zone of the surrounding rock of the roadway, the mudstone around the roadway is selected as the research object as above, and the Hoek–Brown empirical parameter m = 0.639, s = 0.00019 is taken, and the unified strength theoretical parameter b (0, 0.5, 1) is taken. Combined with the actual situation of ground stress distribution, the lateral pressure coefficient λ was selected as 0.5, 0.75, 1.0, 1.25 and 1.5 respectively to observe the distribution of the plastic zone of the surrounding rocks of the roadway.

As can be seen from Fig. 8, the intermediate principal stress has a great influence on the range of plastic zone and displacement size of the surrounding rock of the roadway, when b = 1, the nonlinear double-shear strength criterion is degraded to the nonlinear unity strength criterion, at this time, the effect of the intermediate principal stress is the largest, and the strength potential of the rock mass is maximized, so the plastic range is the smallest. However, when b = 0.5, the plastic range is the largest, indicating that the intermediate principal stress effect exists interval. Within a certain range of variation, the larger the intermediate principal stress is, the smaller the plastic range and displacement are; when the intermediate principal stress exceeds a certain value, the plastic range and displacement decrease with the decrease of the intermediate principal stress.

Fig. 8
figure 8

Boundaries of plastic zones of surrounding rocks with different intermediate principal stresses: (a) b = 0; (b) b = 0.5; (c) b = 1.0.

Full size image

In summary, reasonable consideration of the influence of the intermediate principal stress can not only realize the strength potential of the rock mass, but also more in line with the actual stress state of the rock mass.

Effect of dynamic pressure coefficient on the plastic zone

For the influence of dynamic pressure coefficient on the distribution characteristics of surrounding rock plastic zone, the mudstone around the roadway is still selected as the research object, and the Hoek–Brown empirical parameter m = 0.639, s = 0.00019 is taken. When considering the influence of vertical dynamic pressure D1 on the distribution of the plastic zone, the horizontal dynamic pressure D2 is taken to be 1, and similarly when considering the influence of horizontal dynamic pressure D2 on the distribution of the plastic zone, the vertical dynamic pressure D1 is taken to be 1. Other roadway surrounding rock parameters are the same as above. As shown in Fig. 9, it is the distribution of plastic zone of surrounding rock under the action of dynamic pressure coefficient.

Fig. 9
figure 9

Boundary of plastic zone of surrounding rock with different dynamic pressure coefficients: (a) Vertical dynamic pressure impact situation; (b) Horizontal Dynamic Pressure Impact Situation.

Full size image

From Fig. 9 it can be seen that the dynamic pressure coefficient Di changes from 2.5 to 2.8, the distribution of the shape of the plastic zone of the tunnel surrounding rock changes significantly, and the size of the butterfly lobe of the plastic zone grows exponentially, which is a non-linear relationship.

Comparison with Figs. 7 and 8 above shows that under the influence of mining dynamic pressure, the surrounding rock is more likely to produce “butterfly-type” plastic zone25,26,27,28,29, and the development of butterfly lobe size and range is even larger. With the increase of vertical dynamic pressure, the roadway plastic butterfly leaf formation and rapid expansion, was elongated; peripheral rock plastic area of the butterfly-type theoretically confirms the mining of deep high stress roadway damage generally first from the roadway roof and arch foot, often shear misalignment or extrusion deformation, but also from the side of the dynamic pressure of the roadway compared with the ordinary roadway deformation is greater, more difficult to control.

In order to further explore the change of the radius of the plastic zone under the stress field from the shallow to the deep part of the surrounding rock, the control variable method is adopted to study the change of the radius of the plastic zone by changing the dynamic pressure coefficient Di and the pressure of the surrounding rock under the circumstance that other parameters remain unchanged.

As can be seen from Fig. 10, the overall change rule of the dynamic pressure coefficient and the plastic zone radius of each stress field is similar, whether it is a shallow stress field or a deep stress field, the curve is the first smooth growth, to reach a certain dynamic pressure (Di = 2.5) began to appear a sharp nonlinear growth, the curve is a “sharp head-up type”6. The dynamic pressure coefficient here is defined as the Dξ critical dynamic pressure coefficient.

Fig. 10
figure 10

Curve of dynamic pressure coefficient versus radius of plastic zone. (a) Dynamic pressure versus plastic radius; (b) D1 = 2.8, D2 = 1.0, P0 = 15; (c) D1 = 2.8, D2 = 1.0, P0 = 25; (d) D1 = 2.8, D2 = 1.0, P0 = 20.

Full size image

Simulation and analysis of the plastic zone of the roadway

Rock parameters and numerical modeling

Using the modified nonlinear unified strength theory of rock, the invisibility equation of the boundary of plastic zone of surrounding rock with nonuniform stress field under mining is derived, which is to set the rock mass as an ideal elastic–plastic body. Numerical simulation using FLAC3D is carried out to verify the validity of the theoretically derived invisible equation of the boundary of the plastic zone of the surrounding rock with non-uniform stress field under mining.

  1. (1)

    Selection of rock mass parameters.

    According to the actual burial depth of −850m roadway in the old bottom rock layer is mainly siltstone and mudstone, to select the parameters of the surrounding rock around the roadway. Based on the rock parameters obtained from the indoor test and the coal mine site design and other information, the reasonable and effective rock mass physical and mechanical parameters are finally determined, as shown in Table 3.

Table 3 Equivalent material mechanical parameters of rock mass.
Full size table
  1. (2)

    Modeling

    On the basis of ensuring the accuracy of the simulation results, the model takes the length × width × height = 50m × 3m × 50m, and the radius of the roadway r0 = 2.5 m. The mesh delineation of the model adopts the encircling radial grid. The model size, loading conditions and boundary constraints are shown in Fig. 11a; the rock mass material adopts Hoek–Brown elastic–plastic material mechanical parameters are shown in Table 3.The numerical simulation model is shown in Fig. 11b.

Fig. 11
figure 11

Numerical model and boundary conditions: (a) Model loads and boundary constraints; (b) numerical model.

Full size image

Distribution pattern of plastic zones with different lateral pressure coefficients

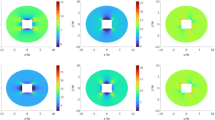
In the simulation, the fixed vertical load is 20MPa, and the change rule of the distribution pattern of the plastic zone of the tunnel enclosure under different lateral pressure coefficients (0.25, 0.5, 0.75, 1.25, 2.0 and 2.5) is realized by transforming the lateral load. And compared with the previous theoretical derivation of the plastic zone morphology under different lateral pressure coefficients, to verify the correctness of the theoretically derived boundary equation of the plastic zone of the surrounding rock of the circular roadway under the condition of non-uniform stress field, as shown in Fig. 12.

Fig. 12
figure 12

Morphology of plastic zones in surrounding rocks with different lateral pressure coefficients: (a) λ = 0.25; (b) λ = 0.5; (c) λ = 0.75; (d) λ = 1.25; (e) λ = 2.0; (f) λ = 2.5.

Full size image

From Fig. 12, it can be seen that the distribution pattern of the surrounding rock plastic zone: the lateral pressure coefficient has an influence on the shape and size of the surrounding rock plastic zone. When the lateral pressure coefficient 0.75 ≤ λ ≤ 1.25, the shape of surrounding rock plastic zone is “oval” and “round”. When the lateral pressure coefficient λ > 1.25 or λ < 0.75, the surrounding rock shows obvious “butterfly-type” plastic zone, and the maximum size of the plastic zone appears at the four sharp corners. When the lateral pressure coefficient λ = 0.25, the plastic zone is “upper butterfly-type”, at this time, the radius of the plastic zone of the surrounding rock at the sharp corners reaches 14.8m, the radius of the plastic zone at the top and bottom is the smallest, which is only 2.5m, and the radius of the plastic zone of the two gangs is the second largest, which is 5.4m. When the lateral pressure coefficient is λ = 2.5, the plastic zone is “under butterfly-type”, at this time, the plastic zone of the top and bottom plates is the smallest, only 4.5m, the radius of the surrounding rock plastic zone at the sharp corner reaches 18.8m, the radius of the plastic zone of the two gangs is the second largest, 8.4m.

Secondly, the range of the plastic zone of the surrounding rock in the roadway has an obvious relationship with the size of the lateral pressure coefficient, when the vertical load is larger (lateral pressure coefficient is less than 1), the range of the plastic zone of the surrounding rock in the vertical direction is larger, while the range of the plastic zone produced in the horizontal direction is smaller. When the horizontal load is larger (lateral pressure coefficient is greater than 1), the range of plastic zone of the surrounding rock in the horizontal direction is larger, while the range of plastic zone generated in the vertical direction is smaller. Through the above numerical simulation, the distribution of the plastic zone of the tunnel rock with different lateral pressure coefficients confirms the existence of the theoretically deduced “butterfly-type” plastic zone and its relationship with the lateral pressure coefficient.

Distribution pattern of plastic zones with different dynamic pressure coefficients

The same use of FLAC3D numerical simulation, fixed vertical load of 20MPa, at the same time in the consideration of vertical dynamic pressure D1 (2.8, 2.5, 1.5) on the distribution of plastic zone, take the horizontal dynamic pressure D2 = 1, in the consideration of horizontal dynamic pressure D2 (2.8, 2.5, 1.5) on the distribution of plastic zone, take the vertical dynamic pressure D1 = 1. Numerical simulation will be obtained at this time under different dynamic load of the distribution pattern of the surrounding rock plastic zone change rule, and with the theoretical solution of the surrounding rock plastic zone boundary equations for comparison, to verify the correctness of the theoretical derivation of the surrounding rock plastic zone boundary equations, as shown in Fig. 13.

Fig. 13
figure 13

Morphology of plastic zones in surrounding rocks with different dynamic pressure coefficients: (a) D1 = 2.8, D2 = 1.0; (b) D1 = 2.5, D2 = 1.0; (c) D1 = 1.5, D2 = 1.0; (d) D1 = 1.0, D2 = 2.8; (e) D1 = 1.0, D2 = 2.5; (f) D1 = 1.0, D2 = 1.5.

Full size image

From Fig. 13 different dynamic pressure coefficient under the roadway surrounding rock plastic zone state can be seen: with the increase of dynamic pressure coefficient, the roadway surrounding rock plastic zone from circular → ellipse → rounded rectangle → butterfly-type transformation, the maximum radius of the plastic zone with the increase of dynamic pressure coefficient increases, and the maximum radius of the plastic zone of the dynamic pressure coefficient of the change of the side pressure coefficient is sensitive to the above. When the dynamic pressure coefficient Di is taken as 1.5, the maximum radius of the plastic zone is about 2.04r0, and when the dynamic pressure coefficient Di is taken as 2.5, the maximum radius of the plastic zone is about 5.85r0, which is about 2.5 times of the increase of the plastic radius comparing with that of the dynamic pressure coefficient Di = 1.5, and the overall is relatively small. However, when the dynamic pressure coefficient Di is taken as 2.8, the maximum radius of the plastic zone is about 15r0, compared with the dynamic pressure coefficient Di = 1.5, the increase in the radius of the plastic zone is about 8.0 times, which further indicates that the larger the dynamic pressure coefficient is, the larger the radius of the plastic zone is, and there is a sudden increase in the amplitude of the radius of the plastic zone and the dynamic pressure coefficient, which is presumed to be between the dynamic pressure coefficients Di = 2.5 and 2.8.

Through the study on the relationship between the dynamic pressure coefficient and the distribution and size of plastic zone, under the influence of dynamic pressure, the surrounding rock is more likely to produce “butterfly-type” plastic zone. The development size and range of the butterfly leaf of the plastic zone are related to the dynamic pressure coefficient, and with the increase of the dynamic pressure coefficient, the butterfly leaf of the plastic zone of the surrounding rock expands rapidly after its formation, which is elongated, indicating that the deformation of the dynamic pressure roadway is larger and more difficult to be controlled than that of the ordinary roadway. The simulation results are consistent with the previous theoretical analysis, confirming the practicality of the theoretical derivation.

Comparison and discussion of theory and simulation

Based on the mechanical environment of −850m roadway, the article establishes the roadway mechanical model of non-uniform stress field under mining by applying the modified nonlinear uniform strength criterion of rock, and derives the invisible equation of the plastic zone of the enclosing rock with non-uniform stress field under mining. The influence of lateral pressure coefficient and Hoek–Brown parameter, intermediate principal stress and dynamic pressure coefficient on the morphology of the plastic zone is analysed by theory and FLAC3D numerical simulation, and the consistency of the two results also verifies the reasonableness of the theoretical solution.

  1. (1)

    Based on the unified strength theory, the Hoek–Brown strength criterion is modified and the nonlinear unified strength theory of rock is established, which considers the influence of intermediate principal stresses and reflects the nonlinear characteristics of rock damage. Based on the modified nonlinear unified strength theory of rock, the invisible boundary equation of the plastic zone of the surrounding rock with nonuniform stress field under mining is proposed. It is found that the geometric distribution of the plastic zone of surrounding rock in the dynamic pressure roadway under mining is closely related to the quality of the rock body and the environment (lateral pressure coefficient λ): when the lateral pressure coefficient λ ≠ 1.0, the plastic zone of surrounding rock develops mainly in the direction of the corners of the roadway, and the whole is similar to the “butterfly-type”.

  2. (2)

    Through the comparative analysis of theoretical and simulation data, the existence of the dynamic pressure coefficient has significant changes on the distribution of the plastic zone morphology of the surrounding rock, the size of the butterfly leaf of the plastic zone grows exponentially, and the range of the plastic zone has a non-linear relationship with the dynamic pressure coefficient. And the intermediate principal stress mainly has a great influence on the range and displacement size of the surrounding rock plastic zone, and the intermediate principal stress effect exists in the interval.

  3. (3)

    Through the study of the dynamic pressure coefficient and the plastic zone radius curve, it is found that whether it is the shallow stress field or the deep stress field, the curve is the first smooth growth, the dynamic pressure coefficient reaches a certain value (about Di = 2.5), the plastic zone radius is the exponential rapid growth, resulting in the plastic zone area can not be converged, the formation of malignant expansion, leading to the surrounding rock to appear in the sudden destabilisation of damage. The influence of dynamic pressure coefficient on the radius of the plastic zone exists Dξ critical dynamic pressure coefficient6.

Mechanism of deformation of surrounding rock in a dynamic pressure roadway

Through the establishment of non-uniform stress field roadway mechanics model under mining, the morphology evolution of surrounding rock plastic zone, plastic zone influencing factors and other in-depth research was carried out, and the destabilization and damage mechanism of −850m roadway was elaborated. Mainly embodied in:

  1. (1)

    Extremely complex dynamic high stress environment

    The −850m roadway itself is in a high stress environment due to the large depth of burial, plus the roadway is arranged in the 805 working face and below the 806 mining area, resulting in the roadway is endowed with a dynamic dynamic pressure and coal pillar bias under the action of a dynamic dynamic pressure, extremely complex mechanical environment. The power source of large deformation damage: −850m roadway buried depth, high stress, static pressure state stress can reach 20–25 MPa, such as considering the dynamic pressure brought by mining (take the empirical value of Di = 2.0–3.0), then the stress environment is as high as 40–75 MPa, resulting in the peripheral rock around the roadway is in the long term in the plastic yielding or limit state.

  2. (2)

    Roadway surrounding rock plasticity area is “butterfly-type” distribution features

    The deformation characteristics of the surrounding rock in the dynamic pressure roadway of deep mining, the damage mode and the development of the plastic zone and the expansion are closely related. Affected by mining, the peripheral rock around the roadway is more likely to form a “butterfly-type” plastic zone at this time, and the development of the butterfly leaf makes the region rock plastic radius Rp, compared with other parts of the obviously larger, plastic damage depth is greater.

  3. (3)

    The overall strength of the surrounding rocks of the roadway is poor.

    The −850m roadway is arranged in the old bottom, and the surrounding rocks are mainly mudstone and siltstone, with more developed structural surfaces. Under the joint action of mining and high stress, the surrounding rock is easy to show the expansion and ductility of soft rock. Moreover, it is easy to swell and disintegrate in contact with water, and has the characteristic of rheology, which greatly reduces the self-supporting capacity of the surrounding rock.

  4. (4)

    There is a critical value of dynamic pressure coefficient.

    According to the dynamic pressure coefficient and the plastic zone radius curve, whether it is shallow stress field or deep stress field, the curve is the first smooth growth, the dynamic pressure coefficient reaches a certain value (about Di = 2.5), the radius of the plastic zone began to appear sharp nonlinear growth. The curve is in the form of a “sharp rise”, which leads to the plastic zone range cannot converge, forming a vicious expansion, which leads to sudden destabilization damage of the surrounding rock. The influence of dynamic pressure coefficient on the radius of plastic zone has Dξ critical dynamic pressure coefficient.

    In summary, the destabilization damage of surrounding rock in −850m roadway belongs to the typical nonlinear large deformation damage of deep high-stress roadway under mining. The destructive mechanism is as follows: under the condition of deep high stress, when the roadway is arranged in the bottom plate of the coal seam, due to the insufficient strength of the original roadway support and the poor structural integrity of the surrounding rock, when the coal seam is mined back to produce the dynamic pressure of mining back to the roadway is very easy to cause large deformation of the surrounding rock damage.

Conclusions and prospects

Conclusions

  1. (1)

    Based on the Hoek–Brown strength criterion, the unified strength theory is modified, and the nonlinear unified strength theory of rock is established, which takes into account the influence of intermediate principal stresses and reflects the nonlinear characteristics of rock damage. Based on the modified uniform strength theory of rock nonlinearity, the invisible equation for the boundary of plastic zone of surrounding rock with nonuniform stress field under mining is proposed. The shape of the plastic zone and its evolution law under mining is studied, and it is found that when λ ≠ 1.0, the plastic zone of the surrounding rock expands in the direction of tilting to the four corners of the roadway, and the whole is similar to the “butterfly-type”, and the more the value of the lateral pressure coefficient λ deviates from l, the more the shape of the plastic zone is similar to the “butterfly-type”. The more the value of lateral pressure coefficient λ deviates from l, the more the shape of plastic zone is similar to “butterfly-type”.

  2. (2)

    The change curve of the dynamic pressure coefficient and the radius of the plastic zone is studied, and it is found that whether it is the shallow stress field or the deep stress field, the curve grows smoothly first, and when the dynamic pressure coefficient reaches a certain value (about Di = 2.5), the radius of the plastic zone grows exponentially, which results in that the range of the plastic zone can not be converged, and forms a malignant expansion, which leads to the surrounding rock to have a sudden destabilizing damage. The influence of dynamic pressure coefficient on the radius of plastic zone exists Dξ critical dynamic pressure coefficient.

  3. (3)

    Based on the theoretical analysis and numerical simulation results, the expansion and distribution law of the plastic zone of the −850 m roadway under the mining movement is obtained, which reveals the deformation and damage mechanism of the deep dynamic pressure back-mining roadway, and it belongs to the nonlinear large deformation damage mode.

Prospects

In the article, the modified nonlinear uniform strength criterion of rock is applied to establish the roadway mechanics model of non-uniform stress field under mining, although the evolution characteristics of the plastic zone of surrounding rock in dynamic pressure roadway of back mining, the distribution law of stress and displacement are obtained. However, the study is under specific working conditions, and its results still have further improvement, mainly manifested as:

  1. (1)

    The article only gives local specific values for horizontal and vertical dynamic pressure to simulate and verify, and there are instantaneous fluctuations of the dynamic pressure coefficient in the actual project, and the direction of principal stresses will also have different deflections, which will have a certain effect on the surrounding rock plastic zone.

  2. (2)

    Based on the modified nonlinear uniform strength theory of rock, the article deduces the invisible equation of the plastic zone of the circular roadway surrounding rock with non-uniform stress field under mining, while the shape of the roadway design in the project is mostly the straight wall and semicircular arch and rectangle, and the shape of the plastic zone of the surrounding rock of the roadway of other shapes and the law of evolution need to be further improved and supplemented.