A double closed loop digital hydraulic cylinder position system based on switching active disturbance rejection control

Jiang, Shouling; Zhao, Guochao; Huang, Fuxian; Liu, Wenfeng; Chen, Ying; Zhang, Long

doi:10.1038/s41598-025-85640-9

Download PDF

Article
Open access
Published: 10 January 2025

A double closed loop digital hydraulic cylinder position system based on switching active disturbance rejection control

Shouling Jiang^1,2,
Guochao Zhao²,
Fuxian Huang¹,
Wenfeng Liu¹,
Ying Chen¹ &
…
Long Zhang¹

Scientific Reports volume 15, Article number: 1556 (2025) Cite this article

2383 Accesses
Metrics details

Subjects

Abstract

A switching active disturbance rejection control (SADRC) strategy was proposed to solve the composite disturbance challenge arising from gap, LuGre friction, hydraulic spring force, and external load disturbance in the double closed-loop digital hydraulic cylinder position control system. Firstly, leveraging the established mathematical model of the double closed-loop digital hydraulic cylinder, the high-order state equation was derived. Subsequently, the high-order double closed-loop digital hydraulic cylinder control system was transformed into a second-order integral series control system using ADRC strategy. Given the pronounced nonlinear characteristics of double closed-loop digital hydraulic cylinders, combined with the characteristics of switching control, a SADRC strategy was proposed, and the stability of the closed-loop system was proved based on Lyapunov theory and switching rules. Finally, the effectiveness of the proposed control method was verified through simulation and experiment. Results indicate that the system's response speed employing the SADRC strategy outperforms the PID control strategy by 32.56%, with a 2.0% reduction in error. The average error in the response speed of the digital hydraulic cylinder and the MATLAB simulation value of the tracking error are 9.0% and 1.50% respectively. Notably, the simulation and experimental results exhibit a consistent overall trend, affirming the feasibility and effectiveness of the control strategy.

Integrating type-2 fuzzy logic controllers with digital twin and neural networks for advanced hydropower system management

Article Open access 11 February 2025

HIL co-simulation of an optimal hybrid fractional-order type-2 fuzzy PID regulator based on dSPACE for quadruple tank system

Article Open access 04 March 2025

Multiple quadrants displacement tracking control of independent metering electro-hydraulic system

Article Open access 20 September 2024

Introduction

The digital hydraulic cylinder holds significant promise in contemporary engineering applications due to its straightforward design, robust resistance to oil contamination, and high precision positioning capabilities¹. For instance, implementing an automatic height adjustment system in a coal mining machine, propelled by a digital hydraulic cylinder, can enhance its precision control. However, the control system of digital hydraulic cylinders faces challenges stemming from nonlinear elements like gap and friction, as well as unpredictable disturbances such as time-varying load disturbances^2,3. This renders the control system susceptible to external disturbances and nonlinear characteristics, making it arduous to meet ideal control requirements in practical settings. Furthermore, various unmeasurable states exist within the digital hydraulic cylinder control system, including the acceleration signal of the digital hydraulic cylinder, speed and acceleration signals of the servo valve spool, and angular speed and angular acceleration signals of the ball screw. Leveraging the state observer method becomes essential to estimate these unmeasurable state quantities, enabling system control based on output feedback^4,5.

Qing et al.⁶ investigated the impact of different valve port configurations on the performance of digital hydraulic cylinders. It was observed that the rectangular valve port exhibits the highest flow gain, with the equivalent flow area decreasing in the order of rectangular, U-shaped, and triangular valve ports under identical spool displacement. Furthermore, the rectangular valve port demonstrated the shortest adjustment time, minimal overshoot, and superior speed characteristics. In reference⁷, the stability of digital hydraulic cylinders was analyzed using the descriptive function method. It was concluded that the error size is directly proportional to the size of the gap. By reducing the gap, lead of the ball screw, and increasing the lead of the feedback nut, the static error of the system can be reduced. Based on the structure and closed-loop control principle of digital hydraulic cylinder, the overall mathematical model of digital hydraulic cylinder was established in reference⁸. It was discovered that fluctuations in oil supply pressure can induce system jitter, and reducing the stepper motor frequency can enhance the positioning accuracy of the cylinder. Kalaiarassan et al.⁹ focused on end-point tracking of a single-link robot arm controlled by a digital hydraulic system. The control signal for trajectory tracking was computed by considering both cylinder pressure and speed, leading to improved performance in low-speed tracking with reduced computational complexity. This approach achieved good controllability in low-speed tracking, with simulation analysis demonstrating a tracking error of nearly 2%. Pan et al.¹⁰ constructed the nonlinear model of digital hydraulic cylinder and controller for the first time, followed by the transformation of the nonlinear problem into a linear matrix inequality solution problem. Subsequently, an anti-saturation compensator was designed. Simulation results showed that the designed controller and compensator ensured system robustness and good dynamic performance. Wang et al.¹¹ introduced a control strategy that combined backstepping control and nonlinear disturbance observer to address various types of disturbances in digital hydraulic cylinders. This control strategy effectively reduced position tracking error, phase lag, steady-state limit cycles, and low-speed crawling phenomena caused by parameter uncertainty and uncertain non-linearity in the system, while improving the response speed of the system and enhancing the system more robust. In reference¹², the sensitivity and feedback accuracy of the feedback system were controlled by adjusting the diameter of the friction wheel, the positive pressure on the piston rod and the modulus of the bevel gear. By employing friction transmission, mechanical impact from the rigid connector was reduced, leading to reduced mechanical wear of components and oil pollution, thereby enhancing the reliability of the system. A cross-coupling control strategy¹³ was proposed based on the inability of digital hydraulic cylinders to adjust in real-time. This control algorithm effectively ensured that the digital hydraulic cylinder tracks the input signals, improving system robustness and synchronization performance, albeit with some remaining static errors. In reference¹⁴, a third-order ADRC based servo valve-controlled hydraulic motor was proposed to address the unstable and nonlinear characteristics of the system. By employing advance prediction to mitigate phase lag introduced by the third-order ADRC controller, the control performance of the ADRC controller was significantly enhanced. Simulation experiments demonstrated that the designed ADRC controller outperformed the traditional PID controller in terms of tracking performance and system robustness. Wang et al.¹⁵ introduced a series controller consisting of ADRC and dead zone inverse compensation to tackle dead zone, parameter uncertainty, and external unknown disturbances in the proportional valve of an electro-hydraulic position servo control system. Simulation and experimental results showcased that the proposed series controller effectively compensated for the dead zone of the proportional valve, thereby improving the system's dynamic performance and position tracking accuracy.

The above references studied the stability and accuracy of digital hydraulic cylinders through numerical simulation and experimental verification, providing both theoretical insights and empirical evidence. However, the single control strategy cannot effectively improve the system performance, and some control algorithms may pose challenges in design and implementation. In reference³, the performance of the digital hydraulic cylinder position control system can be effectively improved by using a composite control strategy. However, there are many controller parameters that need to be adjusted, which are difficult to find and consume a lot of time and effort.

Based on the above analyses, this paper focuses on the existing mathematical model of double closed-loop digital hydraulic cylinders and obtains high-order state equations. To facilitate controller design and implementation, firstly, the high-order double closed-loop digital hydraulic cylinder control system is initially transformed into a second-order integral series control system using ADRC. The ESO is employed to estimate the system states and uncertain disturbances online. Concurrently, leveraging the characteristics of switching control, this paper introduces the SADRC strategy. Subsequently, the system is modeled and simulated using MATLAB simulation software. The performance of the digital hydraulic cylinder position system under the SADRC strategy is evaluated through simulation, and a dedicated test bench is constructed to experimentally validate the effectiveness of SADRC. The control parameters that need to be adjusted for this control strategy are significantly fewer than those outlined in reference³.

State space model of a double closed-loop digital hydraulic cylinder

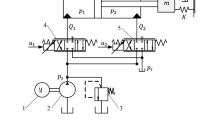
The double closed-loop digital hydraulic cylinder integrates both the internal indirect feedback digital hydraulic cylinder and the indirect digital control hydraulic cylinder. To streamline the structure of the digital hydraulic cylinder, this paper adopts the internal indirect feedback structure , substituting the traditional stepper motor with a higher precision servo motor. Additionally, the encoder and magnetic coupling mechanism of the digital hydraulic cylinder structure are eliminated, and position feedback control is incorporated. This transformation results in a novel type of double closed-loop digital hydraulic cylinder, illustrated in Fig. 1.

The double closed-loop digital hydraulic cylinder consists of several key components: a servo motor, a coupling, a four-way valve spool, an internal indirect feedback mechanism, and a traditional form of hydraulic cylinder. The internal indirect feedback mechanism comprises a ball screw and a valve spool feedback mechanism. The thrust bearing presses the ball screw tightly on the cylinder head. The screw has only one degree of freedom of rotation and both the piston and the nut are fixed. A piston thread pair is formed between the screw and the piston, and the other end of the screw is connected to the right end of the valve spool thread, forming the valve spool thread pair. The right end of the servo motor is connected to the left end of the valve spool by a coupling, and the valve spool has only one degree of axial movement freedom relative to the output shaft of the servo motor, thereby forming a sliding pair of the valve spool.

The structural diagram of the double closed-loop digital hydraulic cylinder position control system is shown in Fig. 2.

Jiang et al.³ discussed the working principle of digital hydraulic cylinder in detail, and established a more comprehensive mathematical model based on the comprehensive analysis of the system composition. This model comprehensively consider the dynamics of the valve spool and feedback mechanism, while covering non-linear factors such as transmission gap, radial leakage of the spool, as well as LuGre friction and non-linear hydraulic springs, which can more realistically reflect the actual situation of the system. This paper will not go into detail here and will directly provide an integrated non-linear state space model.

The system control input is $u_{q}$, the output piston rod displacement is $y = x_{1} = x_{p}$, the system state variable is $x$, the state equation is:

$$ \begin{gathered} x = \left[ {x_{1} ,x_{2} ,x_{3} ,x_{4} ,x_{5} ,x_{6} ,x_{7} ,x_{8} ,x_{9} ,x_{10} ,x_{11} ,x_{12} ,x_{13} ,x_{14} } \right]^{T} \\ = \left[ {x_{p} ,\dot{x}_{p} ,P_{1} ,P_{2} ,x_{v} ,\dot{x}_{v} ,\theta_{s} ,\dot{\theta }_{s} ,\theta_{v} ,\dot{\theta }_{v} ,\theta_{\tau } ,\dot{\theta }_{\tau } ,z,i_{q} } \right]^{T} \\ \end{gathered} $$

(1)

$$ \left\{ {\begin{array}{*{20}c} {\dot{x}_{1} = x_{2} } \\ {\dot{x}_{2} = {{\left[ {A_{1} \left( {x_{3} - mx_{4} } \right) - F_{np} \cos \alpha_{p} - F_{tp} \sin \alpha_{p} - \left( {k_{1} x_{1} + k_{3} x_{1}^{3} } \right) - \sigma_{0} x_{13} + \sigma_{1} \frac{{\left| {x_{2} } \right|}}{{g\left( {x_{2} } \right)}}x_{14} + \left( {\sigma_{2} - \sigma_{1} } \right)x_{2} } \right]} \mathord{\left/ {\vphantom {{\left[ {A_{1} \left( {x_{3} - mx_{4} } \right) - F_{np} \cos \alpha_{p} - F_{tp} \sin \alpha_{p} - \left( {k_{1} x_{1} + k_{3} x_{1}^{3} } \right) - \sigma_{0} x_{13} + \sigma_{1} \frac{{\left| {x_{2} } \right|}}{{g\left( {x_{2} } \right)}}x_{14} + \left( {\sigma_{2} - \sigma_{1} } \right)x_{2} } \right]} {M_{t} }}} \right. \kern-0pt} {M_{t} }} + w_{1} } \\ {\dot{x}_{3} = {{\left[ {Q_{1} - A_{1} x_{2} } \right]\beta_{e} } \mathord{\left/ {\vphantom {{\left[ {Q_{1} - A_{1} x_{2} } \right]\beta_{e} } {\left( {V_{01} + A_{1} x_{1} } \right)}}} \right. \kern-0pt} {\left( {V_{01} + A_{1} x_{1} } \right)}} + w_{2} } \\ {\dot{x}_{4} = {{\left[ { - Q_{2} - A_{2} x_{2} } \right]\beta_{e} } \mathord{\left/ {\vphantom {{\left[ { - Q_{2} - A_{2} x_{2} } \right]\beta_{e} } {\left( {V_{02} - A_{2} x_{1} } \right)}}} \right. \kern-0pt} {\left( {V_{02} - A_{2} x_{1} } \right)}} + w_{3} } \\ {\dot{x}_{5} = x_{6} } \\ {\dot{x}_{6} = {{\left[ {F_{nv} \cos \alpha_{v} - F_{tv} \sin \alpha_{v} - F_{yd} - B_{vp} x_{6} - F_{tg} - F_{fv} } \right]} \mathord{\left/ {\vphantom {{\left[ {F_{nv} \cos \alpha_{v} - F_{tv} \sin \alpha_{v} - F_{yd} - B_{vp} x_{6} - F_{tg} - F_{fv} } \right]} {m_{v} }}} \right. \kern-0pt} {m_{v} }}} \\ {\dot{x}_{7} = x_{8} } \\ {\dot{x}_{8} = {{\left[ {r_{vs} F_{nv} \sin \alpha_{v} + r_{vs} F_{tv} \cos \alpha_{v} + r_{ps} F_{np} \sin \alpha_{p} - r_{ps} F_{tp} \cos \alpha_{p} - T_{fs} - B_{s} x_{8} } \right]} \mathord{\left/ {\vphantom {{\left[ {r_{vs} F_{nv} \sin \alpha_{v} + r_{vs} F_{tv} \cos \alpha_{v} + r_{ps} F_{np} \sin \alpha_{p} - r_{ps} F_{tp} \cos \alpha_{p} - T_{fs} - B_{s} x_{8} } \right]} {J_{s} }}} \right. \kern-0pt} {J_{s} }}} \\ \begin{gathered} \, \dot{x}_{9} = x_{10} \hfill \\ \dot{x}_{10} { = }{{\left[ {{\text{r}}_{\tau } F_{ng} - r_{s} F_{nv} \sin \alpha_{v} - r_{s} F_{tv} \cos \alpha_{v} - B_{vz} x_{10} - T_{fv} } \right]} \mathord{\left/ {\vphantom {{\left[ {{\text{r}}_{\tau } F_{ng} - r_{s} F_{nv} \sin \alpha_{v} - r_{s} F_{tv} \cos \alpha_{v} - B_{vz} x_{10} - T_{fv} } \right]} {J_{v} }}} \right. \kern-0pt} {J_{v} }} \hfill \\ \, \dot{x}_{11} { = }x_{12} \hfill \\ \end{gathered} \\ {\dot{x}_{12} = {{\left[ {k_{t} x_{14} - B_{2} x_{12} - r_{\tau } F_{ng} } \right]} \mathord{\left/ {\vphantom {{\left[ {k_{t} x_{14} - B_{2} x_{12} - r_{\tau } F_{ng} } \right]} J}} \right. \kern-0pt} J}} \\ {\dot{x}_{13} = x_{2} - \sigma_{0} \frac{{\left| {\dot{x}_{2} } \right|}}{{F_{c} + \left( {F_{sc} - F_{c} } \right)e^{{ - \left( {{{x_{2} } \mathord{\left/ {\vphantom {{x_{2} } {v_{sk} }}} \right. \kern-0pt} {v_{sk} }}} \right)^{2} }} }}x_{13} } \\ {\dot{x}_{14} = {{\left[ {u_{q} - Rx_{14} - k_{e} x_{12} } \right]} \mathord{\left/ {\vphantom {{\left[ {u_{q} - Rx_{14} - k_{e} x_{12} } \right]} {L_{0} }}} \right. \kern-0pt} {L_{0} }}} \\ \end{array} } \right. $$

(2)

In the formula (2): where, $w_{1} = {{ - F_{L} } \mathord{\left/ {\vphantom {{ - F_{L} } {M_{t} }}} \right. \kern-0pt} {M_{t} }}$, $w_{2} = {{\left[ { - C_{0} x_{3} - C_{1} \left( {x_{3} - x_{4} } \right)} \right]\beta_{e} } \mathord{\left/ {\vphantom {{\left[ { - C_{0} x_{3} - C_{1} \left( {x_{3} - x_{4} } \right)} \right]\beta_{e} } {\left( {V_{01} + A_{1} x_{1} } \right)}}} \right. \kern-0pt} {\left( {V_{01} + A_{1} x_{1} } \right)}}$,

$w_{3} = {{\left[ { - C_{0} x_{4} + C_{1} \left( {x_{3} - x_{4} } \right)} \right]\beta_{e} } \mathord{\left/ {\vphantom {{\left[ { - C_{0} x_{4} + C_{1} \left( {x_{3} - x_{4} } \right)} \right]\beta_{e} } {\left( {V_{02} - A_{2} x_{1} } \right)}}} \right. \kern-0pt} {\left( {V_{02} - A_{2} x_{1} } \right)}}$.

Considering the hydraulic cylinder load force and leakage as disturbances in the system, namely:

$$ \left\{ \begin{gathered} w_{2} \le \frac{{\beta_{e} P_{s} \left( {C_{1} + C_{0} } \right)}}{{\left| {V_{1} } \right|_{\min } }} \hfill \\ w_{3} \le \frac{{\beta_{e} P_{s} \left( {C_{1} + C_{0} } \right)}}{{\left| {V_{2} } \right|_{\min } }} \hfill \\ \end{gathered} \right. $$

(3)

Therefore the disturbances, $w_{1}$, $w_{2}$ and $w_{3}$ are bounded.

$$ w = \left[ {\begin{array}{*{20}c} 0 & {w_{1} } & {w_{2} } & {w_{3} } & 0 & \cdots & 0 \\ \end{array} } \right]_{1 \times 14} $$

(4)

Then, the system state space expression is:

$$ \left\{ \begin{gathered} \dot{x} = f(x) + g(x)u + p(x)w \hfill \\ z = h(x)x \hfill \\ \end{gathered} \right. $$

(5)

In the formula (4):

$$ f(x) = \left\{ {\begin{array}{*{20}c} {\dot{x}_{1} = x_{2} } \\ {\dot{x}_{2} = {{\left[ {A_{1} \left( {x_{3} - mx_{4} } \right) - F_{np} \cos \alpha_{p} - F_{tp} \sin \alpha_{p} - \left( {k_{1} x_{1} + k_{3} x_{1}^{3} } \right) - \sigma_{0} x_{13} + \sigma_{1} \frac{{\left| {x_{2} } \right|}}{{g\left( {x_{2} } \right)}}x_{14} + \left( {\sigma_{2} - \sigma_{1} } \right)x_{2} } \right]} \mathord{\left/ {\vphantom {{\left[ {A_{1} \left( {x_{3} - mx_{4} } \right) - F_{np} \cos \alpha_{p} - F_{tp} \sin \alpha_{p} - \left( {k_{1} x_{1} + k_{3} x_{1}^{3} } \right) - \sigma_{0} x_{13} + \sigma_{1} \frac{{\left| {x_{2} } \right|}}{{g\left( {x_{2} } \right)}}x_{14} + \left( {\sigma_{2} - \sigma_{1} } \right)x_{2} } \right]} {M_{t} }}} \right. \kern-0pt} {M_{t} }}} \\ {\dot{x}_{3} = {{\left[ {Q_{1} - A_{1} x_{2} } \right]\beta_{e} } \mathord{\left/ {\vphantom {{\left[ {Q_{1} - A_{1} x_{2} } \right]\beta_{e} } {\left( {V_{01} + A_{1} x_{1} } \right)}}} \right. \kern-0pt} {\left( {V_{01} + A_{1} x_{1} } \right)}}} \\ {\dot{x}_{4} = {{\left[ { - Q_{2} - A_{2} x_{2} } \right]\beta_{e} } \mathord{\left/ {\vphantom {{\left[ { - Q_{2} - A_{2} x_{2} } \right]\beta_{e} } {\left( {V_{02} - A_{2} x_{1} } \right)}}} \right. \kern-0pt} {\left( {V_{02} - A_{2} x_{1} } \right)}}} \\ {\dot{x}_{5} = x_{6} } \\ {\dot{x}_{6} = {{\left[ {F_{nv} \cos \alpha_{v} - F_{tv} \sin \alpha_{v} - F_{yd} - B_{vp} x_{6} - F_{tg} - F_{fv} } \right]} \mathord{\left/ {\vphantom {{\left[ {F_{nv} \cos \alpha_{v} - F_{tv} \sin \alpha_{v} - F_{yd} - B_{vp} x_{6} - F_{tg} - F_{fv} } \right]} {m_{v} }}} \right. \kern-0pt} {m_{v} }}} \\ {\dot{x}_{7} = x_{8} } \\ {\dot{x}_{8} = {{\left[ {r_{vs} F_{nv} \sin \alpha_{v} + r_{vs} F_{tv} \cos \alpha_{v} + r_{ps} F_{np} \sin \alpha_{p} - r_{ps} F_{tp} \cos \alpha_{p} - T_{fs} - B_{s} x_{8} } \right]} \mathord{\left/ {\vphantom {{\left[ {r_{vs} F_{nv} \sin \alpha_{v} + r_{vs} F_{tv} \cos \alpha_{v} + r_{ps} F_{np} \sin \alpha_{p} - r_{ps} F_{tp} \cos \alpha_{p} - T_{fs} - B_{s} x_{8} } \right]} {J_{s} }}} \right. \kern-0pt} {J_{s} }}} \\ \begin{gathered} \, \dot{x}_{9} = x_{10} \hfill \\ \dot{x}_{10} { = }{{\left[ {{\text{r}}_{\tau } F_{ng} - r_{s} F_{nv} \sin \alpha_{v} - r_{s} F_{tv} \cos \alpha_{v} - B_{vz} x_{10} - T_{fv} } \right]} \mathord{\left/ {\vphantom {{\left[ {{\text{r}}_{\tau } F_{ng} - r_{s} F_{nv} \sin \alpha_{v} - r_{s} F_{tv} \cos \alpha_{v} - B_{vz} x_{10} - T_{fv} } \right]} {J_{v} }}} \right. \kern-0pt} {J_{v} }} \hfill \\ \, \dot{x}_{11} { = }x_{12} \hfill \\ \end{gathered} \\ {\dot{x}_{12} = {{\left[ {k_{t} x_{14} - B_{2} x_{12} - r_{\tau } F_{ng} } \right]} \mathord{\left/ {\vphantom {{\left[ {k_{t} x_{14} - B_{2} x_{12} - r_{\tau } F_{ng} } \right]} J}} \right. \kern-0pt} J}} \\ {\dot{x}_{13} = x_{2} - \sigma_{0} \frac{{\left| {\dot{x}_{2} } \right|}}{{F_{c} + \left( {F_{sc} - F_{c} } \right)e^{{ - \left( {{{x_{2} } \mathord{\left/ {\vphantom {{x_{2} } {v_{sk} }}} \right. \kern-0pt} {v_{sk} }}} \right)^{2} }} }}x_{13} } \\ {\dot{x}_{14} = {{\left[ { - Rx_{14} - k_{e} x_{12} } \right]} \mathord{\left/ {\vphantom {{\left[ { - Rx_{14} - k_{e} x_{12} } \right]} {L_{0} }}} \right. \kern-0pt} {L_{0} }}} \\ \end{array} } \right. $$

(6)

$$ \left\{ \begin{gathered} g(x) = \left[ {\begin{array}{*{20}c} 0 & \cdots & 0 & 0 & 1 \\ \end{array} } \right]_{1 \times 14}^{T} \hfill \\ p(x) = \left[ {\begin{array}{*{20}c} 0 & 1 & 1 & 1 & 0 & {\begin{array}{*{20}c} \cdots & 0 \\ \end{array} } \\ \end{array} } \right]_{1 \times 14}^{T} \hfill \\ h(x) = \left[ {\begin{array}{*{20}c} 1 & 0 & {\begin{array}{*{20}c} 0 & \cdots \\ \end{array} } & 0 \\ \end{array} } \right]_{1 \times 14} \hfill \\ \end{gathered} \right. $$

(7)

ADRC takes PID control as its core, retaining the advantages of classical control theory and abandoning the dependence of modern control theory on accurate models. It pays more attention to the control rather than the mathematical model of the controlled object. The core of ADRC is to sum up the internal/external disturbances and uncertainties of the system as “unknown disturbances”, then use the extended state observer (ESO) to estimate them, and finally use the controller to compensate for them^16,17. Therefore, ADRC has a better control effect and is more suitable for controlling nonlinear systems. Since the double closed-loop digital hydraulic cylinder is a complex system, combined with the characteristics of switching control and ADRC, a SADRC strategy is proposed. The system structure diagram is shown in Fig. 3.

The ADRC consists of three main parts: a tracking differentiator (TD), an extended state observer (ESO), and a non-linear state error feedback (NLSEF) controller.

Tracking differentiator (TD)

The essence of the TD is to filter the input signal and obtain the differentiation of the input signal, which is a signal processing method. Especially when there is a sudden change in the input signal, TD can provide a smooth input signal to the controller. At the same time, the filtering function of TD can reduce the sudden change signal and prevent the system from overshooting, effectively solving the contradiction between “speed” and “overshoot” of the system, and improving the stability of the system¹⁸.

Based on the ADRC theory, the digital hydraulic cylinder in this paper is equivalent to a second-order system. Assuming a second-order TD is selected, two TDs must be connected in series. If the input command of the system is a sine signal (multi-order differentiable), there is no problem. However, if the system input is a step signal, the derivative of the TD will appear infinite, which is theoretically problematic. Therefore, the TD and ESO in this paper are both third-order. LTD is relatively independent in LADRC, serving as the transition signal $v_{0}$ of the target point and the differential signal $v_{0}^{(i)}$ of any order of the transition signal of the target point, i.e. $v_{1} \to v_{0}$, $v_{i + 1} \to v_{0}^{(i)}$ $\left( {i = 1,2, \cdots n} \right)$. Combining references¹⁹ and²⁰, the second-order LTD given in reference²⁰ is extended to the higher-order SPGH-LTD form, and the specific form of the higher-order LTD is:

$$ \left\{ \begin{gathered} v_{1} = v_{2} \hfill \\ v_{2} = v_{3} \hfill \\ \, \vdots \hfill \\ v_{n} = v_{n + 1} \hfill \\ v_{n + 1} = R^{n + 1} \left( {a_{1} \left( {v_{1} - v_{0} } \right) + a_{2} \frac{{v_{2} }}{R} + \cdots + a_{n + 1} \frac{{v_{n + 1} }}{{R^{n} }}} \right) \hfill \\ \end{gathered} \right. $$

(8)

In the formula (8): R is the adjustment gain that determines the tracking speed, and the coefficient $a_{i} \left( {i = 1,2, \ldots ,n + 1} \right)$ needs to satisfy formula (9).

$$ A = \left[ {\begin{array}{*{20}c} 0 & 1 & 0 & \cdots & 0 \\ 0 & 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ 0 & 0 & 0 & \cdots & 1 \\ {a_{1} } & {a_{2} } & {a_{3} } & \vdots & {a_{n + 1} } \\ \end{array} } \right]_{{\left( {n + 1} \right)\left( {n + 1} \right)}} $$

(9)

In the formula (9): A is Hurwitz matrix, $v = \left[ {v_{1} ,v_{2} , \ldots ,v_{n} } \right]^{T}$.

Extended state observer (ESO)

The function of an ESO is to extend the “disturbance” of the system into a new state variable, with the aim of facilitating the estimation of disturbances. The ESO is the core part of ADRC. It abandons traditional measurement of disturbance effects or precise mathematical models of disturbances, and directly refers to these factors as “total disturbances”. Through real-time online estimation of the system state and “total disturbances”, the original system is transformed into an integral series system by “disturbance compensation”^21,22. In Fig. 3, $z_{1} \sim z_{n}$ represents the observed object state and $z_{n + 1}$ represents the expansion state.

This paper equates the high-order nonlinear system of digital hydraulic cylinders as a complex nonlinear system with disturbances, as demonstrated in the formula (10).

$$ \left\{ \begin{gathered} \dot{x}_{1} = x_{2} \hfill \\ \dot{x}_{2} = f\left( {x_{1} ,x_{2} , \cdots ,x_{14} ,t} \right) + w(t) + bu \hfill \\ y = x_{1} \hfill \\ \end{gathered} \right. $$

(10)

In the Eq. (10): $f\left( {x_{1} ,x_{2} , \ldots ,x_{14} ,t} \right)$ is an unknown function, representing the dynamics of the controlled object, including internal disturbances of the system, and $w(t)$ is an unknown external disturbance. Expanding the total disturbance to a new state variable $x_{3}$, denoted as $x_{3} = f(x_{1} ,x_{2} , \ldots ,x_{14} ,t) + w(t)$. Let $x_{3} = a(t)$, $\dot{x}_{3} = a_{0} (t)$, b is the control gains, then $b \approx b_{0}$. The system (10) can be expanded to formula (11).

$$ \left\{ \begin{gathered} \dot{x}_{1} = x_{2} \hfill \\ \dot{x}_{2} = x_{3} + b_{0} u \hfill \\ \dot{x}_{3} = a_{0} (t) \hfill \\ y = x_{1} \hfill \\ \end{gathered} \right. $$

(11)

In this system, the sum of internal and external disturbances is represented by $a(t)$, and the particular form of the $a_{0} (t)$ expression is no longer important. The system described above was transformed into a linear system, and an observer was then constructed. If the state variable is set to $z$, then there is:

$$ \left\{ \begin{gathered} \dot{z}_{1} = z_{2} - \beta_{01} e_{1} \hfill \\ \dot{z}_{2} = z_{3} - \beta_{02} fal\left( {e_{1} ,\alpha_{1} ,\delta } \right) + b_{0} u \hfill \\ \dot{z}_{3} = - \beta_{03} fal\left( {e_{1} ,\alpha_{2} ,\delta } \right) \hfill \\ \end{gathered} \right. $$

(12)

In the formula(12): z₁, z₂ represents the estimated signal of the state variable x₁, x₂, z₃ represents the estimated signal of the extended state $x_{3}$, and $e_{1} = z_{1} - x_{1}$ represents the observation error, $fal\left( {e_{1} ,\alpha ,\delta } \right)$ is a nonlinear function, and its expression is:

$$ fal(e_{1} ,\alpha ,\delta ) = \left\{ \begin{gathered} \frac{{e_{1} }}{{\delta^{1 - \alpha } }}{ ,}\left| {e_{1} } \right| \le \delta \hfill \\ \left| {e_{1} } \right|^{\alpha } sign(e_{1} ) \, ,\left| {e_{1} } \right| > \delta \hfill \\ \end{gathered} \right. $$

(13)

In the formula(13): the form of the nonlinear function is determined by the parameter $\alpha$, while the size of the linear interval is represented by $\delta$. Subtracts formula (11) from formula (12) results in formula (14).

$$ \left\{ \begin{gathered} \dot{e}_{1} = e_{2} - \beta_{01} e_{1} \, e_{1} = z_{1} - x_{1} \hfill \\ \dot{e}_{2} = e_{3} - \beta_{02} fal\left( {e_{1} ,\alpha_{1} ,\delta } \right) \, e_{2} = z_{2} - x_{2} \hfill \\ \dot{e}_{3} = a_{0} - \beta_{03} fal\left( {e_{1} ,\alpha_{2} ,\delta } \right) \, e_{3} = z_{3} - x_{3} \hfill \\ \end{gathered} \right. $$

(14)

When the system reaches a steady state, all the right-hand sides of the equation converge towards zero, namely:

$$ \left\{ \begin{gathered} e_{2} - \beta_{01} e_{1} { = 0 } \hfill \\ e_{3} - \beta_{02} fal\left( {e_{1} ,\alpha_{1} ,\delta } \right) = 0 \, \hfill \\ a_{0} - \beta_{03} fal\left( {e_{1} ,\alpha_{2} ,\delta } \right) = 0 \, \hfill \\ \end{gathered} \right. $$

(15)

Then, formula (15) can be expressed as:

$$ \left\{ \begin{gathered} e_{2} = \beta_{01} e_{1} \, \hfill \\ e_{3} = \beta_{02} fal\left( {e_{1} ,\alpha_{1} ,\delta } \right) \, \hfill \\ a_{0} = \beta_{03} fal\left( {e_{1} ,\alpha_{2} ,\delta } \right) \, \hfill \\ \end{gathered} \right. $$

(16)

Make $\beta_{02} fal\left( {e_{1} ,\alpha_{1} ,\delta } \right) = \lambda_{02} (e_{1} )e_{1}$, $\beta_{03} fal\left( {e_{1} ,\alpha_{2} ,\delta } \right) = \, \lambda_{03} (e_{1} )e_{1}$. The error in a steady state of the system may be expressed as.

$$ \left\{ \begin{gathered} \left| {e_{1} } \right| = {{a_{0} } \mathord{\left/ {\vphantom {{a_{0} } {\lambda_{03} (e_{1} )}}} \right. \kern-0pt} {\lambda_{03} (e_{1} )}} \, \hfill \\ \left| {e_{2} } \right| = \beta_{01} {{a_{0} } \mathord{\left/ {\vphantom {{a_{0} } {\lambda_{03} (e_{1} )}}} \right. \kern-0pt} {\lambda_{03} (e_{1} )}} \hfill \\ \left| {e_{3} } \right| = \lambda_{02} (e_{1} ){{a_{0} } \mathord{\left/ {\vphantom {{a_{0} } {\lambda_{03} (e_{1} )}}} \right. \kern-0pt} {\lambda_{03} (e_{1} )}} \, \hfill \\ \end{gathered} \right. $$

(17)

From formula (17) above, it can be observed that if $\lambda_{03} (e_{1} )$ is sufficiently large, these estimation errors will converge to zero.

Nonlinear state error feedback control law (NLSEF)

The PID controller deals with the error signal of input and output by linear operation method. In the initial state, this error is directly selected. Because the initial control quantity is too large, the system will cause an overshoot phenomenon. Therefore, the PID controller cannot solve the contradiction between the response speed and the overshoot in the system. After a lot of research, Han Jingqing found that the nonlinear function can deal with the problem of response speed and overshoot^23,24. The application of the nonlinear module in ADRC will achieve excellent results. Using the nonlinear feedback control strategy, the system can select a smaller gain when the error is large or select a larger gain when the system error is small, optimize the system processing information speed, and improve the system control performance^25,26. Figure 4 shows the structure diagram of the NLSEF for n-order system.

In ADRC, to eliminate the error as much as possible, the constructed linear state error feedback control law usually adopts the following nonlinear combination, as shown in the formula (18).

$$ u_{0} = \beta_{1} \cdot fal\left( {e_{1} ,\alpha_{1} ,\delta } \right){ + }\beta_{2} \cdot fal\left( {e_{1} ,\alpha_{2} ,\delta } \right) $$

(18)

The function fal in formula (18) is equivalent to that in formula (13), Where , $\alpha_{1}$$\alpha_{2}$, $\delta$, $\beta_{1}$ and $\beta_{2}$ represent nonlinear parameters, $0 < \alpha_{1} < 1 < \alpha_{2}$. denotes the system state error, and the control variable $u_{0}$ is fitted through a nonlinear function to reduce the system error and avoid high-frequency oscillations.

When the estimated value of the total disturbance $x_{3}$ of the system is obtained, and $b_{0}$ in the formula (11) is known, the control variable may be determined as follows:

$$ u = u_{0} - {{z_{3} } \mathord{\left/ {\vphantom {{z_{3} } {b_{0} }}} \right. \kern-0pt} {b_{0} }} $$

(19)

or

$$ u = {{\left( {u_{0} - z_{3} } \right)} \mathord{\left/ {\vphantom {{\left( {u_{0} - z_{3} } \right)} {b_{0} }}} \right. \kern-0pt} {b_{0} }} $$

(20)

Through the above form transformation, the original nonlinear control system is equivalent to an integral series linear control system, which is called dynamic linear compensation. Therefore, by combining the ESO and the compensation control strategy, a unified method can be used to deal with various control systems such as linear, nonlinear, parameter determination and parameter uncertainty.

Stability analysis of SADRC

In this paper, a revised nonlinear state observer (NLESO) is proposed for the system (10). The NLESO is described as follows:

The solution of the NLESO, which is explored in this chapter, relies on adjusting the parameter $\varepsilon$. Its observer form is :

$$ \left\{ \begin{gathered} \dot{\hat{x}}_{1} = \hat{x}_{2} + \varepsilon g_{1} \left( {\frac{{y(t) - \hat{x}_{1} (t)}}{{\varepsilon^{2} }}} \right) \hfill \\ \dot{\hat{x}}_{2} = \hat{x}_{3} + g_{2} \left( {\frac{{y(t) - \hat{x}_{1} (t)}}{{\varepsilon^{2} }}} \right) + b_{0} u(t) \hfill \\ \dot{\hat{x}}_{3} = \frac{1}{\varepsilon }g_{3} \left( {\frac{{y(t) - \hat{x}_{1} (t)}}{{\varepsilon^{2} }}} \right) \hfill \\ \end{gathered} \right. $$

(21)

In this case, $g_{i} ()$ in the Eq. (21) represents $g_{i1} (y_{1} ) = - k_{i1} y_{1} - \varphi (y_{1} )$, $g_{i2} (y_{1} ) = - k_{i2} y_{1}$ and $g_{i3} (y_{1} ) = - k_{i3} y_{1}$, respectively, wherein $y_{1} = y(t) - \hat{x}_{1} (t)$. Then, the formula (21) can be modified to formula (21).

$$ \left\{ \begin{gathered} \dot{\hat{x}}_{1} = \hat{x}_{2} + \frac{{k_{11} }}{\varepsilon }\left( {y(t) - \hat{x}_{1} (t)} \right) - \varepsilon \varphi \left( {\frac{{y(t) - \hat{x}_{1} (t)}}{{\varepsilon^{2} }}} \right) \hfill \\ \dot{\hat{x}}_{2} = \hat{x}_{3} + \frac{{k_{21} }}{{\varepsilon^{2} }}\left( {y(t) - \hat{x}_{1} (t)} \right) + bu(t) \hfill \\ \dot{\hat{x}}_{3} = \frac{{k_{31} }}{{\varepsilon^{3} }}\left( {y(t) - \hat{x}_{1} (t)} \right) \hfill \\ \end{gathered} \right. $$

(22)

The non-linear function $\varphi$ in formula (22) is:

$$ \varphi (r) = \left\{ \begin{gathered} - {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0pt} 4} \, , \, r \in \left( { - \infty , - {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2}} \right] \hfill \\ {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0pt} 4}{\text{sin(}}r{) }, \, r \in \left( { - {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2},{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2}} \right) \hfill \\ {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0pt} 4} \, , \, r \in \left[ {{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2}, + \infty } \right) \hfill \\ \end{gathered} \right. $$

(23)

The function $\varphi (r)$ in the NLESO is a nonlinear, and the constant $k_{ij}$ is the matrix $E_{i}$ given by Hurwitz as follows:

$$ E = \left( {\begin{array}{*{20}c} { - k_{i1} } & 1 & 0 \\ { - k_{i2} } & 0 & 1 \\ { - k_{i3} } & 0 & 0 \\ \end{array} } \right) $$

(24)

The characteristic equation of formula (24) is:

$$ s^{3} + k_{i1} s^{2} + k_{i2} s + k_{i3} = 0 $$

(25)

The Routh criterion can be obtained since it is equivalent to the Hurwitz stability criterion. The convergence condition of the ESO is as follows:

$$ k_{i1} \cdot k_{i2} > k_{i3} $$

(26)

Lyapunov function V: ${\mathbb{R}}^{3} \to {\mathbb{R}}$ can be defined as:

$$ V(y) = \left\langle {Py,y} \right\rangle + \int\limits_{0}^{y1} {\varphi (s)ds} $$

(27)

Let the positive definite matrix P , Which is the solution of the Lyapunov matrix equation $PE + E^{T} P = - I$ for the positive definite matrix, where I represents the (n + 1) dimensional identity matrix and defines the function V, W: ${\mathbb{R}}^{3} \to {\mathbb{R}}$, $V(\eta ) = \left\langle {P\eta ,\eta } \right\rangle { = }\eta^{T} P\eta$, $W(\eta ) = \left\langle {\eta ,\eta } \right\rangle = \eta^{T} \eta$, $\forall \eta \in {\mathbb{R}}^{n + 1}$. Then:

$$ \lambda_{\min } (P)\left\| \eta \right\|^{2} \le V(\eta ) \le \lambda_{\max } (P)\left\| \eta \right\|^{2} $$

(28)

$$ \sum\limits_{i = 1}^{2} {\frac{\partial V}{{\partial \eta_{i} }}\left( {\eta_{i + 1} - \alpha_{i} \eta_{1} } \right)} - \frac{\partial V}{{\partial \eta_{3} }}\alpha_{3} \eta_{1} = - \eta^{T} \eta = - \left\| \eta \right\|^{2} = - W(\eta ) $$

(29)

and:

$$ \left| {\frac{\partial V}{{\partial \eta_{n + 1} }}} \right| \le \left\| {\frac{\partial V}{{\partial \eta }}} \right\| = \left\| {2\eta^{T} P} \right\| \le 2\left\| P \right\|\left\| \eta \right\| = 2\lambda_{\max } (P)\left\| \eta \right\| $$

(30)

where $\lambda_{\min } (P)$ and $\lambda_{\max } (P)$ represent the maximum and minimum eigenvalues of matrix P, respectively.

For the switching system in this paper, set the matrices $E_{i}$ to be $E_{1} = \left( {\begin{array}{*{20}c} { - 6} & 1 & 0 \\ { - 11} & 0 & 1 \\ { - 6} & 0 & 0 \\ \end{array} } \right)$ and $E_{2} = \left( {\begin{array}{*{20}c} { - 3} & 1 & 0 \\ { - 3} & 0 & 1 \\ { - 1} & 0 & 0 \\ \end{array} } \right)$, respectively. Among them, the eigenvalues of $\left\{ { - 1, - 2, - 3} \right\}$ are $E_{1}$ and $\left\{ { - 1, - 1, - 1} \right\}$ are $E_{2}$, respectively, so both $E_{1}$ and $E_{2}$ satisfy the Hurwitz form of the matrix.

From formula $PE + E^{T} P = - I$, it can be determined that matrices $P_{1}$ and $P_{2}$ are respectively $P_{1} = \left[ {\begin{array}{*{20}c} {1.7} & { - 0.5} & { - 0.7} \\ { - 0.5} & {0.7} & { - 0.5} \\ { - 0.7} & { - 0.5} & {{{23} \mathord{\left/ {\vphantom {{23} {15}}} \right. \kern-0pt} {15}}} \\ \end{array} } \right]$ and $P_{2} = \left[ {\begin{array}{*{20}c} 1 & { - 0.5} & { - 1} \\ { - 0.5} & { \, 1} & { - 0.5} \\ { - 1} & { \, - 0.5} & 4 \\ \end{array} } \right]$. $g_{i} ()$ are respectively $g_{11} (y_{1} ) = - 6y_{1} - \varphi (y_{1} )$, $g_{12} (y_{1} ) = - 11y_{1}$, $g_{13} (y_{1} ) = - 6y_{1}$; $g_{21} (y_{1} ) = - 3y_{1} - \varphi (y_{1} )$, $g_{22} (y_{1} ) = - 3y_{1}$, $g_{23} (y_{1} ) = - y_{1}$.

Directly calculated:

$$ \begin{array}{*{20}c} {\sum\limits_{i = 1}^{2} {\frac{{\partial V_{1} }}{{\partial y_{i} }}\left( {y_{i + 1} + g_{i} (y_{1} )} \right)} + \frac{{\partial V_{1} }}{{\partial y_{3} }}g_{3} (y_{1} )} \\ {{ = } - \varphi^{2} - 5\varphi y_{1} + 2\varphi y_{2} + 2\varphi y_{3} - y_{1}^{2} - y_{2}^{2} - y_{3}^{2} } \\ { = - \frac{21}{{1296}}y_{1}^{2} - \frac{214}{{256}}y_{2}^{2} - \frac{214}{{256}}y_{3}^{2} } \\ { \le 0} \\ \end{array} \quad \begin{array}{*{20}c} {\sum\limits_{i = 1}^{2} {\frac{{\partial V_{2} }}{{\partial y_{i} }}\left( {y_{i + 1} + g_{i} (y_{1} )} \right)} + \frac{{\partial V_{2} }}{{\partial y_{3} }}g_{3} (y_{1} )} \\ {{ = } - \varphi^{2} - \frac{47}{5}\varphi y_{1} + 2\varphi y_{2} + \frac{7}{5}\varphi y_{3} - y_{1}^{2} - y_{2}^{2} - y_{3}^{2} } \\ { \le - \frac{283}{{1280}}y_{1}^{2} - \frac{215}{{256}}y_{2}^{2} - \frac{215}{{256}}y_{3}^{2} } \\ { \le 0} \\ \end{array} $$

(31)

From the above calculation, it can be observed that the two variables $V_{i}$ in the switching subsystem satisfy the Lyapunov function. The switching rule of the system is set as follows:

$$ \sigma (t) = \min \, \arg \left( {V_{1} ,V_{2} } \right) $$

(32)

The smaller $V_{i}$ is selected by the switching rule, which can ensure that the energy of the system is reduced after each switching, and then the ESO is used to find the corresponding observation state. Combined with formulas (16), (18) and (20), the switching controller is finally obtained:

$$ u = \frac{{\beta_{1} fal(e_{\sigma } ,\alpha_{1} ,\delta ){ + }\beta_{2} fal(e_{\sigma } ,\alpha_{2} ,\delta ) \, - z_{\sigma 3} }}{{b_{0} }} $$

(33)

Therefore, based on the switching rule (32) of the system, it can be seen that the SADRC strategy designed in this chapter can ensure the stability of the closed-loop system.

Results

To verify the superiority of the control strategy designed in this paper, the simulation model of the digital hydraulic cylinder position control system is built in the MATLAB/Simulink simulation platform, and the SADRC strategy is compared with the traditional PID control strategy. The digital hydraulic cylinder position system based on SADRC is shown in Fig. 5. In the absence of external interference and square wave disturbance, the system input signals adopt step signal, sine signal, slope signal and custom signal respectively. The influence of two control strategies on the performance of a digital hydraulic cylinder is studied by simulation.

The main parameters of the digital hydraulic cylinder simulation model are shown in Table 1.

Table 1 The structure parameters of digital hydraulic cylinder.

Full size table

Research on the performance of digital hydraulic cylinder position control system without external disturbance

Step response

In the absence of external disturbance, the position command of the step signal is set at 1 s and the amplitude changes from 0 to 60 mm. The simulation time is 10 s. Determine the PID control parameters in this paper through debugging as follows:$k_{p} = 5000$, $k_{i} = 200$, $k_{d} = 100$, filter coefficient is $N = 1$. The parameters of the SADRC are shown in Table 2.

Table 2 SADRC parameters.

Full size table

Figure 6a shows the piston displacement curve, and Fig. 6b shows the piston error curve. It can be seen from Fig. 6a,b that the digital hydraulic cylinder control system is an over-damped system, and there is basically no overshoot. When the adjustment time of the system under the PID control strategy is about 4.3 s, the system is in a stable state, and the static error of the system is 1 mm. When the adjustment time of the system under the SADRC strategy is about 2.9 s, the response speed is increased by 32.56%. At this time, the system is in a stable state, the static error of the system is basically zero, and the position error is reduced by 1.67%. Therefore, the system has higher robustness and faster convergence speed under the SADRC strategy.

Figure 7 is the output voltage curve of the controller. It can be clearly seen from the diagram that the output voltage convergence effect of the SADRC strategy system is significantly faster than the output voltage under the PID control strategy, which further verifies the correctness of Fig. 6.

Figure 8 shows the switching signal of the SADRC system. The switching signal produces multiple switching at 2.9 s. By switching under two types of non-linear ESO, the system reaches a stable state at around 2.9 s, ensuring the stability of the entire closed-loop system.

Sine response

In the absence of external disturbance, for the continuously changing sine position command following the signal, set its frequency to 0.8 rad/s, amplitude to 30 mm, and simulation time to 10 s. The PID control parameters are: $k_{p} = 10000$, $k_{i} = 600$, and $k_{d} = 1000$, filter coefficient is $N = 1000$. The parameters of the SADRC are consistent with Table 2.

Figure 9a shows the piston displacement curve, and Fig. 9b shows the piston error curve. From Fig. 9a,b, it can be seen that the system can track command signal well under both types of control. The maximum static error of the system under PID control is 1.8 mm, while the maximum static error of the system under SADRC is 1.4 mm, and the position error is reduced by 0.67%. Therefore, the system can reduce the tracking error and improve the accuracy of the system by SADRC strategy.

Figure 10 is the output voltage curve of the controller. It can be clearly seen from the Fig. 10 that the output voltage curves of the system under the two control strategies are basically the same. From the enlarged diagram in Fig. 10, it can be seen that although there are very small fluctuations in the output voltage curves by the two controllers, it does not affect the stability of the entire system.

Figure 11 shows the switching signal of the SADRC system. From the Fig. 11, it can be seen that the switching signal only occurs once at 6 s, that is, the two subsystems generate a switching, which can achieve the stable operation of the entire control system.

Slope response

In the absence of external disturbance, for slope control signals, set the slope of the slope to 6 mm/s and the simulation time to 10 s. The PID control parameters are: $k_{p} = 10000$; $k_{i} = 600$; $k_{d} = 1000$; filter coefficient is $N = 1000$. The parameters of the SADRC are consistent with Table 2.

The piston displacement curve and the piston error curve are shown in Fig. 12a,b respectively.

From Fig. 12a it can be seen that the system can effectively track the command signal under both control strategies. From Fig. 12b, it can be seen that the static error of the system under the PID control strategy is 0.5 mm, while the static error of the system under the SADRC strategy is 0.19 mm, and the position error is reduced by 0.52%. At the same time, it can be seen from Fig. 12b) that the error of the system under the SADRC control strategy will immediately reach the steady-state error value, which also shows that the control strategy can improve the rapidity of the system. Comparative analysis shows that the system can track command signals well under both control strategies. However, under SADRC, the static error of the system is effectively reduced, and the accuracy and rapidity of the system are improved.

Figure 13 is the output voltage curve of the controller. It can be clearly seen from the diagram that the output voltage curves of the system under the two control strategies are basically the same. However, the output voltage curves under the two control strategies have slight changes. which further proves the correctness of Fig. 12.

Figure 14 shows the switching signal of the SADRC system. From the Fig. 14, the switching signal has not produced a switching during the operation of the system, which also indicates that the switching system has operated under the second type of nonlinear ESO and the closed-loop system maintains stable operation.

Custom response

In the absence of external interference, for custom signals, set a slope of 30 mm/s for 0 ~ 2 s, then run steadily for 2 s, then run at a slope of -30 mm/s within 4 s, then run steadily for 2 s, and finally run at a slope of 30 mm/s. The PID control parameters are: $k_{p} = 600000$; $k_{i} = 500$; $k_{d} = 1000$; filter coefficient is $N = 1000$. The parameters of the SADRC are consistent with Table 2.

Figure 15a,b show the piston displacement curve and the piston error curve respectively. From the magnification curves in Fig. 15a,b, it can be seen that when the system is under the PID control strategy for 2 s ~ 4 s and 8 s ~ 10 s, the piston will produce obvious oscillation. Among them, the system error is the largest at 0 s ~ 2 s and 10 s ~ 12 s, and the maximum value is 0.1 mm; under the SADRC strategy, the piston basically has no chattering phenomenon. The system error is the largest at 0 s ~ 2 s and 10 s ~ 12 s, the maximum value is 0.05 mm, and the system comprehensive error is reduced by 0.17%. Through comparative analysis, it can be seen that the SADRC strategy can significantly improve the stability of the system and reduce the static error of the system, and effectively improve the system performance.

Figure 16 is the output voltage curve of the controller. It can be clearly seen from the figure that the output voltage curves of the system under the two control strategies are basically the same. However, when the system is under the PID control strategy for 2 s ~ 4 s and 8 s ~ 10 s, the output voltage of the controller is obviously oscillation, which further verifies the correctness of Fig. 15.

Figure 17 shows the switching signal of the SADRC system. When the switching signal is only at about 8.05 s, two nonlinear ESOs produce a switching, which is designed to make the system run stably.

In the absence of external disturbance, the system can be obtained from the above simulation analysis and comparison. In the case of step response, the response speed of the system under the SADRC strategy is 32.56% higher than that under the PID control strategy, and the error is reduced by 1.67%. In the case of sine response, the error of the system under the SADRC strategy is 0.67% less than that under the PID control strategy. In the case of slope response, the error of the system under the SADRC strategy is reduced by 0.52% compared with that under the PID control strategy. In the case of custom response, the error of the system under the SADRC strategy is reduced by 0.17% compared with that under the PID control strategy. When the command signal is different, the traditional the PID parameters need to be greatly modified, while the SADRC parameters do not need to be modified, which saves the workload.

Research on the performance of digital hydraulic cylinder position control system under square wave external disturbance

To further verify the influence of the control strategy designed in this paper on the system performance, the external disturbance force of the system is set to square wave force. The maximum driving load of the digital hydraulic cylinder designed in this paper is 2 T, so the set square-wave force is 10000N. When the system is in the step and ramp command signal, the external disturbance of the system is added between 5 s ~ 6 s. When the system is in the sine and custom command signal, the external disturbance of the system is added between 1.5 s ~ 2.5 s and 2.5 s ~ 3.5 s respectively, and then the tracking characteristics of the system are observed.