Introduction

In the current competitive global market, the efficiency of production and distribution processes is crucial for the profitability and sustainability of manufacturing and logistics enterprises. Permutation flow shop vehicle routing problem (PFSVRP) is a complex scheduling and routing issue that is prevalent in industries such as automotive, electronics, and pharmaceuticals, where just-in-time production and delivery are essential. The optimization of PFSVRP can lead to reduced operational costs, minimized delivery times, and enhanced customer service levels, thereby providing a competitive edge in the market. This paper focuses on PFSVRP, aiming to minimize the total cost of production and transportation through the collaborative optimization of production scheduling and logistics transportation scheduling.

In this paper, PFSVRP is studied. The problem can be briefly described as follows: the orders are processed in the factory, the orders are produced according to the permutation flow shop scheduling problem (PFSP), and then the completed orders are transported to each customer by the vehicles. The objective function is to minimize the sum of production cost and transportation cost. The problem includes discrete manufacturing process and logistics transportation scheduling process. Among them, the discrete manufacturing process considers permutation flow shop scheduling problem; the logistics transportation scheduling process considers vehicle routing problem with time windows (VRPTW).

PFSVRP integrates the complexities of production scheduling with the logistical challenges of vehicle routing. Recent studies have explored innovative optimization techniques, focusing on sustainability, dynamic environments, and advanced algorithmic approaches. Here, we review recent studies that significantly contribute to the field: Abreu et al.1 developed a genetic algorithm for scheduling open shops with sequence-dependent setup times, offering a robust method for handling complex scheduling scenarios. Al-Behadili et al.2 focused on a multi-objective biased randomised iterated greedy for the robust permutation flow shop scheduling problem under disturbances, providing valuable insights into handling uncertainties in PFSVRP. Ali et al.3 addressed a multi-objective closed-loop supply chain under uncertainty, presenting an efficient Lagrangian relaxation reformulation using a neighborhood-based algorithm, which could be applied to PFSVRP for better optimization. Bargaoui et al.4 explored a novel chemical reaction optimization for the distributed permutation flowshop scheduling problem with makespan criterion, introducing a new heuristic approach that could be beneficial for PFSVRP. Bellio et al.5 implemented a two-stage multi-neighborhood simulated annealing for uncapacitated examination timetabling, demonstrating the effectiveness of simulated annealing in solving complex routing and scheduling problems. Fathollahi-Fard et al.6 presented a distributed permutation flow-shop considering sustainability criteria and real-time scheduling, aligning with the growing focus on sustainability in PFSVRP. Fu et al.7 tackled two-objective stochastic flow-shop scheduling with deteriorating and learning effect in an Industry 4.0-based manufacturing system, offering a forward-looking perspective on the integration of advanced manufacturing technologies with PFSVRP. Ghaleb et al.8 focused on real-time production scheduling in the Industry-4.0 context, addressing uncertainties in job arrivals and machines breakdowns, which is crucial for the dynamic nature of PFSVRP. Huang and Gu9 utilized a novel biogeography-based optimization algorithm for the distributed assembly permutation flow-shop scheduling problem, providing a innovative heuristic method that could be adapted to PFSVRP. Jing et al.10 developed local search-based metaheuristics for the robust distributed permutation flowshop problem, emphasizing the importance of robustness in scheduling and routing, a key aspect of PFSVRP.

In recent years, the issue of production and transportation scheduling has attracted the interest of many experts and scholars. Wang et al.11 studied the scheduling problem of a three-stage hybrid flow shop with distribution based on a practical pick-and-distribution system. In order to minimize the maximum delivery time, a mixed integer linear programming model was established. Marandi et al.12 introduced a new integrated scheduling problem of multi-plant production and distribution in supply chain management. This supply chain consisted of many factories that were connected together in the form of a network. The plant produced intermediate or finished goods and supplied them to other plants or end customers distributed in different geographic areas. The problem involved finding a production plan and vehicle routing solution at the same time to minimize the sum of delay costs and transportation costs. Ganii et al.13 studied the integrated scheduling problem of supply chain. A mixed integer nonlinear programming model was introduced, and three multi-objective meta-heuristic algorithms, namely multi-objective particle swarm optimization algorithm, non-dominated sorting genetic algorithm and multi-objective ant colony algorithm, were used to solve the problem. Govindan et al.14 developed a distribution network model in which the routing problem of multi-product vehicles with time Windows was combined as an operational decision with a strategic decision related to network design. In order to solve the model, particle swarm optimization, electromagnetic mechanism algorithm and artificial bee swarm were proposed and combined with variable neighborhood search. Martins et al.15 studied a combination problem of hybrid flow shop and vehicle routing. Aiming at minimizing the service time of the last customer, a partial random variable neighborhood decreasing algorithm was proposed.

Moons et al.16 investigated the job-level scheduling problem of integrated production and distribution, which explicitly took into account vehicle routing decisions in the distribution process. The existing literature on integrated production scheduling and vehicle routing was reviewed and classified. The problem characteristics and corresponding solving methods of the mathematical model were discussed, and the direction of further research was determined. Bahmani et al.17 established an integration model for the two-stage assembly flow shop scheduling problem and vehicle routing distribution problem under the soft time windows, and proposed an improved meta-heuristic algorithm based on whale optimization algorithm. Hou et al.18 proposed an integrated distributed production and distribution problem considering the time windows. An enhanced brainstorming optimization algorithm with a specific strategy was designed to deal with the problem under consideration. Yağmur et al.19 studied a joint production scheduling and outbound distribution planning problem. The goal was to determine the minimum total travel time for vehicles and the delays that might result from delayed delivery. A mixed integer programming formula was proposed. Qiu et al.20 proposed a consideration of hybrid flow workshop production and mixed integer linear programming model for multi-vehicle delivery with travel. An improved meme algorithm was proposed.

Zaied et al.21 reviewed PFSP with completion times and their mathematical models, and also reviewed and discussed most of the methods used to solve PFSP. Bhatt22 used two heuristics, either alone or in combination, to find a solution to PFSP. Wei et al.23 proposed a hybrid genetic simulated annealing algorithm to solve the flow shop scheduling problem. Zhang et al.24 proposed an adaptive step size cuckoo search algorithm based on dynamic balance factors. Firstly, iteration ratio parameters and adaptive ratio parameters were introduced. Then, dynamic balance factor parameters were introduced to adjust the weights of iteration ratio parameters and adaptive ratio parameters. Finally, combining with dynamic balance factors, the calculation method of parameter skewness value and adaptive step strategy were proposed.

Pan et al.25 modeled the multi-travel time-dependent vehicle routing problem with time windows. An iterative algorithm was developed to derive them efficiently. A hybrid meta-heuristic algorithm was designed, which used adaptive large neighborhood search for guided exploration and variable neighborhood descent for intensive development. Fan et al.26 proposed an integer programming model with minimum total cost for multi-depot vehicle routing under time-varying road network. To solve this problem, a hybrid genetic algorithm for variable neighborhood search was proposed. An adaptive neighborhood search frequency strategy and simulated annealing inferior solution acceptance mechanism were used to balance the diversity and exploitability of the iterative algorithm. Chen et al.27 studied the vehicle routing problem with time windows and delivery robot. An adaptive heuristic algorithm for large neighborhood search was proposed. Gmira et al.28 proposed a method for solving time-varying vehicle routing problems with time windows, in which the traveling speed was related to the section in the road network. This solution approach involved a tabu search heuristic.

Commonly used optimization algorithms include simulated annealing29, genetic algorithm30, particle swarm optimization31, ant colony optimization algorithm32 and bat algorithm33,34 Based on the basic principle of the salp swarm algorithm (SSA)35,36, this paper proposes an improved salp swarm algorithm (ISSA) to solve the PFSVRP problem. For the discrete manufacturing process, local search operation is introduced; for the logistics transportation scheduling process, the salp swarm algorithm is applied to the discrete ___domain, and local search strategy is adopted to enhance the search effect of the algorithm. The algorithm is compared with simulated annealing, genetic algorithm and particle swarm algorithm, and the experimental results are given.

The remainder of this paper is organized as follows: Section "Problem description and mathematical model" introduces the problem description and mathematical model. Section "Algorithm design" gives the algorithm to solve the testing problem. The simulation analysis results are presented in Section "Simulation analysis". Section “Conclusion” draws the conclusion.

Problem description and mathematical model

Problem description

This paper studies the PFSVRP problem. The problem can be described as follows: the orders are processed in the factory, \(n\) orders are processed on \(m\) machines, each order has \(m\) processes, each order is processed on different machines, the order is processed in the same order on all machines, each order has its due date, and then the completed orders are delivered to each customer by the vehicles. The objective function is to minimize the sum of production cost and transportation cost. The problem includes discrete manufacturing process and logistics transportation scheduling process. Among them, the discrete manufacturing process considers permutation flow shop scheduling problem37; the logistics transportation scheduling process takes into account vehicle routing problem with time windows38.

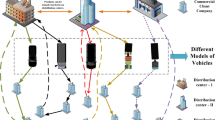
Figure 1 shows the schematic diagram of PFSVRP problem, including 6 orders, 1 factory and 6 customers with 3 processing machines and 3 vehicles.

Fig. 1
figure 1

The schematic diagram of PFSVRP problem.

Full size image

Table 1 presents an example of PFSP. In total, 4 orders and 3 processing machines are included. Among them, each order has 3 processes. As shown in Table 1, the number corresponding to the order represents the processing time of the order on the machine. The unit of processing time is second(s).

Table 1 An example for PFSP.
Full size table

The PFSVRP problem makes the following assumptions.

  1. 1)

    All orders are available at zero time.

  2. 2)

    The machine configuration constitutes a flow shop.

  3. 3)

    The machine is always available, there is no breakdown time and maintenance time.

  4. 4)

    The machine setup time can be ignored.

  5. 5)

    The order is not allowed to be preempted, that is, once the order processing is started, it cannot be interrupted.

  6. 6)

    Assume that the order start time is ignored.

  7. 7)

    Each order belongs to a different customer.

  8. 8)

    The due date of each order is greater than or equal to its completion time.

  9. 9)

    The capacity of each vehicle is the same.

  10. 10)

    Each customer has its own time window.

Mathematical model

Mathematical symbols

The mathematical symbols and meanings of the PFSVRP problem are shown in Table 2.

Table 2 Mathematical symbols for PFSVRP.
Full size table

Objective function

The objective function is to minimize the sum of production cost and transportation cost.

$$\begin{gathered} \min \, F = \, \sum\limits_{i = 1}^{n} {(\max \{ d_{i} - C_{i} ,0\} )dc} + \hfill \\ \, \sum\limits_{i = 1}^{n} {OR_{i} C_{i} c{\prime} } + \hfill \\ \, \sum\limits_{k = 1}^{K} {\sum\limits_{i = 1}^{n} {(y_{ki} + y_{ki}^{^{\prime\prime}} )d_{i}{\prime} b_{k}{\prime} } } + \hfill \\ \, \sum\limits_{k = 1}^{K} {\sum\limits_{i = 1}^{n} {\sum\limits_{l = 1}^{n} {y_{kil}{\prime} d_{il}^{^{\prime\prime}} b_{k}{\prime} } } } \hfill \\ \end{gathered}$$
(1)

Among them, the first item in formula (1) is the delay cost; the second item is the production cost; the third and fourth items are the transportation cost.

Constraints

$$C_{\max } \ge c_{im} , \, i = 1, \ldots ,n$$
(2)
$$\sum\limits_{r = 1}^{n} {x_{ir} } = 1, \, i = 1, \ldots ,n$$
(3)
$$\sum\limits_{i = 1}^{n} {x_{ir} } = 1, \, r = 1, \ldots ,n$$
(4)
$$c_{11} \ge \sum\limits_{i = 1}^{n} {x_{i1} p_{i1} }$$
(5)
$$c_{(h + 1)j} \ge c_{hj} + \sum\limits_{i = 1}^{n} {x_{i(r + 1)} p_{ij} } , \, h,r = 1, \ldots ,n - 1,j = 1, \ldots ,m$$
(6)
$$c_{h(j + 1)} \ge c_{hj} + \sum\limits_{i = 1}^{n} {x_{ir} p_{i(j + 1)} } , \, h,r = 1, \ldots ,n,j = 1, \ldots ,m - 1$$
(7)
$$c_{hj} > 0, \, h = 1, \ldots ,n,j = 1, \ldots ,m$$
(8)
$$x_{ir} \in \{ 0,1\} , \, i = 1, \ldots ,n,r = 1, \ldots ,n$$
(9)
$$\sum\limits_{i = 1}^{n} {y_{ki} } \le 1, \, k = 1,2, \ldots ,K$$
(10)
$$y_{ki} + \sum\limits_{l = 1}^{n} {y_{kli}{\prime} } = \sum\limits_{l = 1}^{n} {y_{kil}{\prime} } + y_{ki}^{^{\prime\prime}} , \, k = 1,2, \ldots ,K, \, i = 1,2, \ldots ,n$$
(11)
$$\sum\limits_{i = 1}^{n} {(y_{ki} + y_{ki}^{^{\prime\prime}} )OR_{i} } + \sum\limits_{i = 1}^{n} {\sum\limits_{l = 1}^{n} {y_{kil}{\prime} OR_{l} } } \le Q, \, k = 1,2, \ldots ,K$$
(12)
$$C_{i} \le C_{\max } , \, i = 1,2, \ldots ,n$$
(13)
$$C_{i} \le d_{i} , \, i = 1,2, \ldots ,n$$
(14)
$$\sum\limits_{{i,l \in S_{k} }} {y_{kil}{\prime} } \le \left| {S_{k} } \right| - 1, \, k = 1,2, \ldots ,K$$
(15)
$$a_{i} \le st_{i} \le b_{i} , \, i = 1,2, \ldots ,n$$
(16)

Here, formula (2) ensures that the maximum completion time is greater than or equal to the completion time of the order on the last machine; formula (3) and (4) ensure that each order in a sequence can occur only once; formula (5) represents the completion time of the first order processed on the first machine; formula (6) ensures that one order cannot be processed by multiple machines at the same time; formula (7) ensures that one machine can only process one order at the same time; formula (8) ensures that the completion time of all processes is greater than zero; formula (9) ensures the value range of decision variables; formula (10) ensures that each vehicle can only transport one order at most; formula (11) ensures that the vehicle is continuous during transportation; formula (12) ensures that the order of vehicle transportation does not exceed its maximum of its capacity; formula (13) ensures that the completion time of each order shall not exceed the maximum completion time; formula (14) ensures that the completion time of each order is less than or equal to its due date; formula (15) ensures that the vehicle does not generate sub-loops during transportation; formula (16) ensures the constraints of time windows for each customer. Here, \(st_{i}\) (actual service start time) is a decision variable representing the service start time for customer \(i\). \(st_{i}\) is not directly calculated from the preceding equations but is determined during the algorithm’s solution process based on vehicle scheduling and route arrangement. The algorithm will consider all customer service time window constraints (as shown in Eq. (16)) and other relevant constraints to determine the \(st_{i}\) for each customer, thereby optimizing the entire logistics delivery plan.

Algorithm design

Coding and decoding of Solutions

Coding of solutions

This section mainly introduces the coding of the solution of PFSP and the solution of VRPTW. The coding of the solution of PFSP consists of two parts, operations sequencing (OS) and machines selection (MS). Here, \(TN = nm\). The coding of the solution of VRPTW contains vehicle routing (VR). The coding of the solution is shown in Fig. 2. Here, the dimension of MS is \(TN\), the dimension of OS is \(TN\) and the dimension of VR is \(n + K - 1\).

  • 1. Operations sequence (OS)

Fig. 2
figure 2

Coding of the solutions.

Full size image

The value on each bit of operations sequencing is represented by a number. For example, the number 1 indicates the first order, and the number 4 indicates the fourth order. The number of occurrences of each order number is equal to the number of machines \(m\). For the example in Table 1, operations sequence can be encoded as OS = [1 4 3 2 1 4 3 2 1 4 3 2], as shown in Fig. 3.

  • 2. Machines Selection (MS)

Fig. 3
figure 3

Coding of solutions for the example of Table 1.

Full size image

The value on each bit of machines selection is represented by the machine number. Based on the selected operation, determine the machine number to which the order is to be processed. The number of occurrences of each machine number is equal to the number of orders \(n\). For the example in Table 1, machines selection can be encoded as MS = [1 1 1 1 2 2 2 2 3 3 3 3], as shown in Fig. 3.

  • 3. Vehicle Routing (VR)

The vertex number is \(n + 1\) (including customers and 1 factory), and the vehicle number is \(K\), and the dimension is \(n + K - 1\). Vehicle routing is coded as a substitution of \((0,1,2, \cdots ,n + K - 2)\). As shown in Fig. 1, \(n = 6\), \(K = 3\), the vehicle routing can be expressed as \((1,2,0,3,4,7,5,6)\), where element \(0\) and elements greater than \(n\) are considered to be the factory \(0\).

Decoding of solutions

This section introduces the decoding of the solution of VRPTW.

The part of vehicle routing is decoded. The element whose value is \(0\) and the elements whose values are greater than \(n\) are both considered to be the factory \(0\). The front and end of vehicle routing are added \(0\) respectively to form a complete VRPTW path. The points passing between the two \(0\) constitutes the access path of a vehicle, which is the decoding of vehicle routing. As shown in Fig. 1, \(n = 6\), \(K = 3\), vehicle routing is \((1,2,0,3,4,7,5,6)\), and its corresponding access path is \((0,1,2,0,3,4,0,5,6,0)\). Therefore, the access path of vehicle 1 is \((0,1,2,0)\), and the access path of vehicle 2 is \((0,3,4,0)\), and the access path of vehicle 3 is \((0,5,6,0)\).

SSA

Salp swarm algorithm is a bio-heuristic optimization algorithm that simulates the swarm behavior of salp swarm. Salps are Marine organisms that navigate and forage in the ocean in groups, a behavior known as a salp chain. The design of salp swarm algorithm is inspired by this group behavior of salps, in particular how they achieve efficient movement and foraging through rapid and coordinated changes.

SSA can be expressed by the following formulas.

$$x_{j}^{1} = \left\{ \begin{gathered} F_{j} + c_{1} ((ub_{j} - lb_{j} )c_{2} + lb_{j} ){ 0}{\text{.5}} \le c_{3} < 1 \hfill \\ F_{j} - c_{1} ((ub_{j} - lb_{j} )c_{2} + lb_{j} ) \, 0 < c_{3} < 0.5 \hfill \\ \end{gathered} \right.$$
(17)
$$c_{1} = 2e^{{ - (\frac{4l}{L})^{2} }}$$
(18)
$$x_{j}^{i} = \frac{1}{2}(x_{j}^{i} + x_{j}^{i - 1} ), \, i \ge 2$$
(19)

Here, \(x_{j}^{1}\) represents the position of the first salp (the leader) in the dimension \(j\). \(F_{j}\) is the position of the food source in the dimension \(j\). \(ub_{j}\) shows the upper bound of the dimension \(j\), and \(lb_{j}\) shows the lower bound of the dimension \(j\). \(c_{2}\) and \(c_{3}\) are the random numbers with the range from zero to one. \(l\) is the number of the current iteration, and \(L\) is the maximum number of iterations. \(x_{j}^{i}\) represents the position of the salp \(i\) (the follower) in the dimension \(j\).

ISSA

ISSA to solve PFSP and ISSA to solve VRPTW are detailed below.

ISSA to solve PFSP

This section describes in detail ISSA to solve PFSP. On the basis of the SSA , local search operation is incorporated, forming an ISSA. Below is a detailed description of the incorporated local search operation.

Select individuals from the population whose fitness values are in the top 20% for local search operation.

For each selected individual, follow these steps.

  • (1) Initialize local search operation parameters.

Set the iteration number \(t\) to start from 1, the maximum number of jobs to be removed as \(D_{\max } = 7\), the number of jobs to be deleted as \(D\), the selection probability for each neighborhood \(q\) as \(P_{q} = 1/D_{\max }\). The current temperature is \(Temp = (T_{0} *\sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{m} {p_{ij} } } )/(n*m*10)\), where \(T_{0}\) is the initial temperature. The maximum number of iterations is \(t_{\max } = n*(n - 1)\). The initial solution is \(\pi_{0}\).

  • (2) Local search process.

From iteration number \(t\) to the maximum number of iterations tmax, based on the current selection probability \(P_{q}\) for each neighborhood, use the roulette method to choose a neighborhood type, determine the size of \(D\), and the neighborhood scale size is \(N(D)\). Select a position \(r\) from the current solution \(\pi\), and then start from this position, continuously remove \(D\) jobs. If \(n - r + 1 \ge D\), then, continuously remove \(D\) jobs \(\pi (r),\pi (r + 1),...,\pi (r + D - 1)\); otherwise, continuously remove jobs \(\pi (r),...,\pi (n)\), and then continuously remove jobs \(\pi (1),...,\pi (D - (n - r + 1))\). Starting from the job \(\pi (r)\), insert it into the best position in the remaining part of the solution, and repeat this process until all jobs are inserted, and thus obtain a new solution \(\pi^{\prime}\). If the objective function value of the new solution \(\pi^{\prime}\) is better than the current solution \(\pi\), then update the current solution \(\pi\) to \(\pi^{\prime}\), and update the neighborhood selection probability, i.e., \(P_{q} = P_{q} + 1/N(D)\).

  • (3) Acceptance criterion.

Update the current temperature, i.e., \(T{\text{emp}} = (T_{0} *\sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{m} {p_{ij} } } )/(n*m*10)\). If the objective function value of the solution \(\pi\) is better than the initial solution \(\pi_{0}\), the acceptance criterion is \(random \le \exp ( - (C_{\max } (\pi ) - C_{\max } (\pi_{0} ))/Temp)\). Where \(C_{\max } (\pi )\) is the maximum completion time of the solution \(\pi\), \(C_{\max } (\pi_{0} )\) is the maximum completion time of the solution \(\pi_{0}\), and \(random\) is a random number, \(random \in [0,1]\). If the acceptance criterion is met, then update the solution \(\pi\) to \(\pi_{0}\).

  • (4) Termination condition.

After completing the local search and acceptance criterion for the individual, the entire optimization process ends.

The pseudocode of local search operation applied in ISSA to solve PFSP is shown in Pseudocode 1.

Pseudocode 1
figure a

Local search operation applied in ISSA to solve PFSP.

Full size image

The steps of ISSA to solve PFSP are shown in Algorithm 1.

Algorithm 1
figure b

ISSA to solve PFSP.

Full size image

ISSA to solve VRPTW

According to the formulas (17), (18) and (19), we redefine the formulas in the discrete ___domain as follows.

Formula (17) can be transformed in the following. Define the food source \(F\) as \(x_{*}\) which refers to the best solution. \(x_{1}\) is the leader which is the first salp. Suppose \(c_{0}\) as \((ub - lb)c_{2} + lb\), where \(c_{2} \in [0,1]\). Here, \(c_{r}\) represents \(2 \times c_{0} \times random\), where \(random \in [0,1]\). However, formula (18) in the continuous ___domain is unchanged. We directly use formula (18) in the discrete ___domain. If \(c_{1} \times c_{0} > c_{r}\), \(x_{1} = x_{*}\). Otherwise, \(x_{1}\) remains unchanged.

Formula (19) can be described as follows. \(x_{i}\) is the \(i\) th follower salp where \(i \ge 2\). Randomly generate \(rand\), where \(rand \in [0,1]\). If \(rand > 0.5\), \(x_{i} = x_{i - 1}\). Here, \(x_{i - 1}\) refers to the last salp. Otherwise, \(x_{i}\) stays the same.

Local search method adopts the large neighborhood search algorithm.

The steps of ISSA used to solve VRPTW are shown in Algorithm 2.

Algorithm 2
figure c

ISSA to solve VRPTW.

Full size image

Simulation analysis

The implementation is programed in Matlab and run on an Intel i7 12700H computer (2.70 GHz CPU) with 16.00 GB RAM.

Performance test of algorithms

The examples of PFSP uses 120 benchmarks39 of Taillard’s instances of permutation flow shop scheduling problem. The goal of PFSP is to minimize the makepan. ISSA is compared with simulated annealing algorithm (SA)40, genetic algorithm (GA)41 and particle swarm algorithm (PSO)42, and the comparison of the algorithms for PFSP is shown in Table 3, where the deviation is defined as \(deviation = \frac{ISSA - BKS}{{BKS}} \times 100\%\). It can be concluded that 57 of the 120 results are obtained by ISSA in precision. Compared with SA, 76 optimal solutions can be obtained by ISSA. Comparing ISSA with GA, 88 optimal solutions can be obtained. Comparing ISSA with PSO, 106 optimal solutions can be obtained. There are 85 results with a deviation of less than 1%.

Table 3 Comparison of the algorithms for PFSP.
Full size table

The iteration convergence times of ISSA solving PFSP to obtain the optimal solution are shown in Table 4. The iteration convergence times usually refers to the number of iterative steps required for an iterative algorithm to achieve a predetermined accuracy or satisfy convergence conditions.

Table 4 The iteration convergence times of ISSA solving PFSP.
Full size table

Based on the iteration convergence times in Table 4, Convergence curve graph is shown in Fig. 4. It can more intuitively display the convergence times.

Fig. 4
figure 4

Convergence curve graph based on Table 4.

Full size image

Examples of VRPTW can be described as follows: V001 to V090 from Solomon benchmark, V091 to V120 from Gehring & Homberger benchmark, as shown in Table 5.

Table 5 Examples of VRPTW.
Full size table

VRPTW aims to minimize the number of vehicles needed (NV) and the total distance (TD). ISSA is compared with SA, GA and PSO and the comparison of the algorithms for VRPTW is shown in Table 6. It can be concluded that among 120 results, 91 better results are obtained by ISSA on NV and TD in precision. On NV and TD, ISSA compared with SA, 113 better results are obtained. 94 better results are obtained by ISSA compared to GA. 104 better results are obtained by ISSA compared to PSO.

Table 6 Comparison of the algorithms for VRPTW.
Full size table

Optimal solution for V091 can be shown as follows.

Optimal Solution:

Number of Vehicles: 20, Total Distances: 2704.5678, Number of Violated Constraint Routes: 0, Number of Violated Constraint Customers: 0

Route1: 0- > 190- > 5- > 10- > 193- > 46- > 128- > 106- > 167- > 34- > 95- > 158- > 0.

Route2: 0- > 177- > 3- > 88- > 8- > 186- > 127- > 98- > 157- > 137- > 183- > 0.

Route3: 0- > 32- > 171- > 65- > 86- > 115- > 94- > 51- > 174- > 136- > 189- > 0.

Route4: 0- > 114- > 159- > 38- > 150- > 22- > 151- > 16- > 140- > 187- > 142- > 111- > 63- > 56- > 0.

Route5: 0- > 170- > 134- > 50- > 156- > 112- > 168- > 79- > 29- > 87- > 42- > 123- > 0.

Route6: 0- > 30- > 120- > 19- > 192- > 196- > 97- > 14- > 96- > 130- > 28- > 74- > 149- > 0.

Route7: 0- > 21- > 23- > 182- > 75- > 163- > 194- > 145- > 195- > 52- > 92- > 0.

Route8: 0- > 62- > 131- > 44- > 102- > 146- > 68- > 76- > 0.

Route9: 0- > 57- > 118- > 83- > 143- > 176- > 36- > 33- > 121- > 165- > 188- > 108- > 0.

Route10: 0- > 148- > 103- > 197- > 124- > 141- > 69- > 200- > 0.

Route11: 0- > 113- > 155- > 78- > 175- > 13- > 43- > 2- > 90- > 67- > 39- > 107- > 0.

Route12: 0- > 93- > 55- > 135- > 58- > 184- > 199- > 37- > 81- > 138- > 0.

Route13: 0- > 60- > 82- > 180- > 84- > 191- > 125- > 4- > 72- > 17- > 0.

Route14: 0- > 45- > 178- > 27- > 173- > 154- > 24- > 61- > 100- > 64- > 179- > 109- > 0.

Route15: 0- > 164- > 66- > 147- > 160- > 47- > 91- > 70- > 0.

Route16: 0- > 73- > 116- > 12- > 129- > 11- > 6- > 122- > 139- > 0.

Route17: 0- > 101- > 144- > 119- > 166- > 35- > 126- > 71- > 9- > 1- > 99- > 53- > 0.

Route18: 0- > 161- > 104- > 18- > 54- > 185- > 132- > 7- > 181- > 117- > 49- > 0.

Route19: 0- > 133- > 48- > 26- > 152- > 40- > 153- > 169- > 89- > 105- > 15- > 59- > 198- > 0.

Route20: 0- > 20- > 41- > 85- > 80- > 31- > 25- > 172- > 77- > 110- > 162- > 0.

Optimal delivery route solved by ISSA for V091 is shown as Fig. 5.

Fig. 5
figure 5

Optimal delivery route solved by ISSA for V091.

Full size image

Optimal solution for V096 can be shown as follows.

Optimal Solution:

Number of Vehicles: 20, Total Distances: 2701.0354, Number of Violated Constraint Routes: 0, Number of Violated Constraint Customers: 0

Route1: 0- > 73- > 116- > 12- > 129- > 11- > 6- > 122- > 139- > 0.

Route2: 0- > 20- > 41- > 85- > 80- > 31- > 25- > 172- > 77- > 110- > 162- > 0.

Route3: 0- > 32- > 171- > 65- > 86- > 115- > 94- > 51- > 174- > 136- > 189- > 0.

Route4: 0- > 164- > 66- > 147- > 160- > 47- > 91- > 70- > 0.

Route5: 0- > 60- > 82- > 180- > 84- > 191- > 125- > 4- > 72- > 165- > 188- > 108- > 0.

Route6: 0- > 177- > 3- > 88- > 8- > 186- > 127- > 98- > 157- > 138- > 0.

Route7: 0- > 133- > 48- > 26- > 152- > 40- > 153- > 169- > 89- > 105- > 15- > 59- > 198- > 0.

Route8: 0- > 114- > 159- > 38- > 150- > 22- > 151- > 16- > 140- > 187- > 142- > 111- > 63- > 56- > 0.

Route9: 0- > 170- > 134- > 50- > 156- > 112- > 168- > 79- > 29- > 87- > 42- > 123- > 0.

Route10: 0- > 190- > 5- > 10- > 193- > 46- > 128- > 106- > 167- > 34- > 95- > 158- > 0.

Route11: 0- > 45- > 178- > 27- > 173- > 154- > 24- > 61- > 100- > 64- > 179- > 109- > 0.

Route12: 0- > 113- > 155- > 78- > 175- > 13- > 43- > 2- > 90- > 67- > 39- > 107- > 0.

Route13: 0- > 93- > 55- > 135- > 58- > 184- > 199- > 37- > 81- > 137- > 0.

Route14: 0- > 30- > 120- > 19- > 192- > 196- > 97- > 14- > 96- > 130- > 28- > 74- > 149- > 0.

Route15: 0- > 148- > 103- > 197- > 124- > 141- > 69- > 200- > 0.

Route16: 0- > 101- > 144- > 119- > 166- > 35- > 126- > 71- > 9- > 1- > 99- > 53- > 0.

Route17: 0- > 21- > 23- > 182- > 75- > 163- > 194- > 145- > 195- > 52- > 92- > 0.

Route18: 0- > 57- > 118- > 83- > 143- > 176- > 36- > 33- > 121- > 17- > 0.

Route19: 0- > 62- > 131- > 44- > 102- > 146- > 68- > 76- > 0.

Route20: 0- > 161- > 104- > 18- > 54- > 185- > 132- > 7- > 181- > 117- > 49- > 183- > 0.

Optimal delivery route solved by ISSA for V096 is shown as Fig. 6.

Fig. 6
figure 6

Optimal delivery route solved by ISSA for V096.

Full size image

Experimental results and analysis

Examples of PFSVRP problem contain examples of PFSP and examples of VRPTW, as shown in Table 7.

Table 7 Examples of PFSVRP problem.
Full size table

The comparison of the algorithms for PFSVRP problem is shown in Table 8. Here, \(c{\prime} = 100\), \(b_{k}{\prime} = 300\). ISSA is compared with SA, GA and PSO. It can be concluded that among 120 results, 87 better results are obtained by ISSA. 111 better results are obtained for ISSA compared to SA. 90 better results are obtained by ISSA compared with GA. ISSA compared with PSO, 108 better results are obtained. We calculate the performance improvement percentage of ISSA algorithm. The performance improvement percentage of the ISSA algorithm can be calculated using the following formula: \(PIP_{ISSA} = \frac{CA - ISSA}{{CA}} \times 100\%\). Here, \(CA\) represents compared algorithms (SA, GA, and PSO). PIS represents the percentage performance improvement of ISSA algorithm compared to SA algorithm. PIG represents the percentage performance improvement of ISSA algorithm compared to GA algorithm. PIP represents the percentage performance improvement of ISSA algorithm compared to PSO algorithm. In this way, the performance advantages of ISSA algorithm compared to other algorithms can be visually demonstrated.

Table 8 Comparison of the algorithms for PFSVRP problem.
Full size table

Conclusion

In this study, we proposed an Improved Salp Swarm Algorithm (ISSA) to address the Permutation Flow Shop Vehicle Routing Problem (PFSVRP). By comparing ISSA with Simulated Annealing (SA), Genetic Algorithm (GA), and Particle Swarm Optimization (PSO), ISSA achieved relatively better results in multiple instances. The practical application of ISSA lies in its direct applicability to real-world industrial problems involving production scheduling and logistics distribution, especially in industries that require just-in-time production and delivery, such as automotive manufacturing and pharmaceuticals.

A direct application of the ISSA algorithm is in the automotive manufacturing industry, where production efficiency and logistics costs directly impact the competitiveness of enterprises. For example, an automobile manufacturing plant may need to schedule the production of multiple orders on several production lines and ensure that the completed orders are delivered to customers on time. The ISSA algorithm can help the factory optimize production scheduling and vehicle delivery routes, reducing the total cost of production and transportation while shortening delivery times. Specifically, the algorithm can determine which production line to process which order and the best delivery sequence for vehicles, thereby achieving collaborative optimization of production and logistics.

For instance, suppose an automobile manufacturing plant has multiple orders that need to be processed on three production lines and the finished components need to be delivered to different customers. The ISSA algorithm can provide the factory with an optimal production and delivery plan that minimizes the total production and logistics costs while meeting customer delivery time requirements. In this way, the ISSA algorithm not only improves production efficiency but also enhances customer satisfaction, providing strong support for the enterprise in fierce market competition.

Future research will explore the integration of ISSA with other intelligent algorithms to solve this problem.