Introduction

Nowadays, with the rapid advancement of industrialization, a significant portion of the products in the industrial chain relies on maritime transportation1,2. According to data from the United Nations Conference on Trade and Development (UNCTAD), maritime transportation is responsible for approximately 80% of international trade goods annually3. With the continuous development of international trade, various challenging issues in maritime transportation are increasingly gaining the attention of researchers. A typical example of these issues is the Maritime Inventory Routing Problem (MIRP)4.

MIRP is a variant of the Inventory Routing Problem (IRP), which is a complex optimization challenge that integrates inventory management with route planning5. IRP requires algorithms to determine the timing and quantity of deliveries to each customer, along with the routing and scheduling of delivery vehicles, to meet the demand for goods in each time period6. MIRP is a special case of IRP in the maritime context, where the task is to optimize the scheduling and routing of cargo ships while managing the inventory levels at the associated ports. Compared to land-based IRPs, MIRPs have the following differences: First, there is no concept of warehouses in MIRPs, and MIRPs involves multiple supply and demand ports, allowing vessels to start and end operations at any port. Second, due to the long-duration or long-distance journeys in maritime transportation, MIRPs require planning multiple sub-periods within the entire journey. Additionally, unlike traditional IRPs that typically involve a fixed number of homogeneous fleets, MIRPs often employ heterogeneous fleets with variable numbers of vessels4. Due to the complexity of maritime transportation, MIRP is actually a highly challenging Mixed-Integer Nonlinear Programming (MINLP) problem7.

Current approaches for solving MIRPs can be broadly divided into two categories: exact algorithms and heuristic algorithms8. Exact algorithms ,such as branch-and-bound9 and dynamic programming10, provide a precise solution to the problem. However, for complex combinatorial optimization problems like MIRPs and IRPs, these exact algorithms often face the issue of combinatorial explosion as the problem size increases. Heuristic algorithms are methods for finding solutions to problems with the help of empirical rules and heuristic strategies. Although heuristic algorithms do not guarantee an optimal solution, they can provide sufficiently good approximate solutions within a reasonable timeframe. Therefore, heuristic algorithms are suitable for solving large-scale or complex problems that are difficult to solve exactly. Because of their robustness and powerful search capabilities, heuristic algorithms have been successfully applied to solve optimization problems in many application areas, including IRPs and MIRPs11,12,13.

However, existing heuristic-based MIRP optimization algorithms still have some limitations. On the one hand, most of the existing heuristic algorithms use single-objective optimization models when solving MIRPs, typically using transportation cost as the optimization objective14,15. Some algorithms consider multiple objectives (such as transportation cost, time cost, and inventory cost) when constructing the problem model. However, during the optimization process, these multiple objectives are still integrated into a single objective function for solving. Essentially, these algorithms are also single-objective optimization algorithms7,16. There are often conflicts between the multiple objectives considered in MIRPs. Single-objective optimization algorithms cannot obtain an optimal solution that simultaneously optimizes multiple conflicting objectives. In such cases, multi-objective evolutionary algorithms (MOEAs) demonstrate significant potential for solving MIRPs due to their ability to simultaneously optimize conflicting objectives. Furthermore, among the few existing multi-objective optimization methods for MIRPs, it is rare to find studies that consider environmental factors such as greenhouse gas emissions as a separate objective. As global trade continues to expand, greenhouse gas emissions from maritime transportation are steadily rising. These emissions not only exacerbate climate change but also harm marine ecosystems. Therefore, integrating environmental factors into multi-objective optimization models has become a crucial consideration when addressing MIRPs17,18.

On the other hand, a common challenge when applying MOEAs to real-world problems is designing efficient encoding mechanisms and search operators. Most evolutionary algorithm-based MIRP optimization approaches use traditional fixed-length encoding mechanisms19. Specifically, in fixed-length encoding mechanisms, the encoding length for different solutions (schedules) is uniform. However, as the problem size expands, the encoding length increases exponentially, significantly raising the algorithm’s computational complexity. Therefore, designing efficient encoding methods has become a pressing issue when using evolutionary algorithms to solve MIRPs. Additionally, when optimizing complex constrained problems like MIRPs, MOEAs are prone to issues such as premature convergence or failure to find feasible solutions. Therefore, designing efficient search operators that leverage ___domain-specific knowledge to guide individuals toward feasible regions, while balancing convergence and diversity, is a key factor affecting the performance of MOEAs.

To address the above issues, this paper proposes a multi-population-based multi-objective evolutionary algorithm (MP-MOEA) to solve MIRPs. Traditional MIRPs typically focus only on transportation and time costs, neglecting environmental factors such as greenhouse gas emissions. MP-MOEA adopts a bi-objective optimization model that not only considers total transportation costs but also introduces greenhouse gas emissions as an independent optimization objective. To improve the algorithm’s search efficiency, MP-MOEA introduces a multi-population-based initialization strategy that employs a three-level dynamic encoding mechanism. This strategy generates multiple individual populations during the initialization phase to enhance population diversity. Furthermore, compared to the fixed-length encoding mechanism commonly used in evolutionary algorithms, the proposed three-level dynamic encoding mechanism effectively reduces the encoding length, thereby lowering the difficulty of problem-solving. To balance population diversity and convergence, this paper introduces three search operators: a hybrid crossover operator, a contribution-based mutation operator, and an individual modification operator. Specifically, the hybrid crossover operator applies two different crossover methods at various stages of MP-MOEA to balance global and local search. The contribution-based mutation operator guides the mutation direction of individuals by calculating their contribution values. The individual modification operator adjusts infeasible individuals based on vessel routes and loading/unloading operations, aiming to increase the proportion of feasible solutions in the individual population. To validate the effectiveness of the proposed algorithm, MP-MOEA has been compared with five state-of-the-art MOEAs on six test cases across three different scales. The experimental results demonstrate the effectiveness of the proposed algorithm. The main contributions of this paper are as follows:

  1. 1.

    Construction of a bi-objective MIRP model that considers total transportation costs and greenhouse gas emissions.

  2. 2.

    A multi-population-based initialization strategy employing a dynamic three-level encoding mechanism is introduced to maintain population diversity and reduce the encoding length.

  3. 3.

    A hybrid crossover operator, a contribution-based mutation operator, and an individual modification operator are designed to improve the search efficiency of the algorithm.

The rest of this paper is organized as follows: Section 2 reviews the existing research on solving IRPs and MIRPs with MOEAs. Section 3 provides a detailed description of the problem formulation. Section 4 elaborates on the proposed algorithm and key operators. Section 5 presents the experimental results and the corresponding analysis. Section 6 offers concluding remarks.

Literature review

As IRPs and MIRPs become increasingly complex, traditional exact algorithms struggle to meet problem-solving demands. Consequently, most current works on IRPs and MIRPs are designed based on heuristic algorithms. Among these heuristic algorithms, MOEAs have been successfully applied to solving IRPs and MIRPs due to their ability to simultaneously consider multiple conflicting objectives, as well as their flexibility and robustness.

Solving IRPs problems using MOEAs

Azuma et al.20 applied the improved version of the strength Pareto evolutionary algorithm 2 (SPEA2), a classic and efficient MOEA, to solve IRPs . In this work, a bi-objective optimization model that simultaneously minimizes inventory costs and transportation costs was adopted. Lv et al.21employed a multi-objective genetic algorithm (GA) to solve IRPs, aiming to minimize inventory, ordering, and transportation costs. The proposed algorithm utilized an elitist preservation strategy and adaptive adjustment strategy to overcome the deficiencies in local search capabilities of GAs, thereby enhancing the algorithm’s convergence speed and global optimization ability. Dongseop22 explored the ___location inventory routing problem (LIRP) with a focus on the time satisfaction of retailers and customers. The first objective of the studied LIRP was to minimize the fixed cost, inventory cost, and routing cost of facility ___location, while the second objective was to maximize the time satisfaction of retailers and customers.Then, an improved GA was introduced to solve the above-mentioned LIRP. Yan and Zhang23 introduced a multi-objective vehicle routing problem model that incorporates soft time window constraints, detailing the earliest and latest service times for customers. Service delivered before the earliest time leads to additional inventory costs, and service provided after the latest time results in penalties. The model is designed to optimize two objectives: minimizing the total transportation costs and minimizing the fleet size required. To tackle this multi-objective optimization problem, an enhanced GA was employed. Li et al.24investigated the ___location-routing-inventory problem with a time window constraint (LRIPTW). This paper devised an optimization model incorporating a soft time window constraint (STW) that concurrently optimizes multiple objectives within the cold chain logistics network, including ___location costs, inventory costs, transportation costs, and penalty costs. Subsequently, an improved multi-objective ant colony optimization algorithm (MACO) was adopted to solve the aforementioned problem.

For IRPs, some studies have already considered environmental factors in problem modeling25,26 developed a bi-objective optimization model for the multi-product and multi-period inventory routing problem, aiming to minimize both transportation costs and greenhouse gas emissions. Alinaghian and Zamani27 proposed a new bi-objective model for green inventory routing problem with the heterogeneous fleet. The first objective function is to minimize the emissions of greenhouse gas pollutants. The second objective function is to minimize the total cost which consists of four parts:the cost of fuel consumed, drivers’wages, the fixed cost of using vehicles and the cost of keeping inventory in the customers’ warehouses.Al-E-Hashem et al.28 have proposed a bi-objective optimization model for IRPs. The first objective of this model is to minimize the expected supply chain costs. The second objective is to minimize the number of vehicles and greenhouse gas emissions.

Solving MIRPs problems using MOEAs

For MIRPs, most of the existing research focuses on constructing single-objective optimization models that aim to minimize total transportation costs7,29,30. However, the inherent complexity of MIRPs means that single-objective optimization models fall short of offering comprehensive solutions. Consequently, the adoption of multi-objective optimization models tailored for MIRPs, along with the deployment of multi-objective evolutionary algorithms to address these multi-objective problems, is garnering growing interest among researchers. Yang et al.31 developed a bi-objective optimization model tailored for the shuttle tanker scheduling problem. This model aims to minimize total operational costs while maximizing system reliability. To tackle this dual-objective optimization problem, the authors introduced an enhanced non-dominated sorting genetic algorithm (NSGAII) incorporating a differential evolution operator. Wibisono and Jittamai2 constructed a bi-objective optimization model for MIRPs, with the proposed objectives being to minimize costs and to minimize the proportional sharing that reflects a fair distribution of total costs. Moreover, an improved GA was employed in their study to solve the aforementioned optimization problem.

Currently, the environmental pollution caused by maritime transportation is of great concern to the international community. However, a review of the literature reveals that research on incorporating environmental factors into multi-objective optimization models for MIRPs is quite limited. Therefore, this paper constructs a bi-objective optimization model for MIRPs that considers both greenhouse gas emissions and transportation costs, and proposes an effective multi-objective evolutionary algorithm, namely MP-MOEA, to solve the constructed problem.

Problem formulation

Problem description

MIRPs involve a heterogeneous fleet of vessels with different load capacities \(V=\left\{ v_{1}, v_{2}, \ldots , v_{k}\right\}\) and a set of ports \(P=\left\{ p_{1}, p_{2}, \ldots , p_{s}\right\}\). The goal of MIRPs is to develop an efficient route planning and cargo handling scheme for each vessel in the fleet, ensuring they meet the cargo demands of multiple ports within the specified time. Figure 1 shows a maritime transportation system. This system includes six ports: some are supply ports providing containers, some are demand ports requiring containers, and some serve as both supply and demand ports. Due to the long durations and distances involved in maritime transportation, the overall planning period in MIRPs is usually evenly divided into multiple sub-periods. Figure 2 illustrates a scheduling plan for four vessels (\(V1 \sim V4\)) transporting two types of containers (a -type and b -type) between six ports (\(P1 \sim P6\)) over six sub-periods (\(T1 \sim T6\)). The four rows in Fig. 2 correspond to the scheduling plans for four vessels. Using the first row as an example, it details the scheduling plan for the first vessel (V1). Specifically, V1 visits port 1 (P1) in the first sub-period (T1), loading 1132 containers of a-type containers and 867 containers of b-type. Then, V1 visits P2 in T2, unloading 932 containers of a-type and unloading 500 containers of b-type. Finally, in T6, V1 visits P4, unloads all containers and completes its voyage. The scheduling plans for the other three vessels can be inferred similarly.

Fig. 1
figure 1

Schematic diagram of a maritime transportation system.

Full size image
Fig. 2
figure 2

Illustration of a schedule plan.

Full size image

Assumptions and symbols

For clarity, the assumptions of the MIRP studied in this paper are listed as follows:

  • Each port can be visited multiple times within a sub-period, but each vessel can visit at most one port per sub-period;

  • Each port has an inventory upper limit and lower limit;

  • Each port has an initial inventory level or initial demand for each type of products;

  • The time window of each port in each sub-period is known in advance;

  • Vessels can start or end their voyage at any port;

  • Fuel consumption varies with different speeds, and vessels also consume fuel while docked at ports;

  • Each vessel’s cargo hold is non-specialized, meaning it can carry any type of container;

  • Vessels unload all their containers upon arriving at the destination port;

  • Vessels arrive at a port before or after the time window will result in penalty costs;

  • Vessels require two types of fuel: diesel (used when operating at ports) and heavy fuel oil (used when sailing at sea).

For ease of reading, the following symbols are used in this paper:

Indices

i, j:

Indices for ports,       \(i, j \in \{1, \cdots , |N|\}\);

v:

Index for vessels, \(v \in \{1, \cdots , |V|\}\);

k:

Index for containers,       \(k \in \{1, \cdots , |K| \}\);

t:

Index for sub-period, \(t \in \{1, \cdots , |T| \}\).

Sets

T:

Set of sub-periods;

N:

Set of ports;

V:

Set of vessels;

K:

Set of containers.

Parameters

\(J_{ik}\):

1, if port i is a supplier of k-type containers; -1, if port i is a consumer of k-type containers; 0, if port i is neither a supplier nor a consumer of k-type containers;

\(C_{ijv}^{t}\):

Heavy fuel oil consumption (tonnes per nautical mile) for vessel v (tonnes per nautical mile) while traveling from port i to port j in sub-period t;

\(F_{iv}\):

Marine Diesel Oil consumption (tonnes per hour) at port i for vessel v;

\(C_{ik}^{O}\):

Operating cost of k-type containers at port i;

\(C_{it}^{S}\):

Penalty cost incurred per hour if a vessel waits at port i before the starting of the time window;

\(C_{it}^{E}\):

Penalty cost incurred per hour at port i when a vessel operates after the ending of the time window;

\(\eta _{it}^{S},\):

\(\eta _{it}^{E}\)Beginning and ending of the time window at port i in sub-period t;

\(L_{ij}\):

Distance between port i and j;

\(P_{Tk}\):

Penalty for shortfall a k-type containers at the end of the entire planning period;

\(H_{Tk}\):

Penalty for k-type containers exceeding the maximum capacity of the port at the end of the entire planning period;

\(W_{NO_{2}}^{T}\):

 Total \(NO_{2}\) emissions;

\(W_{SO_{2}}^{T}\):

Total \(SO_{2}\) emissions;

\(W_{CO_{2}}^{T}\):

Total \(CO_{2}\) emissions;

Binary variables

\(X_{ijv}\):

1, if vessel v sails from port i to port j;

\(W_{iv}\):

1, if vessel v visits port i;

\(y_{ivt}\):

1, if vessel v terminates its route at port i after an operation in sub-period t;

\(Z_{v}^{O}\):

1, if vessel v is not used;

\(O_{ivk}^{t}\):

1, if k-type containers is loaded onto or unloaded from vessel v at port visit i in sub-period t;

\(L_{ivk}^{T}\):

1, if there is a shortfall of k-type containers at port i after the end of the entire planning period;

\(P_{iv}^{E}\):

1, if vessel v terminates its route at port i;

\(S_{itjmv}\):

1, if vessel v initiates its operation in sub-period t at port i and then travels from port i to j and begins its operation in period m at port j.

Real Variables

\(q_{ivk}\):

Amount of k-type containers loaded onto or unloaded from vessel v at port visit i in sub-period t;

\(A_{iv}^{t}\):

Arrival time at port i for vessel v in sub-period t;

\(E_{iv}^{t}\):

Ending time of the operation at port i for vessel v in sub-period t;

\(S_{iK}^{PT}\):

Amount of k-type containers above the maximum level for port i at the end of the entire period;

\(H_{ik}^{t}\):

Inventory of k-type containers at port i in sub-period t;

\(M_{iK}\):

Amount of demand for k-type containers in port i is not met at the end of the entire planning period.

Optimization model

The MIRP used in this paper has two minimization objectives: total transportation cost and greenhouse gas emissions, as shown in Eq. (1). Where, \(f_{1}\) is the total transportation cost, \(f_{2}\) is the greenhouse gas emissions.

$$\begin{aligned} \begin{aligned} \textbf{Minimize}\ F =&\{f_{1}, f_{2}\} \\ f_{1} =&\sum _{t \in T} \sum _{v \in V} \sum _{i ,j \in {N}} C_{ijv}^{t} L_{ij} X_{ijv}+\sum _{t \in T} \sum _{v \in V} \sum _{i \in N} F_{iv}(E_{iv}^{t}-A_{iv}^{t})+ \\&\sum _{t \in T} \sum _{v \in V} \sum _{i \in N} \sum _{k \in K \mid J_{ik} \ne 0} q_{ivtk} C_{ik}^{O} O_{ivk}^{t}+\sum _{t \in T} \sum _{i \in N} \sum _{v \in V} C_{it}^{S}[Max(0,(\eta _{it}^{S}-A_{iv}^{t}))] w_{iv}+ \\&\sum _{t \in T} \sum _{i \in N} \sum _{v \in V} C_{it}^{E}[\operatorname {Max}(0,(E_{iv}^{t}-\eta _{it}^{E}))] w_{iv}+\sum _{v \in V} \sum _{i \in N} \sum _{k \in K \mid J_{i k} \ne 0} M_{ik} P_{Tk} L_{ivk}^{T}+ \\&\sum _{v \in V} \sum _{i \in N} \sum _{k \in K \mid J_{ik} \ne 0} S_{ik}^{PT} H_{Tk} W_{iv}\\ f_{2}=&W_{NO_{2}}^{T}+W_{SO_{2}}^{T}+W_{CO_{2}}^{T} \end{aligned} \end{aligned}$$
(1)

As shown in Eq. (1), the total transportation cost (\(f_{1}\)) is the sum of seven iterms. The first represents the heavy fuel oil consumed by vessels traveling between ports, the second reflects the diesel used by vessels during operations at port, the third is the total operational cost of loading and unloading containers at ports, the fourth is the waiting penalty cost for vessels arriving early at ports, the fifth is the demurrage penalty cost for vessels not completing operations within the designated time window, the sixth is the penalty cost for the total demand shortfall at the demand port after the entire planning period, and the seventh is the penalty cost for exceeding the maximum capacity of ports at the end of the entire planning period. In \(f_{1}\), \(C_{ijv}^{t}\) represents the heavy fuel oil consumption of vessel v sailing from port i to port j , which can be calculated using Eq. (2). Eq. (2) gives the relationship between fuel consumption and speed, derived from the relationship between fuel consumption and speed for a vessel with a capacity of approximately 150,000 cubic meters32. Where, \(S_{ijv}\) represents the sailing speed of vessel v, and \(S_{ijv}^{Min}\) and \(S_{ijv}^{Max}\) represent the minimum and maximum sailing speeds of the vessel, respectively.

$$\begin{aligned} \begin{aligned} C_{ijv}^{t}=0.0036 S_{ijv}^2-0.1015 S_{ijv}+0.8848, \quad S_{ijv}^{Min} \le S_{ijv} \le S_{ijv}^{Max}, \quad \forall i, j \in N, \forall v \in V \end{aligned} \end{aligned}$$
(2)

\(f_{2}\) represents the total emissions of nitrogen oxide, sulfur dioxide, and carbon dioxide, which can be calculated using Eq.s (3)-(7)33. In Eq. (3), \(W_{NO_{2}}^{PT}\) represents nitrogen dioxide emissions while the vessel is operating at the port, which can be calculated using Eq. (4). In Eq. (4), d represents the number of auxiliary engines used during loading and unloading, P is the rated power of the auxiliary engines, A is the load factor of the auxiliary engines during loading and unloading, and \(T_{iv}^{t}\) is the operation time of vessel v at port i during the \(t ^{th}\) sub-period. Eq. (5) represents the nitrogen oxide emissions while the vessel is sailing between ports, where X is the vessel’s tonnage,\(A_{1}\) is the load factor, and \(H_{ijv}^{t}\)is the time taken for vessel v to sail from port i to port j during sub-period t. Eq. (6) and Eq. (7) represent the sulfur dioxide and nitrogen oxide emissions, respectively. Where, \(S_{z}\) is the sulfur content of heavy fuel oil, \(S_{C}\) is the sulfur content of diesel, and \(C_{ivt}^{C}\) represents the amount of diesel consumed by vessel v at port i during sub-period t.

$$\begin{aligned} \begin{aligned} W_{NO_2}^{T}=0.00205\left( W_{NO_2}^{PT}+W_{NO_2}^{ST}\right) \end{aligned} \end{aligned}$$
(3)
$$\begin{aligned} \begin{aligned} W_{NO_2}^{PT}=0.00149 P^{1.14} A^{1.14} d \sum _{t \in T} \sum _{i \in N} \sum _{v \in V} T_{iv}^{t} \end{aligned} \end{aligned}$$
(4)
$$\begin{aligned} \begin{aligned} W_{N O_{2}}^{S T}=0.00149\left( 1.9 X^{0.97} A_{1}\right) ^{1.14} \sum _{t \in T} \sum _{v \in V} \sum _{i, j \in N} H_{i j v}^{t} \end{aligned} \end{aligned}$$
(5)
$$\begin{aligned} \begin{aligned} W_{SO_2}^{T}=2\left( S_{Z} \sum _{t \in T} C_{ijv}^{t}+S_{C} \sum _{t \in T} C_{ivt}^{C}\right) \end{aligned} \end{aligned}$$
(6)
$$\begin{aligned} \begin{aligned} W_{CO_2}^{T}=3.1093\left( \sum _{t \in T} C_{ijv}^{t}+\sum _{t \in T} C_{ivt}^{C}\right) \end{aligned} \end{aligned}$$
(7)

The problem model constructed in this paper includes four sets of constraints based on real-world scenarios: time window constraints, routing constraints, loading and unloading constraints, and inventory constraints.

$$\begin{aligned} E_{iv}^{st} - M_{iv}^{t} \ge 0, \quad \forall i \in N,\forall v \in V,\forall t \in T \end{aligned}$$
(8)
$$\begin{aligned} E_{i v}^{s t} \ge A_{i v}^{t}, \quad \forall i \in N,\forall v \in V,\forall t \in T \end{aligned}$$
(9)
$$\begin{aligned} A_{iv}^{t} \le E_{it}^{time}, \quad \forall i \in N,\forall v \in V,\forall t \in T \end{aligned}$$
(10)
$$\begin{aligned} \left( E_{iv}^{t}+L_{ij} / S_{ijv}-A_{jv}^{t}\right) X_{ijv} \le 0, \quad \forall i \in N,\forall v \in V,\forall t \in T \end{aligned}$$
(11)
$$\begin{aligned} E_{i v}^{t}=A_{i v}^{t}+\sum _{k \in K} T_{i k}^{M} O_{i v k}^{t}+\sum _{k \in K} T_{i k}^{Q} q_{i v k} O_{i v k}^{t}, \quad \forall i \in N,\forall v \in V,\forall t \in T \end{aligned}$$
(12)
$$\begin{aligned} E_{i v}^{s t} \ge E_{i v}^{t-1}, \quad \forall i \in N,\forall v \in V,\forall t \in T ,i > 1 \end{aligned}$$
(13)

Eqs. (8)-(13) detail the time window constraints. Eq. (8) shows that the vessel v must commence operations at the port after the expected arrival time. In Eq. (8), \(E_{iv}^{st}\) represents the time when vessel v begins operations at port i during sub-period t. \(M_{iv}^{t}\) represents the expected arrival time of vessel v at port i during sub-period t. Eq. (10) stipulates that the vessel’s arrival time at the port must not be later than the end of the port’s time window. In Eq. (10), \(E_{it}^{time}\) represents the end time of the time window at port i during sub-period t. Specifically, Eq. (11) specifies that the time ship v arrives at port j must be greater than or equal to the departure time from the preceding port i plus the sailing time between the two ports. Eq. (12) indicates that the end time of vessel v’s operations at port i must equal the start time of the operations plus the total service time, which includes machinery startup time and the time for loading and unloading containers. In Eq. (12), \(T_{ik}^{M}\) represents the time required to start machinery for loading and unloading k-type containers at port i, while \(T_{ik}^{Q}\) represents the time needed to load or unload one k-type container at port i. Eq. (13) shows the vessel should always start its operation at a certain port only after it finishes its operation at the previous period.

$$\begin{aligned} \sum _{i, j \in N} X_{ijv}+Z_{v}^0=1, \quad \forall v \in V \end{aligned}$$
(14)
$$\begin{aligned} \sum _{i, j \in N } X_{ijv}+P_{iv}^{E}=1, \quad \forall v \in V \end{aligned}$$
(15)
$$\begin{aligned} w_{iv}-\sum _{\begin{array}{c} i, j \in N \end{array};j \ne i} X_{jiv}-P_{iv}^{E}=0, \quad \forall v \in V \end{aligned}$$
(16)
$$\begin{aligned} \sum _{t \in T} \sum _{v \in V} y_{ivt} = 1, \quad \forall i \in N \end{aligned}$$
(17)
$$\begin{aligned} \sum _{m, t \in T} \sum _{i, j \in N} s_{i t j m v}-\sum _{m, t \in T} \sum _{i, j \in N} s_{j m i t v}-y_{i v t}=0, \quad \forall v \in V,\ \forall t > 1 \end{aligned}$$
(18)
$$\begin{aligned} w_{iv}, Z_{v}^0 \in \{0,1\}, \quad \forall v \in V,\ \forall i \in \textrm{N} \end{aligned}$$
(19)
$$\begin{aligned} X_{jiv} \in \{0,1\} \quad \forall v \in V, \quad \forall v \in V,\ \forall i, j \in N \end{aligned}$$
(20)
$$\begin{aligned} P_{iv}^{E} \in \{0,1\}, \quad \forall v \in V,\ \forall i \in N \end{aligned}$$
(21)
$$\begin{aligned} y_{ivt} \in \{0,1\}, \quad \forall i \in N, \end{aligned}$$
(22)

Eqs. (14)-(22) describe the routing constraints for vessels. Eq. (14) indicates that vessel v is either used or not used during the scheduling period. Eq. (15) and Eq. (16) indicate that port i can be either the departure port of a sub-voyage or the final port at the end of the planning period. Eq. (17) ensures that the vessel must conclude its route at a certain port. The flow conservation constraint is given by Eq. (18), ensuring that the container flow within the transportation network adheres to real-world conditions. Eqs. (19)-(22) define the binary variable constraints.

$$\begin{aligned} 0 \le q_{ivk} \le C_{v} O_{ivk}^{t}, \quad \forall v \in V,\ \forall i\in N,\ \forall k \in K,\ \forall t \in T \end{aligned}$$
(23)
$$\begin{aligned} Q_{ik}^{MIN} O_{ivk}^{t} \le q_{ivk} \le Q_{ivk}^{MAX} O_{ivk}^{t}, \quad \forall v \in V,\ \forall i \in N,\ \forall k \in K,\ \forall t \in T \end{aligned}$$
(24)
$$\begin{aligned} S_{i t j m v}\left( f_{i v t k}^{o}+J_{i k} q_{j v m k}-f_{j v m k}^{o}\right) =0, \quad \forall v \in V,\ \forall i,j \in N,\ \forall k \in K,\ \forall t,m \in T \end{aligned}$$
(25)
$$\begin{aligned} f_{ivtk}^{o} \ge 0, \quad \forall v \in V,\ \forall i \in N,\ \forall k \in K \end{aligned}$$
(26)
$$\begin{aligned} q_{ivtk} \ge 0, \quad \forall v \in V,\ \forall i \in N,\ \forall k \in K \end{aligned}$$
(27)
$$\begin{aligned} O_{ivk}^{o} \in \{0,1\}, \quad \forall v \in V,\ \forall i \in N,\ \forall k \in K \end{aligned}$$
(28)

Eqs. (23)-(28) define the constraints for loading and unloading containers. Eq. (23) specifies that the number of containers loaded or unloaded from vessel v must not exceed its maximum capacity. In Eq. (23), \(C_{v}\) represents the capacity of vessel v. Eq. (24) indicates that the loading and unloading quantities of the vessel must be within the allowable range of the port. Specifically, the loading quantity of the vessel cannot exceed the port’s inventory, and the unloading quantity cannot exceed the port’s capacity. In Eq. (24), \(Q_{ik}^{MIN}\) represents the minimum unloading quantity of k-type containers at port i. \(Q_{ik}^{MAX}\) represents the maximum unloading quantity of container type k at port i. Eq. (25) states that the containers load of a vessel departing from port i should equal the containers capacity of the vessel departing from port j plus or minus the quantity of containers loaded or unloaded at port j. This means that, over the entire time period, there must be a quantitative consistency between the delivery and consumption of containers at the ports visited. In Eq. (25), \(f_{ivtk}^{o}\) represents the quantity of k-type containers on vessel v when departing from port i during sub-period t. Eqs. (26)-(28) represent the non-negativity constraints and binary variables.

Demand ports:

$$\begin{aligned} S_{ik}^{E}=S_{ik}-\sum _{i \in N} R_{ik} J_{ik}, \quad \forall i \in N,\ \forall k \in K,\ \forall J_{ik}=-1 \end{aligned}$$
(29)
$$\begin{aligned} S_{ik}^{MIN} \le S_{ik}^{MAX}, \quad \forall i \in N,\ \forall k \in K \end{aligned}$$
(30)
$$\begin{aligned} S_{ik} \le 0, \quad \forall i \in N,\ \forall k \in K \end{aligned}$$
(31)
$$\begin{aligned} S_{ik}^{PT} \le 0, \quad \forall i \in N,\ \forall k \in K \end{aligned}$$
(32)

Supply ports:

$$\begin{aligned} S_{ik}^{E}=S_{ik}-\sum _{i \in N} R_{ik} J_{ik}, \quad \forall i \in N,\ \forall k \in K,\ \forall J_{ik}= 1 \end{aligned}$$
(33)
$$\begin{aligned} S_{ik}^{MIN} \le S_{ik}^{MAX}, \quad \forall i \in N,\ \forall k \in K \end{aligned}$$
(34)
$$\begin{aligned} S_{ik} \ge 0, \quad \forall i \in N,\ \forall k \in K \end{aligned}$$
(35)
$$\begin{aligned} S_{ik}^{E} \ge 0, \quad \forall i \in N,\ \forall k \in K \end{aligned}$$
(36)
$$\begin{aligned} S_{ik}^{PT} \le 0, \quad \forall i \in N,\ \forall k \in K \end{aligned}$$
(37)

Eqs. (29)-(37) describe the inventory constraints. Eqs. (29)-(33) respectively represent the calculation of inventory levels for each type of container at the demand port and the supply port from the beginning to the end of each vessel’s visit. \(S_{ik}\) represents the inventory level of k-type containers at the beginning of the visit to port i. \(S_{ik}^{E}\) represents the inventory level of k-type containers at the end of visiting port i. \(R_{ikt}\) represents the demand for k-type containers at port i during sub-period t. Eq. (31) indicates that the initial inventory level of demand k-type containers at demand port i should be less than zero. Eq. (35) indicates that the initial inventory level of supply k-type containers at supply port i should be greater than zero. Eqs. (30) and (34) show that the minimum inventory level \(S_{ik}^{MIN}\) at demand ports and supply ports must be less than their maximum inventory level \(S_{ik}^{MAX}\). Eq. (32) represents the constraint of demand ports, while Eqs. (36)-(37) represent the constraints of supply ports.

Methodology

The MIRPs studied in this paper are large-scale multi-objective MINLPs, which are typically NP-hard and difficult to solve exactly. Therefore, this paper proposes a multi-objective evolutionary algorithm based on a multi-population framework (MP-MOEA) to solve MIRPs.

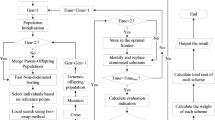
Figure 3 presents the overall framework of MP-MOEA, and the specific steps of the proposed algorithm are provided in Algorithm 1. As shown in Algorithm 1, MP-MOEA first initializes S populations (Line 1). Specifically, MP-MOEA generates multiple populations simultaneously using a multi-population-based initialization operator during the initialization phase to maintain solution diversity. Additionally, the proposed initialization operator employs a three-level dynamic encoding strategy to reduce the encoding length, thereby lowering the difficulty of solving MIRPs. After that, the individual modification operator is applied to repair the solutions in the generated populations, reducing the number of infeasible solutions (Line 2). The modified populations are then merged to form POP (Line 3). During the population update process, a hybrid crossover operator is first used to generate the offspring population OFF (Line 5). Then, the individual modification operator is applied on OFF to increase the proportion of feasible solutions (Line 6). Next, the contribution-based mutation operator is applied to mutate the individuals in OFF (Line 7). Finally, environmental selection is used to select individuals from both POP and OFF to form the updated POP (Line 8). It should be noted that the environmental selection method in this paper uses the Constrained Dominance Principle (CDP)34, which is commonly applied in constrained MOEAs. Specifically, the solutions are first divided into feasible and infeasible sets, with feasible solutions given higher priority. For the feasible set, solutions are ranked based on non-dominated sorting; for the infeasible set, solutions are ranked according to the degree of constraint violation. Since the CDP method is widely used for environmental selection in constrained MOEAs, a detailed description is not provided here. For the specific steps, please refer to the work proposed by Fan et al.34.

As illustrated in Fig. 3, the key operators in MP-MOEA include the multi-population-based initialization operator with a three-level dynamic encoding strategy, the individual modification operator, the hybrid crossover operator, and the contribution-based mutation operator. The following section provides a detailed description of these operators.

Fig. 3
figure 3

Diagram of MP-MOEA.

Full size image
Algorithm 1
figure a

Procedure of MP-MOEA

Full size image

Multi-population-based initialization operator with a three-level dynamic encoding strategy

As shown in Fig. 3, the proposed initialization operator generates S populations simultaneously. Specifically, the different populations contain candidate solutions involving different numbers of vessels. For example, consider three populations: Population 1, Population 2, and Population 3. Population 1 contains candidate solutions involving q vessels, Population 2 contains candidate solutions involving k (\(k \ne q\)) vessels, and Population 3 contains candidate solutions involving m (\(m \ne k \ne q\)) vessels. Therefore, using a multi-population-based initialization operator helps MP-MOEA maintain the diversity of solutions and increase the probability of escaping local optima.

When using evolutionary algorithms to solve real-world problems, an appropriate encoding strategy can effectively reduce the search space, enhancing the algorithm’s search capability. For MIRPs, this paper proposes a three-level dynamic encoding strategy that reduces the encoding length and simplifies the execution of key operators (i.e., crossover and mutation operators).

Assuming there are four vessels in the fleet, Fig. 4 shows the encoding of a solution involving three vessels (the first, third, and fourth vessels). The row corresponding to the second vessel contains no data, indicating that this vessel is not involved in this solution. As shown in Fig. 4, the encoding consists of three parts: Route, Speed, and Container. The “Route” represents the sailing path of a vessel. Since it is assumed that vessels can visit at most one port in each sub-period, the “Route” of a vessel can be initialized as a zero vector of dimension |T|, where |T| is the number of sub-periods. Then, k elements are randomly selected from the zero vector. \(k \in [1, \min \{|N|,|T|\}]\)and |N| is the number of ports. After that, these k elements are replaced with k unique integers randomly selected from the interval [1, |N|]. The “Speed” reflects the sailing speed of a vessel, with its encoding length determined by the number of ports in the vessel’s route. Specifically, if a vessel’s route includes three ports, the “Speed” section will be a 2-dimensional vector, as there is one sailing speed between each pair of adjacent ports. Each element in the speed vector is randomly selected from \([speed_{min}, speed_{max}]\). The “Container” reflects the loading and unloading number of containers for a vessel. Its encoding length is determined by the number of container types and the number of ports in the vessel’s route. Specifically, if the MIRP involves transporting h types of containers and the vessel’s route includes k ports, the “Container” section will consist of \(k-1\) h-tuples (assuming the vessel unloads all containers at the last port). The first h-tuple represents the loading and unloading of containers at the first port the vessel visits. In each h-tuple, a positive value for the i-th element indicates the vessel loads the i-th type of containers, while a negative value indicates the vessel unloads the i-th type of containers.

Fig. 4
figure 4

Illustration of the three-level dynamic encoding strategy.

Full size image

Based on the above description, the lengths of “Speed” and “Container” in the encoding vary for different solutions. Consequently, the overall length of the encoding for different solutions also varies. The decoding process for the solution shown in Fig. 4 is described as follows. As shown in Fig. 4, the first vessel departs from Port 1 in the first sub-period, loading 2,200 units of the first type of container and 1,000 units of the second type. It then sails to Port 3 at a speed of 14.5 knots in the third sub-period, where it unloads 2,000 units of the first type of container and loads 1,244 units of the second type. Afterward, it sails to Port 4 at a speed of 21.4 knots in the fifth sub-period, where it unloads all remaining containers. The “Route,” “Speed,” and “Container” for the second vessel are all empty, indicating that Vessel 2 has no sailing plan throughout the scheduling scheme and is, therefore, idle. The decoding process for the third and fourth vessels can be referenced from the decoding process of the first vessel.

Compared to the traditional fixed-length encoding mechanism, the three-level dynamic encoding mechanism proposed in this paper can effectively reduce the number of decision variables that need to be optimized. For a small-scale transportation task involving 4 ports, 4 vessels, 2 types of containers, and 5 sub-periods, Fig. 4 illustrates a schematic of a candidate solution obtained using the three-level dynamic encoding strategy. As shown in Fig. 4, in the “Route” section, there are at most 4 (number of vessels) \(\times\) 5 (number of sub-periods) = 20 decision variables; in the “Speed” section, there are at most 4 (number of vessels) \(\times\) 3 (number of ports - 1) = 12 decision variables; and in the “Container” section, there are at most 4 (number of vessels) \(\times\) 2 (number of container types) \(\times\) 3 (number of ports - 1) = 24 decision variables. Therefore, for the transportation task described above, the proposed encoding mechanism requires at most 20 + 12 + 24 = 56 decision variables. In contrast, the traditional fixed-length encoding mechanism requires 2584 decision variables, and the number of decision variables can be calculated based on the work proposed by Kumar et al.7. When the task expands to a large-scale maritime transportation scenario involving 14 ports, 10 vessels, 2 types of containers, and 22 sub-periods, the number of decision variables in the traditional fixed-length encoding mechanism grows to 985,096, while the three-level dynamic encoding strategy requires at most 610 decision variables. This demonstrates that the proposed three-level dynamic encoding mechanism can effectively reduce the number of decision variables in real-world MIRPs, thereby decreasing the difficulty of problem optimization.

Individual modification operator

Due to the complexity of the constraints in MIRPs, many candidate solutions generated by algorithms are infeasible. This paper proposes an individual modification operator to enhance the feasibility of the solutions. This operator adjusts candidate solutions by focusing on two main aspects: the loading and unloading number of containers for vessels and the routes of vessels.

(1) Modification for the loading and unloading quantities for vessels

This part focuses on checking the loading and unloading number of containers for vessels at ports as reflected in the candidate solutions and making adjustments to any unreasonable values.

For the initial port, assume that the candidate solution indicates an unloading quantity of \(-a\) (a negative value indicates unloading) for a vessel at the initial port. Since the vessel is empty at the start, if the initial port is a demand port for the k-type containers, the unloading quantity for the k-type containers at the initial port will be adjusted to 0. If the initial port is a supply port for the k-type containers, the unloading status will be changed to loading status, with the loading quantity set to \(\min \left\{ a,b \right\}\) and b is the inventory of the k-type containers in the initial port.

For other ports, if the vessel is loading k-type containers but lacks sufficient capacity or if the port does not have enough inventory of k-type containers, the loading quantity will be adjusted to the minimum of the vessel’s capacity and the port’s inventory of k-type containers. If the vessel unloads k-type containers at a port but the port lacks sufficient capacity, or the vessel does not carry enough k-type containers, the unloading quantity will be adjusted to the minimum of the port’s capacity and the number of k-type containers carried by the vessel.

(2) Modification for the routes of vessels

This part checks whether the vessel routes reflected in the candidate solutions are reasonable and corrects any unreasonable values.

Firstly, check the vessel’s route for duplicate ports and ports with no loading or unloading operations. If any are found, remove the corresponding port from the route.

Secondly, check whether a vessel can sail to the next port within the specified sub-period. If the expected arrival time at the next port is later than the end of the time window within the specified sub-period at the next port, adjust the container loading and unloading quantities at the current port to allow the vessel to reach the next port earlier. As shown in Eq. (38), \(time_{next\_port}^{anticipate}\) is the expected arrival time at the next port, \(time_{Machine\_start\_up}\) is the machinery startup time at the current port, \(P_{next}^{end\_time}\) is the start time of the time window at the current port, \(time_{(un)load}\) is the time required for loading and unloading containers at the current port, and \(time_{Sailing}\) is the sailing time between the current port and the next port. In Eq. (39), \(P_{next}^{end\_time}\) is the end time at the next port, \(time_{(un)load}^{container_{sort}(index)}\) is the loading and unloading time for the container type with the largest quantity carried by the vessel, \(G_{container}^{k}\) is the original loading and unloading quantity of k-type containers for the vessel at the current port in the reference solution, and modified \(G_{container}^{k}\) is the adjusted loading and unloading quantity of k-type containers for the vessel at the current port.

$$\begin{aligned} time_{next\_port }^{anticipate } = P_{current }^{start\_time }+ time _{Machine\_start\_up }+ time_{(un ) load }+ time _{Sailing } \end{aligned}$$
(38)
$$\begin{aligned} \begin{aligned} G_{container}^{k} = G_{container}^{k}- min \{ G_{container}^{k},\frac{time_{next\_port}^{anticipate}-P_{next}^{end\_time}}{time_{(un)load}^{container_{sort}(index)}} \} \end{aligned} \end{aligned}$$
(39)

MIRPs are optimization problems with complex constraints, so the candidate solutions (individuals) found by the algorithm are often infeasible. The individual modification operator proposed in this paper adjusts candidate solutions by focusing on two aspects: the vessel’s loading and unloading operations, and the vessel’s sailing routes, thereby guiding infeasible solutions toward the feasible region. For a transportation task involving 5 ports, 3 vessels, 2 types of containers (a-type and b-type), and 4 sub-periods, Fig. 5 shows an example of how the individual modification operator adjusts a candidate solution. Among the five ports, ports 4 and 5 are demand ports, while ports 1, 2, and 3 are supply ports.

Fig. 5
figure 5

Illustration of the individual modification operator.

Full size image

As shown in Fig. 5 , the second vessel performs an unloading operation for a-type containers at the initial port (port 3). However, since the vessel is empty at the initial port and port 3 is a supply port, the proposed modification operator changes the unloading operation to a loading operation for the second vessel at port 3. The loading quantity is then adjusted according to the description in Section 3.2 (in this example, the loading quantity is adjusted to 2100). In terms of vessel route adjustment, as shown in Fig. 5, the first vessel’s route includes a repeated port (port 1), so the modification operator removes that port and the related decision variables. In the third vessel’s route, port 5 appears, but there are no loading/unloading operations at this port, so the modification operator removes that port and the related decision variables. Additionally, for the third vessel, after detecting that the vessel cannot reach the next port within the prescribed time after loading 2554 b-type containers at port 1, the modification operator adjusts the loading quantity of b-type containers from 2554 to 1500 according to Eq. (39) in Section 3.2. Based on the above description, the individual modification operator optimizes the vessel’s voyage scheduling by adjusting loading/unloading operations and sailing routes, eliminating unnecessary port calls and loading/unloading actions.

Hybrid crossover operator

To enhance the search efficiency of the algorithm, MP-MOEA employs a hybrid crossover operator. This operator includes two commonly used crossover methods in evolutionary algorithms: Simulated Binary Crossover (SBX)35 and Partial-Mapped Crossover (PMX)36. In the hybrid crossover operator, the two crossover methods are applied with different probabilities at different stages of the proposed algorithm. In Eq. (40), \(R_{sbx}\)is the probability of using the SBX, \(R_{pmx}\) is the probability of using the PMX, \(I_{e}\) is the current iteration number, \(G_{e}\) is the total number of iterations, and \(\eta\) is the control parameter.

$$\begin{aligned} \left\{ \begin{array}{ll}R_{s b x}=1, R_{pmx}=0, & I_{e} \le G_{e} / 2 \\ R_{s b x}=1-2 I_{e}(1-\eta ) / G_{e}, R_{pmx}=2 I_{e}(1-\eta ) / G_{e}, & I_{e}>G_{e} / 2\end{array}\right. \end{aligned}$$
(40)

As shown in Eq. (40), when \(I_{e} \le G_{e}/2\), SBX is used. When \(I_{e} > G_{e}/2\), both SBX and PMX are used, with the probability of SBX gradually decreasing and the probability of PMX gradually increasing as the number of iterations increases.

\(\eta\) takes values in the range [0, 1] and is used to control the probability of using SBX and PMX in the later stages of the algorithm. When \(\eta\) is larger, the rates of decrease of \(R_{sbx}\) and increase of \(R_{pmx}\) are slower, meaning the algorithm is more likely to adopt the SBX crossover method. Based on the analysis of the characteristics of SBX and PMX, a larger \(\eta\) value can help the algorithm converge more quickly. When \(\eta\) is smaller, the rates of decrease of \(R_{sbx}\) and increase of \(R_{pmx}\) are faster, meaning the algorithm tends to adopt the PMX crossover method. In this case, the algorithm is more likely to maintain better population diversity.

SBX and PMX are crossover methods based on a single decision variable and a segment of decision variables, respectively. These two crossover methods operate at different levels. If PMX is used in the early stage of the algorithm to directly exchange a segment of decision variables between two parent individuals, it may lead to a rapid decline in the quality of the offspring individuals, as the quality of the parent individuals might also be sub-optimal at this stage. Therefore, only the SBX crossover method is employed in the early stages of the algorithm. As the algorithm progresses, the quality of solutions in the population gradually improves. At the late stage of MP-MOEA, using only the SBX crossover method may result in offspring whose quality is intermediate between the two parent individuals. However, PMX, by performing crossover on a segment of decision variables, can effectively help the algorithm escape local optima. Therefore, in the proposed hybrid crossover strategy, the probability of using PMX gradually increases in the later stage of MP-MOEA.

Fig. 6
figure 6

Illustration of the hybrid crossover operator.

Full size image

Since MIRPs involve scheduling multiple ports, vessels, and types of containers, they are optimization problems with complex decision variables. The hybrid crossover operator proposed in this paper combines the advantages of SBX and PMX, effectively enhancing the algorithm’s search capability in complex decision spaces. Figure 6 illustrates the generation of offspring individuals using the hybrid crossover operator, based on a transportation task involving 5 ports, 3 vessels, 2 types of containers, and 4 sub-periods. The proposed hybrid crossover operator uses the SBX method to generate offspring individuals in the early stages of the algorithm. As shown in Fig. 6, the offspring generated by SBX are distributed around the parent individuals. Since the population diversity is relatively high in the early stages of the algorithm, SBX can effectively help the algorithm generate high-quality offspring individuals. However, in the later stages, as the population begins to converge, SBX may no longer facilitate the search for new regions, potentially causing the algorithm to become trapped in local optima. In the later stages of the algorithm, the hybrid crossover operator is more likely to use the PMX method to generate offspring individuals. PMX performs the crossover operation by exchanging segments of decision variables. As shown in Fig. 6, in PMX, the 1st row of Parent 1 is exchanged with the 3rd row of Parent 2, and the 3rd row of Parent 1 is exchanged with the 2nd row of Parent 2. The generated offspring may be farther from the parent individuals. Therefore, the PMX method can effectively help the algorithm escape local optima and enhance its global search capability.

Contribution-based mutation operator

Based on the characteristics of MIRPs, this paper proposes a contribution-based mutation operator.

The proposed contribution-based mutation operator aims to adjust certain decision variables in the candidate solutions to generate higher-quality solutions. For MIRPs, the candidate solutions found by the algorithm may schedule vessels to unload more at demand ports than the actual port demand. Excessive unloading not only increases unnecessary unloading costs but also extends the overall voyage time of the vessel. Therefore, this paper designs a contribution metric based on the unloading quantity of vessels at demand ports. The decision variables corresponding to the unloading quantities at demand ports are adjusted based on the contribution value to produce solutions with less redundant unloading.

As shown in Eq. (41), the contribution \(CD_{vk}^{it}\) is defined as the ratio of the unloading quantities of k-type containers from vessel v at demand port i to the demand of k-type containers of port i in the t-th sub-period.

$$\begin{aligned} CD_{vk}^{it}=\frac{\text {The discharge volume of ship { v} in port { i} is in sub-period { t}}}{\text {Demand for { k}-type containers at port { i} in sub-period { t}}} \end{aligned}$$
(41)

When \(CD_{vk}^{it}\) is greater than 1, it indicates that the unloading quantity of vessel v exceeds the demand volume at the demand port i, resulting in unloading redundancy. Unloading redundancy incurs additional unloading costs and prolongs the vessel’s operating time. Therefore, in the proposed mutation operator, the contribution of each ship to each demand port on its route is calculated for each sub-period first. If the contribution \(CD_{vk}^{it}\) exceeds 1, the quantity of the k-type containers unloaded by vessel v at port i is adjusted to match the demand for the k-type containers at port i. Since the unloading quantity of vessel v at port i has decreased, it is necessary to trace back to the previous ports the vessel v has visited and reduce the loading quantities at the supply ports accordingly.

Fig. 7
figure 7

Schematic of a transportation task.

Full size image

The proposed contribution-based mutation operator adjusts the unloading quantities of containers at ports by calculating contribution values, thereby reducing redundant operations at the ports. Figure 7 shows a schematic of a transportation task. In Fig. 7, Port 2 requires 50 a-type containers and 10 b-type containers, Port 3 requires 30 a-type containers and 10 b-type containers, Port 1 can supply 80 a-type containers and 50 b-type containers, and the capacity of the transportation vessels is 100 containers. Assume the “container” part of the current solution is {(80, 20); (-55, -10)}, meaning that the vessel loads 80 a-type containers and 20 b-type containers at supply port 1. Upon reaching demand port 2, it unloads 55 a-type containers and 10 b-type containers. The vessel then sails to the final demand port (port 3), where it unloads all remaining containers, i.e., unloading 25 a-type containers and 10 b-type containers. In the contribution-based mutation operator, the contribution value of each demand port for each type of container is first calculated. For example, the contribution value of the a-type containers at demand port 2 is calculated as \(CD_{a}\) = 55/50 = 1.1 (according to Eq. (41)). Since the contribution value is greater than 1, this indicates that the unloading quantity specified by the current solution exceeds the demand at the port 2. Therefore, in this mutation operation, the unloading quantity of a-type containers at port 2 is adjusted to 50, which exactly matches the demand at port 2. A similar adjustment is made for the unloading quantity of b-type containers at port 2. Based on the above description, the contribution-based mutation operator reduces redundant operations by dynamically adjusting the unloading schedules, significantly improving the rationality of port resource allocation.

Computational experiments

Experimental Settings

The test case settings in this section are based on commonly used setups in the maritime transport field7,37,38. In actual transportation, shipping companies typically select their fleets based on factors such as adaptability, resource utilization, risk diversification, and diversity needs. This paper uses six different types of vessels, with parameters including vessel class, container capacity (CC), deadweight tonnage (DWT), sailing speed, and fuel cost listed in Table 1.

Table 1 Parameters of different types of vessels.
Full size table
Table 2 Parameter settings for ports, vessels and containers.
Full size table

Ocean shipping containers are versatile for transporting solid, liquid, and gas-type products, each tailored to specific standard sizes. This section employs three container types: 20-foot standard, 20-foot high-cube, and 40-foot standard containers. To better reflect real-world conditions, the port settings in this study are based on Chinese coastal ports. For example, the experiment uses the ___location information of Chinese coastal ports such as Dandong Port, Dalian Port, Lushun New Port, Yingkou Port, Qinhuangdao Port, Tianjin Port, Yantai Port, Qingdao Port, Lianyungang Port, Wusong Port, and Shanghai Port. Information on ports’ time windows, loading and unloading times and costs for different types of containers, and port storage capacities are refer to data39,40. Detailed settings of all parameters are shown in Table 2. To test the scalability of the proposed algorithm, this study used three different-sized problem scenarios, with a total of six test cases. As shown in Table 3, the small, middle, and large test cases each utilize different numbers of ports, ships, containers, and sub-periods.

Table 3 Parameter settings for problems with different scales.
Full size table
Table 4 Parameter Settings for algorithms.
Full size table

To evaluate the performance of the proposed algorithm, MP-MOEA was compared with seven other state-of-the-art MOEAs:

Adaptive Geometry Estimation-Based MOEA II (AGEMOEAII)41, Constrained Multiobjective Evolutionary Algorithm with Bidirectional Coevolution (BiCo)42, Multi-stage Constrained Multi-Objective Evolutionary Algorithm (MSCEA)43, Non-dominated Sorting Genetic Algorithm II (NSGAII)35 , A Two-Stage Evolutionary Algorithm Based on Three Indicators for CMOPs (TSTI)44, an adaptive neighborhood based evolutionary algorithm with pivotsolution based selection(PiMOEA)45 and A preference-inspired DE for multi and many-objective optimization(PreDEMO)46. The reasons for selecting the aforementioned comparison algorithms are as follows: BiCo, TSTI, AGEMOEAII, PreDEMO, PiMOEA and MSCEA are highly efficient constrained MOEAs proposed in recent years and have demonstrated excellent performance in handling large-scale constrained multi-objective problems. NSGAII is a classic algorithm for solving multi-objective problems and is widely used in various optimization problems.

To ensure the fairness of the experiment, the population size for all algorithms was set to 300, and the maximum number of function evaluations was set to 300,000. The specific parameter settings for the algorithms are shown in Table 4. To evaluate the experimental results, hypervolume (HV) value is used in this paper. The HV metric evaluates the quality of the Pareto front obtained by the algorithm in terms of both convergence and diversity47,48. The value of HV can be calculated using Eq. (42). In Eq. (42), PF represents the Pareto front obtained by the algorithm being evaluated, while \(z^{ref}\) is a predefined reference point that is dominated by all individuals in PF. In Eq. (42), \(c^{i}\) denotes the hypercube formed by the i-th individual in PF and the reference point, while \(volume(c^{i})\) represents the hypervolume of \(c^{i}\). Therefore, the HV metric effectively calculates the volume of the hypercube formed by the individuals in PF and the reference point \(z^{ref}\). Thus, a larger HV value indicates that the Pareto front obtained by the evaluated algorithm is of higher quality. Since the MIRPs solved in this paper are a minimized two-objective optimization problem, \(z^{ref}\) can be generated according to Eq. (43), where P is the set of Pareto-optimal solutions found by algorithms.

$$\begin{aligned} H V\left( P F, z^{\text{ ref } }\right) =U_{i=1}^{|P F|} \text{ volume } \left( c^{i}\right) \end{aligned}$$
(42)
$$\begin{aligned} \begin{array}{l} z^{\text{ ref } }=\left( z_{1}, z_{2}\right) \\ z_{1}=\max _{x \in P} f_{1}(x)+0.1 \\ z_{2}=\max _{x \in P} f_{2}(x)+0.1 \end{array} \end{aligned}$$
(43)

Analysis of Parameters in MP-MOEA

MP-MOEA includes two parameters: S and \(\eta\). The parameter S is used to determine the number of populations in the initialization operator, while \(\eta\) is used to control the selection of different crossover methods in the hybrid crossover operator.

Fig. 8
figure 8

Pareto fronts obtained by MP-MOEA with different values of S.

Full size image

As shown in Fig. 8a–c illustrate the Pareto fronts obtained by MP-MOEA with S set to 1, 2, 3, and 4 across different problem scales. The results indicate that when S = 3, the algorithm achieves the best results for test cases of all three different scales. The reason is that when S is set to a smaller value, it can result in a lack of population diversity, which may prevent the algorithm from finding the global optimum. Conversely, when S is set to a larger value, it can help maintain population diversity but also imposes a significant computational burden, reducing search efficiency. Therefore, in this paper, S is set to 3.

Fig. 9
figure 9

Pareto fronts obtained by MP-MOEA with different values of \(\eta\).

Full size image

As shown in Fig. 9a–c depict the Pareto fronts obtained by MP-MOEA in different-scale test cases when \(\eta\) is set to 0.2, 0.4, 0.6, and 0.8. When \(\eta\) is too small, the probability of SBX becomes smaller, resulting in the failure to produce enough diversified excellent gene fragments. At this time, genes are mainly cross-recombined with PMX, which will lead to the gene fragments in the recombined individuals are not optimal, thus slowing down the population convergence rate and easily falling into local optimization. When the \(\eta\) value is too large, the probability of PMX becomes smaller, and the probability of the inferior gene in an individual being replaced by the corresponding excellent gene fragment in other individuals becomes smaller, which will also lead to the population convergence speed is slow, and it is easy to fall into the local optimal. The results in Fig. 9 show that MP-MOEA achieves the best results when \(\eta\) is set to 0.6. This indicates that \(\eta\) = 0.6 allows the algorithm to strike a good balance between the two crossover methods. Therefore, in this paper, \(\eta\) is set to 0.6.

Comparison of algorithms at different problem scales

Figure 10a–f illustrate the Pareto fronts obtained by each algorithm when solving all six test cases of different scales. Table 5 presents the minimum (best) transportation costs (MT) and the minimum (best) greenhouse gas emissions (ME) obtained by all six algorithms after 30 independent runs for each test case. Table 5 also presents the average HV values obtained by the algorithms after 30 independent runs for each test case.

Fig. 10
figure 10

Pareto fronts for algorithms on test problems with different scales.

Full size image
Table 5 Objective values and HV values of algorithms.
Full size table

As shown in Table 5, for Small case 1, MP-MOEA performs slightly worse than TSTI and MSCEA in terms of ME (greenhouse gas emissions). For the medium-scale test cases, MP-MOEA is inferior to PreDEMO in Middle case 1, and to PreDEMO, TISI, and MSCEA in Middle case 2 in terms of ME. However, for all small-scale and middle-scale test cases, MP-MOEA achieved the best results for HV. The above results indicate that the strategies employed by MP-MOEA effectively helps the algorithm achieve a balance between convergence and diversity. However, the mutation strategy designed in MP-MOEA, which is ___domain-specific, is primarily aimed at reducing redundant unloading operations, specifically to lower transportation costs, i.e., MT. Therefore, while this mutation strategy can assist the algorithm in searching for higher-quality solutions, it mainly focuses on optimizing transportation costs and does not take into account greenhouse gas emissions. The comparison algorithms, such as TISI, PreDEMO, and MSCEA, are designed with efficient evolutionary strategies, which allow them to achieve better results than MP-MOEA in terms of greenhouse gas emissions for some medium and small-scale test cases. For instance, TISI employs a two-stage strategy with different emphases on the three indicators, while PreDEMO introduces a preference-inspired mutation operator and a two-stage environmental selection. These strategies enable the algorithms to perform an efficient search during the evolutionary process. As shown in Table 5, for the large-scale test cases, MP-MOEA achieves the best results for MT, ME, and HV. This is primarily due to the dynamic three-level encoding mechanism, which effectively reduces the dimensionality of the search space. This advantage is more pronounced in larger-scale test cases. The dynamic three-level encoding mechanism and the three search operators enable MP-MOEA to demonstrate superior performance in solving large-scale MIRPs. Specifically, in MP-MOEA, the hybrid crossover operator performs operations at two levels: single decision variables and segments of decision variables. This crossover operator not only enhances the algorithm’s search capability in the decision space but also helps MP-MOEA escape local optima. The contribution-based mutation operator reduces unnecessary container unloading operations, helping the algorithm obtain high-quality solutions. Additionally, the individual modification operator effectively improves the feasibility of offspring.

Table 6 Performance comparison of MP-MOEA, TSTI, and PreDEMO on MT and ME.
Full size table

To more clearly demonstrate the performance of the proposed MP-MOEA on the two objectives, MT and ME, this paper selects two comparison algorithms with better rankings based on the average ranking values from Tables 7, 8, and 9, namely TISI and PreMOEA. In this section, the two selected algorithms are used as baseline algorithms and Table 6 presents the differences in objective function values between the proposed algorithm and the baseline algorithms. The negative values in Table 6 indicate that the proposed algorithm achieved smaller (better) objective values than the baseline algorithm, while positive values indicate that the proposed algorithm obtained larger (worse) objective function values compared to the baseline. For example, compared to TISI, the proposed MP-MOEA reduced approximately 1.22 million USD in MT (transportation costs) for Small case 1, but increased approximately 4.6 tons in ME (greenhouse gas emissions). As can be seen from Table 6 , for some small and medium-scale cases, the proposed algorithm does not achieve improvements on both objectives. For instance, when using TISI as the baseline, the proposed algorithm increased greenhouse gas emissions by 26.3 tons for Middle case 2. When using PreDEMO as the baseline, the proposed algorithm increased greenhouse gas emissions by 9.6 tons for Middle case 1. However, in both of these cases, the proposed algorithm significantly reduced transportation costs compared to the baseline. For large-scale test cases, the proposed algorithm outperforms the baseline on both objectives, showing significant improvements in the results. On the one hand, the encoding mechanism used in this paper effectively reduces the dimensionality of the search space, thus reducing the difficulty of problem-solving. On the other hand, this paper introduces various search operators related to the specific MIRPs, such as the individual modification operator and the contribution-based mutation operator, which can effectively help the algorithm improve search efficiency.

To better compare the performance of the algorithms, this section presents the results of the Friedman test for 8 (k) algorithms on MT (the first objective function) across 6 (N) test cases.Table 7 shows the average ranking results of all algorithms for MT across all test cases.A smaller ranking value indicates better performance of the algorithm. The critical value of the \(F-distribution\) at a 90% confidence level with degrees of freedom \((k - 1)\) and \((k - 1)\times (N - 1)\) is \(F_{0.10} = 2.255\). This value is smaller than the Friedman statistic based on the average rankings, as shown in Table 7. Therefore, the null hypothesis is rejected, indicating a significant difference in the results of the 8 algorithms. According to the pairwise post hoc \(Bonferroni - Dunn\) test, the critical difference at a 90% confidence level is 2.450. This means that if the difference in average ranking between MP-MOEA and any other algorithm exceeds 2.450, MP-MOEA is considered significantly superior to the other algorithm at the 90% confidence level. As shown in Table 7, MP-MOEA is significantly superior to all other comparison algorithms for MT at the 90% confidence level, except for PreMOEA. According to Table 8, the Friedman statistic based on the average ranking results of the algorithms for ME (the second objective function) is 3.05, which is greater than \(F_{0.1}(7,35)\). Therefore, there is a significant difference in the results of the 8 algorithms for ME. Furthermore, as shown in Table 8, the difference in ranking results between MP-MOEA and AGEMOEAII, PiMOEA, BiCo, NSGAII, and PreMOEA exceeds the critical difference according to the Bonferroni-Dunn test for a 95% confidence level, i.e. 2.450. Thus, at the 90% confidence level, MP-MOEA is significantly superior to 5 out of the 7 comparison algorithms for ME, namely AGEMOEAII, PiMOEA, BiCo, NSGAII, and PreMOEA. Similarly, as shown in Table 9, based on the Friedman test and pairwise post hoc Bonferroni-Dunn test, MP-MOEA is significantly superior to all the comparison algorithms in terms of the HV metric at the 90% confidence level. In summary, MP-MOEA outperforms most of the comparison algorithms for each objective function. For the HV metric, MP-MOEA achieved the best results. These findings validate the effectiveness of MP-MOEA in solving MIRPs. These results validate the effectiveness of MP-MOEA in solving MIRPs.

Table 7 Average ranks of various algorithms for the MT.
Full size table
Table 8 Average ranks of various algorithms for the ME.
Full size table
Table 9 Average ranks of various algorithms for the HV.
Full size table

Comparison of running time

Figure 11 shows the average running time of all algorithms after 30 independent runs on all test cases. As shown in Fig. 11, the computation time of all algorithms increases as the problem scale grows from small to large.

Fig. 11
figure 11

Running time of algorithms on different test cases.

Full size image
Fig. 12
figure 12

Pareto fronts of MP-MOEA with different crossover operators.

Full size image

For small-scale test cases, MP-MOEA leads the other algorithms with a computation time of 4.9 minutes for Small case 1 but is slightly outperformed by BiCo for Small case 2. For middle-scale test cases, MP-MOEA achieves the shortest running time for Middle case 1. However, for Middle case 2, MP-MOEA performs slightly worse than MSCE and PreDEMO. For large-scale test problems, MP-MOEA achieves the fastest running time for both Large case 1 and Large case 2. The hybrid crossover operator, contribution-based mutation operator, and individual modification operator in MP-MOEA effectively enhance the algorithm’s search capability, but they require slightly more time compared to basic genetic operators. However, the three-level dynamic encoding mechanism employed in MP-MOEA can significantly reduce the number of decision variables, thereby lowering the difficulty of solving the problem and greatly reducing the required computational time. This reduction in the dimension of the decision space becomes even more pronounced as the problem scale increases, so MP-MOEA demonstrates a clear advantage in running time for large-scale MIRPs.

Fig. 13
figure 13

Pareto fronts achieved by MP-MOEA with and without the contribution-based mutation operator.

Full size image

Investigation of key operators

To elaborate on the influence of the proposed hybrid crossover operator and contribution-based mutation operator on the performance of MP-MOEA, Small case 1, Middle case 1, and Large case 1 are chosen as examples.

Investigation of the hybrid crossover operator

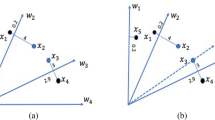
The algorithm that only uses PMX performs the worst among all three algorithms. The PMX crossover method operates based on segments of decision variables, which can easily disrupt high-quality solutions already found by the algorithm, resulting in poor convergence. The algorithm that uses only SBX performs between the one using PMX and the one with the hybrid crossover strategy. The SBX crossover method typically produces offspring with quality between that of the parent individuals, making it prone to local optima when the parent individuals are similar. As shown in Fig. 12, the MO-MOEA using only SBX has poorer convergence and diversity compared to the MP-MOEA with the hybrid crossover operator.

Figure 12a–c illustrates the influence of the hybrid crossover operators on the performance of MP-MOEA across three test cases. It can be observed from Fig. 12 that the performance of MP-MOEA with the hybrid crossover operator is significantly better than that of MP-MOEA using either PMX or SBX alone.

Investigation of the contribution-based mutation operator

Figure 13a–c illustrates the impact of the contribution-based mutation operator on the performance of MP-MOEA across three test cases. Figure 13 indicates that the algorithm’s performance is significantly enhanced by incorporating the proposed mutation operator, which removes unnecessary loading and unloading of containers during transportation, thereby reducing transportation costs and greenhouse gas emissions. The results in Fig. 13 show that using the proposed mutation operator helps MP-MOEA achieve better Pareto fronts on all three test cases.

Table 10 Redundancy of Unloading with and without Mutation Operator Across Different Cases.
Full size table

Table 10 shows the number of redundant unloading containers produced by MP-MOEA with and without the proposed contribution-based mutation operator for Small case 1, Middle case 1, and Large case 1. Note that the results presented are the average values obtained by analyzing each individual in the Pareto-optimal solution set for the three test cases. As shown in Table 10, compared to MP-MOEA that does not use the proposed contribution-based mutation operator, MP-MOEA using the mutation operator significantly reduces the number of redundant unloaded containers. Take Small case 1 as an example for a specific explanation. In Small case 1, Port 1 requires 500 a-type containers, Port 2 requires 900 b-type containers and 800 c-type containers, and Port 3 requires 800 a-type containers. According to Table 10, the solutions obtained by the algorithm using the mutation operator have an average unloading quantity of 534.7 a-type containers at Port 1, resulting in a redundancy of 34.7 containers. In contrast, the solutions obtained without the mutation operator have an average unloading quantity of 691.3 a-type containers at Port 1, with a redundancy of 191.3 containers. For Small case 1, the total redundant unloading quantity for MP-MOEA with the contribution-based mutation operator is 214.4 containers, while the total redundancy for MP-MOEA without the mutation operator is 684.1 containers. In other words, using the contribution-based mutation operator reduces the redundant unloading quantity by 68.7%. For Middle case 1, the total redundant unloading quantity for MP-MOEA using the mutation operator is 732.8 containers, while the total redundancy for MP-MOEA without the mutation operator is 2224.6 containers. Using the mutation operator reduces the redundant unloading quantity by 67.1%. For Large case 1, the total redundant unloading quantity for the algorithm using the mutation operator is 607.1 containers, while the total redundancy without the operator is 2113.8 containers. Using the mutation operator reduces the redundant unloading quantity by 71.2%. As can be seen from Table 10, the contribution-based mutation operator effectively helps MP-MOEA find scheduling solutions with fewer redundant unloading quantities in all three different-scale test cases. This is mainly because the contribution value in the proposed mutation operator is calculated based on the redundant unloading quantity at the port. Guided by the contribution value, the proposed mutation operator helps MP-MOEA search for solutions with reduced redundant unloading quantities.

Case analysis

The MP-MOEA proposed in this paper optimizes both total transportation costs and greenhouse gas emissions. These two objectives are mutually exclusive. Therefore, MP-MOEA ultimately provides a set of Pareto-optimal solutions, among which no single solution is better than the others. Specifically, solution x may superior to solution y in terms of total transportation costs but inferior to y regarding greenhouse gas emissions. To help decision-makers choose suitable solutions based on their needs, this section uses Middle case 2 as an example and analyzes three representative solutions selected from the Pareto-optimal solutions obtained by MP-MOEA. The first solution (referred to as “Solution I”) has the lowest transportation cost and the highest greenhouse gas emissions. The second solution (referred to as “Solution II”) strikes a balance between transportation cost and greenhouse gas emissions. The third solution (referred to as “Solution III”) has the highest transportation cost and the lowest greenhouse gas emissions. As shown in Table 3, the Middle case 2 includes 11 sub-periods through the entire planning period and involves six vessels to be scheduled: one large A-type, four middle C-types, and one small N-type. This task involves two types of containers, with a total transportation gap of 4600 containers.

Table 11 presents the fleet design and vessel scheduling plan corresponding to Solution I. In this scheme, the fleet consists of one large A-type vessel, four medium-sized C-type vessels, and one small E-type vessel. To achieve the objective of minimizing total transportation costs, all six vessels are assigned navigation tasks. As shown in Table 11, each vessel docks at 2 to 3 ports during its voyage. Specifically, vessels 1, 2, and 4 visit two ports within the planning period, while vessels 3, 5, and 6 visit three ports. The total voyage distance is 1853 nautical miles. If following the scheduling plan shown in Solution I, the total transportation cost during the planning period would be 27.0196 million RMB, and the total greenhouse gas emissions would be 1740.25 tons.

Table 12 presents the fleet design and vessel scheduling plan corresponding to Solution. This scheme aims to balance total transportation costs and greenhouse gas emissions. The fleet comprises five vessels, including one small E-type vessel and four medium-sized C-type vessels. The total voyage distance is 1234 nautical miles. If following the scheduling plan shown in Solution II, the total transportation cost during the planning period would be 35.0143 million RMB, and the total greenhouse gas emissions would be 1638.82 tons. Compared to Scheme I, the cost increases by 22.8%, while greenhouse gas emissions decrease by 6.8%.

Table 13 presents the fleet design and ship scheduling plan corresponding to Solution III. This scheme aims to minimize greenhouse gas emissions and involves four vessels, including three medium-sized C-type vessels and one small E-type vessel. The total voyage distance is 1018 nautical miles. The total transportation cost during the planning period is 42.5248 million RMB. Compared to Scheme II, although the transportation cost increases by approximately 17.6%, the greenhouse gas emissions decrease by 9.9%.

A comprehensive analysis of the three schemes reveals significant differences in fleet structure and vessel scheduling design based on different purposes. From the fleet structure perspective, if the goal is to minimize transportation costs, the proportion of large vessels in the fleet will increase. Regarding vessel routing, optimizing for transportation costs or greenhouse gas emissions leads to significantly different routes. If the goal is to minimize greenhouse gas emissions, the planned routes will have a relatively small total voyage distance.

Table 11 Fleet operation plan (corresponding to solution I).
Full size table
Table 12 Fleet operation plan (corresponding to solution II).
Full size table
Table 13 Fleet operation plan (corresponding to solution III).
Full size table

Concluding remarks

This paper constructs a multi-objective optimization model for MIRPs, considering both total transportation costs and greenhouse gas emissions. Based on this multi-objective problem model, a multi-population-based multi-objective evolutionary algorithm (MP-MOEA) is proposed. MP-MOEA incorporates a multi-population-based initialization strategy, an individual modification operator, a hybrid crossover operator, and a contribution-based mutation strategy to enhance the algorithm’s performance. Specifically, the multi-population-based initialization strategy helps the algorithm generate populations with good diversity. Additionally, the proposed initialization operator employs a dynamic three-level encoding mechanism, which effectively reduces the encoding length. The individual modification operator is used to help the algorithm increase the proportion of feasible solutions in the offspring population. The hybrid crossover operator and contribution-based mutation strategy are adopted to improve the algorithm’s search efficiency. The proposed algorithm has been evaluated on six test cases of three different scales, and the statistical results compared with five state-of-the-art algorithms demonstrate the effectiveness of the proposed algorithm.

However, the proposed MP-MOEA only considers a single fleet. Enhancing the proposed algorithm to manage multiple fleets will be a key focus of future research. Additionally, the application of the constructed MIRP model is limited to known fleet numbers and types of operations. Future research could focus on optimizing models and algorithms for parallel operations involving multiple fleets with mixed tasks, further expanding their applicability and efficiency. Moreover, future studies can incorporate more practical constraints into the model to guide actual operations more accurately.