Introduction

The mobile internet provides users with vast resources, but it also brings about the issue of information overload. recommendation systems (RSs) have proven to be effective in mitigating the problem of information overload, leading to their widespread application across various online platforms1,2. The recommendation model based on GNNs captures the complex interactions between users and items by learning the graph structure. This enables the model to better reflect user behavior in the real world, thereby improving the accuracy of the RS3,4. Although the GNN-based recommendation method has achieved good results, there are still some shortcomings in the method. Firstly, the majority of models adopt the supervised learning paradigm for recommendation. However, in real-world scenarios, supervised data is often extremely sparse5. Secondly, traditional models predominantly focus on user behavior and feedback when dealing with user information, potentially overlooking the effective integration of auxiliary data such as knowledge graphs(KGs) into their frameworks6. This is because the rich semantic information in the KG can help the model better understand the deeper reasons behind users’ preferences for certain types of item.

The core idea of unsupervised learning is to help models better understand the structure and characteristics of data by comparing the similarities and differences between them. Due to its ability to reduce reliance on labeled data through data augmentation, unsupervised learning has achieved significant success in tasks such as image retrieval and text classification7,8,9,10. Various methods based on data augmentation have been proposed to address the limitations of current recommendation models based on GNNs11,12,13. Ref14 introduces unsupervised learning in multi-behavior recommendation, enabling the capture of fine-grained differences among users across various behaviors. Ref5 employs three different random dropout techniques to alter the original graph structure for data augmentation. Ref15 designed an adaptive method to dropout relevant nodes or edges in the user-item interaction graph, generating augmented views. Although compared with the GNN-based recommendation method, the use of data augmentation in unsupervised learning has achieved certain results16. If multiple data augmentation methods could be integrated to alleviate the sparsity of labeled data, recommendation models can more comprehensively and accurately capture the complex relationships between users and items, thereby enhancing recommendation quality and user satisfaction.

Fig. 1
figure 1

The working principle of unsupervised learning.

Full size image

The diffusion model generates high-quality samples in a highly stable manner, effectively addressing issues such as mode collapse and gradient vanishing encountered by Generative Adversarial Networks (GANs) during adversarial training. The limited representational capacity of Variational Autoencoders (VAEs) mainly stems from the discrete encoder and decoder they employ. This structure makes it difficult for VAEs to represent complex distributions. In contrast, diffusion models utilize continuous neural networks, capable of representing any continuous distribution. Therefore, diffusion models can better capture complex data distributions, thereby enhancing the quality of generated samples. Compared to traditional generative methods such as GANs and VAEs, Diffusion Models (DMs) and Score-Based Generative Models (SGMs) exhibit more significant advantages in the generation of images, audio, and text17,18,19,20,21. Inspired by DMs, we leverage the powerful generative capabilities of the diffusion process for data augmentation in supervised learning tasks. By integrating two different data augmentation techniques, we propose a novel recommendation model, DARec. In the supervised data augmentation tasks, noise is first introduced into the user-item interaction matrix using forward diffusion to perturb the original data. Subsequently, reverse diffusion is employed to remove the noise and restore the original data. In unsupervised data augmentation tasks, random edge dropout is primarily applied to the user-item interaction graph and the KG. The DARec model optimizes unsupervised and supervised learning by integrating two distinct data augmentation methods, thereby enhancing model performance without relying on large amounts of labeled data. Additionally, in unsupervised data augmentation tasks, DARec also minimizes the distance between positive samples while maximizing the distance between negative samples in the representation space. As illustrated in Fig. 1, let’s assume that User A is interested in sports-related items but not interested in electronics. We consider sports-related items as positive samples and electronics as negative samples. The objective of supervised learning classification is to enable the classification model to recognize specific labels for positive and negative samples. However, in unsupervised learning, the objective is for the model to group positive samples into one category, while negative samples do not belong to that category. In other words, unsupervised learning methods do not require knowledge of the specific names of sports-related items in positive samples or electronic products in negative samples. The model only needs to know which are positive samples and which are negative samples. Assuming the positive samples basketball, badminton, and soccer correspond to features f1, f2, and f3, respectively, while the negative samples phone, tablet, and computer correspond to features f4, f5, and f6, respectively. If positive and negative samples are fed into the same network. The unsupervised learning method can bring features f1, f2, and f3 closer together in the feature space while pushing them further away from features f4, f5, and f6. Exactly, the objective of unsupervised learning is to minimize the distance between positive samples while maximizing the distance between negative samples within a certain feature space. This allows the model to better capture the underlying relationship between the user and the item, thus improving the accuracy of the recommendations.

In summary, the contributions of this study are as follows:

  • Unlike methods that perform data augmentation solely on the user-item interaction graph, DARec utilizes the KG as auxiliary data and employs edge dropout to generate multiple augmented views. Our model can comprehensively capture the features of users and items and perform more granular similarity modeling, thereby generating recommendations that are more interpretable.

  • We attempt to leverage the powerful generative capabilities of diffusion models for data augmentation in supervised learning. Our method aims to minimize disruption to the original data as much as possible.

  • The DARec model integrates two different data augmentation methods, enabling the utilization of newly generated samples from unsupervised learning tasks as inputs for supervised learning models. Additionally, it leverages outputs from supervised learning tasks (such as classification labels) to optimize the unsupervised learning process. This approach effectively addresses the issue of sparse label data and brings about a new breakthrough in the field of RSs.

  • We conducted extensive experiments on three representative datasets, and the results indicate that our DARec model achieves significantly better recommendation performance compared to some representative baselines.

Related work

GNN-based recommendation methods

Recommendation algorithms based on GNNs represent the interactions between users and items as a bipartite graph and employ graph convolution techniques22,23. These methods have outperformed traditional deep learning-based approaches. LightGCN24 simplifies early attempts at using GCNs for collaborative filtering by omitting feature transformation and non-linear activation. UltraGCN25 approximates the limit of infinite-layer graph convolutions directly through constrained loss. It skips the message-passing process of infinite layers to achieve efficient recommendation. To address the issue that existing GNN-based recommendation systems overlook interactions caused by unreliable behaviors (e.g., random clicks), GTN26 introduces a principled graph trend collaborative filtering technique to capture the reliability of interactions between users and items. DGRec27 proposes a diversified GNN-based recommendation system by directly enhancing the embedding generation process.

Unsupervised learning

Unsupervised learning, also known as self-supervised learning, is primarily utilized to learn the intrinsic structure or features of data from unlabeled datasets. This method reduces the cost and time of manual labeling. This makes unsupervised learning particularly effective in many domains, especially when obtaining large amounts of labeled data is challenging28,29,30,31. Recently, some studies have proposed combining GNNs with unsupervised learning to address the issue of sparsity in labeled data during the recommendation process. To enhance the performance of the RS, SMIN utilizes heterogeneous GNNs to learn the complex social relationships between users and items. Furthermore, it proposes a unsupervised learning framework to augment the modeling of higher-order information in the user-item interaction graph32. Ref33 utilizes self-supervised learning to extract additional supervisory signals and untangle users’ preference intents in the latent space, addressing convergence challenges in sequence recommendation. SHT introduces a cross-view self-supervised learning method, employing data augmentation on the user-item interaction graph. On the other hand, by explicitly exploring global collaborative relationships, the model’s robustness to noise perturbations is improved34. To address the issues of data sparsity and long-tail distribution, SSL35 generates additional supervisory signals by masking input information. It utilizes a two-tower DNN to encode the augmented data. Despite the demonstrated effectiveness of data augmentation techniques in the field of unsupervised learning, integrating multiple data augmentation strategies could further alleviate the issue of labeled data scarcity, thereby enhancing the accuracy and personalization of recommendations.

Diffusion-based generative model

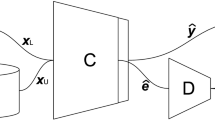
Generative models can learn the distribution of data and generate new samples that are similar but not identical to the training data. This is particularly useful for tasks such as data augmentation, sample generation, image synthesis, and more36. Generative models have a significant advantage in modeling the uncertainty of user behavior in RS. DiffRec37 aims to reduce the damage to user interaction data by minimizing the added noise and learning the generation process in a denoising manner. This method lays the foundation for generative recommendation models. By making modifications to both the forward and backward processes and enhancing the diffusion process, a sequence recommendation method based on the diffusion model was proposed38. Diff-POI39 utilizes the diffusion process and its reverse form to sample from the posterior distribution, further demonstrating the powerful capabilities of denoising diffusion processes and SGMs. The SGMs utilizes the forward diffusion process to smoothly transform data into noise and removes the noise through the reverse process to synthesize fake samples, making it an excellent deep generative model. The Fig. 2 illustrates the specific working principles of SGMs40.

However, SDEs contain a random component, introducing uncertainty and randomness into the system. In our model, we only deal with the user-item interaction matrix, so we only need to use ordinary differential equations (ODEs). ODEs do not include a random component; they are equations involving unknown functions and their derivatives. At each time point, the evolution of the system is entirely determined by deterministic rules.

Fig. 2
figure 2

the specific working principles of SGMs.

Full size image

Ordinary differential equations

ODEs can be defined by the following equation:

$$\begin{aligned} x\left( T \right) = x\left( 0 \right) + \int _0^T {f\left( {x\left( t \right) } \right) } dt \end{aligned}$$
(1)

f is the ODE function describing the time-derivative of x. In practical applications, finding an analytical solution for \(x\left( T \right)\) is often not feasible. The initial value at \(t = 0\) is represented by \(x\left( 0 \right)\). As a result, by integrating the time-derivative of x until \(t = T\), we obtain the solution \(x\left( T \right)\) at the time \(t = T\). In general, to solve this problem, we need to utilize ODE solvers, such as the Runge-Kutta method(RK4), the Euler method. The definition of the RK4 method is as follows:

$$\begin{aligned} x\left( {t + \omega } \right) = x\left( t \right) + \frac{s}{6}\left( {{f_1} + 2{f_2} + 2{f_3} + {f_4}} \right) \end{aligned}$$
(2)

Where \({f_1} = f\left( {x\left( t \right) } \right)\),\({f_2} = f\left( {x\left( t \right) + \frac{\omega }{2}{f_1}} \right)\), \({f_3} = f\left( {x\left( t \right) + \frac{\omega }{2}{f_2}} \right)\), and \({f_4} = f\left( {x\left( t \right) + \omega {f_3}} \right)\).

The definition of the Euler method is as follows:

$$\begin{aligned} x\left( {t + s} \right) = x\left( t \right) + \omega \cdot f\left( {x\left( t \right) } \right) \end{aligned}$$
(3)

Where the pre-configured step size is represented by \(\omega\). Since \(x\left( t \right)\) is updated to \(x\left( {t + \omega } \right)\) with each iteration. The integration problem can be solved by iterating over one of the ODE solvers \(\frac{T}{\omega }\) times with a fixed step size.

Preliminaries

In this section, we will introduce the relevant symbols and definitions used in this study.

Assuming m and n represent the number of users and items, respectively, \(U = \left\{ {{u_1},{u_2}, \ldots ,{u_m}} \right\}\) and \(I = \left\{ {{i_1},{i_2}, \ldots ,{i_n}} \right\}\) denote the sets of users and items, respectively. We first define a user-item interaction matrix \(\mathrm{{R}} \in \left| U \right| \times \left| I \right|\) to represent the interaction behavior of users with different items. Then, based on the matrix \(\mathrm{{R}}\), we construct the user-item interaction graph \({G_{ui}} = \left\{ {U,I,E} \right\}\). We use the user-item interaction graph to represent the interaction relationships between users and items. The set of edges that represent interactions between users and items is denoted by E. If there is an interaction between a user and an item, an edge \({E_{ui}}\) will be established between the user node and the item node. Considering that KG contains rich semantic information, understanding the complex relationship between users and items can be enhanced by introducing KG into RS. We use \({G_k} = \left\{ {\left( {\mathcal{H},\mathcal{R},\mathcal{T}} \right) } \right\}\) to represent the KG, where \(\mathcal{H}\), \(\mathcal{R}\), and \(\mathcal{T}\) respectively denote the sets of head entities, relations, and tail entities. Given the user item interaction graph \({G_{ui}}\) and the KG \({G_k}\), the goal of DARec is to predict the probability that a user will interact with certain items.

Fig. 3
figure 3

The overall architecture of the DARec model. Input Module: the user-item interaction matrix \(\mathrm{{R}}\), the knowledge graph \({G_k}\), and The user-item interaction graph \({G_{ui}}\). Diffusion Module (Supervised Learning): Forward Diffusion: Adds noise to the interaction matrix \(\mathrm{{R}}\) to generate a blurred interaction matrix \({\mathrm{{R}}'}\). Reverse Diffusion: Denoises the blurred matrix to generate an augmented matrix \({\mathrm{{R}}^*}\). The entire process is outlined in Algorithm 1. Graph Augmentation Module (Unsupervised Learning): Edge dropout is performed on the user-item interaction graph \({G_{ui}}\) and the knowledge graph \({G_k}\), generating augmented graph views \(\alpha _1(G_{ui})\), \(\alpha _2(G_{ui})\) and \(\beta _1(G_k)\), \(\beta _2(G_k)\). The entire process is outlined in Algorithm 2.

Full size image

Methodology

The DARec model integrates supervised and unsupervised learning, applying diffusion and edge dropout methods for data augmentation, respectively. Ultimately, recommendation is achieved through joint training. In the supervised learning task, we perform the forward diffusion process and the reverse diffusion process on the user-item interaction matrix for data augmentation. DARec controls the influence of the diffusion process on the original data by adjusting the parameters of the model. This means that the addition of noise is carried out within a controlled range and does not cause fundamental damage to the original interaction matrix. Therefore, our model aims to make the matrix \({\mathrm{{R}}^*}\) as similar as possible to the matrix \(\mathrm{{R}}\). In unsupervised learning tasks, we apply edge dropout to the user-item interaction graph and the KG to generate multiple diverse augmented views. The reason is that this approach not only helps the model to make accurate predictions despite the lack of some interaction information but also minimizes the damage to the original graph structure. Finally, we conduct joint training for the supervised learning task and unsupervised learning task, optimizing their respective loss functions to achieve the optimal performance of the model. During the model training process, unsupervised learning models can generate new features to be used as inputs for supervised learning models. Conversely, outputs from supervised learning models can serve as labels for unsupervised learning models, guiding their learning process. Through this mutual interaction, better utilization of data resources can be achieved, thus enhancing the performance of RSs. Figure 3 illustrates the overall architecture of the DARec model. Our specific work will be detailed in the following subsections.

Supervised learning task

Our Supervised learning task is divided into two key parts: the forward diffusion process and the reverse diffusion process. Specifically, we perform forward diffusion by adding noise to the interaction matrix \(\mathrm{{R}}\), resulting in its blurred matrix \({\mathrm{{R}}'}\). Then, through the reverse process, we remove the noise from the blurred matrix to derive its enhanced matrix \({\mathrm{{R}}^*}\). As shown in Fig. 3 (a), these two processes take full advantage of the generative capabilities of diffusion models for data augmentation. It effectively alleviates the sparsity problem of labeled data in the RS.

Algorithm 1
figure a

Supervised Data Augmentation using Diffusion Model

Full size image

Forward diffusion process

Forward Diffusion aims to model the process by which data goes from clear to progressively noisy. It helps the model to better understand and deal with uncertain data in the real world. The forward diffusion process can be defined as follows:

$$\begin{aligned} F\left( {{T_f}} \right) = F\left( 0 \right) + \int _0^{{T_f}} {f\left( {F\left( t \right) } \right) } dt \end{aligned}$$
(4)

Here, \(F\left( 0 \right)\) represents the initial interaction matrix \(\mathrm{{R}}\) set in our DARec model. f represents a forward diffusion function that approximates \(\frac{{dF\left( t \right) }}{{dt}}\). \({T_f}\) denotes the time of forward diffusion. Therefore, \(F\left( 1 \right)\) can represent an interaction matrix after injecting noise in the forward diffusion process. The specific forward diffusion process is determined by the definition of the function f.

For different purposes, various similar forward diffusion functions have been defined in different fields. In this study, we use the heat equation to define the forward diffusion function f. The heat equation is a mathematical model that describes the diffusion and distribution of heat in a physical system, based on the Newton’s law of cooling which describes the rate of heat loss in a body. The function f is defined as follows:

$$\begin{aligned} f\left( {F\left( t \right) } \right) = k\left( {F\left( t \right) } \right) \left( {\mathop {X - }\limits ^ \sim I} \right) \end{aligned}$$
(5)

The coefficient k, known as the heat capacity, is a hyperparameter in our model that determines the strength of the forward diffusion process. This definition of f bears a resemblance to the low-pass filter commonly used in graph convolutions. Where symbols \(\mathop X\limits ^ \sim\) and I represent the normalized adjacency matrix and the identity matrix, respectively. The operation \(\mathop {X - }\limits ^ \sim I\) represents a matrix operation that applies low-pass filtering to the given matrix. This operation helps preserve the low-frequency information of the matrix while removing high-frequency information, achieving the effect of adding noise to the original matrix.

Reverse diffusion process

As the reverse diffusion process progresses, the noise is gradually removed and the features of the data are gradually restored, and finally a sample close to the original data is generated. The reverse diffusion process can be defined according to the ODE solver:

$$\begin{aligned} R\left( {{T_r}} \right) = R\left( 0 \right) + \int _0^{{T_\mathrm{{r}}}} {r\left( {R\left( t \right) } \right) } dt \end{aligned}$$
(6)

where the matrix \(R\left( 1 \right)\) can be obtained after removing the noise by reverse diffusion function for the input matrix \(R\left( 0 \right)\). \({T_\mathrm{{r}}}\) denotes the time of reverse diffusion. The function r representrs a reverse diffusion function that approximates \(\frac{{dR\left( t \right) }}{{dt}}\). In DARec model, the reverse diffusion function r can be defined by the following formula:

$$\begin{aligned} r\left( {R\left( t \right) } \right) = - r\left( {R\left( t \right) } \right) \mathop X\limits ^ \sim \end{aligned}$$
(7)

The negative sign is used to emphasize the denoising effect on the perturbation matrix, thereby enhancing the restoration ability of the original matrix.

In supervised learning task, leveraging the powerful generative capability of the diffusion model for data augmentation enables the generation of new samples, mitigating the issue of sparse supervised data.

Unsupervised learning task

In unsupervised learning task, DARec mitigates the sparsity of labeled data by constructing supervision signals through data augmentation. This is achieved by randomly dropping edges in the user-item interaction graph and the KG. Edge dropout can simulate scenarios where interactions between certain users and items in the graph are hidden or missing. The purpose of this is to enable the model to learn more robust and generalized representations, as the model needs to adapt to situations with missing information.

Algorithm 2
figure b

Unsupervised Data Augmentation using Edge Dropout

Full size image

We first perform data augmentation on the user-item interaction graph, and this process can be represented by the following formula:

$$\begin{aligned} {\alpha _1}\left( {{G_{ui}}} \right) = \left( {V,M_{ui}^1 \odot E} \right) ,\mathrm{ }{\alpha _2}\left( {{G_{ui}}} \right) = \left( {V,M_{ui}^2 \odot E} \right) \end{aligned}$$
(8)

Where \(M_{ui}^1,M_{ui}^2 \in \left\{ {0,1} \right\}\) represents two different mask vectors generated in the \({G_{ui}}\). The functions \({\alpha _1}\left( \cdot \right)\) and \({\alpha _2}\left( \cdot \right)\) represent our graph augmentation operator, which randomly deletes some user-item interaction data from the edge set E of the user-item interaction graph \({G_{ui}}\). V and E represent the vertex set and edge set in the \({G_{ui}}\), respectively. Similarly, the process of data augmentation on the KG can be represented by the following formula:

$$\begin{aligned} {\beta _1}\left( {{G_k}} \right) = \left( {\mathrm{{V}},M_k^1 \odot \mathrm{{E}}} \right) ,\mathrm{ }{\beta _2}\left( {{G_k}} \right) = \left( {\mathrm{{V,}}M_k^2 \odot \mathrm{{E}}} \right) \end{aligned}$$
(9)

Where \(M_k^1,M_k^2 \in \left\{ {0,1} \right\}\) denotes two different mask vectors generated in the \({G_k}\). The functions \({\beta _1}\left( \cdot \right)\) and \({\beta _2}\left( \cdot \right)\) denote that some user-item interaction information is randomly removed from the edge set \(\mathrm{{E}}\) of the \({G_k}\) with different probabilities. \(\mathrm{{V}}\) and \(\mathrm{{E}}\) denote the vertex set and edge set in the \({G_k}\), respectively.

By adopting the mentioned approach, DARec model can generate various augmented views. Furthermore, our data augmentation scheme aims to minimize damage to the original graph structure and effectively alleviate the issue of missing labeled data.

After data augmentation in the \({G_{ui}}\) and \({G_k}\) , we represent the enhanced views generated from the same node as positive samples \(\left\{ {\left( {h_u^1,h_u^2} \right) |u \in U} \right\}\) and the enhanced views generated from different nodes as negative samples \(\left\{ {\left( {h_u^1,h_v^2} \right) |u,v \in U,u \ne v} \right\}\). DARec uses the generated enhanced views for unsupervised learning. Unsupervised learning aims to bring positive samples closer in the embedding space while increasing the distance between positive and negative samples in the embedding space. The loss function in DARec is defined based on the InfoNCE loss41, and the formula is as follows:

$$\begin{aligned} {L_{\text {unsupervised}}} = \sum \limits _{u \in U} - \log \frac{{\exp \left( {s\left( {h_u^1,h_u^2} \right) /\tau } \right) }}{{\sum \nolimits _{v \in U} {\exp \left( {s\left( {h_u^1,h_v^2} \right) /\tau } \right) } }} \end{aligned}$$
(10)

In the formula, \(\tau\) represents the temperature parameter, and \(s\left( \cdot \right)\) represents the cosine function, which estimates the similarity between positive and negative samples in our model. The loss function is a crucial component of the unsupervised learning framework. Minimizing the loss function encourages the model to learn a representation where similar samples are closer in the embedding space, while dissimilar samples are more dispersed. This contributes to improving the quality of recommendations and enhancing the user experience.

Algorithm 3
figure c

Joint Training of Supervised and Unsupervised Tasks

Full size image

Joint training task

DARec, through the joint training of the supervised learning task and the unsupervised learning task, helps to simultaneously capture semantic relationships of entities in users, items, and the KG in the embedding space. This contributes to improving the accuracy and personalization of recommendations. Specifically, in the supervised learning component, data augmentation is performed on the user-item interaction matrix using the diffusion model. In the unsupervised learning component, data augmentation is achieved by applying edge dropout to the user-item interaction graph and the knowledge graph. The DARec model then employs graph convolution operations from GNNs to extract features, generating the corresponding user and item embeddings \(\left( {{U_{GNN}},{I_{GNN}}} \right)\). Ultimately, joint training is performed by collaboratively optimizing the supervised and unsupervised learning losses to ensure convergence. We choose the Bayesian Personalized Ranking (BPR) loss42 as the loss function for the supervised learning task. By jointly training the loss functions from supervised learning and unsupervised learning, the DARec model is effectively optimized. This implies that the model is not only capable of distinguishing between positive and negative samples through unsupervised learning but also of improving the ranking of positive samples relative to negative ones. The BPR loss function is defined as follows:

$$\begin{aligned} {L_{\text {supervised}}} = \sum \limits _{\left( {u,i,{i^*}} \right) \in O} { - \ln \sigma \left( {{{\mathop y\limits ^ \wedge }_{u,i}} - {{\mathop y\limits ^ \wedge }_{u,{i^*}}}} \right) } \end{aligned}$$
(11)

Where \(\sigma \left( \cdot \right)\) represents the sigmoid function, and \(O = \left\{ {\left( {u,i,{i^*}} \right) |\left( {u,i} \right) \in {O^ + },\left( {u,{i^*}} \right) \in {O^ - }} \right\}\) represents the training data in the model. \({O^ + }\) represents the interaction between users and items, while \({O^ - }\) represents the absence of interaction between users and items. Therefore, the joint training loss of DARec is defined as follows:

$$\begin{aligned} L = {L_{\text {supervised}}} + {\lambda _1}{L_{\text {unsupervised}}} + {\lambda _2}\left\| \Theta \right\| _2^2 \end{aligned}$$
(12)

Where \({\lambda _1}\) represents the parameter determining the strength of the unsupervised learning signal, and \({\lambda _2}\) is the parameter controlling the regularization of the joint loss function. \(\Theta\) represents the learnable parameters in the DARec model.

Time complexity analysis of DARec

Assume that the dimension of the user-item interaction matrix \(\mathrm{{R}}\) is \(m \times n\) (with m users and n items), and the dimension of the adjacency matrix is \(n \times n\). The time complexity of matrix multiplication is \(O(m{n^2})\). Since forward diffusion requires \({T_f}\) iterations, the total complexity is \(O({T_f} \cdot m{n^2})\). Backward diffusion is similar to forward diffusion, and its time complexity is \(O({T_r} \cdot m{n^2})\). Therefore, the overall time complexity of the diffusion model is \(O(({T_f} + {T_r}) \cdot m{n^2})\). The core operation of graph data augmentation is to randomly traverse the edges of the graph and perform edge dropout. Assuming the number of edges in the graph is \(\left| E \right|\), the time complexity of edge dropout is \(O\left( {\left| E \right| } \right)\). The core operation of graph embedding computation is the GNN calculating node embeddings through the adjacency matrix and feature matrix, with the key operation being sparse matrix multiplication. Assuming the number of non-zero elements in the adjacency matrix is \(\left| Y \right|\), and the dimension of the feature matrix is d, the time complexity of each GNN layer is \(O(\left| Y \right| \cdot d)\). Assuming the GNN has L layers, the total complexity is \(O(L \cdot \left| Y \right| \cdot d)\). The total complexity of graph data augmentation and embedding computation is \(O(\left| E \right| + L \cdot \left| Y \right| \cdot d)\). Therefore, the time complexity of DARec is \(O(({T_f} + {T_r}) \cdot m{n^2} + \left| E \right| + L \cdot \left| Y \right| \cdot d)\).

Experiments

To demonstrate the recommendation effectiveness of the DARec model, we conducted comprehensive experiments and addressed the following research questions:

  • RQ1:What is the performance of the DARec framework compared to other types of recommendation methods?

  • RQ2:Can different data augmentation methods in the DARec model enhance recommendation performance?

  • RQ3:How do different parameters in the DARec model affect the recommendation effectiveness?

  • RQ4:How does DARec enhance the training effectiveness of the model?

Experimental settings

Datasets

In this study, we selected three commonly used public datasets in the field of RSs and conducted extensive experiments to validate the effectiveness of DARec.

Yelp2018: This dataset primarily includes user reviews and ratings for various businesses (such as restaurants, shops, etc.), providing personalized recommendations for commercial establishments to users. Datasetlink:https://www.yelp.com/dataset

Amazon-Book: This dataset primarily involves Amazon’s book products. It can be used for book recommendations based on user purchase history, reviews, and other relevant information about books. Datasetlink:https://jmcauley.ucsd.edu/data/amazon/

MIND: The MIND dataset primarily includes user interactions with news articles, such as clicks, reads, and other interactions. It can be used for news recommendations to provide users with a personalized news reading experience. Datasetlink:https://msnews.github.io/

The statistical data for the datasets is shown in Table 1. Since the DARec model needs to use KG data for auxiliary recommendation, we constructed the corresponding KG for the Yelp2018 and Amazon-Book datasets according to similar settings in43. At the same time, we built a KG on the MIND dataset according to the data preprocessing strategy in44. The statistical information for the KG is presented in Table 2.

Table 1 The statistical information for the Yelp2018, Amazon-Book, and MIND datasets.
Full size table
Table 2 The statistical information of KG in the Yelp2018, Amazon-Book, and MIND datasets.
Full size table

Compared models

To illustrate the effectiveness of the DARec model, we compared it with some state-of-the-art baseline models:

  • KGCN45. This is a method that encodes higher-order information in user-item interaction data using relevant attributes from the KG.

  • BPR42. This method is a common recommendation approach that utilizes pairwise ranking loss to rank item candidates.

  • GC-MC46. Designing a graph autoencoder framework based on the user-item interaction graph to construct embeddings for users and items. This framework leverages edge information to enhance recommendation effectiveness.

  • KGAT43. This approach primarily utilizes collaborative filtering concepts, investigating the incorporation of a KG and user behavior data in recommendation tasks. It employs attention mechanisms to reveal the importance of different higher-order connections, aiming to provide more interpretable recommendations.

  • CKE47. This method employs three components to extract semantic features from the structured content, textual content, and visual content of items. It leverages various information from the knowledge base to enhance recommendation effectiveness.

  • LightGCN24. It simplifies the design of GNNs, effectively reducing model complexity and training difficulty while improving training effectiveness.

  • CKAN48. Proposed a heterogeneous propagation strategy that explicitly encodes information from the KG and collaborative information from user-item interactions. It utilizes a knowledge-aware attention mechanism to distinguish the contributions of different neighbors.

  • MVIN49. This method proposes a multi-view model capable of learning feature embeddings for items from user views and entity views.

  • KGIN50. It aims to explore the intent of users’ interest in certain items by leveraging auxiliary item knowledge to mine more granular user-item interaction behaviors.

  • SGL5. It is an advanced unsupervised learning method that effectively addresses the issue of sparse labeled data by utilizing three different data augmentation techniques.

  • KGCL6. This is an excellent data augmentation model. It proposes a graph-enhanced unsupervised learning paradigm to suppress KG noise in the information aggregation process, thereby learning more robust knowledge representations of items.

Evaluation metrics and hyperparameters

The recommendation performance of the DARec model is evaluated using ranking-based metrics, including Recall@N and NDCG@N, where N is set to 20. To ensure fairness and enhance the persuasiveness of the experiments, we adopt the strategy consistent with the settings in50.

In this experiment, we implemented the proposed DARec model and other baselines using PyTorch, and extensively tested the following major hyperparameters:

  • Specifically, The embedding dimension for all methods is fixed at 64 and optimize the DARec model using a learning rate of \(1{e^{ - 3}}\) and a batch size of 2048. The hyperparameters \({\lambda _1}\) and \({\lambda _2}\) are tuned from the ragne \(\left\{ {1{\mathrm{{e}}^{ - 2}},1{e^{ - 3}},1{e^{ - 4}}} \right\}\) for loss balance.

  • We consider using the Euler method and the RK4 method as ODE solvers to solve the integration problem of the diffusion process. For the diffusion process, the solver’s step size \(\frac{T}{\omega } = \mathrm{{K\_s}}\) is adjusted in the range \(\left\{ {1,2,3,4,5} \right\}\), and the terminal time \(\mathrm{{T\_s}}\) is adjusted in the range \(\left\{ {1,2,3,4,5} \right\}\).

Table 3 Performance comparison of the DARec model with other baselines on Yelp2018, Amazon, and MIND Datasets.
Full size table

Overall performance (RQ1)

Table 3 displays the performance comparison between DARec and some representative baseline methods on three datasets. From which we can draw the following conclusions:

Evidently, recommendation methods based on GNNs (e.g., KGAT, CKE, LightGCN) generally outperform traditional recommendation methods (e.g., BPR). This is because recommendation algorithms based on GNNs can propagate information in the graph structure, enabling them to learn and capture complex interaction patterns between users and items. This includes social relationships among users, as well as multi-level relationships between users and items.

It is not difficult to observe that integrating KGs as auxiliary information into recommendation algorithms based on GNNs (e.g., CKAN, MVIN, KGIN) yields significantly better results than using GNN-based recommendation methods alone (e.g., KGAT, LightGCN). Because KGs typically contain attribute information about entities, especially for items that infrequently appear in user behavioral data, these attribute details can be integrated into GNNs to better understand and predict user preferences for such items.

In addition, recommendation algorithms based on unsupervised learning (e.g., SGL, KGCL) outperform recommendation algorithms that integrate KGs (e.g., CKAN, MVIN, KGIN). This reflects that unsupervised learning can achieve favorable recommendation results even in situations where supervised data is sparse, and label information is limited or unavailable.

Compared to methods that do not use data augmentation (e.g., KGIN), DARec improved the Recall and NDCG metrics on the Yelp2018 dataset by 6.74% and 7.79%, respectively. On the Amazon-Book dataset, the Recall and NDCG metrics are improved by 9.47% and 22.99%, respectively. The Recall and NDCG metrics on the MIND dataset respectively improved by 5.27% and 7.40%. The recommendation performance achieved by DARec through integrating different data augmentation methods is superior to using only a single data augmentation method, such as SGL and KGCL. For example, compared with KGCL, DARec’s Recall and NDCG metrics on the Amazon-book dataset are improved by 5.08% and 16.01%, respectively. On the other hand, the improvement of DARec on the Yelp2018 dataset is not very significant, which may be attributed to the sparsity of the dataset. In conclusion, DARec consistently achieves the best results compared to other excellent baselines. This is because traditional recommendation systems are prone to overfitting in data-scarce scenarios. The DARec model employs a diffusion model for data augmentation. By introducing noise into the user-item interaction matrix and using the reverse diffusion process to remove the noise and generate pseudo-labels, it provides additional supervisory signals to the model. Unlike traditional Graph Neural Network methods, DARec generates multiple augmented views of the graph by randomly deleting certain edges while preserving the graph structure. This approach not only enhances the robustness of the graph but also effectively mitigates the impact of label scarcity, thereby improving recommendation performance. We believe that the DARec model breaks through the limitations of traditional methods that rely solely on supervised or unsupervised learning. This fusion of supervised and unsupervised strategies has not been widely applied in recommendation systems, making it highly novel.

Table 4 The impact of data augmentation on the performance of the DARec model.
Full size table

Ablation study of DARec model (RQ2)

The impact of different data augmentation methods on recommendation effectiveness

To study the impact of two data augmentation approaches on the performance of the DARec model and demonstrate their effectiveness, we designed two variants of DARec, namely DARec-RM and DARec-RA, and conducted ablation experiments in three datasets. DARec-RM and DARec-RA represent variants where the data augmentation module was removed from the supervised learning task and the entire model, respectively. From Table 4, it can be observed that the recommendation performance of the DARec model in the three datasets is significantly superior to the other two variants. Specifically, when we remove the data augmentation module from both the supervised learning task and the entire model, the recommendation performance of the DARec model shows a noticeable decline. This phenomenon suggests that by integrating diffusion and edge dropout, two different methods for data augmentation, unexpected recommendation results can be achieved. When we removed the data augmentation module based on the diffusion model, the model’s Recall and NDCG showed a significant drop across all datasets. For instance, on the Amazon-Book dataset, Recall and NDCG decreased by 5.4% and 15.0%, respectively. This is because the pseudo-labels generated by the diffusion model provide additional supervisory signals, compensating for the scarcity of labeled data and enhancing the model’s ability to understand interaction data. When we further removed the data augmentation in the unsupervised learning component, the model’s performance declined even more significantly. For example, on the Yelp2018 dataset, Recall and NDCG decreased by 10.8% and 12.0%, respectively. This indicates that by randomly dropping certain edges in the graph, the model learns how to make more robust recommendation decisions in the presence of missing information. This approach is particularly effective for sparse graph data, as it helps improve the generalization ability of both user and item embeddings. Moreover, our edge dropout technique also minimizes the disruption to the original graph structure.

Fig. 4
figure 4

Influence of Runge-Kuta method (RK4) and Euler method on DARec model.

Full size image

Impact of hyperparameters (RQ3)

In this section, we primarily conducted tests on the relevant hyperparameters of the DARec model to explore how these parameters influence the model’s performance.

The impact of using different ODE solvers during the diffusion process on recommendation performance

From Fig. 4, it can be observed that using RK4 as the ODE solver provides the optimal diffusion performance for DARec. The reason for this situation is that the Euler method, while simple and easy to implement, has relatively low accuracy, especially when dealing with complex diffusion models, which may lead to significant errors. While the RK4 method utilizes more intermediate steps and has better stability, it can to some extent suppress the accumulation of errors, making the solving process more reliable. This makes the RK4 method perform well in diffusion models where high-precision solutions are required.

The influence of step size (\(\mathrm{{K\_s}}\)) and terminal integration time (\(\mathrm{{T\_s}}\)) in the diffusion process on the DARec model

Due to space limitations, we use the Yelp2018 and Amazon-book datasets to verify how different terminal integration times and step sizes in the ODE solver affect the performance of the DARec model. As can be seen from Figs. 5a and 6a, the DARec model achieves the best recommendation when the diffusion step size in the Yelp2018 and Amazon-book datasets is set to 2 and 1, respectively. This shows that using fewer steps is sufficient to solve the integration problem in the ODE solver for diffusion processes. Therefore, setting an appropriate diffusion step size can help the model converge faster and reach the optimal solution, thereby improving training efficiency and recommendation accuracy. However, when the step size is increased to a certain extent, the model has integrated enough information to make accurate predictions, and further increasing the step size will not lead to more performance improvements. From Figs.5b and 6b, it can be seen that the DARec model achieves the best results when the terminal integration time is set to 2.6 and 4 in the Yelp2018 and Amazon-book datasets, respectively. Therefore, setting an appropriate value of \(\mathrm{{T\_s}}\) can help the model to better recover the information processed by noise and improve the accuracy of recommendation. The longer the terminal integration time in the diffusion process, the wider the range of user-item interaction information that the model can integrate. Setting the appropriate terminal integration time helps the model capture more global user preferences and item characteristics, and is able to mine more latent information from limited interaction data. In addition, the slight differences in parameters on different datasets are due to the different characteristics of each dataset, such as interaction data and sparsity.

The impact of Top-N on recommendation performance

Top-N refers to the system generating a ranked list of items for each user based on their predicted preference, and then presenting the top N items from this list to the user. Table 5 reflects the impact of different N values on the recommendation performance. As shown clearly in Fig. 7, when N is set to 20, DARec achieves optimal results across all three datasets. This is because when the value of N is small, the recommendation list contains fewer items. Although the recommended items may be considered the most relevant by the system, the limited quantity often results in a lower recall rate, meaning many items of actual interest to users may not be recommended. Therefore, we fixed the value of N at 20.

The impact of \({\lambda _1}\) and \({\lambda _2}\) on the performance of the DARec model

In our model, the hyperparameters \({\lambda _1}\) and \({\lambda _2}\) are used to balance the supervised learning loss and unsupervised learning loss. In this study, we fixed the value of \({\lambda _2}\) to \(1{e^{ - 3}}\) and searched for the optimal value of \({\lambda _1}\) within the range of \(1{e^{ - 2}}\) to \(1{e^{ - 4}}\). From Table 6 , it can be observed that the model achieves the best performance when the value of \({\lambda _1}\) is \(1{e^{ - 4}}\). This indicates that smaller values of \({\lambda _1}\) reduce the impact of unsupervised learning on the embedding space, resulting in better recommendation performance.

Fig. 5
figure 5

The effects of step size and terminal integration time on the DARec model during the diffusion process in the Yelp2018 dataset.

Full size image
Fig. 6
figure 6

The influence of step size and terminal integration time on the DARec model during the diffusion process in Amazon-book datasets.

Full size image

Case study (RQ4)

Differing from SGL5, we abandoned two data augmentation methods, namely, node dropout and random walks, in the unsupervised learning task. We believe that these two data augmentation methods may not distinguish the importance of edges during model training, potentially leading to the random deletion of crucial information. This deficiency in capturing the structural attributes of the user-item interaction graph may result in suboptimal recommendation performance. Therefore, in the unsupervised learning task of DARec, we exclusively employ edge dropout for data augmentation, avoiding potential damage to the raw data of the user-item interaction graph and KG. This approach is conducive to better capturing the associative relationships between users and items. More importantly, it differs from the approach of solely applying data augmentation in unsupervised learning. We utilize the generative capability of the diffusion model for data augmentation in the supervised learning task. By integrating different data augmentation methods, the model can generate more diverse samples during training, thereby enhancing the model’s generalization ability. Therefore, DARec consistently achieves state-of-the-art recommendation results.

Table 5 The impact of Top-N on recommendation performance.
Full size table
Fig. 7
figure 7

The recommendation performance of different N values on the three datasets.

Full size image
Table 6 The impact of \({\lambda _1}\) on the performance of the DARec model.
Full size table

Conclusion

In this paper, we designed a novel recommendation model called DARec. We perform data augmentation in the supervised learning task by utilizing diffusion on the interaction matrix, and our data augmentation approach in the supervised learning task does not compromise the structure of the interaction matrix. In the unsupervised learning task, we employ edge dropout for data augmentation, aiming to minimize potential disruptions to the interaction graph. Supervised learning can utilize existing labeled data to learn explicit relationships between users and items, thus enabling personalized recommendations. However, labeled data is often limited and may not cover all scenarios. In such cases, unsupervised learning can leverage unlabeled data to explore the underlying structure and features within the data, thereby enriching the knowledge base of RSs. By integrating two different data augmentation methods, the sparsity issue of labeled data in RSs can be addressed. Additionally, we leverage KG mining to discover associative information between entities, uncovering latent relationships hidden in user historical behaviors and item attributes. This aids the RS in a more accurate understanding of user interests and item features. Our unsupervised learning approach can model the similarity between users and items. When new users or items are introduced, they can be compared with other similar users or items. Therefore, this approach can generate more interpretable recommendations. The experiments conducted on three datasets indicate that DARec outperforms various state-of-the-art methods significantly.