Introduction

Since the first high-speed railway (HSR), named as Tokaido Shinkansen, was built in Japan in 1964, HSR has been developing rapidly all over the world in the past decades due to its great advantages of high speed, comfortable ride experience and low-carbon emission1,2. However, high-speed train (HST) also induces vibration related problem, for example, the train-induced vibration may bring severe annoyance to the residents nearby or interfere with the normal function of instruments in the buildings3,4,5. The environmental vibration becomes more serious when HST passes through the soft ground area, for one thing, the speed of HST may exceed the critical velocity of the track-soft ground system, as a result, significant ground vibration will be generated, which has been confirmed by many in-situ vibration tests6,7,8. On the other hand, subgrade settlement or excess pore water pressure (EPWP) are easily built up and accumulated under train vibration load, which also has been validated by the field observation9,10,11. Therefore, strict standards are specified to control the post construction settlement of HSR12.

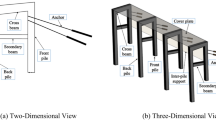
For HSR built in soft ground, piles are widely used to improve the bear capacity of soft soil and reduce subgrade settlement13,14,15. As seen in Fig. 1, there are three typical pile-supported foundations (PSF) in practice, namely pile-net foundation, pile-raft foundation and pile-plate foundation. The embankment with pile-net foundation is usually used for geosynthetics reinforced pile-supported (GRPS) embankment, in which a gravel cushion layer with geosynthetics is laid on the top of pile cap. To reduce the lateral deformation of piles and uneven settlement of embankment, a pile-raft foundation may be adopted, in which a reinforced concrete slab is directly laid underneath the embankment so the gravel layer is buried between the concrete slab and pile heads. When the piles are directly connected with the concrete slab and no gravel layer exists between the slab and pile heads, the pile-raft foundation is then transformed to pile-plate foundation. Pile-net foundation is widely used for HSR in China since it displays good performance in settlement control. Pile-plate foundation is increasingly adopted due to its higher strength, stiffness as well as better settlement control performance. As for pile-raft foundation, it was used for the first time in Beijing-Tianjin intercity railway of China, however, due to its complex construction process, longer construction period, it is gradually replaced by the pile-plate foundation16.

Fig. 1
figure 1

Different types of PSF11.

Full size image

As for the dynamic response characteristics of HSR with PSF in soft ground, extensive studies have been conducted in the past deceases. In general, the researches can be summarized into three categories by the approaches, namely field measurement, model test and numerical modelling. Field measurement can obtain the true vibration characteristics of HSR and provides valuable data for numerical modelling. In China, a series of field tests were conducted on the ground vibrations of Beijing-Shanghai HSR built on embankment with PSF at different sections. For example, Zhai et al.8 measured the vertical ground accelerations of non-ballasted HSR track at different train speeds for the first time and investigated the time-___domain and frequency-___domain response characteristics. Wang et al.17 studied the frequency response characteristics of acceleration and velocity and concluded that the horizontal vibration should not be ignored if the foundation soil is soft. Besides, Feng et al.18, Ren et al.19 and Tang et al.20 also measured the ground vibrations and analyzed the propagation and attenuation characteristics in soft ground. However, such in-situ tests are usually conducted on the surface of ground, vibrations inside the ground are rarely measured, let alone the responses from different types of PSF. Some researchers turn to model tests to investigate the dynamic response characteristics of HSR with PSF. For example, Niu et al.21 conducted model test on the dynamic response of X-section pile-net supported embankment, measured the changes of earth pressure, geogrid strain, settlement and EPWP in the subgrade and soil under train vibration load. Xue et al.22 conducted similar model test and analyzed the frequency characteristics of vertical acceleration under different speeds. Fu23 studied the influence of loading frequency on the dynamic displacement, velocity, and stress of X-section pile-raft foundation. Zhu et al.24 studied the settlement mechanism of pile-raft foundation under high-frequency vertical vibration load by 1 g model test for different sandy grounds. Besides, Liu et al.25 performed 3D model test to investigate the reinforced load in the pile-supported model embankment as the settlement increases. Nevertheless, most model tests are conducted for sandy soil and little attention was paid to the soil–water coupling in soft ground, thus the influence mechanism of PSF on dynamic response of HSR in soft ground needs further study. Currently, it is popular to utilize numerical method to reveal the train-induced vibration of embankment with PSF. Thach et al.26,27 studied the dynamic behaviors of pile-supported embankment under very high train speed using 3D FEM. It confirmed that dynamic response could be significantly reduced by the piles, the vibration resonance behavior was related to PSF rather than the subgrade layer. Tang et al.20 studied the dynamic stress developed in the geosynthetic-reinforced pile foundation and the influences of train speed and pile group layout were analyzed. Gao et al.28 compared the response discrepancy between pile-supported and unreinforced grounds. Li et al.29 investigated the influence of pile on dynamic response using a fully coupled train-track-soil model for the first time and concluded that the existence of pile increased the critical velocity but interfered with the propagation of waves in the soil. In addition, Wang et al.30, Esmaeili et al.31 also used 3D coupled train-track-embankment-reinforced ground model to study the response characteristics of PSF. The existing numerical studies give us an overall knowledge about the influence of PSF, however, the strong nonlinearity and soil–water coupling of soft soil were rarely considered in previous numerical analysis. In fact, the soil–water coupling and nonlinearity are two important features of soft ground, the response characteristics of HSR cannot be revealed with satisfaction unless such two aspects are considered32,33,34. In addition, different types of PSF are adopted for HSR in the engineering, however, their response differences under train vibration load are seldom compared, especially by the soil–water coupled elastoplastic analysis. As a result, the performance of PSF in reducing the train induced vibration cannot be accurately revealed, the dynamic responses among different types of PSF are not clear. By comparing the response characteristics of embankments with different PSFs, the influence mechanism of PSF can be clarified, which enables to gives us an insight to improve the design of PSF to minimize the train induced vibration.

In sum, this paper aims to clarify the response characteristics of HSR with PSF in soft ground based on soil–water coupling FEM. The necessity of soil–water coupling analysis and response discrepancies between embankments with different types of PSF are investigated in detail. The dynamic stress, EPWP, accelerations as well as displacement responses in the embankment and subsoil under different cases are carefully compared. The present study not only contributes to clarify the response characteristics among different PSFs, but also provide a method to evaluate the EPWP and settlement accumulation in soft ground when the effect of long-term train vibrations are considered.

Numerical model and calculation cases

As illustrated in Fig. 2, a 2D FE model for a double-rail HSR is established, the model is referred to Shanghai-Beijing HSR in China, consisting of a low embankment and thick soft subsoil layer. The enlarged embankment model is shown as Fig. 3, the embankment model includes track structure, foundation subgrade and bottom fill, whose thickness and length all conform to the specification of Code TB10621-2014 12. The subsoil layer includes a reinforced surface layer and a soft ground layer, only one soil soft soil layer is considered for simplicity. The soft ground is assumed to be Shanghai silt clay, numbered as ⑤1 layer according to the stratification of Shanghai soils, which is a typical soft soil layer in the Yangtze coastal area.

Fig. 2
figure 2

2D FE mesh in the transverse section of HSR (unit: m).

Full size image
Fig. 3
figure 3

Enlarged view of embankment submodel (unit: m).

Full size image

The transverse size of the subsoil is 140 × 50 m, the truncation length is determined beforehand to ensure the dynamic response in the near field as unaffected as possible. As for the boundary conditions, the lateral boundary is horizontally fixed and the bottom boundary is fixed in both horizontal and vertical direction. For the drainage boundary, the water table is assumed one meter below the ground surface, the bottom boundary is impervious while the lateral boundary and the water table are permeable. The numerical model is carefully meshed with smaller elements in near field and larger elements in far field. There are 8332 elements and 8552 nodes in total in the model and all the materials are modelled by quadrilateral elements. The piles are cast-in-place piles, made of C50 reinforced concrete and the piles and soft ground are assumed to be completely connected. The pile heads locate at the phreatic surface (y =  − 1.00 m) and extend to y =  − 30 m with a diameter of 0.50 m and center-to-center spacing of 3.75 m.

As seen in Table 1, seven numerical calculation cases are considered in this paper to investigate the response discrepancies between soil–water coupling and single-phase calculation types and response discrepancies among different types of PSF. Specifically, Case 1-Case 4 are set to compare the response discrepancies between two different calculation types to verify the necessity of coupling analysis, Case 3 and Case 5–7 are set to compare the response discrepancies among different types of PSF, therefore, their performances in reducing train-induced vibration can be revealed.

Table 1 Numerical calculation cases.
Full size table

Different types of PSF are as illustrated as Fig. 4, in Case 3 and Case 4 only pile foundation is adopted, in Case 5-Case 7, pile-net foundation, pile-plate foundation and pile-raft foundation are adopted, respectively. The primary difference of these PSFs lies in the form of pile head, for instance, the difference between pile-plate and pile-raft foundations is the position of slab, as seen in Fig. 4, the slab is directly connected with pile heads in pile-raft foundation while the slab is laid beneath the embankment and detached from pile heads in the pile-plate foundation. The sizes of pile cap and slab are shown in Fig. 5. The parameters of embankment and PSF are listed in Table 2.

Fig. 4
figure 4

Schematic view of embankments with different types of PSF.

Full size image
Fig. 5
figure 5

Dimensions of pile foundation: (a) pile–net; (b) pile-plate (unit: m).

Full size image
Table 2 Properties of elastic materials8.
Full size table

Cyclic mobility model and soil–water coupling FE-FD scheme

Cyclic mobility model

A sophisticated elastoplastic model named as Cyclic Mobility (CM) model is employed to describe the mechanical behavior of soft ground. The model was proposed by Zhang et al.35 on the concepts of subloading and superloading surfaces as well as considering the stress-induced anisotropy. CM model was originally developed to describe the mechanical behaviors of Toyoura sand, the standard sand in Japan, at different densities and under various loading and drainage conditions. Later, the model was developed to describe the behavior of clayey soils36,37. The yield surfaces of CM model are shown in Fig. 6.

Fig. 6
figure 6

Subloading, normal and superloading yield surfaces in \(p^{\prime}\)-\(q\) stress space.

Full size image

The subloading yield surface for CM model is derived, given in the following form:

$$f = \ln \frac{{p^{\prime}}}{{\tilde{p}^{\prime}_{0} }} + \ln \frac{{M^{2} - \xi^{2} + \eta^{*2} }}{{M^{2} - \xi^{2} }} + \ln \frac{{R^{*} }}{R} - \frac{{\varepsilon_{v}^{p} }}{{C_{p} }} = 0$$
(1)

where the variables in Eq. (1) are defined in general stress state as:

$$\left\{ \begin{gathered} p^{\prime} = \frac{{\sigma^{\prime}_{ii} }}{3},s_{ij} = \sigma^{\prime}_{ij} - p^{\prime}\delta_{ij} ,\eta_{ij} = \frac{{s_{ij} }}{{p^{\prime}}},\eta = \sqrt {\frac{3}{2}\eta_{ij} \eta_{ij} } \hfill \\ \hat{\eta }_{ij} = \eta_{ij} - \beta_{ij} ,\eta^{ * } = \sqrt {\frac{3}{2}\hat{\eta }_{ij} \hat{\eta }_{ij} } ,\xi = \sqrt {\frac{3}{2}\beta_{ij} \beta_{ij} } ,C_{p} = \frac{\lambda - \kappa }{{1 + N}} \hfill \\ \end{gathered} \right. \,$$
(2)

where \(s_{ij}\) is the component of deviator stress tensor,\(\beta_{ij}\) is the component of stress-induced anisotropy tensor, and \(\sigma^{\prime}_{ij}\) is the component of Cauchy effective stress tensor assumed to be positive in compression. The similarity ratio R and R* denote the overconsolidation ratio and structural ratio, respectively. Eight parameters are incorporated into CM model, in which λ, κ, M, v, N are the same as those used in Cam-clay model, the other three parameters are m, a, br, denoting the losing rate of overconsolidation ratio, collapse rate of soil structure, developing rate of stress-induced anisotropy, respectively. The advantage of CM model is that the mechanical behaviors of soil can be simulated with a fixed set of material parameters no matter what loading conditions and drainage conditions may be. The parameters for ⑤1 layer were given in Table 338. The comparison between test and simulated results under drained triaxial compression test is illustrated as Fig. 7. The simulated mechanical behavior of soft ground under cyclic loading is shown as Fig. 8. Up till now, CM model has been widely used in the numerical analyses regarding soil dynamics and earthquake problems, thus the feasibility of CM model has been validated39,40,41,42

Table 3 Model parameters of Shanghai ⑤ 1 layer38.
Full size table
Fig. 7
figure 7

Comparison between test and simulated results of ⑤1 layer under drained compression test.

Full size image
Fig. 8
figure 8

Simulated results of ⑤1 layer subjected to undrained cyclic loading.

Full size image

Field equations for soil–water coupling analysis with FE-FD hybrid scheme

HST induced vibration in saturated soft ground is a typical boundary value problem, in which the field equations for the soil–water coupling problem can be described in u-p formulation based on Biot’s theory43. The kinematic balanced equation and continuity equation of saturated soil subjected to dynamic load are expressed as follows:

$$\left\{ \begin{gathered} \rho \ddot{u}_{i} = \frac{{\partial^{2} \sigma_{ij} }}{{\partial x_{j} }} + \rho b_{i} \hfill \\ \rho^{f} \ddot{\varepsilon }_{ii}^{s} - \frac{{\partial^{2} p_{d} }}{{\partial x_{i} \partial x_{i} }} + \frac{{\gamma_{w} }}{k}\left( {\frac{{\dot{\varepsilon }_{ii}^{s} }}{n} - \frac{1}{{K^{f} }}\dot{p}_{d} } \right) = 0 \hfill \\ \end{gathered} \right.$$
(3)

where ρ is the bulk density of saturated soil, equals to 1.85 × 103 kg/m3 for ⑤1 layer; ρf is fluid density, equals to 1.00 × 103 kg/m3; \(u_{i}^{s}\) is the component of displacement vector of solid skeleton;\(\varepsilon_{ii}^{s}\) is the volumetric strain of solid skeleton; n is the soil porosity; k is the permeability coefficient of soil, equals to 5 × 10−8 m/s for ⑤1 layer; Kf is the bulk modulus of fluid, equals to 2.09 × 109 Pa; pd is EPWP induced by train vibration load; bi is the component of body force vector. The field equations of such soil–water coupling problem are formulated with finite deformation theory and discretized in the time and space ___domain with FE-FD hybrid scheme, which were packaged into FE code named as DBLEAVES44. Therefore, numerical calculation using soil–water coupling dynamic analysis based on CM model were conducted to clarify the dynamic response characteristics of HSR with PSF in soft ground.

High-speed train vibration load

HST vibration load should be determined prior to conducting dynamic numerical calculation. A multiple unit train (MUT) called CRH380A is adopted herein, it consists of eight-car formation, the characteristic length of each car is illustrated as Fig. 9. In the paper, the track irregularity and wheel corrugation are not considered, thus the wheel-rail contact force can be simplified as a series of constant point loads. For CRH380A train, the maximum axle load is 15 tons, thus the maximum wheel-rail force is about 75 kN. The normal running speed of CRH380A is 350 km/h and reaches 380 km/h at maximum, so we considered a speed of 360 km/h (100 m/s) for following analysis.

Fig. 9
figure 9

Schematic diagram of characteristic length of HST CRH380A.

Full size image

A double-layer beam-spring model is used to determine HST vibration load. As illustrated in Fig. 10, the fastener load on the track slab is adopted as train vibration load in this study. In the calculation model, the rail is modelled as infinite Euler beam while the track slab is modelled as discrete Euler beam with a length of 6.50 m. The fastener is simplified as discretely distributed spring/dashpot with a spacing of 0.65 m while the CA mortar layer is modelled as continuous spring/dashpot. Parameters of the calculation model are listed in Table 4. The solution of double-layer beam-spring model is derived using mode superposition method and Runger-Kutta method, finally, the fastener load on the slab can be calculated with Eq. (4).

$$p\left( t \right) = k_{1} \left( {y_{1} - y_{2} } \right) + c_{1} \left( {\dot{y}_{1} - \dot{y}_{2} } \right)$$
(4)

where k1, c1 is the stiffness and damping of the fasteners, respectively; y1, y2 are the respective deflection of rail and track slab at the middle point of the calculation model; \(\dot{y}_{1}\),\(\dot{y}_{2}\) is the corresponding vibration velocity. Finally, the calculated fastener load is illustrated as Fig. 11.

Fig. 10
figure 10

Train vibration load calculation model.

Full size image
Table 4 Parameters of track structure (1/2 track structure).
Full size table
Fig. 11
figure 11

Time history of fastener load.

Full size image

Since 2D numerical analysis is conducted in the paper, the fastener load from Eq. (4) should be equivalent as a linear load per unit length in the longitudinal direction. To determine the equivalent load for 2D model, we first calculate the average load in the longitudinal direction. As referred from Bian et al.45, we first obtain the most unfavorable distribution of fastener load along the longitudinal direction, then the effective distribution length Le of fastener load can be determined. As seen in Fig. 12, the effective length of fastener load within one car is 15.60 m in this study, as a result, the equivalent peak load for 2D model is calculated as follows:

$$\overline{p} = \frac{{\frac{1}{2} \times axle \, load \times 9.8 \times 4}}{{L_{e} }} = \frac{{\frac{1}{2} \times 15 \times 9.8 \times 4}}{15.60} = 18.85 \, {{kN} \mathord{\left/ {\vphantom {{kN} m}} \right. \kern-0pt} m}$$
(5)
Fig. 12
figure 12

Most unfavorable distribution of fastener load.

Full size image

The peak fastener load in Fig. 11 is 28.80 kN, so the load equivalence coefficient can be calculated by 18.85/28.80 (0.654). Finally, the train vibration load for 2D FE model is determined by multiplying the fastener load in Fig. 11 by the load equivalence coefficient, as seen in Fig. 13. By Fast Fourier transformation, the frequency spectrum of 2D train vibration load is shown as Fig. 14. In the following dynamic analysis, the initial stress of the 2D model is first generated according to the self-weight stress, then dynamic numerical calculation based on FE code DBLEAVES is conducted, the Newmark-β method for direct integration in the dynamic calculation is adopted, the integration step for dynamic loading is 0.002 s, sufficient to cover the vibration frequencies of the train vibration load. Rayleigh damping with initial rigidity proportion attenuation is used and the attenuation values for the soils and structures are all set to be 5% and 2%, respectively40.

Fig. 13
figure 13

Train vibration load for 2D model.

Full size image
Fig. 14
figure 14

Frequency spectrum of 2D train vibration load.

Full size image

Numerical results and discussions

Comparison between coupled and single-phase analyses

Vertical dynamic stress

Considering the the symmetry of the 2D FE model, the right half model is chosen for following analysis. The elements and nodes in the embankment at different depths are marked as Fig. 15 and Fig. 16. The vertical dynamic stresses are first presented, for soft ground, the vertical dynamic stress is equal to EPWP for the dynamic stress is almost borne by the water. As illustrated in Fig. 17, the vertical peak stress distributions from these two calculation types are similar, no matter with PSF or without PSF. It indicates that the vertical peak stress from coupled analysis is larger than that from single-phase analysis, implying that the single-phase analysis will underestimate the vertical dynamic stress in the subgrade and subsoil. Reason for the stress difference is related to the stiffness difference between soft ground and single-phase ground. Since the bulk modulus of liquid phase is much larger than that of soil skeleton, therefore, when the void inside the soil skeleton is filled with water, the total stiffness of saturated ground will become much larger than that of single-phase ground. As a result, the vertical vibration in the saturated soft ground encounters greater impedance and results in larger vertical dynamic stress. The peak dynamic stress in PSF is slightly less than that in the unreinforced ground, this is because piles share more dynamic load than the surrounding soil, as a result, the vertical peak stress in the embankment is increased, this phenomenon can also be called “soil arching effect”46.

Fig. 15
figure 15

Elements at different depths.

Full size image
Fig. 16
figure 16

Nodes at different depths.

Full size image
Fig. 17
figure 17

Comparison of vertical peak stresses at different depths: (a) y = 4.0 m; (b) y = 2.93 m; (c) y = 1.78 m; (d) y = 0.25 m; (e) y =  − 0.75 m; (f) y =  − 5.50 m.

Full size image

Acceleration

The peak acceleration comparisons between coupled and single-phase analyses are shown as Figs. 18, 19. As shown in Fig. 18, vertical peak acceleration distributions from the two calculation types are similar, however, the vertical peak accelerations from coupled analysis are much less than those from single-phase analysis, indicating the vertical acceleration would be severely overestimated if coupling analysis is not employed. The vertical peak acceleration differences in the subsoil are further illustrated as Fig. 20. It reveals that there exists an obvious vertical acceleration amplification zone in the unreinforced ground if coupled analysis is considered, however, no amplification zone is predicted from single-phase analysis. The reason is that the existence of water reduces the damping and shear stiffness of saturated soil compared to the single-phase soil, thus the horizontal vibration of soil skeleton in saturated ground can be more easily generated and more fluctuations are induced. In PSF, the vertical accelerations are further reduced, especially when the ground is single-phase ground. Furthermore, the existence of piles also alters the distribution of vertical acceleration, as seen in Fig. 19, the vertical peak acceleration is partitioned by the piles and more fluctuations are induced along the horizontal direction.

Fig. 18
figure 18

Vertical peak accelerations in the embankment: (a) y = 4.20 m; (b) y = 2.65 m; (c) y = 1.50 m; (d) y = 0.00 m; (e) y = −1.00 m.

Full size image
Fig. 19
figure 19

Vertical peak accelerations in the subsoil: (a) Case 1 (coupled); (b) Case 2 (single-phase); (c) Case 3 (coupled + pile); (d) Case 4 (single-phase + pile).

Full size image
Fig. 20
figure 20

Comparison of vertical acceleration response at x = 0 m: (a) time ___domain; (b) frequency ___domain.

Full size image

To further analyze the acceleration difference between the two calculation types, the acceleration responses in the time ___domain and frequency ___domain are both analyzed. As illustrated in Fig. 20a, the amplitude of vertical acceleration from Case 2 (single-phase analysis) experiences faster reduction along the depth direction, from 64.20 cm/s2 at y = 4.2 m to 2.30 cm/s2 at y =  − 20 m, however, the corresponding changes in Case 1 (coupled analysis) is from 54.90 to 3.46 cm/s2. As for the vibration frequency, it is clear to see dominant frequencies in the embankment are similar, however, when the vibration propagates to subsoil, the dominant frequencies from single-phase analysis becomes much smaller than the frequencies from coupled analysis, confirming that vertical vibration attenuates faster in the single-phase soil than in the saturated soft soil. The acceleration response difference in PSF also shows similar results, their comparisons are not discussed here considering the length of paper.

Displacement

The vertical peak displacement comparisons are illustrated as Figs. 21, 22. Vertical peak displacements from coupled analysis are much smaller than those from single-phase analysis due to much larger compressive stiffness in the saturated soft ground. The vertical peak displacements are slightly decreased from the bottom of track slab to its bottom. However, the distributions of vertical peak displacement in the subsoil are significantly different. As seen in Fig. 22, there is an evident displacement trough (around x = 16 m) in the horizontal direction in saturated soft ground, as for single-phase ground, the displacement trough appears at much farther position and is not obvious. The existence of piles greatly changes the distribution of vertical displacement, the vertical displacement distribution becomes more uniform along the depth direction within the pile reinforced area, consequently, the vertical displacement beneath the pile end is much larger than that in unreinforced ground. In sum, the peak displacements in the subsoil from single-phase analysis are much larger than those from coupled analysis, indicating that single-phase analysis underestimates the dynamic displacements in soft ground, therefore, soil–water coupling analysis is necessary to investigate the dynamic response of HSR in soft ground.

Fig. 21
figure 21

Comparison of vertical peak displacements in the embankment: (a) Case1 (coupled); (b) Case 2 (single-phase); (c) Case 3 (coupled + pile); (d) Case 4 (single-phase + pile).

Full size image
Fig. 22
figure 22

Comparison of vertical peak displacement in the subsoil: (a) Case 1 (coupled); (b) Case 2 (single-phase); (c) Case 3 (coupled + pile); (d) Case 4 (single-phase + pile).

Full size image

Response comparison among different types of PSF

Vertical dynamic stress and EPWP

The vertical peak dynamic stresses of embankment with different types of PSF are illustrated in Fig. 23, it is seen that their stress discrepancy is very slight when the distance is far from the pile heads. As depth approaches the pile head, the vertical stress displays stress discrepancy, at y = 0.25 m, the vertical peak stresses from Case 3 (pile only) and Case 6 (pile-net) are similar while those from Case 5 (pile-plate) and Case 7 (pile-raft) are similar, but at y = -0.75 m, the vertical peak stress in all cases become similar, indicating that the dynamic stress difference among different types of PSF concentrates within relatively small area. Besides, the vertical stress from Case 6 (pile-net) is found to be maximum while that from Case 7 (pile-raft) is minimum, implying that the existence of plate is conducive to reduce the stress concentration in the embankment.

Fig. 23
figure 23

Comparison of vertical peak stress comparison above soft ground: (a) y = 4.0 m; (b) y = 2.93 m; (c) y = 1.78 m; (d) y = 0.25 m; (e) y =  − 0.75 m.

Full size image

Peak EPWP generated in soft ground among the four cases is shown in Fig. 24, it is seen that the distribution of EPWP is partitioned by the piles, note that the build-up of EPWP is closely related to the stiffness of PSF, EPWP in Case 5 (pile-plate) is minimum while that from Case 3 (pile only) is maximum, 32.70% decrease from Case 3 (pile only) to Case 5 (pile-raft). The peak EPWP from Case 7 (pile-raft) is slightly larger than that from Case 5 (pile-plate) and less than that from Case 3 (pile only). However, the peak EPWP from Case 7 (pile-raft) is larger than that from Case 6 (pile-net), indicating that the detachment between pile and slab is not suitable to reduce the buildup of EPWP. In addition, EPWP beneath the pile tip is found even larger than EPWP around the pile body, implying that EPWP will be easily accumulated below the pile tips, moreover, the stiffer PSF is, the larger EPWP response occurs beneath the pile tips. Therefore, PSF is very effective to reduce EPWP response in soft ground, yet, EPWP response below the pile tips is increased.

Fig. 24
figure 24

Comparison of EPWP in different cases: (a) Case 3 (pile only); (b) Case 5 (pile-plate); (c) Case 6 (pile-net); (d) Case 7 (pile-raft).

Full size image

Acceleration

The comparison of vertical peak accelerations in the embankment among different types of PSF are shown in Fig. 25. Similarly, the vertical acceleration is closely related to the type of PSF. When the depth is far from the pile head, the vertical acceleration from Case 5 (pile-plate) is maximum, however, when the depth increases, the vertical peak acceleration from Case 3 (pile only) becomes maximum and the peak acceleration from Case 5 (pile-plate) becomes minimum. The reason is that PSF can restrain the vertical vibration in the lower part of embankment, thus the vibration in the upper part can be slightly strengthened.

Fig. 25
figure 25

Comparison of vertical peak acceleration above soft ground: (a) y = 4.20 m; (b) y = 2.65 m; (c) y = 1.50 m; (d) y = 0.00 m; (e) y =  − 1.00 m.

Full size image

The vertical peak accelerations in the subsoil are compared in Fig. 26, similar to the distribution of EPWP, the vertical acceleration is also partitioned by the piles. The stiffness of PSF has important influence on the peak acceleration in the soft ground, acceleration in the pile-plate supported foundation is minimum while that from pile only supported foundation is maximum. Different from EPWP, the pile-raft supported foundation is proved to be more effective in reducing ground vibration than the pile-net supported foundation for the concrete slab can scatter the vertical vibration to farther area than the pile cap, the vertical vibration beneath the embankment bottom thus can be greatly reduced.

Fig. 26
figure 26

Comparison of vertical peak acceleration in different cases: (a) Case 3 (pile only); (b) Case 5 (pile-plate); (c) Case 6 (pile-net); (e) Case 7 (pile-raft).

Full size image

The horzizontal acceerations of embankment from different PSFs is illustrated as Fig. 27, similar to the vertical acceleration, the horizonal acceleration from Case 5 (pile-plate) foundation is maximum when the distance is far from the pile heads , as the depth increases, the peak acceleration from Case 5 (pile-plate) becomes minimum and the horizontal acceleration from Case 1 (pile only) becomes minimum, the horizontal acceleration discrepancy occurs at y = -1.0 m. Therefore, the plate or pile cap above the pile heads has significant influence on the horizontal acceleration of embankment.

Fig. 27
figure 27

Comparison of horizontal peak acceleration above soft ground: (a) y = 4.20 m; (b) y = 2.65 m; (c) y = 1.50 m; (d) y = 0.00 m; (e) y =  − 1.00 m.

Full size image

The horizontal peak acceleration distribution in the subsoil is illustrated in Fig. 28, similar to the vertical peak acceleration, the horizontal peak acceleration in Case 3 (pile only) is maximum while the horizontal accelerations in Case 5 (pile-plate) is minimum. Horizontal acceleration from Case 6 (pile-net) is larger than that from Case 7 (pile-plate), also confirming that the larger stiffness of PSF is, the less peak acceleration may be. In addition, compared to the unreinforced ground, the horizontal acceleration beneath the pile tip in PSF is also increased. Therefore, PSF induces stronger vibration below the pile tips both in the vertical direction and horizontal direction.

Fig. 28
figure 28

Comparison of horizontal peak acceleration in different cases: (a) Case 3 (pile only); (b) Case 5 (pile-plate); (c) Case 6 (pile-net); (d) Case 7 (pile-raft).

Full size image

Displacement

Finally, the vertical peak displacement comparisons are shown in Fig. 29, 30. The peak displacements of embankment with PSF are substantially reduced when compared to the unreinforced ground. As for the peak displacements among different types of PSF, the displacement in the embankment is also closely related to the stiffness of PSF, therefore, the vertical displacement in Case 3 (pile-plate) is minimum, followed by Case 7 (pile-raft), Case 6 (pile-net) and Case 3 (pile only). Nevertheless, as the depth reaches the surface of soft ground, the vertical displacement discrepancy among different PSFs is trivial, in another word, only the vertical displacement in the embankment is significantly influenced by the types of PSF, the displacements response in soft ground are similar.

Fig. 29
figure 29

Comparison of vertical peak displacement above soft ground: (a) y = 4.20 m; (b) y = 2.65 m; (c) y = 1.50 m; (d) y = 0.00 m; (e) y =  − 1.00 m.

Full size image
Fig. 30
figure 30

Comparison of vertical peak displacements in different cases: (a) Case 3 (pile only); (b) Case 5 (pile-plate); (c) Case 6 (pile-net); (d) Case 7 (pile-raft).

Full size image

The distribution of vertical displacement in the subsoil is illustrated in Fig. 30. The displacement distribution from PSF is quite different from the displacement distribution in unreinforced ground, changed. Due to the existence of piles, the vertical displacement within the reinforced area becomes uniform in the vertical direction, moreover, the peak displacements below the pile tips are much larger than that in the unreinforced ground, indicating that PSF can transfers the vertical vibration to deeper ___location directly. To further compare the displacement discrepancy, vertical displacements at different depths are presented as Fig. 31, it is clearly seen that the vertical peak displacements from the four cases of PSF are quite close to each other, indicating that the vertical displacement in soft ground is hardly affected by the pile cap or plate, implying that the vertical displacement of PSF is basically controlled by the piles rather than the pile cap or plate. The horizontal displacements among different types of PSF demonstrate similar characteristics, thus their numerical results are not discussed here.

Fig. 31
figure 31

Comparison of vertical peak displacements along horizontal direction at different depths.

Full size image

Conclusion

This paper aims to clarify the dynamic response of low-embankment with PSF for HSR in soft ground based on soil–water coupling FE-FD scheme combined with a sophisticated elastoplastic model. The response discrepancy between coupling and single-phase calculation types are first compared, then the response characteristics among different types of PSF are investigated in detail. Based on the numerical results, the main conclusions can be summarized as follows:

(1) Soil–water coupled analysis is more reasonable to reveal the dynamic responses of HSR in soft ground, otherwise, the vertical dynamic stress, horizontal acceleration and displacement would be underestimated and the vertical acceleration and displacement would be overestimated. Moreover, coupling analysis can clearly reveal the amplification zone of vertical acceleration in soft ground and the attenuation of ground vibration would be exaggerated if single-phase analysis is adopted.

(2) PSF can significantly reduce the peak EPWP, acceleration and displacement in soft ground, however, the dynamic responses below the pile tips are strengthened because the piles can transfer the ground vibration to deeper ___location directly. As a result, larger EPWP can be built up beneath the pile tips than around the pile body. The stiffer PSF is, the larger EPWP may be generated beneath the pile tips.

(3) Overall, the larger stiffness of PSF, the less peak EPWP, acceleration and displacement may be, thus the existence of plate or cap on the pile head is effective to weaken vibration propagation in soft ground. However, when the distance is far from pile head, the response discrepancy among different types of PSF is trivial.

(4) Due to PSF, the vertical displacement becomes uniform in the vertical direction within the pile reinforced area, therefore, the peak displacements in soft ground from different types of PSF are similar, implying that the displacement is basically controlled by the piles rather than the plate or pile cap.