Introduction

Chemical graph theory, a significant branch of computational chemistry1,2, masterfully merges the sophistication of mathematics with the intricate nature of molecular research. We represent molecules as graphs where atoms are nodes, and bonds are edges. This approach allows researchers to manipulate and scrutinize molecular structures using tools of graph theory, yielding profound perceptions of various chemical phenomena. This methodology has revolutionized the examination of molecular characteristics, the mechanism of reaction, and the interaction within function and structure. Chemical graph theory3,4 forms the basis for developing computational tools and algorithms, which is essential in modern chemistry, driving the advancement of material design, drug discovery, and elucidation of key chemical principles.

Graph theory has emerged as a powerful tool for studying molecular properties, with topological indices offering key insight into the relationship between molecular structure and physicochemical properties. Nevertheless, there is a high demand for the elaboration of more efficient and reliable models that can provide highly accurate predictions of thermodynamic properties of molecules using graph-based descriptors. The topological descriptors represent an important tool to simplify such complicated molecular systems with predictive reliability due to their origin from the association of the vertices within the molecules. Topological indices represent an essential role in QSARs, provide perceptions in many physicochemical characteristics without requiring considerable experimental data, since they encode the structural information in a concise manner. The various molecular features under study by topological indices include solubilities, toxicity, biological activity, and boiling points. This approach enables the patterning of new molecules with desired properties, thus strengthening areas like medicinal chemistry, environmental science, and materials science. Since, the topological descriptors are the basic building blocks, computational chemistry plays a vital role in understanding and explaining the dynamics of molecules within different chemical structures. Graph-theoretic descriptors represent a unique and computationally inexpensive way to investigate many of the molecular properties that are often experimentally cumbersome. An attempt is made here to employ these descriptors for predictive modeling of important thermodynamic properties like entropy (S), formation enthalpy \((\Delta H_f)\), boiling point (BP), refractive index (RI), logarithm of partition coefficient \((\log P)\) and molecular connectivity index \((\omega )\). These properties are critical for understanding the chemical behavior of hydrocarbons, particularly in industrial applications. By examining the relationship between topological indices and thermodynamic properties, this work endeavors to bridge the disciplines of graph theory and molecular thermodynamics. Mostly, degree based topological indices5 are stated as:

$$\begin{aligned} TI\left( \Xi \right) =\sum \limits _{{{\varsigma }_{i}}{{\varsigma }_{j}}\in \Gamma \left( \Xi \right) }{\phi \left( \mathfrak {d}\left( {{\varsigma }_{i}} \right) ,\mathfrak {d}\left( {{\varsigma }_{j}} \right) \right) } \end{aligned}$$

Where, \(\phi \left( y,z \right)\) is defined as mapping of z, y with the property \(\phi \left( z,y \right) =\phi \left( y,z \right)\) and \(\mathfrak {d}\left( {{\varsigma }} \right)\) is the degree of the vertex \(\wp\). Some well-known topological indices of these groups are as follows:

1. Sombor descriptor \(\phi \left( \mathfrak {d}\left( {{\varsigma }_{i}} \right) ,\mathfrak {d}\left( {{\varsigma }_{j}} \right) \right) =\sqrt{\mathfrak {d}{{\left( {{\varsigma }_{i}} \right) }^{2}}+\mathfrak {d}{{\left( {{\varsigma }_{j}} \right) }^{2}}}\),

2. Reduced Sombor descriptor \(\phi \left( \mathfrak {d}\left( {{\varsigma }_{i}} \right) ,\mathfrak {d}\left( {{\varsigma }_{j}} \right) \right) =\sqrt{{{\left( \mathfrak {d}\left( {{\varsigma }_{i}} \right) -1 \right) }^{2}}+{{\left( \mathfrak {d}\left( {{\varsigma }_{j}} \right) -1 \right) }^{2}}}\),

3. Average Sombor descriptor \(\phi \left( \mathfrak {d}\left( {{\varsigma }_{i}} \right) ,\mathfrak {d}\left( {{\varsigma }_{j}} \right) \right) =\sqrt{{{\left( \mathfrak {d}\left( {{\varsigma }_{i}} \right) -\frac{2m}{n} \right) }^{2}}+{{\left( \mathfrak {d}\left( {{\varsigma }_{j}} \right) -\frac{2m}{n} \right) }^{2}}}\), where n, m are the total number of nodes and edges,

4. Banhatti Sombor descriptor \(\phi \left( \mathfrak {d}\left( {{\varsigma }_{i}} \right) ,\mathfrak {d}\left( {{\varsigma }_{j}} \right) \right) =\frac{1}{\sqrt{\mathfrak {d}{{\left( {{\varsigma }_{i}} \right) }^{2}}+\mathfrak {d}{{\left( {{\varsigma }_{j}} \right) }^{2}}}}\),

5. Reduced Banhatti Sombor descriptor \(\phi \left( \mathfrak {d}\left( {{\varsigma }_{i}} \right) ,\mathfrak {d}\left( {{\varsigma }_{j}} \right) \right) ={{\left( \frac{1}{{{\left( \mathfrak {d}\left( {{\varsigma }_{i}} \right) -1 \right) }^{2}}}+\frac{1}{{{\left( \mathfrak {d}\left( {{\varsigma }_{j}} \right) -1 \right) }^{2}}} \right) }^{\frac{1}{2}}}\),

6. Delta Banhatti Sombor descriptor \(\phi \left( \mathfrak {d}\left( {{\varsigma }_{i}} \right) ,\mathfrak {d}\left( {{\varsigma }_{j}} \right) \right) ={{\left( \frac{1}{{{\left( \mathfrak {d}\left( {{\varsigma }_{i}} \right) -\delta \left( \Xi \right) +1 \right) }^{2}}}+\frac{1}{{{\left( \mathfrak {d}\left( {{\varsigma }_{j}} \right) -\delta \left( \Xi \right) +1 \right) }^{2}}} \right) }^{\frac{1}{2}}}\), where \(\delta (\Xi )\) is the minimum degree of the \(\Xi\). A leaf node is a node with degree 1, it is connected to only one other node. Let this leaf node be denoted as \(\mathfrak {d}\left( {{\varsigma }_{i}} \right)\) and its neighboring as \(\mathfrak {d}\left( {{\varsigma }_{j}} \right)\). Let \(\mathfrak {d}\left( {{\varsigma }_{j}} \right) =l\), then

$$\begin{aligned} \sqrt{\mathfrak {d}{{\left( {{\varsigma }_{i}} \right) }^{2}}+\mathfrak {d}{{\left( {{\varsigma }_{j}} \right) }^{2}}}=\sqrt{{{\left( 1 \right) }^{2}}+{{\left( l \right) }^{2}}}. \end{aligned}$$

These mathematical formulations, though comprehensive, offer more than just computational value; they capture essential features of molecular structure that influence key physicochemical characteristics. Descriptors such as the Sombor energy and the Banhatti Sombor energy encode important information about bond connectivity, molecular symmetry, and atomic distribution. These structural attributes are closely correlated with thermodynamic properties, including the boiling point, the enthalpy of formation, and solubility, providing valuable insights into molecular behavior. For more detail see6,7,8.

Methodology

In this section, we present the mathematical formulations of some graph-based descriptors, such as Sombor and Banhatti Sombor energies. These define the relations between the atomic structure and molecular features that are necessary for the prediction of thermodynamic characteristics. The literature has defined a number of different types of matrices. The adjacency matrix inside these is represented by Z. The aforementioned Z of \(\Xi\) on n vertices is a \(n\times n\) whose entries are defined by:

$$\begin{aligned} a_{i,j}= \left\{ \begin{array}{ll} 1, & \hbox {for }\varsigma _i\varsigma _j\in \Gamma (\Xi ), \\ 0, & \hbox {for }\varsigma _i\varsigma _j\notin \Gamma (\Xi ).\\ \end{array} \right. \end{aligned}$$
(1)

Sarkar et al. (2024)9 introduced extended energy matrices for graph structures, demonstrating correlations with molecular properties, including for BHC. The nth order general extended matrix \(Z_{TI}\) is stated as:

$$\begin{aligned} \alpha _{i,j}= \left\{ \begin{array}{ll} \phi \left( \mathfrak {d}\left( {{\varsigma }_{i}} \right) ,\mathfrak {d}\left( {{\varsigma }_{j}} \right) \right) , & \hbox {for }\varsigma _i\varsigma _j\in \Gamma (\Xi ), \\ 0, & \hbox {for }\varsigma _i\varsigma _j\notin \Gamma (\Xi ). \\ \end{array} \right. \end{aligned}$$
(2)

The extended energy of graph is defined as:

$$\begin{aligned} {{\xi }_{TI}}\left( \Xi \right) =\sum \limits _{i=1}^{n}{\left| {{\chi }_{i}} \right| }, \end{aligned}$$

where, \({{\chi }_{1}},{{\chi }_{2}},\ldots ,{{\chi }_{n}}\) are eigenvalues of matrix Z. The extended adjacency matrices of the Sombor, reduced Sombor, and average Sombor descriptors are stated as:

$$\begin{aligned} SO= & \left\{ \begin{array}{ll} \sqrt{\mathfrak {d}(\varsigma _i)^2+\mathfrak {d}(\varsigma _j)^2}, & \hbox {for }\varsigma _i\varsigma _j\in \Gamma (\Xi ), \\ 0, & \hbox {for }\varsigma _i\varsigma _j\notin \Gamma (\Xi ). \\ \end{array} \right. \\ SO_{red}= & \left\{ \begin{array}{ll} \sqrt{(\mathfrak {d}(\varsigma _i)-1)^2+(\mathfrak {d}(\varsigma _j)-1)^2}, & \hbox {for }\varsigma _i\varsigma _j\in \Gamma (\Xi ), \\ 0, & \hbox {for }\varsigma _i\varsigma _j\notin \Gamma (\Xi ). \\ \end{array} \right. \\ SO_{avg}= & \left\{ \begin{array}{ll} \sqrt{(\mathfrak {d}(\varsigma _i)-\frac{2m}{n})^2+(\mathfrak {d}(\varsigma _j)-\frac{2m}{n})^2}, & \hbox {for }\varsigma _i\varsigma _j\in \Gamma (\Xi ), \\ 0, & \hbox {for }\varsigma _i\varsigma _j\notin \Gamma (\Xi ). \\ \end{array} \right. \end{aligned}$$

Now, suppose \(\gamma _{1}^{\left( 1 \right) },\gamma _{2}^{\left( 1 \right) },\ldots ,\gamma _{n}^{\left( 1 \right) }\), \(\gamma _{1}^{\left( 2 \right) },\gamma _{2}^{\left( 2 \right) },\ldots ,\gamma _{n}^{\left( 2 \right) }\) and \(\gamma _{1}^{\left( 3 \right) },\gamma _{2}^{\left( 3 \right) },\ldots ,\gamma _{n}^{\left( 3 \right) }\) are eigenvalues of Sombor descriptors. Then, the Sombor energies are stated as:

$$\begin{aligned} SOE= & \sum \limits _{i=1}^{n}{\left| \gamma _{i}^{\left( 1 \right) } \right| }, \\ S{{O}_{red}}E= & \sum \limits _{i=1}^{n}{\left| \gamma _{i}^{\left( 2 \right) } \right| }, \\ S{{O}_{avg}}E= & \sum \limits _{i=1}^{n}{\left| \gamma _{i}^{\left( 3 \right) } \right| }. \end{aligned}$$

Consider the benzene molecule \((C_{6}H_{6})\), which consists of a ring structure10 with alternating single and double bonds between six carbon atoms. In this representation, each carbon atom is treated as a node, and the bonds between the atoms are represented as edges, forming a graph structure as shown in Figure 1.

Fig. 1
figure 1

Molecular graph of benzene ring.

Full size image

In an adjacency matrix, both the rows and columns correspond to the nodes, while the matrix entries indicate the presence of edges between these nodes. If two atoms are connected by a bond, the corresponding extended energy matrix as shown below:

$$\begin{aligned} Z=\left( \begin{matrix} 0 & \sqrt{8} & 0 & 0 & 0 & \sqrt{8} \\ \sqrt{8} & 0 & \sqrt{8} & 0 & 0 & 0 \\ 0 & \sqrt{8} & 0 & \sqrt{8} & 0 & 0 \\ 0 & 0 & \sqrt{8} & 0 & \sqrt{8} & 0 \\ 0 & 0 & 0 & \sqrt{8} & 0 & \sqrt{8} \\ \sqrt{8} & 0 & 0 & 0 & \sqrt{8} & 0 \\ \end{matrix} \right) \end{aligned}$$

MATLAB and SPSS were selected for their complementary strengths in this study. MATLAB’s versatility in numerical computations, matrix manipulations, and graph-based descriptor calculations makes it ideal for implementing extended energy analyses. Its robust visualization and data analysis capabilities ensure precise handling of complex mathematical operations. SPSS, with its advanced statistical tools and user-friendly interface, excels in regression modeling and evaluating correlations between molecular descriptors and thermodynamic properties. It has support for statistical validation to ensure good results. The combination of computing efficiency from MATLAB and the statistical vigor of SPSS offers a certain balance, ensuring that the results are delivered in an efficient and correct form; thus, both are relevant to this specific analysis. The Banhatti Sombor descriptors are:

$$\begin{aligned} \beta SO= & \left\{ \begin{array}{ll} \frac{1}{\sqrt{\mathfrak {d}{{\left( {{\varsigma }_{i}} \right) }^{2}}+\mathfrak {d}{{\left( {{\varsigma }_{j}} \right) }^{2}}}}, & \hbox {for }\varsigma _i\varsigma _j\in \Gamma (\Xi ), \\ 0, & \hbox {for }\varsigma _i\varsigma _j\notin \Gamma (\Xi ). \\ \end{array} \right. \\ R\beta SO= & \left\{ \begin{array}{ll} {{\left( \frac{1}{{{\left( \mathfrak {d}\left( {{\varsigma }_{i}} \right) -1 \right) }^{2}}}+\frac{1}{{{\left( \mathfrak {d}\left( {{\varsigma }_{j}} \right) -1 \right) }^{2}}} \right) }^{\frac{1}{2}}}, & \hbox {for }\varsigma _i\varsigma _j\in \Gamma (\Xi ), \\ 0, & \hbox {for }\varsigma _i\varsigma _j\notin \Gamma (\Xi ). \\ \end{array} \right. \\ \delta \beta SO= & \left\{ \begin{array}{ll} {{\left( \frac{1}{{{\left( \mathfrak {d}\left( {{\varsigma }_{i}} \right) -\delta \left( \Xi \right) +1 \right) }^{2}}}+\frac{1}{{{\left( \mathfrak {d}\left( {{\varsigma }_{j}} \right) -\delta \left( \Xi \right) +1 \right) }^{2}}} \right) }^{\frac{1}{2}}}, & \hbox {for }\varsigma _i\varsigma _j\in \Gamma (\Xi ), \\ 0, & \hbox {for }\varsigma _i\varsigma _j\notin \Gamma (\Xi ). \\ \end{array} \right. \end{aligned}$$

Suppose that \(\tau _{1}^{\left( 1 \right) },\tau _{2}^{\left( 1 \right) },\ldots ,\tau _{n}^{\left( 1 \right) }\), \(\tau _{1}^{\left( 2 \right) },\tau _{2}^{\left( 2 \right) },\ldots ,\tau _{n}^{\left( 2 \right) }\) and \(\tau _{1}^{\left( 3 \right) },\tau _{2}^{\left( 3 \right) },\ldots ,\tau _{n}^{\left( 3 \right) }\) are the eigenvalues of Banhatti Sombor descriptors. The Banhatti Sombor energies are stated as:

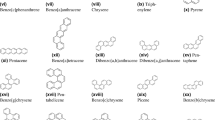
$$\begin{aligned} \beta SOE= & \sum \limits _{i=1}^{n}{\left| \tau _{i}^{\left( 1 \right) } \right| },\\ R\beta SOE= & \sum \limits _{i=1}^{n}{\left| \tau _{i}^{\left( 2 \right) } \right| }, \\ \\ \delta \beta SOE= & \sum \limits _{i=1}^{n}{\left| \tau _{i}^{\left( 3 \right) } \right| }. \end{aligned}$$

The energy of Sombor basically reflects the connectivity in a molecule and may considerably affect the stability, reactivity, and other thermodynamic behaviors of it. In a similar way, the Banhatti Sombor energy reflects the spatial distribution of atoms, which is very important for determining properties such as boiling point and viscosity. By using these graph-based descriptors, we introduce a computationally efficient prediction of thermodynamic properties-a method that will be valuable and an alternative to experimental measurements, which often require a lot of resources and time. In this article, we define the Sombor and Banhatti Sombor energies of BHC11. We conduct an in-depth assessment of their relevance in forecasting numerous thermodynamic characteristics of polycyclic aromatic compounds (PAC). This investigation utilizes a complete dataset comprising 22 BHC available in Table 1. BHC are categorized as hydrocarbons that are unsaturated that are condensed polycyclic and consist of fully conjugated compounds that are primarily planar, featuring specifically \(C_6H_6\). Full conjugation demands all carbon-carbon bonds and carbon atoms to demonstrate the hybridization properties of \(C_6H_6\). While primarily comprising alternant polycyclic aromatic hydrocarbons, this class also encompasses theoretical compounds or potentially unstable such as heptacene and triangulene. This study seeks to fill the gap in reliable and efficient models for predicting the thermodynamic characteristics of BHC12,13. The objective is to investigate the potential of novel graph-based descriptors, including Sombor and Banhatti Sombor energies, in predicting key properties such as boiling point, enthalpy of formation, and retention index. We hypothesize that these descriptors will exhibit strong correlations with thermodynamic properties, providing a computationally efficient alternative to traditional methods14.

Main results and analysis

“Initially, the energies of various molecular structures of BHC in Fig. 2 are determined using the extended adjacency matrix, as illustrated of the heatmap in Fig. 3. In the heatmap, the X-axis represents the energy types calculated from the extended adjacency matrix, while the Y-axis corresponds to the data points. Each cell in the heatmap illustrates the energy value for a specific combination of energy type and molecular structure, with color intensity reflecting the magnitude of the energy. The corresponding energy values are provided in Table 1.

Fig. 2
figure 2

Molecular structures of BHC.

Full size image

Afterwards, we employ MATLAB software to calculate the eigenvalues of these BHC. For the linear regression analysis15, we utilize the statistical tools16 available in SPSS17.

Table 1 Energies of BHC.
Full size table
Fig. 3
figure 3

Energies of BHC.

Full size image

Importance of the graph’s energy

In the following section, using a dataset comprising 22-BHC 1, we examine the connection between Sombor and Banhatti Sombor descriptors with various thermodynamic characteristics of PAC including (BP), (S), \((\Delta H_f )\), (RI), \((\log P)\) and \((\omega )\). The experimental results of BHC are taken from5,9. We find the energies18 of different indices of BHC which are given in Table 1. In the following study, we used the linear regression expression to find the thermodynamic properties. Linear regression analysis is a statistical tool used to predict the value of one variable using another variable’s value. In this analysis, the variable to be predicted is named the dependent variable, while the variable applied to make predictions is referred to as the independent variable. It is stated as

$$\begin{aligned} X=\sigma Y+t, \end{aligned}$$

here, Y is the independent variable, \(\sigma\) is the slope, X is the dependent variable and t is the intercept. By following this, we utilize advanced graph energy matrices, specifically SOE, \(SO_{red}E\), \(SO_{avg}E\), \(\beta SOE\), \(R\beta SOE\) and \(\delta \beta SOE\) as predictor variables, to establish predictive frameworks for S, BP, \(\Delta H_f\), RI, \(\omega\), and \((\log P)\) of BHC19. Through the application of the least squares fitting method, we derive regression designs for entropy (S), enthalpy of formation \((\Delta H_f)\), boiling point (BP), refractive index (RI), the logarithm of partition coefficient \((\log P)\), and molecular connectivity index \((\omega )\) in relation to the Sombor and Banhatti Sombor descriptors. In this article, the symbols \({{\tilde{a}}_{e}}\), \(\Lambda\), \(\Delta\), and \({{\digamma }_{v}}\) denote the standard error of the population, estimation, significance F, and the \(\digamma\)-values, correspondingly.

Models related to SOE

The BP of a matter is the temperature in which the vapor pressure equivalent to the surrounding ambient pressure, causing the liquid to transition into a vapor phase. Entropy measures the amount of thermal energy in a system per unit temperature that cannot be converted into useful work. The standard enthalpy of formation represents the enthalpy change associated with the formation of one mole of a mixture from its component parts, each according to their standard conditions, covered by specified requirements of temperature of 298.15 K and 1, atmosphere pressure. The parameter of thermodynamics assists as main source for assessing the energetic characteristics of stability of substances and chemical reactions. The RI is a essential optical feature stated as the comparison regarding light’s speed in a vacuum to its speed in a given medium. This dimensionless quantity shows how much light slows down when traveling through the medium compared to a vacuum, offering observation into the optical density of the material and influencing events such as reflection and refraction. The \(\log P\), is commonly used to simplify the ratio and analysis of solute partitioning crosswise various frameworks. In this section, we identify the designs of \(\Delta {{H}_{f}}\), S, BP, \(\log P\), RI, and \(\omega\) linked to the SOE.

$$\begin{aligned} BP= & 4.597\times SOE+37.848, \\ \Lambda= & 22,\quad \quad {{\tilde{a}}_{e}}=10.48849, \quad \quad {{\digamma }_{v}}=1846.860, \quad \quad \Delta =3.5262\times {{10}^{-21}}, \\ S= & 0.538\times SOE+58.884, \\ \Lambda= & 22,\quad \quad {{\tilde{a}}_{e}}=4.47957, \quad \quad {{\digamma }_{v}}=138.902, \quad \quad \Delta =1.8681\times {{10}^{-10}}, \\ \omega= & 0.003\times SOE+0.196, \\ \Lambda= & 11,\quad \quad {{\tilde{a}}_{e}}=0.018611, \quad \quad {{\digamma }_{v}}=126.833, \quad \quad \Delta =0.000001, \\ RI= & 4.481\times SOE+11.342, \\ \Lambda= & 22,\quad \quad {{\tilde{a}}_{e}}=9.47192, \quad \quad {{\digamma }_{v}}=2152.083, \quad \quad \Delta =7.751\times {{10}^{-22}}, \\ \end{aligned}$$
$$\begin{aligned} \Delta {{H}_{f}}= & 2.306\times SOE+65.608, \\ \Lambda= & 22,\quad \quad {{\tilde{a}}_{e}}=16.22939, \quad \quad {{\digamma }_{v}}=194.138, \quad \quad \Delta =9.3032\times {{10}^{-12}}, \\ \log P= & 0.053\times SOE+1.067, \\ \Lambda= & 22,\quad \quad {{\tilde{a}}_{e}}=0.19467, \quad \quad {{\digamma }_{v}}=707.470, \quad \quad \Delta =4.4019\times {{10}^{-17}}. \end{aligned}$$

Models related to \(SO_{red}E\)

In this section, we identify the models of \(\Delta {{H}_{f}}\), S, \(\log P\), \(\omega\), RI, and BP linked to the reduced sombor energy.

$$\begin{aligned} BP= & 7.210\times SO_{red}E+65.018, \\ \Lambda= & 22,\quad \quad {{\tilde{a}}_{e}}=12.76813, \quad \quad {{\digamma }_{v}}=1239.747, \quad \quad \Delta =1.8056\times {{10}^{-19}}, \\ S= & 0.836\times SO_{red}E+62.553, \\ \Lambda= & 22,\quad \quad {{\tilde{a}}_{e}}=4.85173, \quad \quad {{\digamma }_{v}}=115.459, \quad \quad \Delta =9.3227\times {{10}^{-10}}, \\ \omega= & 0.005\times SO_{red}E+0.216, \\ \Lambda= & 11,\quad \quad {{\tilde{a}}_{e}}=0.02104, \quad \quad {{F}_{v}}=97.253, \quad \quad \Delta =0.000004, \\ RI= & 7.022\times SO_{red}E+38.181, \\ \Lambda= & 22,\quad \quad {{\tilde{a}}_{e}}=12.51994, \quad \quad {{\digamma }_{v}}=1223.221, \quad \quad \Delta =2.0607\times {{10}^{-19}}, \\ \Delta {{H}_{f}}= & 3.591\times SO_{red}E+80.723, \\ \Lambda= & 22,\quad \quad {{\tilde{a}}_{e}}=17.68387, \quad \quad {{\digamma }_{v}}=160.362, \quad \quad \Delta =5.2234\times {{10}^{-11}}, \\ \log P= & 0.083\times SO_{red}E+1.383, \\ \Lambda= & 22,\quad \quad {{\tilde{a}}_{e}}=0.21725, \quad \quad {{\digamma }_{v}}=564.092, \quad \quad \Delta =3.966\times {{10}^{-16}}. \end{aligned}$$

Models related to \(SO_{avg}E\)

In this section, we identify the models of \(\Delta {{H}_{f}}\), S, BP, \(\log P\), RI, and \(\omega\) linked to the average sombor energy.

$$\begin{aligned} BP= & 21.224\times SO_{avg}E+71.703, \\ \Lambda= & 22,\quad \quad {{\tilde{a}}_{e}}=20.63299, \quad \quad {{\digamma }_{v}}=462.407, \quad \quad \Delta =2.6947\times {{10}^{-15}}, \\ S= & 2.437\times SO_{avg}E+63.799, \\ \Lambda= & 22,\quad \quad {{\tilde{a}}_{e}}=5.44784, \quad \quad {{\digamma }_{v}}=87.437, \quad \quad \Delta =9.6623\times {{10}^{-9}}, \\ \omega= & 0.014\times SO_{avg}E+0.219, \\ \Lambda= & 11,\quad \quad {{\tilde{a}}_{e}}=0.025439, \quad \quad {{\digamma }_{v}}=63.708, \quad \quad \Delta =0.000023, \\ RI= & 20.536\times SO_{avg}E+47.330, \\ \Lambda= & 22,\quad \quad {{\tilde{a}}_{e}}=22.99738, \quad \quad {{\digamma }_{v}}=348.465, \quad \quad \Delta =4.0117\times {{10}^{-14}}, \\ \Delta {{H}_{f}}= & 10.477\times SO_{avg}E+85.897, \\ \Lambda= & 22,\quad \quad {{\tilde{a}}_{e}}=20.53702, \quad \quad {{\digamma }_{v}}=113.728, \quad \quad \Delta =1.0613\times {{10}^{-9}}, \\ \log P= & 0.239\times SO_{avg}E+1.550, \\ \Lambda= & 22,\quad \quad {{\tilde{a}}_{e}}=0.36134, \quad \quad {{\digamma }_{v}}=191.141, \quad \quad \Delta =1.0719\times {{10}^{-11}}. \end{aligned}$$

Models related to \(\beta SOE\)

In the section, we identify the designs of \(\Delta {{H}_{f}}\), S, BP, \(\log P\), RI, and \(\omega\) linked to the \(\beta SOE\).

$$\begin{aligned} BP= & 65.266\times \beta SOE-54.295, \\ \end{aligned}$$
$$\begin{aligned} \Lambda= & 22,\quad \quad {{\tilde{a}}_{e}}=12.76104, \quad \quad {{\digamma }_{v}}=1241.147, \quad \quad \Delta =1.7856\times {{10}^{-19}}, \\ S= & 7.929\times \beta SOE+45.757, \\ \Lambda= & 22,\quad \quad {{\tilde{a}}_{e}}=3.20771, \quad \quad {{\digamma }_{v}}=289.894, \quad \quad \Delta =2.2767\times {{10}^{-13}}, \\ \omega= & 0.044\times \beta SOE+0.124, \\ \Lambda= & 11,\quad \quad {{\tilde{a}}_{e}}=0.01054, \quad \quad {{\digamma }_{v}}=414.499, \quad \quad \Delta =7.7597\times {{10}^{-9}}, \\ RI= & 63.841\times \beta SOE-80.255, \\ \Lambda= & 22,\quad \quad {{\tilde{a}}_{e}}=8.64243, \quad \quad {{\digamma }_{v}}=2589.040, \quad \quad \Delta =1.2388\times {{10}^{-22}},\\ \Delta {{H}_{f}}= & 33.640\times \beta SOE+12.010, \\ \Lambda= & 22,\quad \quad {{\tilde{a}}_{e}}=11.63474, \quad \quad {{\digamma }_{v}}=396.663, \quad \quad \Delta =1.1699\times {{10}^{-14}}, \\ \log P= & 0.752\times \beta SOE-0.012, \\ \Lambda= & 22,\quad \quad {{\tilde{a}}_{e}}=0.18992, \quad \quad {{\digamma }_{v}}=744.306, \quad \quad \Delta =2.6844\times {{10}^{-17}}. \end{aligned}$$

Models related to \(R\beta SOE\)

In this section, we identify the designs of \(\Delta {{H}_{f}}\), S, BP, \(\log P\), \(\omega\), and RI linked to the \(R\beta SOE\).

$$\begin{aligned} BP= & 17.703\times R\beta SOE-76.939, \\ \Lambda= & 22,\quad \quad {{\tilde{a}}_{e}}=23.97916, \quad \quad {{\digamma }_{v}}=337.166, \quad \quad \Delta =5.4821\times {{10}^{-14}}, \\ S= & 2.177\times R\beta SOE+42.163, \\ \Lambda= & 22,\quad \quad {{\tilde{a}}_{e}}=3.57762, \quad \quad {{\digamma }_{v}}=229.123, \quad \quad \Delta =2.0353\times {{10}^{-12}},\\ \omega= & 0.012\times R\beta SOE+0.113, \\ \Lambda= & 11,\quad \quad {{\tilde{a}}_{e}}=0.01649, \quad \quad {{\digamma }_{v}}=164.033, \quad \quad \Delta =4.4131\times {{10}^{-7}}, \\ RI= & 17.382\times R\beta SOE-104.508, \\ \Lambda= & 22,\quad \quad {{\tilde{a}}_{e}}=19.93818, \quad \quad {{\digamma }_{v}}=470.210, \quad \quad \Delta =20.2945\times {{10}^{-15}},\\ \Delta {{H}_{f}}= & 9.246\times R\beta SOE-3.490, \\ \Lambda= & 22,\quad \quad {{\tilde{a}}_{e}}=13.26477, \quad \quad {{\digamma }_{v}}=300.553, \quad \quad \Delta =1.6218\times {{10}^{-13}}, \\ \log P= & 0.204\times R\beta SOE-0.258, \\ \Lambda= & 22,\quad \quad {{\tilde{a}}_{e}}=0.31113, \quad \quad {{\digamma }_{v}}=264.782, \quad \quad \Delta =5.3151\times {{10}^{-13}}. \end{aligned}$$

Models related to \(\delta \beta SOE\)

In this section, we identify the systems of \(\Delta {{H}_{f}}\), S, BP, \(\log P\), RI, and \(\omega\) linked to the \(\delta \beta SOE\).

$$\begin{aligned} BP= & 17.703\times \delta \beta SOE-76.939, \\ \Lambda= & 22,\quad \quad {{\tilde{a}}_{e}}=23.97916, \quad \quad {{\digamma }_{v}}=337.166, \quad \quad \Delta =5.4821\times {{10}^{-14}}, \\ S= & 2.177\times \delta \beta SOE+42.163, \\ \Lambda= & 22,\quad \quad {{\tilde{a}}_{e}}=3.57762, \quad \quad {{\digamma }_{v}}=229.123, \quad \quad \Delta =2.0353\times {{10}^{-12}}, \\ \omega= & 0.012\times \delta \beta SOE+0.113 \\ \Lambda= & 11,\quad \quad {{\tilde{a}}_{e}}=0.01649, \quad \quad {{\digamma }_{v}}=164.033, \quad \quad \Delta =4.4131\times {{10}^{-7}}, \\ RI= & 17.382\times \delta \beta SOE-104.508, \\ \Lambda= & 22,\quad \quad {{\tilde{a}}_{e}}=19.93818, \quad \quad {{\digamma }_{v}}=470.210, \quad \quad \Delta =20.2945\times {{10}^{-15}}, \\ \Delta {{H}_{f}}= & 9.246\times \delta \beta SOE-3.490, \\ \Lambda= & 22,\quad \quad {{\tilde{a}}_{e}}=13.26477, \quad \quad {{\digamma }_{v}}=300.553, \quad \quad \Delta =1.6218\times {{10}^{-13}}, \\ \end{aligned}$$
$$\begin{aligned} \log P= & 0.204\times \delta \beta SOE-0.258, \\ \Lambda= & 22,\quad \quad {{\tilde{a}}_{e}}=0.31113, \quad \quad {{\digamma }_{v}}=264.782, \quad \quad \Delta =5.3151\times {{10}^{-13}}. \end{aligned}$$

Figure 4 displays a detailed scatter plot demonstrating the relationship of the RI with numerous physicochemical and thermodynamic characteristics, comprising BP, \(\Delta H_f\), S, \(\omega\), and \(\log P\), in association with the Sombor energy. This representation with respect to \(SO_{red}E\), \(SO_{avg}E\), \(\beta SOE\), \(R\beta SOE\), and \(\delta \beta SOE\) can be obtained likewise.

Fig. 4
figure 4

Scatter plot between Sombor energy and characteristics of benzenoid hydrocarbons.

Full size image
Fig. 5
figure 5

Correlation heatmap between energies and different characteristics of BHC.

Full size image
Fig. 6
figure 6

Scatter plot matrix between energies and different characteristics of BHC.

Full size image

The Pearson correlation coefficient16,20, often represented by the symbol r, is a prominent statistical tool used to quantify the direction and strength of the linear association between two continuous variables. This coefficient ranges from \(-1\) to 1, where \(r=1\) shows a perfect positive correlation, signifies a perfect negative correlation, and \(r=0\) shows the absence of any linear association. It is critical to note that the r specifically defines linear relationships. Consequently, an r value near zero does not necessarily suggest the absence of any relationship; rather, it indicates the lack of a linear relationship. Furthermore, the The use of the Pearson correlation necessitates certain hypotheses to be met: there exist a linear relationship between the parameters, the parameters should follow a normal distribution and be continuous, with homoscedasticity present,indicating that the independent variable’s variances remain constant at all levels. The calculation of the r is conducted through the following procedure:

$$\begin{aligned} r=\frac{\sum {\left( {{Y}_{i}}-\overline{Y} \right) \left( {{Z}_{i}}-\overline{Z} \right) }}{\sqrt{{{\sum {{{\left( {{Y}_{i}}-\overline{Y} \right) }^{2}}\left( {{Z}_{i}}-\overline{Z} \right) }}^{2}}}}. \end{aligned}$$

In this formula, \(Y_i\) and \(Z_i\) denote the individual data points of the variables, while Y and Z indicate their corresponding means. We examine both the graphical and numerical aspects of the correlation by using heatmap and scatter plot matrix between energies and different characteristics of BHC as shown in Table 2 and in Figs. 5 and 6. The analysis demonstrates that the Sombor energy consistently exhibits the highest correlation with the boiling point BP, the enthalpy of formation \(\Delta H_f\), and the Kovats retention index RI. In contrast, reduced Banhatti Sombor energy shows moderate but significant correlations with entropy S. These findings highlight the predictive capability of specific graph-based descriptors and their importance in characterizing thermodynamic properties.

Table 2 Correlation of energies with different characteristics of BHC.
Full size table

By establishing robust correlations between these properties and graph energies, our models introduce a novel and efficient method for predicting such characteristics based solely on topological data. This approach provides not only improved predictive capability but also a theoretical basis for understanding how molecular topology influences thermodynamic behavior.

Statistical assessment of predictive reliability

The performance of the models was assessed by R-squared and mean squared error (MSE), which were some of the key performance metrics involved. A value of R-squared greater than 0.9 explains that most of the variance in data is described by the model; similarly, a small MSE shows that the model has minimum prediction errors, hence accuracy and efficiency in the prediction of thermodynamic properties. These are testaments to how powerful these graph-based descriptors are with regard to the effective presence of important relationships between structure and thermodynamic properties. The performance of the model in predicting Sombor Energy was evaluated based on MSE and R-squared value, which reflect the accuracy and fitness of the model, respectively. Results for Sombor Energy are described in the following Table 3, and graphical representation in Fig. 7, with a particular focus on its predictive capabilities relative to other molecular properties.

Table 3 Correlation of energies with different properties of BHC.
Full size table
Fig. 7
figure 7

Radar chart for MSE and R-squared for different models.

Full size image

The residual for Sombor Energy is plotted as a means of assessing the goodness of the model. From residual plots, the individual differences between the actual and estimated values are tiny and spread well across; this evidences that the model doesn’t have signs of overfitting or underfitting. For example, among the first five residuals, values such as \(-26.82\), 1.52, and \(-1.93\) indicate some variability but not excessive deviations. Although minor discrepancies were observed in specific molecules, they do not significantly affect the overall predictive strength. These findings confirm the reliability of the proposed model in capturing trends in Sombor Energy across a diverse set of benzenoid hydrocarbons. The trends observed in this study are consistent with established chemical properties of hydrocarbons and align closely with findings from previous research. For example, the strong correlation between Sombor energy and thermodynamic properties such as boiling point BP and enthalpy of formation \(\Delta H_f\) reflects well-documented relationships between molecular connectivity and stability. Additionally, the results reinforce prior evidence supporting the use of graph-based descriptors as computationally efficient predictors. These consistencies not only validate the methodology but also hint at its extension for a wider application in material science and molecular chemistry. In a similar way, further models can be computed for different energies corresponding to MSE, R-squared, and residuals.

Further, it is of utmost importance that such developed models find applications for other classes of molecules, including alkanes, alkynes, and heterocyclic compounds, in order to examine their versatility. In this way, the developed models will be able to test their capabilities in terms of predictive accuracy over a wide range of chemical structures and, hence, give insight into the generalizability of the models. The extension to different molecular types will also establish whether the proposed graph-based descriptors need further refinement in order to enhance their applicability to a wider spectrum of compounds. This will confirm the robustness of the models and their potential for wider use in predictive analysis. To further extend our proposed models, we would highly recommend establishing their respective capabilities in a prediction of generally biological activities, whether compounds exert drug-likeness or have toxicity. Then, the general utility of this graph-based descriptor technique will be possible to evaluate in such vital areas as the discovery of drugs, toxicology, or environmental chemistry. Such an approach will extend application-oriented practicalness of the discussed models and promote further research connected with predictive models.

Conclusion

In this study, we explored several well-established extended energy metrics of graphs, including SOE, \(SO_{red}E\), \(SO_{avg}E\), \(\beta SOE\), \(R\beta SOE\), and \(\delta \beta SOE\). The primary goal was to evaluate their predictive potential for the physicochemical properties of PAC using a dataset of 22 benzenoid hydrocarbons (BHCs). We developed predictive models for key properties, such as, (RI), (BP), \((\Delta H_f)\), (S), \(\omega\), and \(\log P\), based on these topological indices. Our results indicate a strong correlation between the graph-based descriptors and thermodynamic properties, underscoring their effectiveness in predicting molecular characteristics and highlighting their relevance in computational chemistry.