Introduction

Nonlinear partial differential equations (PDEs) have been extensively utilized in recent years to assess numerous physical phenomena in science and engineering. Fluid mechanics, plasma physics, quantum mechanics, nonlinear optics, solid-state physics, physical chemistry, and several other domains of mathematical modeling employ it to characterize intricate phenomena1,2,3,4. Due to the challenges in deriving analytical solutions for non-linear partial differential equations (PDEs), academics have developed several numerical approaches to address these equations. This study has significant implications for social networks, Internet networks, telecommunications, and medical devices. They help us learn more about real-world properties; nonlinear systems have become an important and interesting area of study for modern academics who want to find exact analytical answers to problems. In recent years, several effective methods have been introduced for generating traveling wave solutions of non-linear PDEs. These include the multiple Exp-function method5, the new extended direct algebraic approach6, the sine-Gordon expansion method7, the Bäcklund transformation method8, the sub-equation method9, the modified simple equation method10, the modified Kudryashov method11, the Riccati-Bernoulli sub-ODE method12, and the extended trial function scheme13.

Several contributions to the study of nonlinear systems have been examined. Helal14 conducted a thorough investigation of soliton solutions for PDEs, presenting various methodologies for analytical and numerical analyses. He noted that solitons represent a localized wave with distinct nonlinear characteristics and are solutions to either a nonlinear system of equations or a singular equation. Samir et al.15 effectively utilized a modified extended mapping approach to derive exact traveling wave solutions within a complex nonlinear framework. Tsega explored the numerical solution of two-dimensional unsteady advection-diffusion-reaction equations with variable coefficients. The study focused on the dynamic behavior of these systems under varying parameters. Such equations are crucial for modeling physical and chemical processes in fluid dynamics, environmental science, and reaction kinetics38. Rezazadeh et al.16 applied exponential rational functions and Jacobi elliptic function techniques to investigate wave surfaces, offering valuable insights into the dynamic behavior of the same non-linear model. Savović et al. conducted a study comparing the explicit finite difference method with physics-informed neural networks to solve the Burgers’ equation41. In another work, Savović et al. (2019) demonstrated that the Sine-Gordon equation can be numerically solved using two distinct finite difference methods and advanced physics-informed neural networks42. Gu, Y., et al. delved into the Gerdjikov-Ivanov equation within the realm of nonlinear fiber optics, uncovering elegant closed-form solutions enriched by beta derivatives43. Employing robust and innovative techniques, Gu, Y. illuminated the intricate closed-form solutions of the nonlinear space-time fractional Drinfeld-Sokolov-Wilson problem44. Additionally, Yokus et al.17 derived solitary wave solutions for the non-linear process using the sinh-Gordon function. Fractional partial differential equations (FPDEs) have attracted considerable interest because of their frequent occurrence across various disciplines, including physics, biology, rheology, viscoelasticity, signal processing, and electrochemistry. Recently, significant theoretical progress has been made in this area18. The KdV equation19, the nonlinear Schrödinger (NLS) equation39, the Boussinesq equation40, the KdV-Burgers equation21, the Burgers equation20, the Fisher or Kolmogorov-Petrovskii-Piskunov (KPP) equation22 have been extensively analyzed and numerically investigated in the fields of physics and engineering.

The advection-diffusion-reaction (ADR) equation is a fundamental mathematical model that describes the transport and interaction of substances within various media. It plays a crucial role in disciplines such as biology, chemistry, physics, and environmental science, as it encompasses processes involving advection (transport driven by fluid flow), diffusion (spreading caused by concentration gradients) and reaction (chemical or biological transformations). The solution of the ADR equation presents significant challenges as a result of the varying dominance of advection, diffusion, and reaction under different conditions. For example, in porous media, the time scales associated with these processes can differ by orders of magnitude, adding complexity to the modeling. Numerical methods are often used to approximate solutions, with techniques such as the finite difference method (FDM) being effective in solving nonlinear ADR equations with specific initial and boundary conditions. These approaches provide valuable insight into the stability and efficiency of the solutions. Analytical methods also play an important role in solving ADR equations. For instance, Lie transformations can simplify fractional PDEs by reducing them to fractional ODEs. However, such transformations are not always feasible for time- and space-fractional ADR models. In such cases, hybrid methods are proposed that combine analytical and numerical techniques, offering high precision and broad applicability for the solution of complex ADR problems.

Numerous scientists have already investigated the ADR equation, employing various methodologies across diverse fields and theoretical frameworks. In 2002, Hauke examined the ADR equation employing a basic subgrid scale stabilization method for numerical solutions23. In 2006, Spiegelman and Katz addressed an ADR issue and obtained a numerical solution utilizing a semi-Lagrangian Crank-Nicolson method24. Kaya and Gharehbaghi (2014) discovered the concealed solutions to an ADR equation employing several numerical approaches25. In 2019, Jannelli et al. derived several analytical solutions and presented numerical findings for the ADR equation in both spatial and temporal contexts26. In 2022, Savovic and collaborators released a paper analyzing a comparative investigation employing the ADR equation to simulate exponential-type traveling waves during heat and mass transformation27. This research focuses on the intricate dynamics of the ADR model employing the modified \(\left( \frac{G'}{G^2}\right)\) expansion method for a complete analysis of its exact solutions. Through dynamical analysis, the study seeks to uncover the phase portrait of the system, revealing the various states it can occupy over time. Additionally, it examines the system’s sensitivity to initial conditions, allowing for a deeper understanding of how small variations can lead to significantly different outcomes. This sensitivity highlights the chaotic behavior inherent in the ADR model, where trajectories can diverge rapidly, making long-term predictions challenging. By mapping the phase portrait, the research elucidates the regions of stability and instability within the system, offering crucial insights into its complex behavior and potential applications in various fields for a deeper understanding of chaotic behavior. This multifaceted approach aims to offer valuable insights into the model’s complexities and its broader implications in the field.

Chakrabarty et al. (2024) conducted a dynamical analysis of optical soliton solutions for the complex Ginzburg Landau equation, incorporating Kerr law nonlinearity across classical, truncated M-fractional derivative, beta fractional derivative, and conformable fractional derivative types28. In the same year, Umer et al. investigated the symmetry-optimized dynamical analysis of optical soliton patterns in the Euler-Bernoulli beam equation with flexible support, employing a semi-analytical solution approach29. Raza et al. (2024) performed a dynamic analysis of the modified complex Ginzburg-Landau model in communication systems, deriving new optical soliton solutions30. Rahman et al. (2024) conducted a phase portrait analysis, explored various soliton solutions exhibiting chaotic behavior, and performed a sensitivity analysis of the extended nonlinear Schrödinger equation31. In 2023, Yin et al. investigated the changing behavior of optical pulses using modified Physics-Informed Neural Networks (PINNs). Their study examined soliton solutions, rogue waves, and the parameter identification process for the CQ-NLSE (cubic-quintic nonlinear Schrödinger equation)32. Cui et al. (2023) analyzed the dynamical behavior of the (2+1)-dimensional Heisenberg ferromagnet equation and studied multi-soliton and breather solutions on both constant and periodic backgrounds for the Heisenberg ferromagnet33. Similarly, in 2022, Kaur et al. performed a comprehensive dynamical analysis of soliton solutions for the space-time fractional Calogero-Degasperis and Sharma-Tasso-Olver equations. This research systematically examined the influence of fractional derivatives on the stability, behavior, and propagation of soliton solutions, providing profound insights into the complex dynamics governed by these equations34.

This research is valuable because the ADR equation is widely used in various engineering and physical phenomena, such as soliton dynamics, light transmission, fluid flow, and reaction-diffusion processes in chemical and biological systems. By employing the \(G'/G^2\) expansion method, this study provides exact analytical solutions that are crucial for understanding the intricate interplay between transport, diffusion, and nonlinear reaction mechanisms. These solutions also offer deeper insights into soliton behavior, enabling improved control and optimization in practical applications, including fiber optics, environmental modeling, and plasma physics. The novelty lies in demonstrating the method’s efficacy in handling the intricate balance of advection, diffusion, and nonlinear reaction terms, which are central to understanding phenomena in optical fiber communication, fluid mechanics, and biological systems. By offering new solutions and a versatile framework for analyzing nonlinear equations, this study not only enhances theoretical understanding, but also provides practical tools for optimizing technologies in diverse fields such as telecommunications, environmental science, and plasma physics. Its originality lies in bridging gaps in existing literature and paving the way for future explorations in nonlinear dynamics. Dynamical analysis of the ADR equation involves exploring its stability, bifurcations, and qualitative behavior under various parameter regimes.

Bifurcation analysis is a recognized technique for investigating dynamical systems, providing substantial insights into the behavior of different system components under varying conditions. In this study, bifurcation and chaos theory were employed to enhance our understanding of a related planar dynamical system. Using these analytical tools, we identified system solutions and represented them through phase diagrams. A sensitivity analysis was conducted on the key variables to assess their influence on the system’s behavior. The model was subjected to a comprehensive study under various initial conditions to thoroughly explore its dynamics. This work examines the impact of bifurcation and chaos on the evolution of dynamic systems across diverse contexts, offering novel insights into the system’s intricate characteristics. The findings are original and significant, uncovering the complex processes at play.

The structure of this article is as follows. Section 2 introduces the formulation of the equation and outlines its conceptual framework. Section 3 discusses the modified \(\left( \frac{G'}{G^2}\right)\) expansion method in detail. Section 4 presents graphical representations of the proposed model’s solutions. In Section 5, we analyze the dynamics of the system, providing graphical representations for various initial conditions. Lastly, Section 6 concludes with insights drawn from the model’s findings.

Governing equation

In this paper, we analyze a non-linear ARD equation to explore optimization in function spaces and to derive solitary wave solutions. The proposed equation is expressed by the following36:

$$\begin{aligned} \frac{\partial u(x, t)}{\partial t} = \kappa _1 u(x, t) - \kappa _2 u^2(x, t) - \eta _1 \frac{\partial u(x, t)}{\partial x} + \eta _2 \frac{\partial f(x, t)}{\partial x}. \end{aligned}$$
(1)

In this context, \(u(x, t)\) denotes the primary variable, with \(u_x[f(x, t)] = u_{xx}(x, t)\). Here, \(\eta _1 > 0\) represents the wave propagation speed, while \(\eta _2 > 0\) indicates the diffusion coefficient during propagation. The parameters \(\kappa _1 > 0\) and \(\kappa _2 > 0\) are coefficients within the response term, and \(\mu > 1\) serves as an additional parameter.

This nonlinear Eq. (1) is applicable in various engineering and research domains, including fluid dynamics, electromagnetism, acoustics, and population dynamics. The parameter \(\mu\) reflects the non-linearity of the model, as introducing a non-linear term such as \(u^2(x, t)\) can dramatically influence the behavior and physical characteristics of systems governed by nonlinear advection, reaction, and diffusion equations.

$$\begin{aligned} \begin{aligned} u(x,t) = \phi (\xi ), \ \ \ \xi = p x- q t. \end{aligned} \end{aligned}$$
(2)

In Eq. (2), q represents the velocity of the traveling wave, and p represents the wavenumber of the wave. Upon performing and implementing double integration with the integration constant set to zero, we obtain

$$\begin{aligned} \eta _2 p^2 \phi '' + (q - \eta _1 p) \phi ' + \kappa _1 \phi - \kappa _2 \phi ^2 = 0. \end{aligned}$$
(3)

Modified \(\frac{G'}{G^2}\) Expansion Method

The modified \(\left( \frac{G'}{G^2}\right)\) expansion method is a widely used approach for solving NLPDEs, particularly in the fields of physics, mathematics, engineering, and physical sciences. The process begins by defining the initial conditions and parameters. researchers apply a predefined method to accurately solve the ARD model. Due to its effectiveness, this method is employed to find the exact solution. A detailed explanation of modified \(\left( \frac{G'}{G^2}\right)\) expansion method can be found in37.

$$\begin{aligned} F(u,u_x,u_t,u_{xx},u_{xt},u_{tt},\ldots u_x,u_{xx},u_{xt},u_{tt}\ldots ) = 0. \end{aligned}$$
(4)

Subscripts indicate the derivatives with respect to x and t for the corresponding functions u(x, t).

Step 1: We employ the wave transformation Eq. (3) to transform Eqs. (1) and (2) into an ODE.

$$\begin{aligned} G(\phi ,\phi ',\phi '',\phi ''',\ldots \phi ^{n}) =0. \end{aligned}$$
(5)

Step 2 : Let’s assume that the general solution to the ODE is

$$\begin{aligned} U(\zeta )=\Lambda _{{0}}+\sum _{n=1}^{N}\left\{ \Lambda _n \left( \frac{G'}{G^2}\right) ^n +\Lambda _n \left( \frac{G'}{G^2}\right) ^{-n}\right\} . \end{aligned}$$
(6)

where \(\Lambda _0\) and \(\Lambda _n\) (n=1,2,...N) are detemined later to find the values for the traveling wave solution. Here \(G=G(\phi )\) satisfies the result of the Ricatti equation.

$$\begin{aligned} \left( \frac{G'}{G^2}\right) '=\sigma +\mu \left( \frac{G'}{G^2}\right) +\rho \left( \frac{G'}{G^2}\right) ^2. \end{aligned}$$
(7)

where \(\sigma\), \(\mu\), and \(\rho\) are real constant.

Step 3 : We will use the balancing technique to determine the value of n, which is the difference between the highest order derivative and the highest order non-linear term. By substituting Eq. (16) with Eq. (15) into Eq. (12), we get an algebraic equation that may be expressed as the power of \((\frac{G'}{G^2})\). We solved the algebraic equation by equating the power \((\frac{G'}{G^2})\) to zero and using Maple to obtain the values of \(\Lambda\).

Step 4 : The general solutions of Eq. (14) as follows:

$$\begin{aligned} \left( \frac{G'}{G^2}\right) = \begin{aligned} {\left\{ \begin{array}{ll} \sqrt{\sigma \rho } \left[ \frac{C_1 \cos (\sqrt{\sigma \rho } \, \zeta ) + C_2 \sin (\sqrt{\sigma \rho } \, \zeta )}{C_1 \sin (\sqrt{\sigma \rho } \, \zeta ) - C_2 \cos (\sqrt{\sigma \rho } \, \zeta )}\right] , \mu =0, \sigma \rho >0,\\ -\sqrt{|\sigma \rho |} \left[ \frac{C_1 \sinh (2\sqrt{|\sigma \rho |} \, \zeta ) + C_1 \cosh (2\sqrt{|\sigma \rho |} \, \zeta ) + C_2}{C_1 \cosh (2\sqrt{|\sigma \rho |} \, \zeta ) + C_1 \sinh (2\sqrt{|\sigma \rho |} \, \zeta ) - C_2}\right] , \mu =0, \sigma \rho<0,\\ -\frac{C_1}{\rho \left( \zeta C_1 + C_2\right) }, \ \ \ \ \mu =0, \sigma =0,\rho \ne 0,\\ -\frac{\mu }{2\rho } + \left[ -\frac{\sqrt{\Delta } \left( C_1 \cosh (\frac{\sqrt{\Delta }}{2} \, \zeta ) + C_2 \sinh (\frac{\sqrt{\Delta }}{2} \, \zeta )\right) }{2\rho \left( C_1 \cosh (\frac{\sqrt{\Delta }}{2} \, \zeta ) + C_2 \sinh (\frac{\sqrt{\Delta }}{2} \, \zeta )\right) }\right] \mu \ne 0, \Delta \ge 0,\\ -\frac{\mu }{2\rho } + \left[ -\frac{\sqrt{-\Delta } \left( C_1 \cosh \left( \sqrt{\frac{-\Delta }{2}} \, \zeta \right) - C_2 \sinh \left( \sqrt{\frac{-\Delta }{2}} \, \zeta \right) \right) }{2\rho \left( C_1 \cosh \left( \sqrt{\frac{-\Delta }{2}} \, \zeta \right) + C_2 \sinh \left( \sqrt{\frac{-\Delta }{2}} \, \zeta \right) \right) }\right] , \mu \ne 0, \Delta <0. \end{array}\right. } \end{aligned} \end{aligned}$$
(8)

where \(C_1\) and \(C_2\) are arbitrary constant and \(\Delta =\mu ^2 -4 \sigma \rho\).

Solutions of Modified \(\left( \frac{G'}{G^2}\right)\) expansion method

In this section, we will get the soliton solutions of Eq. (3) by using modified \(\left( \frac{G'}{G^2}\right)\) expansion method. We determine the value of \(n=1\) using the balance technique between \(\phi ''\) and \(\phi ^2\) to get the value from Eq. (3) and substitute it into Eq. (6). We get;

$$\begin{aligned} U(\zeta )= \Lambda _0\ + \Lambda _1\ \left( \frac{G'}{G^2}\right) ^{1}+\Lambda _2\ \left( \frac{G'}{G^2}\right) ^{2}+\Lambda _3\ \left( \frac{G'}{G^2}\right) ^{-1}+\Lambda _4\ \left( \frac{G'}{G^2}\right) ^{-2}. \end{aligned}$$
(9)

By combining Eq. (7) and Eq. (6) into Eq. (3), we derived a nonlinear algebraic expression in which the terms involving \(\left( \frac{G'}{G^2} \right)\) are equated to zero.

$$\begin{aligned} \begin{aligned} \left( \frac{G'}{G^2}\right) ^{4}&:6 p^2 \rho ^2 \Lambda _2 c_2 - \Lambda _2^2 k_2 = 0, \\ \left( \frac{G'}{G^2}\right) ^{3}&:c_2 p^2 \left( 10 \mu \rho \Lambda _2 + 2 \rho ^2 \Lambda _1\right) + 2 (-p c_1 + q) \Lambda _2 \rho - 2 k_2 \Lambda _1 \Lambda _2 = 0, \\ \left( \frac{G'}{G^2}\right) ^{2}&:c_2 p^2 \left( 3 \Lambda _1 \mu \rho + 4 \Lambda _2 \left( \mu ^2 + 2 \rho \sigma \right) \right) + (-p c_1 + q) \left( 2 \mu \Lambda _2 + \rho \Lambda _1\right) \\&+ k_1 \Lambda _2 - k_2 \left( 2 \Lambda _0 \Lambda _2 + \Lambda _1^2\right) =0, \\ \left( \frac{G'}{G^2}\right) ^{1}&:c_2 p^2 \left( \Lambda _1 \left( \mu ^2 + 2 \rho \sigma \right) + 6 \mu \Lambda _2 \sigma \right) + (-p c_1 + q) \left( \mu \Lambda _1 + 2 \sigma \Lambda _2\right) \\&+ k_1 \Lambda _1 - k_2 \left( 2 \Lambda _0 \Lambda _1 + 2 \Lambda _2 \Lambda _3\right) =0,\\ \left( \frac{G'}{G^2}\right) ^{0}&:c_2 p^2 \left( \mu \rho \Lambda _3 + \mu \sigma \Lambda _1 + 2 \rho ^2 \Lambda _4 + 2 \sigma ^2 \Lambda _2\right) + (-p c_1 + q)(-\rho \Lambda _3 + \sigma \Lambda _1) \\&+ k_1 \Lambda _0 - k_2 \left( \Lambda _0^2 + 2 \Lambda _1 \Lambda _3 + 2 \Lambda _2 \Lambda _4\right) =0, \\ \left( \frac{G'}{G^2}\right) ^{-1}&:c_2 p^2 \left( \Lambda _3 \left( \mu ^2 + 2 \rho \sigma \right) + 6 \Lambda _4 \mu \rho \right) + (-p c_1 + q)(- \mu \Lambda _3 - 2 \rho \Lambda _4)\\&+ k_1 \Lambda _3 - k_2 \left( 2 \Lambda _0 \Lambda _3 + 2 \Lambda _1 \Lambda _4\right) = 0, \\ \left( \frac{G'}{G^2}\right) ^{-2}&:c_2 p^2 \left( 3 \mu \Lambda _3 \sigma + 4 \Lambda _4 \left( \mu ^2 + 2 \rho \sigma \right) \right) \\&+ (-p c_1 + q)(-2 \mu \Lambda _4 - \sigma \Lambda _3) + k_1 \Lambda _4 - k_2 \left( 2 \Lambda _0 \Lambda _4 + \Lambda _3^2\right) = 0, \\ \left( \frac{G'}{G^2}\right) ^{-3}&:c_2 p^2 \left( 10 \mu \sigma \Lambda _4 + 2 \sigma ^2 \Lambda _3\right) - 2(-p c_1 + q) \Lambda _4 \sigma - 2 k_2 \Lambda _4 \Lambda _3 = 0,\\ \left( \frac{G'}{G^2}\right) ^{-4}&:6 p^2 \sigma ^2 \Lambda _4 c_2 - \Lambda _4^2 k_2 = 0. \end{aligned} \end{aligned}$$
(10)

We solved the system of algebraic equations using Maple to produce exact traveling wave solutions. We derived the solution of equation as follows:

$$\begin{aligned} \begin{aligned} \rho&= \frac{1}{4} \frac{p^2 \mu ^2 c_2 + k_1}{p^2 \sigma c_2}, \ \ \ \Lambda _0&= \frac{3}{2} \frac{p^2 \mu ^2 c_2 + k_1}{k_2}, \ \ \ \Lambda _1&= 0, \ \ \Lambda _2&= 0, \ \ \Lambda _3&= \frac{6 p^2 \mu \sigma c_2}{k_2}, \ \ \ \Lambda _4&= \frac{6 p^2 \sigma ^2 c_2}{k_2}. \end{aligned} \end{aligned}$$
(11)

The findings were derived by applying the parameter values extracted from the solitary wave solutions presented in Eq. (3).

Case 1: If \(\mu =0\) and \(\sigma \rho >0\),

$$\begin{aligned} \begin{aligned} \phi _1(x,t)&=\frac{3}{2} \frac{\mu ^2 p^2 c_2 + k_1}{k_2} + \frac{6 p^2 \mu \sigma ^2 c_2}{k_2 \sqrt{\sigma \rho } \left( \frac{C_1 \cos (\sqrt{\sigma \rho } \, \zeta ) + C_2 \sin (\sqrt{\sigma \rho } \, \zeta )}{C_1 \sin (\sqrt{\sigma \rho } \, \zeta ) - C_2 \cos (\sqrt{\sigma \rho } \, \zeta )} \right) }\\&\quad + \frac{6 p^2 \sigma ^3 c_2}{k_2 \rho \left( \frac{C_1 \cos (\sqrt{\sigma \rho } \, \zeta ) + C_2 \sin (\sqrt{\sigma \rho } \, \zeta )}{C_1 \sin (\sqrt{\sigma \rho } \, \zeta ) - C_2 \cos (\sqrt{\sigma \rho } \, \zeta )} \right) ^2}, \end{aligned} \end{aligned}$$
(12)

Case 2: If \(\mu =0\) and \(\sigma \rho <0\),

$$\begin{aligned} \begin{aligned} \phi _2(x,t)&=\frac{3}{2} \frac{\mu ^2 p^2 c_2 + k_1}{k_2} - \frac{6 p^2 \mu \sigma ^2 c_2}{k_2 \sqrt{| \sigma \rho |} \left( \frac{C_1 \sinh (2 \sqrt{| \sigma \rho |} \, \zeta ) + C_1 \cosh (2 \sqrt{| \sigma \rho |} \, \zeta ) + C_2}{C_1 \sinh (2 \sqrt{| \sigma \rho |} \, \zeta ) + C_1 \cosh (2 \sqrt{| \sigma \rho |} \, \zeta ) - C_2} \right) } \\&\quad + \frac{6 p^2 \sigma ^4 c_2}{k_2 |\sigma \rho | \left( \frac{C_1 \sinh (2 \sqrt{| \sigma \rho |} \, \zeta ) + C_1 \cosh (2 \sqrt{| \sigma \rho |} \, \zeta ) + C_2}{C_1 \sinh (2 \sqrt{| \sigma \rho |} \, \zeta ) + C_1 \cosh (2 \sqrt{| \sigma \rho |} \, \zeta ) - C_2} \right) ^2}, \end{aligned} \end{aligned}$$
(13)

Case 3: If \(\mu =0\), \(\sigma =0\) and \(\rho \ne 0\),

$$\begin{aligned} \begin{aligned} \phi _3(x,t)&=3/2\,{\frac{{\mu }^{2}{p}^{2}c_{{2}}+k_{{1}}}{k_{{2}}}}-6\,{\frac{{p} ^{2}\mu \,\sigma \,c_{{2}}\rho \left( \left( \zeta \right) \,C_{{1}}+C _{{2}} \right) }{k_{{2}}C_{{1}}}}\\&\quad +6\,{\frac{{p}^{2}{\sigma }^{2}c_{{2} } \left( \rho \left( \left( \zeta \right) \,C_{{1}}+C_{{2}} \right) \right) ^{2}}{k_{{2}}{C_{{1}}}^{2}}}, \end{aligned} \end{aligned}$$
(14)

Case 4: If \(\mu \ne 0\), \(\Delta \ge 0\),

$$\begin{aligned} \begin{aligned} \phi _4(x,t)&=\frac{3}{2} \frac{p^2 \mu ^2 c_2 + k_1}{k_2} + \frac{6 p^2 \mu \sigma c_2}{k_2 \left( -\frac{1}{2} \frac{\mu }{\rho } - \frac{1}{2} \sqrt{\Delta } \frac{\frac{1}{2} C_1 \cosh (\sqrt{\Delta } \, \zeta ) - \frac{1}{2} C_2 \sinh (\sqrt{\Delta } \, \zeta )}{\rho \left( \frac{1}{2} C_1 \cosh (\sqrt{\Delta } \, \zeta ) + \frac{1}{2} C_2 \sinh (\sqrt{\Delta } \, \zeta ) \right) } \right) } \\&\quad + \frac{6 p^2 \sigma ^2 c_2}{k_2 \left( -\frac{1}{2} \frac{\mu }{\rho } - \frac{1}{2} \sqrt{\Delta } \frac{\frac{1}{2} C_1 \cosh (\sqrt{\Delta } \, \zeta ) - \frac{1}{2} C_2 \sinh (\sqrt{\Delta } \, \zeta )}{\rho \left( \frac{1}{2} C_1 \cosh (\sqrt{\Delta } \, \zeta ) + \frac{1}{2} C_2 \sinh (\sqrt{\Delta } \, \zeta ) \right) } \right) ^2}, \end{aligned} \end{aligned}$$
(15)

Case 5: If \(\mu \ne 0\), \(\Delta <0\),

$$\begin{aligned} \begin{aligned} \phi _5(x,t)&=\frac{3}{2} \frac{\mu ^2 p^2 c_2 + k_1}{k_2} + \frac{6 p^2 \mu \sigma c_2}{k_2 \left( -\frac{1}{2} \frac{\mu }{\rho } - \frac{1}{2} \sqrt{-\Delta } \frac{\frac{1}{2} C_1 \cosh (\sqrt{-\Delta } \, \zeta ) - \frac{1}{2} C_2 \sinh (\sqrt{-\Delta } \, \zeta )}{\rho \left( \frac{1}{2} C_1 \cosh (\sqrt{-\Delta } \, \zeta ) + \frac{1}{2} C_2 \sinh (\sqrt{-\Delta } \, \zeta ) \right) } \right) } \\ &\quad +\frac{6 p^2 \sigma ^2 c_2}{k_2 \left( -\frac{1}{2} \frac{\mu }{\rho } - \frac{1}{2} \sqrt{-\Delta } \frac{\frac{1}{2} C_1 \cosh (\sqrt{-\Delta } \, \zeta ) - \frac{1}{2} C_2 \sinh (\sqrt{-\Delta } \, \zeta )}{\rho \left( \frac{1}{2} C_1 \cosh (\sqrt{-\Delta } \, \zeta ) + \frac{1}{2} C_2 \sinh (\sqrt{-\Delta } \, \zeta ) \right) } \right) ^2}. \end{aligned} \end{aligned}$$
(16)

Graphical behavior of wave patterns

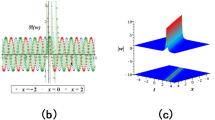
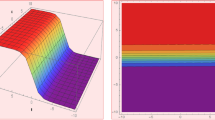
This section analyzes various solutions, evaluating their unique characteristics to examining the physical structures provides insights into the dynamic properties of the solutions for the ARD system. The ADR equation is fundamental for modeling solitons, particularly in systems where transport, dispersion, and non-linear interactions occur simultaneously. In nonlinear fiber optics, the ADR equation describes optical solitons, where the interplay of dispersion and Kerr nonlinearity stabilizes pulse propagation, which is a critical aspect of high-speed communication. Similarly, it models soliton dynamics in shallow water waves, plasma, and thermal transport systems, where nonlinear interactions counteract dispersive effects. In chemical and biological systems, the ADR equation captures reaction-diffusion processes, such as the Belousov-Zhabotinsky reaction and the propagation of nerve signals. By encompassing a wide range of physical phenomena, the ADR equation serves as a unified framework for understanding and applying soliton behavior across multiple disciplines. This study employs the modified \(\left( \frac{G'}{G^2}\right)\) expansion method to generate multiple soliton solutions. The plot illustrates the oscillatory behavior characteristic of soliton-like solutions to the ARD equation. Over time, the amplitude exhibits localized peaks and troughs, signifying the emergence of wave solitons. These waves maintain their form and propagate without attenuation over time, a hallmark of soliton behavior. Figures 1, 2 and 3 highlight intricate interference patterns resulting from the interaction of various waves. The use of distinct coloration enhances the visualization of the oscillation depths and their progression across spatial and temporal domains. Figure 1 illustrates the combination of bright and dark solitons described by Eq. ((12)) with parameters \(k_1 = 1\), \(k_2 = 2\), \(p = 2\), \(q = 2\), \(l = 2\), \(\mu = 1\), and \(c_2 = 2\). Figure 2 depicts the dark soliton described by Eq. ((13)) with parameters \(k_1 = 1\), \(k_2 = 2\), \(p = 2\), \(l = 2\), \(\mu = 0\), and \(c_2 = 2\). Figure 3 represents the kink soliton described by Eq. ((16)) with parameters \(k_1 = 1\), \(k_2 = 2\), \(p = 2\), \(l = 2\), \(\mu = 1\), and \(c_2 = 2\).

Figure 1
figure 1

Combo of bright and dark soliton in this figure where (a) show the 3D, (b) show the 2D and (c) show contour graph of \(\phi _{1}(x,t)\) with \(k_1=1\), \(k_2=2\), \(p=2\),\(q=2\), \(l=2\), \(\mu =1\), \(c_2=2\) with (t = 0.1, 0.3, 0.5).

Full size image
Figure 2
figure 2

Dark soliton in this figure where (a) show the 3D, (b) show the 2D and (c) show contour graph of \(\phi _{2}(x,t)\) with \(k_1=1\), \(k_2=2\), \(p=2\),, \(l=2\), \(\mu =0\), and \(c_2=2\) with (t = 0.1, 0.3, 0.5).

Full size image
Figure 3
figure 3

King soliton in this figure where (a) show the 3D, (b) show the 2D and (c) show contour graph of \(\phi _{5}(x,t)\) with \(k_1=1\), \(k_2=2\), \(p=2\), \(l=2\), \(\mu =1\), and \(c_2=2\) with (t = 0.1, 0.3, 0.5).

Full size image

Dynamical analysis

In this section, we perform a comprehensive dynamical analysis to explore the behavior of the ARD system. We will employ sensitivity analysis, phase portraits45, and chaos theory46 to assess the stability of the ARD model under various initial conditions. Equation (3) serves as the foundational basis for all subsequent computations, owing to its broad applicability across a range of independent variables. This approach allows for a deeper understanding of the system’s response to perturbations, enabling us to identify stable, unstable, and potentially chaotic regimes within the model.

Phase portrait analysis

This analysis allows us to understand how the system’s behavior changes with varying parameters, offering insights into stable and unstable states. By applying bifurcation theory, we can identify critical transitions and the emergence of complex behaviors, such as soliton interactions. These insights are particularly valuable for optimizing optical fiber performance and mitigating non-linear effects. Using bifurcation theory, we analyze the phase dynamics of the SDS system, which arises in optical fibers. Using the Galilean transformation, we convert the Eq. (3) into a planar dynamical system, which can be represented as follows:

$$\begin{aligned} \begin{aligned} {\left\{ \begin{array}{ll} \frac{d\phi }{d\rho } & =S, \\ \frac{dS}{d\rho }& =-\sigma _1 S -\sigma _2 \phi +\sigma _3 \phi ^2. \end{array}\right. } \end{aligned} \end{aligned}$$
(17)

where \(\sigma _1=\left( \frac{q-\eta _1 p}{ \eta _2 p^2}\right)\), \(\sigma _2=\left( \frac{k_1}{\eta _2 p^2 }\right)\) and \(\sigma _3=\left( \frac{k_2}{\eta _2 p^2 }\right)\).

This system exhibits Hamiltonian characteristics and possesses the following;

$$\begin{aligned} G(\phi ,S)=\frac{S^2}{2}+\sigma _1 \frac{S^2}{2}-\sigma _2 \frac{\phi ^2}{2}+\sigma _3 \frac{\phi ^3}{3}=g. \end{aligned}$$
(18)

We focus our investigation on the phase portrait analysis within the parameter space defined by \(\sigma _2\) and \(\sigma _3\) for Eq. (17), where g represents the Hamiltonian constant. According to the dynamical system analysis, the equilibrium points are \(M_1=(0, 0)\) and \(M_2=(V_1, 0)\) along the S-axis, where \(V_1=\frac{\sigma _2}{\sigma _3}\) . The jacobian of the system are;

$$\begin{aligned} det\left( J(\phi ,S)\right) =\left| \begin{array}{cccc} 0 & 1\\ \\ -\sigma _2 +2\sigma _3 \phi & \sigma _1 \\ \end{array} \right| = \sigma _2 -2\sigma _3 \phi . \end{aligned}$$
(19)

If \(J(\phi ,S) >0\), we refer to the point as a center, when If \(J(\phi ,S)<0\), the point is called a saddle, and if \(J(\phi ,S)\) is equal to 0, we refer to the point as a cuspidal. When we change the value of a parameter, we have four different cases.

Case 1: In this case, \(\sigma _2>0\) and \(\sigma _3>0\), we get two equilibrium points: \(M_1=(0,0)\) and \(M_2=(1.5,0)\) using \(\sigma _2=1\) and \(\sigma _3=0.67\). Here we see in Fig. 4\(M_1\) represents the center point, and \(M_2\) represent the saddle point. Furthermore, the influence of \(\sigma _1 S\) has been thoroughly analyzed considering various values of \(\sigma _1\). To illustrate this impact, phase plots corresponding to different scenarios are presented in Fig. 4. These plots provide valuable insights into the dynamic behavior of the system, highlighting how variations in \(\sigma _1\) alter the trajectory patterns and equilibrium stability.

Figure 4
figure 4

Phase portrait analysis of the dynamical system (17) at critical points. (a) Effect of \(\sigma _1 S\) on the planar system (17), assuming \(\sigma _1=1\), \(\sigma _2>0\) and \(\sigma _3>0\). (b) Effect of \(\sigma _1 S\) on the planar system (17), assuming \(\sigma _1=0.7\), \(\sigma _2>0\) and \(\sigma _3>0\). (c) Effect of \(\sigma _1 S\) on the planar system (17), assuming \(\sigma _1=0.3\), \(\sigma _2>0\) and \(\sigma _3>0\). (d) Effect of \(\sigma _1 S\) on the planar system (17), assuming \(\sigma _1=0\), \(\sigma _2>0\) and \(\sigma _3>0\).

Full size image

Case 2: In this case, \(\sigma _2>0\) and \(\sigma _3<0\), we get three equilibrium points: \(M_1=(0,0)\) and \(M_2=(-1.5,0)\) using \(\sigma _2=1\) and \(\sigma _3=-1.5\). Here we see in Fig. 5\(M_1\) represents the center point, while \(M_2\) represents the saddle point. Additionally, the influence of \(\sigma _1 S\) has been thoroughly analyzed by considering various values of \(\sigma _1\). To illustrate this impact, phase plots corresponding to different scenarios are presented in Fig. 5. These graphs provide valuable information on the dynamic behavior of the system, highlighting how variations in \(\sigma _1\) alter the trajectory patterns and the equilibrium stability.

Figure 5
figure 5

Phase portrait analysis of the dynamical system (17) at critical points. (a) Effect of \(\sigma _1 S\) on the planar system (17), assuming \(\sigma _1=1\), \(\sigma _2>0\) and \(\sigma _3<0\). (b) Effect of \(\sigma _1 S\) on the planar system (17), assuming \(\sigma _1=0.7\), \(\sigma _2>0\) and \(\sigma _3<0\). (c) Effect of \(\sigma _1 S\) on the planar system (17), assuming \(\sigma _1=0.3\), \(\sigma _2>0\) and \(\sigma _3<0\). (d) Effect of \(\sigma _1 S\) on the planar system (17), assuming \(\sigma _1=0\), \(\sigma _2>0\) and \(\sigma _3<0\).

Full size image

Case 3: Under this case, \(\sigma _2<0\) and \(\sigma _3>0\), we get three equilibrium points: \(M_1=(0,0)\) and \(M_2=(-1,0)\) by using \(\sigma _2=-0.67\) and \(\sigma _2=0.67\). Here we see in Fig. 6\(M_1\) represents the saddle point, while \(M_2\) represents the center point. Furthermore, the influence of \(\sigma _1 S\) has been thoroughly analyzed considering various values of \(\sigma _1\). To illustrate this impact, phase plots corresponding to different scenarios are presented in Fig. 6. These plots provide valuable insights into the dynamic behavior of the system, highlighting how variations in \(\sigma _1\) alter the trajectory patterns and equilibrium stability.

Figure 6
figure 6

Phase portrait analysis of the dynamical system (17) at critical points. (a) Effect of \(\sigma _1 S\) on the planar system (17), assuming \(\sigma _1=1\), \(\sigma _2<0\) and \(\sigma _3>0\). (b) Effect of \(\sigma _1 S\) on the planar system (17), assuming \(\sigma _1=0.7\), \(\sigma _2<0\) and \(\sigma _3>0\). (c) Effect of \(\sigma _1 S\) on the planar system (17), assuming \(\sigma _1=0.3\), \(\sigma _2<0\) and \(\sigma _3>0\). (d) Effect of \(\sigma _1 S\) on the planar system (17), assuming \(\sigma _1=0\), \(\sigma _2<0\) and \(\sigma _3>0\).

Full size image

Case 4: Under this case, \(\sigma _2<0\) and \(\sigma _3<0\), we get two equilibrium points; \(M_1=(0,0)\), \(M_2=(1,0)\) by using \(\sigma _2=-0.67\) and \(\sigma _3=-0.67\). Here we see in Fig. 7\(M_1\) represents the saddle point, and \(M_2\) represents the center point. Additionally, the influence of \(\sigma _1 S\) has been thoroughly analyzed by considering various values of \(\sigma _1\). To illustrate this impact, phase plots corresponding to different scenarios are presented in Fig. 7. These graphs provide valuable information on the dynamic behavior of the system, highlighting how variations in \(\sigma _1\) alter the trajectory patterns and the equilibrium stability.

Figure 7
figure 7

Phase portrait analysis of the dynamical system (17) at critical points. (a) Effect of \(\sigma _1 S\) on the planar system (17), assuming \(\sigma _1=1\), \(\sigma _2<0\) and \(\sigma _3<0\). (b) Effect of \(\sigma _1 S\) on the planar system (17), assuming \(\sigma _1=0.7\), \(\sigma _2<0\) and \(\sigma _3<0\). (c) Effect of \(\sigma _1 S\) on the planar system (17), assuming \(\sigma _1=0.3\), \(\sigma _2<0\) and \(\sigma _3<0\). (d) Effect of \(\sigma _1 S\) on the planar system (17), assuming \(\sigma _1=0\), \(\sigma _2<0\) and \(\sigma _3<0\).

Full size image

Sensitivity analysis

Various disciplines, including economics, engineering, mathematics, and science, employ sensitivity analysis to assess the impact of input parameters on model solutions. The process entails systematically altering input values within a specified range and observing the resultant changes in output. This facilitates hazard assessment, process improvement, and the development of more informed decisions. We conducted an analysis of three sets of initial conditions to evaluate the sensitivity of the proposed model. The red curve denotes the initial value: \((\phi , S) = (0.1, 0)\). The blue curve denotes the second set \((\phi , S) = (0.15, 0)\), whereas the green curve indicates the third set \((\phi , S) = (0.3, 0)\). Figure 8a–c demonstrates the sensitivity of the system in the intransient period and its relationship with different initial conditions. Figure 8d illustrates the sensitivity resulting from a slight alteration in the initial condition. Figure 9 uses the initial conditions (0.1, 0), (0.15, 0), and (0.3, 0) to illustrate insensitivity during the transient period. Minor modifications to the initial conditions significantly affect the behavior of dynamic systems. We assess the sensitivity of the dynamical system through the initial condition and observe its behavior at both the initial and intransitive times. The application of the initial condition to the system reveals no alteration in the initial state, which is typical behavior. We also observe the system’s behavior during the intransitive period, which indicates sensitivity as shown in Fig. 8d.

Figure 8
figure 8

Sensitivity analysis of systems (17).

Full size image
Figure 9
figure 9

(0.1,0) red, (0.15,0) blue, (0.3,0) green.

Full size image

Chaotic analysis

In this section, we will examine the chaotic patterns of the model under investigation. To investigate these patterns, we intend to introduce an external force \(\Lambda cos( \alpha \xi )\) to the system (17). The intensity of this perturbed component is denoted by the symbol \(\Lambda\), while the frequency is represented by \(\alpha\). Therefore, we can represent the improved system as follows:

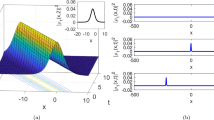
$$\begin{aligned} \begin{aligned} {\left\{ \begin{array}{ll} \frac{d\phi }{d\rho } & =S, \\ \frac{dS}{d\rho }& =-\sigma _1 S -\sigma _2 \phi +\sigma _3 \phi ^2+\Lambda cos( \alpha \xi ),\\ \frac{d T}{d\rho } & =\alpha . \end{array}\right. } \end{aligned} \end{aligned}$$
(20)

where \(T=\alpha \xi\) is the external forces added to the system. We used a variety of techniques to analyze the periodic, quasiperiodic, and chaotic properties of the system (20). We aim to determine the dynamic features of the disrupted system by evaluating various arbitrary physical parameter values. We will investigate the consequences of modifying the parameter value. 3D and 2D phase profiles with time series or Poincare graphs are shown in Fig. 10, with starting values of \(\sigma _2 = 1.3\), \(\sigma _3 = 0.4\), and \(\Lambda = 0.02\) or \(\alpha = 0.1\). Therefore, when the intensity and frequency of the external force are at their minimum, system (20) displays periodic behavior.

Figure 11, shows the three-dimensional plot, the two-dimensional plot, the time analysis, and the Poincaré graph with parameter value \(\sigma _2 = 3.7\), \(\sigma _3 = 0.6\), and \(\Lambda = 0.3\) or \(\alpha = \pi\). With the modifications, the perturbed system (20) displays quasi-periodic behavior. Graphical representations of 3D, 2D, time series, and Poincaré plots are shown in Fig. 12. A temporal analysis is performed using predetermined parameter values: \(\sigma _2 = 6.9\), \(\sigma _3 = 6.7\), and \(\Lambda = 0.4\) or \(\alpha = \frac{\pi }{2}\). An increase in intensity with frequency leads to alterations in the quasi-periodic behavior of the system (20). Figure 13, illustrates the analysis of increasing amplitude and frequency with \(\sigma _2 = 19\), \(\sigma _3 = 29\), and \(\Lambda = 0.7\) or \(\alpha = 2 \pi\). In the redesigned system (20), the findings indicate the existence of chaotic occurrences.

Figure 10
figure 10

Systems (20) exhibit periodic patterns.

Full size image
Figure 11
figure 11

Systems (20) exhibit Quasi-periodic patterns.

Full size image
Figure 12
figure 12

Systems (20) exhibit Quasi-periodic patterns.

Full size image
Figure 13
figure 13

Systems (20) exhibit chaotic patterns.

Full size image

Lyapunov exponent

A Lyapunov exponent is a mathematical metric that measures the rate at which two trajectories diverge over time, starting from proximate initial conditions. This tool is essential for the analysis of chaotic systems; it facilitates the identification of chaos and the assessment of a system’s stability. The analysis of nonlinear dynamics extensively uses Lyapunov exponent because they provide valuable graphical representations of the qualitative behavior of dynamic systems. The Lyapunov exponent holds significant importance in the study of nonlinear dynamical systems due to their diverse applications. As a representation of the chaotic properties of the system, the Lyapunov exponents are represented by the sequence \(\lambda _1\),\(\lambda _2\), and \(\lambda _3\), respectively. Visualization of these exponents over time yielded significant insights into the dynamics of the transformed system (20). Figure 14 illustrates the Lyapunov exponents as a function of time. This makes it possible to find chaotic behaviors in the disturbed dynamical system (20), which is defined by the initial condition (0.7, 0.01, 0) and the parameter values \(\sigma _2 = 6.9\), \(\sigma _3 = 6.7\), and \(\Lambda = 0.4\) or \(\alpha = \frac{\pi }{2}\).

Figure 14
figure 14

Lyapunov exponents.

Full size image

Conclusion

This article explores traveling wave solutions and dynamical analysis of the proposed advection-diffusion-reaction equation. The study emphasizes the identification of the stability criteria and initial conditions required to guarantee the existence of unique solutions. The ADR equation plays a crucial role in describing the behavior of solitons in various physical systems. In nonlinear fiber optics, it governs optical solitons, where the balance between dispersion and Kerr nonlinearity is essential for stabilizing pulse propagation. This stabilization is particularly important for high-speed communication, as it ensures that light pulses can travel long distances without distortion or loss of information. A novel modified \(\left( \frac{G'}{G^2}\right)\) expansion method is utilized to achieve this goal. This approach effectively derives traveling wave solutions, including trigonometric, hyperbolic, rational, periodic, exponential, and mixed trigonometric functions. The proposed method offers several advantages, including simplicity, precision, reliability, and broad applicability in various domains. The study aims to enhance the effectiveness and applicability of the proposed method to a wide range of nonlinear partial differential equations. A systematic approach is employed to generate various soliton profiles and analyze the solutions obtained. Using carefully chosen parameter values, 3D, 2D and contour diagrams were created to emphasize the significance of the proposed model. Figures 1, 2 and 3 shows the graphical representation that effectively illustrates the findings of the study. Additionally, concepts from bifurcation theory are applied to examine the phase portrait of the nonlinear advection-diffusion-reaction model. Figures 4, 5, 6 and 7 presents the phase portrait analysis of the dynamical system under various conditions, while Figs. 8 and 9 demonstrate the system’s sensitivity to minor variations in initial conditions. This sensitivity analysis assesses the system’s response across both transitive and intransitive time scales, verifying its behavior under these changes. The study further investigates chaotic behavior by introducing an external force and analyzing the system’s periodic, quasi-periodic, and chaotic characteristics. Applying a small external force to a system that exhibits periodic behavior allows the dynamical system to maintain equilibrium. As the external force increases, the system transitions to irregular but repetitive quasi-periodic behavior. Further increases in the external force lead to unpredictable chaotic behavior. In addition, we use two-dimensional Poincaré maps to analyze the behavior of dynamic systems and reduce their complexity. These maps offer a visual depiction of the system’s trajectories, facilitating the identification of patterns and stability in planar periodic and quasi-periodic orbits. Figures 10, 11, 12 and 13 show 2D, 3D, temporal profiles, and the Poincaré map that illustrate periodic, quasiperiodic, and chaotic behaviors. Figure 14 shows Lyapunov exponents that provide valuable graphical representations of the qualitative behavior of dynamic systems.