Introduction

The uncertainty principle1, which allows us to simultaneously predict the measurement outcomes for two incompatible observables of a quantum particle, is one of the fundamental features of quantum physics2. Subsequently, Kennard and Robertson generalized the uncertainty relation to a generic formula via variables3,4:

$$\Delta R \cdot \Delta S \ge \frac{1}{2}\left| {\left\langle {\left[ {R,S} \right]} \right\rangle } \right|,$$
(1)

for an arbitrary pair of non-commuting observables \(R\) and \(S\) within a specific system \(\rho\). The variable \(\Delta R{ = }\sqrt {\left\langle {R^{2} } \right\rangle - \left\langle R \right\rangle^{2} }\) with \(\left\langle X \right\rangle\) denoting the expectation value of an observable \(X\), and \(\left[ {R,S} \right]{ = }RS - SR\) represents the commutator. Notably, the lower bound of Eq. (1) is highly dependent on the systematic state \(\rho\), while this will bring about a trivial result if the commutator has zero expectation value. To optimize this state-dependent problem, Deutsch characterized the uncertainty principle with Shannon entropy and put forward the most famous version of uncertainty relation (EUR)5. Afterwards, Kraus6, Maassen and Uffink7 optimized Deutsch’s consequence into.

$$H(X) + H(Z) \ge \log \frac{1}{c}$$
(2)

where the Shannon entropy \(H(Q) = - \sum\nolimits_{i} {x_{i} \log x_{i} }\) with \(x_{i} = \left\langle {\left. {\psi_{i} } \right|\rho \left| {\psi_{i} } \right.} \right\rangle\) and \(Q \in \left\{ {X,Z} \right\}\), the parameter \(c \equiv \max_{i,j} \left| {\left\langle {{\psi_{i} }} \mathrel{\left | {\vphantom {{\psi_{i} } {\varphi_{j} }}} \right. \kern-0pt} {{\varphi_{j} }} \right\rangle } \right|{}^{2}\) is the maximal overlap between any two observables X and Z with \(\left| {\psi_{i} } \right\rangle\) and \(\left| {\varphi_{j} } \right\rangle\), which are the eigenvectors of X and Z respectively.

In 2010, Berta et al. put forward the following quantum-memory-assisted entropic uncertainty relation (QMA-EUR) by virtue of the conditional entropy8. This new relation can be expounded by the uncertainty game between two players, Alice and Bob. First, Bob prepares a pair of particles AB entangled initially and sends A, related to quantum memory B, to Alice. Then Alice performs one of the two measurements X or R and informs Bob of her measurement choice. Bob predicts Alice’s measurement results within minimal uncertainty, which can be described as.

$$S(X|B) + S(Z|B) \ge \log_{2} \frac{1}{c} + S(A|B)$$
(3)

where \(S(A|B) = S(\rho_{AB} ) - S(\rho_{B} )\) is the conditional von Neumann entropy. The quantum system A is measured by Q with \(Q \in (X,Z)\), the post measurement state is \(\rho_{QB} = (\sum\nolimits_{i} ( \left| {\psi_{{_{i} }}^{Q} } \right\rangle_{A} \left\langle {\psi_{{_{i} }}^{Q} } \right| \otimes I_{B} )\rho_{AB} (\left| {\psi_{{_{i} }}^{Q} } \right\rangle_{A} \left\langle {\psi_{{_{i} }}^{Q} } \right| \otimes I_{B} )\) with \(I_{B}\) standing for an identical matrix in the space of particle B, and \(\left| {\psi_{{_{i} }}^{Q} } \right\rangle\) being eigenvectors of Q. It’s worth noticing that when particles A and B are in the state of maximal entanglement, the measurement outcomes for X and Z can be accurately predicted. Owing to a wide application of EUR in the fields of quantum randomness9 quantum key distribution10,11 entanglement witness12,13 and quantum cryptography14, it attracts lots of people’s attention15,16,17,18,19,20. Additionally, there are some studies that can enhance the lower bound of entropy uncertainty relationships12,21,22,23. Especially, Pati et al. proposed a scheme in which quantum discord and classical correlation can be applied to tighten the uncertainty principle in the presence of quantum memory21. Adabi et al. put forward a proposal that Holevo quantity can be effectively utilized to enhance the entropic uncertainty bound and it has a wide range of applications23,24,25,26.

On the other hand, quantum phase transition (QPT) is a fundamental phenomenon and has attracted lots of interest in quantum many-body systems27,28,29. In contrast to classical phase transitions, QPT generally happens at zero temperature, featuring a sudden change in the ground state. In this case, the thermal fluctuations disappear and the quantum fluctuations play a crucial role30,31,32. Additionally, some researchers have found quantum entanglement, quantum correlation, and quantum coherence are able to signal the quantum critical point in quantum spin models33,34,35,36,37. Instead of resorting to two-point spin–spin correlation functions, the quantum renormalization-group (QRG) method is introduced as a tractable statistical method for studying the quantum information properties of critical systems by entering a few sites through the renormalizing of coupling constants38. The QRG method has a simple calculation process and clear physical images, which can help us better study the issues of quantum multibody systems. It is widely used to solve the spin models, including Ising model, XY model, XXZ model, et al.39,40,41,42,43,44,45,46. As we all know, a XXZ model can characterize many useful materials, such as K2CuF4, the antiferromagnetic monolayer NiPS3, twisted bilayer NiPS3 , and so on47,48,49. Generally, the QPT is generated by quantum fluctuations, which are essentially induced by the quantum uncertainty relation of the system. It is of vital significance to use uncertainty to indicate the QPT. However, researches on the relation between the uncertainty and QPT50,51 are still few. In particular, the dynamics of entropic uncertainty relation and its steering between two particles in Heisenberg spin model are attracting increasing attention52,53,54,55. Recently, the relations between EUR and quantum phase transition in one and two-dimensional spin models have been investigated56,57,58.

As we know, the acquisition of tighter low bound in EUR plays an important role in our processing of quantum information tasks. For instance, by applying tighter lower bound, one can attain the tighter bound of the quantum secret key rate, which is of basic importance to enhance the security of quantum key distribution protocols. However, via the QRG method, the dynamical properties of QMA-EUR and the tighter lower bound of EUR in the spin models have been seldom investigated before. In reality, the more tighter lower bound of EUR as well as the relationship between EUR consisting of N-qubit and QPT in the XXZ model have not been studied completely. Invoked by this, we focus on utilizing EUR to investigate the QPT in the XXZ model by means of QRG method. Our results indicate two methods can both be used to obtain tighter lower bound of EUR relationship, one method is to use the difference between quantum discord and classical correlation, and the other way is the use of Holevo quantity, which apparently is a more effective way compared to the former. The tighter the entropy uncertainty relationship is, the higher the accuracy of the predicted results will be. We can obtain the optimal lower bound with the help of Holevo quantity and mutual information. Furthermore, QMA-EUR can evolve into two different saturated values, which can effectively help one to observe the critical points associated with QPT after some iterations step by step. To gain further insight, the scaling behavior and nonanalytic phenomenon of EUR have also been explored. Our study suggests that QMA-EUR deserves to be used to unveil quantum criticality for more quantum many-body systems. Besides, this study might offer a nontrivial insight into many applications in quantum physics including the quantum key distribution, the detection of QPT and the evaluation of the capacity of quantum computation in critical systems.

Results

QRG method in the spin-1/2 XXZ model

The Hamiltonian of spin-1/2 XXZ model on a periodic chain of N sites is.

$$H(J,\Delta ) = \frac{J}{4}\sum\limits_{k = 1}^{N} {(\sigma_{k}^{x} \sigma_{k + 1}^{x} + \sigma_{k}^{y} \sigma_{k + 1}^{y} + \Delta \sigma_{k}^{z} \sigma_{k + 1}^{z} )}$$
(4)

where \(\sigma_{k}^{\alpha } (\alpha = x,y,z)\) are standard Pauli matrices at site k,\(J\) is the exchange constant, \(\Delta\) is the anisotropy parameter, and J, \(\Delta > 0\). For \(\Delta = 1\), the Hamiltonian is SU(2) symmetry invariant, but for \(\Delta \ne 1\), the SU(2) symmetry breaks down to the U(1) rotational symmetry around the z axis. Due to the existence of the rotational symmetry, one can solve the model exactly via Bethe Ansatz. While \(0 \le \Delta \le 1\), the model is known to gapless with quasi-long-range order, in which the correlations diminish polynomially with no magnetic long-range order. For \(\Delta > 1\), the symmetry is reduced to Z2 and the model belongs to the Ising regime. In fact, the third term in the Hamiltonian gives rise to ordering of the system, and as \(\Delta\) approaches infinity, the Néel state converts into the dominant phase of the system. The quantum fluctuations in the system are influenced by the first two terms of the Hamiltonian, resulting in the breaking of the Néel ordering. It is known that a maximum value of concurrence between the two nearest-neighbor sites can be reached due to the competition between the quantum fluctuations and ordering at the critical point \(\Delta = 1\)59,60,61,62,63.

We divide the spin chain into three-site blocks to obtain a self-similar Hamiltonian after each QRG step in Fig. 1. In the standard bases \({\text{\{ }}\left| { \uparrow \uparrow \uparrow } \right\rangle ,\left| { \uparrow \uparrow \downarrow } \right\rangle ,\left| { \uparrow \downarrow \uparrow } \right\rangle ,\left| { \uparrow \downarrow \downarrow } \right\rangle ,\left| { \downarrow \uparrow \uparrow } \right\rangle ,\left| { \downarrow \uparrow \downarrow } \right\rangle ,\left| { \downarrow \downarrow \uparrow } \right\rangle ,\left| { \downarrow \downarrow \downarrow } \right\rangle \}\), the degenerate ground states are given by

$$\left| {\phi_{0} } \right\rangle = \frac{1}{{\sqrt {{2 + }q^{2} } }}\left( {\left| { \uparrow \uparrow \downarrow } \right\rangle + q\left| { \uparrow \downarrow \uparrow } \right\rangle { + }\left| { \downarrow \uparrow \uparrow } \right\rangle } \right)$$
(5)
$$\left| {\phi^{\prime}_{0} } \right.\rangle = \frac{1}{{\sqrt {2 + q^{2} } }}\left( {\left| { \uparrow \downarrow \downarrow } \right\rangle + q\left| { \downarrow \uparrow \downarrow } \right\rangle + \left| { \downarrow \downarrow \uparrow } \right\rangle } \right)$$
(6)

where \(\left| \uparrow \right\rangle ,\left| \downarrow \right\rangle\) are the eigenstates of \(\sigma_{z}\) and \(q = - \frac{1}{2}\left( {\Delta + \sqrt {8 + \Delta^{2} } } \right)\).

Fig. 1
figure 1

The method of Kadanoff’s block renormalization-group for three sites as one block.

Full size image

Then the effective Hamiltonian of the renormalized XXZ chain with staggered DM interaction can read.

$$H^{{{\text{e}}ff}} = \frac{J^{\prime}}{4}\sum\limits_{{\text{k = 1}}}^{N/3} {\left[ {\sigma_{k}^{x} \sigma_{k + 1}^{x} + \sigma_{k}^{y} \sigma_{k + 1}^{y} + \Delta ^{\prime}\sigma_{k}^{{\text{z}}} \sigma_{k + 1}^{z} } \right]}$$
(7)

where the iterative relationship is.

$$J^{\prime} = J(\frac{2q}{{2 + q^{2} }})^{2} ,\,\,\Delta ^{\prime} = \Delta (\frac{q}{4})^{2}$$
(8)

A phase boundary \(\Delta_{c} = 1\) that separates the spin-fluid phase \(\Delta < 1\) from the Néel phase \(\Delta > 1\) can be acquired by considering \(\Delta ^{\prime} = \Delta\).

The QMA-EUR in a three-site model

Similarly, we can achieve the ground-state density matrix \(\rho_{{}} { = }\left| {\phi_{0} } \right\rangle \left\langle {\phi_{0} } \right|\), the result of choosing \(\left| {\phi_{0}{\prime} } \right\rangle\) will be the same. By tracing out the middle site, we derive the reduced density matrix \(\rho_{AB}\),

$$\rho_{AB} { = }\frac{1}{{2 + q^{2} }}\left( {\begin{array}{*{20}c} {q^{2} } & 0 & 0 & 0 \\ 0 & 1 & 1 & 0 \\ 0 & 1 & 1 & 0 \\ 0 & 0 & 0 & 0 \\ \end{array} } \right)$$
(9)

Thus, the left-hand side (LHS) of Eq. (3) representing entropic uncertainty can read as

$$U_{L} = \frac{1}{{2(2 + q^{2} )}}\left( { - 2q^{2} \log_{2} \left( {\frac{{q^{2} }}{{2 + q^{2} }}} \right) + 4(1 + q^{2} )\log_{2} \left( {\frac{{1 + q^{2} }}{{2 + q^{2} }}} \right) - \varsigma \log_{2} \left( {\frac{\varsigma }{{4(2 + q^{2} )}}} \right) - \eta \log_{2} \left( {\frac{\eta }{{4(2 + q^{2} )}}} \right)} \right)$$
(10)

On the other hand, once Alice decides which measurement to perform, the complementarity c of the observables X and Z is a fixed constant. For the observables \(\sigma_{x}\) and \(\sigma_{z}\) , complementarity is always equal to 1/2. Thus, the right-hand side (RHS) of Eq. (3) describing the lower bound of entropic uncertainty (Berta’s bound) is equal to.

$$U_{R} = 1 + S(\rho_{AB} ) - S(\rho_{B} )$$
(11)

We plot entropic uncertainty and the lower bound (Berta’s bound) between the sites A B versus the anisotropy parameter \(\Delta\) in a three-site model in Fig. 2. Obviously, it is worth noticing that both entropic uncertainty and the lower bound display similar characteristics, namely, the value of uncertainty and the lower bound begins with a sharp increase to its maximum, and then slowly reduces and finally ends with a fixed value as \(\Delta\) increases. Besides, when \(\Delta\) takes a relatively large value, the value of RHS is equal to LHS, which indicates the measured entropic uncertainty and lower bound (Berta’s bound) between the sites A B are the same in this situation.

Fig.2
figure 2

Entropic uncertainty and Berta’s lower bound between the sites A B with respect to the anisotropy parameter \(\Delta\) in a three-site model. In this picture, let RHS represent the right-hand side of Eq. (3) and LHS be the right-hand side.

Full size image

Tighter Bound of EUR via quantum discord and classical correlation

It is well known that a tighter lower bound for uncertainty relations can offer information-theoretic security to quantum communication protocols and play a crucial role in many aspects of quantum information science. Here, we concentrate on studying how to improve the lower bound of the entropy uncertainty relation, because the improvement on the lower bound means that we can make more accurate predictions about the uncertainty. According to what Pati et al. presented in ref21, the quantum discord (QD) and classical correlation are applied to probe the tighter bound in spin XXZ model. We can achieve Bob’s uncertainty about both X and Z measurement outcomes as follows:

$$S(X|B) + S(Z|B) \ge \log_{2} \frac{1}{c} + S(A|B) + \max \{ 0,D_{A} (\rho_{AB} ) - J_{A} (\rho_{AB} )\} ,$$
(12)

Here, for convenience, the RHS of Eq. (12) is called Pati’s bound. Note that compared to Eq. (3), the RHS of Eq. (12) has an additional term i.e., \(\max \{ 0,D(\rho_{AB} ) - J(\rho_{AB} )\}\). In Eq. (12), \(D_{A} (\rho_{AB} )\) and \(J_{A} (\rho_{AB} )\) represent QD and classical correlation respectively. Afterwards, through a series of complex calculations, the QD and classical correlation between particles A and B are achieved according to Eq. (12). Then, we can get the Pati’s lower bound by inserting QD and classical correlation into Eq. (12). The performance of entropic uncertainty (blue line), Berta’s lower bound (black line) and Pati’s lower bound (red line) between the sites A B with respect to the anisotropy parameter \(\Delta\) in a three-site model is depicted in Fig. 3. It can be seen that entropic uncertainty, Berta’s lower bound and Pati’s lower bound between the sites A B show similar tendencies, namely, firstly increase then gradually decrease, and finally approach a stable value with the increasing of \(\Delta\) value. When \(\Delta\) takes a relatively large value, the change of Pati’s lower bound coincides with that of Berta’s lower bound. Notably, Pati’s lower bound is closer to the entropy uncertainty than that of Berta’s lower bound, the results demonstrate that the lower bound of measured entropy uncertainty can be enhanced through the implementation of the difference between QD and classical correlation.

Fig.3
figure 3

Entropic uncertainty (blue line), Berta’s lower bound (black blue) and Pati’s lower bound (red blue) between the sites A B as function of the anisotropy parameter \(\Delta\) in a three-site mode.

Full size image

Tighter bound of EUR via Holevo quantity

The Holevo quantity generalized EUR can be utilized to probe the tighter bound in the XXZ model. Based on what Adabi et al. described in ref23, we can obtain Bob’s uncertainty about both X and Z measurement outcomes as follows:

$$S(X|B) + S(Z|B) \ge \log_{2} \frac{1}{c} + S(A|B) + \max \{ 0,\delta \} ,$$
(13)

where \(\delta = I\left( {A:B} \right) - \left[ {I\left( {X:B} \right) + I\left( {Z:B} \right)} \right]\), and \(I\left( {A:B} \right) = S\left( {\rho^{A} } \right) + S\left( {\rho^{B} } \right) + S\left( {\rho^{AB} } \right)\) is the mutual information between A and B, \(I\left( {P:B} \right) = S\left( {\rho^{B} } \right) - \sum\nolimits_{i} {p_{i} S\left( {p_{i} } \right)}\) denotes the Holevo quantity. For simplicity, the RHS of the Eq. (13) is treated as Adabi’s bound. Note that if the mutual information \(I\left( {A:B} \right)\) is more than the sum of information that Alice sends to Bob \(I\left( {X:B} \right) + I\left( {Z:B} \right)\), the above Eq. (13) shows the improvement on Berta’s bound by enhancing the lower bound with the help of the amount of \(\delta\). It is not difficult to achieve the difference between LHS of Eq. (13) and the lower bound, which can be given by \(1 + S\left( {\rho^{A} } \right) - S\left( {\rho^{X} } \right) - S\left( {\rho^{Z} } \right)\), only depending on incompatible measurements X, Z, and \(\rho^{A}\), while irrelative with quantum memory B. By a series of analyses and calculations, we can obtain Adabi’s bound. Similarly, we also plot the entropic uncertainty (blue line), Berta’s lower bound (black blue), and Adabi’s lower bound (red line) between the sites A B with respect to the anisotropy parameter \(\Delta\) in a three-site model in Fig. 4. Compared to Adabi’s bound and Pati’s lower bound (as shown in Fig. 3), the former has a smaller difference compared to entropic uncertainty, resulting in better model performances. Besides, it can be observed that Adabi’s bound coincides with entropic uncertainty, which demonstrates that the application of Holevo quantity and mutual information can give rise to the increasing of lower bound perfectly in this model. Furthermore, we can easily obtain that the difference \(1 + S\left( {\rho^{A} } \right) - S\left( {\rho^{X} } \right) - S\left( {\rho^{Z} } \right)\) is always equal to 0, which may explain that optimal Adabi’s bound is dependent on Alice’s measurement choice. Thus, one can obtain the optimal lower bound as well as accurately predict measurement results by applying Holevo quantity and mutual information. In addition, this method has the potential to be applied to obtain the tighter bound of the quantum secret key rate, which is crucial to improving the security of quantum key distribution protocols.

Fig.4
figure 4

Entropic uncertainty (blue line), Berta’s lower bound (black line), and Adabi’s lower bound (red line) between the sites A B with respect to the anisotropy parameter \(\Delta\) in a three-site model.

Full size image

Dynamical characteristic of the renormalized QMA-EUR

To further investigate the relationship between QMA-EUR and QPT, we focus on obtaining the difference value (U) between LHS and RHS (Beta’s lower bound) of Eq. (3) and depicting U versus \(\Delta\) between site A B in a three-site model in Fig. 5. It can be seen that as the value of \(\Delta\) increases, the difference U gradually decreases. It is worth stressing that U gets maximum as \(\Delta\) is 0, namely, the system changes from XXZ model into XX model. Then, we explore U of the block-block state as a function of \(\Delta\) at different QRG iteration steps in Fig. 6. Every block includes the N/3 spin, and 0th step RG means three sites, 1st means 9 sites, 2nd means 27 sites, nth represents \(3^{n + 1}\) sites, i.e., by enough RG steps, a system of a large size can be scaled into a three-block state. As can be seen from Fig. 6, we notice the plots of U meet in the critical point \(\Delta { = 1}\). Obviously, the value of U about the entire entropic uncertainty relationship in the block-block state is basically at two stable values, namely, \(U = 0.3\) for \(0 < \Delta < 1\), and \(U \to 0\) for \(\Delta > 1\). Additionally, as the size of the system is infinite, U changes most obviously when \(\Delta = 1\), which demonstrates U exhibits a QPT at the critical point in the thermodynamic limit. We may conclude that after a certain number of iterations, the value of QMA-EUR of the whole block-block state can form two saturated values, which are related to two different phases: spin-fluid phase and Néel phase. For \(0 < \Delta < 1\), U get maximum, indicating that the higher the degree of uncertainty is, the less accurate the measurement results are when the system is spin-fluid phase. On the other hand, when the system is spin-fluid phase, U get maximum as \(0 < \Delta < 1\), suggesting the lower the uncertainty is , the more accurate the measurement results will be.

Fig.5
figure 5

The difference value (U) between LHS and RHS (Berta’s lower bound) of EUR versus \(\Delta\) between site A B in a three-site model.

Full size image
Fig.6
figure 6

The value of U as a function of \(\Delta\) at different QRG iteration steps in block-block state.

Full size image

The Fig. 7 depicts the first derivative of U of the entropic uncertainty with respect to \(\Delta\) with the increasing of iteration times. Obviously, as the \(\Delta\) value changes, the curve will experience a sudden change at a certain point, and the extreme point of the change is called the minimum point. Each iteration will cause a change in the minimum value of the curve. As the number of iterations increases, the amplitude of the function graph also increases. The minimum value point of the curve is achieved closer to \(\Delta { = }1\) point. When the iteration reaches the fifth time, the minimum value point of the curve is closest to \(\Delta { = }1\). As the system increases to infinity, the first derivative curve shows a pronounced singular behavior.

Fig.7
figure 7

The first derivative of U with respect to \(\Delta\) at different QRG iteration steps in block-block state.

Full size image

Nonanalytic phenomenon and Scaling behavior

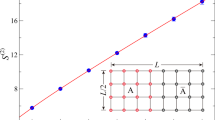
Next, we examine how the variation of \(\left| {dU/d\Delta } \right|_{{\Delta_{\min } }}\) changes relative to the system size \(N\) at \(\Delta { = }1\), with \(\Delta_{\min }\) representing the position of the minimum of \(dU/d\Delta\). The plot of \(\left| {dU/d\Delta } \right|_{{\Delta_{\min } }}\) versus \(\ln (N)\) shown in Fig. 8 where a certain linear behavior is provided obviously. We get the exponent for this behavior is \(\left| {dU/d\Delta } \right|_{\max } \sim N^{\theta }\) with \(\theta { = 0}{\text{.60}}\). Besides, the trend of the minimum point position can be obtained, and as the number of iterations increases, the minimum point \(\left| {dU/d\Delta } \right|_{{\Delta_{\min } }}\) gradually approaches the point \(\Delta { = }1\). A more detailed comparison is achieved that the position of the minimum \(\Delta_{\min }\) of \(dU/d\Delta\) slowly goes to the critical point \(\Delta_{c} = 1\) in Fig. 9. Through a series of numerical analysis and computation, we can obtain that the exponent for this behavior is \(\Delta_{\max } { = }\Delta_{c} + N^{ - 0.46}\). The results convince us that the entropic uncertainty relation can be treated as a signature of quantum phase transition in the XXZ model.

Fig.8
figure 8

The logarithm of the absolute value of minimum,\(\ln (\left| {dU/d\Delta } \right|\Delta_{{{\text{m}} {\text{in}}}} )\), versus the logarithm of chain size, \(\ln (N)\), which is linear and displays a scaling behavior.

Full size image
Fig.9
figure 9

The scaling behavior of U in terms of system size \(N\), where \(\Delta_{\min }\) is the position of the minimum derivative of whole quantum coherence in the XXZ model.

Full size image

Conclusion

In this paper, we utilized the QRG method to investigate the relationship between QMA-EUR and QPT in a spin-1/2 XXZ model. It is found that dynamical behaviors of entropic uncertainty and the lower bound show similar features, namely, first sharply grows , then reduces and finally tends to a fixed value as anisotropy parameter increases. The research unveils that when quantum memory is present, the lower bound of EUR can be enhanced by employing two approaches based on the difference between QD and classical correlation, as well as the Holevo quantity and mutual information. Notably, the optimization effect of the Holevo quantity and mutual information surpasses the former. Besides, it can be observed that Adabi’s bound coincides with entropic uncertainty, demonstrating that Holevo quantity and mutual information can give rise to the increasing of lower bound effectively in this model. It is because that optimal Adabi’s bound is dependent on Alice’s measurement choice. Subsequently, we study quantum critical properties via the difference value U between LHS and RHS of QMA-EUR, and we find through multiple renormalization iterations, U of the entire block-block state converges to two distinct saturated values, corresponding to the spin-fluid phase and Néel phase. Furthermore, after several iterations of the renormalization, we observed that the QMA-EUR of the block-block state exhibits nonanalytic and scaling properties with the entropic uncertainty relation exponent linked to the correlation length. This result demonstrates that the quantum critical properties are connected with the behavior of QMA-EUR. Our researches also show that the numerical technique of QRG method deserves to be used to investigate related issues of QPT for more quantum many-body systems.

Methods

In the uncertainty game, to examine the dynamical characteristic of the measured uncertainty about two-qubit A B in the spin model, we use \(X = \sigma_{x}\) and \(Z = \sigma_{z}\) as the two incompatibility measurements. After the measurement, the new post-measurement states can be expressed as \(\sum\nolimits_{i} ( \left| {\psi_{{_{i} }}^{Q} } \right\rangle_{A} \left\langle {\psi_{{_{i} }}^{Q} } \right| \otimes I_{B} )\rho_{AB} (\left| {\psi_{{_{i} }}^{Q} } \right\rangle_{A} \left\langle {\psi_{{_{i} }}^{Q} } \right| \otimes I_{B} )\), where \(\left| {\psi_{{_{i} }}^{Q} } \right\rangle\) are the eigenstates of the observable \(\sigma_{i}\), and the corresponding density matrix can be given by.

$$\begin{gathered} \rho_{{\sigma_{x} B}} = \frac{{1 + q^{2} }}{{2(2 + q^{2} )}}\left( {\left| {00} \right\rangle \left\langle {00} \right| + \left| {10} \right\rangle \left\langle {11} \right|} \right) \hfill \\ + \frac{1}{{2 + q^{2} }}\left( {\left| {00} \right\rangle \left\langle {11} \right| + \left| {01} \right\rangle \left\langle {01} \right| + \left| {01} \right\rangle \left\langle {10} \right| + \left| {10} \right\rangle \left\langle {01} \right| + \left| {11} \right\rangle \left\langle {00} \right| + \left| {11} \right\rangle \left\langle {11} \right|} \right) \hfill \\ \end{gathered}$$
(14)
$$\rho_{{\sigma_{z} B}} = \frac{{q^{2} }}{{2 + q^{2} }}\left| {00} \right\rangle \left\langle {00} \right| + \frac{1}{{2 + q^{2} }}\left| {01} \right\rangle \left\langle {01} \right| + \frac{1}{{2 + q^{2} }}\left| {10} \right\rangle \left\langle {10} \right|$$
(15)
$$\rho_{B} = \frac{{1{ + }q^{2} }}{{2 + q^{2} }}\left| 0 \right\rangle \left\langle 0 \right| + \frac{1}{{2 + q^{2} }}\left| 1 \right\rangle \left\langle 1 \right|$$
(16)

Whose eigenvalues can be obtained and the corresponding von Neumann entropies can be calculated by \(S(\rho ) = - \sum\nolimits_{i} {\lambda_{i} \log_{2} } \lambda_{i}\) and take on the form as.

$$S(\rho_{{\sigma_{x} B}} ) = - \frac{\varsigma }{{2(2 + q^{2} )}}\log_{2} \left( {\frac{\varsigma }{{4(2 + q^{2} )}}} \right) - \frac{\eta }{{2(2 + q^{2} )}}\log_{2} \left( {\frac{\eta }{{4(2 + q^{2} )}}} \right)$$
(17)
$$S(\rho_{{\sigma_{z} B}} ) = - \frac{2}{{2 + q^{2} }}\log_{2} \left( {\frac{1}{{2 + q^{2} }}} \right) - \frac{{q^{2} }}{{2 + q^{2} }}\log_{2} \left( {\frac{{q^{2} }}{{2 + q^{2} }}} \right)$$
(18)
$$S(\rho_{B} ) = - \frac{1}{{2 + q^{2} }}\log_{2} \left( {\frac{1}{{2 + q^{2} }}} \right) - \frac{{1{ + }q^{2} }}{{2 + q^{2} }}\log_{2} \left( {\frac{{1{ + }q^{2} }}{{2 + q^{2} }}} \right)$$
(19)

Where \(\varsigma = 2 + q^{2} - \sqrt {4 + q^{2} }\), and \(\eta = 2 + q^{2} { + }\sqrt {4 + q^{2} }\).

Quantum discord and classical correlation

Classical correlation can be achieved as \(J_{A} (\rho_{AB} ) = S(\rho_{B} ) - \min S(B|\{ E_{k} \} )\), where \(S(\rho_{B} ) = - Tr(\rho_{B} \log_{2} \rho_{B} )\) and \(S(B|\{ E_{k} \} ) = \sum {P_{k} } S(\rho_{B|k} )\). Then we can obtain quantum discord by \(D_{A} (\rho_{AB} ) = I(A;B) - J_{A} (\rho_{AB} )\), and \(I(A;B) = S(\rho_{A} ) + S(\rho_{B} ) - S(\rho_{AB} )\) is the mutual information between A and B.

Holevo quantity

For a composite quantum state, it is evident that when Alice performs observable measurements on her particle, she will obtain the \(i\) th outcome with probability \(p_{i} = Tr_{AB} \left( {\prod\nolimits_{i}^{A} {\rho^{AB} } \prod {_{i}^{A} } } \right)\) and Bob’s particle will be left in the corresponding state \(\rho_{i}^{B} = \frac{{p_{i} = Tr_{AB} \left( {\prod\nolimits_{i}^{A} {\rho^{AB} } \prod {_{i}^{A} } } \right)}}{{p_{i} }}\). Here \(I\left( {P:B} \right) = S\left( {\rho^{B} } \right) - \sum\nolimits_{i} {p_{i} S\left( {p_{i} } \right)}\) is called the Holevo quantity, which represents an upper bound on the amount of information Bob can access regarding Alice’s measurement outcome.