Introduction

The beam-column connection, a critical component in frame structures, transfers bending moments and shear forces between beams and columns. Prior to the Northridge earthquake, welded connections between beams and columns were optimal for steel frame construction. However, studies after this earthquake revealed extensive and unforeseen brittle fractures in welded steel beam-column connections, shifting this perspective. The primary causes of brittle damage in welds are attributed to irregularities in the weld material and the thermal effects of the welding process1. Two design concepts, termed “strengthening” and “weakening”, were developed to improve ductility and reduce brittle weld damage2. Strengthening involves increasing the flexural strength of the beam-column connections to confine damage within the beams rather than the joints, achieved by adding ribs3, haunches4, or plates5 at the joint. In contrast, weakening entails reducing sections of the beam flanges or webs to localize damage in these areas, as seen in reduced beam section (RBS) connections. Many experimental and analytical studies have confirmed RBS connections as an economical and practical approach for designing seismic-resistant frames6.

Advanced seismic engineering focuses not only on ensuring ductility but also on the recovery of structural functions post-earthquake. A common way to achieve quick functional recovery is by using energy dissipation devices as structural fuses7. These devices concentrate plastic deformation in energy-absorbing components that can be promptly replaced after seismic events8. Examples include replaceable buckling restrained braces9,10, self-centering structural systems11,12,13, dissipative devices like FUSEIS1-1 and FUSEIS1-214, and linked-column frame (LCF) systems15. The LCF system design first proposed by Dusicka and Iwai16 comprises two robust columns connected by replaceable beams and a frame designed to resist bending moments. Dusicka et al.17 conducted a nonlinear pushover analysis on a three-story LCF system to confirm its feasibility, finding that the structure’s functionality can be rapidly restored by replacing the energy dissipation coupling beam when lateral displacement angles range between 0.43% and 1.7%. Malakoutian et al.18 proposed a design approach that ensures a plastic hinge initially forms at the connection between a linked beam and strong column. Shoeibi et al.19,20,21 developed two design strategies for LCF structures grounded in performance-based plastic and force-based seismic design principles, considering interactions between the link-column structure and flexural frame. Other scholars have proposed various enhancements to the LCF system; for instance, Maroofii et al.22 introduced a double-link strut system at the center of the frame to improve seismic performance and performed incremental dynamic analysis to test its effectiveness.

The seismic-resistant system FUSEIS1, developed under the European Research Program “FUSEIS,” consists of two closely spaced strong columns connected by dissipative elements within each story14. In the FUSEIS1-1 variant, these dissipative elements are beams; in FUSEIS1-2, they are pins. Dougka et al.23,24 experimentally analyzed cyclic loading on the FUSEIS1-1 system with energy-dissipating beams featuring open I-, H-, and circular section beams. Similarly, Dimakogianni et al.25 investigated the seismic performance of buildings using FUSEIS1-2. Compared to the LCF system, the FUSEIS1-1 system has more replaceable components, which is not economically advantageous. However, FUSEIS1-1 can be used not only for new structures but also for rehabilitation of existing structures. Tsarpalis et al.26 employed the FUSEIS beam-link system to strengthen existing reinforced concrete buildings and performed incremental dynamic analysis on a nonlinear model in OpenSees. The results indicated an acceptable q-factor, dependent on the selected site and structural configuration.

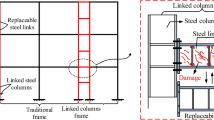
While moment-resisting frames with RBS connections exhibit ductile failure, replacing all damaged steel beams tends to be highly complex, costly, and impractical. To address this, a novel steel frame with a fuse system was designed, where the RBS connections typically distributed at each beam-column junction are centralized as replaceable energy-absorbing components (Fig. 1). This structure resembles an LCF system, but the linked column is replaced with the energy-dissipating system FUSEIS1-1.

Fig. 1
figure 1

Schematic diagram of proposed design.

Full size image

In this paper, the fuse system was modeled using ABAQUS. The accuracy of this model was verified before using it to investigate the influence of the RBS connection beam’s reduced dimensions on the fuse system’s seismic performance. Additional pushover analysis examined the effects of story height, fuse system span, RBS connection beam strength, and fuse system layout on the performance of a steel frame with fuse system. Based on the yielding mechanism of the structure in its ultimate state, the principle of virtual work, and the assumption of small deformation, formulas are established to calculate the elastic lateral stiffness and peaking bearing capacity of a multi-story steel frame with fuse system.

Finite element analysis of fuse system

Description of fuse system

A prototype structure with a 3 × 5 span layout and 6 stories was designed using SAP2000 (ver. v22.2.0) software in accordance with Chinese standards GB 50,017–201727 and GB 50,009–202228. Figure 2 provides a schematic plan and elevation of the steel frame equipped with a structural fuse system. This system comprises two closely spaced, strong articulated columns and multiple replaceable energy dissipation beams, with the articulated columns rigidly connected to the beams. The frame beams and articulated columns are hinged to ensure the transmission of only shear forces while eliminating bending moments. Under seismic loads, the replaceable energy dissipation beams function as fuse elements. The RBS connections are designed to facilitate plastic hinge formation within the fuse system. As illustrated in Fig. 3, end plate bolts connect the RBS beams to the articulated columns so that post-earthquake repairs are relatively cost-effective and straightforward. Transverse stiffeners on the column at the junction of the RBS connection beam prevent local buckling of the column flange.

Fig. 2
figure 2

Steel frame with fuse system.

Full size image
Fig. 3
figure 3

Connections between articulated column and RBS connection beam.

Full size image

Based on the structural design, the cross-sectional dimensions of the steel frame column and articulated column hb × bf × tw × tf are both 400 mm × 400 mm × 13 mm × 21 mm. The dimensions of the frame beam and RBS connection beam are 350 mm × 350 mm × 12 mm × 19 mm and 175 mm × 90 mm × 4 mm × 6 mm, respectively. The end plate is 315 mm × 160 mm × 20 mm, with a bolt diameter of 16 mm. The design of the RBS in the beam must comply with specific geometric criteria to ensure minimal rotation at each limit state. The standards FEMA 35029 and JGJ 99-201530 outline a range of design values for the distance from the end plate to the start of the RBS (denoted as a), the reduction length of the flange (b), and the depth of the flange cut (g), as detailed in Table 1. These standards specify ranges of dimensions, so finite element analysis (FEA) was conducted using the standard module of ABAQUS version 2021 software to evaluate the seismic performance of the fuse system and determine the optimal geometric dimensions31.

Table 1 RBS geometry by code.
Full size table

Material Stress-strain relationship

The yield strength of the steel used in the RBS connection beam should be lower than that of the steel in the frame, as a design feature intended to ensure the energy dissipation system fails before the frame structure does. Accordingly, Q355 steel was used here for the articulated column, end plate, and stiffener, while Q235 steel was used for the RBS connection beam and 10.9-grade high-strength steel for the bolts.

The main hardening modes for steels include isotropic hardening32, kinematic hardening33, and combined hardening34. In this study the steel is modeled with a multilinear kinematic hardening model and the yielding of the members is detected according to the von Mises stress. The Q235 steel was modeled with a triple-line constitutive model and a double-line model was used for Q355 and high-strength steels (Fig. 4). Specific stress and strain values are provided in Table 2, where σy and εy represent the yield stress and strain, respectively; σu and εu are the ultimate stress and strain, respectively; σst and εst mean the destructive stress and the corresponding stress, respectively. The elastic modulus and Poisson’s ratio of steel are 2.06 × 105 MPa and 0.3, respectively.

Fig. 4
figure 4

Stress-strain relationship of steel.

Full size image
Table 2 Material property values.
Full size table

Element type, mesh, interactions

The structural fuse system consists of five parts: articulated columns, RBS connection beams, stiffeners, end plates, and high-strength bolts. These were modeled as general solid elements with incompatible modes (C3D8I). To ensure accuracy and reduce computational costs, the mesh sizes of the articulated column, stiffener, RBS beam, end plate, and bolts were set to 40 mm, 30 mm, 15 mm, 10 mm, and 4 mm35, respectively. The mesh at the connection between the articulated column and RBS beam was refined for greater precision, as shown in Fig. 5.

Fig. 5
figure 5

Element mesh.

Full size image

The weld and surface-to-surface interaction between parts were simulated with “Tie” and “Contact,” respectively. The interaction in the normal surface-to-surface direction was modeled using “Hard Contact” and was represented by the penalty function in the tangential direction. The coefficients of friction corresponding to different contact surfaces are detailed in Table 336.

Table 3 Interaction relationship of the model.
Full size table

In the finite element model, a preload force was applied to the rod of the high-strength bolt to replicate its actual force state. First, a relatively small preload was applied to the bolt rod to establish contact constraints between the nut and the end plate. Second, a complete preload was applied; finally, the length of the bolt rod was fixed to maintain the preload conditions.

Boundary conditions and load application

The bottom of an articulated column in a fuse system is designed to be articulated; this constrains the displacement degrees of freedom in the x-, y-, and z-directions at the bottom of the column, while the rotational degree of freedom around the x-axis is released. The displacement degree of freedom in the x-direction is also constrained to prevent out-of-plane displacement of the structure. The boundary conditions for the fuse system specimen used in this study are shown in Fig. 6.

Fig. 6
figure 6

Boundary conditions.

Full size image

The loading process began with the application of vertical loads at the top of the articulated column. Subsequently, a horizontal cyclic load was applied to the outer flange at the junction between the articulated column and the top RBS connection beam using a displacement-controlled method at 0.5 mm/s. The centroid of the loading surface and the applied surface were coupled before applying displacement load to the coupling point. The loading protocol employed constant amplitude displacement increments at multiples of the yield displacement (Δy), with the first two levels cycled once and subsequent levels cycled twice, as illustrated in Fig. 7. The system was considered to have failed once the bearing capacity of the specimen surpassed the ultimate load and then fell to 0.85 times the maximum load.

Fig. 7
figure 7

Loading process.

Full size image

Verification

A finite element model of the M1 specimen was established, as described in reference23, to validate the feasibility of the proposed modeling approach. The geometric dimensions and finite element model are shown in Fig. 8. The model aligns with the experimental setup in terms of the loading method, constitutive relation, and boundary conditions, so these details are not elaborated further here.

Fig. 8
figure 8

Geometric parameters and finite element modeling of M1 specimen.

Full size image

The comparison of hysteresis, skeleton, and stiffness degradation curves between the experimental and FEA was presented in Fig. 9. The skeleton curve is the envelope formed by interconnecting the peak loads at each controlled displacement loading level of the hysteresis curve, and the stiffness degradation curve is the concatenation of the equivalent stiffness at each controlled displacement loading level. The FEA and experimentally measured curves exhibit close alignment during the elastic stage, while both curves demonstrate similar trends in their evolution throughout the elastoplastic stage. The idealization of material constitutive models and the simplification of interfacial contact interactions between components constitute significant sources of discrepancy between FEA and experimental results.

Fig. 9
figure 9

Comparison of experimental and finite element curves.

Full size image

A comparison of positive and negative elastic stiffness and ultimate bearing capacity is provided in Table 4. Both the experimental tests and FEA revealed greater stiffness and bearing capacity in the negative direction compared to the positive. The ratios of the stiffness and ultimate load capacity obtained from the tests to those from the FEA were 0.93, 1.02, 0.95, and 0.98 in positive and negative directions, respectively, with an average of 0.97. The close agreement between experimental and FEA values confirms the reliability of the FEA results and indicates that the proposed modeling method is suitable for structural fuse systems.

Table 4 Comparison of stiffness and ultimate bearing capacity.
Full size table

Parameter analysis of the fuse system’s seismic performance

Specimen design

To investigate how the reduced size of the replaceable energy dissipation beam affects the seismic performance of structural fuse systems, four series of 12 structural fuse system specimens were designed for parameter analysis. The geometric dimensions and design parameters of the fuse system specimens are shown in Fig. 10; Table 5, respectively. Here, L denotes the length of the RBS connection beam; a, b, and g retain the meanings defined in Sect. "Description of fuse system".

Fig. 10
figure 10

Geometric dimensions of fuse system specimen.

Full size image
Table 5 Specimen design parameters and bearing capacity.
Full size table

Bearing capacity and ductility

The yield displacement (Δy), yield-bearing capacity (Fy), ultimate displacement (Δu), and ultimate bearing capacity (Fu) of each fuse system specimen can be obtained from their load-lateral displacement curves, as shown in Fig. 11. In the load-displacement curve, make a straight line OA tangent to the initial section, intersect with the horizontal line over the peak point at point A, make a vertical line AB intersecting with the curve at point B, connect with OB and extend it to intersect with the horizontal line at point C, and take the displacement at point C as the yield displacement at the corresponding point on the curve as the yield point. The ductility coefficient (µ) is an important indicator of the structure’s deformation capacity, which can be calculated using Eq. (1).

Fig. 11
figure 11

Graphical method of yield load calculation.

Full size image
$$\mu =\frac{{{\Delta _{\text{u}}}}}{{{\Delta _{\text{y}}}}}$$
(1)

Comparing the load-carrying capacities of L-series specimens indicated that extending the RBS connection beam length from 710 to 760 mm led to a 3.3% decrease in yield capacity and a 2.5% decrease in ultimate load capacity, along with a 0.1 reduction in the ductility coefficient. Extending the beam length from 760 to 810 mm resulted in a 2.9% decrease in yield capacity and a 3.2% decrease in ultimate load capacity, accompanied by a 0.1 decrease in the ductility coefficient.

In the A-series specimens, increasing the distance between the start of the RBS and the end plate from 50 mm to 60 mm enhanced the yield and ultimate load capacity by 2.6% and 2.4%, respectively, while the ductility coefficient decreased by 0.1. Following an increase from 60 to 70 mm, the specimen’s yield and ultimate load capacity rose by 3.1% and 2.1%, respectively, while the ductility coefficient decreased by 0.5.

Upon examining the B-series specimens, it was found that the ultimate load-carrying capacity and yield capacity remained nearly unchanged when the length of the RBS connection was reduced between 120 mm and 140 mm, although the ductility coefficient decreased by 0.5 in these cases. Accordingly, selecting a smaller value within the “b” design range is advised.

In the G-series specimens, increasing the weakening depth of the RBS beams from 18 mm to 20 mm resulted in a 3.6% decrease in yield capacity and a 2.2% decrease in ultimate load capacity, while the ductility coefficient increased by 0.2. Increasing the weakening depth from 20 mm to 22 mm led to a 3.7% decrease in yield capacity and a 2.8% decrease in ultimate load capacity, with a 0.2 reduction in the ductility coefficient. As g increased, the ductility coefficient initially increased and then decreased; thus, g should be set at the mid-point within the design range.

Stress analysis of RBS beams in the damage stage

The fuse system was defined to fail when all the weakened sections of the RBS beams reached the yield stress. At this time, the stress change of the top RBS beam was more evident than the other beams, so the top beam was chosen as the research object for stress analysis. A schematic diagram of Paths 1 and 2 on this RBS connection beam is given in Fig. 12. The variations in stress along Paths 1 and 2 are illustrated in Fig. 13.

Fig. 12
figure 12

Schematic diagram of Paths 1 and 2.

Full size image
Fig. 13
figure 13figure 13

Stress distributions along Paths 1 and 2.

Full size image

The stress distributions along Paths 1 and 2 are similar across the different series of specimens. Along Path 1, which corresponds to the length of the RBS connection beam, stress was notably higher at the beam’s weakened flanges compared to the beam’s middle and end locations. Along Path 2, which extends along the height of the web, stresses were higher at the ends near the flanges than at the middle.

Within the specified design range, an increase in the RBS beam length (L) reduced the stress in the middle of the web in the Path 1 direction, and similarly diminished the stress in the middle of the web in the Path 2 direction. With a smaller distance from the start of the weakening flange to the end plate(a), the stress in the middle of the web along Path 1 was higher; stress variations in the web of each specimen along Path 2 were minimal. Altering the value of b had a negligible impact on web stresses in both Path 1 and Path 2 directions. Modifying the value of g similarly exerted little impact on the web stresses in any specimen along Path 1, however, larger g values led to decreased stress in the middle of Path 2.

Pushover analysis of steel frame with fuse system

Modeling in SAP2000

Analytical models were developed using SAP2000 software to verify the yielding sequence of steel frame structures with fuse systems, as shown in Fig. 14. Dead and live loads are applied to the frame beams and RBS beams before pushover analysis, taking into account the effect of gravity. The gravity loads included the dead load and 50% of the design live load. In these models, the bottom of the frame columns are rigidly connected, and the bottom of the fuse system columns are articulated bearings. All components are characterized as plastic hinges. The RBS connection beam and steel frame beam were modeled using deformation-controlled beam bending hinges (M3). The steel bema hinge parameters were determined based on the seismic code FEMA-35637, and the RBS beam hinge parameters were set with reference to past study24. The specific parameter values are detailed in Fig. 15 and Table 6, where B denotes the yield of hinge for the members, IO represents the Immediate Occupancy, LS denotes the Life Safety, CP denotes the Collapse Prevention, C denotes the Collapse stage. For the frame column, a deformation-controlled column bending hinge (P-M2-M3 hinge) was selected, also with default values. The plastic hinge was positioned at the maximum weakening point for the energy dissipation beam, specifically at relative component lengths of 0.158 and 0.842. Conversely, the frame beam and frame column hinges were located at relative component lengths of 0.1 and 0.9, respectively.

Fig. 14
figure 14

Model in SAP2000.

Full size image
Fig. 15
figure 15

MM-θ relation.

Full size image
Table 6 Plastic hinge parameters for steel beam and RBS beam.
Full size table

Typical Load-displacement curve

Figure 16 depicts the typical curve of a steel frame with fuse system under lateral force. Damage to the frame occurs in three stages: immediate, rapid repair to occupancy, and collapse prevention. The dimensions and layout of the steel frame with fuse system are illustrated in Fig. 2.

Fig. 16
figure 16

Typical pushover curve of steel frame with fuse system.

Full size image

Figure 17 shows the plastic hinge distributions identified at three limit states. In the immediate stage (displacement angle 0-0.45%), both the fuse system and the steel frame structure remained elastic, and the resulting load-displacement curve appears as a straight line. In the rapid repair to occupancy stage (displacement angle 0.45–1.13%), plastic hinges began to form in the fuse beam. More plastic hinges developed on the fuse beam as displacement increased, leading to a reduction in structural stiffness. By the end of this stage, most fuse beams had entered the plastic phase while the steel frame remained elastic.

During the collapse prevention stage (displacement angle 1.13–3.24%), plastic hinges emerged in both the fuse system and steel frame. This caused a significant decrease in stiffness, though the structure maintained sufficient ductility and energy dissipation capacity to prevent structural collapse. Upon reaching a displacement angle of 3.98%, the structure reached its ultimate bearing capacity and most components underwent plastic deformation.

Fig. 17
figure 17

Plastic hinge distribution at three limit states.

Full size image

The fuse beam developed plastic hinges within the displacement angle range of the rapid repair stage, whereas the steel frame remained in the elastic stage. Merely replacing the fuse beam could restore the structure’s original functionality in such cases. Consequently, determining the displacement angle’s upper and lower limit values during the rapid repair phase is essential.

Eight models were developed to investigate the effects of story height (H), fuse system span (L), steel strength of the fuse system, and fuse system position on the displacement angle during the rapid repair stage. The design parameters of this pushover analysis model are outlined in Table 7. The variable θr denotes the displacement angle at which the structure enters the rapid repair stage, θp indicates the displacement angle at the onset of the collapse prevention stage, Ke is the lateral stiffness in the structure’s elastic stage, Kr is the stiffness in the rapid repair stage, and Kp is the stiffness as the structure enters the collapse prevention stage.

Table 7 Design parameters of the pushover analysis model.
Full size table

The pushover curves for models with varying H are shown in Fig. 18(a). The overall trends are similar across the three curves, however, the models’ bearing capacities differ significantly. The ultimate bearing capacity of the H3300 model is 7.4% and 17.6% higher than the H3600 and H3900 models, respectively; its elastic stiffness shows increases of 21.40% and 45.36%, respectively. Both ultimate bearing capacity and stiffness appear to decrease as story height increases. However, the displacement angles marking the transition to the rapid repair and collapse prevention stages remain comparatively unchanged.

Pushover curves for models with varying L are provided in Fig. 18(b). Although the three curves largely overlap, there are slight differences in bearing capacity and stiffness among the specimens. However, the displacement angles marking the rapid repair and collapse prevention stage are consistent across the models. These curves also show where altering the fuse beam’s span had a negligible impact on the displacement angle range during the structure’s rapid repair stage.

Pushover curves for models featuring fuse systems with varying steel strengths are presented in Fig. 18(c). These curves coincide until the collapse prevention stage. The model with Q355 steel demonstrates an increase in ultimate bearing capacity of 5.3% and 3.3%, respectively, over those using Q235 and Q275 grades. Higher steel strength appears to result in a higher displacement angle at the onset of the rapid repair stage, while the displacement angle marking the collapse prevention stage remains unchanged. Modifying the steel strength grade did not impact the elastic stiffness of the structure.

Pushover curves for models with various fuse system layouts are depicted in Fig. 18(d). In the S1 model, where the fuse system is positioned at the side span, the structure’s bearing capacity shows an increase of 15.17% compared to the M1 model, which has its fuse system in the middle span. The elastic stiffness also increases by 22.63% in this case. In the S1 layout, the frame beam connected to the column is hinged only in one span of the steel frame, which improves the frame’s performance. Conversely, in the M1 layout, the steel frame has two spans with hinged beams. This reduces the number of bending-resistant connections, leading to lower overall stiffness and capacity.

Fig. 18
figure 18

Pushover curves.

Full size image

This analysis of influencing factors indicates that the building’s height and the fuse system’s ___location significantly impact the bearing capacity and stiffness of the structure. In contrast, the steel strength grade primarily influences displacement angles at the onset of the rapid repair and collapse prevention stages.

Calculating lateral stiffness and ultimate bearing capacity

General

An internal force analysis of the single-story fuse system is depicted in Fig. 19. Given that the linear stiffness of the fuse beam is significantly lower than that of the column and is uniformly distributed vertically, it was assumed that each segment of the energy dissipation beam carried an equal internal force.

Fig. 19
figure 19

Forces in fuse system.

Full size image

The relationship between the overturning moment Mov to the horizontal load F and axial force Nc of the supporting column can be expressed as follows:

$${M_{{\text{ov}}}}=FH={N_{\text{c}}}L$$
(2)

where F is the horizontal load of a single layer, H is the height of the single-layer fuse system, and L is the distance between the axis of the articulated column. The axial force Nc of the articulated column is the sum of the shear forces Vb of the energy dissipation beam segment, as shown in Eqs. (3) and (4), respectively:

$${N_{\text{c}}}={V_{\text{b}}} \times (H/h+1)$$
(3)
$${V_{\text{b}}}={N_{\text{c}}} \times \frac{1}{{(H/h+1)}}=\frac{{FHh}}{{(H+h)L}}$$
(4)

here h is the distance between the axis of the energy dissipation beam segment; (H/h + 1) is the number of energy dissipation beam segments. The bending moment Mb at both ends of the beam can be expressed as:

$${M_{\text{b}}}={V_{\text{b}}} \times \frac{{{L_{\text{b}}}}}{2}=\frac{{FHh{L_{\text{b}}}}}{{2(H+h)L}}$$
(5)

where Lb is the total length of the RBS beam.

Elastic stiffness of Single-layer fuse system

Based on the internal force analysis of the fuse system, the lateral displacement decomposition method was applied to analyze the structure’s lateral stiffness. Under the action of horizontal force, the inter-story displacement (Δ) of the fuse system consists of the displacement due to shear deformation of the RBS beam (Δs) as well as displacement due to bending deformation of the RBS beam (Δm), as shown in Eq. (6):

$$\Delta ={\Delta _{\text{s}}}+{\Delta _{\text{m}}}$$
(6)

The wing edge of the energy-consuming beam section is designed with localized weakening, so it can be assumed that the deepest part of the weakened section forms a hinge before the beam-column node. The corresponding deformation is shown in Fig. 20.

Fig. 20
figure 20

Fuse system deformation.

Full size image

The horizontal displacement Δ of the fuse system at the elastic stage under external force is much smaller than the height of the structure H. The dimensional changes due to deformation can be disregarded, and the following holds:

$${\Delta _{\text{s}}}=H \times {\theta _{\text{s}}}$$
(7)

where θs is the shear deformation displacement angle of the energy dissipation beam segment. Based on the theoretical ultimate bearing capacity of the RBS connection steel frame38, the beam segment shear deformation angle γs can be represented as Formula (8):

$${\gamma _{\text{s}}}=\frac{{{\theta _{\text{s}}}{L_{\text{b}}}}}{{{L_{{\text{RBS}}}}}}=\frac{{{V_{\text{b}}}}}{{G{A_{\text{w}}}}}$$
(8)

Here, LRBS is the distance between the maximum reduced sections of the RBS beam, G is the shear stiffness of the energy dissipation beam segment, and Aw is the cross-sectional area of the web plate of the energy dissipation beam segment. Substituting Eqs. (8) and (3) into Eq. (7) yields:

$${\Delta _{\text{s}}}=\frac{{{H^2}h{L_{{\text{RBS}}}}}}{{G{A_{\text{w}}}(H+h)L{L_{\text{b}}}}}$$
(9)

Similarly, for bending deformation, the relationship between the displacement angle θm created by bending deformation, the bending deformation angle γm and the displacement Δm can be expressed as Eqs. (10), (11) and (12), respectively :

$${\theta _{\text{m}}}=\frac{{{\Delta _{\text{m}}}}}{H}$$
(10)
$${\gamma _{\text{m}}}=\frac{{{\theta _{\text{m}}}{L_{\text{b}}}}}{{{L_{{\text{RBS}}}}}}=\frac{{{V_{\text{b}}}{L_{{\text{RBS}}}}^{2}}}{{12E{I_{\text{b}}}}}$$
(11)
$${\Delta _{\text{m}}}=\frac{{{H^2}h{L_{{\text{RBS}}}}^{3}}}{{12E{I_{\text{b}}}(H+h)L{L_{\text{b}}}}}$$
(12)

where E is the modulus of elasticity of the energy-consuming beam section; Ib is the moment of inertia of the weakened section of the RBS beam.

The lateral deformation of the fuse system must also account for stiffness reductions due to the reduced flanges of the beam. The RBS beam design method established by reference39 introduces bending stiffness reduction coefficients β1, β2, and shear stiffness reduction coefficient β3. Corrections were made to the displacements as follows:

$$\Delta ^\prime_{s}=\frac{2}{{{\beta _1}+{\beta _2}}}{\Delta _{\text{s}}}$$
(13)
$$\Delta ^\prime_{m}=\frac{1}{{{\beta _3}}}{\Delta _{\text{m}}}$$
(14)
$$\Delta ^\prime=\Delta^\prime_{s}+\Delta^\prime_{m}$$
(15)

The elastic lateral stiffness Ke of the fuse system can be determined by correcting the interlayer displacement as depicted in Formula (16):

$${K_{\text{e}}}=\frac{1}{{{{{\Delta}^{\prime}}}}}=\frac{1}{{\frac{{{H^2}h{L_{{\text{RBS}}}}}}{{{\beta _3}G{A_{\text{w}}}(H+h)L{L_{\text{b}}}}}+\frac{{{H^2}hL_{{{\text{RBS}}}}^{3}}}{{6\left( {{\beta _1}+{\beta _2}} \right)E{I_{\text{b}}}(H+h)L{L_{\text{b}}}}}}}$$
(16)

Elastic stiffness of multilayer steel frame with fuse system

The steel frame with fuse system resists horizontal loads through the combined contributions of the fuse system and steel frame. Formula (17) expresses a simplified model for analyzing the lateral stiffness of the overall structure (Fig. 21):

$${K_{\rm{m}}} = {K_{\rm{e}}} + \frac{1}{{\mathop \sum \limits_{i = 1}^s \left( {1/{K_i}} \right)}}$$
(17)
Fig. 21
figure 21

Simplified lateral stiffness model of steel frame with fuse system.

Full size image

Ultimate bearing capacity of Single-layer fuse system

When plastic hinges appear at both ends of all energy dissipation beams in the fuse system, the structure reaches its lateral ultimate bearing capacity. The structural deformation is illustrated in Fig. 22. According to the principle of virtual work, WI=WE, where internal work WI:

$${W_{\rm{I}}} = \mathop \sum \limits_{l = 1}^n \left( {2{M_{{\rm{u,}}l}}\gamma _{\rm{p}}^{\rm{s}} + {V_{{\rm{u,}}l}}{L_{{\rm{RBS}}}}\gamma _{\rm{p}}^{\rm{b}}} \right)$$
(18)

Mu,l and Vu,l are the bending moment and shear force at the plastic hinge of the l-th energy dissipating beam at the limit state, respectively; n is the number of energy dissipation beam segments; γps and γpm is the plastic shear deformation angle and the bending deformation angle, respectively.

Fig. 22
figure 22

Theoretical model of fuse system.

Full size image

The plastic deformation angle (γp) of the energy dissipation beam segment is:

$${\gamma _{\text{p}}}={\gamma _{\text{p}}}^{{\text{s}}}+{\gamma _{\text{p}}}^{{\text{m}}}=\frac{{{\theta _{\text{p}}}{L_{\text{b}}}}}{{{L_{{\text{RBS}}}}}}$$
(19)

which can be substituted into Eq. (18) so that the following holds:

$${W_{\rm{I}}} = \frac{{2\mathop \sum \limits_{l = 1}^n {M_{{\rm{u,}}l}}{\theta _{\rm{p}}}{L_{\rm{b}}}}}{{{L_{{\rm{RBS}}}}}}$$
(20)

The work done by external forces WE is:

$${W_{\text{E}}}=FH{\theta _{\text{p}}}$$
(21)

Because WI=WE, then:

$$F = \frac{{2\mathop \sum \limits_{l = 1}^n {M_{{\rm{u}},l}}{L_{\rm{b}}}}}{{H{L_{{\rm{RBS}}}}}}$$
(22)

The ultimate bending moment Mu of the RBS beam can now be determined based on the yield bending moment My:

$${M_{\text{u}}}=\alpha {M_{\text{y}}}$$
(23)
$${M_{\text{y}}}={C_{{\text{pr}}}}{R_{\text{y}}}{W_{\text{p}}}{f_{\text{y}}}$$
(24)

where α is the cross-sectional shape coefficient, and Cpr is the load-bearing capacity coefficient related to the material’s yield strength, ultimate strength, and strain strengthening; Ry is the steel overstrength coefficient, Wp is the full section modulus at the maximum weakening point of the cross-section, and fy is the yield strength of the material.

Ultimate bearing capacity of multilayer steel frame with fuse system

Once the steel frame with fuse system reaches its limit state, the fuse system and the steel frame collaboratively contribute to energy absorption. Adhering to the design principle of “weak beams and strong columns,” plastic hinges are most likely to form at the base of frame columns and termini of frame beams. This anticipated structural deformation mechanism is illustrated in Fig. 23.

Fig. 23
figure 23

Theoretical model of steel frame with fuse system at limit state.

Full size image

Structural internal work WI’ involves four distinct aspects: fuse system W1, frame beams rigidly connected at both ends (W2), frame beams rigidly connected at one end (W3), and frame column W4:

$${W_{\text{I}}}^\prime={W_1}+{W_2}+{W_3}+{W_4}$$
(25)
$${W_1} = 2\mathop \sum \limits_{l = 1}^n \alpha _l^{\rm{b}}M_{{\rm{y}},l}^{\rm{b}}\left( {\frac{{{L_{\rm{b}}}}}{{{L_{{\rm{RBS}}}}}}} \right)$$
(26)

αlb and Myl are the cross-sectional shape coefficients and yield bending moments of the l-th energy dissipation beam, respectively. Further,

$${W_2} = 2\mathop \sum \limits_{i = 1}^s \mathop \sum \limits_{j = 1}^k \alpha _{i,j}^{\rm{f}}M_{{\rm{y}}i,j}^{\rm{f}}\left( {\frac{{{L_{{\rm{f}},j}}}}{{{L_{{\rm{p}},j}}}}} \right)$$
(27)

αfi, j and Mfyi, j denote the cross-sectional shape coefficient and yield moment of the i-th floor and j-th span frame beam; Lf,j is the span of the frame beam, Lp,j is the distance between the plastic hinges of the frame beam, s is the number of structural layers, and k is the number of steel frame spans.

$${W_3} = \mathop \sum \limits_{i = 1}^s \alpha _{i,1}^{\rm{f}}M_{{\rm{y}}i,1}^{\rm{f}}\left( {\frac{{{L_{{\rm{f}},1}}}}{{{L_{{\rm{p}},1}}}}} \right)$$
(28)
$${W_4} = \mathop \sum \limits_{t = 1}^x \alpha _t^{\rm{c}}M_t^{\rm{c}}$$
(29)

αtc, and Mtc represent the cross-sectional shape coefficient and yield moment of the t-th steel frame column, and x is the total number of steel frame columns.

$$W_{\rm{E}}^\prime = \mathop \sum \limits_{i = 1}^s {F_{\rm{i}}}{H_{\rm{i}}}$$
(30)
$${W_{\text{I}}}^\prime={W_{\text{E}}}^\prime$$
(31)
$$\mathop \sum \limits_{i = 1}^s {F_{\rm{i}}}{H_{\rm{i}}} = {W_1} + {W_2} + {W_3} + {W_4}$$
(32)

Fi is the ultimate lateral force of the i-th layer; Hi is the distance from the i-th layer beam to the column base.

Comparison of calculated values and FEA results

The calculated values and FEA results for elastic stiffness and ultimate bearing capacity are presented in Table 8 for both a single-story fuse system and a steel frame with fuse system. Kcal and Fcal are the calculated elastic stiffness and ultimate lateral force, respectively. Kfea and Ffea are the elastic stiffness and ultimate lateral force determined by FEA, respectively. For the single-fuse system, the average ratios of the FEA results to the calculated values for elastic stiffness and ultimate lateral force are 0.953 and 0.946, respectively. For the steel frame with fuse system, the average ratios of the FEA results to the calculated values for elastic stiffness and ultimate lateral force are 0.968 and 0.963, respectively.

The average discrepancy between the theoretical calculations and FEA values remains below 10%, confirming the feasibility of the proposed calculation method. The FEA values are, however, slightly lower than the calculated values; this is because not all RBS beams develop plastic hinges when the steel frame with fuse system enters the collapse prevention stage.

Table 8 Calculated values vs. FEA results.
Full size table

Conclusion

This paper designs a steel frame structure with fuse system, where RBS connection beams are strategically designed as replaceable energy-absorbing components. Parameter analysis was employed to examine the impact of the RBS connection beam’s reduced dimensions on the seismic performance of the fuse system. The failure mechanisms of the steel frame with fuse system were further examined through pushover analyses. Based on these findings, a calculation method for the steel frame with fuse system’s elastic stiffness and ultimate bearing capacity was established and validated by comparison against FEA results.

The key conclusions of this study can be summarized as follows:

(1) The failure process of the innovative steel frame with fuse system can be divided into three distinct stages: immediate, rapid repair to occupancy, and collapse prevention. During the rapid repair to occupancy stage, non-elastic deformation primarily occurs in the RBS connection beams while the frame beams and columns maintain their elasticity, enabling quick post-earthquake replacement to recover structural functionality.

(2) For the RBS connection beams, the recommended values for the geometric design parameters include a 0.65bf distance from the beginning of the RBS to the end plate, a flange reduction length of 0.65hb, and a flange cut depth of 0.2bf.

(3) Story height significantly affects the stiffness and load-carrying capacity of the steel frame with fuse system. However, both story height and RBS beam span have a negligible effect on the lateral displacement angle during the rapid repair phase. RBS connection beams have a lower steel grade than steel frames, which ensures that the fuse system yields first. Placing the fuse system at the side span was also found to be more effective than positioning it at the center span.

(4) The average ratios of the FEA results for elastic stiffness and ultimate lateral force to the calculated values for the steel frame with fuse system are 0.968 and 0.963, respectively. The error between the calculated results and the finite element values is within 10%, validating the proposed calculation method as a reliable reference for engineering applications.

These conclusions were derived from a hysteretic analysis of the fuse system and pushover analysis of the steel frame with fuse system. Further study of the structural response of steel frames with a fuse system under dynamic loading and its difference from the LCF system will enhance the practical applicability of this design.