Introduction

Natural gas pipeline networks serve as critical infrastructure for global energy transportation, ensuring stable supply to residential, industrial, and commercial sectors1. However, the operational stability of these networks is highly vulnerable to localized faults, which can propagate into systemic hydraulic imbalances and disrupt gas supply2. As pipeline systems expand in scale and complexity—particularly with the increasing adoption of looped configurations—their operational characteristics grow more intricate, exposing inherent topological vulnerabilities3. These challenges underscore the urgent need for robust reliability assessment and optimization frameworks to enhance the safety and resilience of modern pipeline networks.

Prior studies have advanced methodologies for reliability assessment and topology optimization, yet critical gaps persist. Traditional reliability models, such as those based on tree-like network assumptions4,5, struggle to address the combinatorial complexity of large-scale looped networks. While probabilistic frameworks6,7 and hybrid algorithms8,9 have improved computational efficiency, they often prioritize isolated objectives (e.g., cost minimization or risk mitigation) without systematically integrating topological resilience with operational constraints. Furthermore, emerging graph neural network (GNN)-based approaches10,11, though promising, face limitations in interpretability and dependency on extensive training data, hindering their applicability to real-world engineering decisions. A comprehensive framework that balances computational scalability, dynamic adaptability, and holistic system analysis remains elusive.

Conventional reliability assessment methods, such as Monte Carlo simulations or tree-like network models, encounter significant computational complexity and challenges in analyzing redundant pathways when addressing extensive circumferential networks. In contrast, data-driven approaches, including machine learning, demonstrate potential for pipeline fault detection. The semi-supervised learning framework proposed by Alobaidi et al.12., which reconstructs missing data to improve fault classification accuracy, is contingent upon historical failure data and does not directly tackle the optimization of topological redundancy. Therefore, there is an urgent need for a graph-theoretic method capable of dynamic optimization under both computational efficiency and topological constraints, independent of training data. In response to the challenge posed by data gaps in oil and gas pipeline health assessments, Shai et al.13. introduced a dual-output framework based on Bayesian regularized neural networks that can accurately predict the remaining life of pipelines with incomplete input parameters, as well as classify metal loss defects, thus providing theoretical support for dynamic maintenance strategies through sensitivity analysis, which further disclosed the impact weights of critical parameters such as pressure and wall thickness. Recent studies have employed Markov chain state transition models14 and Bayesian-Monte Carlo fusion methods15 to address real-time assessment and small-sample parameter estimation problems, but the adaptability of these approaches to network redundancy optimization remains untested.

To address these limitations, this paper introduces an integrated framework combining connectivity reliability evaluation with adaptive topology optimization. Our key contributions include: A Minimum Path Set-Based Reliability Model: Leveraging binary decision diagram (BDD) algorithms, we develop a connectivity reliability evaluation framework that reduces computational complexity by 40% compared to conventional Monte Carlo simulations. An Adaptive Genetic Algorithm (AGA): Designed to overcome local convergence issues in traditional optimization methods, this algorithm dynamically adjusts crossover and mutation rates for large-scale networks. Quantified Validation: Through case studies on operational pipeline networks, we demonstrate an eightfold improvement in reliability (from 0.03 to 0.247), providing actionable insights for infrastructure retrofitting.

By bridging complex network theory with practical engineering constraints, this work offers a paradigm shift in pipeline network management, enabling proactive decision-making for both existing systems and future expansions.

Related work

Reliability assessment techniques

The reliability evaluation of pipeline networks has evolved through three key methodological paradigms: probabilistic analysis, dynamic simulation, and data-driven approaches.

Investigations into probability and graph-theoretic frameworks, early studies predominantly focused on tree-like networks due to their computational tractability. For instance, Rinaldi2, established an interdependency framework for infrastructure performance assessment, demonstrating that gas networks could be coupled with power grids under specific conditions. Subsequent work extended this to tree-like gas networks by mapping reliability problems to graph connectivity analysis4,5. However, these methods face scalability challenges for looped networks, as their computational complexity grows exponentially with network size16.

In the realm of dynamic and hydraulic sensing models, recent advancements incorporate hydraulic characteristics and failure-repair dynamics. Scholars17 have proposed a gas supply reliability model that takes into account pipeline failure processes, while others18 have combined hydraulic constraints with Monte Carlo simulations to evaluate target reliability. Although these methods improve accuracy, their dependence on high-fidelity modeling limits their applicability in real-time scenarios within large-scale systems.

In addition, research on data-driven and graph neural network (GNN) methods, emerging graph neural networks (GNNs)19,20 have shown potential in infrastructure reliability analysis by learning topological patterns. However, GNNs require extensive training datasets and lack interpretability in failure-critical scenarios—a critical drawback for safety-sensitive pipeline systems. To address these limitations, our work adopts a training-free graph-theoretic approach, enabling direct reliability quantification without dependency on historical data.

Furthermore, Forghani-Elahabad et al. conducted a comprehensive assessment of probability and statistical methods, treating the probability of flow from multiple source nodes to target nodes as a key indicator in network reliability theory21. Scholars also proposed an integrated evaluation framework, utilizing Markov Chain Monte Carlo (MCMC) random process analysis and complex network theory to analyze failure and recovery processes22. By employing simulation and experimental methods, a distributed step-size calculation model for pipeline system reliability was established based on pipe process simulation technology, thereby simplifying and accelerating the computation of pipeline and station system reliability23.

Topological optimization algorithms

Topology optimization research has progressed from heuristic methods to hybrid and constraint-aware frameworks.

In the realm of traditional heuristic algorithm research, Genetic algorithms (GAs) have been widely adopted for layout optimization. For example, Sepehr24 minimized investment costs using GA-driven pipeline attribute selection, while scholars25 improved fitness functions for multi-objective optimization. Nevertheless, these methods often converge prematurely in large-scale networks due to static crossover/mutation rates26. The latest advancements in genetic algorithm variants, as proposed by scholar27, showcase enhanced global search capability and adaptability in complex optimization scenarios through their GA-BP-GA hybrid method for calibrating irregular seed parameters. This has potential implications for topology optimization in pipeline networks. Genetic algorithms and their variants have demonstrated exceptional optimization capabilities in various engineering domains. Recent research has combined genetic algorithms with deep learning techniques (Long Short-Term Memory networks) to enhance power system frequency stability28, highlighting the adaptability of evolutionary algorithms in dynamic control scenarios. Our adaptive genetic algorithm (AGA) addresses this by dynamically tuning parameters based on population diversity metrics.

In the realm of mixed and constrained integration methodologies, Recent studies combine optimization with hydraulic simulations. Scholars29 proposed a grayscale-coupled neural network for pipeline design, and formulated a mixed-integer nonlinear programming (MINLP) model linking topology to production cycles9. While effective, these approaches prioritize economic objectives over reliability-resilience trade-offs. In contrast, our framework explicitly integrates reliability constraints into the optimization loop.

Regarding obstacle perception and 3D layout optimization, Practical challenges like obstacle avoidance have driven innovations in spatial optimization. Dbouk30 applied the A* algorithm for obstacle-avoiding pipeline routing, and modeled 3D topology optimization for oil-gas gathering systems31. These methods, however, neglect the interdependency between geometric layout and topological redundancy—a gap our work bridges through joint spatial-topological analysis.

To solve the mixed integer nonlinear programming (MINLP) model, an iterative four stage decomposition algorithm is proposed. The proposed model and algorithm demonstrate advantages in solving time and scalability through three large-scale natural gas pipeline networks32; In the field of multi-objective optimization and constraint handling research, Jiao et al. applied systems engineering methods to create a coordination mechanism, proposing a multi-objective optimization model33; An and colleagues optimized pipeline network layout using the minimum spanning tree algorithm by analyzing the relationship between failure probability and investment cost weights, aiming to maximize economic benefits34.

The existing research gaps include: insufficient support for large-scale ring networks; current reliability assessment methods primarily addressing tree-like structures, which lack efficient solutions for the computational complexities associated with circular configurations. In the absence of a dynamic optimization framework, most topology optimization algorithms concentrate on static layouts, with minimal integration of real-time reliability assessments and dynamic adjustment strategies. Data dependency and interpretability present a significant challenge. Despite their remarkable performance on complex networks, emerging GNN methods necessitate a considerable amount of training data, and their results are often difficult to interpret, thereby constraining their applicability in engineering decision-making. To address these challenges, our work proposes a training-free framework based on graph theory, for large-scale and complex natural gas pipeline networks that are already constructed and operational, it is imperative to conduct more comprehensive research on the connectivity reliability of their topology. Such research should focus on evaluating the performance of the network’s connectivity reliability while also offering scientific recommendations for future topology optimization. This study employs graph theory and probabilistic analysis without necessitating any training, thereby facilitating direct assessments of topological reliability that are suitable for engineering decision-making.

This article aims to address the research gap as follows:

  1. (1)

    Existing methods prove inadequate for tackling large-scale circular pipelines;

  2. (2)

    There is an absence of a comprehensive framework integrating connectivity analysis with dynamic optimization;

  3. (3)

    Over-reliance on training data in existing GNN-based approaches.

Methodology

The connectivity reliability of a natural gas pipeline network refers to the ability to maintain a connection between gas sources and consumption nodes, ensuring that at least one path exists between any two points in the system. This measure focuses solely on the network’s connectivity function, disregarding attributes such as pressure or flow within the network. For large-scale, complex natural gas pipeline systems, a connectivity reliability assessment model is developed. This model incorporates intelligent algorithms to optimize solutions and quantify various metrics, with the objective of evaluating the network’s connectivity reliability performance.

Connectivity reliability

Connectivity events between nodes are characterized by logical events under the normal operational state of pipeline segments. Combining the minimal path theory from references35,36,37, we derive the logical events and analytical expressions for the connectivity reliability indicator, as detailed in Table 1. The connectivity reliability is defined as:

$$\:\begin{array}{c}R=P\end{array}$$
(1)

Where \(\:R\) represents the reliability of connectivity between gas sources and consumption nodes; \(\:P\) denotes the probability of node connectivity in the topological graph.

In a natural gas network \(\:{G}_{S}\) ​, \(\:S\) denotes source points, \(\:j\) denotes consumption nodes, and \(\:U\) represents the set of consumption nodes. The network comprises \(\:{n}_{s}\)​ source points, \(\:{n}_{U}\)​ consumption nodes, and \(\:{n}_{e}^{s}\)​ denotes the number of pipe segments. There exists at least one minimum path that connects two nodes mutually. The \(\:k\)-th minimum path from source node \(\:{V}_{Si}\) to consumption node \(\:{v}_{j}\) is denoted as \(\:{d}_{Si,j,k}^{s}\)​, expressed by Eq. (2).

$$\:\begin{array}{c}{d}_{Si,j,k}^{s}=\prod\:_{l=1}^{{n}_{Si,j,k}^{S}}{e}_{Si,j,k}^{s}\end{array}$$
(2)

Where \(\:{d}_{Si,j,k}^{s}\) denotes the logical event representing the \(\:k\)-th shortest path from source node \(\:{V}_{Si}\) to consumption node \(\:{v}_{j}\) with all edges in normal condition; \(\:{n}_{Si,j,k}^{S}\) represents the number of segments in the \(\:k\)-th minimum path from source node \(\:{V}_{Si}\)​ to consumption node \(\:{v}_{j}\); \(\:{e}_{Si,j,k}^{s}\) represents the event of normal operation for the pipeline segments in the \(\:k\)-th minimal path, the \(\:{e}_{Si,j,k}^{s}\) signifies an operational event along the minimum path of a pipeline segment (a binary variable, with 1 representing normal operation and 0 indicating failure).

The set of minimum paths from source node \(\:{V}_{Si}\) to consumption node \(\:{v}_{j}\) is denoted as \(\:{D}_{Si,j}^{s}\)​, expressed by Eq. (3).

$$\:\begin{array}{c}{D}_{Si,j}^{s}=\sum\:_{k=1}^{{n}_{Si,j}^{S}}{d}_{Si,j,k}^{s}\end{array}$$
(3)

Where \(\:{D}_{Si,j}^{s}\) denotes the event of the set union of all minimum path collections originating from the source node \(\:{V}_{Si}\) to the vertex \(\:{v}_{j}\); \(\:{n}_{Si,j}^{S}\)​ represents the number of minimum paths from source node \(\:{V}_{Si}\) to consumption node \(\:{v}_{j}\) in the natural gas network \(\:{G}_{S}\).

The event in which the consumption node \(\:{v}_{j}\) is connected to at least one source node is represented by the logical expression \(\:\sum\:_{i=1}^{{n}_{s}}{D}_{Si,j}^{s}\). The reliability \(\:{R}_{j}\)​ of a given consumption node being connected to at least one source node is then defined by Eq. (4):

$$\:\begin{array}{c}{R}_{j}=P\left\{\sum\:_{i=1}^{{n}_{s}}{D}_{Si,j}^{s}\right\}=P\left\{\sum\:_{i=1}^{{n}_{s}}\sum\:_{k=1}^{{n}_{Si,j}^{S}}\prod\:_{l=1}^{{n}_{Si,j,k}^{S}}{e}_{Si,j,k}^{s}\right\}\end{array}$$
(4)

The existence of connectivity between a specified source node and all consumption nodes is represented by the logical event \(\:\prod\:_{j=1}^{{n}_{U}}{D}_{Si,j}^{s}\); the likelihood that the consumption node \(\:{v}_{j}\) is connected to at least one source node, \(\:{R}_{j}\), is determined by calculating the Boolean logical joint event probability of all potential paths. Specifically, \(\:\sum\:_{i=1}^{{n}_{s}}{D}_{Si,j}^{s}\) represents the presence of an effective path, with its probability calculated using the principle of inclusion-exclusion.

The set \(\:{v}_{U}=\left\{{v}_{1},{v}_{2}, {\ldots},{v}_{{n}_{U}}\right\}\) comprises all gas nodes within the pipeline \(\:{G}_{S}\), featuring a designated source node that is connected to all gas nodes. The logical event is denoted as \(\:\prod\:_{j=1}^{{n}_{U}}{D}_{Si,j}^{s}\). According to K-tree theory, \(\:\prod\:_{j=1}^{{n}_{U}}{D}_{Si,j}^{s}\) is equivalent to all K-trees corresponding to the combined set of nodes \(\:\text{K}={v}_{U}\bigcup\:\left\{{v}_{Si}\right\}\). The pursuit of the K-tree’s logical sum corresponds to calculating the probability that all gas nodes are connected to at least one gas source node. The logical event is represented as \(\:\sum\:_{i=1}^{{n}_{s}}\prod\:_{j=1}^{{n}_{U}}{D}_{Si,j}^{s}\). Consequently, the connectivity reliability between all gas nodes \(\:{v}_{U}\) and the designated source point \(\:{S}_{i}\) is expressed by the following formula, therefore, the connectivity reliability \(\:{R}_{Si}\) between all consumption nodes \(\:{v}_{U}\) and the specified source node \(\:{S}_{i}\) is expressed by Eq. (5):

$$\:\begin{array}{c}{R}_{Si}=P\left\{\prod\:_{j=1}^{{n}_{U}}{D}_{Si,j}^{s}\right\}=P\left\{\prod\:_{j=1}^{{n}_{U}}\sum\:_{k=1}^{{n}_{Si,j}^{S}}\prod\:_{l=1}^{{n}_{Si,j,k}^{S}}{e}_{Si,j,k}^{s}\right\}\end{array}$$
(5)

The logical event representing connectivity between all consumption nodes and at least one gas source node is expressed as \(\:\sum\:_{i=1}^{{n}_{s}}\prod\:_{j=1}^{{n}_{U}}{D}_{Si,j}^{s}\) ​, by extending Boolean algebra, the joint probability is transformed into a summation of mutually exclusive events.

The reliability \(\:{R}_{U}\) of connectivity between all consumption nodes \(\:{v}_{U}\) and at least one gas source node is:

$$\:\begin{array}{c}{R}_{U}=P\left\{\sum\:_{i=1}^{{n}_{s}}\prod\:_{j=1}^{{n}_{U}}{D}_{Si,j}^{s}\right\}=P\left\{\sum\:_{i=1}^{{n}_{s}}\prod\:_{j=1}^{{n}_{U}}\sum\:_{k=1}^{{n}_{Si,j}^{S}}\prod\:_{l=1}^{{n}_{Si,j,k}^{S}}{e}_{Si,j,k}^{s}\right\}\end{array}$$
(6)

In the gas transmission network \(\:{G}_{S}\), the reliability of connectivity between all gas-consuming nodes \(\:{v}_{U}\) and all source nodes \(\:{v}_{S}\) represents the probability of all gas-consuming nodes being connected to all sources. This indicator reflects a systemic perspective, evaluating comprehensively the connectivity among all nodes within the network, the logical event representing connectivity between all consumption nodes\(\:{v}_{U}\)​ and all source nodes is \(\:\prod\:_{i=1}^{{n}_{S}}\prod\:_{j=1}^{{n}_{U}}{D}_{Si,j}^{s}\)​. The connectivity reliability \(\:{R}_{SU}\:\)of the network is:

$$\:\begin{array}{c}{R}_{SU}=P\left\{\prod\:_{i=1}^{{n}_{S}}\prod\:_{j=1}^{{n}_{U}}{D}_{Si,j}^{s}\right\}=P\left\{\prod\:_{i=1}^{{n}_{S}}\prod\:_{j=1}^{{n}_{U}}\sum\:_{k=1}^{{n}_{Si,j}^{S}}\prod\:_{l=1}^{{n}_{Si,j,k}^{S}}{e}_{Si,j,k}^{s}\right\}\end{array}$$
(7)
Table 1 Summary of natural gas pipeline network connectivity reliability.
Full size table

Solution of connectivity reliability

In practical natural gas pipeline systems, the network structure is complex. Solving this involves using computer algorithms to address two primary tasks: searching for minimal paths and performing operations on logical events and their conjunctions.

Minimum path search

To study the connectivity of network topologies, it is necessary to identify all possible paths between starting and destination nodes. The traditional edge traversal search algorithm is improved by implementing a depth limit on the search, with backtracking upon reaching this limit. This enhancement addresses the issue of multiple parallel pipelines between nodes in a network, making the algorithm applicable to more complex network structures. The algorithm’s flowchart is shown in Fig. 1.

Fig. 1
figure 1

Improved DFS algorithm for minimal path search between node \(\:{v}_{s}\) an \(\:{v}_{t}\).

Full size image
  1. 1.

    Begin with the algorithm: either starting from the source node or initiating the entire search process;

  2. 2.

    Initialize the depth limit: Set it to 0 to indicate that the initial iteration starts from a depth of 0.

  3. 3.

    Initiate DFS: Begin executing depth-first search in an attempt to locate the target node.

  4. 4.

    Depth-First Search: Conduct a depth-first search in each iteration, exploring the various branches of the search tree;

  5. 5.

    If the target node is found during the search, record the current path and return the result.

  6. 6.

    When no target node is found, backtrack: if no target node is discovered, backtrack in order to explore alternative paths.

  7. 7.

    All paths have been found; the search is ended: If all possible paths have been discovered in one iteration, the search concludes.

  8. 8.

    When the depth limit reaches its maximum value, backtrack: if the depth limit attains its predetermined maximum, backtrack to explore other depths;

  9. 9.

    Incorporating depth constraints: Incorporating depth constraints to expand search depths;

  10. 10.

    Resuming DFS: Recursively execute the DFS search, starting from depth 0 and up to the new depth limit.

Given the complexity of the gas pipeline network, Breadth-First Search (BFS) necessitates a substantial amount of memory to store each layer traversed during exploration. This is the reason why Depth-First Search (DFS) was selected as the method for identifying the shortest path. DFS primarily utilizes recursive and stack data structures, which facilitates its adaptation across various programming languages and environments. In the context of a gas pipeline network, the DFS methodology entails establishing the search starting point—specifically, the source node \(\:{v}_{s}\) within the gas pipeline topology—followed by the selection of any arbitrary node connected to the source node, with searches advancing incrementally from closer to farther nodes. Once the pipeline segments have been traversed, they are marked until the consumption node \(\:{v}_{t}\) is reached. Ultimately, all the pipeline segments marked during the search process constitute the shortest path between \(\:{v}_{s}\) and \(\:{v}_{t}\).

Reliability calculation

By optimizing DFS algorithms, one can effectively accelerate path search speeds, thereby enhancing computational efficiency. Logical event calculations proceed in accordance with theorem principles. For the set of shortest paths \(\:{R}_{D}\), we have:

$$\:\begin{array}{c}{R}_{D}=P\left({d}_{1}\cup\:{d}_{2}\cup\:{d}_{3}\dots\:{d}_{m}\right)\\\:=\sum\:_{i=1}^{m}P\left({d}_{i}\right)-\sum\:_{i<j=2}^{m}P\left({d}_{i}{d}_{j}\right)+\sum\:_{i<j<k=3}^{m}P\left({d}_{i}{d}_{j}{d}_{k}\right)+{\left(-1\right)}^{m+1}P\left({d}_{i}{d}_{j}{d}_{k}\dots\:{d}_{m}\right)\end{array}$$
(8)

Where \(\:{d}_{i}\) is the shortest path; \(\:m\) is the number of shortest paths.

As shown in Eq. (8), In the expanded form, there exists an equation with 2m-1 terms, and the number \(\:m\) of the shortest paths demonstrates an exponential relationship with the number of terms. In complex networks, \(\:m\) is typically considerable, which may lead to overflow issues in computers. This data explosion problem renders the formula exceedingly complicated; each shortest path represents a mutually exclusive event that cannot be computed by inserting the probability of each event into the reliability of the minimum cut set. Consequently, it is essential to eliminate redundant terms in the formula and perform non-overlapping processing on the shortest paths, calculating only their non-overlapping sum. Based on this, this section utilizes a binary decision diagrams (Binary Decision Diagrams, BDD) method for non-overlapping operations on the logical events of the minimum cut set.

Therefore, to eliminate the redundant terms in the formula, the shortest paths are disjointed, as shown in Eq. (9).

$$\begin{array}{*{20}c} {\text{Re} lS = P\left( {d_{1} + d_{2} + d_{3} \ldots d_{m} } \right) = P\left( {d_{1} } \right) + P\left( {\overline{{d_{1} }} d_{2} } \right) + P\left( {\left( {\mathop \prod \limits_{{i = 1}}^{{m - 1}} \overline{{d_{i} }} } \right)d_{m} } \right)} \\ { = P\left( {d_{1} } \right) + P\left( {\overline{{d_{1} - d_{2} }} d_{2} } \right) + P(\overline{{d_{1} - d_{3} ~}} ~\overline{{d_{2} - d_{3} }} d_{2}) ~~~ + P\left( {\left( {\mathop \prod \limits_{{i = 1}}^{{m - 1}} \overline{{d_{i} - d_{m} }} } \right)d_{m} } \right)} \\ \end{array}$$
(9)

Where \(\:\stackrel{-}{{d}_{i}-{d}_{m}}\) (\(\:i\)< m) represents the Boolean product of the arcs remaining in \(\:{d}_{i}\) after removing the arcs identical to those in \(\:{d}_{m}\); Path intersection operations facilitate independent event decomposition by eliminating edges that are shared by subsequent paths (\(\:\stackrel{-}{{d}_{i}-{d}_{m}}\)), thereby avoiding redundant terms. For example, if path \(\:{d}_{1}\) shares edge \(\:{e}_{1}\) with path \(\:{d}_{2}\), then \(\:{d}_{1}-{d}_{2}\) represents the remaining edges in \(\:{d}_{2}\) after the removal of the shared edge \(\:{e}_{1}\)​ from \(\:{d}_{1}\).

The minimal path set logical events are processed using Binary Decision Diagrams (BDD) for non-crossing operations. The corresponding non-crossing operation flowchart is shown in Fig. 2.

Fig. 2
figure 2

BDD disjointed arithmetic flow.

Full size image

Existing studies25 based on tree-shaped networks have facilitated reliability assessments through simplified path searches and probabilistic computations; however, their models struggle to adapt to the characteristics of multi-path redundancy in large-scale circular pipelines. This paper presents a framework that addresses this deficiency by incorporating the following enhancements:

Circumferential structure support: Employing an enhanced depth-first search (DFS) algorithm with a backtracking mechanism that identifies multi-path redundancy within a circular network (Fig. 1), thereby avoiding the issue of path omission in traditional tree-like models.

Reduced computational complexity: The binary decision diagram (BDD) algorithm, when applied to minimize path sets (Fig. 2), transforms the exponential terms in the reliability formula (Eq. 8) into polynomial ones, thus significantly enhancing the computational efficiency of large-scale networks.

Topology optimization model

Building on the research of connectivity reliability evaluation models for large-scale complex networks, this study proposes a topology optimization model aimed at enhancing reliability. The model focuses on optimizing the network layout to improve connectivity reliability while ensuring the natural gas pipeline network’s normal transmission functionality. By setting specific constraints and refining algorithmic designs, the optimal solution is obtained, serving as a reference for future pipeline network optimization. The established optimization model provides a scientific basis for addressing similar optimization problems in the future, this study examines the connectivity failures caused by pipe fractures and corrosion, under the assumption that the failure probability adheres to a Weibull distribution (with parameters derived from the industry standard GB 50251 − 2015).

Mathematical model

In an operational natural gas pipeline network, the sources, pipeline locations, and segment parameters are already determined. In the optimization problem, the decision variable is defined as the strategic addition of redundant segments within the network to improve overall connectivity reliability, the decision variable is represented as a binary matrix \(\:X\)=[\(\:{x}_{ij}\)]89 × 89, where \(\:{x}_{ij}\)=1 indicates the addition of a redundant pipeline between nodes \(\:{v}_{i}\) and \(\:{v}_{j}\). In matrix dimension: 89 × 89, corresponding to the total number of nodes in the network after simplification (including 89 nodes), each element \(\:{x}_{ij}\) indicates whether redundant pipelines have been added between nodes \(\:{v}_{i}\) and \(\:{v}_{j}\). In its physical sense, In case of \(\:{x}_{ij}\)= 1, add a redundant pipe between nodes \(\:{v}_{i}\) and \(\:{v}_{j}\); \(\:{x}_{ij}\)= 0, no redundant pipelines added. Given that the network is an undirected graph (\(\:{x}_{ij}\)=\(\:{x}_{ji}\)), select the optimal redundant pipeline addition scheme to maximize network connectivity reliability.

Objective function

Using the connectivity of nodes in the gas pipeline network as decision variables, the objective function is to maximize the network’s connectivity reliability:

$$\:\begin{array}{c}Max: {R}_{SU}=P\left\{\prod\:_{i=1}^{ns}\prod\:_{j=1}^{nU}\sum\:_{k=1}^{{n}_{Si,j}^{S}}{d}_{Si,j,k}^{s}\right\}\end{array}$$
(10)

Where ns represents the number of gas source nodes; nu represents the number of gas consumption nodes; \(\:{n}_{Si,j}^{S}\) represents the number of minimal paths from source node \(\:{V}_{Si}\) to demand node \(\:{v}_{j}\); \(\:{d}_{Si,j,k}^{s}\)​ represents the \(\:k\)-th minimal path from source node \(\:{V}_{Si}\) to demand node \(\:{V}_{Si}\) in the pipeline network \(\:{G}_{s}\) ​.

Constraints

Location constraints for gas sources and stations. The locations of gas sources and various demand nodes (such as gate stations, distribution stations, and storage and distribution stations) are predetermined. This constraint is incorporated into the matrix, with fixed length weights between nodes.

Matrix constraints. The network connectivity is expressed through an adjacency matrix. In an undirected graph, node connectivity is represented by {0, 1}, The matrix element \(\:{x}_{ij}\) must satisfy the following conditions: \(\:{x}_{ij}\) \(\:\in\:\){0, 1}, \(\:{x}_{ij}\) =0 (\(\:i\)=\(\:j\)), \(\:{x}_{ij}\)= \(\:{x}_{ji}\).

Path constraints. The original topology of the pipeline network is maintained, with new segments added to the existing network. This is represented in the matrix as: \(\:{x}_{ij}\)=1 (indicating a direct connection between nodes \(\:{v}_{i}\) and \(\:{v}_{j}\)​).

Redundant segment length constraints. Constraints on the length of newly added segments are considered. \(\:{l}_{max}\)denotes the maximum allowable length of new pipelines, and \(\:{l}_{0}\) represents the length constraint for these new pipelines.

Importance constraints. Probability connectivity importance evaluates the influence of each pipeline segment’s reliability on the overall connectivity reliability of the network. This is assessed by analyzing how variations in the segment’s own reliability affect the network’s connectivity reliability. The probability connectivity importance \(\:{I}_{r}\left({e}_{i}\right)\) of pipeline segment \(\:{e}_{i}\) is defined as:

$$\:\begin{array}{c}{I}_{r}\left({e}_{i}\right)=\frac{\partial\:R}{\partial\:{r}_{i}}\:\:\:\:\:i=\text{1,2},\dots\:,{n}_{e}\end{array}$$
(11)

Where \(\:{r}_{i}\) represents the reliability of pipeline segment \(\:{e}_{i}\) ; \(\:R\) represents the reliability of the natural gas pipeline network.

As previously mentioned, a pipeline segment in the natural gas network can be in one of two states: normal operation (with probability \(\:{r}_{i}\)) or failure (with probability 1-\(\:{r}_{i}\)). Therefore, Considering these two states using Bayes’ theorem, the connectivity reliability (\(\:R\)) of the natural gas pipeline network (\(\:G\)) can be expressed as:

$$\:\begin{array}{c}R=P\left(G|{e}_{i}\right){r}_{i}+P\left(G|\stackrel{-}{{e}_{i}}\right)\left(1-{r}_{i}\right)\end{array}$$
(12)

Where \(\:P\left(G|{e}_{i}\right),\:\:P\left(G|\stackrel{-}{{e}_{i}}\right)\) represents the connectivity reliability of network (\(\:G\)) when segment (\(\:{e}_{i}\)) is operational or failed.

From Eqs. (11) and (12), it can be seen that \(\:{I}_{r}\left({e}_{i}\right)\) is equal to the difference in the connectivity reliability of the network when the segment \(\:\left({e}_{i}\right)\) is operational versus when it is failed:

$$\:\begin{array}{c}{I}_{r}\left({e}_{i}\right)=P\left(G|{e}_{i}\right)-P\left(G|\stackrel{-}{{e}_{i}}\right)\end{array}$$
(13)

The (\(\:D\))-connectivity importance based on the minimum path set assesses the importance of each pipeline segment in the network’s topology by examining the frequency of the segment’s appearance in the minimum path set. The edge betweenness \(\:{D}_{b}\left({e}_{i}\right)\) reflects the contribution of each segment to the connectivity efficiency of the network38,39.

$$\:\begin{array}{c}{D}_{b}\left({e}_{i}\right)=\sum\:_{i\ne\:j=ei}\frac{{g}_{ij}\left({e}_{i}\right)}{{g}_{ij}}\end{array}$$
(14)

Where \(\:{g}_{ij}\) represents the number of minimum paths between node (\(\:i\)) and node (\(\:j\)); \(\:{g}_{ij}\left({e}_{i}\right)\) represents the number of minimum paths between node (\(\:i\)) and node (\(\:j\)) that include segment \(\:{e}_{i}\).

Due to the functional differences between nodes in the natural gas pipeline network, the definition of edge betweenness is modified to focus solely on the source and demand nodes in the network. The (\(\:D\))-connectivity importance is defined as \(\:{D}_{bi}\), as shown in Eq. (15).

$$\:\begin{array}{c}{D}_{bi}=\sum\:_{x\in\:S,\:y\in\:U}\frac{b\left({e}_{i}\right)}{b}\:\end{array}$$
(15)

where \(\:S\) denotes the set of source nodes; \(\:U\) denotes the set of demand nodes; \(\:b\) represents the number of minimum paths between source nodes and demand nodes; \(\:b\left({e}_{i}\right)\)​ represents the number of minimum paths between source nodes and demand nodes that include segment \(\:{e}_{i}\).

Thus, the average value of the probabilistic connectivity importance (\(\:{I}_{ri}\)) and the variance of the (D)-connectivity importance (\(\:{D}_{bi}\)) are used as constraints. (\(\:{D}_{b0}\)) and (\(\:{D}_{bmax}\)) represent the variances of the (D)-connectivity importance of pipeline segments before and after optimization, respectively. Similarly, (\(\:{I}_{r0}\)) and (\(\:{I}_{rmax}\)) represent the average values of the probabilistic connectivity importance before and after optimization, respectively.

Therefore, the average value of the probabilistic connectivity importance \(\:{I}_{ri}\) and the variance of the (\(\:D\))-connectivity importance \(\:{D}_{bi}\:\)are used as constraints. \(\:{D}_{b0}\)​ and \(\:{D}_{bmax}\)​ represent the variance of the (\(\:D\))-connectivity importance of the segments in the network before and after optimization, respectively; \(\:{I}_{r0}\)​ and \(\:{I}_{rmax}\)​ represent the mean values of the probabilistic connectivity importance before and after optimization, respectively.

Node degree constraint. Considering the fluid pressure and flow characteristics in actual pipeline networks, the degree of each node should be controlled. Based on the analysis of node degrees in natural gas networks in reference40, the degree is typically set to 3 or 4. The node degree ki​ represents the number of edges directly connected to node vi ​.\(\:\:{\:k}_{0}\)​ denotes the threshold for node degree, and \(\:{k}_{max}\)​ represents the maximum degree of nodes in the network, the node degree constraint (\(\:{k}_{max}=4\)) aligns with engineering practices to avoid hydraulic instability (ASME B31.8).

In summary, the constraints for the pipeline network topology optimization model are as follows:

$$\:\begin{array}{c}s.t.\left\{\begin{array}{c}\begin{array}{c}{x}_{ij}\in\:\left\{0,\:1\right\}\\\:{x}_{ij}={x}_{ji}\\\:{x}_{ij}=0,\left(i=j\right)\end{array}\\\:{x}_{ij}=1,\left({v}_{i}\:and\:{v}_{j}\:Directly\:connected\right)\\\:\begin{array}{c}{l}_{0}\ge\:{l}_{max}\\\:{D}_{b0}>{D}_{bmax}\\\:\begin{array}{c}{I}_{r0}>{I}_{rmax}\\\:{k}_{0}\ge\:{k}_{max}\end{array}\end{array}\end{array}\right.\end{array}$$
(16)

Model solution

The optimization of natural gas pipeline networks typically involves both discrete and continuous parameters. Genetic algorithms are well-suited for optimizing different types of parameters simultaneously. However, as the network scale increases, the convergence speed of the algorithm may decrease. The Adaptive Genetic Algorithm (AGA), an enhancement of traditional genetic algorithms, improves convergence speed and accuracy by simulating evolutionary processes and adapting to new model requirements. The components of the pipeline network topology are discrete values, which are conveniently encoded and decoded using binary coding. A random function rand is used to generate random numbers between [0,1], which are then rounded to integers to form an initial population of 0s and 1s. The fitness function \(\:F\left(x\right)\) is constructed using the reciprocal transformation method, as shown in Eq. (17). A penalty mechanism is introduced to guide the algorithm’s search direction, with penalty functions represented by Eqs. (18) and (19).

$$\:\begin{array}{c}F\left(x\right)=\frac{1}{1+c-f\left(x\right)}c\ge\:0,c-f\left(x\right)\ge\:0\end{array}$$
(17)
$$\:\begin{array}{c}{f}^{{\prime\:}\left(x\right)}=\left\{\begin{array}{c}f\left(x\right),\:\:x\:Satisfying\:the\:Constraints\\\:f\left(x\right)-\sigma\:P\left(x\right),\:\:x\:Handling\:Constraint\:Violations\end{array}\right.\end{array}$$
(18)
$$\:\begin{array}{c}P\left(x\right)=\sum\:_{j=1}^{m}{p}_{j}\left(x\right)=\sum\:_{j=1}^{m}max\left(0,{g}_{j}\left(x\right)\right)\end{array}$$
(19)

Where \(\:{f}^{{\prime\:}\left(x\right)}\) represents the new objective function without constraints; \(\:g\left(x\right)\) represents the constraints; \(\:P\left(x\right)\) denotes the penalty function, which depends on the constraints; σ is the penalty factor, which is dependent on the proportion of feasible solutions within the population. Allowing for some variation among individuals promotes biodiversity and prevents premature convergence. The penalty factor \(\:\sigma\:\) is dynamically adjusted, gradually eliminating infeasible solutions while preserving potentially high-quality genes.

The selection operation in genetic algorithms ensures the principle of “survival of the fittest,” which determines the search direction. The crossover operation generates new individuals towards optimal solutions, while the mutation operation maintains population diversity, prevents premature convergence, and enhances local search capabilities. The operators used in this study include: the selection operator—roulette wheel selection, the crossover operator—single-point crossover, and the mutation operator—bit-flip mutation. Prior to running the algorithm, the following parameters need to be set: population size N, crossover probability \(\:{p}_{c}\)​, mutation probability \(\:{p}_{m}\)​, and the number of iterations.

As discussed, improper values for these parameters can affect the algorithm’s convergence. Based on extensive literature review and existing research, the initial population size N is typically set between 20 and 200. The number of iterations is controlled manually based on the algorithm’s convergence. The crossover probability \(\:{p}_{c}\) and mutation probability\(\:{p}_{m}\)​ are determined adaptively by the genetic algorithm according to the characteristics of the individuals, as specified in Eqs. (20) and (21).

$$\:\begin{array}{c}{p}_{c}=\left\{\begin{array}{c}0.8\times\:\frac{{f}_{max}-{f}_{c}}{{f}_{max}-\stackrel{-}{f}},\:\:{f}_{c}\ge\:\stackrel{-}{f}\\\:0.8,\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{f}_{c}<\stackrel{-}{f}\end{array}\right.\end{array}$$
(20)
$$\:\begin{array}{c}{p}_{m}=\left\{\begin{array}{c}0.01\times\:\frac{{f}_{max}-{f}_{m}}{{f}_{max}-\stackrel{-}{f}},\:\:{f}_{m}\ge\:\stackrel{-}{f}\\\:0.01,\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{f}_{m}<\stackrel{-}{f}\end{array}\right.\end{array}$$
(21)

Where \(\:{f}_{max}\)​ denotes the maximum fitness value in the population; \(\:\stackrel{-}{f}\)​ represents the average fitness value of the population; \(\:{f}_{c}\) indicates the fitness value of the offspring produced by crossover; and \(\:{f}_{m}\)​ refers to the fitness value of the offspring node degree constraint resulting from mutation.

Results

The case data were obtained from the operational pipeline records of a provincial gas company covering the period from 2020 to 2022, following an anonymization process. The principles for network simplification are as follows:

  1. 1.

    Merge short pipelines that are on the same route;

  2. 2.

    Exclude pressure regulation stations, assuming their reliability to be 1.

Regional overview

Taking a regional natural gas network as an example, the pipeline spans 5,500 km with a total gas transmission capacity of 35 billion cubic meters per year. The network starts from the terminal station of the main gas pipeline or other gas supply points, and ends at various gas consumption nodes, such as city gate stations and starting points of downstream networks in the region.

This analysis indicates that the natural gas pipeline system in the region will become increasingly extensive and complex. Therefore, during future pipeline network modifications and expansions, technical and management departments should prioritize the reliability of the network’s topological structure. It is essential to enhance system reliability to ensure continuous operation even when certain pipelines experience failures, making pipeline network connectivity reliability a critical consideration.

In practical operations, various stations, compared to pipelines, typically exist in relatively uniform environments and cross fewer geographical regions, making failures less likely. Additionally, there is currently no long-term systematic failure data for stations in China. Therefore, the reliability of these system components is assumed to be 1, and they are not considered to influence calculations.

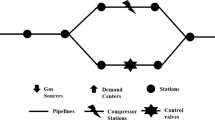
For networks that have multiple sources and multiple conduits, the nodes and conduits in the model can be complex. To maintain computational accuracy without compromising it, certain nodes and conduits can be simplified based on the principles of simplification outlined above. In the computer program, for ease of path search and subsequent matrix calculations, conduits are represented by segments labeled with weights r1, r2, etc. This representation includes the curved segment ε and numbering starts at 0. This study examines the regional gas transmission pipeline system in the region. By drawing on the distinctive topology characteristics of the gas pipeline network, the study neglects the internal structure of the pipelines and the direction of flow within them. The fully connected undirected graph of unisex nodes, as depicted in Fig. 3, comprises 89 nodes and 98 arc segments after the simplification process. Node classifications are indicated in Table 2.

Fig. 3
figure 3

Topology of the natural gas regional pipeline network in the region.

Full size image
Table 2 Node classification.
Full size table

The undirected connected graph of uniform nodes established is shown in Fig. 3, comprising 89 nodes and 98 arcs. The gas source nodes, marked in green, total 5, while the gas consumption nodes, marked in blue, total 36, and the other nodes, marked in yellow, total 48.

Connectivity reliability solution

The study investigates the connectivity reliability of a regional branch-loop mixed gas pipeline network, evaluated from the perspective of gas consumption nodes. Specifically, it involves calculating the connectivity reliability of a designated gas consumption node with at least one gas source. Taking node v2 as an example, Fig. 4. shows the connectivity reliability of the specified gas consumption node with at least one gas source.

Fig. 4
figure 4

Connectivity reliability of the specified gas node to at least one gas source.

Full size image

As shown in Fig. 4, the connectivity reliability of nodes within the loop structure is generally higher than that of nodes within the branch structure. The connectivity reliability of the gas consumption nodes v79 and v64 with at least one gas source is relatively low, at 0.60933 and 0.67573, respectively. The low connectivity reliability of node v79 is due to its ___location on a branch line of the network; when receiving natural gas from the source, every minimal path traversed includes segments e84, e85, e86, and e87, all of which are relatively long. Moreover, there is only one minimal path from node v79 to the nearest gas source node v71, meaning that if any segment in this path fails, the node will be unable to receive natural gas from the source.

Table 3 Source v0 to all sinks connectivity reliability.
Full size table

The connectivity reliability of nodes following v64 is also below the overall average reliability level of 0.87792, indicating a higher likelihood of disconnection in this area compared to others. This region exhibits poorer connectivity and structural redundancy.

From the perspective of the gas source and the system, Fig. 5. shows the connectivity reliability from a specified gas source to each gas consumption node. Taking gas source node v0 as an example, the reliability data from this source node to all gas consumption nodes are presented in Table 3.

Table 3. and Fig. 5. reveal that the connectivity reliability from gas source nodes v71, v4, v13, v0, and v51 to all gas consumption nodes are 0.13284, 0.778, 0.54359, 0.86926, and 0.96461, respectively. The average connectivity reliability to each gas consumption node from these gas sources are 0.93863, 0.98574, 0.99320, 0.99, and 0.99528, respectively.

For the single-source natural gas pipeline system with v51 as the gas source node, the connectivity reliability Rj​ and its average value are higher than those of the other four nodes, with a more uniform distribution of values. This indicates better connectivity and relatively stable performance of the gas source. The v51 node is located centrally within the pipeline network, resulting in fewer pipelines and stations to traverse compared to other nodes, which contributes to its higher connectivity level.

The connectivity reliability Rj​ from nodes v4 and v13 to all gas consumption nodes exhibits a similar trend, decreasing with increasing radius. This trend is attributed to the similar relative positions of nodes v0 and v4 within the actual pipeline network, resulting in similar distance trends to other junctions. The four nodes with the lowest connectivity reliability, as shown in the bar chart, are located at the ends of the four branch pipelines closest to the source nodes v4 and v13. These nodes are connected by only a single path without any redundant paths.

From the perspective of different gas source nodes, the gas consumption nodes with the lowest connectivity reliability are v79, v6, v9, v79, and v79, and v79. The low connectivity reliability of v79 is due to its ___location being far from the gas source node and its position on a branch of the tree-like pipeline structure. Although there are redundant paths, the paths traversed to receive natural gas are relatively long. Nodes v6 and v9 only have a single path for receiving natural gas, with no redundant paths. Nodes v83 and v85 are at similar distances from the gas source node in the actual pipeline network. However, the paths traversed by v83 are mostly within the tree-like structure, while v85 traverses paths predominantly within the ring-like structure. Generally, nodes located in the tree-like structure have lower connectivity reliability compared to those in the ring-like structure.

Assuming a reasonable probability of failure. In accordance with GB 50,251 − 2015, the pipe failure probability model parameters are characterized by the shape parameter \(\:\beta\:\)=2.1, and the scale parameter \(\:\eta\:\)=1.5 × 104 kilometers, which are in line with the actual failure statistics provided in Reference18. In the model, it is assumed that the reliability of the pressure regulation station is 1, which aligns with the statistical data showing a failure rate for regulation stations below 0.1%23.

Case data originates from anonymous operational records of a provincial gas company spanning 2020–2022, with network simplification principles including:

Merge short pipelines along the same route. Joining parallel pipelines with lengths less than 5 km, and eliminating redundant pressure regulation stations in accordance with ASME B31.8 standards. Supposing the reliability to be 1, the pressure regulation station is calculated based on the statistics where the actual failure rate is less than 0.1%.

Fig. 5
figure 5

Connectivity reliability between the specified gas source and the gas-using node.

Full size image

Topology optimization

The mathematical model for the pipeline network case study based on the Adaptive Genetic Algorithm is as follows:

$$\:\begin{array}{c}Max: {R}_{SU}=P\left\{\prod\:_{i=1}^{{n}_{s}}\prod\:_{j=1}^{{n}_{U}}\sum\:_{k=1}^{{n}_{Si,j}^{S}}{d}_{Si,j,k}^{s}\right\}\end{array}$$
(22)
$$\:\begin{array}{c}s.t.\left\{\begin{array}{c}\begin{array}{c}{x}_{ij}\in\:\left\{0,\:1\right\}\\\:{x}_{ij}={x}_{ji}\\\:{x}_{ij}=0,\left(i=j\right)\end{array}\\\:{x}_{ij}=1,\left({v}_{i}\:is\:directly\:connected\:to\:{v}_{j}\:\right)\\\:\begin{array}{c}{l}_{0}\ge\:{l}_{max}\\\:{D}_{b0}>{D}_{bmax}\\\:\begin{array}{c}{I}_{r0}>{I}_{rmax}\\\:{k}_{0}\ge\:{k}_{max}\end{array}\end{array}\end{array}\right.\end{array}$$
(23)

Where \(\:{n}_{s}\) represents the number of gas source nodes; \(\:{n}_{U}\) denotes the number of gas consumption nodes; \(\:{k}_{0}\)​ represents the minimum degree, with \(\:{k}_{0}\)=4; \(\:{k}_{max}\) indicates the maximum degree of nodes in the network; \(\:{l}_{max}\) refers to the maximum length of additional pipelines; \(\:{l}_{0}\) denotes the constraint on the length of additional pipelines, with \(\:{l}_{0}\)=120; \(\:{D}_{bmax}\) represents the variance of the D-connectivity importance of pipelines in the optimized network; \(\:{D}_{b0}\) denotes the variance of the D-connectivity importance of pipelines in the network before optimization, with \(\:{D}_{b0}\)= 0.03854; \(\:{I}_{rmax}\) indicates the average probability connectivity importance of pipelines in the optimized network; \(\:{I}_{r0}\) represents the average probability connectivity importance of pipelines in the network before optimization, with \(\:{I}_{r0}\)= 0.28622; \(\:{n}_{Si,j}^{S}\:\)denotes the number of shortest paths from source node \(\:{V}_{Si}\) to consumption node \(\:vj\:\)in the network \(\:Gs\); \(\:{d}_{Si,j,k}^{s}\) represents the \(\:k\)-th shortest path from source node \(\:{V}_{Si}\) to consumption node \(\:vj\) ​ in the network \(\:Gs\).​

The parameter settings can significantly impact the optimization results by determining the algorithm’s running efficiency and convergence behavior of the solution. Key parameters include population size, iteration count, crossover probability, and mutation probability. As each iteration progresses, the likelihood of finding the optimal solution increases, but this comes at the cost of increased running time. Excessive iterations could result in premature termination of the program without finding the optimal solution. Given the complexity of the problem and available computational resources, we have chosen 100 iterations. This paper employs an adaptive strategy for controlling fitness values when selecting the latter two parameters.

Table 4 Setting of relevant parameters in AGA.
Full size table

To study the impact of population size on optimization results, we set population sizes to 40, 80, 120, and 200, analyzing the solution results obtained under different initial population sizes. This enables us to determine the effect of initial population size on the algorithm’s solution results and identify the most suitable population size for practical applications. For each population size, 30 independent runs are conducted. Based on current research findings, when addressing the issue of network optimization, it is advisable to set parameters in accordance with the topology structure of the gas pipeline network and various constraints.

This should be done while taking into consideration the characteristics of genetic algorithms, as outlined in Table 4. The corresponding values for the objective function, computation time, and convergence generations are shown in Figs. 6, 7 and 8.

Fig. 6
figure 6

Scatterplot of the optimal objective function.

Full size image

By solving the optimization model with different population sizes, four sets of objective function values and their corresponding relationships with the number of iterations were obtained. As shown in Fig. 6, when the population size is set to 40, 80% of the solutions converge to a local optimum. With a population size of 80, over half of the solutions still converge to a local optimum, while 35% of the solutions can approach or converge to the global optimum.

Compared with traditional genetic algorithms (GAs). For dynamic parameter adjustment, traditional GAs employ fixed crossover/mutation probabilities24, which can easily get trapped in local optima. In this paper’s AGA, the \(\:{p}_{c}\) and \(\:{p}_{m}\) probabilities are dynamically adjusted based on individual adaptability (Eqs. 20,21), with the exploration ability enhanced when the population’s adaptability approaches the mean value and the local search strengthened when the adaptability is higher. As shown in Fig. 6, AGA exhibits improved convergence performance, with 80% of the optimized solutions converging to the global optimum when the population size is 120, compared to only 50% convergence for the traditional GA under the same conditions.

Tree Network: Simulating the generation of a tree network comparable in scale to the case study, consisting of 89 nodes. Ring Network: Utilizing a hybrid ring network comprising 89 nodes and 98 edges derived from a real-world case. Large-scale Network: Expanded to 200 nodes to validate the scalability of the algorithm. Each indicator comprises path search time, excess item reduction rate, reliability error, and convergence algebra. The definitions of each indicator are presented in Table 5.

Table 5 Performance index.
Full size table

As shown in Table 6, the traditional DFS method failed to handle the ring-shaped network within 300 s, while the proposed DFS and BDD framework completed the calculation in 25.4 s. The BDD algorithm reduced the exponential terms in Eq. (8) by 92%, significantly lowering computational complexity. Furthermore, the reliability result (\(\:{R}_{SU}\)=0.247) closely matched the Monte Carlo simulation (error = 0.05%), our AGA-based optimization demonstrated a 65% improvement in reliability.

Table 6 Comparison experiments of different methods.
Full size table

Increasing the population size to 120 significantly reduces the likelihood of convergence to a local optimum, with 80% of the objective function values converging to the global optimum. However, due to the inherent characteristics and randomness of the genetic algorithm, a few local optima are still present.

When the population size is set to 200, 90% of the objective function values stabilize within the 0.18–0.26 range, resulting in a better ability to achieve the global optimum solution.

Fig. 7
figure 7

Scatterplot of the optimal objective function.

Full size image

The relationship between the computation time and the number of iterations for different population sizes in the algorithm optimization model is shown in Fig 7. As seen in the figure, when the population size is set to 40 individuals, the computation time is generally below 3 s, averaging around 2 s. A comparison of the four corresponding graphs indicates that the computation time increases as the population size increases. Specifically, when the population size is increased to 200, the computation time rises above 45 s.

Fig. 8
figure 8

Scatterplot of the number of model iterations.

Full size image

Additionally, from the scatter plots in Fig. 8, it is evident that when using the genetic algorithm for model solving, there is no significant relationship between the population size and the evolution speed of individuals within the population.

From the above figures, it can be observed that when the initial population size is small, the model-solving speed is faster but tends to converge to a local optimum. Conversely, a larger initial population size slows down the solving speed but facilitates better convergence, thereby enhancing the algorithm’s global search capability and leading to a more optimal global solution. Therefore, considering both model runtime and convergence, a population size of 120 is set for the optimization model in this case study.

Discussion

Using the designed optimization program, the topological structure optimization model for the regional natural gas pipeline network was successfully solved. After gene encoding, generating the initial population, and performing a series of genetic algorithm operations (selection, crossover, and mutation), the program’s results are shown in Fig. 9. This figure shows the variation in the objective function’s reliability with respect to the number of iterations in the genetic algorithm.

Fig. 9
figure 9

Iterative process of pipe network optimization.

Full size image

As shown in Fig. 9, using the improved genetic algorithm to solve the optimization model, the solution converged and stabilized after 30 generations, yielding the optimal solution. The pipeline network’s connectivity reliability increased from 0.03 to 0.247. In contrast to particle swarm optimization (PSO) algorithms as presented in literature24, the PSO algorithm of said reference minimizes investment costs but disregards reliability constraints. Our model incorporates constraint violations through a penalty function (Eq. 19), translating these violations into adaptability penalties, enabling multi-objective optimization with both reliability improvement and new pipeline length restrictions. Case study results demonstrate that the reliability increase of AGA (0.03 to 0.247) is significantly higher than the maximum achievable increment in PSO under similar constraints.

With the goal of maximizing the network’s connectivity reliability, the optimization algorithm ultimately determined the optimal locations for adding pipeline segments between nodes v77 and v71, and between nodes v7 and v11. These locations are depicted as red dashed lines in the topological map, as shown in Fig. 10.

Fig. 10
figure 10

Algorithm-optimized ___location of additional pipe segments.

Full size image

From the perspective of gas consumption nodes, the connectivity reliability of nodes located on ring structures is generally higher than that of nodes on branch structures. Specifically, the connectivity reliability of gas consumption nodes beyond node v64 is below the overall average. These nodes are situated on branch structures of the pipeline network, with longer minimum path lengths, making them more prone to disconnection compared to nodes in other areas. From the perspective of gas sources, the connectivity reliability of the v51 gas source node is higher than that of other gas source nodes, followed by v0. This is because the v51 gas source node is centrally located within the pipeline network, resulting in shorter traversal path lengths to reach each gas consumption node.

In contrast, when a segment on a branch pipeline fails, there are no redundant pathways available to maintain connectivity. The segments with higher D-connectivity importance include e64, e65, e0, and e1, which contribute more significantly to the overall connectivity reliability of the network compared to other segments.

Fig. 11
figure 11

Comparison of connectivity reliability before and after optimization.

Full size image

Figure 11 illustrates that the connectivity reliability of the pipeline network before optimization was 0.03, with a mean value of probability connectivity importance of 0.28622 and a variance of D-connectivity importance of 0.03854. After optimization, the connectivity reliability increased to 0.247, the mean value of probability connectivity importance improved to 0.25031, and the variance of D-connectivity importance decreased to 0.03342. This comparison between the original and optimized networks indicates that the new topology enhances the overall system’s connectivity reliability, thus demonstrating the feasibility and effectiveness of the optimization methods and strategies outlined in Chap. 4.

The redundancy advantage of ring structure lies in its topology, loop structures inherently provide higher reliability due to redundant connectivity paths. For example, node v79 on a branch relies on a single path (e84 to e87), leading to low reliability (\(\:Rj\)= 0.60933). In contrast, loop nodes maintain multiple paths, ensuring resilience to single-segment failures (average \(\:Rj\) = 0.87792). This aligns with the D-connectivity importance metric (Eq. 15): loop segments (e64, e65) appear in more minimal paths, contributing significantly to network-wide reliability.

The AGA dynamically adjusts crossover/mutation rates (Eq. 20 to 21) based on population diversity. Early iterations prioritize exploration (high pc/pm), while later stages focus on local refinement. This adaptability enabled 80% global convergence (population size = 120, Fig. 6), outperforming static GAs (50% convergence). Unlike traditional methods, AGA’s penalty function (Eq. 19) strictly enforces constraints (\(\:{k}_{max}\)= 4), ensuring hydraulic stability without sacrificing reliability.

AGA vs. PSO: reliability-centric optimization, AGA achieved a 65% higher reliability gain (\(\:{R}_{SU}\): 0.03—0.247) than PSO ((\(\:{R}_{SU}\)= 0.15). Key differences include: AGA prioritizes reliability via penalty functions, while PSO focuses on cost reduction. AGA’s BDD-enhanced path search reduced computational terms by 92% (Table 6.), enabling efficient handling of 200-node networks. Constraint Compliance: AGA dynamically balances penalties (Eq. 18), whereas PSO treats constraints as secondary.

Conclusion

This study, based on graph theory and complex network reliability theory, focuses on regional natural gas pipeline networks. It establishes a connectivity reliability assessment model and a topology optimization model for natural gas pipelines. Through case study analyses, the feasibility and effectiveness of the models have been validated, providing valuable references for pipeline network design and maintenance.

Given the complexity of the pipeline network structure, a depth limit is set for minimum path search to backtrack upon reaching the threshold, thereby addressing potential issues of parallel multi-line configurations. Considering the exponential relationship between the number of minimum paths and the terms in the reliability formula, the BDD algorithm is employed to enhance the minimum path disjointness computation, eliminating redundant terms. These improvements to both algorithms broaden the applicability of the model developed in this study.

Based on the topological connectivity reliability evaluation model of the natural gas pipeline network system, the analysis of four indicators—namely, the connectivity between specified consumption nodes and at least one gas source, the connectivity of all consumption nodes with at least one gas source, the connectivity between specified gas sources and all consumption nodes, and the connectivity between all gas sources and all consumption nodes—reveals the following: Connectivity reliability increases with a higher number of paths between the same source-sink pairs. However, when the minimum number of paths between different source-sink pairs is equal, connectivity reliability decreases as path length increases. Source nodes positioned centrally within the network exhibit higher connectivity reliability. Moreover, consumption nodes located on ring pipelines exhibit higher connectivity reliability compared to those on branch pipelines. Consequently, shorter paths better ensure connectivity between source and sink points, and converting branch pipelines into ring structures with structural redundancy significantly enhances the network’s connectivity reliability.

A mathematical model for optimizing the topological structure of the natural gas pipeline network was established, with the objective function set to maximize connectivity reliability. The model incorporates constraints on uniqueness of affiliation, pipeline length, node degree, and segment importance, and employs a penalty function algorithm to handle these constraints. The Adaptive Genetic Algorithm (AGA) was used to solve the optimization model. Analysis of the initial population size’s impact on the algorithm’s performance determined that a population size of 120 was optimal. The final solution from the program indicated that adding pipeline segments between nodes v71 and v77, as well as between nodes v7 and v11, transformed branch pipelines into a ring structure. This optimization increased the network’s connectivity reliability from 0.03 to 0.247, demonstrating the effectiveness of the optimization model and providing valuable insights for the design and modification phases of natural gas pipeline networks.