Introduction

Binary optimization has been applied to a wide range of applications across various fields, from network design in telecommunications1,2,3 and vehicle routing in transportation4,5,6 to structural optimization in material sciences7,8,9,10,11,12,13,14. Various strategies have been used for binary optimization, such as discrete particle swarm optimization (DPSO)5,15, genetic algorithm (GA)16,17, quadratic unconstrained binary optimization (QUBO)8,9, and artificial bee colony (ABC)18,19. Recently, an active learning scheme has been proposed to efficiently solve binary optimization tasks to accelerate the discovery of optimal designs in the field of nanophotonics (e.g., planar multilayer (PML) structures, stratified grating systems)7,8,9,11,12,13,14 and material science (e.g., high-entropy alloys)10. This active learning method is iterative and actively accumulates a sparse training dataset consisting of binary vectors and the associated figure-of-merits (FoMs). It uses a second-order factorization machine (FM)20 to project the design task onto a QUBO model with the training dataset, then leverages quantum annealing (QA)21 to quickly solve the QUBO problem. For example, Kitai et al.7 and Kim et al.8 used the FM-based active learning to design radiative coolers using 40-dimensional binary vectors. They identified an optimal structure with 2000–5000 iterations, which cover ~ 10–7% of all the possible binary vector states.

The key to the active learning scheme is that a machine learning model can accurately capture the N-dimensional hypervolume of the original binary space near the global and local optima with the actively accumulated sparse training dataset 22,23. Here, the optimum refers the optimal binary vector yielding the minimum or maximum FoM, or close to it; essentially, it is the point that achieves the target objective. Thus, in each iteration, the formulated machine learning surrogate model should be optimized to identify the best candidate binary vector, which is hopefully near the global optimum. The identified candidate binary vector is then accumulated in the training dataset, which is important for iteratively refining the model and improving its accuracy. However, the FM-based surrogate model in active learning has limitations. The surrogate model (i.e., QUBO model) constructed by the FM includes only linear and quadratic terms, which cannot capture higher-order interactions (e.g., third order, fourth order, and so on) in the N-dimensional hypervolume space20,24. Consequently, while the QA can identify the best candidate binary vector from the formulated QUBO model, this vector may not be of high quality due to the limitations of the FM in describing the optimization hyperspace.

On the other hand, convolutional neural networks (CNNs), which are traditionally used for image processing tasks25,26 such as image classification and object detection, can act as surrogate models to approximate complex objective functions. As CNNs are well-suited for feature hierarchies thus efficiently extracting interactions in discrete input variables, they can potentially capture the complexity of the N-dimensional hypervolume of the binary space with multiple convolutional layers and activations. However, CNNs are a feed-forward neural network where data flows in one direction from the input layer to the output layer27. The optimization of CNN-based surrogate models, therefore, has to leverage external optimization strategies (e.g., DPSO, ABC, or GA), which are often trapped in local minima or maxima as the dimension of the binary space increases28. Recently, Partel et al.29 proposed the so-called ‘extremal learning,’ which identifies the inputs that minimizes (or maximizes) the output of a neural network in regression problems with frozen parameters (e.g., weights and biases). Extremal learning is, however, designed specifically for continuous variable inputs. Thus, it is not yet known whether the extremal learning is effective for discrete-variable input (i.e., binary input). Additionally, formulating accurate surrogate models based on CNNs may be more computationally expensive than those based on FMs for supervised learning (e.g., CNNs may require more training data than FMs)30.

In this study, we propose an inverse binary optimization (IBO) scheme to enhance a CNN-based surrogate function within active learning frameworks and demonstrate its performance in optimizing nanophotonic structures. The IBO employs an extremal learning approach to fix the parameters of a pre-trained CNN while introducing soft variables to identify the optimal input binary vector via backward propagation. Using the CNN-IBO active learning scheme, we optimize a PML structure designed to transmit visible light in the solar spectrum, with binary vectors of length up to N = 40. We benchmark the performance of the CNN-IBO against conventional binary optimization methods, such as DPSO and exhaustive enumeration, and study the influence of parameters like the IBO learning rate. For binary vectors of length N ≥ 40, we apply the CNN-IBO active learning to design various nanophotonic applications, including visible-light filter based on PML structure and asymmetric-light transmitters based on stratified grating structure, and compare the results with the FM-QA method. We find that CNN-IBO can achieve optimal designs with fewer optimization cycles (i.e., a smaller number of training datasets) than FM-QA, highlighting its potential as a promising alternative in binary optimization.

Model and method

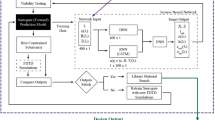
The binary optimization to design nanophotonic structures is based on the active learning scheme (see Fig. 1a), which consists of the following steps: (i) accumulating the training dataset (\(X\)) consisting of binary vectors (\({\overrightarrow{x}}_{i}\in {\left[\text{0,1}\right]}^{N}\)) and associated outputs (i.e., FoMs) (\({y}_{i}\in {\mathbb{R}}_{\ge 0}\)), \(X=\left\{\left({\overrightarrow{x}}_{1},{y}_{1}\right),\dots ,\left({\overrightarrow{x}}_{l},{y}_{l}\right)\right\}\); (ii) formulating a surrogate function (\({\widehat{y}}_{i}=f({\overrightarrow{x}}_{i})\)) with the training dataset; (iii) optimizing the surrogate function to discover a candidate of the optimal binary vector (\({\overrightarrow{x}}_{*}\)) that minimizes the surrogate function (\({\overrightarrow{x}}_{*}={\text{argmin}}_{{\overrightarrow{x}}}f({\overrightarrow{x}})\) or \({\widehat{y}}_{*}=f({\overrightarrow{x}}_{*})\)); (iv) evaluating the candidate vector by solving Maxwell’s equations (e.g., transfer matrix method, TMM). If the candidate vector is already included in the training dataset, a randomly generated binary vector and the associated FoM are added instead; (v) updating the training dataset, and repeating steps (ii), (iii), and (iv). Further details of the active learning scheme can be found in References8,9. It is noted that the active learning scheme utilizes both exploration and exploitation, since the training dataset used for formulating a surrogate function contains both discovered binary vectors and randomly generated binary vectors.

Fig. 1
figure 1

Active learning using convolutional neural networks (CNN) and inverse binary optimization (IBO). (a) An active learning scheme consisting of five steps to automatically identify the optimal nanophotonic structure. (b) A schematic of the CNN framework for pre-training step, depicted in step (ii) of the active learning scheme. The framework consists of two parts: convolutional (Conv) layers and fully-connected (FC) layers. (c) A strategy for IBO of a pre-trained CNN with backward propagation of error, depicted in step (iii) of the active learning scheme. The sky-blue colored nodes indicate fixed parameter values in the Conv and FC layers.

Full size image

The surrogate function is based on a CNN (see Fig. 1b) consisting of the input layer with N nodes, convolutional (Conv) layers (i.e., kernel 1-Conv1 layer, kernel 2-Conv2 layer, etc.), fully-connected (FC) layers (i.e., FC1 layer and FC2 layer), and the output with a single node. In the initial layers, a kernel with the size of five was utilized to extract features from a broader receptive field. In the deeper layers, a kernel with the size of three was employed to increase the depth of network, allowing it to learn more complex and diverse features. For step (iii), an IBO strategy is used (see Fig. 1c) by freezing parameters in the trained CNN, where the IBO can identify \(\vec{x}_{*}\) yielding \(\hat{y}_{*}\) by introducing the soft variable vector \(\vec{z}_{ } = \left\{ {z^{1} , z^{2} ,...,z^{N} } \right\} \in \left[ {{\mathbb{R}}_{ \ge 0} } \right]^{N}\) with gradient descent as:

$$\begin{aligned} \left( {z^{m} } \right)_{t + 1} & = \left( {x^{m} } \right)_{t} - Lr {\text{A}}\left( {\frac{{\partial E\left( {\theta ,{\vec{\text{z}}}} \right)}}{{\partial z^{m} }}} \right), \\ \left( {x^{m} } \right)_{t + 1} & = \left\{ {\begin{array}{*{20}c} {1,\;\left( {z^{m} } \right)_{t + 1} \ge 0.5} \\ {0,\;\left( {z^{m} } \right)_{t + 1} < 0.5} \\ \end{array} } \right. , \\ \end{aligned}$$
(1)

where \(\left( {z^{m} } \right)_{t}\) is the m-th element of \(\vec{z}_{ }\) at iteration t in the gradient descent, \(x^{m}\) is the m-th element of \(\vec{x}_{*}\), \(Lr\) is the learning rate, \({\text{A}}\) is the function for adaptive moment estimation (i.e., Adam optimizer31), and \(E\left( {\theta ,{\vec{\text{z}}}} \right)\) is the error function which can be defined as:

$$E\left( {\theta ,{\vec{\text{z}}}} \right) = a ,{\text{ where}} \hat{y} = f\left( {{\vec{\text{z}}}} \right) ,$$
(2)

where \(\theta\) denotes the collection of the weights and biases, which are frozen, in the formulated CNN-based surrogate function. The calculation of the gradient of the error function \(E\left( {\theta ,{\vec{\text{z}}}} \right)\) with respect to each element (\(z^{m}\)) of \({\vec{\text{z}}}\) can be performed by leveraging backward propagation of errors as:

$$\begin{aligned} \frac{\partial E}{{\partial {\text{z}}^{m} }} & = \mathop \sum \limits_{l}^{{L_{1,m} }} \frac{\partial E}{{\partial \alpha_{l}^{1} }}\frac{{\partial \alpha_{l}^{1} }}{{\partial {\text{z}}^{m} }}, \\ \frac{\partial E}{{\partial \alpha_{j}^{k} }} & = \mathop \sum \limits_{l}^{{L_{k + 1,j} }} \frac{\partial E}{{\partial \alpha_{l}^{k + 1} }}\frac{{\partial \alpha_{l}^{k + 1} }}{{\partial \alpha_{j}^{k} }},\quad {\text{for}}\;1 \le k < D \\ \frac{\partial E}{{\partial \alpha_{1}^{D} }} & = \hat{y}\frac{{\partial g_{o} }}{{\partial \alpha_{1}^{D} }}, \\ \end{aligned}$$
(3)

where \(\alpha_{j}^{k}\) is the product-sum-plus-bias for node j in layer k, \(L_{k,m} is\) a specific set of nodes in layer k connected to node m in layer k−1, and \(g_{o}\) is the activation function of the output layer (D-th layer).

Result and discussion

Benchmarking study of IBO in active learning scheme

To benchmark the performance of IBO in active learning, we selected the design task of a visible-light filter with a PML structure in the solar spectrum as a testbed. This PML structure is supposed to perfectly transmit visible photons while reflecting ultraviolet and near-infrared photons in the solar spectrum (see Fig. 2a), which is challenging in terms of design due to the large parametric space8. This design task was first introduced in the reference8, where active learning was used with the FM-QA method. In our study, we aim to overcome the limitations of the FM-based surrogate function in active learning by proposing the CNN-IBO. Given the variety of binary optimization tasks, our choice of the visible-light filter as a testbed is intentional, as it allows us to focus on this specific design task to compare the optimization performance between the FM-QA and the CNN-IBO. The PML has a thickness of 1200 nm, which is divided into an N number of pseudo layers. Each pseudo layer is either SiO2 or TiO2, assigned to a binary digit of ‘1’ for SiO2 and ‘0’ for TiO2. This allows a PML structure to be encoded as a binary vector \(\vec{x}_{i} \in \left[ {0,1} \right]^{N}\). The output \(y_{i}\) for a binary vector can be calculated as

$$y_{i} = \frac{{10\int_{{\uplambda _{{\text{i}}} }}^{{\uplambda _{{\text{f}}} }} {\left[ {{\text{S}}\left( \uplambda \right)\left( {T\left( \uplambda \right) - T_{{\text{I}}} \left( \uplambda \right)} \right)} \right]^{2} {\text{d}}\uplambda } }}{{\int_{{\uplambda _{{\text{i}}} }}^{{\uplambda _{{\text{f}}} }} {{\text{S}}\left( \uplambda \right)^{2} {\text{d}}\uplambda } }}$$
(4)

where \(T\left( {\uplambda } \right){ }\) and \(T_{{\text{I}}} \left( {\uplambda } \right)\) are, respectively, the transmittance of the designed and target PML, and \({\text{S}}\left( {\uplambda } \right)\) is the AM 1.5G solar spectrum, \({\uplambda }\) is the wavelength of the incident photon, \({\uplambda }_{{\text{i}}}\) and \({\uplambda }_{{\text{f}}}\) are 300 nm and 2500 nm, respectively. In Eq. (4), a smaller output (\(y_{i}\)) is preferred for the PML structure (e.g., an ideal visible-light filter has \(y_{i}\) = 0). \(T\left( {\uplambda } \right){ }\) is obtained by solving Maxwell’s equations with the transfer matrix method. The active learning starts with an initial dataset of 25 (i.e., \(X = \left\{ {\left( {\vec{x}_{1} ,y_{1} } \right), \ldots ,\left( {\vec{x}_{l} ,y_{l} } \right)} \right\}\), l = 25), and stops at l = 2025 (for N = 16, 20, and 24) and l = 3025 (for N = 32, and 40) for the benchmarking study.

Fig. 2
figure 2

Benchmarking study of CNN-IBO-based active learning. (a) (Top) Schematic model of the planar multilayer (PML) structure for the benchmarking study. (Bottom) The target transmitted irradiance as a function of wavelength. The background grey-colored area shows the AM1.5 G solar spectrum. (b–f) The optimized output (\({\widehat{y}}_{*}\)) of the CNN-based surrogate function by the IBO method as a function of the optimization cycle at (b) N = 16, (c) N = 20, (d) N = 24, (e) N = 32, and (f) N = 40. For comparison, the optimized outputs by the exhaustive enumeration (EE) method and the discrete particle swarm optimization (DPSO) method are also shown. For (b–f), the right panel shows the projected density of optimized outputs over optimization cycles: (blue) DPSO, (black) EE, (red) IBO. (g) The minimum output (\({y}_{i}\)) in the training dataset as a function of the optimization cycle using CNN-IBO-based active learning at various N = 16, 20, 24, 32, and 40.

Full size image

The benchmarking results are shown in Fig. 2b–f, where active learning with IBO was performed for N = 16, 20, 24, 32, and 40. The results plot the output (\(\hat{y}_{*}\)) of the surrogate function for the identified optimal binary vector (\(\vec{x}_{*}\)) as a function of optimization cycles. For comparison, exhaustive enumeration (EE) and discrete particle swarm optimization (DPSO) were also used to optimize the surrogate function at each optimization cycle, and their results were also plotted. The EE method can identify the global optimal vector of the surrogate function, but it is limited by computational resources. In our study, for N > 24, the EE method could not be used due to the computational limitations (e.g., insufficient random-access memory). DPSO, a meta-heuristic method, is known to efficiently solve binary optimization problems. In Fig. 2a, for N = 16, 20, and 24, it is seen that the optimized outputs by the IBO method are very close to the global minimum identified by the EE method and are lower than those obtained by DPSO. It is evidenced by the density-of-output distributions (see the sub-panels on the right side of each panel in Fig. 2a), showing that the distributions for IBO and EE nearly coincide each, while those for DPSO deviate and show higher values. The deviation becomes more pronounced for N = 32 and 40. These results demonstrate that IBO can efficiently discover the optimal binary vector close to the global solution of the surrogate function, indicating its methodological compatibility with the CNN-based surrogate function. We note that for N = 32 and 40, it could not be verified whether the optimized outputs by the IBO method are close to the global optimal values since EE is too computationally expensive to be performed to find the absolute global minimum.

The results of active learning with IBO are shown in Fig. 2g. This figure tracks the minimum of the output (\(y_{i}\)) in the training dataset as a function of the optimization cycles, referred to as the “\(y_{min}\) history plot” for each N case. The \(y_{min}\) history plot demonstrates a continuous reduction of \(y_{min}\) as the number of the optimization cycle increases, a characteristics typically observed in the previous studies using active learning8. For N = 16, we verified that active learning identified the global optimal binary vector, which is identified by calculating the outputs for all binary vectors using TMM (see Figure S1 in Supporting Information), indicating that the CNN-IBO can find the global optimal point through exploration and exploitation. As the length of the binary vector increases, active learning discovers better structures yielding lower output values. Specifically, the case of N = 40 (or 32) achieved much better optimized structure than that of N = 20 (or 16). These results indicate that active learning with CNN-IBO effectively optimizes the design of the PML structure for the given target function. We also investigated the feature map of the CNN-based surrogate function at N = 24 (see Figure S2 in Supporting Information). The colored visualization of the first convolutional layer reveals the characteristics of binary input variables, while the visualization of the last layer shows a distinguishable distribution that varies with the FOM values. Specifically, the color distributions for input binary vectors associated with lower FOM values are similar to one another, indicating that the CNN effectively captures the parametric space relevant to the design task. This suggests that the CNN is capable of generalizing across inputs with similar conditions, an important aspect of its ability to model the underlying design parameters accurately.

On the other hand, the performance of the IBO depends on the learning rate (\(Lr\)) of the gradient descent. We investigated the error function (\(E\)) as a function of the gradient descent iteration (t in Eq. (1)) with various \(Lr\) values: 0.25, 0.5, 1.0, and 2.0 for N = 24, as shown in Fig. 3. For each iteration, the error function value at the locally optimized soft variable is depicted as blue dots, while the value for the projected binary space (i.e., local optimal binary vector) is shown as red dots. At learning rates of 0.25 and 0.5, the IBO appears to be trapped in a local optimum (a local optimal binary vector) after t = 100, which cannot be overcome by additional iterations. At the learning rate of 1.0, the trapping issue is not observed. The IBO identifies various local optimal binary vectors as well as optimized soft variables, with the error function values continuously decreasing as the number of iteration increases. At a higher learning rate of 2.0, the optimization performance is slightly compromised, resulting in slightly higher optimal error function values compared to those at \(Lr\) = 1.0. These results suggest that an appropriate learning rate should be determined to maximize the performance of the IBO.

Fig. 3
figure 3

The IBO characteristics depending on the learning rate (Lr). (a–d) The output of the error function as a function of the iteration of the IBO method at various (a) Lr = 0.25, (b) Lr = 0.5, (c) Lr = 1, and (d) Lr = 2. The surrogate function used for (a) to (d) is a pre-trained CNN at N = 24 and the 2,205 training dataset. The global minimum is obtained by the EE method.

Full size image

Performance comparison between CNN-IBO and FM-QA methods

Next, we compare the performance of active learning with CNN-IBO to the FM-QA method. For this comparison, we selected two distinct design tasks studied in Refs. [8,9]: optimizing a PML structure with four material bases (SiO2 = 00, Si3N4 = 01, Al2O3 = 10, TiO2 = 11) for the given output function of Eq. (2); and identifying a one-dimensional stratified grating (OSG) structure that achieves asymmetric-light transmittance with the output function, given by : \(1-({T}_{F}-{T}_{B})\), where \({T}_{F}\) (or \({T}_{B}\)) is the forward (or backward) transittance at the wavelength of 600 nm. For the PML task, the structure is assumed to consist of twenty-four pseudo layers, each with a thickness of 50 nm, resulting in N = 48 (424 = 248) (see Fig. 4a). For the OSG task, the grating has a unit cell with a periodic length of 450 nm. The unit cell consists of five thin layers: the middle layer has a thickness of 50 nm, while the other layers each have a thickness of 20 nm. Each layer is discretized into ten rectangular pixels, except the middle layer (see Fig. 4b). A rectangular pixel can be either dielectric (air for the top layer, otherwise SiO2) or Ag, and can be assigned ‘0’ for dielectric or ‘1’ for Ag. This configuration of OSG can be encoded as a binary vector with a length of N = 40. We noted that the learning rates for these two different design tasks were optimized and set to ‘Lr = 1.0’ for both cases (see Figure S3 in Supporting Information).

Fig. 4
figure 4

Performance comparison between the CNN-IBO and FM-QA methods for designing various nanophotonic structures. (a) and (b) The minimum output in the training dataset as a function of the optimization cycle for designing (a) a visible-light filter based on PML and (b) an asymmetric-light transmitter based on a one-dimensional stratified grating (OSG). The data for FM-QA in (a) is from Ref. [8] and in (b) from Ref. [9]. The green-colored dotted line depicts the mean value of the minimum outputs from five different optimizations using CNN-IBO. The green-colored area represents the range of maximum and minimum values, with the minimum value is highlighted by a solid line. Insets: schematics of nanophotonic structures and encoding strategies. The green (or orange) arrow indicates the schematic of the optimized structure using the CNN-IBO (or FM-QA) method. (c–f) The parity plots of CNN-based and FM-based surrogate functions for cases (a) and (b). The datasets used for the parity plots are from the results of CNN-IBO in (a) and (b). (g) The transmittance irradiance of the optimized PML structure using FM-QA and CNN-IBO as a function of wavelength. (h) The forward and backward transmittance of the optimized asymmetric-light transmitter using FM-QA and CNN-IBO as a function of wavelength.

Full size image

We investigated the \({y}_{min}\) history plots of the CNN-IBO for the design tasks, as shown in Fig. 4a, b. The history plots of the FM-QA are sourced from Ref.8 for the PML tasks and Ref.9 for the OSG tasks. The CNN-IBO method was tested with five trials each for both the PML and OSG tasks, and the history plots display statistical data, including the average, minimum, and maximum values, as a function of the optimization cycles. In both cases, the CNN-IBO effectively minimizes the \({y}_{min}\) values, leading to rapid convergence in the history plots as optimization cycles increase. It is evident that the CNN-IBO achieves convergence with fewer optimization cycles compared to the FM-QA across all trials. This consistent performance is observed in both the PML and OSG tasks despite differences in their respective hypervolume spaces. We also investigated the parity plots for both cases, as shown in Fig. 4c–f. For the parity plots, we used the dataset at the optimization cycle of 3000, actively accumulated by the CNN-IBO. In the selected dataset, 80% is used for formulating the CNN (or FM) surrogate function, and 20% is used for validation. It is clear that the CNN-based surrogate function possesses better accuracy than the FM-based surrogate function. The CNN surrogate function for the PML task has an R2 score of 0.997 for the training set and 0.917 for the validation set, and for the OSG task, it has an R2 score of 0.997 for the training set and 0.876 for the validation set. These scores are much higher than those of the FM cases (see Fig. 4d, f), and the scores of the validation set are generally considered a good fit. This is also supported by the stable training curves of the validation and training data sets (see Figure S4 in Supporting Information), where early stopping was applied based on the validation loss to prevent overfitting. It is noted that the R2 score value of the validation data depends on the volume of the CNN, the architecture (e.g., deep neural network, DNN), or the training criterion (e.g., regularization) (see Figure S5 in Supporting Information). With the reduced volume CNN, the R2 scores of the validation set are 0.9150 for the visible-light filter case and 0.8565 for the asymmetric-light filter case, which are similar but slightly lowered. The DNN and CNN with regularization cases show a noticeable drop in the R2 scores of the validation set, ranging from 0.82 to 0.87, which are, however, still acceptable values. These results indicate that the CNN-IBO method not only effectively captures the N-dimensional hypervolume space but also performs robustly regardless of the specific characteristics of the hypervolume. It also suggests that the CNN can better describe the complexity of the hypervolume of binary space near the optimal point, accounting for the observed optimization performance of the CNN-IBO compared to the FM-QA in the history plots in Fig. 4a, b. We noted that QA is expected to identify the global optimal binary vector (or a local optimal vector very close to the global point) of a given QUBO problem 21,32,33,34,35,36. Thus, it is reasonable to assume that the performance of the FM-QA method is limited by the accuracy of the FM surrogate model.

The converged (\({y}_{min}\)) values identified by the CNN-IBO for both PML and OSG tasks are similar to those obtained by the FM-QA, indicating comparable optical performance. However, the optimal structures identified by the CNN-IBO differ from those by the FM-QA. For instance, the PML structure from the CNN-IBO is “00 00 11 11 01 01 00 00 00 00 11 11 00 00 00 11 11 00 00 00 11 11 00 00”, whereas the FM-QA identifies “11 11 00 00 00 11 11 00 00 00 11 11 00 10 10 11 11 11 11 10 10 10 11 11”. Despite these structural differences, the transmitted irradiance spectra are very similar (see Fig. 4g), with slight variations between 830 and 860 nm. This characteristic is also observed in the OSG task, where the optimal configurations differ, yet the forward and backward transmittance remain similar (see Fig. 4h). These results imply the existence of multiple local optima with similar optical performance but different structural configurations. In CNN-IBO, for example, the number of locally optimal binary vectors with an output < 1.1 \(\times {y}_{min}\) is 83 for the PML task and 6 for the OSG task. This abundance of viable structures may provide users with a degree of freedom in their choice, allowing them to select based on factors like fabrication costs or specific constraints, such as material availability, manufacturing precision, or structural stability.

Conclusion

In conclusion, the CNN-IBO active learning method effectively optimized the design tasks of PML structures by mapping them onto binary optimization problems. For 16 \(\le\) N \(\le\) 40, the CNN-IBO method demonstrated conventional characteristics of binary optimization using an active learning scheme and efficiently identified optimal PML-based visible-light filter. Within the active learning framework, IBO discovered optimal binary vectors with significantly lower output values compared to the DPSO method for a given CNN-based surrogate function. For higher dimensions (N \(\ge\) 40), the CNN-IBO method needed fewer optimization cycles than the FM-QA method to identify the optimal designs of visible-light filter and asymmetric-light transmitters. This efficiency is attributed to the capability of the CNN-based surrogate function to capture the complexity of the hypervolume in binary space. However, further investigation is needed to assess the performance of IBO in very high-dimensional binary optimization (e.g., N ~ 100). Additionally, the performance of the IBO should be examined for various kinds of binary optimization problems, and the current strategy of the IBO, which leverages continuous variables and rounds back to binary values, may need to be modified or improved. The IBO method can also be applied to optimize discrete variable or hybrid (e.g., discrete and continuous) variable optimization problems by leveraging deep neural networks. Also, the active learning with the CNN-IBO strategy can be applied to structural design tasks compatible with discrete or binary optimization. For example, lattice optimization37, including high-entropy alloys and quaternary semiconductor alloys, can leverage active learning with the CNN-IBO method. Each atom can be mapped with binary digits, and their optimal composition for a good figure-of-merit may be identified. A different architecture, such as a DNN-based surrogate function, can alternatively be used for the CNN-based surrogate model, which can potentially leverage the IBO strategy for optimization.