Introduction

Permeability is a key parameter for reservoir evaluation, and the accuracy of this parameter calculation will directly affect the development effect of the reservoir. Due to the strong heterogeneity and complex pore structure of carbonate reservoirs, the traditional permeability interpretation model established by logging data has been unable to meet the needs. Therefore, how to use logging data to accurately predict the permeability of carbonate reservoirs is also a major difficulty in current research1,2,3,4.

At present, the traditional carbonate reservoir permeability calculation model mainly adopts the idea of clastic reservoir evaluation, using the correlation between core porosity and permeability to derive the permeability calculation model, or using the empirical formula of permeability, but the two methods are applied to the evaluation of carbonate reservoirs, and the results varied widely. In recent years, with the rapid development of artificial intelligence, more and more experts and scholars have been applying machine learning algorithms to geophysical logging permeability interpretation5,6,7,8,9,10. Yang Jian et al11 used an improved BP neural network model to predict the logging permeability, and achieved certain application results; Wang Xinglong et al12 used C5.0 Decision-tree algorithm to interpret the permeability of carbonate reservoir; Gu Yufeng et al13 used a particle swarm optimization algorithm for parameter optimization of the gradient Decision-tree, and established a model for the permeability of clastic reservoir; Zhang Yanan et al14 proposed to construct a logging interpretation model for the permeability of complex carbonate reservoir by using hybrid simulated annealing-genetic algorithm-random forest algorithm; Han Rubing et al15phase-control carbonate reservoir layers, and then use BP neural network for permeability prediction. Although the above method has played a certain application effect in permeability logging interpretation, due to the slow convergence speed of the model, easy over-fitting and high complexity of the model, the above algorithm cannot be widely used in logging interpretation. Compared with BP neural network, traditional Decision-tree, Random Forest and other algorithms, XGBoost algorithm adds regularization terms, the fitting model refinement, having the advantages of high efficiency, high scalability, and high prediction accuracy, and being widely used in reservoir evaluation16,17. Therefore, this paper takes the strong heterogeneous carbonate reservoir of Longwangmiao Formation in Moxi Block of Anyue Gas Field as an example. Based on the optimization of permeability sensitive logging curves, the XGBoost algorithm based on simulated annealing genetic algorithm (SA-GA) optimization is proposed to establish the logging permeability prediction model of carbonate reservoir. The optimization model can obtain the global optimal solution and the convergence speed is faster than the single optimization algorithm such as particle swarm optimization (PSO) and genetic algorithm (GA), which can give full play to the performance of XGBoost.

Overview of the study area

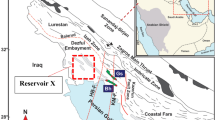
In 2013, the high-yield Anyue super-large gas field was discovered in the Longwangmiao Formation of the Sichuan Basin.This gas field is the oldest and largest single super-large marine gas reservoir discovered in China at this stage. Moxi block of Anyue gas field is located in Weiyuan-Longnvsi structural group in the gentle structural area of the middle slope of the ancient uplift in central Sichuan. The main production layer Longwangmiao Formation is widely developed carbonate reservoirs, which have the characteristics of diverse lithology, complex pore structure and strong heterogeneity. The horizontal and vertical spatial distribution of this kind of carbonate rocks is well connected. The reservoir lithology is a large set of dolomite, and some core thin sections are shown in Fig.1. The reservoir lithology is mainly medium-fine-grained dolomite, with residual granular (sandy and oolitic) structures (Fig.1a, c, e). The main types of reservoir space are intergranular and intercrystalline solution pores (Fig.1b, e), followed by intercrystalline pores, and some well sections develop cavities and fractures (Fig.1d-f, g), with strong heterogeneity of the reservoir.

Figure 1
figure 1

Core electron microscope and cast photos of carbonate reservoir in the study area. (a) Moxi 17, Longwangmiao Formation, 4612.50–4612.61, fine-silt crystal sand debris dissolved pore dolomite, \(\times\)20, single polarization; (b) Moxi 17, 4628.07–4628.34, medium-coarse grained sandstone lithic dissolved pore dolomite, intergranular dissolved pore development, partially filled asphalt, \(\times\)20, single polarization; (c) Moxi 13, 4640.15–4640.30, fine-medium crystalline dissolved pore dolomite, the dissolved pores see the asphalt ring edge, \(\times\)20; (d) Moxi 13, 4606.28, fine-grained residual sand debris dissolved pore dolomite, cave development, single polarization, \(\times\)20; (e) Moxi 12, 4622.05–4622.21, medium-fine-grained residual sandy dolomite, intergranular solution pore development, casting body, single polarization, \(\times\)20; (f) Moxi 12, Longwangmiao Formation, 4636.82–4637.10, fine-grained sand-clastic dolomite, see mesh seam development; (g) Moxi 12, 4628.32–4628.50, Longwangmiao Formation, fine-powder crystal residual sandy dolomite, fracture, casting body, single polarization, \(\times\)20.

Full size image

According to the analysis data of the core of the Longwangmiao Formation, the porosity of the small rock samples with porosity greater than 2%, ranges from 2.02% to 12.11%, with an average of 4.16%. Among them, the porosity of more than 4% accounted for 44.23%, more than 6% accounted for 13.74%. The permeability ranges from 0.0001 mD to 108.1 mD, with an average of 0.87 mD. The ones with permeability greater than 0.01 mD accounted for 54.84%, those with permeability greater than 0.1 mD accounted for 23.4% and those with permeability greater than 1 mD accounted for 9.14%. It can be seen that the reservoir of Longwangmiao Formation is characterized by medium porosity and medium permeability. Excluding the influence of fractures, the porosity-permeability relationship of the reservoirs in the study area was established, as shown in Fig. 2, it is not difficult to see that the pore structure of the reservoir has the characteristics of partial high porosity and low permeability and low porosity and high permeability. It can be found that the correlation between porosity and permeability of carbonate reservoirs in the study area is not obvious.

Figure 2
figure 2

Image of reservoir porosity and permeability relationship in the study area.

Full size image

Principle of SA-GA-XGBoost method

Principle of XGBoost

Friedman first proposed the Gradient Boosting Decision Tree algorithm (GBDT) in 2001, which is an algorithm that combines, Decision-tree and gradient boosting, the algorithm constructs a weak classifier function by making the loss function obtained from each round of iteration descend along the gradient direction, and the results of multiple weak classifiers are combined with certain weights to form a strong classifier as the final prediction output18. XGBoost is an optimized algorithm of GBDT, which is characterized by the fact that the model can automatically utilize the CPU to perform multi-threaded parallel computation, which is faster, and the second-order expansion of the loss function by the Taylor’s formula makes the prediction accuracy higher, and the addition of the regular term can constrain the descent of the loss function and the overall complexity of the model. The XGBoost objective function expression is as follows:

$$\begin{aligned} Obj=\textstyle \sum _{i=1}^{n}l\left( {y}_{i},\hat{{y}_{i}}\right) +\sum \varOmega \left( {f}_{k}\right) \end{aligned}$$
(1)

Where: \(l\left( {y}_{i},\hat{{y}_{i}}\right)\) denotes the loss error, \(\varOmega \left( {f}_{k}\right)\) denotes the regular term, \(\hat{{y}_{i}}\) is the model prediction value, \({y}_{i}\) is the true value of the ith sample, k is the number of trees, and \({f}_{k}\) is the model of the kth tree.

The expression for the regular term is specified as follows:

$$\begin{aligned} \varOmega \left( {f}_{k}\right) =\gamma J+1/2\lambda {\left\| \omega \right\| }^{2} \end{aligned}$$
(2)

Where: J is the number of leaf nodes of each classification regression tree; \(\omega\) is the sum of the weights of the leaf nodes of that tree; \(\gamma\) and \(\lambda\) are penalty coefficients, which can be adjusted in specific applications.

When the tth iteration is performed, the objective function is second-order Taylor expanded and the infinitesimal term is removed to obtain:

$$\begin{aligned} Obj=\textstyle \sum _{i=1}^{n}\left[ l\left( {y}_{i},{\hat{{y}_{i}}}^{\left( t-1\right) }\right) +{g}_{i}{f}_{t}\left( {x}_{i}\right) +\frac{1}{2}{h}_{i}{{f}_{t}}^{2}\left( {x}_{i}\right) \right] +\varOmega {f}_{t}+C \end{aligned}$$
(3)

Where: C is a constant term; \({g}_{i}=\partial {\hat{y}}^{\left( t-1\right) }l\left( {y}_{i},{\hat{{y}_{i}}}^{\left( t-1\right) }\right)\), denotes the first-order derivative of \({g}_{i}=\partial {\hat{y}}^{\left( t-1\right) }l\left( {y}_{i},{\hat{{y}_{i}}}^{\left( t-1\right) }\right)\) with respect to \({\hat{{y}_{i}}}^{\left( t-1\right) }\); \({h}_{i}={\partial }^{2} {\hat{y}}^{\left( t-1\right) }l\left( {y}_{i},{\hat{{y}_{i}}}^{\left( t-1\right) }\right)\), denotes the second-order derivative of \(l\left( {\hat{{y}_{i}}}^{\left( t-1\right) }\right)\) with respect to \({\hat{{y}_{i}}}^{\left( t-1\right) }\).

Let \({G}_{j}=\textstyle \sum _{i\in {I}_{j}} {g}_{j}\), \({H}_{j}=\textstyle \sum _{i\in {I}_{j}} {h}_{j}\), be brought into Eq. 3 and simplify the objective function to finally obtain:

$$\begin{aligned} Obj=-\frac{1}{2}\textstyle \sum _{j=1}^{T}\frac{{G}_{j}^{2}}{{H}_{j}+\lambda }+\lambda J \end{aligned}$$
(4)

SA-GA parameter optimization

Since XGBoost has to set many empirical parameters in modeling, such as the number of leaf nodes in the regression tree, the learning rate and the regularization coefficient, etc., optimization is necessary to ensure the modeling quality. The simulated annealing algorithm (SA) can jump out of the local values to find the global optimal solution; the genetic algorithm (GA) has the characteristics of fast convergence and is not easy to overfitting.The SA-GA algorithm combines the two algorithms to make up for the shortcomings of the GA, which has the disadvantage of local self-optimization in the rapid convergence, and the SA, which has the disadvantage of slow convergence and prone to oscillation. It has the characteristics of stronger search ability, faster convergence speed and better adaptability to complex problems, so that it can give full play to the advantages of the respective algorithms19,20,21. The specific steps are as follows:

  1. (1)

    Initialize the population. Randomly generate n individuals as the XGBoost regression tree volume, learning rate, maximum regression depth, regular term coefficient, the sum of the minimum sample weights of the leaves, and the minimum splitting gradient descent value, and set the maximum number of iterations as Mmax, and set the annealing initial and cutoff temperatures.

  2. (2)

    Calculate the fitness function. The adaptation function in the algorithm is the error function, and its expression is:

    $$\begin{aligned} f=\frac{1}{n}\textstyle \sum _{i=1}^{n}{\left( {y}_{k}-y\right) }^{2} \end{aligned}$$
    (5)
  3. (3)

    Selection, crossover, and mutation. Evaluate the population and select the excellent individuals based on the individual fitness, the expression is:

    $$\begin{aligned} {p}_{i}=\frac{{f}_{i}}{\textstyle \sum _{i}^{n}{f}_{i}} \end{aligned}$$
    (6)
  4. (4)

    Local update using Metropolis criterion. Simulated annealing operation is performed on the new individuals after crossover and mutation, and the expression is:

    $$\begin{aligned} P\left( \varDelta E,T\right) ={e}^{\frac{\varDelta E}{{K}_{b}T}} \end{aligned}$$
    (7)
  5. (5)

    Iteration ends. The optimization search ends when the maximum number of iterations is reached, otherwise (1)-(4) are repeated.

The flowchart of the SA-GA-XGBoost method is shown in Fig.3.

Figure 3
figure 3

Flowchart of the SA-GA-XGBoost algorithm. Standardization of logging data: select the core analysis data as the training set. Optimization of permeability characteristic parameters: by calculating the correlation coefficient between logging curve and permeability, the characteristic parameters are optimized. Initialize model parameters: set the initial parameters of the model, and optimize the SA-GA algorithm to obtain the optimal parameters. Establish XGBoost model: according to the optimal parameters, establish the algorithm model, predict the test set, and obtain the prediction results.

Full size image

Analysis of application examples

Standardization of logging data

Due to the different dimensions of different logging curves, the order of magnitude gap between the data is too large, which affects the calculation speed and accuracy of the model, so it is also necessary to preprocess the data before learning and training. In this paper, the standard deviation normalization formula is used to standardize all data samples (Eq. 8). Since the resistivity curve is a nonlinear logarithmic characteristic curve, it needs to be logarithmically transformed and then normalized.

$$\begin{aligned} X=\frac{x-\bar{x}}{\delta } \end{aligned}$$
(8)

Where: X is the normalized data, x is the sample data, \(\bar{x}\) is the sample mean, and \(\delta\) is the sample data standard deviation.

Permeability characterization carameter optimization

Since different logging sequences have certain responses to the logging permeability of carbonate reservoirs, such as natural gamma, neutron porosity, density, acoustic wave, resistivity, etc., and the interpretation conclusions by using single logging response has serious multi-resolution, the selection of logging characteristic parameters has a direct impact on the efficiency of the prediction model as well as the reliability of the results when establishing the permeability prediction model. In this paper, three correlation coefficients (Eq. 9, 10, 11), Pearson’s coefficient, Kendall’s coefficient, and Spearman’s coefficient, which are commonly used in statistics, are prioritized to calculate the correlation between various types of logging curves and permeability22.

$$\begin{aligned} {r}_{p}= & \frac{\sum \left( {x}_{i}-\bar{x}\right) \left( {y}_{i}-\bar{y}\right) }{\sqrt{\sum {\left( {x}_{i}-\bar{x}\right) }^{2}\sum {\left( {y}_{i}-\bar{y}\right) }^{2}}} \end{aligned}$$
(9)
$$\begin{aligned} {r}_{k}= & \frac{c-d}{\frac{1}{2}n\left( n-1\right) } \end{aligned}$$
(10)
$$\begin{aligned} {r}_{s}= & 1-\frac{6\sum {d}_{i}^{2}}{n\left( {n}^{2}-1\right) } \end{aligned}$$
(11)

Where: \({r}_{p}\), \({r}_{k}\), \({r}_{s}\) denote Pearson’s coefficient, Kendall’s coefficient, and Spearman’s coefficient, respectively; \({x}_{i}\), \({y}_{i}\) are sample data, and \(\bar{x}\), \(\bar{y}\) are sample data averages; n is the number of sample data, c is the number of consistent values in the subjective and objective assessment values, and d is the number of values in which the subjective assessment values are not the same as the objective assessment values; and \({d}_{i}\) is the number of rank differences in the paired variables.

Using three kinds of correlation coefficients to calculate the input parameters, the correlation coefficients \(\left| r\right|\) of each logging response characteristics and permeability were obtained, and the results are shown in Table 1, the correlation coefficients \(\left| r\right|\) are in the range of 0–1, and the larger value indicates the higher degree of correlation.

Table 1 Results of different correlation coefficient analysis.
Full size table

The correlation results between logging response and permeability calculated by the three correlation coefficients are basically the same, according to the principle that the correlation coefficient is greater than 0.5, this paper selects five permeability-sensitive logging curves of CNL, DEN, DT, \(\ln {RT}\) and GR as inputs, and integrally selects 10 core wells in carbonate rocks of the Longwangmiao Formation of Muxi block in Anyue Gas Field, with a total of 200 core data, of which 80% of the total 160 samples constitute the model training set, and 20% of the total 40 samples constitute the test set to establish the permeability logging prediction model.

Constructing the SA-GA-XGBoost prediction model

In the XGBoost algorithm model, the setting of various parameters will affect the prediction accuracy and convergence effect of the model. In this paper, the initial parameters of the model are set as follows, the regression tree volume k=100, the learning rate =0.01, the maximum regression depth max-depth=3, the regular term coefficient =0.1, the sum of the minimum sample weight of the leaf min-chile-weight=0.1, and the minimum splitting gradient descent. When using SA-GA to optimize the XGBoost parameters, the number of iterations is set to 200, the number of populations is set to 50, and the temperature reduction parameter is set to 0.98. When the number of iterations is greater than 120, the optimization results are also close to the global optimal solution, and the parameter optimization takes 0.5 h. The optimal parameters of the XGBoost are finally obtained as shown in Table 2.

Table 2 Optimal XGBoost parameters after SA-GA optimization.
Full size table

Model results validation analysis

Using the established SA-GA-XGBoost model, 40 samples of the test set are predicted, and the prediction results are shown in Fig. 4a, the correlation coefficient \({R}^{2}\) between the core permeability and the predicted permeability reaches 0.94, and meanwhile, in order to validate the prediction effect of the model, The adjusted \({R}^{2}\) and root mean square error (RMSE) commonly used in statistics are selected (Eq. 12, 13). The adjusted \({R}^{2}\) is 0.887 and RMSE is 0.132. In order to compare the prediction effect of the model after parameter optimization, this paper also uses the conventional XGBoost algorithm and same data to model and predict, and the results are shown in Fig. 4b, with the correlation coefficient \({R}^{2}\) of 0.88 and the adjusted \({R}^{2}\) is 0.774 and RMSE is 0.215. It is not difficult to see that after entering the model after SA-GA parameter optimization, the adjusted \({R}^{2}\)is increased by 0.113, RMSE is increased by 0.083, and the accuracy of prediction results is significantly improved. In order to verify the extrapolation ability of the SA-GA-XGBoost model, this paper uses the ten-fold cross-validation method to validate all the sample data, the data set was randomly divided into 10 copies, one of which was selected as the test set, and the remaining 9 were used as the training set for 10 training and testing23, and the results are shown in Fig. 5, the average value of the error mean of the SA-GA-XGBoost model is 0.15, indicating that the model has certain generalization ability and effectiveness. and the prediction accuracy meets the needs of logging interpretation.

$$\begin{aligned} Adjusted {R}^{2}=1-\left[ \frac{\left( 1-{R}^{2}\right) \left( n-1\right) }{n-k-1}\right] \end{aligned}$$
(12)

Where: \({R}^{2}\) is the model coefficient of determination; n is the number of samples; k is the number of predictors.

$$\begin{aligned} RMSE=\sqrt{\frac{1}{n}\textstyle \sum _{i=1}^{n}{\left( \hat{{y}_{i}}-{y}_{i}\right) }^{2}} \end{aligned}$$
(13)

Where: \({y}_{i}\) denotes the true value of permeability; \(\hat{{y}_{i}}\) denotes the predicted value of permeability; n denotes the total number of samples of the training set data.

Figure 4
figure 4

Prediction results of permeability evaluation model. (a) SA-GA-XGBoost model; (b) XGBoost model.

Full size image
Figure 5
figure 5

The result of 10-fold cross-validation.

Full size image
Figure 6
figure 6

Comparison of permeability model prediction in well M8.

Full size image

Comparison of model application

The established SA-GA-XGBoost model is practically applied to the prediction of logging permeability of carbonate reservoir in M8 well in the study area, in order to compare the prediction effect, the traditional pore-permeability plate method and the BP neural network are used to predict the permeability of M8 well, the prediction results of the three methods are shown in Fig. 6. It can be seen that all the three prediction methods can reflect the change of reservoir permeability. However, the prediction accuracy is significantly different. The prediction results of BP neural network and SA-GA-XGBoost models are in good agreement with the core permeability. There is a significant deviation between the low and high permeability values in the BP permeability evaluation model, while the SA-GA-XGBoost model has a good application effect in the whole well section, and the error is small, especially in the low permeability interval, the advantage is more obvious. The adjusted \({R}^{2}\) and RMSE of the three models were calculated respectively. The adjusted \({R}^{2}\) of the porosity and permeability plate method was 0.672, and the RMSE was 0.364. The adjusted \({R}^{2}\) of the BP neural network was 0.738, and the RMSE was 0.253. The adjusted \({R}^{2}\) of the SA-GA-XGBoost model was 0.876, and the RMSE was 0.142. Therefore, the SA-GA-XGBoost permeability evaluation model can fully reflect the difference of logging response characteristics. The model has strong stability and high calculation accuracy. It is more suitable for the permeability evaluation of carbonate reservoirs with complex pore structure and strong reservoir heterogeneity.

Conclusion

For the evaluation of logging permeability of Cambrian Longwangmiao Formation carbonate reservoirs in the Moxi block in central Sichuan, an XGBoost carbonate reservoir permeability prediction model based on SA-GA optimization is proposed from the optimization of model parameters, and it has been applied well in the study area, and meanwhile, the following understandings have been achieved:

  1. (1)

    The correlation between different logging response characteristics and permeability is calculated by three correlation coefficients, and five permeability-sensitive logging curves of CNL, DEN, DT, \(\ln {RT}\), and GR with higher correlation are identified as input parameters of the model, which simplifies the model calculations and improves the prediction accuracy at the same time.

  2. (2)

    Using simulated annealing genetic algorithm, the parameter of XGBoost model is optimized to improve the generalization ability of the prediction model and the reliability of the results, and the prediction effect meets the actual needs of the study area.

  3. (3)

    Compared with the traditional network model, the SA-GA-XGBoost model has the advantages of high precision and strong generalization ability. In the future, it can also be applied to carbonate fracture identification and other aspects to provide more accurate and efficient reservoir parameter prediction for oil and gas exploration.