Multi-objective particle swarm optimization algorithm for task allocation and archived guided mutation strategies

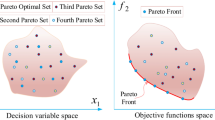
Multi-objective optimization problems (MOPs)^1,2,3 are widely used in the fields of machine learning, recommender systems, financial cloud computing, and software engineering, etc., where real-world problems usually involve multiple optimization objectives. Finding an optimal solution is extremely difficult because there are often conflicts between objective functions^4,5. To find a compromise solution between different objectives, a Pareto optimal solution set (POS)⁶ is introduced, and these solutions constitute a Pareto optimal frontier (PF) in the objective space⁷. Many new algorithms have been proposed and optimized to enhance the performance of MOPs⁸, such as Particle Swarm Optimization (PSO)⁹, Genetic Algorithm (GA)¹⁰, Ant Colony Optimization (ACO)¹¹, African Vulture Optimization Algorithm (AVOA)¹², and Multi-Objective Adaptive Guided Differential Evolutionary Algorithm (MOAGDE)¹³.

Among many improved algorithms, DTDP—EAMO¹⁴ utilizes fast non-dominated sorting to divide the population into three sub-populations and then introduces a two-stage multi-population adaptive mutation strategy with a dual external archive mechanism, which maintains convergence and diversity of the sub-populations and archives high-quality solutions to help the populations get rid of the local optimums, promote information exchange, and finally select high-quality solutions to reorganize the new population¹⁵. Another study¹⁶ proposes a convergence contribution evaluator that does not rely on additional parameters or predefined reference points, and its design is inspired by the concept of ideal points of Pareto frontiers and partitioning strategies. MSC-PSO¹⁷ enhances the global search capability through population partitioning, and TSO-DF¹⁸ evaluates the elite solutions for guiding the search by fusing the convergence and diversity information without sacrificing the diversity of the solutions. The method screens the optimal solutions by merging convergence and diversity metrics as a single ranking criterion. MOPSO, which is derived from the PSO extension, is widely used in solving multi-objective optimization problems due to its simple structure and fast convergence rate¹⁸. In addition, the MOFS-REPLS algorithm¹⁹, LDANet²⁰, and EAL-PDM²¹ also show their advantages in different fields, respectively. MOFS-REPLS algorithm improves the performance of multi-objective optimization in various ways, such as unique coding format, optimized initialization strategy, and double archiving mechanism; LDANet improves the performance of lung substance segmentation through innovative structure; the pair-based early active learning algorithm proposed by EAL-PDM solves the data labeling problem in the early active learning of pedestrian re-identification and improves the model performance.

Although MOPSO has significant advantages in optimization performance, there is still room for improvement when facing complex problems. There are many limitations in traditional MOPSO: The population is handled in a single way, which is difficult to cope with the complex search space and dynamic changes, and it may be too concentrated in the optimization of certain objectives, leading to slow convergence or premature convergence; the variation operation is based on simple random perturbations, which is insufficiently diversified, and the setup of the mutation probability is inflexible, which makes it difficult to balance the exploration and exploitation; the maintenance of the external archive relies on the basic criterion, which is insufficiently reflecting the diversity of the non-dominated solution. External archive maintenance relies on basic guidelines, which do not reflect the diversity of nondominated solutions and is prone to the loss of important solutions; the traditional individual optimal updating suffers from dimensional pressure and selection unfairness. In this paper, we address the potential problems of MOPSO by combining multiple mechanisms and propose TAMOPSO.

For one thing, the traditional unified treatment of the population tends to concentrate on the particle population in a local region prematurely, which reduces the diversity of the solution set and weakens the global optimization ability. To solve this problem, numerous studies have attempted to divide the population. For example, MOCPSO²² uses shift density estimation (SDE)²³ to calculate the population fitness score and randomly divide the population; ecemAMOPSO²⁴ divides the subpopulation according to the order of particle convergence; Ran Cheng and Yao Chu Jin²⁵ propose an angular penalization distance (APD) method to balance convergence and diversity; MOMTPSO²⁶ combines objective space partitioning and adaptive migration distance with the adaptive migration distance method. Combining target space partitioning and adaptive migration; the Football Team Training Algorithm (FTTA) of²⁷ and the two-population evolutionary algorithm of dealing with the population partitioning problem from different perspectives, respectively, to improve the search efficiency and algorithm performance. However, the current population partitioning methods still have the problems of a single partitioning standard and lack of dynamic adaptability. Therefore, this paper proposes to use population uniformity as a weighting factor for population division.

Second, the variation operation is crucial in MOPSO. It increases population diversity, avoids premature convergence, and enhances the global search capability while fine-tuning the particles when they are close to the optimal solution, realizing the balance between global and local search, and improving the quality of the solution. Moazen²⁸ proposes the exponential mutation operator;²⁹ proposes a particle swarm algorithm that combines elite learning; the algorithm of³⁰ adopts an adaptive response strategy, and the FDDE algorithm of³¹ uses a differential evolution strategy and integrates individual fitness and diversity contributions, and the Flower Pollination Algorithm (FPA)³² has also been applied in optimization problems. However, the existing variation operations have problems such as difficulty balancing global and local searches, high parameter sensitivity, poor stability, and low effective variation rates.

The Lévy flight strategy brings new opportunities to improve the performance of MOPSO population variability. Many previous researches have achieved remarkable results: in 2010, Xin-She Yang and Suash Deb’s team first introduced it into the firefly algorithm to avoid the algorithm falling into the local optimum through long-distance jumps in order to improve the optimization ability; in 2012, Kenneth V. Price and other scholars integrated it into the differential evolution algorithm to enhance the diversity of populations and improve the convergence speed and accuracy; in 2015, Carlos A. Coello Coello’s team applied Lévy flights in a multi-objective optimization algorithm to make the Pareto solution set distribution better. These studies confirmed the effectiveness of the Lévy flight strategy in different dimensions and provided theoretical and practical foundations for applying the strategy in the variational operation of TAMOPSO. However, when applying Lévy flight to MOPSO, problems such as population degradation due to too large step size, underdevelopment of localization when relying solely on it, and parameters needing to be adjusted manually may occur. The adaptive control The Lévy flight variation strategy proposed in this paper adaptively adjusts the variation method by detecting the archived growth rate, which reduces the parameter sensitivity and decreases the difficulty of adjustment while effectively improving the effective variation rate.

Third, in practice, the solutions in the archive may be overly concentrated, especially in the multidimensional objective space. Most algorithms lead to this problem by relying only on nondominated ordering to select archived solutions and not sufficiently introducing a diversity maintenance strategy. García³³ proposes a method based on nondominated ordering of metrics, Luo et al.³⁴ guide the selection of particles by establishing reference vectors and uniformly distributed vectors, and PRMOPSO³⁵ maintains the archive by using projected points and reference points. However, these methods have the limitation of being difficult to accurately measure particle diversity and mixing in low diversity contributing particles, which affects the overall diversity of the archive. To this end, this paper adopts a novel method to calculate the local uniformity of archived particles as a contribution influence factor and collaborates with adaptive grids to measure and remove particles with low contributions to improve the archive maintenance effect.

Fourth, the traditional multi-objective particle swarm optimization algorithm has limitations in individual optimal updating. On the one hand, the dimension pressure problem is highlighted with the increase of dimension, and it is difficult to process the information effectively in the traditional way, leading to the increase of computational complexity and the decline of algorithm performance. On the other hand, the selection unfairness problem makes the evaluation criteria unreasonable and biased towards certain particles, affecting the overall search effect and convergence speed. The self-weight robust LDA (SWRLDA) method proposed in³⁶ effectively avoids problems such as optimal mean computation. The L2 paradigm selection of individual optimum has two major advantages: relieving dimensionality pressure and improving selection fairness.

To summarize, TAMOPSO proposed in this paper innovates and improves the traditional MOPSO through population partitioning, task allocation, adaptive mutation strategy, archive maintenance, and individual optimal selection method. Compared with existing MOPSO algorithms, the innovativeness of TAMOPSO can be summarized as follows:

1. 1.

   Adaptive Particle Comprehensive Ranking: The algorithm combines the convergence, diversity, and evolutionary state of the particles to propose a comprehensive score for the particles and adaptively divides the population by ranking the comprehensive score of each particle; finally, the algorithm assigns a specific task for evolutionary search according to the characteristics of each population of particles to improve the performance of the algorithm.

2. 2.

   Adaptive Lévy flight variation: In this paper, we use the archived information as a feedback factor for the population variation rate, and the algorithm realizes the adaptive switching of the dual-mode variation strategy (global Lévy flight and local normal perturbation) according to the feedback factor. This not only reduces the sensitivity to parameters and the difficulty of parameter tuning but also effectively enhances the effective mutation rate through the targeted mutation approach.

3. 3.

   Archiving maintenance based on local uniformity: By combining the global and local densities of particles in the archive, a new metric is proposed to maintain the archive. The index takes into account both the global particle distribution and the individual particle distribution, which improves the accuracy of archive maintenance.

4. 4.

   Improved Individual Optimal Update: The traditional individual optimal update faces the problems of dimensional pressure and unfair selection. For this reason, in this paper, non-dominated particles are selected as individual optimal particles by making a Pareto comparison between the current generation particles and the previous generation particles. For the mutually non-dominated particles, the distance between the particle paradigm (paradigm in the n-dimensional case) and the super-ideal point is calculated, and the particle with the closest super-ideal point is selected as the individual optimum.

Subsequently, Section Related work introduces the basics of MOPs and PSOs and related work; Section "Proposing the TAMOPSO algorithm" elaborates the proposed algorithm and process in detail, running through the basic ideas and algorithmic implementations; Section "Algorithm comparison and result analysis" describes the parameter design and performance metrics and demonstrates the effectiveness of TAMOPSO through algorithmic comparative test evaluations; and, finally, Section "Conclusion" concludes the research work on TAMOPSO.

Multi-objective optimization problem

Multi-objective optimization problems contain multiple objective functions \({f}_{1}\left(x\right),{f}_{2}\left(x\right),\dots ,{f}_{m}\left(x\right)\), which are usually conflicting. It is not possible to optimize the values of all objective functions at the same time, even under an optimal solution, so the relationship between the objectives needs to be weighed. A multi-objective optimization problem is generally represented as (in terms of the minimum problem):

where \(x=({x}_{1},{x}_{2},\dots ,{x}_{n})\) is the vector of decision variables,\(x\in {R}^{n}\), \(n\) is the dimension of the decision variables. \({f}_{1}\left(x\right),{f}_{2}\left(x\right),\dots ,{f}_{m}\left(x\right)\) is the objective function, each \({f}_{i}\left(x\right)\) corresponds to an objective to be optimized and \(m\) is the number of objectives.

The constraints usually include equal and unequal constraints, denoted as:

where \({g}_{j}\left(x\right)\) is the inequality constraint, \({h}_{k}\left(x\right)\) is the equality constraint, \(p\) and \(q\) are the number of these constraints, respectively.

Particle swarm optimization

PSO was proposed by Kennedy and Eberhart³⁷ in 1995 and belongs to the category of group intelligence. PSO simulates the movement of a group of particles in the solution space. Each particle represents a potential solution, and the particle searches for the optimal solution by continuously adjusting its speed and position:

where \({x}_{i}\left(t\right)\) and \({x}_{i}\left(t+1\right)\) denote the positions of the particle relations generating \(t\) and \(t+1\), respectively. \({v}_{i}\left(t\right)\) and \({v}_{i}\left(t+1\right)\) denote the velocities of the \(t\) and \(t+1\) generations, respectively. The inertia weight \(\omega\) controls the inertia of the particle along the direction of the original velocity. \({c}_{1}\) and \({c}_{2}\) are the learning factors for personal and global experience, respectively. \({r}_{1}\) and \({r}_{2}\) are randomly generated values on the interval \([\text{0,1}]\). \({pBest}_{i}\) is the optimal position experienced by particle I during the search process, and \({gBest}_{i}\) denotes the particle’s personal optimal solution (i.e., self-perception). is the best position experienced by all particles in the whole population and denotes the best solution for all particles (i.e., population cognition).

Pareto ranking

Definition 1

Pareto dominance relationship.

Let \(x\) and \(y\) be two solution vectors in a multi-objective optimization problem, both of which have multiple objective function values. A solution \(x\) is said to Pareto dominate \(y\), denoted \(x<y\) if for all objective functions \({f}_{i} (i=\text{1,2},\cdots ,m\text{ is the number of objective functions})\), there is \({f}_{i}(x)<{f}_{i}(y)\), and there exists at least one objective function \({f}_{j}\) such that \({f}_{j}(x)<{f}_{j}(y)\).

Intuitively, if \(x\) is not worse than \(y\) on all objectives and is better than \(y\) on at least one objective, then \(x\) dominates \(y\). If two solution vectors, \(x\) and \(y\), have neither \(x<y\) nor \(y<x\), then the summation is said to be mutually non-dominating.

Definition 2

Pareto ranking.

1. 1.

   Initialization: For each particle in the particle swarm, set its Pareto rank to 1 and initialize the set of dominating particles and the set of dominated particles to empty.

2. 2.

   Calculate the dominance relationship: Iterate through each pair of particles x and y in the particle swarm and judge the dominance relationship between them according to the definition of the Pareto dominance relationship. If x dominates y, add y to the dominating particle set of x, and at the same time add x to the dominated particle set of y. If y dominates x, do the opposite; if x and y do not dominate each other, do not perform any operation.

3. 3.

   Determine the Pareto front (first layer): Iterate over all particles and find those particles whose set of dominated particles is empty, which constitutes the Pareto front, i.e., the first layer of the Pareto optimal solution, marking their Pareto rank as 1.

4. 4.

   Recursively determine the other layers: for the particles in each layer of the Pareto optimal solution that has been determined, iterate through the particles in their set of dominated particles. If all the dominated particles of a particle have been assigned a Pareto rank, then set the Pareto rank of that particle to the maximum of the Pareto ranks of all its dominated particles plus 1. Repeat this process until all particles have been assigned a Pareto rank.

In this section, the specific procedure of the proposed TAMOPSO algorithm is described in detail. Among them, Section Core framework of TAMOPSO describes the overall framework of the TAMOPSO algorithm, Section "Population segmentation and tasking strategies" elaborates on the proposed population partitioning and task allocation strategy, Section Adaptive control of the Lévy flight variation strategy demonstrates the Lévy flight variation operation with adaptive control, and regarding the maintenance method of the archive and the individual optimal updating strategy, they are elaborated in Section Uniform contribution margin metrics guide archive maintenance strategies and Section Individual optimal update strategy, respectively. Moreover, the motivation for introducing the corresponding new features in the algorithm is clearly explained at the end of each subsection.

Core framework of TAMOPSO

This section outlines the core framework of TAMOPSO. As shown in Fig. 1, TAMOPSO proposes the establishment of reference vectors to divide the population, task-allocation search strategy, individual optimal selection, archive maintenance, and adaptive mutation mechanism, aiming to improve the search efficiency and optimization effect. Its basic process is as follows:

Core framework of TAMOPSO.

Full size image

First, the algorithm randomly initializes the population to provide a starting point for the subsequent search process. The population is divided into three subpopulations by creating reference vectors. This classification process is based on the relationship between the reference vectors and the individuals, with the aim of classifying the particles in the population into different subpopulations by integrating their fitness and spatial characteristics, thus making the subsequent optimization process more targeted. For the different subpopulations, the algorithm assigns different search strategies, respectively. This differentiation of strategies permits a suitable search approach for individuals with different characteristics in the population. For example, while some subpopulations focus on local search, others may focus on global search, thus improving the search efficiency of the algorithm.

When performing a population search, the algorithm not only focuses on the current optimal particle but also keeps track of the global optimal particle by maintaining an archive. The selection of individual optimal particles is based on the dominance relationship between the particles of the previous and current generations and the paradigm to ensure that high-quality particles are selected as much as possible. For non-dominated particles, if the archive is not full, they are added directly; if the archive is full, some particles are eliminated, and the particles in the archive are updated according to the uniform contribution index.

In addition, the algorithm introduces a mutation operation to guide the population to explore efficiently in the search space through an adaptive mutation strategy. This operation employs a mutation model based on Lévy flights, which can perform jumping search in the global range to avoid falling into local optima. The adaptive mechanism allows the mutation operation to dynamically adjust to the current population growth rate, switching between global and local mutation to improve the mutation efficiency.

Finally, the algorithm optimizes the quality of the particles by continuously and iteratively updating the population and eventually storing the globally optimal particles in the archive. The individual strategies in the process work closely together to drive the algorithm towards a more optimal solution.

Population segmentation and tasking strategies

Population segmentation strategy

The traditional multi-objective particle swarm optimization algorithm adopts a single population evolution mode, and the global unified treatment is prone to premature convergence and Pareto frontier distribution diversity defects. To address this problem, TAMOPSO proposes a dynamic swarm optimization framework based on adaptive reference vectors: firstly, we construct a set of directional reference vectors based on the geometric features of the target space and then divide the population into multiple co-evolving sub-populations through the distribution of the particles in the reference vectors to reflect the convergence and diversity of the particles; each sub-population focuses on searching a specific region of the Pareto front so as to achieve autonomous trade-offs and diversity maintenance among conflicting targets. First, the number S of reference vectors is calculated by Eq. (6), which depends on the dimension (M) and resolution (H) of the target space.

where the resolution (H) denotes the number of segmentation segments on each target dimension. It determines the distribution density of the reference vectors in the target space. Specifically, the larger the value of H, the more finely the target space is divided and the greater the number of reference vectors generated. This helps to steer the population distribution more finely, avoid premature convergence, and maintain diversity.

The generation of reference vectors depends on the dimensionality of the target space, and the coordinates of each reference vector are determined by the values of angles uniformly distributed on the unit circle (2-dimensional) or hypersphere (high-dimensional). Assuming that the target space is 2-dimensional, the reference vectors are uniformly distributed on the unit circle in the first quadrant, with angles ranging from 0 to uniformly distributed \(\pi /2\). For each reference vector \({r}_{j}\), its coordinates can be computed using the following equation:

where: \({\theta }_{j}\) is the angle of the reference vector, uniformly distributed over the range of \([0,\pi /2]\).

In n-dimensional space, point V in n-dimensional space on the sphere can be generated by the following equation:

where each component \({v}_{i}\) can be calculated by:

where \(r\) is the radius of the ball (for the unit sphere \(r=1\)) and \({\theta }_{1}{\theta }_{2},\cdots ,{\theta }_{n-1}\) is an \(n-1\) angular parameter, usually uniformly distributed in the interval \([0,\uppi ]\) or \([0,2\uppi ]\).

For particle \(i\), the angle \({\theta }_{ij}\) is calculated as in Eq. 10; the angle between the particle and each reference vector can be obtained, which in turn leads to the relative position of each particle in the target space. Next, the fitness values are Pareto-ranked, and then the angle and fitness value rankings of each particle with the reference vector are normalized separately. The normalization method for both the angle and fitness value rankings is the minimum–maximum normalization method (Eq. 12), which linearly maps the angle and fitness value rankings data into the [0,1] interval to ensure that they are weighted and summed at a uniform scale. The angle score \(As\) and fitness ranking score \(Fs\) of each particle are obtained after ranking the normalized particle angle and fitness values. Where \(As\) reflects the proximity of the particle to the reference vector and \(Fs\) reflects the superiority of the particle in multi-objective optimization. These two scores are weighed and summed by adjusting their relative weights using the population homogeneity factor \(\varphi\) (Eq. 12), thus combining \(As\) and \(Fs\) (Eq. 13) to calculate the combined particle priority score \(Ps\). The effect of the uniformity factor \(\varphi\) is that it can adaptively change the focus of the population division according to the distribution of the population during each iteration to avoid falling into a local optimum.

in Eq. 10, \({f}_{i}\) is the fitness value vector of the particle, \({r}_{j}\) is the reference vector, and \(\Vert {f}_{i}\Vert \cdot \Vert {r}_{j}\Vert\) is the dot product of the fitness value vector and the mode of the reference vector.

in Eq. 11, \({X}_{N}\) is the normalized particle angle or fitness value ranking, \({X}_{i}\) is the angle that needs to be normalized, and \(min(X)\) and \(max(X)\) are the minimum and maximum values of the angle and fitness value ranking in the particle.

where: N is the size of the population; \(\left(\genfrac{}{}{0pt}{}{N}{2}\right)=\frac{N(N-1)}{2}\) is the number of solution pairs in the population, denoting the number of combinations of all the different solution pairs; \({x}_{i}\) and \({x}_{\text{j}}\) are the vectors of the objective values of the two solutions; M is the dimensionality of the objective space; and \({F}_{max}\) and \({F}_{min}\) are the maximum and minimum values of each objective dimension in the population, respectively. Finally, the particle composite priority score \(Ps\) is obtained:

The priority \(Ps\) scores of all the particles are sorted and based on the sorting result, the particles are divided into three classes: subpopulation \({P}_{A}\) (highest priority), subpopulation \({P}_{B}\) (medium priority), and subpopulation \({P}_{C}\) (lowest priority) in the ratio of 1:3:1.The pseudo-code for the division of the population is given in Algorithm 1 of.

The \(Ps\) score is a key measure of particle quality and is well constructed. It uses the evolutionary state of the population as the weight \(\varphi\) and integrates the \(As\) and \(Fs\) scores. As reflects the distribution of particles in the reference vector, and the angle between the particles and the reference vector can reflect the diversity of particles, the angle is discrete, the diversity is good, and the distribution of particles is uniform and extensive, while the angle is concentrated, the diversity is poor. \(Fs\) score is based on the ranking of the particle fitness values; the particles with smaller fitness values are ranked higher, and they get a higher \(Fs\) score, which is the visualization of the convergence of particles. The higher the score, the better the convergence is. The higher the score, the better the convergence.

To reasonably combine \(As\) and \(Fs\), the number of high-quality particles in the archive is examined to reflect the evolutionary state of the particles, which is set as the adaptive weight. In the early stage of evolution, the diversity of the population is important, and the adaptive weights account for a large proportion in the calculation of the \(Ps\) score; \(As\) evolution advances and the particles tend to converge, the adaptive weights are adjusted to make the fs play a greater role so as to comprehensively synthesize the strengths and weaknesses of the different states of the particles.

Based on this, we can accurately classify the population in different evolutionary states according to the \(Ps\) score. For the classified particles, tasks are assigned according to their characteristics, such as allowing particles with good diversity but insufficient convergence to explore new spaces and particles with good convergence to perform local search optimization, improving the optimization effect and pushing the particles to approach the optimal solution.

In order to improve the optimization refinement, the population particles are divided into three parts according to 1:3:1. The first part is used to explore the initial search direction; the middle three parts balance the exploration and convergence in different evolution stages to optimize the quality of the solution; the last part deeply polishes the better solution region to ensure the high precision of the solution. Through this division and synergy, the particles play the maximum performance in their respective areas to enhance the performance of the optimization system.

Population segmentation.

Full size image

Tasking strategy

A single search strategy is often difficult to effectively balance the conflicts between different goals. To alleviate the pressure of localized search and, at the same time, improve the search efficiency of each subpopulation, a new speed-controlled search mechanism is assigned based on the subpopulation characteristics.

The subpopulation \({P}_{A}\) contains the best particles in the population and is therefore small. They are in the high-quality region of the Pareto front and solution space, and their task is to focus on further optimizing the existing excellent solutions. Therefore, their main task is to further improve the accuracy and quality of the solutions through local optimization. Inspired by³⁸ a search mechanism with velocity pause (Fig. 2a) for the characteristics of \({P}_{A}\) subpopulation, a velocity decay factor \({r}_{t}\) Eq. (14) and a velocity pause threshold \(\gamma\) Eq. (15) are added to this search mechanism, where \({r}_{t}\) gradually decays with the population evolution during iterations to improve the search accuracy, where the velocity pause threshold R is based on the particles in the archive per iteration exchange rate changes adaptively.

where \(\beta =0.8\) controls a constant for the decay rate; \(rk\) and \(sk\) are the particles removed from the archive and introduced into the archive in each iteration, respectively; \(NS\) is the number of particles in the archive; \(t\) is the number of current iterations; and \(T\) is the maximum number of iterations.

Search strategy for subgroups \({P}_{A}\) and \({P}_{B}\).

Full size image

During the search process when the archive growth rate is large it will allow a small portion of the particles in the subpopulation \({P}_{A}\) to move with a small probability of velocity pause i.e. the same velocity as in the previous iteration while the remaining portion performs the decelerated search mechanism. The subpopulation \({P}_{A}\) particle velocity position is updated in the following way:

where the setup parameters take the values \({c}_{1}=0.5\); \({r}_{1}\) and \(r\) are uniform random numbers between [0,1].

Subpopulation \({P}_{B}\) is the most numerous subpopulations and is mainly responsible for the global search. Since these particles are still some distance away from the optimal solution, they have a greater potential to explore other regions of the solution space. By increasing the number of particles, the diversity of the population can be enhanced, effectively avoiding premature convergence to the local optimal solution, thus ensuring a more comprehensive and extensive search process. The particles of the subpopulation \({P}_{B}\) take on the tasks of global search and local optimization. Inspired by the search mechanism in²², in this paper, by introducing the repulsion mechanism \(RD\) and adaptive deceleration \({r}_{t}\), this repulsion mechanism helps the particles to disperse (Fig. 2b), enhances the coverage of the solution space, and prevents over-concentration in certain regions. It enables them to effectively explore multiple regions of the solution space to avoid premature convergence, while gradually improving the quality of the solution. Overall, the subpopulation \({P}_{B}\) maintains the population diversity and pushes the algorithm to converge towards the global optimal solution through a strong global search capability and certain local optimization strategies. The subpopulation \({P}_{B}\) particle velocity positions are updated as follows:

where the setup parameter takes the value:\({c}_{2}=0.8\); \({c}_{3}=0.1\);

The subpopulation \({P}_{C}\) contains the worst 40 particles, which are located at the edge of the solution space or in regions far from the ideal solution, are less well adapted and have a higher Pareto ranking, meaning that they dominate fewer solutions. The angle to the reference vector is larger, showing that their target values are more directionally different from the ideal solution. The main task of the particles of the subgroup \({P}_{C}\) is to accelerate the convergence to the global optimum (Fig. 3), which is enhanced by the global search. The velocity position update formula for subgroup \({P}_{C}\) is as follows:

where the setup parameter takes the value of \({c}_{4}=1.5\);

Search strategy of \({P}_{C}\).

Full size image

In the TAMOPSO algorithm, global search and local optimization problems in multi-objective optimization problems are solved by establishing reference vectors to simultaneously improve the efficiency and convergence accuracy of the algorithm. By dividing the population into different subpopulations, each subpopulation can focus on a specific optimization task, resulting in a broader and finer exploration in the solution space. Three different search tasks are assigned for the three subpopulations; the task of subpopulation \({P}_{A}\) is to focus on further optimizing the existing excellent solutions, the particles of subpopulation \({P}_{B}\) take on the tasks of global search and local optimization, and the main task of the particles of subpopulation \({P}_{C}\) is to accelerate the convergence to the global optimum. Such a division of labor allows the algorithm to search for potential high-quality solutions in a larger range, and at the same time to converge quickly when approaching the optimal solution, and ultimately to obtain a high-quality solution. Pseudo-code for task allocation is given in Algorithm 2.

Task Assignment.

Full size image

Adaptive control of the Lévy flight variation strategy

The variation operation in common MOPSO usually relies on a small range of random perturbations, which tends to cause the particles to oscillate in a local region of the search space and fall into a local optimal solution, which prevents effective global search. Too large a variation amplitude may lead to population degradation. And when the magnitude of variation is too small, the particle population may oscillate around the known solution, slowing down the convergence speed and making it difficult to further improve the quality of the solution. In addition, a fixed or limited variation amplitude may cause the particle population to fall into a local region with local oscillations, which in turn leads to premature convergence and a lack of global search capability, especially in multi-peak optimization problems, where the variation frequency and amplitude fail to be dynamically adjusted, resulting in inefficient search.

In the TAMOPSO variational design, Lévy flights are used as a way of global variability and combined with local variability to balance global and local fine variability. The step size \({L}_{i}\) (Eq. 20) generated by the Lévy distribution has a strong jumping property, which enables the particles to make a wide range of jumps and jump out of the local optimal region, avoiding the local oscillations and search limitations of the traditional variational methods.

where \({u}_{i}\) and \({v}_{i}\) are random variables sampled from the normal and Lévy distributions, respectively. \(\beta\) is a parameter of the Lévy distribution that takes the value \(1<\beta \le 2\) over the range and determines the heavy-tailed nature of the distribution.

Global and local variation in the variation operation is switched according to the variation probability \(\gamma\) (Eq. 15). The mutation probability \(\gamma\) gradually decays with iterations, thus allowing the particle swarm to perform extensive global exploration at the beginning of the search and refine the search through local perturbations at a later stage. In addition, the inclusion of an archival growth rate factor in the mutation probability ensures that the particles do not continue to make excessive jumps as they approach the optimal solution, which avoids population degradation and improves the mutation efficiency. This adaptive mutation strategy improves the convergence speed of the particle population and ensures that the particles can find the global optimal solution more accurately in the final stage. The global and local particle mutation formulas are as follows:

where \(P\left(j,j\right)\) and \(P\left(k,j\right)\) are two randomly selected particles; \(r\) is a random number; \(\varepsilon\) is the magnitude of the perturbation controlling the local variation; In this paper, we set the size \(\varepsilon = 0.1\); a smaller perturbation allows the particles to be fine-tuned around their current position, which helps the algorithm to exploit the promising regions that have been found; \({u}_{i}\sim \text{N}(0,{\sigma }^{2})\) is a normally distributed random variable controlling the direction of the jumps;\(\sigma\) is a scale factor for the Lévy flight step:

where \(\Gamma\) is the Gamma function, which is a generalization of the factorial; \({v}_{i}\sim \text{N}(\text{0,1})\) is a standard normally distributed random variable that controls the scale of the jumps; and \(\beta\) is a parameter of the Lévy distribution, which usually takes values between \(1<\beta \le 2\), and controls the shape of the distribution of steps.

Adaptive Control of Lévy Flight Variation.

Full size image

Compared with the traditional Lévy flight implementation, the adaptive control mechanism of TAMOPSO focuses on global exploration (large jumps in Lévy flights) at the early stage of the search through the dynamically decaying variance probability \(\gamma\) and gradually shifts to local perturbations at the later stage for refined exploitation, which solves the problem of ineffective jumps or local oscillations at the later stage due to the fixed probability of the traditional method; meanwhile, TAMOPSO suppresses large jumps at the later stage by combining a dual-mode variance strategy (global Lévy flights and local normal perturbations) with a dynamically decaying At the same time, TAMOPSO suppresses large jumps in the late stage by dynamically decaying the mutation probability \(\gamma\) and the archival growth rate factor to avoid population degradation and combines the dual-mode mutation strategy (global Lévy flight and local normal perturbation) to achieve adaptive switching of the stage, complemented by the dynamically adjusted Lévy parameter \(\beta\) and the scale factor \(\sigma\), to synergistically optimize the distribution of the step lengths and the search strengths to reduce the dependence on manual parameter tuning. These improvements allow the algorithm to balance global exploration and local exploitation in multi-peak optimization, significantly improving convergence speed, solution quality, and the ability to avoid premature stagnation. The pseudo-code of Algorithm 3 gives the pseudo-code of the Lévy flight variant with adaptive control.

Uniform contribution margin metrics guide archive maintenance strategies

There are several major problems with common archive maintenance strategies. First, the dominance relationship judgment is inefficient, the dominance between particles needs to be compared frequently, and the computational complexity will rise rapidly when the number of particles increases. Second, if the archive is not limited, the number of particles may keep increasing, leading to increased storage and computational pressure. In addition, archiving usually suffers from insufficient diversity of solutions and easy loss of boundary solutions. Meanwhile, the range of the target space expands or contracts with particle changes, and the fixed grid division cannot be dynamically adjusted, which affects the adaptability of the dynamic target space. Finally, in high-dimensional spaces, the distribution of solutions tends to be biased towards certain target dimensions, leading to insufficient coverage of other dimensions, which affects the equilibrium of solutions. These problems significantly affect the performance of the algorithm, especially in the case of high dimensionality and diversity requirements, which poses a higher challenge to the archive design.

To address the above challenges this paper proposes a new metric-guided archive maintenance strategy. When the archive does not reach the threshold, the algorithm only compares the non-dominated particles in the population after iteration with the particles in the archive in a Pareto comparison, if the new particles dominate the particles in the archive, the dominated particles are deleted from the archive; if the new particles are dominated by the particles in the archive, the new particles are ignored directly, which reduces the size of the archive and the computational redundancy, and improves the efficiency. When the archive capacity exceeds the limitation threshold of 200, particles are filtered by grid division and new indicators. An adaptive grid (hypercubic grid in high dimensions) is established based on the fitness values of the particles in the archive and the candidate new particles, In the process of generating the adaptive grid, firstly, for each objective function dimension, the basic range is determined according to the maximum and minimum values of the particle adaptation value, and the boundary is extended outward by 5% (if all the values are the same, the extension of the unit range is mandatory); then the extended range is equally divided into 49 intervals, and 50 equally spaced grid splitting points are generated; finally, by judging the ___location of the particle’s adaptation value in each dimension in each interval, the corresponding multidimensional grid index is determined. This process ensures that the distribution of particles in the target space is uniformly quantified by dynamically adjusting the grid boundaries and interval divisions, providing the basis for subsequent density calculation and diversity maintenance. After establishing the adaptive mesh, each particle is assigned to the grid \(g\left({x}_{j}\right)\) in the target space:

For each mesh \({g}_{i}\), the particle density is defined as \(d\left(g\right)=\sum_{j=1}^{N}\mathcal{J}\left({x}_{i}\in g\right)\) where \(\mathcal{J}(\cdot )\) (Eq. 24) is an indicator function of whether the particle belongs to the mesh \({g}_{i}\). The value is 1 when the condition inside the parentheses is true; otherwise, the value is 0. For each particle l, check whether its grid indexes in all dimensions are equal to that of the ith particle, and if they are equal, then the counts are added by 1. Finally, the counts of all the particles are summed up, and the density of the grid where the ith particle is located is obtained.

After obtaining the grids and grid densities, all the particles in the densest grids are selected, and then the local uniformity contribution \(\mu\) (Eq. 25) metric is calculated for these particles; the particles in the high-density grids are measured by the local uniformity contribution metric, and some of the particles that have the smallest contributing to the archive uniformity by the number of exceeding the threshold (The threshold is a predefined size for the archive, which is set to 200, the population size, and setting the threshold to the archive size ensures that the high-quality particles in the archive are maintained within the predefined value for archive maintenance) are deleted (Fig. 4). In high-dimensional target spaces, the distribution of certain target dimensions may dominate the archive update, leading to uneven coverage. The distribution balance between local neighboring particles is measured by the new metric uniform contribution index, which prioritizes the retention of particles that contribute more to the uniformity.

where \({\overline{f} }_{i}=\frac{1}{N}\sum_{j=1}^{N}{f}_{i}({x}_{i})\) is the mean value of the ith objective; \(kNN\left({x}_{i}\right)\) is the set of nearest neighbor solutions, and the algorithm selects two particles as a nearest neighbor; and \(f\left({x}_{i}\right)\) denotes the value of the ith objective.

Uniform contribution factor guides archival maintenance.

Full size image

It is important to note that this mesh is built adaptively and will dynamically adjust (Eq. 27) the mesh boundaries according to the range of target values of the current particles to ensure the adaptability of the target space. Adapting to the dynamic changes in the target space improves the robustness of the archive update.

In addition, extending the mesh boundary through (Eq. 27) ensures that the boundary solution is preserved. Increasing the retention probability of the boundary solution ensures the integrity of the Pareto front.

TAMOPSO provides a fine-grained design treatment for archive maintenance, which solves common archive updating and maintenance problems. First, the diversity of the archive is effectively maintained through dynamic grid partitioning and density-driven particle screening to avoid excessive concentration of particles in the target space. Specifically, the algorithm can dynamically adjust the grid division according to the fitness values of the particles and preferentially retains the particles in low-density regions, thus ensuring the uniform distribution of the optimized solutions in the target space. In addition, the archive capacity is effectively controlled, and the archive size is maintained by eliminating particles in high-density regions when the capacity is exceeded, and avoiding the loss of critical solutions (e.g., boundary solutions). This is achieved through adaptive extension of the boundary and the computation of the uniformity contribution factor, allowing the archive to not only reflect the convergence of the Pareto front, but also to fully cover the target space. Redundant computations are also reduced through efficient dominance relation checking, which improves the speed of updating the archive and can significantly enhance the efficiency of the algorithm, especially when the number of particles is large. Finally, the ability to adjust the mesh and archive content according to the particle distribution ensures that a good solution distribution is always maintained in the dynamically changing target space. The algorithmic flow of the new index-guided archive maintenance strategy is given in Algorithm 4.

New indicators guide archive maintenance policies.

Full size image

Individual optimal update strategy

In traditional optimization algorithms, the update of the individual optimal solution usually relies on the comparison of single-objective fitness. Specifically, particles will choose the solution with a smaller fitness value to update their individual optimal solution. Although this approach performs well in single-objective optimization problems, it often faces problems such as dimensionality pressure and unfair selection in multi-objective optimization problems or more complex optimization problems.

\({P}_{best}\) update strategy.

Full size image

To solve these problems, this paper proposes an individual optimal solution updating method based on the Pareto dominance criterion and \({L}_{2}\) paradigm (\({\text{L}}_{\text{n}}\) paradigm in the n-dimensional case). Specifically, when particles update individual optimal solutions, the Pareto dominance criterion is first utilized to compare the fitness of the solutions. The Pareto dominance criterion can consider the relative relationship between multiple objectives simultaneously, rather than relying solely on the fitness value of one objective. When the fitness vectors between particles do not dominate each other, traditional methods are often unable to fairly choose which solution is superior. In this case, relying solely on the fitness of one objective to update the individual optimal solution may lead to unreasonable results, and it may even appear that some solutions are over-optimized while others are ignored. To solve this problem, when the solutions between particles are not dominated by each other, the algorithm selects the solution that is closer to the super-ideal point by calculating the \({L}_{2}\) paradigm distance between the particle fitness vector and the super-ideal point (where the super-ideal point is chosen to be the zero point). In this way, the algorithm can select a solution more fairly in a multi-objective optimization problem, avoiding over-optimization of one objective while considering the optimization of other objectives, ensuring the balance and effectiveness of the global optimization. Algorithm 5 demonstrates the individual optimal update strategy.

Parameter settings and performance indicators

TAMOPSO employs 22 test problems from three benchmark suites, ZDT³⁹, UF⁴⁰ and DTLZ⁴¹, to evaluate the algorithm performance. These test problems cover different difficulty levels; problems like ZDT1-ZDT3 are relatively basic, while some of the problems in the UF and DTLZ series are more complex. Complex problems may have multimodal, discontinuous, or irregular PF shapes, which make it difficult for the algorithms to find the optimal solution and place higher demands on the algorithms searching ability and their ability to balance convergence and diversity. In terms of dimensionality, the number of decision variables is different; in the two-objective test problem, the number of decision variables is set to 30 for ZDT1-ZDT3 and UF1-UF7 and 10 for ZDT4 and ZDT6, while in the three-objective test problem, the number of decision variables is 30 for UF8-UF10, 7 for DTLZ1, 12 for DTLZ2-DTLZ6, and 22 for DTLZ7, and the different The different dimensions mean that the algorithm needs to deal with different sizes of the solution space, and the increase in dimensionality will increase the difficulty of the algorithm in searching for the optimal solution. In terms of objective space characteristics, these problems have different PF shapes, such as concave, convex, multimodal, discontinuous, and irregular, etc. The PFs of the ZDT series may have specific geometrical shapes, while the UF and DTLZ series of problems cover more complex shapes, and these different characteristics can be used to check whether the algorithms can make the solutions as close to the real PFs and good on them as possible when they deal with different types of optimization problems. to the real PF and well-distributed over it.

The relevant parameter settings are presented in Table 1, where FEs denote the maximum number of evaluations. With five existing MOPSO algorithms (CMOPSO⁴², NMPSO⁴³, MPSOD⁴⁴, MOPSOCD⁴⁵, MOPSO) and five MOEA algorithms (DGEA⁴⁶, SPEAR⁴⁷, MOEADD⁴⁸, NSGAIII⁴⁹, IDBEA⁵⁰) Comparison experiments were conducted. To ensure fairness, the parameter settings of all comparison algorithms were consistent with the original text. Each algorithm was run independently 30 times on each test problem. The mean (mean) and standard deviation (Std) of the IGD and HV values were recorded, and the best results for IGD and HV are shown in bold. All experiments were implemented on an AMD Ryzen 7 4800U with Radeon Graphics 1.80 GHz, Windows 11, via MATLAB R2022b. source code for the comparison algorithms is provided by PlatEMO⁵¹.

Performance evaluation indicators

In this paper, the inverse generation distance (IGD)⁵² and hypervolume (HV)⁵³ are used as evaluation metrics for algorithm performance. Although both metrics can synthesize convergence and diversity, a single metric cannot fully evaluate the experimental algorithm. Therefore, these two metrics will be used to evaluate the performance of TAMOPSO with the selected MOPSO and MOEA algorithms.

The IGD (Eq. 28) provides important information about the accuracy of the algorithm and the quality of the solution set by measuring the distance between the approximate solution set and the true Pareto frontier. A smaller value of IGD indicates that the algorithm is closer to the true Pareto frontier in terms of solution quality and distribution.

where \({P}^{*}\) denotes the set of uniformly distributed solutions along PF in the objective space; \(S\) is the Pareto optimal set obtained by the algorithm; and \(dist\left({x}^{*},S\right)\) is the minimum Euclidean distance between solution \({x}^{*}\) and solution \(S\) in \({P}^{*}\);

HV (Eq. 29) is used to measure the volume covered by the solution set in the objective space, which can effectively assess the overall quality of the solution set, especially for problems with high dimensionality of the objective space. HV reflects the dominance and diversity of the optimized solution set, and it is one of the key metrics for assessing the performance of multi-objective optimization algorithms.

where \({Z}^{*}={Z}_{1}^{*},{Z}_{1}^{*},\cdots ,{Z}_{m}^{*}\) is the reference point in the target space where all Pareto optimal solutions dominate; \(\delta\) is the Lebesgue measure.

Comparison of experimental results

Comparison of IGD and HV with five existing MOPSOs

Tables 2 and 3 show the mean and standard deviation of IGD and HV obtained by the six MOPSO algorithms (CMPSO, MOPSO, MOPSOCD, MPSOD, NMPSO, and TAMOPSO) after 30 independent runs on 22 test problems. According to the test results in the table, TAMOPSO performed the best among the 22 test problems, obtaining 11 best IGD values and 10 best HV values, making it the algorithm with the highest number of best results among all the algorithms. In addition, to ensure that the conclusions are statistically reliable, a normality test was carried out on all HV and IGD values in the algorithm. The test results show that some of the data do not conform to normal distribution. In view of this, we introduced a non-parametric statistical hypothesis testing approach to the experimental results. The Wilcoxon rank sum test⁵⁴ was applied to assess whether there was a significant difference between the different algorithms at a significance level of \(\alpha = 0.05\). In each of the corresponding tables, the last row of the data is denoted by the symbols “ + ,” “-,” and “≈,” respectively: The results of the other algorithms are significantly better than those of TAMOPSO, significantly lower than TAMOPSO, and like TAMOPSO at the statistical level.

Table 2 demonstrates the significant advantages over the other five MOPSOs. Specifically, in the ZDT series, TAMOPSO outperforms the other five algorithms in four test problems, and only slightly underperforms the algorithm CMOPSO in the ZDT6 problem. However, TAMOPSO performs particularly well in the UF series, outperforming the other five algorithms in all six test problems, showing its strong optimization ability in high-dimensional problems. Although in the DTLZ series, TAMOPSO’s advantage is more limited, outperforming the other algorithms in only one test problem, when considering the 22 test functions of the three series, ZDT, UF, and DTLZ, TAMOPSO occupies a dominant position in 11 test problems, outperforming all the other algorithms in terms of number. This result indicates that TAMOPSO has a more stable and comprehensive advantage in solving complex multi-peak and multi-objective optimization problems.

As can be seen from the HV-based performance evaluation results in Table 3, TAMOPSO still obtains the largest number of the best HV results. In the ZDT4 test problem, TAMOPSO shows a significant advantage even though the five MOPSO algorithms have an HV value of 0, indicating that MOPSO is unable to converge at the final iteration, whereas TAMOPSO can achieve better convergence at the final iteration. This further validates the superior performance of TAMOPSO in terms of convergence and diversity.

Combining the predominance of IGD and HV in Tables 2 and 3, it can be concluded that TAMOPSO optimizes the particle swarm search process by introducing an advanced mechanism, which improves the algorithm’s global search ability and local accuracy. In the tests of ZDT series and UF series, the performance of TAMOPSO is even better, reflecting that the algorithm has strong adaptability and performance in dealing with high dimensional and complex objective optimization problems. In the DTLZ series, although the performance is not as good as the former two, it still shows better stability and reliability. Overall, TAMOPSO performs well on several standard test functions, especially in the ZDT series and UF series, and shows obvious advantages in overall optimization quality, solution efficiency and global convergence compared with the other five particle swarm algorithms.

Comparison of IGD and HV with five existing MOEAs

To further validate the performance of the TAMOPSO algorithm, this paper compares it with five common multi-objective evolutionary algorithms MOEAs (DGEA, IDBEA, MOEADD, NSGAIII, SPEAR). Tables 4 and 5 show the mean and standard deviation of these six algorithms on IGD and HV metrics, respectively, after 30 independent runs on 22 standard test problems.

Based on the IGD evaluation results in Table 4, the overall performance of TAMOPSO is significantly better than the other five algorithms on the ZDT, UF and DTLZ series of problems. In the ZDT series of problems, TAMOPSO performs well in all the test problems, only ZDT4 is second only to MOEADD while the other IGD values are lower than the other algorithms, which indicates that it is able to better converge to the Pareto front and maintain the diversity of the solution set, especially in the face of the complex nonlinear Pareto front, and it shows its strong global search ability. TAMOPSO also outperforms the other algorithms in the UF series of problems, with significantly lower IGD values than the other algorithms in most of the test problems, demonstrating its search efficiency in high-dimensional spaces and its ability to deal with goal conflicts. Although TAMOPSO outperforms other algorithms in only two test problems in the DTLZ series of problems, it still ranks second in most of the problems, showing strong robustness and stability, especially in dealing with complex high-dimensional problems.

In the HV evaluation results in Table 5, TAMOPSO’s performance is not as impressive as in the IGD metrics but still shows a relatively clear advantage. For the ZDT series, TAMOPSO outperforms the other five algorithms in terms of HV on four problems, and only slightly lags and fails to outperform the algorithm NSGAIII on the ZDT4 problem, which indicates that TAMOPSO is still capable of balancing the goal conflicts and converging the Pareto frontiers. For the UF series, TAMOPSO also leads to several test problems, and it outperforms the other algorithms in terms of HV on five test problems, showing its excellent optimization ability in high-dimensional problems. In contrast, TAMOPSO’s HV value in the DTLZ series is slightly less impressive, and although it exceeds the other algorithms in only one test problem, it still performs relatively well in the other test problems, placing it at the top of the list.

Overall, TAMOPSO performs well in several test problems of the ZDT and UF series, demonstrating strong global search capabilities and adaptability to multi-objective optimization problems. In the DTLZ series of problems, TAMOPSO maintains a good optimization performance despite facing higher dimensionality and complex Pareto frontiers, proving its robustness and stability in complex multi-objective problems. Overall, the excellent performance of TAMOPSO on these test functions shows that it is an efficient and adaptable multi-objective optimization algorithm suitable for handling a wide range of complex multi-objective optimization tasks.

Visual comparison of algorithms

Box plots measure algorithm stability

Figure 5 illustrates a box plot based on the IGD value data for the MOPSO and MOEAs algorithms in Tables 2 and 4. The 1 to 11 on the horizontal axis represent different algorithms: CMOPSO, MOPSO, MOPSOCD, MPSOD, NMPSO, DGEA, IDBEA, MOEADD, NSGAIII, SPEAR, and TAMOPSO, respectively. By scrutinizing the box plots corresponding to these algorithms, we can intuitively find that the box gap of TAMOPSO is significantly smaller, and the upper and lower quartile intervals of its box are relatively narrow. This phenomenon indicates that TAMOPSO exhibits the smallest solution set volatility among all the algorithms, suggesting that its stability is significantly better than the other algorithms in different runs. Therefore, TAMOPSO is not only able to obtain better solution quality but also has higher stability when solving multi-objective optimization problems, which makes it more reliable and advantageous in practical applications.

Box plots of 10 comparison algorithms and TAMOPSO on ZDT3, UF9, and DTLZ6 test problems.

Full size image

Comparison of Pareto frontiers

Figures 6, 7, and 8 show the distribution of Pareto-optimal solution sets for the ten comparison algorithms (CMOPSO, MOPSO, MOPSOCD, MPSOD, NMPSO, DGEA, IDBEA, MOEADD, NSGAIII, and SPEAR) versus TAMOPSO on the test problems ZDT3, UF9, and DTLZ6. By observing the distribution of the solution set in the figure, we can intuitively see that TAMOPSO outperforms other algorithms in both its convergence to the PF and its distribution on the PF.

Distribution of Pareto-optimal solution sets for the 10 algorithms compared and TAMOPSO on the ZDT3 test problem.

Full size image

Distribution of Pareto-optimal solution sets for the 10 algorithms and TAMOPSO on the UF9 test problem.

Full size image

Distribution of Pareto-optimal solution sets for the 10 compared algorithms and TAMOPSO on the DTLZ6 test problem.

Full size image

Figure 6 For the bi-objective test problem ZDT3, the performance of TAMOPSO is particularly outstanding compared to the other comparison algorithms. First, intuitively, only CMOPSO and TAMOPSO have solution sets that are both uniformly distributed and converge to the true Pareto front. In particular, the solution set of TAMOPSO not only shows strong convergence to the frontier but also shows a more uniform distribution of the solution set. By analyzing the data in Table 2, the solution set of TAMOPSO is more significant in approaching the true Pareto frontier compared to CMOPSO. This indicates that TAMOPSO has a greater ability to guide the convergence of the solution set to more accurately approximate the true optimal solution. In addition, the solution sets of the other compared algorithms either fail to approach the true Pareto frontier sufficiently in terms of convergence, or there are obvious localized concentrations in the distributions, resulting in a more limited diversity of solution sets. For the three-objective test problem UF9, the advantages of TAMOPSO are even more obvious.

Figure 7 shows the distribution of the solution sets of the 11 algorithms on this problem, and TAMOPSO can satisfy two key requirements at the same time: one is convergence, and the other is diversity of solution sets. As can be seen from the figure, the solution set of TAMOPSO not only converges perfectly to the true Pareto frontier but also has a uniform distribution of solution sets covering the entire range of the Pareto frontier. In contrast, the solution sets of other algorithms either have obvious deficiencies in convergence or are concentrated in a certain localized region, resulting in inadequate coverage of the Pareto front and poor diversity of the solution sets. For example, some algorithms form locally concentrated solution sets in certain parts of the frontier, failing to effectively cover the entire diversity region of the Pareto frontier. Therefore, the performance of TAMOPSO in the UF9 problem is significantly better than other algorithms both in terms of diversity and convergence, indicating that it can better balance the accuracy and diversity of the solution set in high-dimensional multi-objective optimization problems.

Finally, Fig. 8 shows the performance of the 11 algorithms under the complex multi-objective test problem DTLZ6. In this problem, TAMOPSO still performs well and can achieve a good balance of both convergence and diversity. Although CMOPSO, MOPSOCD, NMPSO and TAMOPSO are all able to converge to the true Pareto front, the distribution of the solution sets shows that only CMOPSO and TAMOPSO can distribute the solution sets uniformly over the Pareto front, ensuring better diversity. In contrast, although MOPSOCD and NMPSO also converge to the true frontier, their solution sets are unevenly distributed with obvious concentrated regions, which may lead to over-convergence of locally optimal solutions in some cases, limiting the diversity of solution sets. Therefore, TAMOPSO not only excels in convergence, but also has a significant advantage in maintaining the diversity of solution sets. In summary, TAMOPSO performs well in multi-objective optimization problems with strong convergence and excellent diversity of solution sets and can provide solution sets that are uniform and close to the true Pareto frontier in different test problems, which is significantly better than the other compared algorithms.

Comparison of convergence trajectories

To further validate the performance of the algorithms, we compared the convergence speeds of ten existing algorithms with TAMOPSO on three classical test problems, ZDT3, UF9 and DTLZ6, and made a visual comparison. By observing the convergence trajectories of the algorithms in Fig. 9, it can be clearly seen that TAMOPSO is able to reach the optimal IGD value earlier compared to the other compared algorithms. This phenomenon indicates that TAMOPSO is not only able to effectively guide the convergence of the populations, but also significantly accelerates the convergence process, showing a strong convergence speed advantage. Specifically, TAMOPSO can quickly find solutions closer to the true Pareto frontier in each round of iterations, thus reducing the number of iterations in the optimization process. This accelerated convergence speed is of great significance for solving complex multi-objective optimization problems, as it can provide high-quality solution sets in a shorter period, which greatly improves the computational efficiency of the algorithm.

10 comparison algorithms and TAMOPSO on ZDT3, UF9, DTLZ6 test problems Convergence trajectory plot.

Full size image

Friedman rank test

The Friedman rank test is an ideal tool when dealing with the comparison of multiple algorithms with multiple test problems. By statistically analyzing significant differences in algorithm performance, the Friedman rank test can help to more accurately determine the strengths and weaknesses of different algorithms without the stringent data distribution requirements of traditional methods. Its support for multiple comparisons makes it possible to more effectively evaluate the combined performance of algorithms when faced with complex multi-objective optimization problems.

From the IGD values of the TAMOPSO algorithm and the Friedman rank test results of each compared algorithm in Table 6, TAMOPSO consistently ranks first in the rank rankings of the ZDT and UF series of problems, which shows its excellent performance in these problems. Despite its relatively weak performance in the DTLZ series of problems, which leads to its lower rank in this series, overall, TAMOPSO still maintains the first place in the rank ranking, which fully proves its balanced advantage in terms of diversity and convergence. This suggests that TAMOPSO can provide more stable and better solutions when dealing with different types of multi-objective optimization problems, especially in the ZDT and UF series of optimization problems.

The analysis of the Friedman rank test results of TAMOPSO in terms of HV values versus each of the compared algorithms in Table 7 also shows that TAMOPSO once again ranked first in the rankings of the ZDT and UF series, which further validates its combined advantages in terms of convergence and diversity. Despite the dip in rank on the DTLZ problem set, resulting in its third place in overall HV, this result also reveals the potential room for improvement of the TAMOPSO algorithm on the DTLZ test problems. Thus, despite TAMOPSO’s slightly inferior performance on some of the test problems, its overall superiority is still evident, especially on the ZDT and UF problems, demonstrating the algorithm’s strong potential and scalability in the field of multi-objective optimization.

Sensitivity analysis of experimental parameters

This subsection develops a sensitivity analysis around the algorithm’s parameters, aiming to provide insights into the following key elements: assessing how variations in parameter values affect the algorithm’s performance in different test problems; determining the optimal or recommended parameter ranges for various scenarios; and demonstrating TAMOPSO’s robustness under different configurations.

Six representative test problems, namely ZDT1, ZDT2, UF3, UF4, DTLZ6, and DTLZ7, are selected for the experiment, which covers multi-objective optimization scenarios of different types and difficulties and can comprehensively and efficiently reflect the effects of parameter changes on the performance of the algorithm. In the experiments, the algorithm parameters C1, C2, C3, and C4 are emphasized for testing. Because the inertia weight W in this paper is adaptively transformed by high-quality particles in the test archive, to ensure the accuracy and validity of the experimental results, the inertia weight is not tested in this parameter sensitivity analysis experiment.

The experiments were conducted with different values for each parameter: 0.1, 0.5, 1, and 1.5 for C1; 0.4, 0.8, 1.2, and 1.6 for C2; 0.05, 0.1, 0.15, and 0.2 for C3; and 0.5, 1, 1.5, and 2 for C4. The experimental data are organized as shown in Table 8 to evaluate the performance of the algorithm in different test problems by comparing the IGD values with different parameter settings. Evaluate the impact of parameter changes on the performance of the algorithm in different test problems.

From the data in the table, the different values of each parameter have different impacts on the performance of the algorithm under different test problems. For parameter C1, when C1 = 0.5, the number of preferences reaches half, while the number of preferences for other parameters does not reach half; for parameter C2, only when C2 = 0.4 is preferred in ZDT1, and most of the remaining preferences occur when C2 = 0.8; among the values of C3, the largest number of preferences is found when C3 = 0.1; the experimental parameter preferences of C4 are similar to that of C2, and five out of six test problems are preferred when C4 = 1.5, and only when C4 = 1 is preferred; C4 = 1 is preferred by the algorithms of all the test problems. The experimental parameter preference for C4 was like C2, with 5 out of 6 test problems at C4 = 1.5 and only 1 out of 6 test problems at C4 = 1 in DTLZ7.

It is thus determined that the optimal or recommended parameter ranges under these test problems is C1 = 0.5, C2 = 0.8, C3 = 0.1, and C4 = 1.5. Under this parameter combination, the algorithm has the highest number of optimal numbers in different test problems, which suggests that it has a better robustness under different configurations, which is more conducive to the algorithm to achieve a good performance in the multi-objective optimization scenario. This series of experimental results provides a strong parameter selection basis for the practical application and further optimization of the algorithm and fully demonstrates the robust characteristics of TAMOPSO under different configurations.

Ablation study

In this paper, multiple strategies are innovatively combined to achieve the optimization of the MOPSO algorithm. To deeply investigate the actual effectiveness of each strategy in the algorithm, an ablation experiment is designed, which evaluates the impact of these mechanisms on the overall performance of the algorithm by removing specific mechanisms from the algorithm.

Specifically, the TAMOPSO algorithm was set up to compare its performance with four variants of the algorithm: firstly, TAMOPSO with the removal of the individual optimal update strategy (labeled TAMOPSO—234); secondly, TAMOPSO with the removal of the population delimitation and task allocation strategy (labeled TAMOPSO—134); thirdly, TAMOPSO with the removal of the uniform contribution metrics guiding the archival maintenance strategy (labeled TAMOPSO—124); and the fourth is TAMOPSO (labeled TAMOPSO—123), which removes the Lévy flight variation strategy for adaptive control. During the experiments, the parameter settings of these four variants of the algorithm were kept identical to those of TAMOPSO to ensure a fair and accurate comparison of the algorithms’ performance.

Subsequently, the four variants of the algorithms were tested on problems in the ZDT, UF and DTLZ test suites, respectively. Each test problem was run independently for 30 times, and the results of each run were recorded and statistically analyzed for the IGD and HV metrics to obtain the mean and standard deviation of these two metrics, and the comparison results are presented in Tables 9 and 10. Meanwhile, Wilcoxon rank sum test is applied to detect the significance of the performance difference between TAMOPSO and the four variants of the algorithm.

From the experimental results, in the IGD data table in Table 9, the four variants of the algorithm are 0, 2, 0, and 3, while the original TAMOPSO algorithm has as many as 17; similarly, in Table 10, the four variants of the algorithm are 1, 2, 0, and 4, while the original TAMOPSO algorithm has 12. These data fully confirm that the organic combination of the four strategies significantly improves the comprehensive performance of TAMOPSO and plays a crucial role in the algorithm.

In this paper, a novel multi-objective optimization algorithm is proposed to overcome the problems of premature convergence, lack of diversity, and difficult coordination of inter-objective conflicts in traditional algorithms by introducing multiple mechanisms. First, for the uniform distribution of the population, the algorithm assigns proportionate weights to the convergence and diversity of each particle and optimizes the evolutionary process by using a sub-population strategy. Second, it is difficult to balance the target conflicts with a single search strategy. A new speed control mechanism is designed to adjust the search strategy according to the subpopulation characteristics, which improves the local search efficiency and balances the relationship between exploration and exploitation. In terms of mutation operation, an adaptive Lévy flight mutation strategy is proposed to balance the global and local search by detecting the growth rate and local mutation of the archive, which effectively reduces the difficulty of parameter adjustment and improves the mutation rate. To better approximate the Pareto frontier, this paper also innovatively introduces the concept of archive particle uniformity contribution factor to optimize the archive quality by deleting low contribution particles. Finally, to address the problems of unfair selection and dimension pressure of individual optimal updates in traditional algorithms, this paper selects optimal particles by Pareto comparison and \({L}_{2}\) paradigm, which significantly improves the fairness of selection and reduces the dimension pressure. These innovative mechanisms enable the algorithm to show significant advantages in terms of convergence speed, solution set diversity and global optimization capability. Through in-depth comparative analysis of experimental results, the TAMOPSO algorithm was comprehensively compared with five existing MOPSO algorithms and five MOEA algorithms from multiple dimensions such as convergence, diversity, and stability. Its performance on 22 standard benchmark problems was evaluated. The experimental results show that TAMOPSO demonstrates significant advantages in terms of convergence, diversity, and stability in these benchmark problems, outperforming the other comparison algorithms.