Introduction

The digital economy (DE) has recently experienced remarkable development worldwide, and its potential impact on environment is a topic of great interest (Lange et al. 2020; Tranos et al. 2013; Lyu et al. 2023; Di Vaio et al. 2022). The International Energy Agency predicts that the widespread use of digital technologies could reduce the cost of oil and gas production by 10 to 20%. In China, DE has been identified as a crucial driver to promote high-quality economic development (Chen et al. 2022; Liang and Li 2023; Huang and Zhang 2023). The Chinese government has recognized the importance of DE and has included it in the “14th Five-Year Plan” for the country’s development, with a clear focus on promoting green development through the digital transformation.

Utilizing DE to achieve China’s low-carbon transition requires giving priority to improving carbon total factor productivity (CTFP) (Lin and Xu 2018; Li et al. 2021; Su et al. 2023). However, measuring the impact of DE on CTFP is the first challenge that must be addressed. While the term “DE” was introduced by Tapscott (1996), there is no uniform definition of the concept in academic literature. Bukht and Heeks (2018) classified DE into three levels: the core level, which includes DE infrastructure; the middle level, comprising digital services and platform economy; and the output level, encompassing economic activities driven by DE. Building on this classification, Chen et al. (2022) defined DE more broadly, covering the entire process from the underlying technical foundation of DE to the output activities of DE, including four key dimensions: digital information base, internet platform, digital technology, and new economic models and industries. By incorporating these four dimensions into the measurement of DE, this paper presents a more comprehensive approach to measuring DE development than existing studies (Bai and Zhang 2021; Huang et al. 2019).

The second difficulty in investigating the impact of DE on CTFP is how to address the endogeneity issue caused by the reverse causality between DE and CTFP, and the correlation between the measurement error of CTFP and the residual in the regression equation. Although a few studies have explored the impact of the DE on carbon emissions (Dong et al. 2022; Li and Wang 2022) and energy efficiency (Wang and Shao 2023), these studies have not fully addressed the issue of endogeneity, and consequently, the findings they report may be biased. To overcome this difficulty, this paper constructs a novel analytical framework that can examine the impact of DE on CTFP and estimates its potential for reducing carbon emissions. By using the endogenous stochastic frontier approach (endogenous SFA), this paper can address the critical issues that previous research has not fully accounted for, such as endogeneity resulting from potential reverse causality between DE and CTFP, as well as correlations between measurement error of CTFP, which is calculated by data envelope analysis (DEA) or stochastic frontier analysis (SFA), and the residual in the regression equation. By overcoming these challenges, we can accurately estimate the impact of DE on CTFP and the potential for carbon emissions reduction and apply it to the case of China using the prefecture-level city data from 2004 to 2017.

The findings show that DE has a positive and significant impact on CTFP in China once the endogeneity issue of DE is addressed. The positive effect is mainly through changes in production methods (efficiency improvement and green innovation) and optimization of urban environmental regulation and governance (environmental regulation). Moreover, the positive effect of DE on CTFP is stronger for residents with higher green awareness, cities with lower resource abundance, and higher levels of human capital. Additionally, a balanced development of DE has the potential to achieve greater CO2 emission reductions. Finally, this paper provides some important policy implications for policymakers in achieving a successful low-carbon transition in China, including further developing DE, promoting the adoption of energy-efficient technologies, increasing the investments on corporate green innovation and balancing the regional development of DE.

This article makes three contributions. First and foremost, a novel analysis framework is constructed that can effectively address the estimation bias and endogeneity problems that arise from traditional methods of estimating the impact of different factors on carbon efficiency. Specially, the endogenous SFA approach is adopted, which offers several key advantages over traditional two-step approaches (to measure the efficiency in the first stage and regress it on the impact factors in the second stage). When the non-efficiency term is correlated with the residual term in the regression equation of the second stage, consistent estimates of the coefficients of the variable of interest cannot be obtained. This issue is resolved by the one-stage approach utilized in this paper, which also does not require bootstrap correction for the standard deviation of the estimated parameters (Trans and Tsionas 2013; Kutlu 2010).

Moreover, the endogeneity problem inherent in traditional stochastic frontier models can lead to inconsistent parameter estimates. The maximum likelihood method, commonly employed for parameter estimation in stochastic frontier models, requires modeling based on the joint distribution of the explanatory and endogenous variables when endogeneity is present. However, this process becomes more complex when the residual terms contain both bilaterally and unilaterally distributed inefficient terms, as is typical in traditional regression. The endogenous SFA method employed in this study effectively addresses both the endogeneity problem due to the correlation between the two-sided error and one-sided error, between the measurement error of CTFP, which is measured by DEA or SFA, and the residual in the regression equation, as well as the endogeneity problem due to the correlation between the regression variables and the residuals of the two-sided error term (Karakaplan and Kutlu 2017). As a result, this method allows for a more scientifically rigorous and accurate assessment of the effect of any factors on CTFP, and it can be applied in other studies.

Second, a new and comprehensive indicator for measuring the development of DE is constructed based on its four connotations, namely digital information, internet platform, digital technology, and new economic and business models. This new indicator enables a more comprehensive and precise measurement of DE development in Chinese cities, by including DE technologies that are not considered in previous studies.

Finally, we apply the analysis framework to the case of China, and estimate both the impact of DE on CTFP and the carbon emissions reduction potential. Given that carbon reduction is a pressing issue and improving CTFP should be of utmost importance for policymakers, this paper provides the empirical evidence that developing DE can serve as a valuable means to achieve carbon emissions reduction.

Because this paper is mainly conducted from the macro perspective, we concentrate our data on the city level. In the future, we can further extend the research to firm level and yield more nuanced findings.

Literature review

The impacts of digital economy

Research on the green development effects of DE has only recently emerged, and recent studies suggest that DE does contribute to the low-carbon transformation and sustainable development of the economy. Tapscott (1996) first proposes the term “digital economy”, defining it as an economic system that makes extensive use of information and communication technologies. As an important engine of the new round of technological revolution and industrial innovation (Wei et al. 2023), the impact of DE has attracted extensive attention from academics. Most of the existing studies focus on the impact of DE on economic development and enterprise efficiency. For example, studies have found that the development of DE can promote economic growth (Guo et al. 2023; He et al. 2022), enhance enterprise innovation (Peng et al. 2023), optimize organizational structure (Bloom et al. 2012), increase energy efficiency (Zhang et al. 2022) and improve total factor productivity (Pan et al. 2022).

Several recent studies suggest that DE contributes to low-carbon transformation and sustainable development (Cheng et al. 2023). For instance, Cao et al. (2021) demonstrate that digital finance significantly contributes to energy and environmental performance in China. Yu (2022) find that internet technology enhances the green development of industry, while Haseeb et al. (2019) deem that the use of the internet significantly reduces carbon emissions and promotes green total factor energy efficiency in industry. Ma et al. (2020) believe that the use of big data in energy-intensive industries can predict energy consumption parameters and production status in the production process, leading to improved energy efficiency. However, digital finance, internet, blockchain, and big data technologies only represent a subset of DE technologies and may not fully reflect the effects of DE. Other studies suggest that the introduction of DE technology can significantly promote China’s green economic growth (Zhang et al. 2022) or have a positive impact on the efficiency of urban green development (Luo et al. 2022). The main mechanisms through which DE affects green development include reducing carbon dioxide emissions (Yi et al. 2022; Haseeb et al. 2019) and significantly improving energy efficiency (Wu et al. 2021).

Carbon total factor productivity and its influencing factors

The concept of carbon emission efficiency, measured by carbon intensity (CO2 emissions per unit of GDP), has limitations in accurately measuring productivity gaps between actual and optimal production units due to the lack of consideration for other input factors such as labor and energy (Wang et al. 2013). In response, measuring carbon emission efficiency within a total factor framework has gained traction among scholars, referred to as CTFP (Zhou et al. 2010; Zhang and Choi 2013; Zhou and Tang, 2021). While the data envelopment analysis (DEA) method has been commonly used to measure CTFP, its nonparametric nature does not account for random disturbances in the production process, resulting in inefficient confidence intervals and the inability to handle statistical noise and outliers (Lin and Du 2015; Coelli et al. 2005). Although some scholars use Bootstrap in DEA methods for statistical inference and testing, Coelli et al. (2005) argue that the use of Bootstrap in the DEA framework can only deal with the variability of the sample and cannot take into account statistical noise. Not only that, the results obtained by DEA method are easily disturbed by outliers in the sample, thus making the efficiency measures unrobust. Stochastic frontier analysis (SFA) can overcome the above shortcomings of DEA method and is applied to analyze the CTFP in China in this paper.

To address these limitations, this paper proposes the use of stochastic frontier analysis (SFA) to analyze CTFP in China. SFA can overcome the shortcomings of the DEA method, offering a more robust measurement of efficiency. However, prior literature on factors influencing production efficiency typically follows a two-step approach, employing SFA or DEA in the first step to measure production efficiency and regression analysis in the second step to explore the effects of different factors. Yet, omitting factors and measurement error that may impact efficiency in the first step may lead to inconsistent parameter estimates in the second step (Wang and Schmidt 2002; Liu et al. 2020), regardless of whether the two-sided error is correlated with influencing variables or not. Previous studies have examined the effects of various factors, such as manufacturing agglomeration (Zhang and Tu 2022), foreign trade (Lin and Liu 2015), and structural transformation (Liu and Lin 2020).

The present body of literature offers a valuable foundation for studying the correlation between DE and green development. However, certain issues remain unresolved. Firstly, as a relatively new concept, the measurement of DE development levels is still in its early stages and lacks a unified standard. Most existing studies utilize single dimensions of DE, such as the degree of internet development or the digital financial inclusion index, as indicators of DE. Consequently, they fail to consider DE technology in their measurements, leading to an incomplete reflection of the actual situation of DE development.

Secondly, in terms of research methodology, the “two-step approach” for examining the impact of DE on CTFP may lead to biased parameter estimates. Similarly, the traditional “one-step” stochastic frontier analysis (SFA) method may produce biased estimates due to the correlation between DE and inefficiency or the two-sided error term. Using the one-step SFA method, the correlation between DE and non-efficiency or random disturbance terms may also result in biased estimates. While many studies have proposed various approaches to overcome the problems in the “two-step” approach, they usually assume the independence between the one-sided error term and two-sided error term or between the two-sided error and frontier regressors (Guan et al. 2009; Tran and Tsionas 2015; Amsler et al. 2016). In line with Karakaplan and Kutlu’s (2017) method, we employ the endogenous SFA method to examine the impact of China’s DE on CTFP and provide policy implications for future DE development and achieving a low-carbon transition based on our findings. Finally, few studies have delved into the effects of DE on China’s CTFP, and the existing evidence of the underlying mechanisms is insufficient.

Theoretical analysis

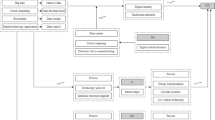
As a nascent economic and social development phenomenon, DE is capable of circumventing the geographical limitations of economic activities, mitigating transaction costs and resource mismatches, enabling data sharing, promoting enterprise innovation, and enhancing efficiency changes, which can significantly contribute to the advancement of high-quality and green development in China. Based on the existing studies, this paper specifically focuses on the transformations in production methods and the optimization of urban environmental governance as the underlying mechanisms by which DE can positively affect CTFP in China. These hypotheses are graphically illustrated in Fig. 1.

Fig. 1
figure 1

The mechanisms of DE to promote green development.

Full size image

Firstly, DE has the potential to facilitate significant changes in production methods. Primarily, DE plays a pivotal role in promoting green development by enhancing operational and production management efficiency, as well as energy efficiency. By integrating digital technology into traditional industries, DE optimizes the production mode of these industries and improves their operational efficiency and resource utilization (Bai and Zhang 2021). Luo and Li (2015) highlight the internet’s capacity to reduce information transfer costs, dismantle information barriers, and bolster manufacturing efficiency. Shi (2016) contends that internet technology decreases transaction costs and optimizes resource allocation. Utilizing digital information technology to monitor, analyze, and manage product and process information effectively curbs resource and energy waste in production processes, fostering efficiency gains. Furthermore, employing digital technologies such as big data, cloud computing, and artificial intelligence aids in overcoming fragmentation and information asymmetry in business decision-making, thereby enhancing labor productivity, operational management efficiency, and ultimately reducing energy consumption. Consequently, this study posits the first research hypothesis:

H1: DE positively impacts CTFP by augmenting production efficiency.

Second, DE contributes to green development through the promotion of technological innovation. DE has the potential to enhance innovation collaboration and knowledge sharing within enterprises by integrating digital technologies such as big data, the internet of things, and cloud computing into traditional industries, ultimately promoting the role of digital technology empowerment (Bai and Yu 2021; Han et al. 2014; Bertschek et al. 2013; Kohli and Melville 2019). Moreover, the application of internet technology increases the likelihood of knowledge acquisition and transformation into innovation, which demonstrates its capacity to drive innovation activities in manufacturing. Additionally, the adoption of multifaceted smart energy systems and new power systems supported by digital technologies provides the necessary technological framework for green transformation. Furthermore, DE reduces the cost of information dissemination and enhances the efficiency of innovation sharing and dissemination (Paunov and Rollo 2016). In the process of optimizing the digital transformation and innovation capacity of cities, it creates an environment conducive to innovation and attracts innovative talents, effectively promoting technological innovation and green development. Hence, the second research hypothesis is as follows:

H2: DE can positively impact CTFP by promoting technological innovation.

Finally, DE plays a crucial role in optimizing urban environmental regulation and governance and enhancing the efficiency of urban resource recycling (Jin et al. 2024). The development of DE offers a technological catalyst for environmental regulation across various industries, thereby facilitating the green transformation. Firstly, digital technology emerges as a novel tool for environmental regulation. Environmental protection agencies employ cutting-edge technologies such as big data, industrial internet, internet of things, satellite remote sensing, and smart environmental monitoring systems to monitor real-time environmental indicators, including pollution emissions, enabling prompt awareness of energy utilization dynamics and pollution emissions within cities (Xu et al., 2022). Zhang et al. (2018) discover that big data technology can effectively identify energy intensive industries and detect energy wastage, thus presenting new opportunities for energy conservation and emission reduction in the manufacturing sector. Furthermore, the application of digital technology in environmental protection regulation curtails environmental fraud and data distortion, thereby compelling the transition to low-carbon practices. Hence, this paper proposes the third research hypothesis:

H3: DE can positively influence CTFP by enhancing environmental regulation.

Data and methodology

Data

This paper employs the panel data of 223 cities in China from 2004–2017 due to data availability. The reason for limiting the research interval is that the fixed asset investment data at the prefectural level are temporarily unavailable in 2018 and beyond, so it is not possible to estimate the capital stock of each prefecture since 2018 on. Additionally, data on import and export trade volume of enterprises in each prefecture before 2004 is significantly lacking. The primary sources of the original data used in this research include the China City Statistical Yearbook, the Enterprise Search database, and the annual reports of each listed company. The variables used in the study and their sources are described below:

  1. (1)

    Carbon total factor productivity

This paper employs several input and output variables to measure the CTFP of each city, including capital stock, labor, energy, gross industrial output, and carbon dioxide emissions. In line with Lin and Tan (2019), the capital stock is calculated based on fixed asset investment data of each city, using the perpetual inventory method. Electricity consumption is used to measure energy, given its availability at the city level. The CO2 emissions data are sourced from the Center for Global Environmental Research website, which provides global CO2 emissions data. To ensure comparability, we aggregate the 1kmx1km raster data to the level of each prefecture-level city.

  1. (2)

    The level of development of DE

The lack of a unified standard for measuring DE has been a subject of debate in the literature. To address this issue, Chen et al. (2022) establish a theoretical framework for DE in the context of China’s development, and present the scientific definition of DE. Drawing on this theoretical framework, this paper develops a set of measurement indices to assess the level of DE development. The indices are constructed from four perspectives of digital information: internet platform, digital technology, new economic and business models. The specific measures for each sub-index are outlined in Table 1.

Table 1 Formation of DE indicator.
Full size table

Digital information

In this paper, we consider two dimensions: information foundation and information impact. Specifically, we use the proportion of information transmission computer service employees in each city to the total number of employees as a proxy variable for information foundation, and the telecommunication business income to measure information impact.

Internet platform

The number of internet broadband access users and the number of cell phone users are used to measure it.

Digital technology

This paper employs Python technology and uses the word frequency ratio of digitalization-related terms in the annual reports of business discussion and analysis contents of listed companies in each city as a proxy variable for the technology application penetration of listed companies.

New and business mode

The number of enterprises whose main business content includes e-commerce in each city is from the Enterprise Search Database, and the number of enterprises whose main business includes e-commerce of each city per unit of area is used to measure the level of digital transaction basis of the city.

  1. (3)

    Control variables

Other control variables used include economic development, industrial structure (ind_str), and trade openness (openness). The logarithm of GDP of each city, the share of tertiary industry in each city, and the ratio of import/export trade and foreign direct investment to GDP of each city are used to indicate them respectively.

  1. (4)

    Mechanism variables

This paper examines the role of DE in improving CTFP through three mechanisms: efficiency improvement effect, technological innovation effect, and environmental regulation effect. The measurement of total factor energy efficiency (TFEE), a crucial indicator of efficiency improvement, utilizes various variables such as labor, electricity consumption, capital, and gross industrial output of each city from 2004 to 2017. To capture the impact of technological innovation, we use the number of green utility models applied for and approved for each city in each year as a percentage of the total number of utility model patents applied for in the region that year. The proxy variable for environmental regulation is represented by the comprehensive industrial solid waste utilization rate for each city. Descriptive statistics for the variables used in the analysis are presented in Table 2.

Table 2 Descriptive statistics of all the variables.
Full size table

Model specification

Based on the analysis in Section “Theoretical Analysis”, DE is posited to enhance CTFP by improving energy efficiency, fostering green innovation, and optimizing the environmental regulation. However, the casual relationship between DE and CTFP is complex, as highlighted by the potential for reverse causality, where CTFP could in turn influence the development and deployment of digital technologies. Additionally, inaccuracies in measuring CTFP may confound the relationship, leading to endogeneity issues in the regression analysis. Studies in the field, such as those by Dong et al. (2022), Zhang et al. (2022) and Wang and Shao (2023), have begun to investigate these complexities but have stopped short of addressing the full spectrum of endogeneity concerns. Our approach is informed by this gap in the literature and aims to construct a robust analytical framework. By adopting the endogenous SFA, our model accounts for the endogeneity caused by bidirectional causality between DE and CTFP and the correlation between the nonefficiency term and regression residual, which are typically overlooked. This methodology is supported by the theoretical assertion that a more sophisticated econometric treatment is necessary to discern the true impact of DE on CTFP. Such a treatment is in accordance with recent advancements in the field (Karakaplan and Kutlu 2017; Karakaplan and Kutlu 2019), providing a more precise and theoretically justified estimation of the effects of DE, thus contributing to the body of knowledge with evidence-based insights into policy and strategic implications for sustainable economic development. In the following part, we will first define CTFP and then derive the model we estimate.

Definition of CTFP

In order to model CTFP, this paper needs to first define it. First, we define the environmental production technology (PT) as follows:

$$PT=\{(K,L,E,Y,C{O}_{2})|(K,L,E)can\;produce(Y,C{O}_{2})\}$$
(1)

where, K, L, E and Y indicate capital, labor, energy and GDP, respectively.

According to Zhou et al. (2010), we define the carbon Shephard distance function as follows:

$${D}_{c}(K,L,E,Y,C{O}_{2})=\sup \{\delta |(K,L,E,Y,C{O}_{2}/\delta )\in PT\}$$
(2)

Carbon Shephard distance function measures the maximum percentage reduction in CO2 emissions that can be achieved when holding the environmental production technology, capital, labor, energy, and output in the economic production process constant (Coelli et al., 2005). In this setting, if the ideal minimum emissions of carbon dioxide are represented by\(C{O}_{2}^{\ast }\), the CTFP can be expressed as

$$CTFP=C{O}_{2}^{\ast }/C{O}_{2}=1/{D}_{c}(K,L,E,Y,C{O}_{2})$$
(3)

Model specification

To avoid the possible estimation bias caused by model misspecification, the carbon Shephard distance function form is assumed to be:

$${\mathrm{ln}}\,{D}_{c}^{t}({K}_{i}^{t},{L}_{i}^{t},{E}_{i}^{t},{Y}_{i}^{t},C{O}_{2i}^{t})={\alpha }_{i}+f({\mathrm{ln}}\,{K}_{i}^{t},\,{\mathrm{ln}}\,{L}_{i}^{t},\,{\mathrm{ln}}\,{E}_{i}^{t},\,{\mathrm{ln}}\,{Y}_{i}^{t},\,{\mathrm{ln}}\,C{O}_{2i}^{t},t)+{v}_{it}$$
(4)

Where, αi is the individual fixed effect; vit is the error term.

The specific form of \(f({\mathrm{ln}}\,{K}_{i}^{t},\,{\mathrm{ln}}\,{L}_{i}^{t},\,{\mathrm{ln}}\,{E}_{i}^{t},\,{\mathrm{ln}}\,{Y}_{i}^{t},\,{\mathrm{ln}}\,C{O}_{2i}^{t},t)\) is unknown and we use its second order Taylor expansion at \(({\mathrm{ln}}\,\overline{K},\,{\mathrm{ln}}\,\overline{L},\,{\mathrm{ln}}\,\overline{E},\,{\mathrm{ln}}\,\overline{Y},\,{\mathrm{ln}}\,\overline{CO}_{2},0)\) to represent it, where, \(\mathop{K}\limits^{\_\_},\mathop{L}\limits^{\_\_},\mathop{E}\limits^{\_\_},\mathop{Y}\limits^{\_\_},\mathop{C{O}_{2}}\limits^{\_\_\_\_}\) is the mean value of the variables, respectively. Therefore, we can get:

$$\begin{array}{c}{\mathrm{ln}}\,{D}_{c}^{t}({K}_{i}^{t},{L}_{i}^{t},{E}_{i}^{t},{Y}_{i}^{t},C{O}_{2i}^{t})={\alpha }_{i}+{\beta }_{k}{k}_{i}^{t}+{\beta }_{l}{l}_{i}^{t}+{\beta }_{e}{e}_{i}^{t}+{\beta }_{y}{y}_{i}^{t}+{\beta }_{c}{c}_{i}^{t}+{\beta }_{t}t\\\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad +{\beta }_{kl}({k}_{i}^{t}\cdot {l}_{i}^{t})+{\beta }_{ke}({k}_{i}^{t}\cdot {e}_{i}^{t})+{\beta }_{ky}({k}_{i}^{t}\cdot {y}_{i}^{t})+{\beta }_{kc}({k}_{i}^{t}\cdot {c}_{i}^{t})\\\qquad\qquad\qquad\qquad\qquad +{\beta }_{le}({l}_{i}^{t}\cdot {e}_{i}^{t})+{\beta }_{ly}({l}_{i}^{t}\cdot {y}_{i}^{t})+{\beta }_{lc}({l}_{i}^{t}\cdot {c}_{i}^{t})\\\qquad\qquad\qquad\qquad\qquad\qquad +{\beta }_{ey}({e}_{i}^{t}\cdot {y}_{i}^{t})+{\beta }_{ec}({e}_{i}^{t}\cdot {c}_{i}^{t})+{\beta }_{yc}({y}_{i}^{t}\cdot {c}_{i}^{t})\\\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad +{\beta }_{kk}{({k}_{i}^{t})}^{2}+{\beta }_{ll}{({l}_{i}^{t})}^{2}+{\beta }_{ee}{({e}_{i}^{t})}^{2}+{\beta }_{yy}{({y}_{i}^{t})}^{2}+{\beta }_{cc}{({c}_{i}^{t})}^{2}\\\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad +{\beta }_{tk}(t\cdot {k}_{i}^{t})+{\beta }_{tl}(t\cdot {l}_{i}^{t})+{\beta }_{te}(t\cdot {e}_{i}^{t})+{\beta }_{ty}(t\cdot {y}_{i}^{t})+{\beta }_{tc}(t\cdot {c}_{i}^{t})+{\beta }_{tc}{t}^{2}+{v}_{it}\end{array}$$
(5)

where, \({k}_{i}^{t}=\,{\mathrm{ln}}\,{K}_{i}^{t}-\,{\mathrm{ln}}\,\overline{K}\), \({l}_{i}^{t}=\,{\mathrm{ln}}\,{L}_{i}^{t}-\,{\mathrm{ln}}\,\overline{L}\), \({e}_{i}^{t}=\,{\mathrm{ln}}\,{E}_{i}^{t}-\,{\mathrm{ln}}\,\overline{E}\), \({y}_{i}^{t}=\,{\mathrm{ln}}\,{Y}_{i}^{t}-\,{\mathrm{ln}}\,\overline{Y}\), \({c}_{i}^{t}=\,{\mathrm{ln}}\,C{O}_{2i}^{t}-\,{\mathrm{ln}}\,{\overline{CO}}_{2}\).

Since carbon Shephard distance function is homogeneous of degree one in terms of carbon dioxide emissions, we can get:

$${\mathrm{ln}}\,{D}_{c}^{t}({K}_{i}^{t},{L}_{i}^{t},{E}_{i}^{t},{Y}_{i}^{t},C{O}_{2i}^{t})=\,{\mathrm{ln}}\,C{O}_{2i}^{t}+\,{\mathrm{ln}}\,{D}_{c}^{t}({K}_{i}^{t},{L}_{i}^{t},{E}_{i}^{t},{Y}_{i}^{t},1)$$
(6)

Plugging Eq. (5) into (6), we can get:

$$\begin{array}{c}{\mathrm{ln}}\,{D}_{c}^{t}({K}_{i}^{t},{L}_{i}^{t},{E}_{i}^{t},{Y}_{i}^{t},C{O}_{2i}^{t})={c}_{i}^{t}+\,\mathrm{ln}\,{\overline{CO}}_{2}+{\alpha }_{i}+\left[{\beta }_{k}{k}_{i}^{t}+{\beta }_{l}{l}_{i}^{t}+{\beta }_{e}{e}_{i}^{t}+{\beta }_{y}{y}_{i}^{t}+{\beta }_{t}t\right.\\ +{\beta }_{kl}({k}_{i}^{t}\cdot {l}_{i}^{t})+{\beta }_{ke}({k}_{i}^{t}\cdot {e}_{i}^{t})+{\beta }_{ky}({k}_{i}^{t}\cdot {y}_{i}^{t})\\ +{\beta }_{le}({l}_{i}^{t}\cdot {e}_{i}^{t})+{\beta }_{ly}({l}_{i}^{t}\cdot {y}_{i}^{t})+{\beta }_{ey}({e}_{i}^{t}\cdot {y}_{i}^{t})\\ +{\beta }_{kk}{({k}_{i}^{t})}^{2}+{\beta }_{ll}{({l}_{i}^{t})}^{2}+{\beta }_{ee}{({e}_{i}^{t})}^{2}+{\beta }_{yy}{({y}_{i}^{t})}^{2}\\\qquad\qquad\qquad\qquad\left. +{\beta }_{tk}(t\cdot {k}_{i}^{t})+{\beta }_{tl}(t\cdot {l}_{i}^{t})+{\beta }_{te}(t\cdot {e}_{i}^{t})+{\beta }_{ty}(t\cdot {y}_{i}^{t})+{\beta }_{tc}{t}^{2}\right]+{v}_{it}\end{array}$$
(7)

Rearrange the terms:

$$\begin{array}{ll}-{c}_{i}^{t}={\beta }_{i}+\left[{\beta }_{k}{k}_{i}^{t}+{\beta }_{l}{l}_{i}^{t}+{\beta }_{e}{e}_{i}^{t}+{\beta }_{y}{y}_{i}^{t}+{\beta }_{t}t+{\beta }_{kl}({k}_{i}^{t}\cdot {l}_{i}^{t})+{\beta }_{ke}({k}_{i}^{t}\cdot {e}_{i}^{t})+{\beta }_{ky}({k}_{i}^{t}\cdot {y}_{i}^{t})\right.\\\qquad\quad +{\beta }_{le}({l}_{i}^{t}\cdot {e}_{i}^{t})+{\beta }_{ly}({l}_{i}^{t}\cdot {y}_{i}^{t})+{\beta }_{ey}({e}_{i}^{t}\cdot {y}_{i}^{t})+{\beta }_{kk}{({k}_{i}^{t})}^{2}+{\beta }_{ll}{({l}_{i}^{t})}^{2}+{\beta }_{ee}{({e}_{i}^{t})}^{2}+{\beta }_{yy}{({y}_{i}^{t})}^{2}\\\qquad\quad \left.+\,{\beta }_{tk}(t\cdot {k}_{i}^{t})+{\beta }_{tl}(t\cdot {l}_{i}^{t})+{\beta }_{te}(t\cdot {e}_{i}^{t})+{\beta }_{ty}(t\cdot {y}_{i}^{t})+{\beta }_{tc}{t}^{2}\right]+{v}_{it}-{u}_{it}.\end{array}$$
(8)

among which, \({u}_{it}=\,{\mathrm{ln}}\,{D}_{c}^{t}({K}_{i}^{t},{L}_{i}^{t},{E}_{i}^{t},{Y}_{i}^{t},C{O}_{2i}^{t})\), \({\beta }_{i}=\,{\mathrm{ln}}\,\overline{CO}_{2}+{\alpha }_{i}\).

Assuming\({v}_{it} \sim N(0,{\sigma }_{v}^{2})\),\({u}_{it}={\sigma }_{u}({Z}_{it};{\varphi }_{u}){u}_{i}^{\ast }\) and \({u}_{i}^{\ast } \sim {N}^{+}(0,1)\), if the variable influencing the inefficiency is endogenous, Eq. (8) is an endogenous SFA model. Following Karakaplan and Kutlu (2017) and Karakaplan and Kutlu (2019), we can estimate the parameters in Eq. (8).

Baseline results

This paper employs principal component analysis to measure the DE development index in each region, and Fig. 2 illustrates the temporal change trend. The results show that China’s DE development index has demonstrated a steady upward trajectory from 2004 to 2017, with an average value that has risen from 0.22 in 2004 to 1.17 in 2017, representing an average annual growth rate of 13.7%. The South China region exhibits the highest level of DE development, followed by East China. North China and Southwest China have relatively similar levels of DE development. However, Northwest and Northeast China are the least developed regions in terms of DE. Before 2012, Central China is lagged behind in DE development, but it surpasses Northwest and Northeast after that. The subsequent section delves deeper into the effects of DE development on CTFP.

Fig. 2
figure 2

The time change trend of DE indicator.

Full size image

Ensuring consistent parameter estimation results requires addressing endogeneity, which can lead to over or underestimating the impact of DE on CTFP. Two main sources of endogeneity arise. First, there exists a reverse causality between DE and CTFP. In regions with higher CTFP, firms may generate more profits, resulting in higher tax revenues for local governments. Local governments may then use these funds to introduce preferential policies for DE development, potentially overestimating the impact of DE on CTFP. Conversely, if DE technology contributes to increased CTFP, firms may expand their production scale, and short-sighted management may lead to reduced investment in DE technology despite higher profits, underestimating the impact of DE on CTFP.

Second, numerous factors influence CTFP, and due to data limitations, it is challenging to control for all relevant variables in empirical analyses, resulting in potential omitted variable bias. Although regional fixed effects can be controlled to mitigate the influence of non-time-varying factors, it remains difficult to account for the effects of other time-varying factors. For instance, regions with a high concentration of firms exhibiting high CTFP may also exhibit higher levels of DE development, leading to an overestimation of DE’s impact. Conversely, regions with a larger proportion of firms with low CTFP may face limited resources for DE development, resulting in an underestimation of DE’s impact on CTFP. To address these concerns, this paper employs an endogenous stochastic frontier analysis approach, which allows for the identification of the net effect of DE development on CTFP, while mitigating potential endogeneity issues in the estimation process.

To account for the regional and temporal variation of the DE development index, this paper adopts a more comprehensive instrumental variable strategy than merely relying on the historical post office and telephone penetration. Using only these variables may not adequately control for urban fixed effects, resulting in potential omitted variable bias. Therefore, following Nunn and Qian (2014), this paper incorporates the number of post offices per 10,000 people in 1984, the number of telephones per person in 1984, and the number of internet users in the previous year. The new interaction terms serve as instrumental variables to capture the digital economic development index. This approach provides a more robust and nuanced identification strategy for the endogeneity issue and enables us to obtain more reliable estimates of the causal relationship between DE and CTFP.

Table 3 presents the estimation results for the impact of DE on CTFP. To compare the results of dealing with the endogeneity of DE, we also present the estimation results without treating the endogeneity (Model EX). The table is divided into four parts. The first part presents the dependent variable, which is the left-hand side of Eq. (8), and the explanatory variables are the right-hand side of Eq. (8), which constitute the frontier side for measuring CTFP. The second part presents the dependent variable as carbon total factor inefficiency, and the results show that the effect of DE on it is significantly positive when the endogenous problem is not solved and significantly negative when the endogeneity is addressed. Therefore, the effect of DE on CTFP will be underestimated when the endogeneity of DE is not addressed. The analysis demonstrates that DE plays a substantial role in enhancing CTFP, and its positive impact is statistically significant at the 1% level after accounting for its endogeneity. Specifically, a 10% increase in the level of DE development leads to a 0.25% rise in CTFP, all else equal, once the endogeneity issue of DE is addressed. This economic interpretation underscores the crucial contribution of DE to productivity growth and highlights the importance of tackling its endogeneity for reliable estimates of its impact. To assess the validity of the instrumental variable, the results of the first-stage regression, which is presented in column 1 of Table 5, indicate that the instrumental variables still meet the correlation condition, and the F-value is greater than 10, thereby there is no weak instrumental variable problem.

Table 3 The impact of DE on CTFP.
Full size table

Comparing to the existing literature, no consistent conclusions about the impact of digital economy on carbon emissions have been reached so far. For example, Wang et al. (2022) find that if the digital economy index is increased by one percent, CO2 emissions will be decreased by 0.886% in China. Lyu et al. (2023) deem that digital economy serves to the increase of carbon emission efficiency. Tan et al. (2024) also think digital economy can promote the low-carbon development. However, Zhang et al. (2022) conclude that digital economy development intensifies CO2 emissions. There is no study on the impact of digital economy on carbon total factor productivity up now.

The third part of Table 3 presents a test that examines the necessity of employing the endogenous SFA approach. The results strongly reject the null hypothesis that DE is exogenous at the 1% significance level. This further underscores the importance of using the endogenous SFA approach to address the endogeneity issue. Moving on to the fourth part, it provides the estimation results of CTFP. The findings demonstrate that both the mean efficiency and median efficiency will yield over estimates of CTFP if the endogeneity of DE is not properly accounted for.

The foregoing results suggest that the development of DE has a positive impact on CTFP. To assess the robustness of this finding, we re-estimate Eq. (8) using different instrumental variables for DE, varying the construction method of the DE indicator, and constructing the frontier surface using the Cobb-Douglas (C-D) production function. The first two columns of Table 4 display the results of using the cross product term of the telephone penetration rate (i.e., number of telephones per 10,000 people) in 1984 and the number of internet users in the previous year as an instrumental variable for DE development. The effect of DE on CTFP remains significantly positive and its magnitude is very similar to the results obtained from the benchmark regression, indicating that the findings are robust to the use of different instrumental variables. The first-stage regression outcomes in column 2 of Table 5 demonstrate that the new instrumental variable still satisfies the correlation condition and has an F-value greater than 10, suggesting that the model does not suffer from a weak instrumental variable problem.

Table 4 Robustness checks.
Full size table
Table 5 The results of first stage using IV approach.
Full size table

The present study employs principal component analysis to synthesize the DE indicator in the baseline regression. To ascertain the impact of alternative methods for constructing the DE indicator, we normalize each variable measuring the four connotations of DE and compute its arithmetic mean to gauge the degree of DE, as suggested by Bai and Zhang (2021). The results of the robustness test are shown in the middle two columns of Table 4, which demonstrates that the positive impact of DE on CTFP remains unaffected.

Furthermore, since the SFA method is utilized in this paper and the measurement of CTFP is reliant on the specification of the production function, we employ the Cobb-Douglas (C-D) production function to construct the frontier and evaluate the effect of DE on CTFP. This is unlike the trans-log production function used in the benchmark regression. The findings presented in the last two columns of Table 4 suggest that the impact of DE on CTFP is significantly positive, while the results of the endogeneity test underscore the necessity of using the endogenous SFA method. Thus, these results confirm the robustness and reliability of the benchmark regression outcomes.

Mechanism analysis

The preceding analysis posits that the development of DE positively impacts CTFP. In this section, we delve deeper into this relationship and explore three mechanisms through which DE affects CTFP, namely, the efficiency improvement effect and technological innovation effect, and the optimization of environmental regulation and governance. First, the improvement of business management efficiency and production methods resulting from DE reduces energy intensity and improves CTFP in the short-term with a constant energy mix (Han et al. 2019; Bai and Zhang 2021). Second, DE promotes technological innovation by facilitating collaboration, knowledge sharing, and technology diffusion among enterprises, leading to further improvements in CTFP at both the firm and regional levels (Bertschek et al. 2013; Paunov and Rollo 2016). Additionally, DE can serve as an innovative tool for environmental regulation, where data processing technologies such as the internet, satellite remote sensing, and smart environmental monitoring systems are used to monitor energy use and pollution emissions in real-time, enabling timely environmental regulation and governance (Xu et al. 2022).

By improving business management efficiency and production methods, DE enhances CTFP in the short-term with a constant energy mix. This is achieved by reducing energy intensity and optimizing production methods. Furthermore, the positive effects of DE on CTFP can be amplified through its contribution to technological innovation. The advent of digital technologies like big data, the internet of things, and cloud computing enhances collaboration and knowledge sharing within firms and reduces the cost of technology diffusion across firms, leading to further improvements in CTFP at both the firm and regional levels. Lastly, the deployment of DE technologies in environmental regulation and governance has the potential to revolutionize the monitoring and regulation of energy use and pollution emissions. By facilitating real-time monitoring of pollutant and CO2 emissions of each enterprise, environmental protection departments can optimize the regulation process and minimize the environmental impact of economic activities.

This study utilizes proxy variables for efficiency improvement, green innovation, and environmental regulation to investigate the impact of DE on CTFP. Specifically, TFEE (Zhang and Wu 2011), the proportion of green utility model patents applied for and obtained in the region to the total number of patents (Liu and Xiao 2022), and the industrial solid waste disposal rate (Xie et al. 2015) are used as indicators of efficiency improvement, green innovation, and environmental regulation, respectively. The results in Table 6 confirm that DE positively affects regional CTFP by enhancing production efficiency, promoting technological innovation, and improving environmental regulation. To address the endogeneity of DE, an interaction term of the number of historical post offices and the number of internet users in the previous year is utilized as an instrumental variable. The results show that the instrumental variables meet the correlation condition and that there is no weak instrumental variable problem. Thus, hypotheses 1 to 3 are supported by the empirical evidence.

Table 6 Mechanism analysis.
Full size table

Heterogeneous analysis

In addition to determining the effects of DE on CTFP and the underlying mechanisms, policy makers may also wish to ascertain whether the impact of DE on CTFP varies across cities. This section conducts three heterogeneity analyses to address this question, examining the public’s green awareness, the abundance of regional resources, and the level of human capital advancement.

The green and low-carbon awareness of the public

To peak carbon emissions in 2030 and achieve carbon neutral in 2060 goals, it is crucial to increase public awareness of green and low-carbon practices and encourage their participation in energy conservation and emission reduction. The level of green awareness among the public plays a significant role in moderating the impact of DE on CTFP. It is expected that the effect of DE on CTFP will vary significantly between regions with strong and weak public awareness. To test this hypothesis, this section divides the 223 cities in China into two subgroups based on their level of green and low-carbon awareness, using survey data from the China General Social Survey (CGSS) in 2013, and conducts separate regression analyses.

To measure the green and low-carbon awareness of the public, this paper employs the mean score of the respondent’s environmental protection behavior in 2013, as reported in question B22 of the China General Social Survey (CGSS), which includes ten questions. The median of this indicator is used to divide the sample into two subsamples, with stronger and weaker public awareness. The regression results for the two subsamples are presented in Table 7.

Table 7 Heterogeneous analysis- the green and low-carbon awareness of the public.
Full size table

The results reveal that in regions with stronger awareness of green and low-carbon among the public, the development of DE has a significant and positive impact on CTFP. In particular, when DE development increases by 10%, CTFP rises by 0.37%. However, in regions where the population’s awareness of green and low-carbon is weaker, the development of DE does not contribute to the improvement of CTFP, as depicted in Fig. 3. Hence, in order to enhance CTFP and attain the objective of “double carbon” through DE development, it is imperative to raise awareness about green and low-carbon practices and encourage active public participation in green and low-carbon initiatives.

Fig. 3
figure 3

The impact of DE on carbon total factor inefficiency.

Full size image

Resource abundance

When a region is rich in natural resources, it is expected that the productivity improvement through DE might be neglected as the high income from the resource abundance can be an alternative source of economic growth (Gylfason 2001). Additionally, local business operators may not prioritize energy-efficient use of resources, resulting in lower productivity growth (Papyrakis and Gerlagh 2007). However, resource abundance can also reduce energy transportation costs, leading to lower production costs for firms and potentially increasing CTFP.

To investigate the possibility of a “resource curse” effect on the relationship between DE and CTFP, we adopt the share of mining industry employees in the total local population of each city as a measure of resource abundance. This division allows us to create two subgroups of the sample: cities with higher and lower resource abundance. Our findings, as shown in Table 8, reveal that the impact of DE on CTFP is insignificant in regions with higher resource abundance. This outcome is likely due to two factors. First, the abundance of natural resources may lead to complacency among local residents, resulting in a neglect of productivity improvement as a contributor to economic growth. Second, resource-rich regions may be less motivated to pursue energy-efficient practices, as the abundance of natural resources may reduce the incentives for firms to focus on energy conservation. In contrast, we find that DE can significantly increase CTFP in regions with lower resource abundance (as depicted in Fig. 3). When the level of DE increases by 10%, CTFP can increase by 0.49%. Therefore, our results indicate a “resource curse” effect on the impact of DE on CTFP.

Table 8 Heterogeneous analysis- resource abundance.
Full size table

Human capital

DE relies heavily on digital knowledge and information as the primary production factor, and modern information networks serve as the primary carrier. Key technologies encompass mobile internet, cloud computing, big data, artificial intelligence, internet of things, 5G, blockchain, among others. The development and application of these technologies are dependent on high-quality human capital. Moreover, innovation is closely tied to the level of human capital, and high-quality human capital is better equipped for technological innovation (Huang et al. 2013). Furthermore, high-quality human capital can optimize the use of energy technologies and equipment to improve energy production efficiency. Additionally, high-quality human capital is more aware of energy conservation, which leads to greater attention paid to energy efficiency improvement (Yin et al. 2008). Therefore, if DE has a significant impact on CTFP, the positive contribution of DE should be more evident in regions with higher quality human capital compared to those with lower quality.

To examine the hypothesis presented above, this study employs the proportion of college and above enrolled students to the total population of each city as a proxy for the level of advanced human capital in that region (Liu and Liu 2014). The entire sample is divided into two subgroups based on the median of the advanced human capital index. The findings presented in Table 9 reveal that DE significantly enhances CTFP in regions with a higher advanced human capital index, but it does not have a significant effect in regions with a lower advanced human capital index (as demonstrated in Fig. 3). In terms of economic significance, a 10% increase in DE in regions with a higher advanced human capital index results in a 0.43% increase in CTFP.

Table 9 Heterogeneous analysis- human capital.
Full size table

Further analysis: the carbon reduction potential of optimizing the regional DE development

The preceding section demonstrates the positive impact of DE on CTFP. This section shifts the focus to examine the extent to which this improvement can lead to the reduction of CO2 emissions, a crucial factor in determining the potential of leveraging DE to reduce carbon emissions in China. Three scenarios are discussed. In Scenario 1, it is assumed that the DE level of each city can reach the maximum value within its corresponding province annually. In Scenario 2, the assumption is made that the DE level of each city can reach the maximum value within its corresponding region (Northeast, North, East, Central, South, Southwest, and Northwest) annually. Scenario 3 assumes that the DE level of each city can reach the maximum value of the entire country annually. Scenarios 1–3 correspond to the balanced development of DE within the province, the region, and the whole country, respectively. The reduction potential of CO2 emissions in each region in different scenarios is related to the disparity in the level of DE development within each province, each region, and the entire country, as well as its historical CO2 emissions.

Based on the estimations of the positive impact of DE on CTFP conducted in Section “Data and methodology”, the corresponding changes in CTFP can be derived when the DE development index varies across different scenarios, allowing for the calculation of the potential CO2 reduction. Table 10 presents the relevant findings. East China exhibits the highest potential for CO2 emission reduction resulting from enhanced DE development, with reductions amounting to 153.41 Mt, 920.47 Mt, and 970.15 Mt in Scenarios 1–3, respectively. Conversely, Southwest China demonstrates the lowest potential for CO2 emission reduction, with reductions of 24.35 Mt, 62.83 Mt, and 163.12 Mt in Scenarios 1–3, respectively. The CO2 emission reduction potential of North China and Central China is similar in Scenario 1, whereas in Scenario 2, the reduction potential in North China surpasses that in Central China. This discrepancy primarily arises from the greater disparity in the level of DE development among cities in North China compared to those in Central China.

Table 10 Reduction potential of CO2 emissions (million tons).
Full size table

Furthermore, the analysis of different scenarios reveals that each region exhibits the highest potential for CO2 emission reduction in Scenario 3, followed by Scenario 2, and the lowest potential in Scenario 1. This pattern arises due to the variations in DE development levels across the entire country, which are more substantial compared to the differences observed among different regions. For China as a whole, the carbon dioxide emission reduction potential across the three scenarios amounts to 564.91 Mt, 1973.39 Mt, and 3502.86 Mt, respectively. In terms of global carbon dioxide emissions in 2020, which stood at 31.98 billion tons, the potential carbon emission reduction resulting from optimizing China’s DE development level during the period from 2004 to 2016 accounts for 1.8, 6.2, and 11.0% of global carbon dioxide emissions, respectively. Moreover, in comparison to China’s total CO2 emissions in 2020 (9,893.5 Mt), the carbon reduction potential in the three scenarios reaches 5.7, 20.0, and 35.4%, respectively. These findings underscore the significant potential for carbon dioxide emission reduction through the promotion of DE development and the narrowing of DE disparities among different regions.

Conclusions and policy recommendations

This paper constructs a novel framework that can analyze the impact of DE on CTFP by well addressing the endogeneity issue. After applying it to the case of China, we examine the impact of DE on CTFP and explore the potential CO2 emission reduction arising from optimizing the regional DE development. To be specific, by utilizing prefecture-level city data from 2004–2017 in China, this paper first constructs a DE development index that combines four major aspects of DE development, namely digital information, internet platforms, digital technologies, and new economic and business models. Then, this paper applies an endogenous SFA approach to explore the impact of DE on CTFP, the mechanisms as well as the heterogeneity.

The results reveal several findings. First, within the study interval, China’s DE development exhibits a significant upward trend. South China experiences the largest and fastest growing speed in DE development, followed by East China, while Southwest China lags behind. Second, DE has a significant positive effect on CTFP. This effect holds true using different instrumental variables, DE development indicators, and forms of stochastic frontier production functions. Third, the effect of DE on CTFP is more significant in cities with higher awareness of green and low-carbon in the public, lower abundance of resources, and more developed human capital. Fourth, mechanism analysis shows that DE’s primary impact paths on CTFP are improving total factor energy use efficiency, promoting regional green innovation level, and strengthening the degree of urban environmental regulation. Finally, under the scenario of optimally balanced regional DE development, DE can lead to a greater potential for CO2 emission reduction.

In light of the results presented in this study, several policy recommendations are offered. Firstly, this paper shows that the development of DE can significantly enhance the CTFP, making it an essential tool in realizing China’s “double carbon” objectives. Compared to the conventional carbon intensity index, CTFP considers not only CO2 emissions and economic output, but also all other factor inputs throughout the economic production process. Therefore, the development of DE can effectively reduce carbon emissions without increasing other inputs of production or sacrificing economic output. This win-win scenario supports China’s high-quality development objectives, and highlights the need for continued promotion of DE in the future.

Furthermore, the mechanism analysis reveals that DE exerts its impact on CTFP through several channels, including enhancing TFEE, driving green innovation, and facilitating local environmental regulation. Given the limited feasibility of making major adjustments to China’s primary energy mix in the short term, alternative strategies are necessary to achieve significant CO2 emission reductions. Accordingly, it is recommended to further promote the adoption of energy-efficient technologies and increase investment and incentives for corporate green innovation. Moreover, there is a need to expedite the integration and innovation of DE and green technology. Although the development of DE and green technology has been incorporated into China’s national medium- and long-term strategic plan, their full integration remains incomplete. It is imperative to align the advancement of DE with the application of key technologies such as big data, cloud computing, and 5G in the realm of local energy conservation and environmental monitoring. Additionally, leveraging digital technology can foster research and development efforts as well as innovation in green technologies that address pollution, carbon reduction, recycling, and regeneration. To further maximize the emissions reduction potential of DE, it is essential to raise public awareness of green and low-carbon practices. In terms of talent development, there is a need to expedite the training of multidisciplinary professionals who possess expertise in both DE and green technology, facilitating cross-pollination of knowledge and skills across disciplines. By nurturing such composite talents, the transformative potential of DE in emission reduction can be effectively harnessed.

Additionally, it is crucial to emphasize the importance of balanced regional development of DE to unlock its full potential for CO2 emission reduction. In this regard, future efforts should be directed towards two key aspects. Firstly, the acceleration of digital park construction in leading cities should be prioritized, leveraging the advanced digital technologies available in these cities to serve as exemplars for driving national digital transformation. Secondly, equal attention should be given to promoting the development of DE at the provincial, regional, and national levels. In regions where digital technology lags behind, expediting the establishment of advanced digital technology enterprises and fostering collaborations with energy-intensive industries in areas such as pollution supervision, clean production, and smart manufacturing would be instrumental in maximizing the carbon emission reduction effects of DE. By adopting a balanced approach to DE development, the potential for CO2 mitigation can be more effectively realized.

This study takes a macro perspective, concentrating on city-level economic and carbon emissions data to capture overarching trends. Future research could pivot to the firm level, enabling a detailed analysis of individual company dynamics. This would provide a deeper understanding of the microeconomic forces that influence the low carbon transformation within the broader economic patterns identified. Such an approach would enrich our findings, offering more nuanced insights that could guide both policymakers and business strategists.