Introduction

Terrestrial water storage (TWS) is the sum of all water resources stored on the land surface and in the subsurface as the net residual among precipitation, evaporation, and runoff over land. It is an essential component of the hydrological cycle that determines freshwater availability on Earth1 and reverses the sign of the rate of sea level rise when more water is stored on the continents2. In regions experiencing frequent water scarcity, TWS often provides the last critical buffer against extreme droughts through natural water storage systems such as underground aquifers, glaciers, and wetlands. TWS also regulates Earth’s energy budget, affects biogeochemical cycles, maintains freshwater ecosystems, and enables socioeconomic development3.

The global TWS is affected by climate change and exacerbated by multi-faceted human activities. Climate change impacts TWS because it accelerates the hydrological cycle through enhancing evapotranspiration and altering precipitation patterns across the globe. The climate-induced variations in the global TWS pose multiple risks to human and natural systems worldwide, in particular in the vulnerable regions where changes in the hydrological cycle on people and ecosystems are observed4. On the other hand, human activities, such as the impoundment of fresh water in reservoirs and groundwater mining, exacerbate the TWS variations in time and space as these activities contribute to changes in water and energy budgets which are tightly coupled through changes in phase. Given the rapid population growth and urbanization coupled with climate change as a multiplier, the water insecurity issues will likely to be magnified in many vulnerable places, resulting in water-related risks and social unrest such as political instability, forced migration, social conflicts, and injustice5,6. Monitoring global TWS is thus crucial for understanding of the status of the global hydrological cycle, freshwater availability over time and space, and socio-hydrological responses to climate change.

Yet, it is difficult to obtain long-term trends in global TWS due to limited global observation records, decadal climate variability, highly uneven hydrological responses to climate change, and complicated interactions between climate, hydrological, and social systems2,7,8. Although recent development of big Earth data, especially the effort from different research centers to process the data from the Gravity Recovery and Climate Experiment (GRACE) and GRACE-Follow On (GRACE-FO) missions2,9 at various levels, has made it possible to assess global TWS change and anomalies, providing evidence to confirm changes in the global hydrological cycle predicted by hydroclimate models10, these data only cover a short period of time which makes it hard to understand climate-driven interannual-to-decadal variability in TWS2,11,12,13. However, some studies have been able to estimate linear trends in TWS and TWS anomalies from a short time series that helped to explain the natural spatial-temporal variability in TWS14,15,16. To address the data limitation and missing consideration of human factors, global hydrological and land surface models have been widely integrated into observation data to evaluate large-scale climate change and/or human impacts on TWS8,14,17,18,19,20,21,22,23. Among these attempts, the detection of climate change signals in global TWS and the identification of drivers behind TWS anomalies have rarely been investigated but need to be addressed to manifest the interplay between climate change and global TWS variability2.

To examine anthropogenic climate change in observations or model simulations, climatologists usually apply detection and attribution (D&A) techniques which aim to determine whether modeled patterns of climate change and their magnitude are consistent with observations24. Detection of the evolving climate signals in observation data is usually based on identifying characteristic space-time patterns, typically referred to as fingerprints25,26. In Hasselmann’s early work, an optimal fingerprint pattern was derived to maximize the signal-to-noise ratio, often defined as the leading empirical orthogonal function of the multi-model average from forced model simulations27,28. Recently, ridge regression has been used to optimally estimate “regression coefficient” to produce weights that maximize climate change signals against internal climate variability for the target variable29. The regression coefficient’s spatial distribution provides weights for locations around the globe; once the weights are applied to all locations, their weighted average fits the target variable the best. Despite the advanced understanding of global TWS systems and their improved representations in global hydrological models (GHMs) and land surface models (LSMs)30,31, only a few regional studies have used D&A techniques to track climate change signals in river flow32,33,34. An important question yet to be addressed is whether externally forced climate changes are detectable in freshwater availability at the global scale35. The lack of work on this is partly due to the weakened global average signal in changes in precipitation28, as the precipitation varies in the sign of change with regions under climate change, and thus they cancel each other out in the global average10,36,37. On the other hand, the application of D&A techniques requires long-time data of terrestrial water mass to identify climate change signals through observed TWS at the global scale. Such data are impossible with the technical capacity and resources available to date, but efforts have been made by reconstructing past TWS anomalies using meteorological data and GRACE observations11,38,39,40,41.

TWS at the regional scale fluctuates with hydrological fluxes, namely precipitation, evaporation, and runoffs, which are strongly affected by daily weather patterns and extreme hydrological events such as floods and droughts. Weather events and climatological anomalies, driven by cyclones, frontal systems, stationary eddies and other atmospheric processes, often occur at much smaller scales than continental scales. While synoptic patterns and large-scale atmospheric circulations can influence hydrometeorological conditions over broader regions, the drying and wetting effects of weather events tend to occur on more localized or regional scales. The effects of daily weather and extreme events on global TWS can be significantly attenuated due to the spatial average of the regional scale variations across the globe. Thus, it is possible to extract secular TWS trends from daily meteorological variables such as temperature and moisture through sophisticated statistical techniques.

Crucially, traditional D&A methods typically demand a congruence in the spatial distribution of linear TWS trends between observations and model simulations. This poses a challenge, given the existing limitations in GHMs and LSMs, for precisely reproducing substantial trends observed in GRACE at regional scales16 (Supplementary Fig. 1). In the present study, we follow the machine learning approach developed in recent work by Sippel et al.29 to extract fingerprints that encapsulate the relationship between anomalies of the annual global average of terrestrial water storage (AGTWS, excluding Greenland and Antarctica) and global weather patterns, represented by daily surface air temperature and specific humidity. It is noteworthy that, unlike traditional D&A methods that rely on the spatial distribution of linear TWS trends, the method used in our study uses only AGTWS trend which is well captured by numerical models to some extent (see Supplementary Fig. 2a). In doing so, we firstly derived TWS and meteorological data from seven physically based GHMs and LSMs models provided by the ISIMIP2b protocol42 (Supplementary Table 1). Four general circulation models (GCMs)—GFDL-ESM2M, HadGEM2-ES, IPSL-CM5A-LR, and MIROC5—were used to obtain climate variables, including near-surface air temperature, relative humidity, wind speed, precipitation, and surface downwelling longwave and shortwave radiation. Secondly, regularized linear regression models (i.e., ridge regression) were trained, using the retrieved data, to linearly relate AGTWS anomalies to daily weather patterns of surface air temperature and specific humidity and to obtain fingerprints as maps of regression coefficients. Three radiative forcing scenarios were considered: the historical climate (HIST, 1861–2005), a stringent greenhouse gas emission scenario (RCP2.6, 2006–2099), and a medium stabilization scenario (RCP6.0, 2006–2099). The bias-adjusted meteorological forcing and socioeconomic and human-influence data were downscaled to a 0.5° × 0.5° global grid43 (Supplementary Table 2). We used the ISIMIP multi-model archive42 for extracting fingerprints, estimating the distribution of AGTWS under natural variability and predicting future AGTWS in both RCP2.6 and RCP6.0 scenarios. Further, we retrieved GRACE data from the mascon solutions by the Center for Space Research, Goddard Space Flight Center, and Jet Propulsion Laboratory to evaluate the simulated AGTWS and uncertainties, with the missing months gap-filled by the linear interpolation. Next, we assessed detection beyond climate models on a daily basis using four daily reanalysis datasets which were then projected onto the extracted fingerprints to estimate AGTWS anomalies until 2021: the 20th Century Reanalysis version 3 (1861–2015)44, ERA5 (1979–2021)45, the NCEP/NCAR Reanalysis 1 (1948–2021)46, and the NCEP-DOE Reanalysis 2 (1979–2021)47. Whether climate change is detectable can then be determined by testing against the null hypothesis that the predicted AGTWS anomalies cannot be distinguished from natural climate variability.

Results

Spatial fingerprints detectable from daily weather patterns

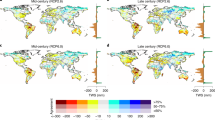
The AGTWS fingerprints and their variations at latitudinal bands are presented in Fig. 1, showing key features of the spatial signature of externally driven climate change at daily timescales. The spatial distribution of the AGTWS fingerprints optimizes the climate signal against the noise of natural variability, because ridge regression reduces weights in regions with large natural variability. Thus, this process leads to a reduction in the absolute values of regression coefficients in these regions29. Ridge regression may even change the sign of regression coefficients if natural variability in these areas is large enough48. As shown in Fig. 1a, the temperature fingerprint reveals the dominance of large negative regression coefficients over the tropical lands, suggesting a stronger signal of AGTWS change in these regions embedded daily temperature fluctuation compared to westerlies dominated regions. Larger temperature coefficients in the tropics occur because the tropical regions have less synoptic-scale disturbances than the extratropics. The negative coefficients are potentially caused by a consistent increase in evapotranspiration and melting of ice and snow across the globe, both of which reduce TWS through warming (Fig. 1a).

Fig. 1: The annual average fingerprint of external forcing and its variations at latitudinal bands.
figure 1

The global fingerprint presented as a map of regression coefficients extracted from global weather patterns of daily surface air temperature (a) and specific humidity (c), and their variations at latitudinal bands for land grid cells (b and d). The values over the ocean are masked to focus on the AGTWS responses over land. The color map is reversed to match a general decreasing trend in AGTWS (see Fig. 2), corresponding to an increase in surface air temperature and a reduction in specific humidity (both are shown as red shadings).

Full size image

It is worth noting that although direct human influences, such as land cover change49, crop irrigation50, and reservoir operations50,51, can contribute to the TWS changes at the regional scale, ensemble hydrological simulations have shown that the projected change in global TWS could primarily be attributed to climate forcings21. It should also be noted that the D&A analysis at the global scale decreases the noise caused by the internal climate variability which typically occurs at regional scales27. For example, TWS anomalies in several regions can be associated with El Nino/Southern Oscillation (ENSO) variability52; thus, the signals identified in the fingerprint are unlikely to be caused by natural variability alone—stochastically, it is almost impossible for natural variability to produce the same sign across the globe.

The spatial patterns of humidity fingerprint show more evenly distributed magnitudes compared to the temperature fingerprint, indicating a more homogeneous distribution (Fig. 1b). Negative coefficients are observed over most of the land areas in the Northern Hemisphere and along the Equator. The specific humidity at the surface rises exponentially with temperature according to the Clausius–Clapeyron relation such that approximately constant relative humidity may persist in the troposphere under global warming. Nevertheless, ridge regression decreases the absolute values of negative coefficients (that is, increases the coefficients) or even assigns positive coefficients at mid- and low-latitudes in the Southern Hemisphere (especially in Australia and South America) because climate variables in these regions are strongly related to interannual variability of the ENSO. In this way, ridge regression reduces the degree to which internal variability projects onto the humidity fingerprint, therefore ensuring robustness of D&A to uncertain internal variability. These features of the ridge regression fingerprints are consistent with previous work using a similar method53,54.

Daily predictions from models and reanalyses

A time series of AGTWS anomalies for each day in a given year was yielded through projecting daily model simulations (Fig. 2a) and reanalysis data (Fig. 2b) onto the extracted fingerprints. The results show a broad congruency between the two sets of AGTWS estimates over different intervals, especially from the early 1960s onwards when decreasing trends are perceptible in both models (Fig. 2a) and the average of reanalyses (Fig. 2b). The 2.5th–97.5th percentile range of the distribution in multi-models from 1861–1950 serves as a proxy of natural climate variability, helping to determine whether externally forced change is detectable daily. While the early 20th century warming (1910–45) was believed to be attributed to the Atlantic multidecadal variability55, growing evidence is highlighting the pivotal role of human-induced radiative forcing during this warming period56. Thus, it is conservative to use this proxy for the distribution of AGTWS under natural variability.

Fig. 2: AGTWS estimates from models and reanalysis datasets.
figure 2

Time series of AGTWS anomalies estimated from the multi-model mean (a) and reanalysis datasets (b). Shadings indicate the range of multi-model results. Two dashed lines indicate the 2.5th and 97.5th percentile of the distribution of AGTWS anomalies from the multi-model results for the 1861–1950 historical period, respectively.

Full size image

As can be seen in Fig. 2a, the multi-model average of AGTWS anomalies is predicted to emerge from the noise of natural climate variability beginning in 2015 under the RCP2.6 scenario. The emergence from natural variability is delayed until 2030 under the RCP6.0 scenario, probably because of the larger climate variability in higher emission scenarios due to enhanced ENSO variability53,54. Notably, the early 20th-century warming (from 1910–1945) in the period 1861–1950 has been associated with changes in external radiative forcing55. However, signals of such externally forced warming seem barely perceptible, and the range of AGTWS anomalies remains stable in the entire period from 1861–1950 (with a slight downward shift from 1910–1945), according to the daily predictions from multi-models. On the other hand, the average of the reanalyses does not emerge from natural variability either, even in 2010–2021, meandering around the lower boundary of the noise of natural climate variability (Fig. 2b). Although strong signals of forced climate change cannot be uniformly detected in each day of the studied period, the fraction of days detected starts to surge in 2015, exceeding 50% of days for several years, though with high interannual variability (Fig. 3).

Fig. 3: Emergence of externally forced change from natural climate variability in reanalysis datasets at the global scale.
figure 3

The fraction of days in which climate change signals have emerged from natural variability (that is, below the 2.5th percentile in the multi-model 1861–1950 distribution).

Full size image

As opposed to its application in the global temperature29, the application of the daily detection technique in global TWS shows distinct features. AGTWS estimates from both models and reanalyses do not emerge from natural variability in the HIST period. Changes in global TWS could largely rely on climate forcings. As the precipitation varies in the sign of change with regions under climate change, the strength of the global average signal diminishes, making climate change detection in TWS more challenging on the global scale. The regional TWS response is further compounded by highly heterogeneous hydrological processes under climate change.

Daily detections at continental scales

We further compare fingerprints at continental scales with previous studies on TWS changes at regional scales, which provide clues to deduce dominant processes causing changes in TWS. The regularized linear regression models show good performance metrics on the daily pattern of surface air temperature and specific humidity over different continents (Supplementary Fig. 3). Previous work has revealed an observation-based global map of TWS responding to direct human impacts, climate change, and natural climate variability7. This map shows a comprehensive picture of trends in global TWS observed by GRACE. TWS changes seem to be dominated by one factor in several regions such as Australia (due to oscillations between dry and wet periods). In large continents such as Asia, however, causal mechanisms are more intricate and difficult to identify on the global TWS landscape. Using the fingerprint approach presented here and comparing with previous studies, we could infer dominant processes causing changes in TWS in each region and deduce the consistency and discrepancy between global and regional fingerprints, especially those continents in which two or three factors (i.e., human impacts, climate change, and natural climate variability) play a critical role. Specifically, if the fingerprint in a respective area at both regional and global scales is consistent, the TWS anomalies in this area are highly correlated to the global mean TWS anomalies, and vice versa. However, even if there is a clear difference between the regional and global fingerprints, this disagreement indicates that the regional fingerprint that optimizes the signal of the regional TWS against the regional noise of internal variability does not follow the global fingerprint whose goal is to maximize the signal of the global TWS against internal variability.

Africa

The simulated TWS variations in Africa generally agree with AGTWS variations, and high negative regression coefficients are seen over central and southern Africa in the temperature fingerprint, indicating the effect of rising temperatures on increased evapotranspiration and its subsequent impact on African TWS (Fig. 4a). The sign of regression coefficients in the humidity fingerprint is not uniform over the continent partly due to the afore-mentioned algorithm of ridge regression to ensure robustness of D&A to the uncertainty of changes in internal variability (Fig. 4g). The hydroclimatic variations in precipitation are believed to increase in most parts of Africa except its west coast57 in a warmer world.

Fig. 4: The annual average fingerprint of external forcing and TWS estimates from models on different continents.
figure 4

The regional average fingerprint is presented as a map of regression coefficients extracted from weather patterns of daily surface air temperature (a–f) and specific humidity (g–l) in Africa, Asia, Australia, Europe, North America, and South America. The color map is reversed to match a general decreasing trend in regional TWS corresponding to an increase in surface air temperature and a reduction in specific humidity (both shown as red shadings). The values over the ocean are masked out to focus on the TWS regional mean responses over land. The time series of TWS anomalies is estimated from the multi-model mean (m–r). Shadings indicate the range of multi-model results. Two dashed lines indicate the 2.5th and 97.5th percentile of the distribution of TWS anomalies on each continent from the multi-model results for the 1861–1950 historical period, respectively.

Full size image

The predicted time series of TWS anomalies is below the natural climate variability for the entire studied period under both the RCP2.6 and RCP6.0 scenarios (Fig. 4m). This result shows strong signals of human-induced climate change over Africa, in agreement with the highest fraction of days (over 60% no matter what reanalysis dataset is used) in which climate change is detectable on this continent with reanalysis datasets compared to other continents by the end of the study period (Fig. 5). Previous studies have attributed the GRACE-derived trend in Africa to natural variability (i.e., a climatic shift in precipitation in Southern Africa; precipitation variations driven by large-scale climatic oscillations in the Amazon and Congo basins)7,58 and anthropogenic causes (i.e., extraction of groundwater over the Saharan aquifers, deforestation in the Congo basins, and the dam impoundment in tropical western Africa)59. Here, we examine TWS changes from a different angle. Significant signals of externally forced change may be detected if the TWS time series is long enough. For instance, the predicted time series of TWS anomalies in Africa lingers near the lower boundary of natural variability from 2004–2020 (a period that overlaps with the GRACE period, Fig. 4m). Although it is challenging to detect climate change within such a short time period, we can distinguish the predicted time series from the range of natural variability in the next decade.

Fig. 5: Emergence of externally forced change from natural climate variability in reanalysis datasets over different continents.
figure 5

The fraction of days in which climate change signals have emerged from natural variability (that is, below the 2.5th percentile in the multi-model 1861–1950 distribution) in Africa (a), Asia (b), Australia (c), Europe (d), North America (e), and South America (f).

Full size image

Asia

The temperature fingerprint in Asia agrees well with the global temperature fingerprint: High negative regression coefficients concentrated in low latitudes, regions with relatively low internal variability, namely India, central and eastern China, and Mainland Southeast Asia (Fig. 4b). Strong signals of anthropogenic climate change in TWS anomalies are detected over southern India and Mainland Southeast Asia due to warmer climates. While the declining TWS trends in the North China Plain are commonly viewed as the result of irrigation-induced groundwater depletion60, climate change signals are also detectable in the temperature fingerprint over this region. Even though the GHMs/LSMs in the ISIMIP project contain components of human activities such as land-use change, irrigation, reservoir operation, and fertilizer use (see Methods), it is still challenging to completely extract direct human impacts from our results. However, direct human impacts on TWS are mostly confined within irrigated agricultural zones, and secondary impacts over non-irrigated regions are negligible; thus, such human impacts are negligible in global and continental mean TWS anomalies estimated in this study. Over the Tibetan Plateau, the regional humidity fingerprint shows large positive coefficients, possibly because ridge regression algorithms reduce the degree to which internal variability projects onto the humidity fingerprint. Previous work using the attribution experiments from the CLIVAR Climate of the 20th Century Plus Project has shown that trends in summer precipitation over the south Tibetan Plateau are primarily controlled by internal variability61.

Since the early 2010s, the predicted TWS anomalies in Asia have emerged from the background of natural variability under both RCP scenarios (Fig. 4n). Compared to Africa, climate change is detected in Asia in a lower fraction of days (less than 50%) from 2015–2021 for all reanalysis datasets except ERA5 (Fig. 5b).

Australia

The regional temperature (humidity) fingerprint reveals negative (positive) coefficients over most parts of the Australian continent (Fig. 4c, i). Precipitation reduction in the Southern Hemisphere mid-latitudes will further decrease TWS in Australia due to the larger landmass in the Northern Hemisphere and rising global temperatures62. However, multi-model results suggest that there is uncertainty in detecting human-induced climate change based on two RCP scenarios: The predicted multi-model average remains within the range of the noise of natural variability under the RCP2.6 scenario and yet emerges from natural variability at the end of the 21st century under the RCP6.0 scenario (Fig. 4o).

Our D&A analysis gets well agreement with previous GRACE-based studies that the TWS trend in Australia is mostly attributed to natural variability7,63. Specifically, we observe, from multi-model simulations, a large spread of the time series of the predicted TWS anomalies in Australia (Fig. 4o), indicating a widespread background of natural variability. Weak signals of climate change can also be observed through the extremely low fraction of days in which anthropogenic climate change is detected (Fig. 5c). Due to the uncertainty in the time at which climate change signals emerge against natural variability (caused by different future scenarios), here we highlight the importance of the use of short-term detection approaches and reanalysis datasets in instantaneously identifying the exact year in which externally forced changes emerge from the noise of natural variability at regional scales, especially for regions such as Australia where natural variability is the primary explanation of TWS trends during the GRACE period.

Europe

Being consistent with previous projections21, a decline in TWS in Europe in response to regional warming is indicated by the negative coefficients in the temperature fingerprint for most parts of Europe except northern Europe (Fig. 4d, j). High negative values of regression coefficients in the humidity fingerprint can be found over parts of northern Europe, agreeing with the observed dipole pattern of European runoff trends64. Local specific humidity in northern Europe will increase in response to climate change, with an increase in high-latitude precipitation28, while model simulations have projected that TWS will decline in Europe. As a dominant factor in natural climate variability, the North Atlantic Oscillation (NAO) has a well-known influence on the river flow in Europe65. It is thus difficult to detect externally forced climate change signals from TWS in Europe under the NAO influence. Using the traditional D&A approach and model simulations, previous work can capture the observed dipole pattern of the river flow in pan-European regions, but only if anthropogenic emissions are accounted for35. Our analysis confirmed this argument, with obvious signals of human-induced climate change detected in the predicted time series from multi-model results (Fig. 4p) and in the fraction of days from reanalysis datasets (Fig. 5d).

North America

Negative regression coefficients are seen in the regional temperature fingerprint, with high absolute values for regions in the central and eastern United States and most of Mexico due to less synoptic noises compared to higher latitudes (Fig. 4e). For the regional humidity fingerprint, high positive regression coefficients are found in relatively arid areas along the Rocky Mountains and on the west coast of the United States and large negative coefficients in the northern parts of the continent (Fig. 4k). The temperature fingerprint reveals negative implications of changes in surface air temperature over the midwestern United States for North American TWS. Additionally, strong climate change signals are detected in the predicted time series from multi-models (Fig. 4q) and in the fraction of days from reanalysis datasets (Fig. 5e). A previous D&A study identified human-induced changes in observed river flow and snowpack over the western United States from 1950–1999, but changes in precipitation cannot be distinguished from natural climate variability32. In the central part of the Rocky Mountains, a combined water balance and tree ring study found that moderate warming alone (in the absence of considerable changes in precipitation) could still have critical adverse impacts on water availability66.

South America

In South America, the regional temperature fingerprint shows considerable negative coefficients in the majority of the Amazon rainforest except its southern part, whereas the humidity fingerprint reveals positive coefficients in the central and southern parts of the Amazon rainforest (Fig. 4f, l). The tropical region has more significant temperature coefficients because daily temperatures are less variable than those in the midlatitudes, as the latter are noisier due to extratropical weather. Although these fingerprints reasonably reflect the response of South American TWS to rising temperatures in the Southern Hemisphere, climate change is barely detected in terms of the fraction of days from reanalysis datasets (Fig. 5f). Precipitation over South America, particularly in the Amazon, is significantly impacted by interannual variability of the ENSO and the tropical Atlantic meridional sea surface temperature (SST) gradient67. The time series of model-predicted TWS anomalies on this continent has a large spread which makes anthropogenic climate change much harder to detect from the noise of natural variability (Fig. 4r). These may help to explain why the GRACE-observed TWS trend in South America has been mostly attributed to natural climate variability7.

Discussion

In this study, we have used statistical learning techniques to extract externally forced fingerprints from global weather patterns of daily surface air temperature and specific humidity. Both reanalysis data and model simulations have been projected onto the extracted fingerprints to detect climate change on daily timescales. The selection of daily surface air temperature and specific humidity as predictors was based on the fact that climate change can influence the Earth system through changing the surface air temperature and the atmospheric moisture that alters the latent heat29. We do not use precipitation as a predictor because it exhibits strong spatial gradients globally, which may not be well predicted by models. In some cases, averaging precipitation over latitude bands is used to reduce internal variability in the D&A method27. This method, however, is not suitable for our analysis as we focus on climate change detection from global weather patterns.

According to the results, we found that the daily predictions obtained from models and reanalyses are consistent, but weak climate change signals are detected in global TWS compared to the global temperature reported in the previous literature29,68. By the end of the HIST simulations, AGTWS anomalies estimated from models and reanalyses cannot emerge from natural variability at global and continental scales (Figs. 2, 4). GHMs and LSMs demonstrate the ability to simulate observed trends in AGTWS, but with an underestimated amplitude (Supplementary Fig. 2a), probably due to their incapability of accurately reproducing large TWS trends in GRACE observations at regional scales16. Fingerprints derived from these GHMs and LSMs may underestimate signals in global TWS. Relatively weak signals in global TWS may also be attributed to other reasons. First, GHMs/LSMs simplify processes (e.g., surface water and groundwater processes) in the hydrological cycle and thus are limited by the corresponding simplifying approximations. Second, the expected physical response to external forcing is influenced by a variety of uncertainties in model-structure-related water storage compartments and capacity16, radiative forcing and socioeconomic scenarios, and meteorological forcings. Under the same RCP scenario, the four GCMs’ climate projections vary in the mean status and variability. Key uncertainties that result in a large spread of natural variability could come from inter-model disagreement on runoff responses even though common meteorological forcing data are used69. Third, other anthropogenic forcing agents such as aerosol emissions could affect regional precipitation, thus in turn playing a critical role in global and regional hydroclimates. Anthropogenic aerosol emissions cause large discrepancies in global precipitation response among GCMs through their different representations of aerosol–cloud interactions70,71. The signals of greenhouse gas forcing in global drought are robustly detectable in the first half of the 20th century, yet the signals are possibly counteracted by the increase in anthropogenic aerosol emissions in the mid-century (1950–1975)72. A recent study73 has shown the effectiveness of nonlinear machine learning techniques, such as convolutional neural networks (CNN), in identifying signals that are beyond the reach of ridge regression. Advances in deep learning may provide useful tools for revealing global warming’s influence, even in variables with high natural climate variability.

Although relatively weak signals of human-induced climate change are detected in global TWS in the HIST period which is in line with previous studies74,75, the detected fraction of days started to climb in 2015. Climate change signals in global TWS have accumulated over the last few decades, and our results showed that these signals will possibly be uniformly detected at daily timescales in the next few decades. Moreover, by employing a daily detection approach that incorporates cross-validation with extensive climate reanalyses and modeling datasets, our study effectively overcomes the obstacles posed by the large internal climate variability and overcomes the constraint posed by limited observations of TWS at a global scale, facilitating the detection of warming-induced TWS trends at daily time intervals. The model-derived fingerprints may be complementary to the study of GRACE-derived TWS trends. Strongly decreasing TWS trends shown by the GRACE data7 alone call attention to the importance of improving current models that allow the incorporation of hydrological processes such as groundwater pumping and snowmelt to match independent observations. In this study, we reported that global TWS, excluding Antarctica and Greenland, mainly resides in the Northern Hemisphere, and the most pronounced signature for temperature is in the tropics and Southern Hemisphere due to the large signal-to-noise ratio therein. The signal of forced climate change under RCP6.0 emerges later than that under RCP2.6, most likely due to higher climate variability under higher emission scenarios. The AGTWS is expected to decrease by about 40 kg m−2 under RCP6.0, compared to about 20 kg m−2 under RCP2.6.

In conclusion, the ability to detect climate change signals in TWS from the global weather patterns on daily timescales has wide implications for climate science, the hydrological cycle, and climate adaptations. Our work is a first attempt to extend short-term detection and attribution to the water cycle. Because global and regional weather patterns are expected to be updated daily as time proceeds, this method can help detect climate change signals at the earliest possible moment using daily global data. This would be critical in regions such as Australia and South America, where only natural signals have been detected recently, but possible signals of anthropogenic climate change will be identified at a pivot point in the future. Furthermore, our study revealed that the already limited freshwater availability will likely become scarcer around the globe as we found a significant decline in the annual global average of TWS in response to global warming. The declining freshwater storage under climate change will jeopardize water ecosystem services worldwide as TWS provides a buffer against climate extremes such as droughts. The loss of water ecosystem services will exacerbate water-related risks on human and natural systems. Our findings therefore would be informative to adaptive management and the identification of nature-based solutions to climate change.

Methods

Hydrological simulations and meteorological forcing data

Seven GHMs and LSMs were used to simulate AGTWS, essential components (e.g., groundwater, snow, ice, and soil moisture), and primary hydrological processes through the terrestrial hydrological cycle (Supplementary Table 1). All GHMs/LSMs consider human activities (e.g., land-use change, population growth, and economic development; https://www.isimip.org/documents/258/ISIMIP2b_protocol_22May2017.pdf). Historical land-use patterns are from the HYDE3.2 data76, and future land-use projections are generated by the land use model MAgPIE77.

Climate variables were obtained from four general circulation models (GCMs): GFDL-ESM2M, HadGEM2-ES, IPSL-CM5A-LR, and MIROC5, and included near-surface air temperature, relative humidity, wind speed, precipitation, and surface downwelling longwave and shortwave radiation. We evaluated hydrological simulations from 27 ensemble members (Supplementary Table 2). The bias-adjusted meteorological forcing and socioeconomic and human-influence data were downscaled to a 0.5° × 0.5° global grid43. All simulations were performed under the ISIMIP2b protocol42. Three radiative forcing scenarios are considered in this study: the historical climate (HIST, 1861–2005), the stringent greenhouse gas emission scenario (RCP2.6, 2006–2099), and a medium stabilization scenario (RCP6.0, 2006–2099). We selected these two RCPs, as they are the only scenarios for which hydrological outputs from up to seven models are available in the ISIMIP2b simulations. We considered two socioeconomic scenarios, which represent human influences such as land use, nitrogen deposition, fertilizer input, and water management. With most selected models, the simulation of land use and socioeconomic conditions varies (denoted as histsoc) in the historical climate (HIST), while it is fixed at the 2005 level (denoted as 2005soc) in the future climate (RCP2.6 and RCP6.0).

Observations and reanalysis data

GRACE observations from April 2002 to July 2021 were used to evaluate the simulated AGTWS. To derive uncertainties, GRACE mascon solutions from the Center for Space Research, Goddard Space Flight Center, and Jet Propulsion Laboratory were all used78,79,80. Data for the months not available on GRACE observations were gap filled using linear interpolation. A consistent reference period (2002–2021) was used to compute the climatological seasonal cycle and to compare the GRACE-observed and simulated anomalies. As the HIST simulation ended in 2005, we combined the results from HIST (2002–2005) with RCP2.6 (2006–2021) to cover the entire evaluation period.

The reanalyses were used to assess daily detection beyond climate models. We used four daily reanalysis datasets: the 20th Century Reanalysis version 344 (1861–2015), ERA545 (1979–2021), the NCEP/NCAR Reanalysis 146 (1948–2021) and the NCEP-DOE Reanalysis 247 (1979–2021).

Climate change detection and statistical learning technique

The daily climate change detection method used in this study is based on a widely used fingerprint approach25,26,27,72. Following a procedure identical to the one used in this fingerprint approach29, we first extracted fingerprints from multi-model outputs to encapsulate the relationship between AGTWS anomalies and daily weather patterns of surface air temperature and specific humidity (Eq. (1)), generating geographical patterns of regression coefficients. To extract the fingerprint, we used regularized linear models because they yield relatively smooth regression coefficients in space, even if predictors include spatially correlated climate variables81,82. The time series of AGTWS anomalies is stored in a vector S of length n, where n denotes the number of days in the training samples. The geographical patterns of daily surface air temperature and specific humidity are stored in an n × p matrix M, where p denotes the number of geographical predictors. The estimated fingerprint \(\hat{{\boldsymbol{\beta }}}\) is a p-dimensional vector of geographical regression coefficients.

$$\text{S}=M\hat{{\boldsymbol{\beta }}}+{\boldsymbol{\varepsilon }}$$
(1)

Second, reanalysis data were projected onto the extracted fingerprint \(\hat{{\boldsymbol{\beta }}}\) to evaluate the agreement between reanalyses \({\hat{{\bf{S}}}}_{{\rm{rea}}}\) and model simulations \({\hat{{\bf{S}}}}_{\mathrm{mod}}\) (which can be obtained by projecting the multi-model results in those days not used for training onto \(\hat{{\boldsymbol{\beta }}}\)). We also projected model simulations of natural variability (which are not used for training, as specified in the next subsection) onto \(\hat{{\boldsymbol{\beta }}}\) to estimate the control distribution of AGTWS anomalies under natural variability (\({\hat{{\bf{S}}}}_{{\rm{nat}}}\)).

$${\hat{{\bf{S}}}}_{{\rm{rea}}}={M}_{{\rm{rea}}}\hat{{\boldsymbol{\beta }}}$$
(2)
$${\hat{{\bf{S}}}}_{{\rm{nat}}}={M}_{{\rm{nat}}}\hat{{\boldsymbol{\beta }}}$$
(3)

Next, we assessed whether climate change is detectable by testing against the null hypothesis that the predicted AGTWS anomalies (\({\hat{{\bf{S}}}}_{\mathrm{mod}}\) or \({\hat{{\bf{S}}}}_{{\rm{rea}}}\)) is indistinguishable from the control distribution under natural variability (\({\hat{{\bf{S}}}}_{{\rm{nat}}}\)). The aforementioned climate change detections are mainly based on physically based model simulations. To advance our understanding of the time when climate change signals emerge, we further determine whether externally forced climate change is detectable on a daily basis by testing daily predictions \({\hat{{\bf{S}}}}_{{\rm{rea}}}\) (derived from the reanalyses) against the distribution under natural variability (\({\hat{{\bf{S}}}}_{{\rm{nat}}}\)). Supplementary Fig. 4 illustrates this daily climate change detection method.

Data processing

Prior to extracting the fingerprint, we preprocessed all model data from the ISIMIP project. We derived monthly TWS simulations from seven GHMs/LSMs along with the climate forcing data, including daily surface air temperature and specific humidity under the HIST, RCP2.6, and RCP6.0 scenarios. All daily meteorological data were regridded to a 0.5° × 0.5° global grid. Because several reanalyses (e.g., ERA5 and the NCEP-DOE Reanalysis 2) start in 1979 while the HIST simulations end in 2005, we chose 1979–2005 as the reference period to calculate the climatological seasonal cycle. For each model, the 31-day rolling mean seasonal cycle (centered on day i) was computed using daily surface air temperature and specific humidity from 1979–2005 and then subtracted from the daily value on each day (day i) on each grid cell. AGTWS anomalies (in the year corresponding to day i) were area-weighted based on monthly TWS anomalies from global grid cells (excluding Greenland and Antarctica) relative to the 1979–2005 mean seasonal cycle.

Multi-model data under three scenarios were used for fingerprint extraction. First, we chose three days per month for training: the 5th, 15th, and 25th. Next, regularized linear models (ridge regression) were trained to extract fingerprints. We then trained the statistical model for each month as previous studies have shown that the extracted climate response to external forcing can vary with the seasonal cycle25,29. To increase the sample size for each month, we included samples from the previous and subsequent month for training. To extract robust fingerprints across the multi-model archive, a resampling method, ‘leave-one-model-out’ cross-validation, was performed to derive an accurate estimate of the model prediction. We iteratively left out one of seven GHMs/LSMs (k = 7) for each training process. All seven training processes used data from k – 1 GHMs/LSMs, each of which was driven by four sets of meteorological forcing data (Supplementary Table 2). We determined the ridge regression parameter λ which yielded a fingerprint (\({\hat{{\boldsymbol{\beta }}}}_{{\boldsymbol{j}}}\), j = 1, 2, 3, …, 7) as a set of regression coefficients for each training process. Finally, we obtained the final monthly fingerprint (\(\hat{{\boldsymbol{\beta }}}\)) through averaging over all seven fingerprints (\({\hat{{\boldsymbol{\beta }}}}_{{\boldsymbol{j}}}\)).

To measure prediction errors, we predicted AGTWS anomalies (\({\hat{{\bf{S}}}}_{\mathrm{mod}}\)) for day i with data that are not used in the training process. We separately assessed the prediction error metrics (e.g., RMSE) for each model. We also obtained the predicted ensemble mean AGTWS anomalies by averaging over seven independent predictions from seven fingerprints. The predicted ensemble mean was then compared with the ensemble mean of seven GHMs/LSMs’ outputs by evaluating the pertinent prediction error metrics. To construct estimates of natural variability, daily predictions from 1861–1950 (\({\hat{{\bf{S}}}}_{{\rm{nat}}}\)) were used as a reference distribution of AGTWS anomalies under natural variability.

In addition, to obtain daily predictions beyond climate models, we projected the daily reanalysis datasets onto \({\hat{{\boldsymbol{\beta }}}}_{{\boldsymbol{j}}}\). The data preprocessing of the reanalyses followed the same procedure: daily data were re-gridded to a 0.5° × 0.5° grid, and the 31-day rolling mean seasonal cycle was subtracted from each day (day i) on each grid cell.