Introduction

Absorbing aerosol particles are mainly emitted from biomass burning and fuel combustion for transportation, industrial, and household activities, as well as from dust aerosol particles emitted from soil erosion (e.g. during dust storms over deserts) and agricultural activities. Absorbing aerosol particles significantly affect the transmission of solar radiation in the atmosphere and are widely regarded as a principal source of low regional air quality1,2,3. Aerosol absorption is typically expressed by the single scattering albedo (SSA), i.e. the ratio of aerosol absorption to the total aerosol extinction (the sum of absorption and scattering) in the atmosphere. SSA is a key variable for describing aerosol radiative forcing and, thus, the direct effect of aerosols on climate change. Furthermore, absorbing aerosols adversely affect air quality and health4, as well as on snow melt contributing to Arctic amplification and the retreat of glaciers5,6,7. Therefore, accurate estimates of SSA are critical for decreasing the uncertainty in investigations of aerosol effects on air pollution and climate change8,9,10.

Satellite remote sensing allows the optical characteristics of global aerosols to be captured11,12. However, the intensity of the reflected radiation in radiative transport is affected by both aerosol scattering and absorption, which are difficult to distinguish in satellite remote sensing retrieval13. In particular, for polar-orbit satellites with a single view, the inversion of various aerosol properties is underdetermined because of the limited number of independent observations14.

Candidate regional aerosol models used in typical aerosol inversion algorithms are typically derived via a cluster analysis of specific ground observation data15,16. Every predefined aerosol model exhibits known aerosol properties and different models exhibit different optical properties. SSA can be obtained using these models. For example, for the Dark Target algorithm developed for aerosol retrieval using moderate-resolution imaging spectroradiometer (MODIS) data over dark surfaces, five aerosol models (continental, moderately absorbing, non-absorbing, strong absorbing, and spheroid) were defined based on the analysis of sun photometer data in the global aerosol robotic network (AERONET)17,18. For each aerosol model, the SSA at 550 nm was fixed at values of 0.89, 0.92, 0.95, 0.87, and 0.9519. Hence, only a few discrete SSA values can be assigned using this algorithm, which results severely biased SSA results.

Researchers have attempted to retrieve parameters to characterise aerosol absorption, such as SSA or absorbing aerosol optical depth (AOD), from satellite observations. Satheesh et al.20 used the MODIS AOD product to retrieve aerosol absorption from ozone monitoring instrument (OMI) data, and the MODIS aerosol algorithm was discovered to be independent of the aerosol layer height (ALH). Although the OMI can provide both AOD and SSA products, the ALH must be assumed in advance21,22,23. Subsequently, MODIS retrieval is performed to constrain the AOD in OMI retrieval, which can improve the assessment of aerosol absorption24. Jeong and Hsu25 proposed an algorithm known as the aerosol single-scattering albedo and layer height estimation (ASHE) algorithm, which can provide biomass burning smoke (BBS) SSA and the ALH using a combination of MODIS, OMI, and Cloud-Aerosol Lidar with Orthogonal Polarization satellite sensors, and the corresponding shape and magnitude of spectral BBS SSA inversion results agreed well with the AERONET data (the deviation between them was within ± 0.03). However, this study only compared 4-day biomass aerosol SSA data to test the ASHE algorithm, the former of which do not contain sufficient data to verify the stability of the algorithm. Jeong et al.26 developed an optimal-estimation (OE)-based aerosol inversion algorithm based on OMI observations, and the results showed that the OE-based SSA (correlation coefficient (R = 0.33)) at 388 nm was consistent with AERONET SSA and comparable to the operational SSA (R = 0.34). Bao et al.27 proposed an inversion algorithm to indirectly obtain daily SSA results using a visible infra-red imaging radiometer suite sensor in East Asia. The algorithm combines the three basic aerosol components in a 6 S model to obtain several aerosol models and then selects the optimal aerosol model to obtain the optimal SSA value. The SSA inversion accuracy is higher under higher aerosol loading (AOD > 0.5) (R2all AOD = 0.426 and R2AOD > 0.5 = 0.571 at 550 nm). Wang et al.28 also regarded the aerosol models as unknowns and are determined based on the mixture of aerosol components (DU, BrC, BC, and AS), and the results are more reliable than the official SSA of MODIS. In addition to using only wavelengths in the ultraviolet and visible bands for SSA retrieval, the use of polarisation can provide additional information, thus providing a method for the detection of aerosol optical properties. Dubovik et al.29 developed a generalised retrieval of atmospheric and surface properties (GRASP) to retrieve the SSA for a POLDER/PARASOL sensor. The global GRASP/model SSA correlation coefficient was 0.348 compared with that of the AERONET at 443 nm, and researchers have proven that the retrieval accuracy can be improved during aerosol enrichment (R = 0.639 when AOD > 1.5)30,31.

Currently, research pertaining to SSA inversion is mainly focused on polar orbit satellites, whereas research pertaining to geostationary satellites is limited. Compared with polar orbit satellites, geostationary satellites have higher temporal resolution, which is of great research significance for studying the dynamic changes in aerosol optical properties14. Yoshida et al.32 constructed the advanced Himawari imager (AHI) retrieval technique and utilised the optimal estimation algorithm to invert the AOD and SSA at 500 nm; however, the SSA showed a low correlation of 0.304 when compared with AERONET’s observations, because the verification results show that the variable range of the satellite’s SSA is small, leading to significant deviation33.

Herein, an Algorithm for the retrieval of Single scattering albedo over Land (ASL) based on the geostationary satellite Himawari-8/AHI data is presented. Section 2 describes the results of the SSA inversion are presented and validated using ground-based AERONET data. The validation results are compared with the operational Japan Meteorological Agency (JMA) SSA results for the same period. The Section 3 is discussion of this paper. The Section 4 describes data source, the atmospheric radiative transfer forward model and the surface albedo model used in this study and the manner by which these models are used to construct the SSA retrieval algorithm. Additionally, the SSA and asymmetry factor sensitivity analysis are presented.

Results

Spatiotemporal distribution of retrieved SSA datasets over study area

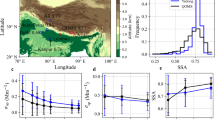
The ASL algorithm was applied to the AHI data to retrieve the SSA in the study area from January to September 2020. The spatial distributions of the AHI-retrieved SSA on 16 February 2020 from 00:00 to 08:00 UTC are presented in Fig. 1. The overall spatial distributions of the SSA over the study area were similar throughout the day, with high values over Australia and the North China Plain (near 40 N, 110E) and low values over Southeast Asia (near 20 N, between 80E and 100E). However, the spatial distributions over different regions changed by the hour, indicating the short-term variability of the aerosol absorbing properties, which can only be observed over such large areas using instruments on geostationary satellites. The low SSA (<0.9) over Southeast Asia indicates a relatively high proportion of absorbing aerosols in this region, which may be related to high emissions from biomass burning and the industry34.

Fig. 1: Maps of SSA retrieved using ASL algorithm over study area on February 16th 2020.
figure 1

a–i represent the SSA values of observation time from 0:00 – 08:00 UTC.

Full size image

Validation of ASL-retrieved SSA and comparison with JMA SSA data

The inversion results were evaluated and compared with the AERONET observations. To compare the results from the ASL algorithm with the JMA SSA, the latter were evaluated against AERONET SSA data for the same period. Based on the validation of these datasets through comparison with collocated AERONET SSA data, a quantitative comparison of the ASL SSA and JMA SSA was performed. In this regard, statistical metrics, including the correlation coefficient (R) and root-mean-square error (RMSE), mean absolute error (MAE), mean bias error (MBE), and expected error (EE, ±0.05) were used to evaluate the accuracy27,35. The AERONET SSA retrieval results from observations within ±30 min of the satellite overpass were averaged, and the satellite-retrieved SSA was averaged over a 50 km × 50 km region around the AERONET station27,36,37,38,39.

Scatterplots of the ASL SSA and JMA SSA vs. the AERONET SSA are shown in Fig. 2. To compare the AHI and AERONET SSA at the equivalent wavelength, the AERONET SSA was corrected to the AHI wavelengths at 470 and 500 nm via interpolation from 440 nm and 675 nm, respectively36. A total of 1071 collocated AHI/AERONET data points were obtained (Fig. 2a); the R was 0.7284 and the linear regression function was SSAASL = 0.60*SSSAERONET + 0.38. Meanwhile, MAE = 0.0319, MBE = 0.00324, and RMSE = 0.0427. Approximately 80.11% of the ASL SSAs were within the uncertainty range of △SSA = ( ± 0.05 + SSAAERONET)27. To validate the JMA SSA (Fig. 2b), 1766 collocated data pairs were used. The correlation between the JMA SSA and AERONET SSA was less significant than that for the ASL SSA data, with R = 0.0969, MAE = 0.0413, MBE = 0.00179, RMSE = 0.0654, and SSAJMA = 0.04*SSSAERONET + 0.90. Approximately 74.29% of the retrieval results were within the uncertainty of the ± 0.05 EE envelope. Clearly, the JMA SSA does not include the lower values provided by the ASL and AERONET, as shown by the comparison of the data presented in Fig. 2a and b.

Fig. 2: Scatter plots of satellite SSA vs. AERONET-derived SSA data over study area from January to September 2020.
figure 2

a ASL SSA and b JMA SSA vs. AERONET SSA data over study area. Middle dashed lines (red), side dashed lines (red), and solid lines (green) are the 1:1, EE (±5% + SSAAERONET), and linear regression lines, respectively. The upper-left text denotes the MAE, MBE, RMSE, EE, R, linear regression function, and number of matching points (N).

Full size image

The number of collocated SSA data points for the ASL SSA was smaller than that for the JMA SSA. For the inversion of the ASL SSA, a 2 × 2 pixel window in a cloud-free state must be implemented for two consecutive observations, and for both observations, an AOD value must be available. These conditions are not always fulfilled; in addition, some invalid inversion values with SSA ≥ 1.0 appear in the inversion results, which are invalid values and will not be included in the validation results. This also results in a relatively small number of matching points for ASL validation; therefore, the number of successful SSA retrievals and, thus, the number of match-ups for the ASL SSA is smaller than that for the JMA SSA.

In addition, the previous discussion included all the successful ASL SSA retrievals. Based on AERONET studies, the retrieval at low AODs (<0.4 at 440 nm) is less reliable40,41, which is similarly indicated in “Methods“ herein (the retrieval for low AODs (<0.4 at 470 nm) is less reliable). Therefore, the ASL SSA validation was repeated for cases where AOD > 0.4. As expected, the results in Fig. 3 showed better agreement between the ASL SSA and AERONET SSA, with an R value of 0.8627; the linear regression function was SSAASL = 0.73*SSAAERONET + 0.26, and the MAE, MBE, and RMSE were 0.0251, 0.01138, and the 0.0342, respectively. Furthermore, 84.58% of the ASL SSA was within the uncertain range of the ±0.05 EE envelope. The results above show that the correlation of the SSA retrieved by the ASL method agrees better with the ground-based observation when the aerosol load is high.

Fig. 3: Scatter plot of ASL-retrieved SSA vs.
figure 3

AERONET SSA for AOD > 0.4 at 470 nm over study area for the period from January to September 2020. Middle dashed lines (red), side dashed lines (red), and solid lines (green) are the 1:1, EE (±5% + SSAAERONET), and linear regression lines, respectively. The upper-left text denotes the MAE, MBE, RMSE, EE, R, linear regression function, and number of matching points (N).

Full size image

Discussion

In this study, an algorithm for the inversion of ASL was proposed for application to AHI data over land. The algorithm is based on the USM model and iteratively uses multi-pixel and multi-time data. In the inversion process, the known AOD and BRDF shapes were used to determine the aerosol SSA based on the optimal estimation method. The ASL algorithm was applied to the AHI data to invert the SSA over land for the Himawari-8 full-disk observation encompassing Asia and Australia for a period of 9 months. The results were evaluated using AERONET-derived SSA data. A comparison of the results with the JMA SSA data over the same area and time period, using AERONET data as reference, indicated the better performance of the ASL results, which agreed well with AERONET reference data, where the latter showed much lower SSA values than the JMA product. However, ASL retrieval requires the availability of multiple cloud-free pixels and the availability of AOD over these pixels, i.e. conditions that cannot be fulfilled at all times, thus resulting in lower coverage. And when the equations were iterated, sometimes there would be no solution state. Therefore, there are fewer matching points in verification results.

Methods

Data

The AHI is an imager on board the Himawari-8 geostationary meteorological satellite that was launched by the JMA in 2014. The AHI observes the full disk image every 10 min and the radiances in 16 channels at wavelengths from 0.47 to 13.28 μm, with a spatial resolution of 0.5–2 km42. In this study, AHI L1b data at 0.47 μm were used for SSA retrieval, because the blue wavelengths are sensitive to absorbing aerosols, which are good for estimation SSA27. The study area was (80°E–180°E, 60°S–60°N) over land, and the study period was from January to September 2020. The results were compared with those of aerosol products retrieved from the AHI observations by the JMA, which were distributed free of charge. In this study, we used level 2 SSA products (Version03) at 0.500 μm with a spatial resolution of 5 km and a temporal resolution of 10 min36 (further referred to as “JMA SSA”), retrieved daily between 0:00 and 8:00 UTC. The AHI official L1 and SSA products were obtained from JAXA (http://www.eorc.jaxa.jp/ptree/, last accessed on 30 November 2023). Hourly high-precision AHI AOD datasets used as inputs in this study were obtained from She et al.43, according to the validation results with AERONET measurements, the accuracy of this dataset is higher than JMA AOD and comparable to MODIS C6 AOD.

The SSA derived from AERONET sun photometer measurements was used to validate the retrieved SSA. AERONET sun photometers provide direct solar irradiance and sky radiance measurements along the solar principle plane and solar almucantar40,44. The SSA is provided at four wavelengths (440, 675, 870, and 1020 nm) and has a low uncertainty of ± 0.03 when AOD > 0.4 at 440 nm40,41. Data from all available AERONET sites in the study area (Supplementary Table 1) were used for validation. These datasets are available for free from the AERONET website (https://aeronet.gsfc.nasa.gov/, last accessed on 17 December 2023).

Forward model

The atmospheric forward radiative transfer model used in this study was proposed by these research articles45,46. This model, referred to as the USM model herein, describes the top of the atmosphere reflectance (TOA) as the sum of Un-scattered, Single-scattered, and Multiple-scattered components, as shown in Eq. (1) and Supplementary Fig. 1(a)-(c). The meaning of each parameter used in Eq. (1) are listed in Table 1.

$$\begin{array}{l}{\rho }^{TOA}({\theta }_{s},{\theta }_{v},\varphi )=\\ {I}_{0}(\tau ,{\Omega }_{{\rm{v}}})+{I}_{1}(\tau ,{\Omega }_{{\rm{v}}})+{I}_{m}(\tau ,{\Omega }_{{\rm{v}}})/{{F}_{0}^{\text{'}}}|{\mu }_{s}|\\ =\rho ({\theta }_{s},{\theta }_{v},\varphi ){e}^{-G\tau }+\frac{\omega {P}_{t}({\Omega }_{{\rm{v}}},{\Omega }_{{\rm{s}}})}{4(|{\mu }_{s}|+{\mu }_{v})}(1-{e}^{-G\tau })+\frac{{I}_{m}(\tau ,{\Omega }_{{\rm{v}}})}{{{F}_{0}^{\text{'}}}|{\mu }_{s}|}.\end{array}$$
(1)
Table 1 Description of the USM model parameters
Full size table

In (1), SSA (\(\omega\)) is expressed as an independent variable in \({I}_{1}\left(\tau ,{\varOmega }_{v}\right)\) and \({I}_{m}\left(\tau ,{\varOmega }_{v}\right)\) (for the detailed expressions of \({I}_{1}\left(\tau ,{\varOmega }_{v}\right)\) and \({I}_{m}\left(\tau ,{\varOmega }_{v}\right)\), see Li et al.45), the value of which can be obtained from the analytical solution of this equation. The total atmospheric scattering phase function (\({P}_{t}\left({\varOmega }_{v},{\varOmega }_{s}\right)\)), SSA (\(\omega\)), and asymmetry factor (g) are expressed in Eq’s. (2), (3) and (4).

$${P}_{t}({\varOmega }_{v},{\varOmega }_{s})=\frac{{\tau }_{{\mathrm{r}}}{{\mathrm{P}}}_{{\mathrm{r}}}(\Theta )+{\tau }_{{\mathrm{a}}}{{\mathrm{P}}}_{{\mathrm{a}}}(\Theta )}{{\tau }_{r}+{\tau }_{a}}.$$
(2)
$$\omega =\frac{{\tau }_{r}{\omega }_{r}+{\tau }_{a}{\omega }_{a}}{{\tau }_{r}+{\tau }_{a}}.$$
(3)
$$g=\frac{{\tau }_{r}{g}_{r}+{\tau }_{a}{g}_{a}}{{\tau }_{r}+{\tau }_{a}}.$$
(4)

The aerosol scattering phase function (\({P}_{a}\left(\varTheta \right)\)) can be calculated using the Henyey–Greenstein function as follows47:

$${P}_{a}(\varTheta )={P}_{H-G}(\varTheta )=\frac{1-{g}_{a}^{2}}{{[1+{g}_{a}^{2}-2{g}_{a}\cos (\Theta )]}^{1.5}}.$$
(5)

For molecular Rayleigh scattering, \({g}_{r}=0,{\omega }_{r}=1,{\tau }_{r}=0.00864{\lambda }^{-(3.916+0.074\lambda +\frac{0.05}{\lambda })}\), and \({P}_{r}\left(\varTheta \right)=\{3\left[1+{\cos }^{2}\left(\varTheta \right)\right]/4\}\)48.

Surface BRDF/albedo model

Land surface bidirectional reflectance was calculated using a semi-empirical kernel-driven BRDF model. The most widely used model for simulating the BRDF shape is the Ross–Thick–Li–Sparse (RTLS) model, which is utilised to generate the MODIS BRDF product, MCD4349. It describes the land surface BRDF in terms of three angular kernels, which represent three major scattering processes: isotropic (iso), volume scattering (vol), and geometric optical (geo) in Eq. (6). The meanings of the various parameters used in the RTLS model are listed in Table 2.

$$\begin{array}{c}\rho ({\theta }_{s},{\theta }_{v},\varphi )=\\ {f}_{iso}{K}_{iso}({\theta }_{s},{\theta }_{v},\varphi )+{f}_{vol}{K}_{vol}({\theta }_{s},{\theta }_{v},\varphi )+{f}_{geo}{K}_{geo}({\theta }_{s},{\theta }_{v},\varphi ).\end{array}$$
(6)
Table 2 RTLS model parameter description
Full size table

Equation (6) can be simplified to Eq. (7)50, which effectively reduces the number of unknown surface parameters in the inversion process.

$$\begin{array}{l}\rho \left({\theta }_{s},{\theta }_{v},\varphi \right)=\\ {f_{\!iso}}\left[\left(1+\frac{{f_{\!vol}}}{{f_{\!iso}}}\right)\cdot {K}_{vol}({\theta }_{s},{\theta }_{v},\varphi )+(\frac{{f_{\!geo}}}{{f_{\!iso}}})\cdot {K}_{geo}({\theta }_{s},{\theta }_{v},\varphi )\right].\end{array}$$
(7)

MCD43C2 data provide the isotropic coefficient (\({f}_{{iso}}\)), volume scattering coefficient (\({f}_{{vol}}\)), and geometric optical scattering coefficient (\({f}_{{geo}}\)) in seven wavebands from the visible to the near-infra-red region at a spatial resolution of 5 km. In many studies, \({f}_{{iso}}\) was assumed to change with time, the BRDF shape was assumed to be relatively stable in a month and between different spectral channels, and the shape of BRDF43,50 can be characterized by ratios of \({f}_{{vol}}\) and \({f}_{{geo}}\) to \({f}_{{iso}}\). Therefore, in this study, the \({f}_{{vol}}/{f}_{{iso}}\) and \({f}_{{geo}}/{f}_{{iso}}\) ratios were obtained from the MCD43C2 products and aggregated into monthly averages with a spatial resolution of 10 km.

Once \({f}_{{iso}}\) is obtained, we can compute the bi-hemispherical reflectance in the multiple scattering radiance (\({I}_{m}\left(\tau ,{\varOmega }_{v}\right)\)) process, which is the white-sky albedo of MODIS products, using the BRDF shape provided. The white-sky albedo α can be expressed as follows51:

$$\alpha ={f_{\!iso}}(\lambda ){H}_{iso}+{f_{\!vol}}(\lambda ){H}_{vol}+{f_{\!geo}}(\lambda ){H}_{geo}.$$
(8)

Where \({H}_{{iso}}=1\),\({H}_{{vol}}=0.189184\), and \({H}_{{iso}}=-1.377622\).

Sensitivity analysis

We analysed the sensitivity of Eq. (1) in solving the SSA (Fig. 4). In this regard, we used the following values: \({\theta }_{s}={\theta }_{v}=\varphi =30^\circ\); wavelength, 0.47 μm; and AOD values of 0.0001, 0.05, 0.1, 0.15, 0.2, 0.4, 0.6, 1.0, 1.5, 2.0, and 2.5. Five typical aerosol models (continental, moderately-absorbing, non-absorbing, absorbing, and dust) were selected, and the SSA and g values for these five models are shown in Supplementary Table 252. Two surface types (vegetation in Fig. 4a and desert in Fig. 4b) were considered, and the standard deviation of the TOA value calculated under different aerosol models is shown in Table 3 for each AOD step value. The data in Table 3 show that when AOD is low (AOD < 0.4), the TOA estimated by different SSA values barely changes, indicating that the retrieved SSA value is not accurate at this time. When AOD > 0.4, the TOA estimated using different SSA values began to differentiate. The higher the AOD value, the more significant is the differences, indicating that the TOA under high aerosol loading is sensitive to changes in the SSA, which is consistent with ground-based AERONET data41.

Fig. 4: Sensitivity analysis of SSA based on USM model.
figure 4

a Vegetated areas (dark surface, 34°40′5.21″N, 116°58′28.79″E), fk = 0.070750, 0.035759, 0.09853. b Desert areas (bright surface, 42°12′58.52″N, 117°7′21.93″E); fk = 0.279533, 0.162176, 0.054849. The fk (k = iso, vol, or geo) are obtained from the monthly mean value of MCD43C2 products in February.

Full size image
Table 3 TOA standard deviation (s.d.) of five typical aerosol models under different AOD conditions
Full size table

In order to further analyze the impact of SSA and g on the inversion results, we took the bright surface as an example and conducted sensitivity analysis on SSA and g respectively. The observation angle and AOD change step were consistent with the above. SSA ranges from 0.7, 0.8, 0.9 to 0.99, and g from 0.65, 0.7–0.75, as shown in Supplementary Fig. 2 and Supplementary Fig. 3. In Supplementary Fig. 2a–c, when AOD > 0.4, the estimated TOA for different SSA values can be clearly distinguished, indicating that the accuracy of inversion can be guaranteed in this case. In Supplementary Fig. 3a–d, when SSA = 0.7, the difference in estimated TOA for g under different AOD values is not significant, and when the AOD load is high, TOA hardly changes with the change of AOD. As SSA gradually increases, the estimated TOA will show more significant differences, indicating a lack of sensitivity in g when targeting high load aerosols with strong absorption.

Inverse method

The L1b AHI/Himawari-8 data provided by the JMA and the AHI-AOD datasets produced by She et al.43 were used in the ASL algorithm. The L1b data included a cloud mask determined based on the method of Lim et al.42. The theoretical basis for the algorithm in this study comes from the different spatiotemporal scale differences between the Earth’s land surface and aerosols. The land surface undergoes significant changes in space, but the short-term changes are minimal, while the optical properties of aerosols can undergo rapid changes over time, but the changes are relatively small within a spatial range of about 50–60 km53,54. For the AHI sensor, its high-frequency observation characteristics can provide high-resolution observation images. Although the observation zenith angle of geostationary satellites is always fixed, the solar zenith angle changes with time, resulting in changes in the scattering angle of the two observations. Therefore, it has natural multi angle observation characteristics, effectively avoiding the problem of insufficient observation information caused by single angle observation. So the ASL is based on the following assumptions: (1) the surface BRDF \({f_{{\!iso}}}\) does not change within 1 h; (2) the aerosol optical properties (SSA, g) in the 20 km × 20 km pixel window (2 × 2 pixel window) remain unchanged54,55; and (3) the aerosol optical properties (SSA, g) remain unchanged for 1 h. The MODIS MCD43C2/BRDF product was used for the treatment of surface reflectance. For a fixed BRDF shape, information regarding the aerosol optical properties and BRDF \({f}_{{iso}}\) can be estimated from multiple time and pixel window observations available from the AHI. For the general condition, we used N × N pixel windows and K observations for the inversion. N2 + 2 unknowns, N2 BRDF isotropic coefficients, and two parameters can be used to characterise the aerosol optical properties (SSA, g), provided that the AOD is known. In total, the K × N2 equations exist. The number of equations must not be less than the number of unknowns to ensure robust retrieval.

$$K\times {N}^{2}\ge {N}^{2}+2.$$
(9)

The solution of inequality shown in Eq. (9) can be realised for K = 2 and N = 2. The schematic diagram is shown in Supplementary Fig. 4. For the iterative method, we selected the OE method26. The cost function \(c(x)\) is expressed as:

$$c\,(x)={(y-F(x))}^{T}{S}_{\varepsilon }^{-1}(y-F(x))+{({x}_{a}-x)}^{T}{S}_{a}^{-1}({x}_{a}-x).$$
(10)

In Eq. (10), \(x\) represents the unknown parameters (\({f}_{{iso}}\), SSA, and g) to be determined, \({x}_{a}\) the prior value of the unknown parameter, \({S}_{a}\) the prior covariance matrix, and \({S}_{\varepsilon }\) the AHI TOA observation error-covariance matrix. Considering that the AHI TOA at 0.47 μm is independent at different pixel positions and for the same pixel at different times56, \({S}_{\varepsilon }\) is expressed as a diagonal matrix of the spectral reflectance multiplied by the radiometric calibration accuracy. \({f}_{{iso}}\), SSA, and g are independent of time and space; therefore, \({S}_{a}\) is a diagonal matrix. The initial values of SSA and g were set to 0.9 and 0.65, respectively, and the initial value of \({f}_{{iso}}\) from MCD43C2 products. An extremely low SSA value (0.7) was set as the weak constraint of the component SSA of the diagonal matrix \({S}_{a}\). The effective value range of SSA is [0-1]. To avoid invalid iterations, we calculated the SSA values of AERONET in the study area and found that the SSA values range from 0.6 to 1.0. Therefore, if SSA < 0.6 or SSA ≥ 1.0 occurs during the iteration process, the iteration will stop and the inversion results will be considered invalid. The constraint of the diagonal matrix \({S}_{a}\) on \({f}_{{iso}}\) was set to the greater of two values: (1) the uncertainty of the MODIS BRDF product (10%) or (2) the standard deviation of \({f}_{{iso}}\) per month. To minimise the cost function, we used the Levenberg–Marquardt method to perform the inversion iteration. The whole inversion process is shown in Supplementary Fig. 5.