Main

Molecular property prediction is widely considered one of the most important tasks in drug discovery. Traditional wet-lab experiments are time consuming and require a huge and incessant investment1,2. With artificial intelligence, researchers have studied molecular property prediction models to assess the clinical trial success rate and therapeutic potential of drug candidates, or even directly predict whether a compound will receive US Food and Drug Administration approval, substantially speeding up drug development and avoiding costly late-stage failures.

With the increasing availability of chemical experimental data, researchers have adopted pre-training models on extensive collections of unlabelled molecules, followed by fine-tuning on a limited number of labelled molecules for a specific task3,4,5,6. Most of these self-supervised learning (SSL) methods on molecules are purely data driven, focusing on exploiting the intrinsic information of molecular graphs without any prior chemical knowledge7,8,9,10. Moreover, with the enormous chemical space, these models rely heavily on pre-training datasets and may not generalize well to different downstream prediction tasks. Additionally, models that capture only the topology of molecular graphs and simple construction rules generally yield low interpretability. Therefore, it is important to leverage the fundamental chemical knowledge as a prior to guide the model to explore the chemical semantics of molecules at the microscopic level and discover meaningful patterns in both pre-training and fine-tuning.

As a typical SSL method, contrastive learning has attracted more research interest. To construct similar pairs and maximize agreement between them, existing methods rely on universal graph augmentation techniques that include node deletion, edge perturbation and subgraph extraction11. However, these techniques can be unsuitable for molecular graphs due to the considerable impact of adding or removing chemical bonds or atoms, which can alter the molecule’s properties and identity12. Moreover, most existing methods consider only the connections between atoms established by chemical bonds, and thus do not fully explore the underlying relations of atoms in a molecular graph, which also highlights the key to incorporating external ___domain knowledge.

Another neglected issue is that the pre-training tasks differ greatly from the downstream tasks. Directly applying pre-trained representations to downstream tasks may result in suboptimal performance. In this Article, to address this, we propose providing a chemical prompt during fine-tuning based on fundamental chemical knowledge to bridge this gap. Inspired by prompt-tuning13, an emerging paradigm that has demonstrated remarkable performance on a wide range of natural language processing tasks14,15,16,17, it is crucial to devise appropriate prompts for molecular graphs based on fundamental chemical knowledge to enable more reliable predictions.

To this end, we propose a chemical element-oriented knowledge graph (ElementKG), which integrates basic knowledge of elements and functional groups in an organized and standardized manner. Then we exploit the contained fundamental chemical knowledge as a prior in both pre-training and fine-tuning, and propose a novel knowledge graph-enhanced molecular contrastive learning with functional prompt (KANO).

Firstly, we construct a chemical ElementKG based on the Periodic Table (https://ptable.com) and Wikipedia pages (https://en.wikipedia.org/wiki/Functional_group). ElementKG offers a comprehensive and standardized view from a chemical element perspective, which forms the foundation of our work. ElementKG covers the class hierarchy of elements, the chemical attributes of elements, the relationships between elements, the corresponding functional groups, and the connections between functional groups and their constituent elements.

Second, we introduce an element-guided graph augmentation in contrastive pre-training. Specifically, we augment the original molecular graph under the guidance of element knowledge in ElementKG, extracting rich relations between elements and associations between atoms that share the same element type but are not directly connected by chemical bonds. The resulting augmented graph respects the chemical semantics within molecules and establishes essential connections between atoms that go beyond the structural information. On top of this, a contrastive learning framework is developed to avoid indiscriminate implantation of external knowledge and to mitigate injection noise by allowing the two graph views to complement each other.

Third, we propose functional prompts to bridge the gap between pre-training contrastive tasks and downstream molecular property prediction tasks. As sets of atoms bonded together in a specific pattern, functional groups play a crucial role in determining the properties of the parent molecule18 and are therefore closely related to downstream tasks. Therefore, in fine-tuning, we utilize the functional group knowledge in ElementKG to generate functional prompts, prompting the pre-trained model to recall task-related knowledge.

Finally, we thoroughly evaluate KANO on 14 various molecular property prediction tasks, demonstrating its superiority over competitive baselines. We also conduct extensive experiments to verify the necessity of each component of KANO, and to investigate its robustness and interpretability.

Results

Overview of KANO

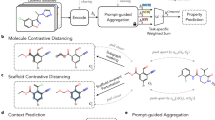
In this paper, we propose KANO, a new KG-enhanced molecular contrastive learning with functional prompt method, which consists of three main components: (1) ElementKG construction and embedding, (2) contrastive-based pre-training and (3) prompt-enhanced fine-tuning. An overview of KANO is shown in Fig. 1.

Fig. 1: Overview of KANO.
figure 1

a, ElementKG construction and embedding. We collect basic element knowledge from the Periodic Table and functional group knowledge from Wikipedia pages to build ElementKG. Then we apply the KG embedding method to obtain the embeddings of all entities and relations in ElementKG. b, Contrastive-based pre-training. We use an element-guided graph augmentation strategy based on element knowledge of ElementKG to convert the original molecular graph G into the augmented molecular graph \(\tilde{G}\), establishing essential connections between atoms beyond the inherent structure. The graph encoders are then trained to maximize the agreement between these two graph views to avoid excessive knowledge injection in \(\tilde{G}\). c, Prompt-enhanced fine-tuning. We leverage functional group knowledge of ElementKG to generate a corresponding functional prompt for each molecule, stimulating the pre-trained graph encoder to recall the learned molecular property-related knowledge and bridging the gap between the pre-training contrastive tasks and the downstream tasks. The resulting prompt-enhanced molecular graph is then fed into the pre-trained graph encoder for molecular property prediction.

Full size image

ElementKG construction and embedding

Chemical ___domain knowledge is critical for molecular analysis, and integrating it into structured data can make it more standardized and easier to use. Some researchers have built KGs from public chemical databases and scientific literature to extract associations between chemicals and diseases or drug pairs19,20. However, in contrast to these approaches, we focus on the most fundamental chemical knowledge—the chemical elements. Over more than a century, the Periodic Table has evolved into an interrelated and complete system of elements, revealing the inherent laws of the complex real world and enabling chemical research to achieve a fundamental leap from phenomenon to essence. While a recent study11 developed a KG that incorporates elements and their corresponding chemical attributes, its basic relations are inadequate for accommodating thorough and well-organized fundamental chemical knowledge. To provide a holistic view of the Periodic Table, we construct an element-oriented KG that combs the class hierarchy, data properties and object properties of elements. Additionally, we recognize the importance of functional groups and their close relationship to chemical elements, and thus, we collect relevant knowledge about functional groups from Wikipedia pages to make ElementKG more informative.

Figure 2a shows a snapshot of ElementKG, which consists of two levels: instance level and class level, coloured as red and blue, respectively. At the instance level, chemical elements and functional groups are represented as entities in ElementKG, denoted by red blocks. To record various chemical attributes of each element (for example, electron affinity and boiling point) and the composition of each functional group (for example, bond type), we apply data properties that attach literal data type values to an entity. The dotted block represents the data properties of the entity in the red block above it. Furthermore, as indicated by the red arrows, we establish associations between entities through object properties, such as chemical attribute relations between elements and the inclusion relations between elements and functional groups. We then classify all entities on the basis of their commonalities, resulting in the class level of ElementKG. Entities are assigned to the corresponding classes via rdf:type, denoted by dashed black arrows. The blue blocks represent different classes, while the blue arrows reflect the inclusion (rdfs:subClassOf) or disjointness (owl:disjointWith) between them. In particular, the subClassOf relations between classes form the class hierarchy, which serves as the backbone of ElementKG. The construction details can be found in Methods, and the statistics of ElementKG are displayed in Supplementary Information.

Fig. 2: Illustration of ElementKG and its embedding process.
figure 2

a, A snapshot of ElementKG. ElementKG contains the class hierarchy, data properties, object properties and entities of both elements and functional groups. b, The process of ElementKG embedding. We derive a corpus of three documents (structure document, lexical document and combined document) from ElementKG, considering the structural topology, literal semantics and correspondence between entity IDs and literal words in ElementKG, respectively. We then train a language model to learn entity and relation embeddings from this corpus. This process enables the integration of element and functional group knowledge into a unified representation, which facilitates downstream molecular property prediction.

Full size image

To comprehensively explore the structural and semantic information and obtain meaningful representations of all entities, relations and other components in ElementKG, we adopt a KG embedding approach based on OWL2Vec* (ref. 21). For further elaboration, please see Methods.

Contrastive-based pre-training

After obtaining ElementKG and its embeddings, we aim to incorporate it into pre-training to enhance the model’s understanding of fundamental ___domain knowledge. We employ a contrastive learning method to pre-train a graph encoder on a large set of unlabelled molecules, using the basic element knowledge in ElementKG. Traditional graph augmentation techniques for creating positive pairs of contrastive learning often involve dropping nodes or perturbing edges, which can violate chemical semantics within molecules. To address this issue and establish more meaningful connections between atoms, we propose an element-guided graph augmentation approach for constructing positive pairs in contrastive learning.

As shown in Fig. 1b, we begin by identifying the element types present in a given molecule (for example, C, N and O) and retrieving their corresponding entities and relations from ElementKG (for example, (N, hasStateGas, O), (O, inPeriod2, C)). This forms an element relation subgraph that describes the relationships between elements using their associated entities and relations. We link the element entity nodes in this subgraph to their corresponding atom nodes in the original molecular graph to create an augmented molecular graph that integrates fundamental ___domain knowledge and captures the essential associations between atoms that share the same element type, even if they are not directly connected by chemical bonds. Our approach preserves the topology structure while incorporating important chemical semantics. Additional details about the input features and the triple definition can be found in Supplementary Information.

On top of this, we employ a contrastive learning framework to train the graph encoder by maximizing the consistency between the original molecular graph and the augmented molecular graph, without indiscriminately embedding element knowledge in the augmented graph. Given a minibatch of N randomly sampled molecules, we create a set of 2N graphs by transforming their molecular graphs \({\{{G}_{i}\}}_{i = 1}^{N}\) into augmented graphs \({\{\tilde{{G}_{i}}\}}_{i = 1}^{N}\) using element-guided graph augmentation. Following refs. 12,22, we treat the 2(N − 1) graphs other than the positive pair within the same minibatch as negatives, where a positive pair consists of the original molecular graph Gi and its augmented molecular graph \(\tilde{{G}_{i}}\). We apply a graph encoder f(⋅) to extract graph embeddings \({\{{{{{\boldsymbol{h}}}}}_{{G}_{i}}\}}_{i = 1}^{N}\) and \({\{{{{{\boldsymbol{h}}}}}_{\tilde{{G}_{i}}}\}}_{i = 1}^{N}\) from the two graph views, and a non-linear projection network g(⋅) to map these embeddings into a space where the contrastive loss is applied, resulting in two new representations \({\{{{{{\boldsymbol{z}}}}}_{{G}_{i}}\}}_{i = 1}^{N}\) and \({\{{{{{\boldsymbol{z}}}}}_{\tilde{{G}_{i}}}\}}_{i = 1}^{N}\). Finally, a contrastive loss is used to maximize the consistency between positive pairs while minimizing the agreement between negative pairs. For further details, refer to Methods.

Prompt-enhanced fine-tuning

After pre-training, the molecular graph encoder needs to be fine-tuned for downstream property prediction. Specifically, the input molecular graph G is fed into the pre-trained graph encoder f(⋅) to extract the graph embedding hG, which is then fed into the predictor to output the property value. To bridge the gap between the pre-training contrastive tasks and downstream tasks, we propose to use functional group knowledge as prompts to stimulate the pre-trained graph encoder.

As shown in Fig. 1c, we generate the functional prompt from the functional group knowledge of ElementKG. First, we detect all functional groups in the input molecule, retrieve their corresponding entity embeddings in ElementKG and construct a mediator with a learnable embedding to capture the importance of each functional group. We then apply a self-attention mechanism to the embedding of the mediator (coloured in red) and the embeddings of the functional group entities to comprehensively aggregate their semantics and obtain the functional prompt. Finally, the functional prompt is added to the original representation of each atom node in the input molecular graph with a learnable scale parameter to produce the prompt-enhanced molecular graph, which is then fed into the pre-trained graph encoder and a predictor for molecular property prediction. The technical details of functional prompts are provided in Methods.

KANO boosts the performance of property prediction

Molecular properties of interest can vary widely in scale, ranging from macroscopic influences on the human body to microscopic electronic properties, such as drug side-effects23, the ability to inhibit human immunodeficiency virus (HIV) replication24 and hydration free energy3. To assess the effectiveness of KANO, we evaluated its performance on datasets in four categories: physiology, biophysics, physical chemistry and quantum mechanics. For more information on the datasets and baselines, please refer to Supplementary Information.

Tables 1 and 2 present the results of various supervised and SSL methods. #Molecules represents the number of molecules in each dataset, and #Tasks indicates the number of binary prediction tasks in each dataset.

Table 1 Test performance of different models on eight classification benchmarks of physiology and biophysics. The first five models are supervised learning methods, while the last eight are self-supervised methods. The mean and standard deviation of test ROC-AUC (%) on three independent runs are reported
Full size table

Table 1 reports the test receiver operating characteristic-area under curve (ROC-AUC,%) on classification tasks in physiology and biophysics. Key observations include: (1) KANO consistently outperforms other methods on all eight datasets, with a significant improvement of 3.79%, showcasing its effectiveness. (2) KANO performs well on multiple-task learning datasets such as Tox21, ToxCast, SIDER and MUV. In particular, KANO achieves a 3.39% improvement on the ToxCast dataset with 617 binary classification tasks. The robust performance indicates that its representations cover diverse molecular semantics.

Table 2 presents the test performance of regression tasks in physical chemistry and quantum mechanics. The key observations are as follows: (1) KANO receives top scores among supervised and self-supervised models, surpassing previous records by a relative improvement of 15.8% on all six regression tasks. (2) KANO’s fine-grained chemical understanding helps it achieve remarkable accuracy on quantum mechanical datasets, even surpassing models that incorporate additional 3D information9. (3) KANO greatly helps tasks with limited label information, as evidenced by the average improvement of 21.7% on small datasets ESOL and FreeSolv with only 1,128 and 642 labelled molecules, respectively.

Table 2 Test performance of different models on six regression benchmarks of physical chemistry and quantum mechanics. The first five models are supervised learning methods, and the last six are self-supervised methods. The mean and standard deviation of test root mean square error (for ESOL, FreeSolv and Lipophilicity) or mean absolute error (for QM7, QM8 and QM9) on three independent runs are reported
Full size table

In summary, KANO outperforms other models in all benchmarks, demonstrating the effectiveness of integrating ElementKG into the pre-training and fine-tuning stages. KANO not only outperforms other SSL methods but also demonstrates its superiority over supervised methods, providing a competitive advantage for generalization to a broader chemical space.

Richer knowledge in KG leads to more robust representations

ElementKG is essential in the KANO framework as it guides molecular augmentation and functional prompt generation. To determine the contributions of its various components, we evaluate KANO’s performance using different KG components, such as class hierarchy, data property and functional group knowledge. We only prune ElementKG’s components during pre-training and keep the experimental settings for fine-tuning consistent with the original KANO approach.

Extended Data Fig. 1a reveals that: (1) KANO with the complete ElementKG architecture (‘complete ElementKG’) outperforms the other versions across all datasets, highlighting the indispensability of each component. (2) Removing class hierarchy (‘w/o class hierarchy’) results in performance degradation, accentuating the significance of class division and transitive relations between subclasses in refining and transferring fundamental ___domain knowledge. (3) Excluding functional groups from ElementKG (‘w/o functional group’) causes a noticeable drop in performance, underscoring the critical role of functional groups. (4) Excluding data properties of entities (‘w/o data properties’) almost always perform the worst, emphasizing the importance of chemical attributes.

To further investigate the impact of data properties, which each element contains more than 15 of, we mask a certain proportion of them and report the test performance on four categories of tasks. Extended Data Fig. 1b shows the test results for varying keeping rates of data properties. Notably, the model’s performance consistently improves as the proportion of retained properties increases, verifying that richer data properties provide more comprehensive fundamental knowledge and consequently enable the learning of more robust molecular representations.

Contrastive learning produces a high-quality feature space

The quality of a representation space can be evaluated by two key properties: alignment and uniformity25. The former indicates that similar samples should be mapped to nearby embeddings, while the latter suggests that feature vectors should be uniformly distributed on the unit hypersphere, preserving as much data information as possible. In Fig. 3, we compare the molecular representations produced by our method with those obtained by other methods, including a supervised model (CMPNN26), a representative predictive method (GROVER8) and a contrastive method with universal augmentation strategy (MolCLRCMPNN11).

Fig. 3: Alignment and uniformity analysis.
figure 3

a, Alignment analysis. We show t-SNE visualization of molecular representations to investigate the similarity of molecules with the same scaffold. Different colours represent different scaffolds, with a lower DB index indicating better clustering separation. b, Uniformity analysis. Molecular feature distributions are plotted with Gaussian KDE in \({{\mathbb{R}}}^{2}\) (darker colours indicate more points fall in the region), along with KDE on angles (that is, arctan2(y, x) for each point \((x,y)\in {{{{\mathcal{S}}}}}^{1}\)) for a clearer presentation.

Full size image

Alignment analysis

We visualize representations of the molecules with different scaffolds by t-distributed stochastic neighbour embedding (t-SNE)27 to test whether molecules with the same scaffold would have similar representations. The scaffold, which represents the core structure of a molecule, is a fundamental concept in chemistry and provides a basis for systematic investigations of molecular cores and building blocks28. Molecules with different scaffolds typically have very different chemical properties. We choose the seven most common scaffolds from each dataset (Tox21, QM7 and BBBP) and distinguish the scaffolds with different colours. As shown in Fig. 3a, the model without pre-training cannot distinguish molecules with these scaffolds, and the predictive and contrastive methods show only slight improvement. In contrast, KANO produces more distinctive clusters with the lowest Davies–Bouldin (DB) index.

Uniformity analysis

To examine the uniformity of the learned molecular representations, we first map them onto the unit hypersphere \({{{{\mathcal{S}}}}}^{1}\) using t-SNE27, and then visualize the density distributions of the representations on \({{{{\mathcal{S}}}}}^{1}\) using non-parametric Gaussian kernel density estimation (KDE)29 in \({{\mathbb{R}}}^{2}\). We also show the density estimations of angles for each point on \({{{{\mathcal{S}}}}}^{1}\) to present the results more clearly. Figure 3b illustrates the feature and density distributions of the molecular representations learned by our model and the three baselines on the Tox21, ToxCast and ClinTox datasets. In the first three columns, the distributions of the representations are relatively highly clustered with sharp density distributions. In the last column, the distribution becomes more uniform, and the density estimation curves are markedly less sharp.

From Fig. 3, we observe that our model can map molecules with the same scaffold to similar representations, and the pre-trained representations have a more uniform distribution than the baselines. Our ElementKG and KG-guided contrastive learning framework enable KANO to capture globally intrinsic molecular characteristics by normalizing the filtering of knowledge and perceiving global structural insights. Supplementary Information provides additional visualizations of KANO pre-trained representations.

Functional prompts enable explainable predictions

In Extended Data Fig. 2, we compared KANO’s performance with functional prompts with that without prompts and evaluated two alternative architectures that integrated functional group knowledge through adding and concatenating to each atom. Results show that the model with functional prompts performs better than the one without, with an 8.41% relative improvement. Furthermore, adding and concatenating functional group features were proven to be suboptimal choices, emphasizing the effectiveness of functional prompts.

Since functional prompts act as a bridge between pre-training contrastive tasks and downstream molecular property prediction tasks, we are interested in their potential to provide ___domain-specific interpretability. We visualize the attention weights of functional groups in molecular graphs from four property categories in Fig. 4. (1) The first example is from the Tox21 (ref. 30) public database, which measures the toxicity of compounds. We observe higher attention weights for pyridyl and azo functional groups, followed closely by primary amine. Interestingly, pyridyl and primary amine groups can combine to form 2,6-diaminopyridine, a major component of secondary hepatotoxins and skin sensitizers31. Azo-containing compounds, such as azo dyes, exhibit carcinogenic and mutagenic properties, making them highly significant32. (2) The second example is a human β-secretase 1 (BACE-1) inhibitor from the BACE dataset33. The molecule assigns more attention to amidine, carboxamide and secondary ketimine, which form the imidazole component. In addition, pyridyl and phenyl also receive more attention. These findings align with previous research34,35, suggesting that the aromatic heterocycle family inhibits BACE-1. (3) The third sample is from FreeSolv36, which focuses on the hydration free energy of small molecules in water. Fluoro and hydroxyl groups receive higher attention due to fluoro’s strong electron-acquiring ability and hydroxyl’s hydrophilicity, affecting the molecule’s interaction force with water. Additionally, carboxyl groups with strong polarity receive more attention weights. (4) The final molecule is from QM7 (ref. 37), recording the atomization energies of molecules. Alkenyl and carboxamide groups receive more attention due to the higher bond energy of the carbon–carbon double bond and the stability of the amide bond, requiring more energy to break them apart into separate atoms. The interpretability exploration illustrates how functional prompts bridge the gap between pre-training tasks and downstream tasks by invoking relevant functional group knowledge from the molecular property prediction task perspective.

Fig. 4: Investigation of interpretability of functional prompts.
figure 4

Attention visualization examples of different functional groups in four data categories. The attention weights reflect the functional groups’ significance to the global characteristics of the molecule, extracted from the final self-attention layer and normalized. Darker colours indicate higher attention weights.

Full size image

Conclusion

In this study, we presented KANO, a novel approach that enhances molecular property prediction tasks by incorporating chemical ___domain knowledge. KANO achieved superior performance on 14 molecular benchmarks by leveraging ElementKG, a KG that organizes the knowledge of elements and functional groups. KG-guided pre-training allowed KANO to obtain a high-quality molecular representation space, while functional prompts captured meaningful chemical substructures relevant to downstream tasks.

While KANO has shown promising performance, it may still have some limitations. For instance, ElementKG may not fully capture molecular system complexity, and the current functional prompts may not be able to capture long-range interactions between substructures. To address these limitations, we suggest several interesting future directions. Firstly, extending ElementKG to cover other areas of chemistry and integrating it with other existing KGs could provide a more comprehensive understanding of molecular systems. Secondly, studying the interpretability of KANO’s learned representations and the chemical knowledge captured by the functional prompts could provide insights for molecular design and optimization. Finally, exploring the possibility of combining KANO with other techniques to improve its performance on small datasets and accelerate drug discovery could be a promising direction to pursue.

Methods

ElementKG construction and representation

We constructed ElementKG by integrating knowledge from the Periodic Table and Wikipedia pages, providing a holistic view of the element class hierarchy, the chemical attributes of elements and functional groups, and the relations between them. The detailed construction process is shown in Fig. 2 and described below.

First, we extracted the class hierarchy from the collected knowledge of elements and functional groups, which serves as the backbone of ElementKG. As shown in the upper part of Fig. 2, blue blocks represent different classes and blue arrows reflect the containment or disjoint relations between them. For example, the rdfs:subClassOf construct between the class ReactiveNonmetals and the class Nonmetals means that the set of entities in ReactiveNonmetals is a subset of entities in Nonmetals. Also, every entity in the Ester class is a member of its parent class, GroupContainingOxygen. It is important to note that the subclass relations are transitive, implying that the ReactiveNonmetals class is also a subclass of the Element class. However, since literal names can be insufficient to differentiate between different classes, we defined disjointness for the classes and added disjointness axioms using owl:disjointWith. For example, the disjointness between the Metals and Nonmetals classes indicates that an element entity in the Metals class cannot be a member of the Nonmetals class at the same time. Using the class hierarchy, we assigned corresponding entities to each class via rdf:type, with both C and O elements in red blocks being members of the ReactiveNonmetals class.

Second, we compile a list of chemical attributes sourced from the Periodic Table and assign them as data properties to each entity in ElementKG (the dotted block). Over 15 data properties, including hasName, hasAtomic, hasDensity and hasIonization, are associated with each element. On the other hand, for functional groups, we record the type of bonds they contain. For instance, CarboxylhasBondType contains single and double bonds, while Phenyl contains both single and aromatic bonds.

Third, we use object properties (red directional arrows) to model the relationships between entities in ElementKG. To achieve this, we discretize the continuous chemical attribute values of elements and use them as object properties (for example, inRadiusGroup1 and inWeightGroup2) to connect element entities to each other. For instance, the triple (C, inRadiusGroup1, O) indicates that the entities C and O are both in Radius Group 1, while (C, hasStateGas, O) means that they are both in the gaseous state. We add symmetric characteristics to these object properties, which means that (O, hasStateGas, C) also holds when given (C, hasStateGas, O). Since ElementKG is primarily element oriented, we do not directly add object properties to functional groups. Instead, we establish the connection between element and functional group entities through the isPartOf object property, which indicates that the element is involved in the formation of the functional group.

To fully explore the structural and semantic information and obtain meaningful representations of all entities, relations and other components in ElementKG, we employ a KG embedding approach based on OWL2Vec* (ref. 21). As illustrated in Fig. 2b, this approach involves two steps: (1) extracting a corpus from ElementKG, including a structure document, a lexical document and a combined document, and (2) training a language model on the corpus to obtain high-quality KG embeddings38. The structure document captures the graph structure and the logical constructors by computing random walks for each target entity and combining the traversed relations and entities into sentences. For example, a random walk of depth 3 starting from the element C would result in the sentence (C, inRadiusGroup1, O, rdf:type, ReactiveNonmetals). The lexical document includes sentences parsed from the structure document. For example, the sentence above can be parsed as (‘C’, ‘in’, ‘radius’, ‘group1’, ‘O’, ‘type’, ‘reactive’, ‘nonmetals’). To establish the correspondence between entities and their literal names, we replace each word in the lexical document with the corresponding entity in the structure document, resulting in a combined document. That is, the example above can be converted to a set of sentences: (C, ‘in’, ‘radius’, ‘group1’, ‘O’, ‘type’, ‘reactive’, ‘nonmetals’), (‘C’, inRadiusGroup1, ‘O’, ‘type’, ‘reactive’, ‘nonmetals’) and so on. These three documents are merged into a single document, which is then used to train a word2vec39 model with the skip-gram architecture. Finally, we obtain embeddings for each entity and relation in ElementKG, which we use for input feature initialization of the augmented molecular graph and functional prompt generation.

Contrastive learning framework

We employ a contrastive learning framework to learn the representations of molecular graphs. Given a minibatch of size N, we generate 2N graphs by transforming the N original molecular graphs into N augmented molecular graphs. The original molecular graph Gi and its augmented version \({\tilde{G}}_{i}\) constitute a positive pair (Gi, \({\tilde{G}}_{i}\)), while (Gi, Gj)j≠1 and \({({G}_{i},\tilde{{G}_{j}})}_{j\ne 1}\) form negative pairs.

After capturing the graph representations using the graph encoders f(⋅), a non-linear transformation g(⋅) called the projection network maps both the original and augmented graph representations to a latent space where the contrastive loss is calculated, as proposed in simCLR40. We adopt a two-layer perceptron (MLP) to perform the projection. Then, we use the normalized temperature-scaled cross-entropy (NT-Xent) loss function40 to train the graph encoders to maximize the agreement between positive pairs and the discrepancy between negative pairs.

Let \({{{\rm{sim}}}}({{{{z}}}}_{1},{{{{z}}}}_{2})=\frac{{{{{z}}}}_{1}^{\top }{{{{z}}}}_{2}}{\left\Vert {{{{z}}}}_{1}\right\Vert \cdot \left\Vert {{{{z}}}}_{2}\right\Vert }\) denote the cosine similarity between ℓ2 normalized z1 and z2. The loss function for a positive pair \(({G}_{i},{\tilde{G}}_{i})\) is defined as

$$\begin{array}{l}{\ell }_{i}=\\-\log \frac{{e}^{{{{\rm{sim}}}}\left({{{{z}}}}_{{G}_{i}},{{{{z}}}}_{{\tilde{G}}_{i}}\right)/\tau }}{\mathop{\sum }\nolimits_{k = 1}^{N}{{\mathbb{1}}}_{[k\ne i]}\left({e}^{{{{\rm{sim}}}}\left({{{{z}}}}_{{G}_{i}},{{{{z}}}}_{{G}_{k}}\right)/\tau }+{e}^{{{{\rm{sim}}}}\left({{{{z}}}}_{{\tilde{G}}_{i}},{{{{z}}}}_{{\tilde{G}}_{k}}\right)/\tau }\right)+\left({e}^{{{{\rm{sim}}}}\left({{{{z}}}}_{{G}_{i}},{{{{z}}}}_{{\tilde{G}}_{k}}\right)/\tau }+{e}^{{{{\rm{sim}}}}\left({{{{z}}}}_{{\tilde{G}}_{i}},{{{{z}}}}_{{G}_{k}}\right)/\tau }\right)},\end{array}$$
(1)

where \({{\mathbb{1}}}_{[k\ne i]}\) is an indicator function that evaluates to 1 if k ≠ i, τ is a temperature parameter and z represents the latent representation. The numerator of the contrastive loss measures the agreement between the positive pair, while the denominator calculates the sum of the agreement between each graph and the other 2N − 1 graphs. This means that the latent representation \({{{{\boldsymbol{z}}}}}_{{G}_{i}}\) of the original graph should consider the similarity with not only other original graph latent vectors \({\{{{{{\boldsymbol{z}}}}}_{{G}_{k}}\}}_{k\ne i}\) but also all augmented graphs \({\{{{{{\boldsymbol{z}}}}}_{{\tilde{G}}_{k}}\}}_{k = 1}^{N}\). The latent representation of the augmented graph \({{{{\boldsymbol{z}}}}}_{{\tilde{G}}_{i}}\) also follows the same calculation process. Finally, the loss is computed across all positive pairs in the minibatch.

Prompt generator

To stimulate the pre-trained model to recall the relevant knowledge learned before, we design a prompt generator fprompt to produce a prompt xprompt based on ElementKG and the input molecular graph G, that is, xprompt = fprompt(G, ElementKG). We detect all functional groups contained in G using the open-source package RDKit41 and retrieve the corresponding functional group entities in ElementKG on the basis of their names. Then we obtain the embeddings of functional group entities {x1, …, xm} using the KG embedding method, where m is the number of detected functional groups. To capture the importance of functional groups, we construct a learnable vector as the mediator (denoted as x0) and then apply the self-attention mechanism42 on both the embeddings of the mediator and functional groups. Specifically, the input X = {x0, x1, …, xm} is first projected into the query/key/value vector:

$${{{Q}}}={{{X}}}{{{{W}}}}^{Q},{{{K}}}={{{X}}}{{{{W}}}}^{K},{{{V}}}={{{X}}}{{{{W}}}}^{V},$$
(2)

where WQ, WK, \({{{{W}}}}^{V}\in {{\mathbb{R}}}^{d\times d}\) and d is the hidden dimension. The self-attention mechanism calculates the attention weight between queries and keys, and then multiplies by the value. The output embedding is formulated as

$${{{{X}}}}^{{\prime} }={{{\rm{softmax}}}}\left(\frac{{{{Q}}}{{{{K}}}}^{{{{\rm{T}}}}}}{\sqrt{d}}\right){{{V}}}.$$
(3)

We implement two self-attention layers and obtain the embedding of the mediator \({{{{x}}}}_{0}^{{\prime} }={{{{X}}}}^{{\prime} }[:,0]\), which reflects the combined contributions of functional groups with varying importance. We then feed it into a fully connected layer followed by layer normalization43 to obtain the functional prompt

$${{{{x}}}}_{{{{\rm{prompt}}}}}={{{\rm{LayerNorm}}}}({{{W}}}\cdot {{{{x}}}}_{0}^{{\prime} }).$$
(4)

Finally, we add the prompt xprompt to the original representation of each atom node in G with a learnable scale parameter α, resulting in the new input feature of a node v in G expressed as \({{{{x}}}}_{v}^{{\mathrm{new}}}={{{{x}}}}_{v}+\alpha \cdot {{{{x}}}}_{{{{\rm{prompt}}}}}\). We then feed this prompt-enhanced molecular graph into the pre-trained graph encoder, followed by a prediction network for downstream molecular properties.

Graph encoder architecture

A molecular graph can be represented as \(G=({{{\mathcal{V}}}},{{{\mathcal{E}}}})\), where \({{{\mathcal{V}}}}\) denotes a set of nodes and \({{{\mathcal{E}}}}\) denotes a set of edges. Each edge is bidirectional. Let xv denote the initial features of node v, and \({{{{x}}}}_{{e}_{(u,v)}}\) as the initial features of edge e(u, v). In particular, for atoms and bonds in the original molecular graph, we extract different initial features for them following specific chemical rules, as detailed in Supplementary Information.

Taking Fig. 1b as an example, for the augmented graph, we take the element entity embeddings obtained above as the initial features of element nodes. The initial feature of an edge between every two element nodes is obtained by mean pooling of the embeddings of multiple relations between the corresponding element entities in ElementKG. Following the same feature extraction method in the original molecular graph, we obtain the initial features of atoms and bonds. The edges between elements and their corresponding atoms are distinguished by different random initialization features, that is, the dashed edges with the same colour represent the same initial features while different colours indicate different representations.

Given the graph structure, node features and edge features, our goal is to learn a graph encoder f(⋅) that maps the input graph to a vector representation. In our case, we implement CMPNN26 as the graph encoder, which improves graph embeddings by strengthening the message interactions between edges and nodes.

Firstly, to update the node hidden states, each node \(v\in {{{\mathcal{V}}}}\) aggregates representations of their incoming edges instead of its neighbouring nodes in G. The intermediate message vector is obtained as

$$\begin{array}{lll}{{{{m}}}}^{k}(v)&=&{{{\rm{AGGREGATE}}}}\left(\left\{{{{{h}}}}^{k-1}\left({e}_{(u,v)}\right),\forall u\in {{{{\mathcal{N}}}}}_{v}\right\}\right)\\ &=&\mathop{\sum}\limits_{u\in N(v)}{{{{h}}}}^{k-1}\left({e}_{u,v}\right)\odot {\mathrm{pooling}}\left(\mathop{\sum}\limits_{u\in N(v)}{{{{h}}}}^{k-1}\left({e}_{u,v}\right)\right),\end{array}$$
(5)

where k denotes the current depth of the message passing, the pooling operator is a max pooling function and ⊙ is an element-wise multiplication operator. Here we apply max pooling to highlight the edges with the highest information intensity, as the hidden state of a node is mainly based on the strongest message from incoming edges. Then, the node’s current hidden state hk−1(v) is concatenated with the message vector mk(v) and fed through a communicative function to update the node’s hidden state hk(v):

$$\begin{array}{lll}{{{{h}}}}^{k}(v)&=&{{{\rm{COMMUNICATE}}}}\left({{{{m}}}}^{k}(v),{{{{h}}}}^{k-1}(v)\right)\\ &=&\sigma \left({{{{W}}}}^{k}\cdot {{{\rm{CONCAT}}}}\left({{{{h}}}}^{k-1}(v),{{{{m}}}}^{k}(v)\right)\right),\end{array}$$
(6)

where the hidden state hk(v) acts as a message transfer station that receives incoming messages, integrates them and sends them to the next station. The specific communication function is implemented by feeding both the node and edge features into an MLP followed by a rectified linear unit (ReLU) activation.

Secondly, we extract message of the edge e(v, w) by subtracting its inverse edge information from the hk(v):

$${{{{m}}}}^{k}\left({e}_{(v,w)}\right)={{{{h}}}}^{k}(v)-{{{{h}}}}^{k-1}\left({e}_{(w,v)}\right),$$
(7)

where e(w, v) is the inverse edge of e(v, w). To update the edge hidden states, we first feed the edge intermediate message \({{{{m}}}}^{k}\left({e}_{(v,w)}\right)\) into a fully connected layer and add it with the initial edge feature \({{{{x}}}}_{{e}_{(u,v)}}\). We apply a ReLU activation function to the output and use it as the intermediate message vector for the next iteration. This procedure can be mathematically expressed as

$${{{{h}}}}^{k}\left({e}_{(v,w)}\right)=\sigma \left({{{{x}}}}_{{e}_{(u,v)}}+{{{W}}}\cdot {{{{m}}}}^{k}\left({e}_{(v,w)}\right)\right).$$
(8)

Thirdly, after K iterations, one more round of interaction is applied:

$${{{m}}}(v)={{{\rm{AGGREGATE}}}}\left(\left\{{{{{h}}}}^{K}\left({e}_{(u,v)}\right),\forall u\in N(v)\right\}\right),$$
(9)

then the final node representation h(v) of the graph is obtained by gathering the message from incoming edges, the current node representation and the initial node feature:

$${{{h}}}(v)={{{\rm{COMMUNICATE}}}}\left({{{m}}}(v),{{{{h}}}}^{K}(v),{{{{x}}}}_{v}\right).$$
(10)

Finally, a readout operator is applied to get the whole graph representation:

$${{{{h}}}}_{G}=\mathop{\sum}\limits_{v\in {{{\mathcal{V}}}}}{{{\rm{GRU}}}}({{{h}}}(v)),$$
(11)

where GRU is the gated recurrent unit introduced in ref. 44.

Experimental setup

Pre-training and downstream dataset

In the pre-training phase, we pre-train KANO using 250,000 unlabelled molecules sampled from ZINC15 (ref. 4), a public access database containing purchasable drug-like compounds. In the fine-tuning phase, we use 14 benchmark datasets from MoleculeNet5, comprising 678 binary classification tasks and 19 regression tasks. The datasets cover molecular data from a wide range of domains, such as drugs, biology, physics and chemistry. We perform three independent runs on three random-seeded scaffold splitting for all datasets, except QM9, with a train/validation/test ratio of 8:1:1. Scaffold splitting45 is a more challenging splitting method that splits molecules according to their scaffolds (molecular substructures) and can better evaluate the generalization ability of the models on out-of-distribution data samples. For the QM9 dataset, we follow the random splitting setting of most related works11,46 for comparison. Supplementary Information contains more details about the datasets.

Implementation details

Since the raw data are in the form of molecular SMILES, which is a line notation for describing the structure of chemical species using short ASCII strings, we utilize the open-source chemical analysis tool RDKit to convert them into 2D molecular graphs and extract the atom and bond features. The initial features of atoms are determined by their associated eight attributes (for example, chirality, hybridization and atomic mass), and the bonds are embedded by their four related attributes (for example, bond type and conjugated), as detailed in Supplementary Information.

In contrastive pre-training, we utilize the Adam optimizer with a learning rate of 3 × 10−5 to optimize the NT-Xent loss and set the temperature parameter τ to 0.1. We apply an MLP with a ReLU activation function as the projection network. The model is trained with a batch size of 1,024 and 50 epochs.

In prompt-enhanced fine-tuning, we use RDKit to detect the functional groups in each molecule. We apply two self-attention layers on all functional groups and the mediator. The output is fed into a fully connected layer, which is then layer normalized. We adopt a two-layer MLP as the property prediction network. For classification tasks, we utilize the binary cross-entropy (BCE) loss combined with the sigmoid layer (BCEWithLogits loss) when training the graph encoder and the property prediction network, while for regression tasks, we apply the mean squared error loss. The Adam optimizer is applied to the graph encoder with a learning rate ranging from 1 × 10−4 to 1 × 10−3 for all datasets, and the learning rate of the prompt generator is five times that of the graph encoder. We train the model on the training set and search hyper-parameters on the validation set for the best results. The training is set to 100 epochs. We implement fine-tuning of the pre-trained model three times with a batch size of 256 to report the average and standard deviation of performance on the testing set, using ROC-AUC for classification tasks and mean absolute error/root mean square error for regression tasks. KANO is implemented using Pytorch and runs on a Ubuntu Server with NVIDIA GeForce RTX 3090Ti graphics processing units.