Introduction

Modelling and understanding geoscience processes is crucial to predicting natural phenomena and mitigating the impacts of environmental challenges under global change. Earth system processes are typically represented by governing equations in the form of symbolic models, which describe how the values of unknown variables change in response to variations in one or more known variables1. Governing equations inherently entail concepts of time, space, causality, and generality, defining the evolution of geophysical, -chemical, -biological, -mechanical and ecological processes2 with interpretability and accessibility. Historically, the paradigm for establishing governing equations in geosciences has been rooted in constructive and principled theories (Box 1). The former approach derives equations for phenomena based on first principles, such as conservation laws, symmetries, physical regulations, and phenomenological behaviours3. The latter approaches are empirical or semi-empirical generalisations summarised and parameterised to capture the main features. For centuries, the classical paradigm has resulted in ubiquitous canonical governing equations in geosciences across various scales and processes, which are illustrated in Fig. 1a. These equations are fundamental to Earth and climate sciences4.

Fig. 1: Examples of governing equations in geosciences.
figure 1

a Geoscience processes in the Earth system are described by different governing equations derived from the conventional equation discovery paradigm. b Representative governing equations in four typical geoscience domains: hydrology, ecology, seismology, and atmospheric science. These equations are of various forms, including algebraic, ordinary, and partial differential equations.

Full size image

Despite the historical success, the natural processes we study today are often more complex and multifaceted rather than simple and single processes, such as modelling coupled dynamic components of the Earth system (e.g., atmosphere, ocean, biosphere, cryosphere, carbon-water-nutrient cycling, ecological dynamics). Limited knowledge makes it hard to define accurate variables, and simplifying assumptions can lead to errors and oversimplifications that don’t reflect real-world complexity5. This is true even for basic equations, such as empirical equations for the physical properties of gases that are not entirely ideal6, let alone in subsystems dominated by nonlinearity, stochasticity, multiscale couplings, nonequilibrium behaviour, and spontaneous behaviour6. In addition, scientific discoveries that adhere to the classical paradigm rely on the creative and intellectual insight of scientists and require continuous trial-and-error approaches for incremental improvement7. Nevertheless, scientists are also limited in processing and analysing hidden patterns that are not immediately apparent in complex datasets. Consequently, progress in establishing and refining the governing equations in these systems has been slow over the past several decades.

With advances in sensor and data storage technologies, diversified data within the Earth system have become more accessible, which offers an alternative chance to understand the Earth system8,9. These data are primarily used to develop data-driven predictive models10,11, often making accurate predictions by identifying complex patterns in large datasets. Nevertheless, they sometimes tend to be associated with increased model and computational complexity and reduced transparency12. The fundamental goal of geosciences is to derive a concise, interpretable, and meaningful understanding of complex natural phenomena.

In this Perspective, we introduce and discuss the data-driven equation discovery and argue that it can integrate the power of data-driven methods and the strengths of governing equations. Figure 2 provides a comparison of these methods. Data-driven equation discovery is defined as automatically distilling the hidden patterns from data and transforming them into an interpretable and concise symbolic representation. As a result, it combines the ability of data-driven models to extract laws that conform to predictive patterns with the simplicity and transparency of equations. Data-driven equation discovery is relevant to practical geoscience applications and potentially essential for pioneering geoscientific discoveries. Specifically, it represents an opportunity to move beyond conventional (semi-)empirically parameterised equations (e.g., numerous empirical equations in evapotranspiration modelling13 and autotrophic respiration modelling14), thereby improving the modelling accuracy with transparency. It may also resolve controversies in the forms of various conventional governing equations, such as the ongoing debate over the structure of the advection-diffusion equation15. Moreover, the discovery and formulation of equations are naturally driven by data, which occurs spontaneously. This process not only overcomes the difficulties associated with calibrating and estimating equation parameters but also accelerates scientific discovery by improving the efficiency and effectiveness of exploration processes.

Fig. 2: Comparison of different approaches for modelling and understanding geoscience processes.
figure 2

Based on phenomena and observed data, scientists summarised and proposed governing equations, the equations are accurate, reliable, transparent to a certain extent and also simple. The pure data-driven models based on artificial intelligence perform higher accuracy while lacking reliability and transparency and are too complex. The new data-driven equation discovery can integrate their merits.

Full size image

We first provide overviews of the conventional and data-driven equation discovery and discuss how the emergence of the new data-driven discovery could bring significant advantages to geoscience. We then underscore the potential challenges and envision advancing geosciences through data-driven discovery. We aim to foster a deep integration of data-driven discovery into the practice of geoscientists, contributing to more accurate, efficient, and comprehensive modelling, understanding, and management of the complex Earth system.

Conventional governing equations in geosciences

Conventionally, in geoscience, the philosophy of deriving governing equations (i.e., mathematical modelling) is based on first principles or (semi-)empirical approaches3 (see Box 1). Scientists first postulate and conceptualise a formulation based on observations or (theoretical) experiments. This formulation is then subject to validation, refinement, and updating, driven by logical reasoning and scientific or engineering research insights. Many classical governing equations are initially derived by empirical summarization, with subsequent scientific progress revealing their derivability from first principles. Figure 1b provides example equations in different disciplines within geosciences.

However, establishing such equations requires a deep understanding of complex processes by experienced scientists. In cases where a system is not thoroughly understood, the equation-building process can be susceptible to human cognitive biases, particularly in determining which simplifications and assumptions are reasonable or in selecting the most appropriate physical principles. For instance, the formation and dissipation of clouds remain poorly understood, resulting in physics-based cloud parameterization equations that are based on incomplete knowledge and are prone to inaccuracies16, thereby weakening our ability to predict climate dynamics. Geoscientists often simplify fine-scale phenomena through parameterisation, such as first-order degradation of empirically defined carbon pools17. In some cases, they may also rely on empirical formulas, guided by their intuition, to capture the salient features of these processes. A typical example is evapotranspiration modelling, where empirical equations describe many physical transformations. For instance, stomatal conductance, a key intermediate variable, is commonly expressed as a product of several environmental factors18 or through a linear relationship with the rate of photosynthesis19. Similarly, aerodynamic and thermal dynamics roughness lengths are estimated using various semi-empirical models20,21,22. These approaches often result in crucial yet intangible parameters that are difficult to determine in practice. Furthermore, human factors can introduce errors into the derived equations or make the equation form questionable. For instance, the derivation of equations that describe unsaturated soil moisture movement based on the Darcy-Buckingham law has long been controversial in hydrology23. Furthermore, determining the appropriate form of reaction-diffusion equations is a continuing debate primarily influenced by scale effects15, which consistently limits our understanding and modelling of complex subsurface flow. Additionally, the conventional paradigm of equation discovery, which is mainly scientist-driven and reliant on intuition, often necessitates an iterative process of trial and error that may lead to a slow pace of scientific progress. In summary, despite its historical achievements, this paradigm may not effectively capture the ever-growing demands for deeper scientific understanding of the increasingly complex Earth system processes we study today.

Towards new data-driven equation discovery

Recently, the big Earth data9 has been accessible, which is characterized by its considerable volume, diverse sources, and rapid generation (e.g., CMIP-6 data24). In addition, with the increasing abundance of computational resources, scientific artificial intelligence approaches have emerged25. There is a growing effort on the automatic discovery of governing equations directly from data26,27. To the best of our knowledge, the earliest study of data-driven equation discovery can be attributed to Gerwin28, Langley29, Falkenhainer and Michalski30, who proposed heuristic methods to derive the mathematical functions from a large and complex space of possible formulations using informed search. Data-driven equation discovery was starting to become feasible. Subsequently, Koza demonstrated that genetic programming (GP) could discover symbolic governing equations from data31. During this time, GP was successfully applied in geoscience. For instance, Babovic and Keijzer32 discovered the equation describing the additional resistance to flow induced by flexible vegetation from data.

The modern paradigm of data-driven discovery is traced to seminal work by Bongard and Lipson33 and Schmidt and Lipson34 through improved GP, who successfully automated the discovery of equations for dynamical systems and conservation laws from data. However, GP typically has inherent limitations, such as computational intensity, susceptibility to overfitting, and difficulties with convergence if not properly balanced35,36. These limitations become prohibitive for high-dimensional systems described by PDEs. However, PDEs play a critical role in simulating dynamic systems and phenomena with spatial and temporal variations, including applications in geosciences such as climate modelling and natural disaster prediction5. A few years later, Brunton et al.35 introduced a new data-driven discovery framework known as sparse regression to address this challenge and reignite enthusiasm in the field28,36. It led to numerous subsequent works to extend to discover chaotic and complex PDEs from data, such as PDEs with parameter dependencies37,38, which significantly expand the potential applications within geoscience. In addition, the rapid development of deep learning technologies has begun to address a long-standing high sensitivity to noise and data-hungry39,40,41. In addition, the studies on the identification of coordinates for governing equations, state variables, and implicit representations (i.e., learning an operator that encapsulates the system characteristics)42,43, may provide another avenue for data-driven equation discovery.

Nowadays, this emerging data-driven discovery paradigm has underpinned wide-ranging applications, including biology6,44, materials45, and also geosciences, such as subsurface hydrology46, ocean modeling47,48,49 and climate science16,50,51. Despite its enormous potential and widespread attention42, its opportunities remain underappreciated in the geoscience community, primarily because of the disconnect between the advances and the challenges and needs of geosciences. Therefore, we introduce the data-driven equation discovery in detail and discuss leveraging it to benefit geosciences in the following sections.

How to realise data-driven equation discovery in geosciences

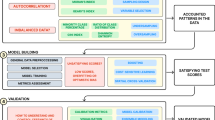
The overview of the data-driven equation discovery workflow in practice is shown in Fig. 3, and an example is given in Box 2. An important part of data-driven equation discovery is to select proper approaches, whose objective is to employ reasonable strategies to reduce search space effectively, as brute force search is considered non-deterministic polynomial-hard (NP-hard)52, which means that solving it quickly becomes impractical as the size of the problem grows. The equation discovery from data differs from traditional inverse modelling and black-box system identification. The latter aims to estimate the parameters or coefficients from data53, where the equation structure is usually partly given.

Fig. 3: The overview of the data-driven equation discovery workflow in practice.
figure 3

The first step is data collection and preprocessing, then selecting proper approaches based on specific tasks. A detailed description of different approaches can be found in Supplementary Note 1. Based on the selected algorithms, the governing equations can be discovered. Finally, the discovered equations should be validated and physically interpreted.

Full size image

Figure 4 provides an overview of methods for realising data-driven equation discovery in geosciences. A detailed description of approaches is given in Supplementary Note 1. We divide data-driven equation discovery approaches into two primary categories: symbolic regression and sparse selection algorithms, based on whether the algorithms can generate an infinite variety of equation forms. Symbolic regression utilises various search methods to generate infinite combinations of symbolic formulae, mainly including genetic programming33,34, heuristic symbolic regression28,54, mixed-integer nonlinear programming approaches55,56, deep reinforcement learning39,57, and large-scale pre-trained Transformers58,59. They only require data on the variables of interest, including preprocessed data (e.g., derivatives). The ability of symbolic regression makes it well suited to uncovering complex governing equations that describe the underlying symbolic relationships between multiple variables in geoscience. For instance, it can be employed to explore intricate governing equation relationships between evapotranspiration flux and various meteorological parameters and vegetation variables using large amounts of data, where the exact physical mechanism is still unclear. In contrast, sparse selection algorithms, including sparse regression35,36,60 and equation learner networks (EQL)61,62 aim to select the most appropriate equation from a predefined pool of symbolic combinations. They are efficient for systems with a solid understanding of the underlying functional form. Sparse regression and EQL have their own application scopes. Sparse regression is widely used to discover the underlying PDEs because there are often discernible patterns in the modelling of PDEs. EQL networks can seamlessly interface with high-dimensional data, such as satellite imagery, enabling end-to-end learning processes and exploring these hidden mechanisms behind high-dimensional data.

Fig. 4: Data-driven equation discovery approaches in geosciences.
figure 4

The approaches can be divided into two main categories: symbolic regression and sparse selection algorithms. It is noted that some methods inherently utilise deep learning techniques as part of their core algorithms. At the same time, some can be structured to be compatible with deep learning, allowing for integration that enhances their capabilities. A detailed description of each approach is given in Supplementary Note 1.

Full size image

The benchmarks of accuracy, speed, and tolerance to data noise for symbolic regression methods63,64,65,66 and sparse regression67 have been performed. It has shown that sparse regression has a low computational cost and few hyperparameters. In contrast, symbolic regression approaches provide an opportunity to discover underlying equations with complex structures, while the main limitation is computational cost. Deep learning-based approaches are more robust to noisy and sparse data such as deep reinforcement learning. They are therefore recommended to deal with geoscientific applications where flawed datasets are common43. In terms of required prior information, sparse regression needs more ___domain expert input and assumptions, such as the general form of the underlying governing equations. Therefore, sparse regression could fail if incorrect or incomplete prior information is introduced, i.e., the candidate library matrix in sparse regression36. In contrast, symbolic regression can realise learning from scratch, while we can incorporate some physical information in different ways to discover the underlying equations accurately.

Nowadays, most of the proposed algorithms have open-source code available. For example, PySR and SymbolicRegression.jl68, implemented in the Python and Julia languages, encapsulate symbolic regression methods. PySindy69, developed in Python, can be used for sparse regression. These tools can significantly lower the technical barriers to implementing advanced and complex algorithms, paving the way for geoscientists to engage in data-driven equation discovery. It is worth noting that this field is rapidly evolving, so close attention is necessary to obtain algorithms with superior performance, especially considering accuracy, speed, and robustness.

Opportunities for advancing geosciences

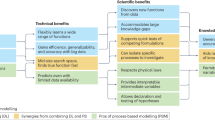
Data-driven equation discovery provides promising opportunities for advancing geosciences. Figure 5 summarizes these aspects, and the detailed descriptions are as follows.

Fig. 5: The overview of opportunities for using data-driven equation discovery to advance geosciences.
figure 5

Based on various datasets collected in the Earth system, data-driven discovery is expected to discover new equations, thereby enhancing existing equations, model transparency, and finally accelerating scientific discoveries. In turn, it will also facilitate the collection of higher-quality data.

Full size image

Enhancing classical governing equations

The conventional derivation of equations inevitably involves a degree of empiricism, such as selecting and defining variables, conditional assumptions, and simplifications. The new paradigm offers an alternative to these locally empirical methods and promotes improved subsequent derivation, leading to better structure governing equations. For example, it allows the exploration of improved forms of water retention curve equations in subsurface hydrology70 or the study of moisture sensitivity of soil heterotrophic respiration71.

Replacing black-box models with explicit expressions

Due to long-standing challenges in parameter calibration and estimation and precision issues, many geoscience equations are being replaced by black-box models, such as those based on machine learning. Through the data-driven discovery paradigm, it is possible to derive equation models that maintain consistent performance and offer greater interpretability and physical relevance. For instance, in hydrology, this approach allows for deriving hydro-pedotransfer functions with precise and explicit forms72. Additionally, these explicit governing equations may facilitate a more straightforward assessment of potential underlying biases learned from the data, offering an advantage over the opacity of black-box models. For instance, recently, it showed that data-driven equation discovery can learn new physics for the atmosphere and replace costly modules in cloud parameterizations16,47.

Improving traditional controversial governing equations

When a system is not entirely understood, the derivation process may be prone to cognitive biases. These biases can introduce errors in the equations or lead to significant controversy in their formulation. The data-driven paradigm can address such controversies. A pertinent example is using fractional-order equations in Earth systems characterised by scale or memory effects73, whose rationality could be clearer and often sparks debate. Applying the new approach could provide clarity and resolve these ongoing controversies.

Uncovering missing equations

The new paradigm is adept at uncovering previously unrecognised variables or processes, particularly in data-rich scenarios. Integrating interdisciplinary data across the geosciences can reveal complex interactions that may remain elusive when individual disciplines are considered separately. For example, climate scientists can use these newly discovered equations to refine climate models, deepening our understanding and improving climate change predictions. An explicit expression for the concentration-flow relationship (C-Q) may be found in water quality science. Similarly, it may be possible to establish equations linking vegetation structure to radar backscatter in satellite biomass mapping74,75.

Accelerating scientific discoveries and high-quality data collection

The real-time nature of the data-driven discovery approach bypasses the need for slow, theory-based development from first principles, potentially accelerating the pace of scientific discovery in geoscience. Moreover, the increasing emphasis on data-driven methods in this field may promote advancements in data collection technologies, leading to the acquisition of more diverse and high-quality datasets.

Challenges and potential solutions

Despite the promise, several challenges must be addressed before fully realising the benefits of data-driven discovery for geosciences. From our perspective, these challenges encompass three main aspects: data, geoscience processes, and validations, which are briefly summarised in Table 1. These challenges do not diminish the potential of the new paradigm but rather represent opportunities for collaboration between geoscientists and data scientists to promote artificial intelligence as a truly powerful tool to advance geoscience.

Table 1 Overview of challenges for data-driven equation discovery in geosciences
Full size table

Data perspective

  1. (1)

    Discovering governing equations from sparse and noisy geoscientific data: While data is becoming increasingly abundant, there are still instances in many geoscientific domains where accurate and extensive datasets still need to be improved. This data sparsity is characterised by temporal and spatial coverage inconsistencies, which will persist as a long-term feature despite the potential for richer datasets in the future76. Additionally, they are frequently corrupted by noise, involving diverse noise sources, uncertainties, data missing, and gaps. Data-driven discovery is required to deal with sparse and noisy data29,40. Generally, direct observations often involve state variables such as temperature, pressure, and concentration. However, equation discovery tasks typically rely on derivatives of these variables with respect to space and time to capture dynamic changes. Obtaining these derivatives involves numerical approximations that can introduce errors affecting the accuracy of the discovered equations77. Conventional finite difference methods78 would quickly deteriorate when dealing with sparse and noisy data. Fortunately, several approaches have been developed to discover equations from such data, such as smoothing methods79,80, weak-form formulas81, targeted denoising methods82,83, and deep neural networks40,55. The selection depends on the specific types of geoscience processes and should be carefully chosen84,85. For instance, the low-rank property of physical system dynamics can be utilised to preprocess large-scale observational datasets86. Continued efforts are needed to deal with datasets characterised by extreme noise and significant sparsity.

  2. (2)

    Distilling underlying equations from high-dimensional big Earth data: Recently, certain geoscience domains have experienced notable shifts in data access, mainly attributed to the proliferation of satellite-based and in-situ sensors10,76 (e.g., International Soil Moisture Network87 provides a large amount of in-situ soil moisture measurements). Harnessing these vast and varied data and extracting meaningful insights has proven to be a challenge76,88. Data-driven equation discovery has provided opportunities to make sense of this data deluge. For example, it has been demonstrated that EQL networks can be seamlessly integrated with high-dimensional data to explore hidden mechanisms and discover governing equations89. When dealing with these complex in-suite data, one limitation is that these data need an effective coordinate system. Data-driven equation discovery approaches may only succeed with proper coordinates. For example, when dealing with irregular measurements (e.g., temperature at different locations) in a complicated geometry, coordinate transformations are inevitable to obtain equations for temperature dynamics. Fortunately, systematic and automated discovery of the latent coordinate representation has been realised, such as deep autoencoder networks90,91,92,93,94. It is possible to discover proper coordinates and equations from unorganized measurement data. Another limitation is the need for considerable computational resources when dealing with large datasets40. The amount of data that can be ingested and utilised positively correlates with available computing resources. Recently, some emerging efficient computing methods, including parallel processing, distributed computing, and dedicated hardware such as GPUs, have shown promise in solving this challenge12.

  3. (3)

    Leveraging imbalance data to find governing equations: It is an obvious feature that some parts of the Earth system have more available data than others; for example, above-ground data are richer than below-ground76. Imbalanced data can lead to potential implicit biases in data-driven models, thus affecting the discovered equations. For instance, the accuracy of wet and dry end coefficients is reduced when the soil water flow equation is derived from datasets with fewer observations of extreme wet and dry scenarios95. To minimise the impact of data imbalance, data preprocessing is straightforward but effective, such as controlling the data distribution or augmenting the data with deep learning methods to make the data richer and more balanced. However, such simple preprocessing may only be feasible for univariate governing equation discovery. However, using unbalanced multivariate data to find governing equations for multiple processes still needs further research. One possible strategy is to integrate multi-fidelity deep learning96 and generative deep learning97 with equation discovery tasks. Multi-fidelity deep learning can integrate data from multiple sources to improve the accuracy of discovered equations. Generative deep learning can create synthetic data that enhances the dataset, enabling more accurate and robust identification of the underlying equations governing the system. In summary, biases hidden in unbalanced datasets should be treated with caution and the equations found need to be carefully validated to ensure reasonable results.

Geoscience perspective

Complex geophysical, -chemical, and -biological processes are common in geoscience and play a crucial role in shaping the Earth’s surface, climate, and geological features. These processes involve multiple interacting components, can occur on transient to extended time scales, and usually span multiple spatial scales. Data-driven equation discovery provides effective ways to describe these interactions but also faces several challenges, as listed below. These challenges are often interrelated rather than isolated in real-world scenarios, necessitating a holistic consideration.

  1. (1)

    Equation discovery for nonlinear processes with parameter dependencies: Many geoscience processes exhibit nonlinear behaviour and can vary significantly in space and time, and the heterogeneity can introduce parametric variability into the underlying governing equations. Several challenges remain to overcome. For instance, sparse regression can discover nonlinear PDEs when nonlinear terms are included in the candidates, but this can be difficult when dealing with a new system98. In addition, symbolic regression may easily converge prematurely when searching for complex nonlinear equations, which is inefficient and impractically slow. A worthwhile step could be integrating some geophysical information, such as symmetry and dimensional analysis, as it can speed up the search process. On the other hand, due to the coupled effects of parametric dependencies and equation structure on geoscientific dynamics, it is hard to separate and identify them. Group sparse regression38,99,100 and the kernel approach101 have been applied to resolve it. Nevertheless, it is still intractable when dealing with highly nonlinear and complex coefficient fields, common in various geoscientific domains. For example, hydraulic conductivity, one of the parameters in the groundwater flow equation, can vary in magnitude by several orders of magnitude on microscopic spatial scales. Furthermore, key vegetation parameters in global carbon cycle models also vary spatially, mainly as a function of biodiversity102. In addition, current methods rely primarily on assumptions such as smoothness and symmetry, which are absent in some systems. Therefore, further approach development is still needed101.

  2. (2)

    From data to governing equations for multiscale interactions: Geoscience processes can span multiple spatial and temporal scales. While micro-scale interactions may be well described by governing equations derived from first principles, the macroscopic behaviour may sometimes fail to follow directly. For example, in the groundwater flow, the assumptions of homogeneity and continuity are typically based on the representative elementary volume scale, a virtual volume that may not hold at larger or smaller scales103. Despite these modelling difficulties, observational data is much more accessible for some macroscopic interactions. A notable direction is combining the data-driven discovery with microscopically simulated data46,104,105. Since microsimulation does not assume any macroscopic governing equations a priori, it can be a valuable approach to verify already derived governing equations106 and to reveal yet unknown macroscopic governing equations104. For instance, macroscale PDE for proppant transport in subsurface geoscience has been successfully discovered104. Experimental data can also be explored: an example is the quantitatively accurate equation for weakly turbulent fluid flow, albeit in a complicated and high-dimensional nonequilibrium system, discovered from velocity field measurements107. These pioneering works have demonstrated the potential of discovering multiscale interactions governing equations from data.

  3. (3)

    Identifying equations with multiple connected processes: Geoscience processes often involve numerous interacting factors and require multiple and multivariable governing equations to describe them. Data-driven equation discovery can potentially find multiple interrelated process equations, which may lead to insights into cross-temporal and cross-scale linkages. For instance, the study of terrestrial ecosystem dynamics can significantly benefit from holistically identifying the equations of multiple interacting factors such as vegetation succession and competition, root zone water transport, plant allocation to leaves, stems, and roots, and impacts of fire on vegetation states and atmospheric emissions108. An essential prerequisite for identifying equations with multiple interrelated processes is the definition of appropriate variables. In a high-dimensional system, the relevant set of state variables is typically unknown, and identifying them is generally a laborious task that demands considerable scientific effort. Defining compact and complete variables is essential for discovering parsimonious governing equations. The automatic identification of interpretable and physically consistent state variables remains a challenging and intractable problem. Methods such as geometric manifold learning, a machine learning approach for dimensionality reduction by uncovering the intrinsic structure or geometry of high-dimensional data, have been devised to automate the discovery of fundamental variables hidden in time-series data109 or high-dimensional data (e.g., video data)110. These advances in data-driven discovery methods hold promise for addressing the bewildering variety of information that confronted early scientists109,110,111.

  4. (4)

    Extracting equations for geoscience processes with uncertainty and identifiability: In various processes and phenomena within the Earth system, there are inherent, unavoidable factors of uncertainty. This uncertainty can originate from multiple aspects, for example, natural variability can introduce stochastic elements. It is crucial to discover equations to capture the uncertainty and extrapolate better in different uncertain scenarios112. Discovering stochastic equations from data in the presence of such uncertainty is a complex task. However, approaches such as variational Bayesian inference make it feasible to learn stochastic governing equations and quantify uncertainties directly from data113,114,115,116. In addition, adopting techniques such as sensitivity analysis117 and ensemble methods118 is promising to address the uncertainties in the equation discovery tasks. Moreover, many geoscience processes often occur as nonequilibrium, such as transient behaviour and critical thresholds or abrupt transitions, making it challenging to identify equations that account for sudden changes in behaviour. The task of inferring non-stationary dynamics from stochastic observations, explored in recent studies119, is a critical step in this direction.

Validation perspective

Generally, the formulation of governing equations should follow Occam’s Razor, balancing parsimony with accuracy120. However, assessing the complexity of the underlying equation before its discovery and validation remains challenging. Pareto frontier analysis34 is recommended to address this, which involves using a series of progressively complex formulas to improve accuracy incrementally. For instance, independent validation for sets of proposed governing equations for the carbon cycle has allowed the determination of their optimal complexity given the information content of the calibration data121. Moreover, information criteria have been used to select the best equations that balance model parsimony and predictive power, such as the Akaike information criterion122, the Bayesian information criterion123 and the Bayesian machine scientist113. However, these information criteria, which are often derived under the assumption that the likelihood function is based on Gaussian errors, may not work well when dealing with non-Gaussian noise, which is common in geoscience, as many complex natural processes are not well-described by simple Gaussian distributions. In addition, automated interpretation of newly revealed governing equations is generally limited and still requires careful validation by geoscientific ___domain experts to ensure that the equations align with established principles and theories55. In practice, it is helpful to incorporate known physical constraints124 into data-driven discovery approaches or to leverage prior knowledge to guide discovery approaches. Models must obey built-in conservation laws or certain symmetries for the discovered equations to be consistent with established principles. It is worth noting that the selection of constraints should be reasonable, as it might also introduce biases. Furthermore, data-driven equation discovery has been preliminarily shown to understand hidden functional relationships and generalize them from observations to unknown parameter spaces62. It initially indicates that it is a powerful tool to help us model complex geoscience processes, but further validation is needed in the future.

Summary and future perspectives

Geoscience communities are confronted with increasingly intricate scientific questions, prompting the exploration of more advanced methods to resolve these challenges better. In this Perspective, our contributions are introducing the data-driven equation discovery to meet the unique needs of modern geosciences. Through the detailed discussions about the potential opportunities, we advocate that the new data-driven discovery is helpful in modelling and understanding numerous processes within the Earth system, especially those with potentially complicated mechanisms and available observational datasets. It is highly relevant to a wide range of geoscientists in their everyday research routines, aligning with the diverse research needs across the field. We argue that although the discovered equations are not necessarily meant to be causal, they frequently serve the purpose of creating a highly detailed testbed for the study of feedback. This is the first time we have objective measures of (semi)parametric model evaluation, intercomparison and selection learned from data.

We advocate that this emerging field provides opportunities for interdisciplinary collaboration, enabling the cooperative development of more advanced and adapted methods for geoscience, as they cannot be solved by either geoscientists or data scientists alone. Developing these interdisciplinary approaches and using interdisciplinary data in geosciences can reveal scientific insights that would be difficult to discover if individual disciplines were studied in isolation but are easy and feasible for data-driven equation discovery.

Furthermore, it is important to note that, like most data-driven methodologies, the selection of datasets can introduce bias, which can subsequently impact the final equations generated. To mitigate this, techniques such as cross-validation should be employed to minimise the potential for errors. Moreover, the equations obtained must be interpreted in a logical and rational manner to guarantee their scientific validity and coherence. In conclusion, we highlight that data-driven equation discovery should be employed for scientific discovery in a comprehensive and responsible manner.

We believe that data-driven equation discovery is expected to consistently facilitate our comprehension of geoscience processes and even reshape the foundations of geosciences. The discovered insights have the potential to challenge existing geoscientific theories and models. While the initial response from the community may lean towards scepticism or resistance, sustained scientific validation over time could lead these innovative insights to redefine fundamental concepts in geosciences. In the past few years, we have witnessed artificial intelligence’s remarkable and rapid success in applied geoscience endeavours. We anticipate that data-driven methods will soon offer similarly significant contributions to our scientific understanding by aiding in the discovery of governing equations, which have seen slow progress in the field over the past decades.