Introduction

In quantum mechanics, closed systems are governed by Hermitian Hamiltonians and are termed Hermitian systems. In contrast, non-Hermitian systems—characterized by non-Hermitian Hamiltonians—are typically employed to model open systems1,2. The Hermiticity of the Hamiltonian ensures real eigenvalues and orthogonal eigenstates in Hermitian systems, whereas non-Hermitian Hamiltonians yield complex eigenvalues and non-orthogonal eigenstates3,4,5. A defining feature of non-Hermitian systems is the exceptional point (EP), where eigenvalues and eigenstates coalesce simultaneously—a phenomenon absent in Hermitian systems6,7,8. The emergence of EPs endows non-Hermitian systems with extraordinary properties, sparking significant scientific interest9,10,11,12. Nevertheless, realizing such systems in quantum mechanics remains challenging. Therefore, research efforts are increasingly focusing on classical domains, where EPs and non-Hermitian phenomena play pivotal roles in optics8,13,14,15, mechanics16,17,18, acoustics19,20,21,22, thermotics23,24, and beyond.

Among classical wave systems, metasurfaces25,26,27,28, a novel two-dimensional artificial structure of the metamaterial, have garnered significant attention due to their precise and versatile control over the amplitude29,30,31,32,33, phase34,35,36, and polarization37,38,39 of incident waves. Compared to three-dimensional metamaterials, metasurfaces not only break through the electromagnetic properties of traditional materials but also overcome the processing difficulty of three-dimensional structures, offering unprecedented advantages for device integration and miniaturization. As inherently open systems that radiate energy into their surroundings40,41,42, metasurfaces provide an exceptional platform for realizing non-Hermitian effects. By adjusting the structure geometry and material composition, one can precisely tailor the system’s loss, enabling advanced manipulation of wave amplitude, phase, and polarization43,44. Therefore, in non-Hermitian metasurfaces, optical loss transitions from a technical limitation to a pivotal design parameter, unlocking novel physical phenomena and applications45,46,47.

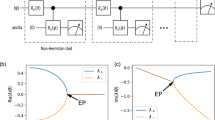
Recently, non-Hermitian metasurfaces have gained increasing prominence, playing an important role in polarization and phase control48,49,50, diffraction engineering51,52, sensing53,54,55,56,57, imaging58,59, and other applications. To date, several detailed reviews have been conducted on non-Hermitian systems60,61,62,63. However, current reviews still focus more on common non-Hermitian systems and applications rather than the theoretical analysis methods themselves, leading to a lack of summarization of the theoretical and analytical methods for non-Hermitian metasurfaces. In fact, two distinct analytical frameworks have been established for non-Hermitian metasurfaces64,65,66, corresponding to resonant EPs and scattering EPs as illustrated in Fig. 1. The latter can be further classified based on specific scattering coefficient configurations within the scattering matrix (S-matrix).

Fig. 1: EP clarifications and applications.
figure 1

According to the different analytical methods, the EP of the metasurface can be divided into two types: resonant EP96,97, related to the mode evaluation, and scattering EP78,79,117,127,131,133, related to the S-matrix. Based on different element combinations, the scattering EP can be further clarified. The insets are reprinted with permission from ref. 78, ref. 79, ref. 97, ref. 117. and ref. 127, from ref. 131. permitted under the Creative Commons license CC BY 4.0 and from ref. 133. permitted under the Creative Commons CC BY license.

Full size image

This review provides a systematic classification of non-Hermitian metasurfaces based on these different theoretical approaches. Section 2 begins with the most common non-Hermitian system—the parity-time (PT) symmetric system—and identifies two distinct types of EPs by analyzing different types of PT-symmetric systems. The resonant EP is detail analyzed in section 3, where we first derive eigenvalues of non-Hermitian Hamiltonians via the Schrodinger equation, then present a complete analytical framework for EP determination using coupled-mode theory (CMT) through a two-mode two-port metasurface. Also, various applications based on the resonant EP are listed. Section 4 establishes universal criteria for scattering EPs through generalized S-matrix analysis, specifically examining four S-matrix types (diagonal-reflection, diagonal-transmission, reflection-only, and transmission-only) with their unique EP conditions and applications. Furthermore, a comparative analysis highlights the physical connections and distinctions between these EP classes. We conclude with an outlook on future research trajectories in this field.

Parity-time symmetric systems and exceptional points

In this section, we focus on the most common and discussed class of non-Hermitian systems, PT-symmetric systems, and corresponding properties of EPs. Three different types of situations are detail discussed in the following: Hamiltonian is PT-symmetric, S-matrix is PT-symmetric, and other properties are PT-symmetric.

Unlike Hermitian systems that conserve energy, non-Hermitian systems exchange energy with the environment and their Hamiltonians \({\boldsymbol{H}}\) generally possess complex eigenvalues. However, in 1998, it was discovered3 that even non-Hermitian systems can have real eigenvalues when the PT-symmetry is preserved, namely \({\boldsymbol{HPT}}={\boldsymbol{PTH}}\). Here, P is the parity operator, while T is the time reversal operator. This discovery triggered a surge of research focused on PT-symmetric systems67,68,69,70,71,72. A simple PT-symmetric system can be created if the gain and loss of the system reach equilibrium. In a non-Hermitian PT-symmetric system, when tuning the coupling strength, the eigenvalues can have a transition between real and complex numbers, which corresponds to the PT-symmetric phase and the PT-broken phase of the system. In the strong coupling region, the imaginary part of the eigenvalues degenerates while in the weak coupling region, the real part of the eigenvalues degenerates. The transition point is called the EP of the system where all eigenvalues and eigenvectors degenerate73,74, the orange dot in Fig. 2a.

Fig. 2: Different EP analytical approaches and corresponding theoretical models.
figure 2

a Schematic diagram of a variation of Hamiltonian eigenvalues with coupling strength. When both the real and imaginary part of eigenvalues degenerates, the system is at EP, which is represented by the orange dot in the figure. b Theoretical models of the resonant EP and the scattering EP, and the general expressions for the corresponding physical quantities, are given under the model. \({\omega }_{i}\), \({\gamma }_{i}\) is the eigenfrequency and loss of the i-th mode, and \({\mu }_{{ij}}\) is the coupling coefficient from the i-th mode to the j-th mode.

Full size image

In addition to analyzing the non-Hermitian property through the Hamiltonian of the system, in more cases such as metasurfaces, the scattering fields of the system become more significant. Therefore, it is preferable to acquire the scattering characteristics of the system with a PT-symmetric S-matrix, which focuses specifically on the scattering coefficients rather than the symmetry and symmetry-breaking phase change of the S-matrix. Besides, researchers have explained the symmetry of the S-matrix in detail and proposed a technique for analyzing non-Hermitian systems using the S-matrix. Following this method, the non-Hermitian system can be viewed as a resonator coupled to several scattering channels. When the system is PT-symmetric, the S-matrix of the system satisfies \(\left({PT}\right){\boldsymbol{S}}\left({\omega }^{* }\right)\left({PT}\right)={{\boldsymbol{S}}}^{-1}(\omega )\). Therefore, eigenvalues of the S-matrix are either unimodular or form pairs whose moduli are inverses of each other, corresponding to the symmetric phase and symmetric-broken phase, respectively. That means, in the symmetric phase, eigenstates are PT-symmetric and stay unchanged, whereas, in the symmetric-broken phase, eigenstates break PT-symmetry in pairs, which means one is amplified and the other is dissipated75,76,77,78.

Besides, several systems are referred to as PT-symmetric because other systematic matrices satisfy the PT-symmetric conditions. For different system characteristics, different PT-symmetry matrices are constructed. For instance, a PT-symmetric matrix can be constructed from the Hamiltonian of the system. Based on this, eigenvalues and eigenstates can be solved to examine the polarization properties79,80,81,82. When the coupling strength of two resonators changes from strong to weak, the orientations of the eigenstate ellipses also change, implying that the phase of the system changes from a symmetric state to a symmetry-broken state. Under this circumstance, EP separates these two regions where only the circularly polarized solution exists, which means the coalescence of the eigenmodes. Besides, to better explore the scattering properties of a PT-symmetric metasurface, a transfer matrix is constructed to show the unique transmission phenomenon at an EP83. This can also be combined with other physical theories, such as the nonlinear effect, to achieve nonreciprocal transmission84.

From the analysis methods of the PT-symmetric systems, we can see that totally distinct analytical approaches exist for studying non-Hermitian systems that can be classified into two categories based on their analytical perspectives. Consequently, the EPs obtained through these methods can also be classified into two types. One is called the resonant EP, which is derived from the Hamiltonians, and the other is called the scattering EP obtained directly from the S-matrix (transfer matrix). The corresponding theoretical models are shown in Fig. 2b. It is worth noting that significant differences exist between these two analytical methods in terms of their eigenvalues and eigenstates. The resonant EP is analyzed based on mode evolution, where the energy exchange between the system and the external environment is viewed as the coupling between the intrinsic mode of the system and the ambient incident field. The eigenvalues of this method are the complex frequencies of resonance modes, while the eigenstates are associated with the near field of the metasurface. In contrast, the scattering EP is analyzed from the perspective of scattered fields, where the system is modeled as resonators coupling with scattering channels. The eigenvalues are denoted by the scattering coefficients, and the eigenstates are related to the far field of the metasurface. The detailed derivation process of these two approaches and the unique properties of the EPs will be presented in the following sections.

Resonant EP

Non-Hermitian Hamiltonians and exceptional points

According to the Schrodinger equation, the wave function of the system meets

$$i{{\hslash }}\frac{\partial }{\partial t}\left|{{\psi }}\right\rangle ={\boldsymbol{H}}\left|{{\psi }}\right\rangle,$$
(1)

where

$$\left|{{\psi }}\right\rangle =\left(\begin{array}{c}{\psi }_{1}\\ {\psi }_{2}\\ \begin{array}{c}\vdots \\ {\psi }_{n}\end{array}\end{array}\right)$$

is the set of states of the system, \(\hslash\) is the Plank constant, and \({\boldsymbol{H}}\) is the Hamiltonian describing the energy of the system. When concerned about a non-Hermitian system with coupled gain and loss modes, the simplest Hamiltonian can be expressed as

$${\boldsymbol{H}}=\left(\begin{array}{cc}{\omega }_{1}+{ig} & \mu \\ \mu & {\omega }_{2}-i\gamma \end{array}\right),$$
(2)

where \({\omega }_{1,2}\) are the frequencies of the resonators, \(\mu\) is the coupling coefficient, \(g\) is the gain of one resonator, and \(\gamma\) is the loss of the other.

Before solving the EP problem of the system, we present a general expression for the eigenvalues of a \(2\times 2\) matrix first, aiding in the subsequent eigenvalues solution of the Hamiltonian or the S-matrix. For a \(2\times 2\) matrix \({\boldsymbol{A}}=\left(\begin{array}{cc}a & b\\ c & d\end{array}\right)\), the eigenvalues are derived from \(\det \left(x{\boldsymbol{I}}-{\boldsymbol{A}}\right)=0\), that means

$${x}_{1,2}=\frac{a+d}{2}\pm \sqrt{\frac{{\left(a-d\right)}^{2}}{4}+{bc}}$$
(3)

Therefore, when solving for the eigenvalues later, the elements will be carried over directly instead of repeating the calculation process.

Returning to the Hamiltonian shown in Eq. 2, when two resonators have the same resonant frequency, \({\omega }_{1}={\omega }_{2}={\omega }_{0}\), the eigenvalues of the Hamiltonian is

$${\lambda }_{1,2}={\omega }_{0}+i\frac{g-\gamma }{2}\pm \sqrt{{\mu }^{2}-\frac{{\left(g+\gamma \right)}^{2}}{4}}.$$
(4)

The system reaches EP when the eigenvalues coalesce \({\lambda }_{1}={\lambda }_{2}\), that is, the coupling coefficient, gain, and loss need to fulfill the condition that \(\mu =\frac{|g+\gamma| }{2}\).

To get an intuitive understanding of the eigenvalues and eigenstates evolution near an EP, we consider a classical PT-symmetric system of two resonators, where the gain and loss are balanced, which means \(g=\gamma\). Thus, the eigenvalues are given by \({\lambda }_{\mathrm{1,2}}={\omega }_{0}\pm \sqrt{{\mu }^{2}-{\gamma }^{2}}\). When \(\mu > \gamma\), the eigenvalues are real with their imaginary parts degenerating, leading to the system being in the PT-symmetric phase. Under this circumstance, let \(\frac{\gamma }{\mu }=\sin \left|\alpha \right|,\left|\alpha \right| < \frac{\pi }{2}\), then the normalized eigenvectors in the PT-symmetric phase can be expressed as \({\left[\begin{array}{cc}1 & {\pm e}^{-i\alpha }\end{array}\right]}^{T}\). On the Bloch sphere, this represents a pair of distinct points moving toward each other as \(\alpha\) increases. When \(\left|\alpha \right|=0\), the eigenvectors are orthogonal, while when \(\left|\alpha \right|=\frac{\pi }{2}\), the two eigenvectors are degenerated. When \(\mu < \gamma\), the eigenvalues become complex conjugates with degenerate real parts, corresponding to the system being in the PT-symmetric broken phase. In this case, let \(\frac{\gamma }{\mu }=\cosh \theta,\theta > 0\), then the eigenvectors be \({\left[\begin{array}{cc}1 & {\pm {ie}}^{-\theta }\end{array}\right]}^{T}\). When \(\theta =0\), the eigenvectors are equal. By gradually increasing the \(\theta\), the eigenvectors become increasingly non-orthogonal and separated on the Bloch sphere. When \(\mu =\gamma\), the eigenvalues coalesce, and the system reaches an EP.

However, in practical analyzes of non-Hermitian metasurfaces, the challenges in achieving strict PT-symmetry often lead to systems dominated solely by lossy resonators, rather than balanced loss-gain configurations. Furthermore, experimental limitations typically restrict measurable quantities to the scattering coefficients of the metasurface. This necessitates extending analytical frameworks beyond the intrinsic Hamiltonian parameters to explicitly establish a rigorous theoretical bridge between the observable scattering properties and the underlying non-Hermitian Hamiltonian parameters. Due to the particular structure of the metasurface, coupling arises among the eigenmodes and between the eigenmodes and the incident field (assuming there is an incident electromagnetic wave), forming new coupled resonant modes with corresponding eigenvalues and eigenstates of the system.

Since non-Hermitian systems inherently exchange energy with their environment, the eigenmodes are characterized by complex frequencies—where the real part represents the oscillation frequency and the imaginary part quantifies the modal gain or loss rate. These modes are defined as quasi-normal modes (QNMs)85,86,87. In coupled QNM systems, the QNM coupling theory88 establishes a comprehensive framework to calculate coupling coefficients between individual modes, enabling the prediction of hybridized mode properties based on isolated mode parameters. Another theoretical analysis approach is the temporal coupled-mode theory (TCMT), a widely adopted analytical tool in EP studies of non-Hermitian systems. A critical distinction between these methodologies lies in the frequency dependence of the coupling coefficients, which will be discussed in the following parts. Notably, under weak coupling and low-loss conditions, the frequency-dependent coupling coefficient derived from QNM coupling theory becomes approximately independent of frequency. This means the generalized QNM coupling theory can be reduced to the TCMT formalism, indicating that the traditional TCMT is a special form of the QNM coupling theory with weak coupling and low loss. Given the easy analysis of coupled-mode theory (CMT) compared to QNM-based approaches, we employ CMT here to analyze coupled systems. Through CMT, we establish explicit connections between the Hamiltonian parameters (e.g., resonance frequencies, coupling coefficients) and the measurable scattering coefficients of the metasurface. This linkage allows direct mapping of the system’s intrinsic non-Hermitian properties to its far-field optical responses. Below, we show the generalized CMT-based modeling procedure for such systems.

Considering the system contains n modes and m ports, the general expression of the CMT can be written as follow64,89:

$$\frac{d}{{dt}}{\boldsymbol{a}}=\left(j{\mathbf{\Omega }}-{\mathbf{\Gamma }}\right){\boldsymbol{a}}+j{\bf{{X}}}{\boldsymbol{a}}+{{\mathbf{{K}}}}^{T}\left|{{\boldsymbol{s}}}_{+}\right\rangle$$
(5)
$$\left|{{\boldsymbol{s}}}_{-}\right\rangle =-\left|{{\boldsymbol{s}}}_{+}\right\rangle +{\boldsymbol{{\rm K}}}{\boldsymbol{a}}$$
(6)

where the vector \({\boldsymbol{a}}{{=}}{\left({a}_{1},{a}_{2},\cdots,{a}_{n}\right)}^{T}\) represents the amplitude of each mode of the system, and the modulus of the element \({|{a}_{i}|}^{2}\) represents the energy of each mode. Γ matrix is a diagonal matrix whose diagonal element is the decay rate of each mode, including the radiation and non-radiation parts. Ω is a \(n\times n\) diagonal matrix with the information on modes’ resonant frequency and

$${\bf{{X}}}{{=}}\left(\begin{array}{cccc}0 & {\mu }_{12} & \cdots & {\mu }_{1m}\\ {\mu }_{21} & 0 & \cdots & {\mu }_{2m}\\ \vdots & \vdots & \ddots & \vdots \\ {\mu }_{n1} & {\mu }_{n2} & \cdots & 0\end{array}\right)$$

is the coupling coefficient matrix between each mode. The resonant modes can be excited by the incident waves \(\left|{{\boldsymbol{s}}}_{{{+}}}\right\rangle ={\left({s}_{1+},{s}_{2+},\cdots,{s}_{m+}\right)}^{T}\) from Port 1 to m. And

$${{\boldsymbol{{\rm K}}}}^{T}=\left(\begin{array}{cccc}{\kappa }_{11} & {\kappa }_{12} & \cdots & {\kappa }_{1m}\\ {\kappa }_{21} & {\kappa }_{22} & \cdots & {\kappa }_{2m}\\ \vdots & \vdots & \ddots & \vdots \\ {\kappa }_{n1} & {\kappa }_{n2} & \cdots & {\kappa }_{{nm}}\end{array}\right)$$

is a \(n\times m\) matrix and represents the coupling strength between each mode and the incident waves. Based on the CMT, we can relate the desired scattering coefficients of the metasurface to the physical parameters of the system, building a bridge between theoretical parameters and practical experimental measurements.

In the following part, we take the non-Hermitian metasurface with two modes coupled to two ports as an example to show the entire process of the resonant EP derivation in detail. The model is shown in the inset of Fig. 3a, where Port 1 contains the incident and reflectance light, while Port 2 contains the incident and transmittance light. In the framework of CMT, the time evolution of mode amplitudes can be expressed as

$$\left\{\begin{array}{c}\frac{d}{{dt}}{a}_{1}=\left(j{{\omega }}_{1}-{\Gamma }_{1}\right){a}_{1}{{+}}j{\mu }_{21}{a}_{2}{{+}}{\kappa }_{1}{s}_{+}\\ \frac{d}{{dt}}{a}_{2}=\left(j{{\omega }}_{2}-{\Gamma }_{2}\right){a}_{2}{{+}}j{\mu }_{12}{a}_{1}{{+}}{\kappa }_{2}{s}_{+}\end{array}\right.,$$
(7)

where \({\omega }_{i}\) and \({\Gamma }_{i}\) are the resonant frequency and decay rate of the i-th mode, \({\mu }_{{ik}}\) describes the coupling strength between the two modes, and \({\kappa }_{i}\) represents the coupling to the external port. It is worth noting that in the QNM coupling theory, all coupling coefficients, whether between modes or between modes and scattering channels, can be calculated through integrals of the eigenfields88 and are generally dependent on frequency. In weakly coupled and low-loss systems, CMT is also accurate in analyzing the system, where the coupling coefficients are often considered constant and independent of frequency, often obtained by fitting the spectral function. For reciprocal systems, mode coupling is symmetric, which means \({\mu }_{12}={\mu }_{21}\).

Fig. 3: Theoretical schematic of resonant and scattering EPs.
figure 3

a Schematic diagram of the EP metasurface137. The inset is the theoretical mode model of the resonant EP in one unit of the metasurface. The resonators have their resonant modes with both intrinsic loss and radiative loss. Coupling occurs between modes and between modes and incident light. According to our derivation, EP can be reached by tuning the coupling strength and the structures. b Theoretical models of the scattering EP of the metasurface. The metasurface can be regarded as a two-port device. It is worth noting that there is no wave propagation at the channel \({A}_{2}\) if \({A}_{1}\) is the channel of incidence. \({B}_{1}\) and \({B}_{2}\) are the channels of reflection and transmission, respectively. The schematic diagram in (a) reprinted with permission from ref. 137. Copyright 2023 American Chemical Society.

Full size image

Then the reflected waves of the metasurface can be expressed as

$${s}_{-}=-{s}_{+}+{\kappa }_{1}{a}_{1}+{\kappa }_{2}{a}_{2}$$
(8)

Thus, the reflection of the metasurface can be easily obtained by \(R={\left|r\right|}^{2}={\left|\frac{{s}_{-}}{{s}_{+}}\right|}^{2}\).

Next, we will show how to get resonant EP conditions in this system. To simplify the calculation, here we assume the system is reciprocal, which means \({\mu }_{12}={\mu }_{21}=\mu\). Firstly, a transformation from the time ___domain to the frequency ___domain can be made: \(\frac{d}{{dt}}\to j\omega\), so the Eq. 7 can be written as

$$\left(\begin{array}{cc}j\left(\omega -{{\omega }}_{1}\right)+{\Gamma }_{1} & -j\mu \\ -j\mu & j\left(\omega -{{\omega }}_{2}\right)+{\Gamma }_{2}\end{array}\right)\left(\begin{array}{c}{a}_{1}\\ {a}_{2}\end{array}\right)=\left(\begin{array}{c}{\kappa }_{1}\\ {\kappa }_{2}\end{array}\right){s}_{+}.$$
(9)

Under these circumstances, the Hamiltonian of the system, defined in Schrödinger-like form \(\frac{d}{{dt}}\left|\varphi \right\rangle =-j{\boldsymbol{H}}|\varphi \rangle\), becomes

$${\boldsymbol{H}}=\left(\begin{array}{cc}{{\omega }}_{1}+{\Gamma }_{1} & \mu \\ \mu & {{\omega }}_{2}+{\Gamma }_{2}\end{array}\right)$$
(10)

The eigenvalues of this Hamiltonian are

$${\lambda }_{1,2}=\frac{{{\omega }}_{1}+{{\omega }}_{2}+j\left({\Gamma }_{1}+{\Gamma }_{2}\right)}{2}\pm \frac{\sqrt{{\left[\left({{\omega }}_{1}-{{\omega }}_{2}\right)+j\left({\Gamma }_{1}-{\Gamma }_{2}\right)\right]}^{2}+4{\mu }^{2}}}{2}.$$
(11)

When the resonant frequencies of the two modes are equal, \({{\omega }}_{1}={{\omega }}_{2}={{\omega }}_{0}\), the eigenvalues can be written as

$${\omega }_{1,2}={\lambda }_{1,2}={{\omega }}_{0}+\frac{j\left({\Gamma }_{1}+{\Gamma }_{2}\right)}{2}\pm \frac{\sqrt{4{\mu }^{2}-{\left({\Gamma }_{1}-{\Gamma }_{2}\right)}^{2}}}{2}.$$
(12)

According to the definition of the EP, the eigenvalues and eigenstates of the system coalesce at the EP, which requires the parameters to satisfy \(2\mu =\left|{\Gamma }_{1}-{\Gamma }_{2}\right|\). Then the corresponding reflectance of the metasurface is given by

$$R={\left|\frac{{s}_{-}}{{s}_{+}}\right|}^{2}={\left|\frac{{{\kappa }_{1}}^{2}\left[j\left(\omega -{{\omega }}_{0}\right)+{\Gamma }_{2}\right]+{{\kappa }_{2}}^{2}\left[j\left(\omega -{{\omega }}_{0}\right)+{\Gamma }_{1}\right]+2{j\kappa }_{1}{\kappa }_{2}\mu }{\left(\left[j\left(\omega -{{\omega }}_{0}\right)+{\Gamma }_{1}\right]\left[j\left(\omega -{{\omega }}_{0}\right)+{\Gamma }_{2}\right]\right)-{\mu }^{2}}\right|}^{2}.$$
(13)

The expressions for reflection and eigenvalues demonstrate that the poles of the scattering coefficient correspond directly to the system’s eigenvalues. Furthermore, the degenerate point of these scattering coefficient poles coincides with the degenerate point of the Hamiltonians, which marks the EP of the system. Under this condition, the eigenstates become degenerate and the eigenfield distribution transitions from a symmetric profile to a localized one.

Based on the previous description, although the parametric conditions of resonant modes at the EP can be directly derived, determining the complex resonant frequencies during the design process remains challenging. Therefore, this method typically identifies whether the system reaches the EP through the coalescence of eigenvalues. In practice, parameter fitting based on spectral data is commonly employed. However, the fitting process becomes highly complicated if performed after each adjustment of the metasurface structure, as achieving the EP in a single attempt is nearly impossible. Generally, by tuning the metasurface structure, the EP is considered to exist within the adjustment range of the structural parameters when the fitted resonance frequency and loss rate exhibit intersection and non-intersection behavior. Ultimately, the approximate ___location of the EP can be determined by iteratively adjusting the parameters and performing multiple fits.

Applications

When the system operates in the vicinity of the EP, numerous applications emerge. One of the most prominent applications of resonant EPs is sensing, leveraging the ultra-high sensitivity exhibited by the system near the EP90,91,92. It has been demonstrated that the bifurcation nature of second-order non-Hermitian degeneracies at the EP can significantly enhance the sensitivity of resonant structures to external perturbations. Specifically, for a second-order EP, the splitting of eigenfrequencies is proportional to the square root of the perturbation, expressed as \(\Delta \omega \propto \sqrt{\varepsilon }\), where \(\varepsilon\) denotes the perturbation strength and \(\Delta \omega\) represents the frequency splitting between resonant modes. Similarly, a higher order of the EP can further enhance the sensitivity by \(\Delta \omega \propto {\varepsilon }^{1/N}\), where \(N\) is the order of the EP. Thus, sensors designed near the EP have been studied in lots of physical systems93,94,95 and next we will focus on sensor applications based on non-Hermitian EP metasurfaces. For example, shown in Fig.4a, a third-order EP was realized using a PT-symmetric coupled cavity system consisting of three cavities96. These cavities were designed to exhibit loss, neutrality, and gain, respectively, enabling a third-root enhancement in sensitivity to external perturbations. In non-PT-symmetric systems, EP sensors have been experimentally studied. A non-Hermitian metasurface was designed to reach an EP by using a multilayered periodic plasmonic structure that breaks the symmetry97, which is shown in Fig.4b, and demonstrated that a non-Hermitian system operating at the EP exhibits significantly higher sensitivity than one operating at a diabolic point (DP) under small perturbations. Additionally, as shown in Fig.4c, the sensitivity of the EP in a plasmon-exciton hybrid system has been investigated. The system, composed of a gold nanorod and a monolayer of \({\rm{W}}{{\rm{Se}}}_{2}\), was designed such that the resonant frequencies and loss rates coalesce simultaneously, confirming the system’s operation at the EP98. The sensitivity of the EP-based sensor was significantly enhanced compared to a single-rod sensor. However, EP sensors are highly susceptible to nanofabrication errors. The extreme sensitivity of systems at the EP means that even minor fabrication imperfections can cause the system to deviate from the EP. Moreover, the EP can amplify noise effects, raising concerns about the signal-to-noise ratio (SNR) of EP-based sensors99,100,101. Research efforts have also focused on mitigating noise impacts on sensor resolution and improving dynamic stability102,103,104,105.

Fig. 4: Applications for metasurfaces with resonant EP.
figure 4

a Schematics of the PT-symmetric coupled cavity system96 with three cavities that exhibit loss, neutral, and gain are shown in blue, gray, and red, respectively. b Resonant EP metasurface for sensing97. Left panel: Schematic of a multilayered periodic plasmonic structure made of two plasmonic resonators array with detuned resonances. Right panel: Resonance splitting \(|\varDelta {\omega }_{{EP}}|\) (red circles) and the logarithm of \(|\varDelta {\omega }_{{DP}}|\) (blue squares) versus the logarithm of the perturbation of (\(\varDelta n\)). The slopes are 0.5 and 1 respectively. c Sensitivity of the EP in a plasmon-exciton hybrid system98. Left panel: Schematic of the plasmon-exciton system composed of a gold nanorod and a monolayer \(W{{Se}}_{2}\). Right panel: Variation of the difference of resonant frequencies and the loss rate of the plasmon-exciton system and the resonant frequency and the loss rate of the GNR sensor in response to the change of the environmental refractive index. d PT-symmetric systems and the coherent perfect absorption-lasing point106. Left panel: Semilog plot of S-matrix eigenvalue intensities versus frequency. Right panel: Trajectories of S-matrix poles and zeros and the corresponding log of the transmittance. (a)(b)(c)(d) reprinted with permission from ref. 96, ref. 97, ref. 98. and ref. 106, respectively.

Full size image

In addition to sensing, resonant EPs are of growing significance in photonic systems. In particular, PT-symmetric structures can exhibit scattering singularities, such as the CPA-lasing point, which often appear near the parameter regimes where the non-Hermitian Hamiltonian hosts EPs. The CPA-laser point is a unique feature of PT-symmetric systems106, characterized by the coalescence of a pole and a zero of the S-matrix on the real frequency axis (Fig. 4d right panel). Under such conditions, the system can simultaneously function as a laser and a coherent absorber, depending on the relative phase and amplitude of the incident fields. A CPA absorber refers to a configuration in which all incident energy is perfectly absorbed by the system, with zero outgoing fields. In contrast, the CPA laser spontaneously emits in the amplifying eigenstate when the system reaches the lasing threshold, corresponding to a real-frequency pole of the scattering matrix. In certain systems, this scattering singularity may also coincide with a Hamiltonian EP, revealing a deeper correspondence between modal coalescence and extreme scattering behavior.

While the conventional CPA-laser point involves radiative mode degeneracy, recent studies have demonstrated that EPs can also emerge from the coalescence of incoming solutions of the wave equation, leading to so-called absorbing EPs or CPA-EPs. These configurations give rise to distinct spectral features, such as quartic absorption line shapes, and have been experimentally realized in optical microcavity systems to enable broadband coherent perfect absorption107. Furthermore, by integrating EP physics with massively degenerate cavity architectures, a new class of CPAs has been proposed, capable of achieving broadband and wavefront-independent absorption. These MAD-EP-CPA (Massively Degenerate EP CPA) systems represent a promising step toward practical, robust, and geometry-tolerant perfect absorbers108.

The approach to analyzing metasurfaces directly through mode evolution is relatively straightforward, as the complex resonant frequencies of the modes can be directly obtained from fitting. However, due to the challenges associated with parameter fitting, resonant EPs have been studied less extensively compared to other types of EPs.

EP in the scattering matrix

Scattering matrix and exceptional point

Since scattering coefficients are central to non-Hermitian metasurfaces, a practical strategy is to directly identify EPs via the S-matrix. Metasurfaces can be considered multi-port devices so that the S-matrix can serve as a reliable depiction of the link between the scattering coefficients of metasurfaces. For a metasurface with m ports, the relationship between its input and output ports can be written as

$$\left(\begin{array}{c}{o}_{1}\\ {o}_{2}\\ \begin{array}{c}\vdots \\ {o}_{N}\end{array}\end{array}\right)=\left(\begin{array}{ccc}\begin{array}{cc}{S}_{11} & {S}_{12}\\ {S}_{21} & {S}_{22}\end{array} & \cdots & \begin{array}{c}{S}_{1N}\\ {S}_{2N}\end{array}\\ \vdots & \ddots & \vdots \\ \begin{array}{cc}{S}_{N1} & {S}_{N2}\end{array} & \cdots & {S}_{{NN}}\end{array}\right)\left(\begin{array}{c}{i}_{1}\\ {i}_{2}\\ \begin{array}{c}\vdots \\ {i}_{N}\end{array}\end{array}\right),$$
(14)

where \({i}_{p}\) and \({o}_{q}(p,q=\mathrm{1,2},\ldots,N)\) corresponds to the input and output ports, respectively. It is noted that the expression shown above is a general form and scattering coefficients \({S}_{{ij}}\) can be replaced by reflection or transmission coefficients leading to different S-matrices. Various forms of the S-matrices and their corresponding EP will be elucidated in the following part of this section.

Considering a \(N\times N\) S-matrix shown in Eq. 14, when all the eigenvalues and eigenstates of the S-matrix degenerate, the non-Hermitian system is at a high-order EP, while when only a subset of the eigenvalues and eigenstates undergo degeneracy, the system is said to be at an nth-order EP. Furthermore, the matrix presented in Eq. 14 can be split into smaller matrices, each of which indicates the scattering relationship between certain channels109. To simplify the analysis process, we consider a metasurface with two ports as an example and the input and output ports of the metasurface can be related by the S-matrix:

$$\left(\begin{array}{c}{o}_{1}\\ {o}_{2}\end{array}\right)=\left(\begin{array}{cc}{S}_{11} & {S}_{12}\\ {S}_{21} & {S}_{22}\end{array}\right)\left(\begin{array}{c}{i}_{1}\\ {i}_{2}\end{array}\right).$$
(15)

Substituting the S-matrix into Eq. 3, the eigenvalues of the system are

$${\lambda }_{1,2}=\frac{{S}_{11}+{S}_{22}}{2}\pm \sqrt{\frac{{\left({S}_{11}-{S}_{22}\right)}^{2}}{4}+{S}_{12}{S}_{21}}.$$
(16)

When two eigenvalues degenerate, the system is at the EP, and scattering coefficients should satisfy

$$\left|{S}_{11}-{S}_{22}\right|=2j\sqrt{{S}_{12}{S}_{21}}.$$
(17)

In this case, the eigenvalues are equal \({\lambda }_{1}={\lambda }_{2}=\frac{{S}_{11}+{S}_{22}}{2}\). When the system operates at an EP, only eigenstate-matched incident waves can efficiently couple into the degenerate eigenmodes, leading to extreme selectivity in mode excitation.

Although we have only demonstrated the process to find the eigenvalues of a second-order S-matrix, the methodology used for finding the eigenvalues of higher-order S-matrices and determining whether the system is at the EP is similar. In the following part of the section, we will focus more on the second-order EP.

Different types of the S-matrix and corresponding EP

When it comes to non-Hermitian metasurfaces, there are different types of S-matrices present due to various structures of metasurfaces and different research focuses. To standardize terminology, we classify the four forms of S-matrices as follows: (i) reflection-only matrix (all elements correspond to reflection coefficients), (ii) transmission-only matrix (all elements correspond to transmission coefficients), (iii) diagonal-reflection matrix (diagonal elements are reflection coefficients with others being transmission coefficients), and (iv) diagonal-transmission matrix (diagonal elements are transmission coefficients with others being reflection coefficients).

The process of obtaining eigenvalues for each matrix form is similar, and the system reaches an EP when the eigenvalues and eigenstates coalesce. The specific derivation of the EP for S-matrices will not be discussed in detail in this article. Subsequently, Table 1 summarizes the EP conditions for all forms of S-matrices. Among these, the first group—the diagonal-reflection matrix—can be directly derived from the definition of the S-matrix, making it the most intuitive and general form, though it is less commonly used in practice110,111. By rearranging the port order, a diagonal-transmission S-matrix can be obtained, which resembles the second group of matrices and finds extensive application in various fields112,113,114,115,116. Additionally, here we group the reflection-only matrix and the transmission-only matrix due to their similar forms and potential applications. These S-matrices are typically derived from the transfer matrix and are closely related to the metasurface structure and the specific problem under investigation. Reflection-only matrices usually represent metasurfaces with only reflection and no transmission, often featuring a metallic base layer that acts as a reflective surface. Conversely, for metasurfaces where transmittance is the primary focus, the corresponding S-matrix often includes only transmittance. Both reflection-only and transmission-only matrices are highly effective for analyzing the polarization properties and phase transitions of metasurfaces.

Table 1 EP conditions for different forms of scattering matrices
Full size table

Furthermore, when the non-Hermitian metasurface is reciprocal, the S-matrices and EP conditions can be significantly simplified. Their simplified expressions are summarized in Table 2. For the diagonal-reflection matrix and the diagonal-transmission matrix, the transmission coefficients at both ports are identical in the reciprocal metasurface system, i.e, \({t}_{1}={t}_{2}\). For the reflection-only matrix, two common S-matrix expressions exist under the reciprocity condition: equality of diagonal elements or equality of anti-diagonal elements. In the case of the transmission-only matrix, reciprocity implies that the anti-diagonal elements are identical. Since the diagonal-reflection matrix is rarely used in practice, we will focus on providing detailed descriptions and corresponding applications of the remaining three types of matrices.

Table 2 EP conditions for reciprocal metasurfaces
Full size table

Diagonal-transmission S-matrix

When the transmission coefficients in the S-matrix are identical the EP condition simplifies to \({r}_{1}{r}_{2}=0\), indicating that the system reaches an EP if either reflection coefficient vanishes. Consequently, the diagonal-transmission S-matrix can be utilized to design unidirectional reflectionless devices. For instance, a chip-scale metamaterial near the PT-symmetry phase transition point was experimentally demonstrated to achieve unidirectional reflection117, which is shown in Fig. 5a. The transfer matrix was employed to calculate the eigenvalues of the S-matrix. Additionally, in Fig. 5b, c, non-ideal PT-symmetry metamaterials, consisting of two vertically placed resonators, are shown to achieve unidirectional reflectionless propagation and works based on far-field coupling118 and phase coupling119, respectively, were proposed. The far-field-coupling-based metamaterial is insensitive to the polarization of the incident light due to the ring structure, while the phase-coupling-based one adjusts the EP by polarization of the incident light. In addition to PT-symmetric metamaterials, non-PT-symmetry multi-layer metasurface was also proposed and investigated the polarization-dependent unidirectional reflection in the vicinity of the EP120, which is shown in Fig. 5d where the strong dependence on incident light polarization has the potential for near-field imaging and optical encryption. Also, the dual-band unidirectional reflectionless propagation was achieved by a polarization-insensitive metasurface consisting of two circle-hole resonators121.

Fig. 5: Applications for metasurfaces with EP of the scattering matrix.
figure 5

a Simulated electric field amplitude distribution of light in a chip-scale metamaterial along the +z/−z direction117. b, c Schematic of a unit cell of the non-ideal PT-symmetry metasurface structure118,119. d Unidirectional reflectionless metasurface120. Left panel: Schematic diagram of the unidirectional reflectionless effect in the metasurface. Right panel: Simulated electric field. e Schematic diagram of the unidirectional retro-reflection effect of the loss-assisted metasurface123. f Schematics of extreme OAM chirality at the perfectly chiral EP125. a, d, f reprinted with permission from ref. 117, ref. 120. and ref. 125, respectively. b reprinted with permission from ref. 118. © Optical Society of America. c from ref. 119. permitted under the Creative Commons license CC BY 4.0. e reprinted with permission from ref. 123. Copyright 2020 American Chemical Society.

Full size image

Reflection-only S-matrix

For reciprocal non-Hermitian metasurface systems, two distinct reflection-only S-matrix formulations arise from different analytical frameworks. The first framework, based on reflection directions, defines the S-matrix elements as specular and retro-reflection coefficients. Specifically, Port 1 exhibits specular reflection \({r}_{1}\) and retro-reflection \({r}_{2}\), while Port 2 corresponds to \({r}_{3}\) and \({r}_{4}\). Under reciprocity, the specular reflection coefficients of both ports become identical, leading to the S-matrix: \(S=\left(\begin{array}{cc}{r}_{0} & {r}_{1}\\ {r}_{2} & {r}_{0}\end{array}\right)\), where \({r}_{0}\) denotes the specular reflection and \({r}_{1}\), \({r}_{2}\) represents the retro-reflection for Ports 1 and 2, respectively. The system reaches an EP when \({r}_{1}{r}_{2}=0\), which provides a direct pathway to design a unidirectional retroreflector122. With loss engineering, a metasurface working at the EP was reported as shown in Fig. 5e, showing extraordinary angular asymmetry to exhibit unidirectional retro-reflection123, where reflection from one side of the incidence is completely suppressed while reflection from the other side is highly efficient. Furthermore, polarization-insensitive asymmetric optical devices leveraging a fourth-order EP have been realized, exhibiting extraordinary angular asymmetry under different polarization incident lights124. Besides, chirality is inherently linked to asymmetry studies. To transcend conventional two-state polarization limits, as shown in Fig. 5f, a mirror-symmetry-broken metasurface was proposed, achieving the perfect chiral EP for extreme chirality via orbital angular momentum (OAM)125. Additionally, unidirectional retro-reflection has been demonstrated at the scattering EP in the visible126.

On the other hand, when considering the polarization properties, the S-matrix \(\left(\begin{array}{cc}{r}_{{xx}} & {r}_{{xy}}\\ {r}_{{yx}} & {r}_{{yy}}\end{array}\right)\) characterizes polarization conversion, where \({r}_{{ij}}\) denotes the reflection coefficient from i-polarized incident to j-polarized reflection, and reciprocity leads to \({r}_{{xy}}={r}_{{yx}}=r\). Studies have revealed that non-Hermitian metasurfaces shown in Fig. 6a exhibit nontrivial topological features near the EP of the S-matrix127. When encircling the EP, a 2π phase transition could be induced, leading to reflected circle phase conversion. Leveraging this mechanism, a vertical Fourier metasurface was proposed to achieve asymmetric manipulation of wavefront via paired EPs, demonstrating full-color holograms128. Moreover, with the demand for dynamic tunability of EPs in optical, an electrical tunable non-Hermitian metasurface was demonstrated, enabling voltage-controlled topological phase transition129. Meanwhile, Phase-change materials (PCMs) enable dynamically reconfigurable control of reflection and transmission properties in the terahertz (THz) regime130.

Fig. 6: Applications for metasurfaces with EP of the scattering matrix.
figure 6

a EP metasurface with 2π phase transition127. Left panel: Perspective and (bottom) top view of the metasurface designed in reflection. Right panel: Simulated CP conversion coefficients \({r}_{+-}\). b Asymmetric transmission EP metasurface131. Left panel: Variation of the transmission matrix components in the circularly polarized basis when passing over the metasurface. Right panel: Transmission spectrum of the metasurface. c Metasurface with chiral EP enhanced asymmetry polarization133. Left panel: Parameter space surrounding EP on the Riemann surface. Right panel: Variation of the eigentransmission magnitude and eigenpolarization ellipse angle along the cyclic variation. d Metal–graphene hybrid metasurface with switchable scattering characteristics134. Left panel: Magnitudes, phase, and polarization eigenstates for the eigenvalues of the S-matrix obtained at different EF values. Right panel: Polarization eigenstates are represented on the Poincare ́ sphere. a, d reprinted with permission from ref. 127. and ref. 134, respectively. b from ref. 131. permitted under the Creative Commons license CC BY 4.0. c from ref. 133. permitted under the Creative Commons CC BY license.

Full size image

Transmission-only S-matrix

When considering the transmission-only matrix, polarization conversion receives more attention. The form shown in Table 2 is expressed using the linear polarization basis where \({t}_{{xy}}={t}_{{yx}}\) due to reciprocity. However, it is more intuitive to present the matrix in the circular polarization basis instead, which is shown in Eq. 18.

$${T}_{{cir}}=\left(\begin{array}{cc}{t}_{++} & {t}_{+-}\\ {t}_{-+} & {t}_{--}\end{array}\right)=\frac{1}{2}\left(\begin{array}{cc}\left({t}_{{xx}}+{t}_{{yy}}\right)+j\left({t}_{{xy}}-{t}_{{yx}}\right) & \left({t}_{{xx}}-{t}_{{yy}}\right)-j\left({t}_{{xy}}+{t}_{{yx}}\right)\\ \left({t}_{{xx}}-{t}_{{yy}}\right)+j\left({t}_{{xy}}+{t}_{{yx}}\right) & \left({t}_{{xx}}+{t}_{{yy}}\right)-j\left({t}_{{xy}}-{t}_{{yx}}\right)\end{array}\right)$$
(18)

Under these circumstances, it is easy to find that \({t}_{++}={t}_{--}\), so that the system reaches EP when the transmittance matrix satisfies \({t}_{+-}{t}_{-+}=0\). By designing a non-Hermitian metasurface containing two orthogonally oriented split-ring resonators with overlapping resonant frequencies but different losses, the parameter space around the EP is accessible131 as shown in Fig. 6b. When encircling around the EP, the eigenstates swap and the geometric phases accumulate on only one of the states. Asymmetric transmission and an abrupt phase flip are also observed on this structure, which can be utilized for active polarization modulators and sensitive biosensors. Recently, graphene as a gate is combined with the metal to realize active tuning of the metasurface132, and the chiral EP of the transmission-only matrix shown in Fig. 6c leads to enhanced asymmetry polarization conversion133. Besides, PCMs such as \({{\rm{VO}}}_{2}\) are used to realize switchable reflection and transmission characteristics134 as shown in Fig. 6d.

In the following part of this section, we take a two-mode coupled metasurface with two ports as an example to demonstrate the detailed derivation of eigenvalue calculations and EP conditions. The derivation process is shown as follows, and the corresponding model is illustrated in Fig. 3b. Analogous to the resonant EP, CMT is employed to establish a physically intuitive model. Such a metasurface system can be described by equations similar to Eq. 7 for resonant EPs, but with distinct incident waves in the two channels, \({s}_{1}^{{in}}\) and \({s}_{2}^{{in}}\). The relations between incident and outgoing fields are expressed as

$$\left(\begin{array}{c}{s}_{1}^{{out}}\\ {s}_{2}^{{out}}\end{array}\right)=\left(\begin{array}{c}{s}_{1}^{{in}}\\ {s}_{2}^{{in}}\end{array}\right)+\left(\begin{array}{cc}{\kappa }_{1} & 0\\ 0 & {\kappa }_{2}\end{array}\right)\left(\begin{array}{c}{a}_{1}\\ {a}_{2}\end{array}\right).$$
(19)

Introducing the S-matrix \({\boldsymbol{S}}\), the input-output relation becomes:

$$\left(\begin{array}{c}{s}_{1}^{{out}}\\ {s}_{2}^{{out}}\end{array}\right)={\boldsymbol{S}}\left(\begin{array}{c}{s}_{1}^{{in}}\\ {s}_{2}^{{in}}\end{array}\right).$$
(20)

Rewriting Eq. 9 in matrix form:

$$\left(\begin{array}{cc}{{\kappa }_{2}}^{2}\left({\Delta }_{1}-j{\Gamma }_{1}\right) & -{\kappa }_{1}{\kappa }_{2}\mu \\ -{\kappa }_{1}{\kappa }_{2}\mu & {{\kappa }_{1}}^{2}\left({\Delta }_{2}-j{\Gamma }_{2}\right)\end{array}\right)\left(\begin{array}{c}{\kappa }_{1}{a}_{1}\\ {{\kappa }_{2}a}_{2}\end{array}\right)={{-j\kappa }_{1}}^{2}{{\kappa }_{2}}^{2}\left(\begin{array}{c}{s}_{1}^{{in}}\\ {s}_{2}^{{in}}\end{array}\right)$$
(21)

where \({\Delta }_{i}=\omega -{{\omega }}_{i}\). The left-hand matrix can be regarded as the effective Hamiltonian

$${\boldsymbol{H}}=\left(\begin{array}{cc}{{\kappa }_{2}}^{2}\left({\Delta }_{1}-j{\Gamma }_{1}\right) & -{\kappa }_{1}{\kappa }_{2}\mu \\ -{\kappa }_{1}{\kappa }_{2}\mu & {{\kappa }_{1}}^{2}\left({\Delta }_{2}-j{\Gamma }_{2}\right)\end{array}\right).$$
(22)

In order to distinguish between the Hamiltonians corresponding to the resonance EP and the scattering EP, we call Eq. 10 the resonance Hamiltonian and Eq. 22 the scattering Hamiltonian. Combining Eqs. 19–22, the input-output relationship further simplifies to

$$\left(\begin{array}{c}{s}_{1}^{{out}}\\ {s}_{2}^{{out}}\end{array}\right)={\boldsymbol{S}}\left(\begin{array}{c}{s}_{1}^{{in}}\\ {s}_{2}^{{in}}\end{array}\right)=\left({\boldsymbol{I}}-j{{\kappa }_{1}}^{2}{{\kappa }_{2}}^{2}{{\boldsymbol{H}}}^{-1}\right)\left(\begin{array}{c}{s}_{1}^{{in}}\\ {s}_{2}^{{in}}\end{array}\right).$$
(23)

Thus, the S-matrix can be expressed as

$${\boldsymbol{S}}={\boldsymbol{I}}-j{\kappa }_{1}^{2}{\kappa }_{2}^{2}{{\boldsymbol{H}}}^{-1}={\boldsymbol{I}}-j\frac{{\kappa }_{1}^{2}{\kappa }_{2}^{2}}{\det \left({\boldsymbol{H}}\right)}{{\boldsymbol{H}}}^{{\boldsymbol{* }}},$$
(24)

where \({{\boldsymbol{H}}}^{{\boldsymbol{* }}}\) is the adjoint matrix of \({\boldsymbol{H}}\). Consequently, the eigenstates of \({\boldsymbol{S}}\) are the same as those of \({\boldsymbol{H}}\), provided \({\boldsymbol{H}}\) is diagonalizable. Then the eigenvalues of \({\boldsymbol{H}}\) are given by

$$\begin{array}{l}{\lambda }_{H}=\left\{{\kappa }_{2}^{2}\left({\Delta }_{1}-{\rm{j}}{\Gamma }_{1}\right)+{\kappa }_{1}^{2}\left({\Delta }_{2}-j{\Gamma }_{2}\right)\right.\\\quad\;\;\left.\pm\sqrt{{[{\kappa }_{2}^{2}\left({\Delta }_{1}-{\rm{j}}{\Gamma }_{1}\right)-{\kappa }_{1}^{2}\left({\Delta }_{2}-j{\Gamma }_{2}\right)]}^{2}+{4\kappa }_{1}^{2}{\kappa }_{2}^{2}{\mu }^{2}}\right\}/2.\end{array}$$
(25)

The eigenvalues and eigenstates of the \({\boldsymbol{S}}\) matrix are

$${\lambda }_{S}=1-j{\kappa }_{1}^{2}{\kappa }_{2}^{2}{\lambda }_{H}^{-1},$$
(26)
$${\upsilon }_{S}=\left(1,\{[{\kappa }_{2}^{2}({\Delta }_{1}-{\rm{j}}{\Gamma }_{1})-{\lambda }_{H}]/({\kappa }_{1}{\kappa }_{2}\mu )\}\right)$$
(27)

respectively. Assuming here \({\Delta }_{1}=\omega -{{\omega }}_{1}=0,{\Delta }_{2}=\omega -{{\omega }}_{2}=0\), the EP occurs when the eigenvalues and eigenvectors coalesce, which requires:

$$2\left|{\kappa }_{1}{\kappa }_{2}\mu \right|=\left|{\kappa }_{2}^{2}{\varGamma }_{1}-{\kappa }_{1}^{2}{\varGamma }_{2}\right|$$
(28)

At this point, \({\lambda }_{H}={-(j\kappa }_{2}^{2}{\Gamma }_{1}+j{\kappa }_{1}^{2}{\Gamma }_{2})/2\) and the eigenvalues of the S-matrix are degenerated to one real number. The corresponding eigenvectors of the S-matrix become degenerate \({\upsilon }_{S}=(1,\pm j)\). This implies chiral eigenstates at the EP, corresponding to left- and right-handed circularly polarized modes. This methodology proves particularly practical for polarization and phase analysis near the metasurface’s EP, explaining why most studies on polarization characteristics near non-Hermitian metasurface EPs currently adopt the S-matrix approach.

Difference and relations between resonant EP and scattering EP

The preceding sections have comprehensively analyzed the theoretical foundations and applications of both resonant and scattering EPs. Here, we establish a unified analytical framework by systematically comparing their distinctions and connections.

Starting from definitions, resonant EPs originate from the non-Hermitian degeneracy of resonant characteristics, where eigenvalues and eigenvectors of the resonant Hamiltonian become degenerate simultaneously. These EPs typically emerge in discrete-mode coupling systems (e.g, optical microcavities, mechanical resonators) and are intrinsically linked to the non-Hermiticity of bound or quasi-bound states. Physically, they are associated with scattering poles of the resonant Hamiltonian according to Eq. 24. In contrast, scattering EPs originate from degeneracies in scattering zeros of the scattering Hamiltonians, governing open-system phenomena such as unidirectional reflectionless transmission and perfect absorption.

Despite differing physical contexts, both EP classes exhibit fundamental non-Hermitian signatures. First, mathematical description via eigenvalue/eigenstate coalescence in their respective Hamiltonians (resonant Hamiltonians for resonant EPs; scattering Hamiltonians for scattering EPs). Second, topological braiding of eigenvalue trajectories in the complex plane when encircling EPs in parameter space. Recent studies have shown that the energy spectra of resonant states and scattering states undergo topological braiding near the EPs135. Specifically, the eigenvalues and eigenvectors exhibit winding behavior around the EPs, and their braiding structures have opposite chirality. In some cases, scattering EPs and resonant EPs can be regarded as manifestations different from the same system. For example, bound states in the continuum in the complex plane have been proven to be the degeneracy points of the eigenvalues of the resonant and the scattering Hamiltonian. This unification not only deepens the understanding of non-Hermitian physics but also provides a theoretical foundation for designing multifunctional metasurfaces with tailored EP-enabled functionalities.

Conclusion

In this review, we provide a comprehensive analysis of prevalent techniques for characterizing EPs in non-Hermitian metasurfaces and categorize them into two distinct theoretical types. The Resonant EP typically investigates mode evolution in metasurfaces while the scattering EP directly analyzes the S-matrix of metasurfaces. As previously mentioned, while the resonant EP may seem more intuitive regarding the evolution of the mode, the existing work is scarce when compared to the scattering EP. This method relies solely on fitting parameters to determine whether the system is at the EP, which makes the analysis process more difficult and time-consuming. In addition, it is worth noting that there is a missing dimension in the process of EP analysis, which has not been elaborated and analyzed in most of the work136. Further investigation is necessary to determine whether it has any impact on the analysis of non-Hermitian systems. The scattering EP is more prevalent in current studies on non-Hermitian metasurfaces. The majority of these studies concentrate on analyzing the polarization of the metasurface’s electromagnetic field. Also, we categorize the scattering EP into four specific forms based on the different combinations of scattering coefficients.

By using appropriate theoretical and analytical methods, we can scrutinize the properties and traits of EPs. This review classifies the theoretical analysis methods of non-Hermitian metasurface EPs and offers clear insights into the theoretical analysis for achieving non-Hermitian systems or EP applications, filling the theoretical analysis gap in this promising field.