Introduction

Ancient murals are precious human cultural heritages, which record a wealth of historical memory information of human life, religion, culture, and art activities1. Due to long-time exposure to environments and human activities, most of these ancient murals have suffered from various damages and degradations such as cracks, scratches, flaking, and other diseases2. These diseases may greatly reduce the cultural and artistic values of ancient murals. Therefore, automatic and accurate detection of damaged regions in murals has become a critical and urgent work for cultural heritage protection communities. At present, most researchers rely on manual methods to calibrate damaged and diseased areas in murals, which is extremely time-consuming and labor-intensive3. The use of modern computer technology for automatic detection of mural disease areas can greatly reduce the workload of mural restoration personnel.

In recent years, researchers have made preliminary progress in the field of automatic detection of ancient mural damages. Turakhia et al.4 utilized order-statistic filtering and tensor voting to automatically detect crack regions and used them as inputs for Canny edge detection for crack repair. Wu et al.5 used two morphological methods (top-hat and below-hat) to design multi-scale structural elements to mark the diseases of Tang Dynasty tomb murals. Jaidilert et al.6 proposed a semi-automatic detection method based on seed region growing for cracks in Thai murals. This method requires users to provide seed points, which complicates the prediction process of mural-damaged areas. Cao et al.7 proposed an improved region-growing algorithm for the murals of the Song Dynasty in the Kaihua Temple. The method cannot accurately calibrate the flaking regions with significant variations in color and brightness. Zhang et al.8 applied RGF filtering in murals to smooth image details and preserve their edges. This processing method is more suitable for murals with obvious differences between damaged and intact areas. Zhang et al.9 used a local optimal hierarchical clustering extraction algorithm to form an information mask for mural diseases. The approach requires manual intervention. However, the abovementioned methods either have low accuracy or suffer from high computational complexity. There still exist limitations and challenges when dealing with complex image environments.

With the advancement of deep learning technology, some researchers have begun to make preliminary attempts to use deep learning approaches to detect mural damage. Lin et al.10 used the minimum noise fraction transform and trained a back propagation neural network to classify damaged and normal areas in mural images. Huang et al.11 designed a multi-path convolutional neural network (CNN) to detect mural damage. which is applicable to damaged images under different lighting conditions. Yu et al.12 proposed a model based on U-Net to detect paint-peeling diseases in temple murals. Wu et al.13 proposed a lightweight YOLOv5-based detection model to improve the detection performance. Cao et al.14 combined the lightweight network MobileNetV2 with PSPNet to improve segmentation accuracy and, meanwhile, reduce computation time. Hu et al.15 proposed a new hierarchical multi-scale encoder–decoder framework that uses an attention-convolution dual-branch module to predict damaged areas in complex background murals. Wu et al.16 proposed a dual-attention detection network based on ConvNeXt for accurately identifying cracks in tomb murals.

Although the above techniques are capable of detecting specific mural damages, there still exist some challenges for a mural damage detection approach. Firstly, many ancient murals contain diverse contents and complex structures. This makes it very difficult for an approach to accurately detect the damaged regions of murals. Secondly, some murals have significant differences in the area of damage. This will pose difficulties for algorithms that simultaneously detect large-scale damage and small holes. Thirdly, most deep neural networks need large amounts of training data. The quality of the training datasets will affect the performance of a damage detection model.

To address these challenges, we propose an innovative network that has a great ability to detect damaged regions of murals, even though the murals contain complex structures and abundant semantic contents. The main contributions of this paper include the following four points: (1) We design a damage detection model for ancient murals based on multi-scale boundary and region feature fusion (MBRF). The model contains two sub-networks: global information generator (GIG) and detail information generator (DIG). The GIG integrates global features to predict coarse-damaged regions, whereas the DIG utilizes the predicted coarse-damage regions to generate a refined map of the damaged regions of murals. (2) We employ the Res2Net residual convolutions to extract multi-level features and design a global decoder (GD) to integrate multi-level deep features. (3) We propose a bilateral guided fusion (BGF) module to extract and fuse the boundary and the region features. We introduce a reverse attention (RA) module to capture boundary details, and we design a group receptive field (GRF) module to extract the region features. (4) For network training, we collect 100 high-quality images of damaged murals, and expand them to 5000 by use of data augmentation techniques.

Proposed method

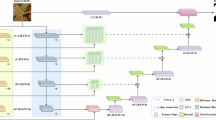
Most of the damaged regions in ancient murals have irregular shapes and complex backgrounds. It is very difficult to detect the damaged regions of the mural images. Regions and their boundaries are crucial features for detecting mural damage. Therefore, the extraction of these features plays an important role in guiding the detection of damaged murals. Motivated by this point, we propose a multi-scale boundary and region feature fusion (MBRF) model for detecting damaged ancient murals. Figure 1 illustrates the overall architecture of the MBRF model. The model can be divided into two sub-networks: global information generator (GIG) and detail information generator (DIG). Two sub-networks collaborate to optimize the features from coarse to fine.

Fig. 1
figure 1

The overall architecture of the proposed model.

Full size image

Given an input-damaged mural image \(I\in {{\mathbb{R}}}^{H\times W\times C}\), the GIG extracts different levels of features from image I, and integrates the three deep-level features using a global decoder (GD). The GD focuses on predicting the coarse locations of damaged mural regions and then generates a global mask map Mg. We use the global mask map and three deep-level features as inputs to DIG. DIG refines features under the guidance of Mg. It gradually extracts fuzzy boundary details and region features and then generates refined feature maps at different scales. The last feature map is processed through a sigmoid function to generate a final prediction map.

Global information generator (GIG)

The high-level features in the network have high resolution. These features contain rich semantic information and can preliminarily predict the damaged regions in ancient murals. We design a global information generation network, also referred to as the global information generator (GIG) in this work, to predict the coarse position of the damaged regions. Given an input image \(I\in {{\mathbb{R}}}^{512\times 512\times 3}\), GIG generates a mask map containing global information. GIG consists of the Res2net residual blocks17 and a global decoder. We use residual blocks as input layers to extract features at four levels \(\left\{{F}_{i}| 1\le i\le 4\right\}\) of the input image. Compared with ordinary convolution, residual convolution blocks increase the receptive field of the convolutional layer and, therefore, can improve the ability to extract global and local information.

Notice that the context of ancient murals is complex, and the multi-level features extracted from the early input layers of the network are insufficient for damage detection. Directly fusing these features can easily lead to information loss. Therefore, we propose a global decoder (GD) to capture the global context information as much as possible. Figure 2a illustrates the architecture of the GD, we take, \({F}_{2}\in {{\mathbb{R}}}^{64\times 64\times 512}\), \({F}_{3}\in {{\mathbb{R}}}^{32\times 32\times 1024}\) and \({F}_{4}\in {{\mathbb{R}}}^{16\times 16\times 2048}\) as the input features of GD. The GD module is divided into the following three main parts:

Fig. 2: The architectures of global decoder.
figure 2

a GD module, b residual convolution (RC) module, c multi-resolution fusion (MRF) module, and d pooling fusion (PF) module.

Full size image

(a) Residual convolution (RC) module (Fig. 2b). The module connects two residual blocks by residual concatenation18. Each residual block consists of a Grouped Normalization layer19, a Gelu activation function20 and a 3 × 3 convolutional layer. The RC unifies the channels of each input feature to 64.

(b) Multi-resolution fusion (MRF) module (Fig. 2c). This module employs 3 × 3 convolution with different dilation factors21 to extract multi-resolution features and concatenate these features across channel dimensions. This module effectively expands the receptive field and further improves the ability to extract features.

(c) Pooling fusion (PF) module (Fig. 2d). In order to match the features (extracted by MRF) at different scales, we perform a convolution operation on these features to obtain \({F}_{c}^{2}\in {{\mathbb{R}}}^{64\times 64\times 64}\), \({F}_{c}^{3}\in {{\mathbb{R}}}^{32\times 32\times 64}\), and \({F}_{c}^{4}\in {{\mathbb{R}}}^{16\times 16\times 64}\). The intermediate output features \({F}_{a}\in {{\mathbb{R}}}^{32\times 32\times 64}\) and \({F}_{b}\in {{\mathbb{R}}}^{16\times 16\times 64}\) are defined as

$${F}_{a}={f}_{1\times 1}\left({\rm{P}}({F}_{c}^{2})\oplus {F}_{c}^{3}\right)\otimes {\rm{P}}({F}_{c}^{2})$$
(1)
$${F}_{b}={f}_{1\times 1}\left({\rm{P}}({F}_{c}^{3})\oplus {F}_{c}^{4}\right)\otimes {F}_{c}^{4}$$
(2)

where \({f}_{1\times 1}\left(\cdot \right)\) denotes the convolution operation with a kernel size of 1 × 1, ⊕ denotes element-wise addition, ⊗denotes matrix multiplication, \({\rm{P}}\left(\cdot \right)\) denotes the pooling operation. Afterwards, we obtain the output feature FPF by using \({F}_{{\rm{PF}}}={\rm{P}}({F}_{a})\oplus {f}_{1\times 1}\left({F}_{b}\right)\), and let them pass a 3 × 3 convolution to form the global mask map \({M}_{g}\in {{\mathbb{R}}}^{16\times 16\times 1}\).

Detail information generator (DIG)

The goal of the sub-network DIG is to generate detailed information of damaged murals based on the predicted global mask map Mg. DIG mainly consists of three cascaded bilateral guided fusion (BGF) modules (combined with residual connections) to achieve feature optimization from coarse to fine. This process can be formulated as \({M}_{{\rm{out}}}={f}_{1\times 1}\left({\rm{BGF}}(F,{M}_{{\rm{in}}})\oplus {M}_{{\rm{in}}}\right)\), where \({\rm{BGF}}\left(\cdot \right)\) denotes the BGF module. Under the guidance of Mg, through the iterative process of three BGF modules, the GIG can predict three refined feature maps \({M}_{{\rm{out1}}}\in {{\mathbb{R}}}^{16\times 16\times 1}\), \({M}_{{\rm{out2}}}\in {{\mathbb{R}}}^{32\times 32\times 1}\), and \({M}_{{\rm{out3}}}\in {{\mathbb{R}}}^{64\times 64\times 1}\). Mout3 is passed through the sigmoid activation function to generate a final damage prediction map. The details of the GIG network are shown in Fig. 1.

The BGF modules build the connections between damaged regions and boundary information. Figure 3 illustrates the architecture of the BGF module. We up-sample Min to obtain a feature map Mup with the same size as F, and then use Mup to process F in two branches. One branch is used to focus on the detailed features of the damaged boundary. The other branch is used to enhance the features of the damaged region.

Fig. 3
figure 3

The architecture of the bilateral guided fusion (BGF) module and the detail of the RA module.

Full size image

The global mask map Mg comes from the early layers of the network and can only capture the coarse locations of damaged regions without fine features. Feature maps generate blurry boundaries during damage detection. To solve this problem, we introduce the reverse attention (RA) module22. In the first branch to capture the boundary detail information. Figure 3 shows the details of the RA module. After the up-sampled feature map passes through a sigmoid function and a reverse operation, we can obtain a reverse attention map \({M}_{{\rm{RA}}}\in {{\mathbb{R}}}^{H\times W\times 1}\), which erases the already identified damaged region. The reverse attention map is defined as

$${M}_{{\rm{RA}}}=1-\sigma \left({M}_{{\rm{up}}}\right)$$
(3)

where \(\sigma \left(\cdot \right)\) denotes the sigmoid activation function. Then, we use the formula \({F}_{{\rm{RA}}}=F\otimes \varepsilon \left({M}_{{\rm{RA}}}\right)\) to calculate a reverse attention weight \({F}_{{\rm{RA}}}\in {{\mathbb{R}}}^{H\times W\times C}\), where \(\varepsilon \left(\cdot \right)\) denotes the expansion operation, which expands the single channel of the same channel MRA to the same channel as F. By calculating this weight, the network can focus on detecting previously ignored regions, thereby extracting boundary and fine features from complementary regions.

The RA module effectively improves the problem of boundary blurring, but it is prone to losing contextual information outside the boundary. Inspired by the receptive field block 23, we designed a grouped receptive field module (GRF) in the second branch to enhance the ability of region feature extraction. Figure 4 illustrates the architecture of the GRF. We split the input feature F along the channel into four groups by using \({F}_{\rm{s}}^{i}={\rm{Split}}\,{({f}_{1\,\times\,1})(F)}{({i}=1,2,3,4)}\) to reduce the computational complexity. \({\rm{Split}}\left(\cdot \right)\) denotes the spilt operation. In the four groups, we set the convolutions with different kernel sizes and dilation factors to expand the receptive field of the module. The features of neighboring groups are fused by element-wise addition. In this way, multi-scale information between different levels can complement each other to capture richer semantic information. Next, the GRF module calculates the output feature by using the following formula:

$${F}_{{\rm{GRF}}}=f\left({\rm{C}}\left({F}_{v}^{1},f\left({F}_{v}^{2}\right),f\left({F}_{v}^{3}\right),f\left({F}_{v}^{4}\right)\right)\oplus {F}^{{\prime} }\right)$$
(4)

where \({\rm{C}}\left(\cdot \right)\) denotes the concatenate operation. Through the two-branch processing, the model simultaneously extracts boundary detail features Mline and region enhancement features Fregion, obtaining a comprehensive representation of the damaged regions. The above operations can be expressed as

$$\left\{\begin{array}{l}{M}_{{\rm{line}}}=f\left({F}_{{\rm{RA}}}\right)\\ {F}_{{\rm{region}}}={f}_{3\times 3}\left({F}_{{\rm{GRF}}}\otimes {M}_{{\rm{up}}}\right)\end{array}\right.$$
(5)

where \(f\left(\cdot \right)\) is the convolution operation. Finally, we perform a matrix addition operation on Mregion and Fregion to obtain the refined feature FBGF. Through this gradual erasing and optimization strategy, the model can establish the relationship between regions and boundaries, and obtain accurate and refined damage detection results.

Fig. 4
figure 4

The architecture of the group receptive (GRF) field module.

Full size image

Loss function

In this paper, we employ deep supervision24 to compute the loss function. Our loss function is described as

$$L={L}_{{\rm{iou}}}^{\omega }+{L}_{{\rm{bce}}}^{\omega }$$
(6)

where \({L}_{{\rm{iou}}}^{\omega }\) and \({L}_{{\rm{bce}}}^{\omega }\) denote the weighted IoU loss25 and the weighted binary cross entropy (BCE)26 loss, respectively.

Given an input image I, we compute the loss function for the feature maps Mg, Mout1, Mout2, Mout3, and Mout4 generated at four different stages of the network. These feature maps are up-sampled to make their resolution the same as the size of the ground truth G. The overall loss function of the network can be expressed as

$${L}_{{\rm{total}}}={\lambda }_{i}\mathop{\sum }\limits_{i=1}^{3}L\left({M}_{{\rm{out}}i}^{{\rm{up}}},G\right)+{\lambda }_{{\rm {g}}}L\left({M}_{{\rm {g}}}^{{\rm{up}}},G\right)$$
(7)

where λi and λg denote the weights for different stages. In our experiment, λ1, λ2, and λ3 are set to 1, 0.3, and 0.2, respectively, λg is set to 0.1.

Experimental results and analysis

To verify the detection performance of the proposed model, we conduct experiments on real damaged ancient murals. Since mural damage detection is inherently an image segmentation problem, we compare the proposed model with four segmentation approaches: U-Net27, EGE-UNet28, M2SNet29, and PraNet30. For a fair comparison, all approaches are trained on the same mural image dataset. We evaluate the mural detection results using four objective metrics: Dice coefficient(Dice)31, Precision (Pre)32, Recall (Re)32, and Mean Absolute Error (MAE)33. We also perform ablation experiments for each module of the proposed model.

Training settings

The experiments are implemented using the PyTorch framework and run on the Windows platform. The hardware environment is configured with NVIDIA GeForce RTX 2080Ti GPU. In the training process, the size of each mural image is 512 × 512 pixels, and we use the Adam optimizer. The initial learning rate is set to 1.0 × 10−3. All experiments are conducted under consistent conditions.

Dataset

Due to the limitation of available mural data, we have to use mural data as much as possible for network training to ensure its performance. In this study, we build a dataset called DHMural, which contains 100 mural images from the Mogao Grottoes of Dunhuang (366–1368). This dataset contains ancient mural images from different dynasties and styles. To alleviate the over-fitting problem, we expand the training samples using data augmentation techniques34, including random rotation, mirror flipping, and crop. Through data augmentation, we expand the training samples to form a dataset of 5000 mural images. In the experiment, we divide the dataset into a training set and a validation set in a ratio of 8:2 (4000 images for training and 1000 images for validation). To test the performance of the network, we select 324 representative mural images that are independent of the training set.

To assess the generalization ability of the proposed model, we collect 345 mural images of ethnic minority in Yunnan, and create a corresponding data set called YNMural. This dataset includes murals images from the Zhilin Temple in Honghe and the Baisha Ancient Town in Lijiang. Note that the YNMural dataset have different painting styles and historical backgrounds with the DHMural murals.

The two mural datasets are manually annotated by mural disease researchers as ground truth images. Each image contains varying numbers, shapes, and sizes of damaged regions. All mural images are resized to 512 × 512 pixels.

Experiment on DHMural dataset

In this subsection, we test our model over the DHMural dataset. Figure 5 shows six images with varying degrees of damage and the detection results of all five comparative approaches. It can be seen that the 1st and 2nd images have some small damaged regions which are difficult to distinguish from the backgrounds. Our model can successfully detect these damaged regions. For the 3rd and 4th images with continuous large damage regions, our model not only finds the damaged regions but also can accurately detect the boundaries of the damaged regions. The 5th and 6th images have cluttered damaged regions. They are somewhat challenging tasks. It can be seen that the detection results of our model show more resemblance with the Ground Truth images than the other four comparative approaches.

Fig. 5
figure 5

Detection results of five approaches on the DHMural dataset.

Full size image

We also provide a quantitative comparison by use of Dice, Pre, Re, and MAE on the detection results of all test mural images. The larger the value of Dice, Pre and Re, the better the detection result. The smaller the value of MAE, the better the result. Table 1 shows the quantitative evaluation metrics of five approaches on the DHmural dataset. It can be seen that our model outperforms other four approaches in all four evaluation metrics.

Table 1 The evaluation metrics of five approaches on the DHMural dataset
Full size table

Experiment on YNMural dataset

In this test, we perform our model over the YNMural dataset. This dataset has different painting styles and historical backgrounds with the DHMural. Figure 6 gives five mural images and the damage detection results of five comparative approaches. The 1st, 2nd, and 3rd images have simple backgrounds and obvious damaged regions. Our model can not only detect large-scale damaged regions but also obtain clear and continuous boundaries. The 4th and 5th images have lots of cluttered damaged regions. In these difficult tasks, our model can find most of the damaged regions. Table 2 shows the objective evaluation metrics of five approaches on the YNMural dataset. It can be seen that our model achieved better evaluation metrics than the other two comparison approaches. In this test, our model shows good generalization ability when detecting various types of damaged murals.

Fig. 6
figure 6

Detection results of five approaches on the YNMural dataset.

Full size image
Table 2 The evaluation metrics of five approaches on the YNMural dataset
Full size table

Ablation study

In this subsection, we perform ablation experiments on the proposed core modules to verify their impact on the detection results. We take the Res2net residual blocks as the baseline network (referred to as Baseline). We respectively add the proposed global decoder (GD) and the bilateral guided fusion (BGF) module to the baseline and abbreviate these two operations as Baseline+GD and Baseline+BGF. We add the introduced reverse attention (RA) module to the baseline and abbreviate this operation as Baseline+RA.

Figure 7 gives five test mural images and a visual comparison of the ablation experiment results for four different models. It can be seen that the Baseline model performs poorly in this test. It fails to detect small damaged regions. The Baseline+GD model can suppress the interference of background information, reduce information loss, and improve the detection performance of damaged regions. The Baseline+RA model refines the boundaries of damaged regions and enhances attention to detail information. However, this model ignores contextual information outside the boundaries, resulting in inaccurate regional localization. On the basis of the RA module, the Baseline+BGF model incorporates the grouped receptive field (GRF) module to enhance the extraction of regional features. It can be seen that this model makes up for the shortcomings of the RA module, and can simultaneously capture local detail features and global regional features. By comparison, our complete model (MBRF) can detect more complete regions and generate continuous boundaries by integrating the advantages of each module. The model shows the best visual effects in this test.

Fig. 7
figure 7

Results of the ablation experiment.

Full size image

Table 3 shows the objective evaluation metrics of five test models. As compared with the Baseline network, the detection results for each proposed module show obvious improvement in Dice, Pre, and Re metrics. The MAE values of each module are lower (better) than the baseline network. This shows that each proposed module plays an important role in mural damage detection.

Table 3 The objective evaluation metrics of four test models
Full size table

Conclusion

In this study, we propose a multi-scale boundary and region feature fusion (MBRF) model for damage detection in ancient murals. This model is a two-stage network consisting of a global information generator (GIG) and a detail information generator (DIG). The GIG is designed to capture global information and thus can predict a global mask map of damaged mural regions. DIG can accurately detect completely damaged regions under the guidance of the global mask map predicted by GIG. Our model is tested on the DHMural and the YNMural datasets. Experimental results show that the model can accurately detect various types of damaged regions in ancient murals. Compared with the baseline network, the proposed MBRF model improves the Dice coefficient by 5.2 percentage points and 6.2 percentage points, respectively. The model also achieves better results in visual effects and objective evaluation metrics as compared to the other four existing approaches.

Because the styles of ancient murals in various parts of China are different, there are many kinds of diseases, and their characteristics are very different. This paper takes the collected murals in the Mogao Grottoes of Dunhuang and the ethnic minority murals in Yunnan as the research objects. Due to the limited amount of ancient mural data, although data augmentation techniques are used to make up for the lack of training data sets, these expanded data have information redundancy. This may affect the performance and generalization ability of the network model to a certain extent. Moreover, the lack of high-quality data limits the model’s ability to detect damaged murals of different styles, and the robustness of the model needs to be further improved. This research work provides a new idea and reference for intelligent detection of ancient mural disease areas in various places in China and all over the world. It is a new attempt and exploration to automatically detect ancient mural disease areas using deep learning methods. In future work, we will continue to explore the latest developments in deep neural networks and enhance the learning ability of the model. At the same time, we need to continuously expand the ancient mural dataset of different styles, and design a more adaptable mural damage detection model.