Introduction

Ancient murals, as irreplaceable cultural heritage, are often subjected to damage caused by natural and environmental factors such as humidity, temperature fluctuations, and human destruction. Cracks, discoloration, and missing portions frequently appear in ancient mural images, making their restoration a critical and challenging task1,2,3. Traditional restoration methods typically rely on manual techniques, which are not only labor-intensive but also prone to inconsistency due to varying skill levels and interpretations of the restorers4,5.

Traditional mural restoration methods can be divided into three main categories: local restoration, patch-based restoration, and techniques based on partial differential equations (PDEs). Local restoration is widely used to address minor damages, where missing or damaged areas are filled based on surrounding pixel values. These methods are computationally efficient and are suitable for small-scale problems6. However, their effectiveness diminishes with extensive damage and often leads to noticeable seams or texture inconsistencies 7.

Patch-based restoration methods (e.g., the Criminisi algorithm) identify matching blocks from undamaged regions to restore missing parts6. These methods perform well for simple textures but often struggle with complex patterns or large-scale damages, leading to blurry results when residual information is insufficient3,4. To address this, Cao et al. introduced adaptive sampling and local search strategies to improve patch selection and maintain structural consistency8.

Techniques based on partial differential equations (PDEs), including the total variation model, aim to preserve smoothness by minimizing intensity variations. These methods are effective and computationally simple for small-scale restorations4. Nevertheless, their tendency to oversmooth complex textures can result in detail loss, particularly in regions with intricate patterns7.

While traditional methods have limitations, they remain valuable for preserving the original artistic style and texture of murals. However, due to their labor-intensive nature and limited applicability to complex or large-scale damages, integrating these methods with digital technologies is necessary to achieve better results9. As a result, there is growing interest in developing automated restoration technologies that can address these challenges more consistently and effectively.

With the rapid development of artificial intelligence (AI), deep learning has become a powerful tool for solving image restoration problems. Deep learning has revolutionized image restoration by providing data-driven solutions capable of handling complex damages with higher accuracy and efficiency2,10. Early models based on convolutional neural networks (CNNs) utilized contextual information to address minor damages10,11,12,13. Despite their successes, CNN-based methods often struggle with irregular and large-scale damages, posing challenges in reconstructing structural details.

Generative adversarial networks (GANs), known for their ability to generate realistic details, have been widely applied to restoration tasks. Models such as those by Zhang et al. 14 and Yu et al. 15 showed significant improvements in restoring missing areas by refining textures and ensuring consistency. In the context of mural restoration, specialized GAN architectures, including skip connections and multi-scale feature optimization, have further enhanced performance2,16.

Transformer-based models have broken the boundaries of restoration by capturing long-range pixel dependencies. Zamir et al. 17 proposed a Transformer architecture optimized for high-resolution images, excelling in preserving fine details. Other methods, such as those by Alimanov and Islam18, combine transformers with cycle consistency techniques to improve restoration quality.

Diffusion models represent recent advancements, excelling in restoring both global structures and fine details. These models are based on Markov chain theory19,20, gradually adding and removing noise to reconstruct clean images. Conditional diffusion models, such as RainDiffusion21, introduce new frameworks for targeted restoration tasks, while DDNM22 enhances restoration without additional training by using identity equations. Innovations such as RDDM23 integrate degraded images into the diffusion process, providing strong guidance and improved results.

Despite their advantages, traditional diffusion models face limitations when generalized across multiple tasks. Approaches like DiffUIR24 address this by selectively guiding the refinement of task-specific distributions, enabling universal restoration across different scenarios. In mural restoration, diffusion models are particularly useful as they maintain both structural integrity and fine details, making them an essential tool for balancing artistic and technical requirements2,25.

Diffusion-based methods are particularly advantageous for mural restoration as they excel in tasks that require global structure restoration and local texture reconstruction. The ability of diffusion models to learn complex image distributions makes them highly suitable for various image restoration tasks, including denoising26, super-resolution27,28, and inpainting29. By formulating the image restoration problem as a stochastic process, these models provide a flexible framework to handle various forms of degradation, ranging from noise to missing image regions. This flexibility is further enhanced through the use of stochastic differential equations (SDE), which provide a continuous-time formulation of the diffusion process20,30.

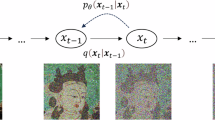
This study proposes a novel mural restoration framework based on diffusion, combining a heterogeneous UNet architecture with two custom-designed modules: the pixel space augmentation block (PSAB) and the dual channel attention block (DCAB). PSAB enhances global feature extraction by focusing on pixel-level augmentation, while DCAB refines local details through a channel attention mechanism. This combination enables the model to balance global structure restoration with fine texture recovery, making it highly effective for complex mural restoration tasks. The diffusion process in mural restoration can be regarded as the gradual degradation and subsequent recovery of the GroundTruth mural image, as illustrated in Fig. 1. The forward diffusion process q(zt∣zt−1) introduces noise into the clean image, simulating the types of degradation typically affecting murals over time. The reverse diffusion process pθ(zt−1∣zt, x), conditioned on the observed degraded mural image x, iteratively estimates and removes the injected noise, eventually restoring the original image. This iterative denoising process allows the model to reconstruct missing details while preserving global structures and fine textures, which are crucial for high-quality mural restoration. In addition, the proposed method is designed to handle large-scale damage and missing regions in mural images, outperforming traditional methods in both qualitative and quantitative evaluations6,16,31.

Fig. 1: The forward diffusion q(zt∣zt−1) (dashed arrows) progressively degrades the GroundTruth mural image z0.
figure 1

Guided by the latent space learned from the distribution of GroundTruth images, the conditional reverse diffusion pθ(zt−1∣zt, x) (solid arrows) iteratively estimates and removes the injected noise, restoring the degraded mural image x.

Full size image

The main contributions of this study are summarized as follows:

  • A novel diffusion-based mural restoration framework is proposed, integrating a heterogeneous UNet architecture to improve restoration quality across global and local feature domains.

  • Two key modules are designed and implemented: the pixel space augmentation block (PSAB) and the dual channel attention block (DCAB), which enhance the model’s ability to handle complex mural restoration tasks by focusing on pixel-level augmentation and channel attention, respectively.

  • The proposed method demonstrates state-of-the-art performance in mural restoration tasks, particularly excelling in handling large-scale damage and preserving fine details across multiple mural datasets.

Methods

Denoising diffusion probabilistic models for mural restoration

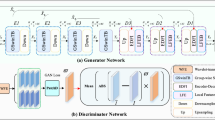
The proposed mural restoration model is based on the denoising diffusion probabilistic models (DDPM) framework and incorporates a heterogeneous UNet architecture. The overall structure of the network is depicted in Fig. 2. The model consists of a forward diffusion process where noise is gradually added to the clean mural images, followed by a reverse diffusion process that restores the clean image from noise. The forward process is responsible for corrupting the image with Gaussian noise over several steps, while the reverse process is learned using a neural network.

Fig. 2: The architecture of the proposed Network for mural restoration.
figure 2

The random mask information is added to the clear images to simulate the missing information that may occur in degraded input images in real-world scenarios. The input t in the ResBlock represents the encoded time step.

Full size image

The network architecture integrates two key components: the dual channel attention block (DCAB) and the pixel space augmentation block (PSAB). These modules help enhance both channel-wise and pixel-level features during the restoration process. The DCAB focuses on spatial and channel-wise feature extraction, while the PSAB ensures that fine-grained pixel details are preserved and enhanced. Together, these components enable the model to effectively restore damaged murals with high fidelity.

Next is the core DDPM framework that supports the diffusion and recovery process.

Denoising diffusion probabilistic models (DDPM)19 define a forward diffusion process q that gradually injects Gaussian noise into mural images z0 ~ q(z0) over T diffusion time steps in a Markovian manner. This noise injection follows a linear variance schedule β1 < ⋯ < βt, where βt ∈ (0, 1):

$$q({z}_{t}| {z}_{t-1})={\mathcal{N}}({z}_{t};\sqrt{1-{\beta }_{t}}{z}_{t-1},{\beta }_{t}I)$$
(1)
$$q({z}_{1:T}| {z}_{0})=\mathop{\prod }\limits_{t=1}^{T}q({z}_{t}| {z}_{t-1})$$
(2)

Directly sample any noisy mural image zt with αt = 1−βt and \({\bar{\alpha }}_{t}=\mathop{\prod }\nolimits_{i = 1}^{t}{\alpha }_{i}\):

$$q({z}_{t}| {z}_{0})={\mathcal{N}}({z}_{t};\sqrt{{\bar{\alpha }}_{t}}{z}_{0},(1-{\bar{\alpha }}_{t})I)$$
(3)
$${z}_{t}=\sqrt{{\bar{\alpha }}_{t}}{z}_{0}+\sqrt{1-{\bar{\alpha }}_{t}}{\epsilon }_{t}$$
(4)

where \({\epsilon }_{t} \sim {\mathcal{N}}(0,I)\). To make the model tractable, this study conditions the posterior distribution q(zt−1∣zt) on z0 using Bayes’ theorem:

$$q({z}_{t-1}| {z}_{t},{z}_{0})={\mathcal{N}}({z}_{t-1};{\tilde{\mu }}_{t}({z}_{t},t),{\tilde{\beta }}_{t}I)$$
(5)

where the mean and variance are:

$${\tilde{\mu }}_{t}({z}_{t},t)=\frac{1}{\sqrt{{\alpha }_{t}}}\left({z}_{t}-\frac{{\beta }_{t}}{\sqrt{1-{\bar{\alpha }}_{t}}}{\epsilon }_{t}\right),\quad {\tilde{\beta }}_{t}=\frac{1-{\bar{\alpha }}_{t-1}}{1-{\bar{\alpha }}_{t}}{\beta }_{t}$$
(6)

The reverse diffusion process p approximates the posterior distribution and restores the original mural images from noise. Starting from the prior \(p({z}_{{\rm {T}}})={\mathcal{N}}({z}_{{\rm {T}}};0,I)\), the neural network predicts:

$${p}_{\theta }({z}_{t-1}| {z}_{t})={\mathcal{N}}({z}_{t-1};{\mu }_{\theta }({z}_{t},t),{\Sigma }_{\theta }({z}_{t},t))$$
(7)
$${p}_{\theta }({z}_{0:T})=p({z}_{{T}})\mathop{\prod }\limits_{t=1}^{T}{p}_{\theta }({z}_{t-1}| {z}_{t})$$
(8)

The model is trained by optimizing the variational lower bound:

$$\begin{array}{l}{{\mathcal{L}}}_{{\rm{vlb}}}={{\mathbb{E}}}_{q}\left[{{\mathcal{D}}}_{{ {KL}}}(q({z}_{{T}}| {z}_{0})\parallel p({z}_{{T}}))-\log {p}_{\theta }({z}_{0}| {z}_{1})\right.\\\qquad\,\,\,\,\left.+\,\sum _{t > 1}{{\mathcal{D}}}_{{ {KL}}}(q({z}_{t-1}| {z}_{t},{z}_{0})\parallel {p}_{\theta }({z}_{t-1}| {z}_{t}))\right]\end{array}$$
(9)

Σθ(zt, t) in the reverse process is not learned but fixed, and the mean is parameterized as

$${\mu }_{\theta }({z}_{t},t)=\frac{1}{\sqrt{{\alpha }_{t}}}\left({z}_{t}-\frac{{\beta }_{t}}{\sqrt{1-{\bar{\alpha }}_{t}}}{\epsilon }_{\theta }({z}_{t},t)\right)$$
(10)

The training objective simplifies to

$${{\mathcal{L}}}_{{\rm{simple}}}={{\mathbb{E}}}_{t,{z}_{0},{\epsilon }_{t}}\left[\parallel {\epsilon }_{t}-{\epsilon }_{\theta }({z}_{t},t){\parallel }^{2}\right]$$
(11)

Conditional diffusion models for mural restoration

In the context of mural restoration, conditional diffusion models map the damaged mural images x to their clean counterparts z0. The forward diffusion process applies noise progressively to the clean mural images, following the same diffusion framework as in DDPM, while the reverse process is conditioned on the damaged image x.

The conditional reverse process is defined as

$${p}_{\theta }({z}_{0:T}| x)=p({z}_{T})\mathop{\prod }\limits_{t=1}^{T}{p}_{\theta }({z}_{t-1}| {z}_{t},x)$$
(12)
$${p}_{\theta }({z}_{t-1}| {z}_{t},x)={\mathcal{N}}({z}_{t-1};{\mu }_{\theta }({z}_{t},x,t),{\Sigma }_{\theta }({z}_{t},x,t))$$
(13)

Here, the noise prediction ϵθ(zt, x, t) is conditioned on the damaged mural image x, and the network is trained using a modified loss function:

$${{\mathcal{L}}}_{{\rm{cond}}}={{\mathbb{E}}}_{t,{z}_{0},{\epsilon }_{t}}\left[\parallel {\epsilon }_{t}-{\epsilon }_{\theta }({z}_{t},x,t){\parallel }^{2}\right]$$
(14)

By conditioning the reverse process on the input damaged mural image, the model can learn to gradually restore the original mural while accounting for the specific characteristics of the damage in x.

Heterogeneous UNet architecture

Similar to other image-to-image translation diffusion models32, this study conditions the input damaged image x in the reverse diffusion process by concatenating it with the noisy enhanced output zt. The model architecture employs a UNet network similar to Ooi et al. 33, with modifications to the attention layers based on. The proposed model integrates a heterogeneous UNet architecture specifically designed for mural restoration, consisting of both encoding and decoding stages, and incorporates specialized attention mechanisms to effectively handle the intricacies of mural features. Specifically, two key modules are introduced within the UNet: the dual channel attention block (DCAB) and the pixel space augmentation block (PSAB).

The pixel space augmentation block (PSAB) is designed to enhance pixel-level details by applying attention mechanisms in the spatial ___domain. Specifically, PSAB refines the input features through a sequence of convolutions and activations, emphasizing important spatial regions, as shown in the architecture in Fig. 3. The block performs a two-stage feature enhancement, where features are first compressed and then mapped back to the original dimensions through interpolation. This process generates an attention mask that highlights critical areas in the input. The final step applies this mask multiplicatively to the input, allowing the network to focus on the most relevant pixel-level details.

Fig. 3
figure 3

The architecture of the proposed pixel space augmentation block. The input feature x is processed through parallel convolutional paths. One path extracts contextual features, which are upsampled and passed through a sigmoid activation to generate an attention map m. The final output \({\tilde{x}}\) is obtained via element-wise multiplication of x and m, as denoted by the circled dot symbol.

Full size image

Mathematically, PSAB can be formulated as

$${c}_{1}={\text{Conv}}_{1}(x),\quad {c}_{2}={\text{Conv}}_{2}({c}_{1})$$
(15)
$${v}_{{\rm{max}}}={\text{MaxPool}}\,({c}_{2})$$
(16)
$${c}_{3}=\,{\text{ReLU}}\,\left({{\text{Conv}}}_{3}({v}_{{\rm{max}}})\right)$$
(17)

Here, x represents the input feature map, and c1 is the result of the first convolutional layer Conv1, which applies a 1 × 1 convolution to compress the input channels. The second convolution Conv2 reduces the spatial dimensions by using a stride of 2, and vmax is the result of applying max pooling over c2, which extracts the most prominent spatial features. The ReLU activation is applied to vmax after it passes through Conv3, further refining the spatial information.

$$m=\sigma \left({\text{Conv}}_{4}\left({c}_{3}+{\text{Conv}}_{f}\left({c}_{1}\right)\right)\right)$$
(18)
$$\tilde{x}=x\cdot m$$
(19)

Next, an interpolation step restores the spatial dimensions of c3 to match the input size. Concurrently, c1 undergoes an additional convolution through Convf, and the sum of c3 and this transformed c1 is processed by Conv4. The result is passed through a sigmoid activation σ, generating the attention mask m, which is then applied to the input feature map x to produce the enhanced feature map \(\tilde{x}=x\cdot m\). This mask allows the network to enhance important pixel-level details by amplifying or suppressing specific regions in the input.

The dual-channel attention block (DCAB) is designed to enhance both channel-wise and spatial feature representations by splitting the input feature map into two branches, as depicted in the architecture in Fig. 4. Each branch processes the input differently to capture complementary information. The first branch undergoes a series of convolutions and a channel attention mechanism, while the second branch is directly combined with the modulated first branch and then subjected to its own attention mechanism. The fusion of these two branches results in a more refined and focused feature representation, which is critical for restoring fine details in mural images.

Fig. 4
figure 4

The architecture of the proposed dual channel attention block. The input x is split into two branches, x1 and x2. The upper branch undergoes convolution and channel attention (CA) to generate modulation tensor A, which is used to modulate x1 via element-wise scaling. The lower branch applies a CA module to generate B and modulates x2 similarly. The modulated features are concatenated and passed through 1×1 convolutions to produce the output as \({\tilde{x}}\). “C” indicates concatenation.

Full size image

The input feature map x is split into two parts, x1 and x2. The first part, x1, undergoes a series of convolutional layers followed by a channel attention mechanism, which can be mathematically described as

$$A=\sigma \left(\,{\text{CA}}\_{\text{Conv1}}({\text{Conv}}\,({x}_{1}))\right)$$
(20)

In this formula, Conv(x1) represents a sequence of three convolutional layers applied to x1, with LeakyReLU activations after each convolution. The result of these convolutions is then passed through a channel attention mechanism, denoted as CA_Conv1, which generates the attention map A. The sigmoid function σ is applied to normalize the attention map, ensuring that the values are within the range [0, 1]. This attention map highlights the most important channels from x1, allowing the model to focus on the most relevant features.

After attention is applied, the modulated output A ⋅ x1 is concatenated with x2, which has not been altered at this stage:

$$P=\,{\text{concat}}\,({x}_{2},A\cdot {x}_{1})$$
(21)

Here, concat (x2, A ⋅ x1) refers to the concatenation of the attention-modulated x1 with the unmodified x2. This step preserves information from both channels and creates the intermediate feature map P, which combines the enhanced features from x1 and the unaltered features from x2.

Next, x2 undergoes its own channel attention mechanism to generate the attention map B:

$$B=\sigma \left(\,{\text{CA}}\_{\text{Conv2}}\,({x}_{2})\right)$$
(22)

In this formula, CA_Conv2(x2) represents the application of a second channel attention mechanism directly to x2. Similar to the previous step, the sigmoid function σ ensures that the values of the attention map B are normalized. This attention map modulates the values of x2, allowing the model to emphasize the most important features from this branch.

Finally, the modulated x2 (i.e., B ⋅ x2) is concatenated with the original (unmodified) x1, forming the intermediate feature map Q:

$$Q=\,{\text{concat}}\,({x}_{1},B\cdot {x}_{2})$$
(23)

In this step, the unaltered x1 is concatenated with the modulated x2 (i.e., B ⋅ x2), allowing both the raw and attention-enhanced features from x2 to be combined with x1. This creates the feature map Q, which captures complementary information from both branches.

The final output is obtained by fusing the feature maps P and Q, and the resulting output is denoted as \(\tilde{x}\):

$$\tilde{x}=\,{\text{Fuse}}\,(P,Q)$$
(24)

In this final formula, \(\tilde{x}\) represents the output of the DCAB module, where Fuse(P, Q) is a 1 × 1 convolution applied to the concatenated feature maps P and Q. This fusion step merges the information from both branches, generating the final output that incorporates the enhanced features from both channel-wise and spatial attention mechanisms.

Training objective

The complete training objective combines the simplified DDPM loss, the variational lower bound (VLB), and the conditional diffusion loss, as follows:

$${{\mathcal{L}}}_{\theta }={{\mathcal{L}}}_{{\rm{simple}}}+\lambda {{\mathcal{L}}}_{{\rm{vlb}}}+\gamma {{\mathcal{L}}}_{{\rm{cond}}}$$
(25)

Here, \({{\mathcal{L}}}_{{\rm{simple}}}\) minimizes the prediction error of the noise in the reverse diffusion process. The variational lower bound \({{\mathcal{L}}}_{{\rm{vlb}}}\) ensures that the reverse process approximates the true posterior, and \({{\mathcal{L}}}_{{\rm{cond}}}\) ensures the network is conditioned on the input damaged mural image during the restoration process. The balancing factors λ and γ control the relative contributions of these losses during training. In the experimental setup, the values of λ and γ are 0.1 and 0.01, respectively.

Results

This section presents the experimental setup, results, and comparative analysis of the diffusion-based mural restoration model proposed in this study. The performance of the proposed network is evaluated and compared against several state-of-the-art mural restoration methods. Furthermore, this study demonstrates the model’s capacity to handle various types of mural degradation and analyzes the contribution of key components such as the dual channel attention block (DCAB) and the pixel space augmentation block (PSAB).

Experimental setup

Dataset

Experiments are conducted on a dataset consisting of ancient mural images, specifically focusing on Tang Dynasty murals. The dataset includes 56,338 images, with 50,704 images designated for training and 5634 for testing. The training images are complete, while the test images contain synthetic damage, created by applying irregular masks to simulate real-world mural degradation such as cracks, discoloration, and missing parts.

Evaluation metrics

To evaluate the effectiveness of the restoration model, several standard image quality metrics are used, including:

  • Peak signal-to-noise ratio (PSNR): PSNR measures the ratio between the maximum possible power of a signal and the power of corrupting noise that affects the fidelity of the restored image. It is calculated in terms of the logarithmic difference between the original and restored image intensities. A higher PSNR indicates better restoration performance, as it implies less distortion relative to the original image.

  • Structural similarity index measure (SSIM): SSIM assesses image quality based on changes in structural information, taking into account luminance, contrast, and structural components. It evaluates the similarity between the restored and original images from a human visual perception perspective, focusing on how the structural details of the images are preserved during restoration. SSIM is often preferred in applications where maintaining perceptual quality is more important than pixel-to-pixel accuracy.

  • Learned perceptual image patch similarity (LPIPS): LPIPS is a perceptual metric designed to quantify the visual similarity between the restored and ground truth images. It uses a pre-trained neural network model to extract features from the images, capturing the high-level perceptual characteristics, such as textures and semantic content. LPIPS works by comparing image patches, simulating how human observers perceive differences between image regions. Unlike PSNR and SSIM, which focus on low-level pixel values or structural information, LPIPS is more subjective, as it reflects human perceptual judgments on the quality of images, making it particularly useful for assessing restoration tasks where texture and perceptual fidelity are crucial.

An irregular mask dataset12 is used to create damaged images. Four state-of-the-art methods are compared with the proposed method: AST34, Uformer35, MPRNet36, and MIRNetv237. These methods were chosen for comparison because they have performed well in many real-world applications and therefore permit an accurate assessment of the performance and advantages of the proposed method across a wide range of metrics and aspects.

Experimental conditions

The diffusion-based network is trained using the Adam38 optimizer with a learning rate of 0.0001. During training, the network underwent approximately 350,000 training iterations with a batch size of 16. These parameters were carefully fine-tuned to improve the overall learning process of the network, ensuring that the model captures intricate mural details while maintaining stability during training. Experiments were conducted on a single platform using an NVIDIA RTX 3090 GPU.

Experimental results

Figure 5 illustrates several mural restoration results obtained by the proposed method and the state-of-the-art techniques used for comparison. The diffusion-based model demonstrates superior performance in both preserving fine details and restoring the overall structure of degraded mural images.

Fig. 5: Comparative restoration results between the proposed method and other state-of-the-art models.
figure 5

a Origin images, b damaged images, c AST, d Uformer, e MPRNet, f MIRNetv2, g GAN-based, and h Proposed.

Full size image

The quantitative results of these comparisons are presented in Table 1. Among them, the upward arrow means that the larger the indicator, the better, and the downward arrow means that the smaller the indicator, the better. The proposed model outperforms several competitive models, achieving higher PSNR and SSIM scores while maintaining a low LPIPS value. This indicates that the model excels in both perceptual quality and structural consistency, making it more suitable for delicate tasks such as mural restoration.

Table 1 Quantitative comparison of PSNR, SSIM, and LPIPS values across different methods
Full size table

Comparison of experimental results

Quantitative comparison

Table 1 shows the performance of the proposed method compared to other state-of-the-art restoration techniques. The integration of PSAB and DCAB modules leads to a notable improvement in PSNR, with an increase of 23.43% compared to MPRNet and 20.72% compared to AST. In addition, the SSIM value shows a significant enhancement, with a 15.01% improvement over MPRNet and 10.47% over AST. These results highlight the effectiveness of the proposed approach in improving both perceptual quality and structural similarity for complex mural image restoration.

In addition, we added results for the Diffusion+UNet, Diffusion only, and UNet only models, and presented a detailed comparison in Table 1. The comparison shows that the performance is poor when using only UNet, with the PSNR being 8.4638 dB lower than that of the proposed model. The best performance is achieved with the Diffusion+UNet model, where the metrics show significant improvement compared to both the Diffusion only and UNet only models.

Qualitative comparison

Figure 5 illustrates the restoration results for various methods applied to several mural images. The comparison clearly shows that the proposed method consistently provides superior restoration quality across all samples, maintaining structural accuracy and minimizing artifacts.

In Sample 2, where delicate textures and faded colors are affected, AST (Fig. 5c) struggles to restore the intricate surface details, resulting in a flatter appearance, while MPRNet (Fig. 5e) overly smooths certain areas, losing important texture information. In contrast, the proposed method (Fig. 5h) preserves these fine details and maintains better color consistency, avoiding the tonal discrepancies seen in Uformer (Fig. 5d).

In Sample 4, the proposed method (Fig. 5h) excels in seamlessly blending the repaired areas with the original mural, especially in regions with complex patterns of damage. While MIRNetv2 (Fig. 5f) introduces noticeable artifacts and AST (Fig. 5c) produces blurry edges, the approach accurately restores these edges and retains the fine-grained textures that other methods fail to capture.

In Sample 6, where sharp edge recovery is crucial, both MPRNet (Fig. 5e) and Uformer (Fig. 5d) generate either jagged or overly smoothed edges, detracting from the mural’s original appearance. The proposed method (Fig. 5h), however, restores these edges with greater precision, and the overall tonal balance is more natural, avoiding the color inconsistencies seen in MIRNetv2 (Fig. 5f) and the noise artifacts present in AST (Fig. 5c).

A detailed analysis is conducted based on the zoomed-in comparison of Sample 1 (shown in Fig. 6), to better emphasize the restoration performance of the proposed method relative to other non-GAN-based approaches. The results of the GAN-based (Fig. 6g) method exhibit significant local information loss and are plagued by noise interference. The GAN-based (Fig. 6g) method uses the model from ref. 39.

Fig. 6: Zoomed-in comparison of Sample 1 with other methods.
figure 6

a Origin images, b damaged images, c AST, d Uformer, e MPRNet, f MIRNetv2, g GAN-based, and h proposed.

Full size image

In this enlarged view of Sample 1, AST (Fig. 6c) struggles with maintaining the sharpness and continuity of fine details, particularly in areas with intricate line structures. The restored regions appear overly smooth, lacking the texture and clarity of the original. Uformer (Fig. 6d), while slightly better at preserving some texture, introduces blurring and fails to accurately reconstruct high-frequency details, especially in regions with fine patterns. MPRNet (Fig. 6e), although capable of reducing noise, results in an overly smoothed appearance, particularly noticeable in areas requiring precise boundary transitions.

In contrast, the proposed method (Fig. 6h) demonstrates a superior ability to restore these intricate details with minimal loss of texture. The lines and patterns are much clearer, and the transitions between different areas of the mural are handled with greater precision. This zoomed-in analysis further emphasizes how the method excels in preserving the natural textures of the original mural while reducing artifacts that are evident in the other methods. MIRNetv2 (Fig. 6f), while decent in restoring color, introduces unwanted artifacts that detract from the overall visual fidelity, which the method effectively avoids.

This closer inspection reveals the advantages of the proposed approach in maintaining a more coherent and authentic restoration, preserving both the texture and structure of the original mural.

Overall, the qualitative comparison shows that the proposed method produces restorations that are visually consistent and faithful to the original murals, particularly in regions with complex and significant damage.

Ablation study

To further understand the contributions of the PSAB and DCAB modules in the proposed model, as well as the effects of different sampling steps, an extensive ablation study is conducted. The study systematically investigates the removal of key components and the impact of varying the sampling steps. Table 2 summarizes the quantitative results, while Figs. 7 and 9 provide visual comparisons across different configurations and sampling steps.

Table 2 Ablation study results showing the performance impact of removing PSAB and DCAB
Full size table
Fig. 7: Visual comparisons for the ablation study.
figure 7

a Origin images, b damaged images, c without DCAB, d without PSAB, e without DCAB&PSAB, and f proposed.

Full size image

The pixel space augmentation block (PSAB) plays a critical role in pixel-level feature extraction, allowing the model to capture intricate details essential for the restoration process. When PSAB is removed (as seen in Fig. 7d), there is a significant drop in both PSNR and SSIM, as pixel-level augmentation is essential for high-quality restoration. The quantitative results, where the PSNR drops from 35.7325 to 30.8117 dB, and SSIM decreases from 0.9285 to 0.8842, reflect the importance of PSAB in maintaining fine detail, especially in challenging mural restoration tasks. Fig. 8 provides a zoomed-in view, where the absence of PSAB leads to a noticeable loss of sharpness and fine detail, particularly in areas with intricate textures, such as the small cracks and edges in the mural. Without PSAB, the model struggles to accurately restore these subtle details, resulting in a visibly smoother and less authentic reconstruction.

Fig. 8: Zoomed-in visual comparisons for the ablation study.
figure 8

a Origin images, b damaged images, c without DCAB, d without PSAB, e without DCAB&PSAB, and f proposed.

Full size image

Similarly, the dual channel attention block (DCAB) is responsible for refining channel-wise dependencies, enhancing the model’s ability to capture detailed texture and features. Its removal (as shown in Fig. 7c) negatively impacts the model’s performance, with PSNR decreasing to 31.7809 dB and SSIM to 0.8517. Without DCAB, the model struggles to focus on relevant channel features, resulting in less effective noise reduction and texture restoration. The zoomed-in results in Fig. 8 show this clearly, with the image without DCAB exhibiting a less distinct separation between textures and a flattening of fine patterns. These differences are particularly evident in the regions where high-frequency textures are crucial, highlighting how DCAB helps maintain clarity and definition in the restored images.

When both PSAB and DCAB are removed (Fig. 7e), the restoration quality further deteriorates, with PSNR and SSIM values falling to 29.5371 dB and 0.8397, respectively. The zoomed-in images in Fig. 8 further illustrate the substantial loss of detail, particularly in intricate areas like cracks and textures that require both pixel-level enhancement and channel-wise attention. This combined absence results in a washed-out appearance with fewer preserved details, demonstrating how the two modules work synergistically to balance pixel-level and channel-level processing, which is crucial for optimal mural restoration.

In addition to the module-specific ablation, the impact of different sampling steps on restoration quality is examined, as depicted in Figs. 9 and 10. This part of the study explores the effect of varying the number of sampling steps (T) in the diffusion process. Starting from a minimal number of steps (T = 2), the model struggles to perform an accurate restoration (Fig. 9c). The zoomed-in results in Fig. 11 clearly demonstrate this, where regions of high texture complexity remain blurred and incomplete due to the insufficient number of steps. As the number of sampling steps increases (T = 5 in column (Fig. 9d), T = 10 in column (Fig. 9e), and T = in column (Fg. 9f)), the quality of restoration steadily improves. With T = 20, the details become sharper, and the restored textures exhibit higher fidelity, striking a good balance between restoration accuracy and computational efficiency.

Fig. 9: Sampling step comparison in the ablation study.
figure 9

a Origin images, b damaged images, c T = 2, d T = 5, e T = 10, f T = 20, and g T = 500.

Full size image
Fig. 10
figure 10

PSNR and SSIM over different sampling steps (T) in the diffusion process. Red solid lines indicate PSNR (Peak Signal-to-Noise Ratio), and green dashed lines indicate SSIM (Structural Similarity Index).

Full size image
Fig. 11: Zoomed-in sampling step comparison.
figure 11

a Origin images, b damaged images, c T = 2, d T = 5, e T = 10, f T = 20, and g T = 500.

Full size image

Increasing the steps further to T = 500 (Fig. 9g) results in additional improvements in fine details and overall image quality. However, as seen in Fig. 10, the improvements become more marginal compared to the computational cost, indicating that while higher sampling steps can yield enhanced results, the trade-off between performance and efficiency needs to be carefully considered. Fig. 11 shows that while the details at T = 500 are slightly better, particularly in areas with small cracks and high-frequency textures, the differences are less pronounced compared to T = 20. Thus, T = 20 offers a practical balance for most cases, achieving high-quality restoration with reasonable computational effort.

The quantitative and visual results both highlight the importance of selecting an appropriate number of sampling steps to achieve the best performance without unnecessary computational overhead. A smaller number of steps results in lower-quality restorations, while a very large number of steps leads to minimal improvements at the cost of additional computation.

In summary, the ablation study shows that both the PSAB and DCAB modules are crucial for high-quality mural restoration, and an optimal number of sampling steps is necessary for achieving a balance between performance and efficiency.

In addition, the impact of different hyperparameter choices on the model is validated in Tables 3 and 4. In Eq. (25), λ is the balancing coefficient of \({{\mathcal{L}}}_{{\rm{vlb}}}\), and γ is the balancing coefficient of \({{\mathcal{L}}}_{{\rm{cond}}}\). We analyze the effect of hyperparameters γ and λ on model performance by changing one while keeping the other fixed. The performance is best when λ is set to 0.1 and γ is set to 0.01.

Table 3 The PSNR and SSIM values for different values of λ
Full size table
Table 4 The PSNR and SSIM values for different values of γ
Full size table

Restoration of original damaged murals

The effectiveness of the proposed model is further demonstrated by applying it to real-world damaged murals. The restoration results are shown in Fig. 12, where each column represents different stages of the restoration process. Figure 12a shows the original damaged mural images, and Fig. 12b highlights the damaged areas in green for clarity. Figure 12c provides the realistic damage masks based on the actual deterioration observed in the murals, while Fig. 12d showcases the results restored using the proposed method.

Fig. 12: Restoration results for real-world mural damage.
figure 12

a Origin images, b damaged areas marked in green, c realistic damaged mask, and d proposed.

Full size image

The approach effectively preserves both the global structure and the fine details of the murals, offering a well-balanced restoration that maintains the integrity of the original artwork. Specifically, the method excels in reconstructing intricate patterns and textures, which are often lost in other restoration techniques. In areas with large-scale damage, the restoration process, although challenged, produces transitions between restored and original regions that are smooth and free from noticeable repair artifacts, ensuring that the restoration does not detract from the mural’s historical value.

The ability of the method to reconstruct damaged murals with minimal visual disturbances has significant implications for the preservation of cultural heritage. By enabling high-quality restoration of murals, this research contributes to the preservation and prolonged life of these invaluable cultural assets, helping to protect and showcase the history and artistry they represent for future generations.

To validate the model’s effectiveness in restoring real damaged murals, we chose to use the Dunhuang Murals dataset for restoration. As shown in Fig. 13, due to the age of the Dunhuang murals, the pigment layer has become raised, brittle, and even partially detached. After restoration using our model, the results show vibrant colors with high saturation.

Fig. 13: Restoration results on the Dunhuang dataset (real-world damaged images).
figure 13

Input image and restored image.

Full size image

Discussion

In this work, a novel diffusion-based model for ancient mural restoration is introduced, addressing the challenges of both global structural damage and intricate local detail reconstruction. The proposed model integrates a heterogeneous UNet architecture enhanced by two key components: the pixel space augmentation block (PSAB) and the dual channel attention block (DCAB). The PSAB focuses on enhancing pixel-level features, while the DCAB refines channel-wise information, enabling the network to efficiently restore both large-scale damages and fine-grained textures commonly seen in ancient murals.

Experimental results demonstrate the effectiveness of this approach, with the model outperforming several state-of-the-art mural restoration techniques in terms of PSNR, SSIM, and LPIPS metrics. The proposed network not only preserved structural integrity but also achieved superior perceptual quality by reducing visual artifacts and enhancing image consistency.

Key findings of this study include:

  • The integration of PSAB and DCAB significantly improved the model’s ability to restore both global mural structures and delicate textures, offering a balanced approach to large-scale and detailed image restoration.

  • The diffusion-based framework proved particularly effective in handling complex and irregular degradation patterns in mural images, demonstrating robustness and high performance across various evaluation metrics.

  • The model achieved superior visual quality in real-world mural restoration tasks, with seamless transitions between restored and original regions, preserving the cultural and historical integrity of the artwork.

Although the model shows promising results, there are areas for further improvement. In particular, handling large-scale continuous damage still presents some challenges, and future work could explore more advanced techniques for long-range attention or hierarchical feature extraction. Additionally, expanding the dataset to include murals from different cultural backgrounds and restoration conditions could enhance the model’s generalizability.

Overall, this study contributes a powerful new approach to the digital preservation and restoration of cultural heritage murals, leveraging the strengths of diffusion models to restore images with high fidelity and perceptual quality. This work marks a significant step forward in automating and improving the mural restoration process, aiding in the preservation of these invaluable cultural treasures for future generations.