Introduction

Due to the diffraction limit and the fast normal decay of evanescent waves, the spatial resolution of conventional optical microscopes is typically about one-half to one-quarter of the wavelength1,2. Scanning near-field optical microscope (SNOM) has been proven as one of the promising techniques3,4,5,6,7 to break this limit and provide super-resolution optical measurement for the identification of surface plasmon (SP), infrared spectroscopy emission, and so on8,9,10,11,12. It combines near-field optical imaging techniques with scanning probe microscopy. As such, the imaging resolution depends more on the probe radius than the working wavelength. According to the structure of the probe, SNOM is divided into aperture type (a-SNOM)13,14,15 and non-porous type (or scattering type, s-SNOM). s-SNOM has higher resolution and better stability because of a smaller tip radius and higher vibration frequency, making it more accurate to control the near-field tip-sample interactions. Theoretically, s-SNOM can obtain a measurement resolution equivalent to the size of the probe tip. However, there is a large amount of scattered background signal between the probe and the sample16. Therefore, there is an urgent demand to reduce the background signal for high-resolution measurement.

To obtain near-field signals with a high signal-to-noise ratio17, from the perspective of frequency modulation, scientists have proposed homodyne interference18, heterodyne interference19, and pseudo-heterodyne interference20 techniques. The homodyne interferometry method has to move the reference mirror precisely twice and then integrate the signal to obtain a near-field image. Heterodyne interferometry usually uses an acoustic-optic modulator to control the frequency of the interfering optical path, which is commonly used at visible wavelengths. Pseudo-heterodyne interferometry modulates the phase of the interference by applying a mirror with a given vibration frequency. These methods adopt different interferometric configurations to reduce the influence of ambient light on the measured signal, meaning that multiple optics and complex optical paths are required. This brings out the problems of stability and reproducibility. Therefore, the effective extraction of pure near-field signals is challenging.

It has been found that the near-field signal and imaging properties highly depend on the excitation wavelength21,22. In recent years, s-SNOM has been applied mainly in the near-infrared and terahertz bands to reveal the dielectric constant, SPs, and emission spectroscopy of different materials21,23,24. Besides, it has been pointed out that each order of the near-field mode has its own imaging characteristics and varies dramatically when measuring low-dimensional samples. Determining a proper order helps to get a better result23,25,26.

In this paper, the scattering model of incident light of different wavelengths on different sample surfaces is established through the finite-difference time-___domain method, and the ideal excitation wavelength is obtained in theory. The scattered near-field signals were excited and collected when the probe approached the sample, obtaining the scattering near-field signals at different distances and orders at the wavelength of 1550 nm. The change rule of the near-field scattering signals was analyzed based on experiments and simulations. The near-field optical imaging of two-dimensional nanomaterials was achieved, and the generation and transmission of SPs on graphene-silicon (Gr-Si) steps and carbon nanotubes were verified. These experimental results proved that this is a new method to observe the propagation of SPs. Near-field optical imaging of microparticles on the surface of gold films yielded a lateral resolution higher than that of atomic force microscopy (AFM).

Measurement principle

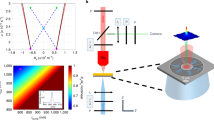
Figure 1a presents the schematic of the measurement principle. Due to the excitation of near-field light, collective charge oscillations are formed between the conductor and the dielectric, called SPs27,28. It includes various types involving electron density waves that propagate along the surface of the conductor (surface plasmon polaritons, SPPs) and electron oscillations on sub-wavelength nanoparticles (localized surface plasmon). Usually, this conductor-dielectric interface refers to a metal-air interface, especially the gold-air interface. However, graphene also has very high conductivity and a low refractive index, which creates good conditions for light-excited SPPs29,30. Based on this, the near-field images of Gr-Si steps, multi-walled carbon nanotubes (MWCNTs), and gold nanoparticles on gold film can be measured with near-field optical microscopy.

Fig. 1: Schematic of s-SNOM principle and comparison of higher-order signals (2nd–7th).
figure 1

a The schematic diagram of the measurement principle of s-SNOM. b The electric field strength from the 2nd to the 7th order. c Signal-to-noise ratio (SNR) values from the 2nd to the 7th order

Full size image

The intermittent contact mode (semi-contact mode) of AFM was used in the experiment, and the first-order vibration frequency of the probe (Nanoworld, ARROW-NCPt) in the vertical direction is Ω. For the light scattered from the spherical tip of the AFM probe, the measurable intensity \({E}_{sca}\) is usually described by an improved dipole model31. For the polarization of the light field under ambient conditions, the measurable intensity \({E}_{sca}\) is:

$${E}_{sca}\sim \left|\frac{{(1+{r}_{p})}^{2}{\alpha }_{t}}{1-\frac{{\alpha }_{t}\beta }{16\pi {(R+z)}^{3}}}\right|{E}_{inc}=\sigma {E}_{inc}$$
(1)

where \(z\) is the tip-sample spacing, \({r}_{p}\) is the Fresnel reflection coefficient of the sample, \({E}_{inc}\) is the electric field of the incident light, \(\beta =(\varepsilon -1)/(\varepsilon +1)\) is the response function of the sample with a permittivity of\(\varepsilon\), and \({\alpha }_{t}\approx 4\pi {R}^{3}({\varepsilon }_{r}-1)/({\varepsilon }_{r}+2)\) is the tip polarizability, which is related to the tip radius \(R\) and tip permittivity \({\varepsilon }_{t}\). Use \(\sigma\) to characterize the relationship between \({E}_{sca}\) and \({E}_{inc}\), which is called the probe-sample interaction. The distance between the probe and the sample changes sinusoidally, so the scattered near-field light is sinusoidally modulated, which can be written as \(\sigma =s{e}^{i\varphi }\), where \(s\) is the vibration amplitude and \(\varphi =\varOmega t\) is the phase. \(\sigma\) can be rewritten as:

$$\sigma ={\sigma }_{0}+{\sigma }_{1}\,\cos (\varOmega t)+{\sigma }_{2}\,\cos (2\varOmega t)+{\sigma }_{3}\,\cos (3\varOmega t)+\mathrm{..}.$$
(2)

where \({\sigma }_{n}\) is the amplitude of the nth-order component. The amplitude \({E}_{sca}^{n}\) of the nth-order near-field signal \({S}_{n}={\sigma }_{n}\,\cos (n\varOmega t)\) can be obtained through demodulation with a lock-in amplifier (Zurich, MFLI-5MHz). Since the near-field signal and the background signal interfere in free space, the demodulated near-field signal contains an undesirable background signal. s-SNOM near-field information requires at least high-order information above \({S}_{2}\). In this paper, the near-field signals of \({S}_{2}-{S}_{7}\) were obtained by improving the excitation and collection optical paths. The relationship between the amplitude \({E}_{sca}^{n}\) and the probe-sample distance \(z\) during the needle-down process is shown in Fig. 1b. Since the real near-field signal only occurs at the contact point between the needle tip and the sample, as z increases, the smaller the amplitude \({E}_{sca}^{n}\) indicates that the demodulated signal contains more near-field signals. At the same time, \({\eta }_{n}={E}_{z}/{E}_{0}(n=2,3,\cdots 7)\) is defined to represent the ratio of the near-field signal to the background signal. \({E}_{z}\) and \({E}_{0}\) are the amplitudes of \({S}_{n}\) when the probe-sample distance is z and 0, respectively. The smaller \({\eta }_{n}\) means the smaller the background signal of \({S}_{n}\) at the distance \(z\). Figure 1c shows the curve of\(E\) changing with \(z\). The previous experiments have shown no near-field interaction between the probe and the sample when \(z > 100nm\).

As can be seen from Fig. 1b, c, the \(\eta\) of \({S}_{2}\), \({S}_{3}\) and \({S}_{4}\) do not show a monotonically decreasing trend and take higher values when z < 50 nm; when 50 nm ≤ z < 1000 nm, \(\eta\) of \({S}_{3}\) and \({S}_{4}\) are relatively smaller, and \(\eta\) of \({S}_{2}\) is close to 0.5. This shows that it has a high background signal and cannot perform near-field imaging; \({S}_{3}\) and \({S}_{4}\) have a small amount of background signal, but the contrast of near-field imaging is low. The subtle signals will be overwhelmed by noise, making high-resolution measurements impossible. \({S}_{5}\), \({S}_{6}\) and \({S}_{7}\) have good performance. When z < 40 nm, \(\eta\) decreases monotonically; when z ≥ 40 nm, \(\eta\) is less than 0.1, which meets the requirements of high-resolution measurement. However, since the initial amplitude \(\eta\) of \({S}_{6}\) and \({S}_{7}\) is low, it can be seen that \(\eta\) still fluctuates after \(z\) exceeds 50 nm, which is affected by system noise, while \(\eta\) of S5 is more stable because \({E}_{0}\) is higher. This relationship illustrates the sharp attenuation of the measurable intensity when the distance between the tip and the sample becomes larger, and the advantages of higher-order near-field optical signals (especially the \({S}_{5}\) order) in high-resolution near-field optical imaging. This function predicts the sharp attenuation of the measurable intensity \({E}_{sca}\) when the distance between the tip and the sample becomes larger and then characterizes the correlation between the scattering intensity from the sample and light wavelength. Therefore, the appropriate incident light wavelength can be determined by the simulation of the scattering intensity of carbon nanotubes and graphene.

Equation (1) indicates that the measurable intensity of scattering depends highly on the properties of the material and the excitation wavelength when the tip-sample distance is constant. Therefore, we simulated the situation where the excitation light and the probe are 2 nm above the Gr/Si and carbon nanotubes(diameter 10 nm)/Si junction with wavelengths of 660 nm, 980 nm, and 1550 nm, respectively. The dielectric constants of graphene and carbon nanotubes at different wavelengths of incident light were set according to the results of previous studies32,33.

Simulations were performed using time-___domain finite element difference (FDTD) solutions. As shown in Fig. 2a, c, when excited with 1550 nm, the intensity of the scattered light on graphene (left) is stronger than that of Si (right). Besides, the intensity change at the Gr-Si step is sharp, showing a significant edge enhancement effect.

Fig. 2: FDTD simulations of near-field excitation in silicon-graphene step structures and silicon-supported carbon nanotubes.
figure 2

The near-field intensity distribution of a Gr-Si step and b carbon nanotube. c The electric field intensity of the yellow line in (a). d The electric field intensity of the yellow line in (b)

Full size image

When changing the wavelength, we can see the highest scattering intensity at 1550 nm, while it’s close to zero at 660 nm since no SP is excited.

As shown in Fig. 2b, d, carbon nanotube shows similar behavior while the intensity is a bit higher at 660 nm. These phenomena result from the high absorption of graphene and carbon nanotubes in the near-infrared band. Therefore, the peak at 1550 nm has the highest intensity. A higher absorption rate means stronger coupling between free electrons and photons, which leads to strong SP resonance34,35.

Experiments and analysis

In this experiment, we used the NTEGRAII commercial AFM system of NT-MDT, and the s-SNOM function realized by building an external optical path. The incident light source is a Thorlabs SC4500 1.3–4.5 μm fiber laser, and the detector is Thorlabs PDA20CS2. In previous studies36,37, parameters have been provided for optimizing near-field scattered signals. Generally speaking, the optimization effect of vibration frequency on high-order near-field signals is not obvious, but a higher vibration frequency can improve the signal-to-noise ratio of collecting high-order near-field scattered signals, so a probe with a higher resonance frequency (Nanoworld NCPt) is selected.

Near-field optical imaging of Gr-Si step

Compared to traditional metal materials such as gold and silver, a new two-dimensional material, graphene, has the characteristics of single atomic layer thickness, Dirac electronic properties, and high carrier mobility, showing great promise in optoelectronics38,39,40,41,42. The plasmon excited has the advantages of a higher wavelength compression ratio and electrostatic tunability. Since the first experimental observations in 2011, graphene plasmons have shown great potential for applications in photodetectors43,44,45, nanoscale waveguides46,47,48, electrically tunable lasers49, and molecular sensors50, etc51.

Figure 3a shows the 3rd-order near-field image of a Gr-Si step, with an inset of an AFM image. Both images reveal the boundary, but the AFM image presents only the topography, while the near-field image displays a clear difference in the scattering intensity on both sides of the interface, providing information on the different material properties. Fig. 3b presents the 5th-order near-field image in the same region. Compared with Fig. 3a, the low-order image blurs, and the grain and edges can not be nicely resolved. In contrast, the high-order image provides a detailed profile at the interface and reveals the standing waves formed when the SPPs propagate at the edge of graphene. Figure 3d shows the scattering intensity of the white dashed line marked in Fig. 3b. A steep intensity increase happens at the transition boundary from Si to Gr, indicating the excitation and propagation of the Gr SPs at the edge of the step. Moreover, the excitation intensity and propagation efficiency of the SPs at the edge are significantly higher than when graphene is entirely in contact with the flat Si substrate. This is because the edge region behaves like a suspended membrane, consistent with previous research results52. Figure 3c presents the intensity difference diagram obtained by taking the difference between the symmetrical positions in the simulation. The Boltzmann fitting curve is consistent with the measured results in Fig. 3d. Based on these results, as a product of graphene curling, it can be predicted that carbon nanotubes have better plasma propagation capabilities43.

Fig. 3: AFM and SNOM characterization of silicon-graphene step structures.
figure 3

a The 3rd-order (low-order) near-field optical image of a Graphene-Si step. Inset: the corresponding AFM image. b The 5th-order (high-order) near-field optical image of the Graphene-Si step. c Difference of scattering intensity between graphene and Si. d Scattered signal intensity values at the white dotted line. The curves of the measured image and the simulated image are well-matched

Full size image

High-order near-field optical imaging of carbon nanotubes

Previous research has been carried out by adhering carbon nanotubes on the tip of the AFM to increase the aspect ratio of the probe to achieve higher resolution and large aspect-ratio measurement capability53,54,55. Due to the excellent optical and electrical properties of carbon nanotubes, they exhibit light-guiding properties in the near-infrared band; it is foreseeable that carbon nanotubes will be adhering to near-field optical microprobes to improve the resolution of near-field optical microscopy and the ability to measure large aspect-ratio structures.

We use MWCNT dispersion as the base liquid to synthesize the single MWCNT. Since carbon nanotubes exist as clusters in the solution, the concentration of the prepared solution is extremely low, which makes it possible to obtain the single MWCNT by multiple ultrasonic dispersions and centrifugations. The solution was then dropped onto a Si wafer and evaporated to dryness.

Figure 4a presents the AFM topography of the tube. Figure 4b presents the near-field optical measurement of the single MWCNT, which was performed at a wavelength of 1550 nm using a high-order signal. The profile of the white dotted line is shown in Fig. 4d. The red frame of Fig. 4d shows that the scattered light intensity in the middle of the MWCNTs is stronger than on both sides, which looks different from the simulation results in Fig. 4c. The reason is that SNOM imaging is a scanning process, and the signal is collected at every point during the process, which leads to a sharp decline and enhancement in Fig. 4d. This is consistent with the results of the red dotted frame in Fig. 4c, and it proves that the near-field enhancement is caused by SPs produced by carbon nanotubes when excited with 1550 nm light. Therefore, the carbon nanotubes were identified. A fully recognizable “bulge” in the middle indicates local enhancement.

Fig. 4: AFM and SNOM characterization of silicon-supported carbon nanotube.
figure 4

a The AFM image of CNT. b The 5th-order near-field optical image of CNT. c Simulated scattering intensity of carbon Nanotubes. d The scattered light intensity distribution on white dotted lines

Full size image

Measurement and comparison of near-field optical imaging of gold film surface particles

In the previous research, the plasmonic enhancement of gold in the near-infrared band was predicted theoretically56. Here, as shown in Fig. 5b, we take the model of two-coupled gold nanoparticles on the surface of the gold film to study the plasmonic effect, and the diameter of gold nanoparticles set in the simulation is 60 nanometers with a 10 nm gap. The dielectric constant value of gold nanoparticles was used by Magnozzi et al.57 as the dielectric constant value used in this simulation. Figure 5c presents the simulated field distribution of this structure under an excitation wavelength of 1550 nm. An unusually strong surface plasma enhancement can be observed between the two coupled gold nanoparticles. This helps to improve the resolution of the near-field imaging. s-SNOM can simultaneously acquire AFM topography and near-field optical images. Thus, we measured the particles on the surface of the gold film using both AFM and 5th-order near-field imaging techniques, as presented in Fig. 5d, e. We compare two adjacent areas at the same positions in the two measurements, highlighted by the dotted lines 1 and 2. The topography curve corresponding to the dotted line 1 is shown in Fig. 5f, while that of the dotted line 2 is shown in Fig. 5g. It can be seen that the near-field light intensity measured at the gap between the two gold particles is higher than that of the gold particles, which proves the enhancement of the near-field intensity at the wavelength of 1550 nm. This is the evidence of the excitation of the SP between the gold particles. The resolution is obtained by measuring the resolvable interval between two adjacent gold particles. In order to obtain a comparable full width at half maxima value, in Fig. 5f, g, the blue dotted line at the common half-height of the gap measured in the near-field optical image and the AFM topography image is taken as the measurement reference. Other half-height positions (red and black dotted lines) are on the two lines, respectively. The AFM result of the particle gap in line 1 is 21.7 nm, while the near-field measurement value is 10.7 nm. For line 2, they are 19.6 nm and 9.6 nm, respectively. The difference is because the accuracy of near-field measurement does not completely depend on the probe tip topography. Therefore, the measurement error caused by the convolution of the tip and the sample can be effectively reduced. The lateral resolution is much better than the AFM’s in the circumstances.

Fig. 5: Characterization, simulation setup and results of gold nanoparticles on gold films.
figure 5

a SEM image of gold nanoparticles on gold surface sample. b A model developed to simulate the plasma enhancement effect between two gold nanoparticles with a spacing of 10 nm on a gold film. c Field distribution of the excited gold particles on the gold film surface. d The AFM image of particles on the gold film surface. e The 5th-order near-field optical microscope image of particles on the gold film surface. f The AFM and near-field optical topography in line 1. g The AFM and near-field optical topography in line 2. It can be seen that the AFM image is relatively blurry, while the SNOM image is quite sharp

Full size image

Conclusions

We studied the near-field light scattering signals of different orders in the near-infrared band. The 5th-order signal shows good signal-to-noise ratio and stability, which is beneficial for high-order near-field optical imaging. The detection of SP excitation and propagation on the surface using s-SNOM is realized, which expands the application of s-SNOM in near-field imaging. Measurements of graphene-Si nano-step and carbon nanotube showed that under excitation of 1550 nm, plasmon excitation and propagation occurred at both the edges of graphene and the surface of carbon nanotubes. In addition, the measurement results of the method on gold films showed that this method can achieve a higher lateral resolution than the AFM. This paper offers an advanced approach for high-resolution measurement of low-dimensional materials with s-SNOM, owning great potential for sensitive nanoscale imaging.