Introduction

In recent years, the demand for highly sensitive and accurate sensors has surged, particularly in the fields of Micro-Electro-Mechanical Systems (MEMS) technology. These advancements are driven by the growing need for precise measurements in various applications, such as Automotive Safety and Navigation1,2, environmental monitoring3,4, biomedical diagnostics5, and industrial automation6,7. MEMS sensors offer advantages like miniaturization, low power consumption, and the ability to integrate multiple functions on a single chip, making them highly attractive for modern sensing applications. As the complexity of these applications increases, so does the requirement for sensors capable of detecting multiple signals simultaneously.

Mode-localized sensors have emerged as a popular solution for signal detection due to their high sensitivity8. Mode localization9,10,11,12 is an extension of Anderson localization13 in structure dynamics and is usually manifested in the periodic structure of weakly coupled resonators (WCRs). When a small disorder is applied, the mode shape of the WCRs will be drastically changed and the vibration energy will mostly be confined to some specific modes of the WCRs. Various MEMS sensors based on the mode localization phenomenon have been widely used in various applications such as accelerometers14,15,16,17,18,19, mass sensors8,20, electrometers21,22,23,24, electric field strength sensors25, electric current sensors26 and voltage sensor27.

However, conventional MEMS sensors, particularly those based on coupled resonators, face significant limitations when it comes to simultaneously measuring multiple signals. When multiple signals are input, they cause shifts in the sensor’s resonant frequencies, leading to significant cross-sensitivity due to mutual interference between the signals. This interference not only reduces measurement sensitivity and accuracy but also hampers the overall performance in practical applications. Therefore, achieving synchronous detection of different signals while maintaining the sensitivity of mode-localized sensors remains a key challenge in this field.

To tackle this challenge, this paper introduces a novel approach using weakly coupled resonators with a constant-drive technique. By stabilizing the resonator’s driving frequency, the method effectively reduces the cross-sensitivity, enabling precise synchronous detection of two distinct signals. This paper details the design, experimental validation, and performance analysis of the method, demonstrating its potential to improve mode-localized sensor functionality in multi-signal scenarios.

Results and discussion

Structure of the dual signals sensor

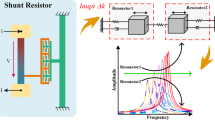
The schematic diagram of the dual signals sensor (DSS) structure is shown in Fig. 1a. The structure consists of WCRs, sense electrodes, drive electrodes, tune electrodes, and anchors. The core component is the WCRs, which comprises three individual resonators with equal stiffness (k1 = k2 = k3 = k), connected by two couplers. The coupling stiffness between the resonators is significantly lower than the stiffness of the resonators themselves (kc < <k), allowing for weak coupling.

Fig. 1: Structure and equivalent model of DSS.
figure 1

a Structure diagram of DSS; b Mass–spring model of DSS

Full size image

The three resonators are arranged horizontally and connected in series via the two couplers, with all resonators oscillating exclusively in the vertical direction. They are fixed at the anchors and activated by the drive electrodes. An AC signal is applied to the resonators through the drive electrodes, producing the output signal, which is detected by the sense electrodes.

The tune electrode adjusts the resonator’s stiffness by applying voltage, compensating for manufacturing variations to ensure same stiffness across all three resonators. In this paper, the two signals are input by applying voltage to the tune electrodes of resonator 1 and resonator 3. Both perturbations cause significant changes in the amplitude ratio between resonators 1, 2, and 3. Finally, the input voltage is determined by measuring the amplitude ratios AR1 (A2/A1) and AR2 (A2/A3), respectively. Table 1 presents the design parameters of the DSS.

Table 1 Parameters of the DSS
Full size table

Transduction mechanism

Figure 1b illustrates the equivalent mass-spring model of the DSS under ideal conditions (without damping). The stiffness and mass of the three resonators are identical (k1 = k2 = k3 = k, m1 = m2 = m3 = m). Two signals introduce stiffness disturbances to resonator 1 and resonator 3, respectively. The dynamic equation for the DSS is given in Eq. (1).

Figure 1b shows the equivalent mass and spring model of the DSS in ideal conditions (damping not considered). The stiffness and mass of three resonators are identical. Two signals cause stiffness perturbations to resonator 1 and resonator 3 (Δk1, Δk2), respectively. The dynamic equation for the DSS is as Eq. (1).

$$\left[\begin{array}{ccc}m & 0 & 0\\ 0 & m & 0\\ 0 & 0 & m\end{array}\right]\left[\begin{array}{c}{\ddot{x}}_{1}\\ {\ddot{x}}_{2}\\ {\ddot{x}}_{3}\end{array}\right]+\left[\begin{array}{ccc}k+{k}_{c}+\varDelta {k}_{1} & -{k}_{c} & 0\\ -{k}_{c} & k+2{k}_{c} & -{k}_{c}\\ 0 & -{k}_{c} & k+{k}_{c}+\varDelta {k}_{2}\end{array}\right]\left[\begin{array}{c}{x}_{1}\\ {x}_{2}\\ {x}_{3}\end{array}\right]=\left[\begin{array}{c}0\\ 0\\ 0\end{array}\right]$$
(1)
$$\left[\begin{array}{ccc}-m{\omega }^{2}+k+{k}_{c}+\varDelta {k}_{1} & -{k}_{c} & 0\\ -{k}_{c} & -m{\omega }^{2}+k+2{k}_{c} & -{k}_{c}\\ 0 & -{k}_{c} & -m{\omega }^{2}+k+{k}_{c}+\varDelta {k}_{2}\end{array}\right]\left[\begin{array}{c}{A}_{1}\\ {A}_{2}\\ {A}_{3}\end{array}\right]=0$$
(2)

The resonator undergoes simple harmonic motion, and by substituting the mode equation x=Asin(ωt + φ) into Eq. (1), a linear system of equations for the amplitude, as shown in Eq. (2), can be derived.

The two disturbances, Δk1 and Δk2, correspond to the amplitude ratio outputs as follows:

$$\left\{\begin{array}{c}A{R}_{1}=\frac{{A}_{2}}{{A}_{1}}=\frac{-m{\omega }^{2}+k+{k}_{c}+\varDelta {k}_{1}}{{k}_{c}}\\ A{R}_{2}=\frac{{A}_{2}}{{A}_{3}}=\frac{-m{\omega }^{2}+k+{k}_{c}+\varDelta {k}_{2}}{{k}_{c}}\end{array}\right.$$
(3)

The amplitude ratio AR1 between resonator 2 and resonator 1, and the amplitude ratio AR2 between resonator 2 and resonator 3, correspond to the two input disturbances Δk1 and Δk2, respectively. From Eq. (3), it is known that AR1 is related to and the resonant frequency. The input of k2 causes changes in omega, which in turn leads to changes in the output AR1. Similarly, k1 affects AR2 in the same way. This is the fundamental reason for the mutual interference between the two signals. The resonant frequency can be determined by setting the determinant of the coefficient matrix in Eq. (2) to zero. The result is as Eq. (4).

$$\begin{array}{c}{(-m{\omega }^{2}+k+{k}_{c})}^{3}+(\varDelta {k}_{1}+\varDelta {k}_{2}+{k}_{c}){(-m{\omega }^{2}+k+{k}_{c})}^{2}\\ +(\begin{array}{c}\varDelta {k}_{1}\varDelta {k}_{2}+\varDelta {k}_{1}{k}_{c}+\varDelta {k}_{2}{k}_{c}-2{k}_{c}^{2}\end{array})(-m{\omega }^{2}+k+{k}_{c})\\ +\varDelta {k}_{1}\varDelta {k}_{2}{k}_{c}-{k}_{c}^{2}(\varDelta {k}_{1}+\varDelta {k}_{2})=0\end{array}$$
(4)

The amplitude ratio AR1 between resonator 2 and resonator1, and the amplitude ratio AR2 between resonator 2 and resonator 3, correspond to the two input disturbances Δk1 and Δk2, respectively. As shown in Eq. (3), AR1 is related to the resonant frequency. The input of Δk2 causes a change in ω, which in turn alters the output AR1. Similarly, Δk1 affects AR2 in the same way. This mutual interference between the two signals is the fundamental reason for their interaction. The resonant frequency can be determined by setting the determinant of the coefficient matrix in Eq. (2) to zero, resulting in the following expression (4).

From Eq. (4), the first resonant frequency of the WCRs can be determined. Since the DSS structure is theoretically fully symmetrical, this paper focuses solely on analyzing the effects of Δk1 and Δk2 on the output of AR1. By Eq. (3) and Eq. (4), the relationship between k1 and k2 with respect to AR1 can be derived. As shown in Fig. 2a, AR1 has a linear relationship with Δk1, but decreases as Δk2 increases. The larger the AR1, the greater the influence of k2 on AR1. Therefore, it is not feasible to simultaneously detect two signals by mode-localized phenomenon.

Fig. 2: Theoretical analysis of synchronous detection of dual signals.
figure 2

a The variation trend of AR1 with Δk1 and Δk2; b The variation trend of AR2 with Δk1 and Δk2; c AR1 varies with Δk1 and Δk2 (0–0.5 N/m)

Full size image

From Eq. (3), it can be concluded that the mutual interference between the two signals is due to changes in the resonant frequency caused by the signals. To address this, this paper proposes a constant-drive mode for weakly coupled resonators, where the resonators are driven at their natural resonant frequencies without altering the driving frequency. By substituting Δk1 = 0 and Δk2 = 0 into Eq. (4), the natural resonant frequencies of the undisturbed resonators can be obtained, as shown in Eq. (6).

$$(-m{\omega }^{2}+k+{k}_{c})(-m{\omega }^{2}+k)(-m{\omega }^{2}+3{k}_{c})=0$$
(5)
$$\left\{\begin{array}{lll}{\omega }_{1}=\sqrt{\frac{k}{m}}\\ {\omega }_{2}=\sqrt{\frac{k+{k}_{c}}{m}}\\ {\omega }_{3}=\sqrt{\frac{k+3{k}_{c}}{m}}\end{array}\right.$$
(6)

By substituting Eq. (6) into Eq. (3), the relationship between AR1 and Δk1 at three different frequencies is derived, as shown in Eq. (7). In constant-drive mode, the sensitivity of Δk1 to AR1 is 1/kc, which is the same as in the mode localization effect, demonstrating that this method does not suffer from a loss of sensitivity. The relationship between Δk1 and Δk2 for AR1 in constant-drive mode is shown in Fig. 2b. Therefore, the sensitivity of AR1 to Δk2 is zero, indicating that there is no interference between the detection of Δk1 and Δk2.

$$\left\{\begin{array}{ll}A{R}_{11}=\frac{{A}_{2}}{{A}_{1}}=\frac{{k}_{c}+\varDelta {k}_{1}}{{k}_{c}}\\ A{R}_{12}=\frac{{A}_{2}}{{A}_{1}}=\frac{\varDelta {k}_{1}}{{k}_{c}}\\ A{R}_{13}=\frac{{A}_{2}}{{A}_{1}}=\frac{-2{k}_{c}+\varDelta {k}_{1}}{{k}_{c}}\end{array}\right.$$
(7)

To more clearly illustrate the differences between the two methods, this paper quantitatively analyzes the detection interference of the two signals over a range of 0–0.5 N/m, with a step of 0.05 N/m. In this analysis, the spring constant k is 290 N/m, the mass m is 1.4 × 10−8 kg, and the coupling strength kc is 0.1 N/m.

As shown in Fig. 2c, the sensitivity of the constant-drive mode is 10 N/m and remains constant with Δk2 increases, with no deviation in AR1 caused by Δk2. Therefore, there is not cross-sensitivity for constant-drive mode. In contrast, the sensitivity of the mode-localized method is 9.46 N/m when k2 = 0, but sensitivity decreases with k2 increases. The maximum deviation in AR2 caused by Δk1 is 1.22, resulting in a sensitivity of AR2 to Δk1 being 2.44 N/m, which corresponds to a cross-sensitivity of 25.8%.

The constant-drive mode sensitivity is higher than that of the mode-localized method, which is due to a nonlinear region at the mode-localized method’s lower initial working point28, lowering the overall sensitivity. Thus, the constant-drive mode proposed in this paper not only preserves the sensitivity of the Mode-localized sensor but also eliminates interference between the two signals.

Finite element analysis of the DSS

Through the theoretical analysis the effectiveness of the constant-drive mode for dual-signal synchronous detection can be established. However, this theoretical analysis is based on undamped conditions, leaving the impact of damping interference on the dual signals unclear. Due to the complexity of theoretical analysis in the presence of damping, this paper employs finite element simulation (FEM) to analyze both methods. This approach not only verifies the level of interference in detecting the two signals within a damped system but also reveals the amplitude variation patterns of each resonator, contributing to a better understanding of the overall sensing process.

The results of the FEM simulation are shown in Fig. 3. Figure 3a displays the three natural frequencies of the DSS, with the resonant frequencies of the three resonators being 22,937.07 Hz, 22,940.86 Hz, and 22,946.31 Hz, respectively. The corresponding initial amplitude ratios are 1, 0, and 2, which align with Eq. (7).

Fig. 3: Simulation analysis of synchronous detection of dual signals.
figure 3

a Simulation Mode of DSS; b–d The amplitude variation trend of resonators 1, 2, and 3 with Δk1 and Δk2; e, f AR1 and AR2 variation trend with Δk1 and Δk2. g AR1 variation trend with and Δk2 of two methods; h Cross-sensitivity of two methods

Full size image

In the constant-drive mode, the amplitude variation of resonators 1, 2, and 3 with respect to changes in Δk1 and Δk2 is shown in Fig. 3b, c, and d, respectively. The amplitudes of the three resonators decrease as Δk1 and Δk2 increase. Specifically, the amplitude of resonator 1 decreases more rapidly with Δk1 than with Δk2, while conversely, the amplitude of resonator 3 decreases more rapidly with Δk2 than Δk1. Thus, unlike the mode-localized effect, where energy is redistributed throughout the system, the constant-drive method essentially represents the dissipation of overall energy. Both disturbances reduce the amplitudes of all three resonators. However, for the primary disturbance, such as Δk1 affecting resonator 1, the faster decrease in amplitude provides AR1 with high sensitivity to Δk1. On the other hand, Δk2 causes the amplitudes of resonators 1 and 2 to decrease proportionally, keeping AR1 unchanged and thus eliminating the interference from k2 on AR1. The trends of AR1 and AR2 with respect to Δk1 and Δk2 are shown in the Fig. 3e, f. The Fig. 3e, f indicates that AR1 and AR2 exhibit a good linear relationship with Δk1 and Δk2, respectively, and are essentially unaffected by changes in the other signal, consistent with Fig. 2b.

The effect of Δk1 on AR2 in the mode-localized method is shown in the Fig. 3g. Both theoretical and FEM simulation results indicate the same trend: as Δk1 increases, the change in AR2 also increases, but the rate of change slows down, with results of 1.22 and 1.04, respectively. The discrepancy between these results may be due to differences in coupling stiffness. In the constant-drive mode, the effect of Δk1 on AR2 is shown in the Fig. 3h. Theoretically, Δk1 has no impact on AR2. However, in simulations, Δk1 influences AR2 in the same pattern as the mode-localized method but with significantly lower intensity, resulting in a slight effect with a cross-sensitivity of 0.054%. The energy redistribution in the mode-localized effect involves not only the transfer of energy between two resonators but also the coupling between different modes within each resonator. In the absence of damping, these modes remain completely decoupled, and the constant-drive mode effectively isolates energy transfer between different resonators, resulting in zero cross-sensitivity. However, when damping is introduced, it alters the mode energy distribution, leading to energy leakage from one mode to another. This disrupts the perfect isolation achieved in the undamped case, resulting cross-sensitivity to emerge. As a result, despite being significantly lower in magnitude compared to the mode-localized method, a similar pattern of cross-sensitivity is observed in simulations, driven in damping-induced condition. A similar energy transfer mechanism has been reported in related studies29.

This paper clarifies the amplitude variation patterns of the three resonators through FEM simulation, explains the detection mechanism of the constant-drive mode for dual-signal detection, and reaffirms the effectiveness of the constant-drive mode in reducing crosstalk between the two signals, decreasing the cross-sensitivity by over 1000 times.

Experimental principle and environment

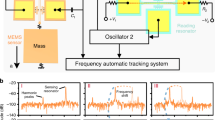
An experimental schematic of a DSS is displayed in Fig. 4. As shown in Fig. 4a, the experiment is performed in a vacuum chamber with a pressure of 0.022 Pa. DSS incorporates three resonators, each designed with differential outputs to minimize common mode noise30. As depicted in Fig. 4b, the differential signals are amplified using charge amplifiers (AD8605) and instrumentation amplifiers (AD8221). The device and interface circuit are powered by an external power supply. An AC drive signal is provided through a lock-in amplifier, which also receives the signal from the interface circuit. Since the lock-in amplifier has only two input channels, it can only receive signals from two resonators at a time. Therefore, the selected approach is to keep resonator 2 constantly connected, while resonators 1 and 3 are alternately connected.

Fig. 4: Experimental setup and procedure.
figure 4

a Photo of the experimental environment DSS; b Experimental principle of the DSS; c The process of stabilizing the driving force

Full size image

In this experiment, the lock-in amplifier was used to provide an AC drive signal and to perform detection using both the mode-localized method and the constant-drive mode. In the mode-localized method, the lock-in amplifier’s PID module is used for closed-loop control of the DSS, continuously tracking the DSS resonant frequency as the two signals are input. In the constant-drive mode, the lock-in amplifier’s open-loop frequency sweep function is initially used to determine the resonators’ operating frequency, which is then set as the AC drive frequency and kept constant.

As shown in Fig. 4c. The phase-locked amplifier begins by generating a reference signal from a high-precision crystal oscillator. This reference signal is then compared with the signal produced by a voltage-controlled oscillator (VCO). The phase difference between the two signals is detected and processed by a phase-locked loop (PLL), which adjusts the VCO’s frequency to match the reference signal. The PLL continuously fine-tunes the VCO, ensuring the output signal’s frequency remains stable and locked to the reference, providing high accuracy and stability.

Amplitude frequency response

A 10 V DC bias voltage was applied to the weakly coupled resonators, and then the stiffness of the three resonators was equalized by adjusting the stiffness of resonators 1 and 3 by two tune electrodes positioned around them. After the adjustment, the tuning voltages for resonators 1 and 3 were 21.611 V and 9.36 V, respectively.

The study tested the frequency response of the resonators under different tuning voltages to better analyze the two methods. As shown in the Fig. 5a–d, in the mode-localized method, the amplitude of Resonator 1 increases with the input of Δk1, while the amplitude of Resonator 2 decreases. With the input of Δk2 the amplitudes of both Resonators 1 and 2 increase. In contrast, for the constant-drive method, regardless of whether Δk1 or Δk2 is input, the amplitudes at the initial resonance frequencies of both resonators will reduce. Therefore, the fundamental difference between the two methods lies in the fact that modal localization detects the signal through energy redistribution, while constant-drive detects it through energy loss. The response of Resonator 3 is almost identical to that of Resonator 1, so it is not presented here. In the following sections, the sensitivity and cross-sensitivity of the two methods will be tested and analyzed.

Fig. 5: Amplitude frequency response and sensitivity test results.
figure 5

a Amplitude of Resonator 2 variation trend with voltage tune1; b Amplitude of Resonator 1 variation trend with voltage tune1; c Amplitude of Resonator 2 variation trend with voltage tune2; d Amplitude of Resonator 1 variation trend with voltage tune2; e The AR1 variation trend with Δk1 in constant-drive and mode-localized method; f The AR2 variation trend with Δk2 in constant-drive and mode-localized method

Full size image

Sensitivity experiment

The voltage sensitivity of the resonator is directly proportional to the difference between the tune voltage and the DC bias voltage. Due to variations in these voltage differences, there can be a significant disparity in voltage sensitivity between resonator 1 and resonator 3. Therefore, voltage sensitivity directly to calculate cross-sensitivity is not appropriate. This study converts voltage into stiffness for sensitivity analysis. The conversion relationship between voltage and stiffness is shown in Eq. (8). To ensure that the input stiffness ranges for the two signals correspond, the input ranges for resonators 1 and 3 are set as follows: 21.611 V to 21.591 V with a step size of 2 mV, and 9.36 V to 9.86 V with a step size of 5 mV. The relationship between voltage and stiffness signals is shown in Table 2.

$$|{k}_{e}|=\frac{\varepsilon A}{{d}^{3}}={({V}_{dc}-{V}_{tune})}^{2}\frac{\varepsilon A}{{d}^{3}}$$
(8)
Table 2 Conversion relationship between voltage and stiffness
Full size table

Sensitivity tests were conducted on the DSS in both constant-drive mode and mode-localized method, with the results shown in Fig. 5. Figure 5e displays the output relationship between AR1 and Δk1 in both modes, with no Δk2 input during the testing process. As Δk1 increases from 0 to 0.0192 N/m, in constant-drive mode, AR1 increases from 2.99 to 4.64, while in mode-localized method, AR1 increases from 3.08 to 4.72. The fitted lines for the constant-drive and mode-localized methods are represented by Eqs. (9) and (10), with sensitivities of 85.24/(N/m) and 84.86/(N/m), respectively.

Figure 5f displays the output relationship between AR2 and Δk2 in both modes, with no Δk1 input during the testing process. As Δk2 increases from 0 to 0.0161 N/m, in constant-drive mode, AR2 increases from 2.00 to 3.70, while in mode-localized method, AR1 increases from 2.13 to 3.84.

The fitted lines for the constant-drive mode and mode-localized methods are represented by Eqs. (11) and (12), with sensitivities of 111.09/(N/m) and 112.29/(N/m), respectively. The experimental results are consistent with the FEM simulation results, indicating that the sensitivity of constant-drive method is basically consistent with the mode-localized method.

$$A{R}_{1}=85.24{k}_{1}+3.09$$
(9)
$$A{R}_{1}=84.86{k}_{1}+3.17$$
(10)
$$A{R}_{2}=111.09{k}_{2}+1.94$$
(11)
$$A{R}_{2}=112.29{k}_{2}+2.23$$
(12)

Dual signal synchronization detection Experiment

The input ranges for resonators 1 and 3 are set as follows: 21.611 V to 21.591 V with a step size of 4 mV, and 9.36 V to 9.86 V with a step size of 10 mV. The interference test results for the two signals in the constant-drive mode are shown in Fig. 6. When resonators 1 and 2 are connected to the lock-in amplifier, the amplitude variation of resonators 2 and 1 with respect to k1 and k2 is shown in Fig. 6a, b. As Δk1 increases from 0 to 0.0192 N/m and Δk2 increases from 0 to 0.0161 N/m, the amplitude of resonator 2 decreases from 186.5 mV to 142.4 mV, and the amplitude of resonator 1 decreases from 59.7 mV to 30.3 mV. The corresponding AR1 is shown in Fig. 6e. When Δk2 = 0, as k1 increases from 0 to 0.0192 N/m, AR1 increases from 3.126 to 4.656. However, with the input of Δk2, AR1 also responds to Δk2. The variation trend of AR1 with respect to Δk2 is shown in Fig. 6g. As Δk2 increases from 0 to 0.0161 N/m, the deviation produced by AR1 gradually increases. The cross-sensitivity generated by mode-localized and constant-drive methods are 26.3% and 3.1%, respectively.

Fig. 6: Results of synchronous detection of dual signals.
figure 6

a–d The amplitude variation trend of resonators 1, 2, and 3 with Δk1 and Δk2; e, f AR1 and AR2 variation trend with Δk1 and Δk2; g AR1 variation trend with and Δk2 in constant-drive and mode-localized methods; h AR2 variation trend with and Δk1 in constant-drive and mode-localized methods

Full size image

When resonators 2 and 3 are connected to the lock-in amplifier, the amplitude variation of resonators 2 and 1 with respect to Δk1 and Δk2 is shown in Fig. 6c, d. As Δk1 increases from 0 to 0.0192 N/m and Δk2 increases from 0 to 0.0161 N/m, the amplitude of resonator 2 decreases from 189.0 mV to 161.7 mV, and the amplitude of resonator 1 decreases from 88.4 mV to 42.1 mV. The corresponding AR2 is shown in Fig. 6f. When k1 = 0, as Δk2 increases from 0 to 0.0161 N/m, AR2 increases from 2.137 to 3.844. However, with the input of Δk2, AR2 also responds to Δk2. The variation trend of AR2 with respect to Δk1 is shown in Fig. 6h. As Δk2 increases from 0 to 0.0192 N/m, the deviation produced by AR2 gradually increases. The cross-sensitivity generated by mode-localized and constant-drive methods are 28.7% and 1.1%, respectively.

Discussion

This paper introduces a constant-drive method that enables the simultaneous detection of two signals by a three-degree-of-freedom WCRs. Unlike existing three-degree-of-freedom mode-localized sensors31, where the stiffness of the middle resonator is set much higher than that of the other two to reduce coupling and enhance sensitivity, this study equalizes the stiffness of all three resonators and measures their vibration amplitudes. In previously reported designs, only the two outer resonators typically participate in signal detection, and therefore, they can only detect a single signal.

This study is the first to provide a theoretical analysis of the signal interference mechanism in WCRs, explaining the underlying causes. When multiple signals are input, each one induces a shift in the resonance frequency of the WCRs, which in turn causes changes in the vibration amplitude of each resonator. This results in significant cross-sensitivity between the different signals.

This study employs the first-order natural frequency of weakly coupled resonators (WCRs) for constant-drive operation to reduce cross-sensitivity. The analysis is conducted through theoretical modeling, FEM simulation, and experimental validation. The theoretical analysis shows that, without considering damping, the constant-drive method can completely eliminate signal interference, reducing cross-sensitivity to zero, while the mode-localized method yields a cross-sensitivity of 25.8%. FEM simulations, accounting for damping, reveal that the constant-drive method achieves a cross-sensitivity of just 0.054%. Experimental validation further confirmed the method’s effectiveness, with cross-sensitivity between the two signals measured at 3.1% and 1.1%, respectively. Additionally, results from the theoretical analysis, FEM simulation, and experiments all demonstrate that the sensitivity of the constant-drive method is nearly identical to that of the mode-localized method, preserving the high sensitivity characteristics of mode-localized sensors.

The experimentally measured reduction in cross-sensitivity did not fully align with the theoretical and simulation results, likely due to factors such as manufacturing tolerances, residual stress, and environmental influences. Fabrication imperfections may introduce asymmetries in resonator geometry and coupling stiffness, which can increase the feedthrough current and amplify cross-sensitivity. Additionally, residual stress may disrupt the coupling balance, resulting in a significant difference in detection sensitivity between the two signals. Furthermore, external disturbances, including temperature fluctuations and mechanical vibrations, can affect the vibration state of resonator, introducing additional cross-sensitivity not accounted for in simulations. Despite the differences between theory and experiment, the experimentally measured cross- sensitivity of the DSS reached levels comparable to similar devices, such as biaxial accelerometers32,33,34,35, demonstrating its practical application value.

The method proposed in this paper is a general approach that utilizes constant-frequency drive and can be applied to almost any coupled resonator-based sensor. By modifying the front-end sensing structure and changing the voltage input to force or electric field input, the system can be adapted into a multi-axis force or electric field sensor. Additionally, by designing the resonators in a vertical configuration, the method can be extended to a biaxial accelerometer. Compared to standalone mode-localized sensors, this approach is expected to have lower power consumption due to the elimination of complex frequency-tracking circuitry.

This study validates the potential of the constant-drive method to advance the development of sensors based on weakly coupled resonators, marking a significant contribution to the field.

Conclusion

This study presents a novel approach for the synchronous detection of dual signals using a three-degree-of-freedom weakly coupled resonator system. By utilizing a mode-locking technique, we effectively decouple the interactions between multiple signals, thereby eliminating crosstalk and enhancing sensitivity. The experimental and finite element analysis results demonstrate that the constant-drive mode maintains sensitivity comparable to closed-loop modal localization methods while ensuring minimal interference between the signals. This advancement not only broadens the functional capabilities of MEMS sensors but also offers a reliable solution for applications requiring simultaneous detection of multiple parameters. The findings contribute significantly to the development of high-performance sensing technologies in various fields.

Materials and fabrication

The DSS was fabricated using a dicing-free silicon-on-insulator (SOI) process36,37 with a 50 μm thick device layer, as shown in Fig. 7. The process started with the formation of the back cavity, which reduced release time and minimized footing effects. AZ4620 was selected as the positive photoresist for the 450 μm base layer, with a thickness of 7–8 μm. The silicon wafer was etched in an ICP chamber down to the middle oxide layer, followed by immersion in acetone for 30 min to dissolve the photoresist.

Fig. 7: Fabrication process of the DSS.
figure 7

a Patterning process for the bottom layer; b ICP etching of the base layer; c, d Photoresist removal and gold deposition on the substrate; e Patterning of the structural layer and attaching the support chip; f ICP etching of the structural layer; g Photoresist and support chip removal; h Chip release

Full size image

Next, a metal layer was patterned, and gold (Au) electrodes were deposited at a thickness of 300 nm. The lateral corrosion error during Au removal was kept under 5 μm. Photoresist was also used for the 3 μm structural layer, and the silicon wafer was bonded to the support, applying uniform pressure to ensure proper adhesion and avoid gaps that could affect thermal conductivity.

Afterward, the silicon wafer was etched to the middle oxide layer, as shown in Fig. 7h, separating the DSS chip from the wafer frame. The bonded wafers were then immersed in acetone for 30 min to release the silicon from the supporting wafers. Finally, the box layer self-separated, allowing the device and support to detach after the box layer release.