Abstract
Historically, eloquent functions have been viewed as localized to focal areas of human cerebral cortex, while more recent studies suggest they are encoded by distributed networks. We examined the network properties of cortical sites defined by stimulation to be critical for speech and language, using electrocorticography from sixteen participants during word-reading. We discovered distinct network signatures for sites where stimulation caused speech arrest and language errors. Both demonstrated lower local and global connectivity, whereas sites causing language errors exhibited higher inter-community connectivity, identifying them as connectors between modules in the language network. We used machine learning to classify these site types with reasonably high accuracy, even across participants, suggesting that a site’s pattern of connections within the task-activated language network helps determine its importance to function. These findings help to bridge the gap in our understanding of how focal cortical stimulation interacts with complex brain networks to elicit language deficits.
Similar content being viewed by others
Introduction
Many older studies supported the paradigm that eloquent cortical functions, such as language, may be highly localized to specific brain areas1,2,3. More recent studies support the recruitment or suppression of activity in broad cortical networks during both task-driven and resting states4. In particular, vast networks in temporal, parietal, and frontal lobes, as well as subcortical nuclei, may participate in different perceptual, cognitive, and productive subtasks of language5,6,7,8,9,10,11,12. In neurosurgical patients, direct electrocortical stimulation (DES) is used to identify focal regions of the human neocortex that are presumably indispensable for proper execution of speech and language function and thus are avoided to reduce postoperative language deficits13,14,15,16,17. However, the mechanisms by which DES affects the cortical processing of language and speech are not clearly understood18. In particular, it is not clear what is special about the focal sites identified as critical to language or speech by DES when broad networks are active during speech and language behaviors.
Graph theoretic approaches are a powerful and flexible means of studying brain networks via estimates of either functional or structural correlates between brain sites (or nodes)19. Functional MRI studies have suggested the presence of multiple communities (groups of correlated nodes, a.k.a. modules) in functional brain networks that reorganize dynamically according to task demands20,21. This is dependent on specialized and flexible connector nodes that support network reconfiguration between task states and help integrate information between relatively more stable brain network modules22,23,24,25. Lesions to these connectors lead to greater changes in network organization than damage to nodes important for within-module communication (“local hubs”)26. Experimental inhibition of connector nodes, and not neighboring nodes, causes disruption during working memory tasks27. On the other hand, simulated lesions of more globally connected nodes (“global hubs”) also have widespread effects on the network28. Whether this type of modularity plays a role in language networks, and how connector nodes and global hubs relate to language function and the effects of DES, is unknown. We therefore hypothesized that areas defined to be critical to speech and language by DES would be those that played a key role in integrating information across the language network.
In this work, we examine the properties of language networks using task-based electrocorticography (ECoG). We use the high-gamma (Hγ, 70–150 Hz) band from ECoG recorded during the performance of a language task to estimate functional connectivity between the sampled brain regions. We assess measures of node-based global, inter-regional (inter-community), and local connectivity within these networks, and find that critical language areas—in particular those that cause language errors when stimulated—function as connector nodes between submodules (communities) in the language network. We further demonstrate that these areas can be predicted by their network signatures alone, suggesting that the pattern of connections formed by critical language areas informs their function and is relatively preserved across participants.
Results
Patient data
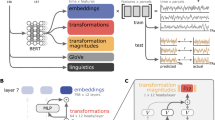
An overview of the experimental design may be found in Fig. 1, and a diagram providing intuition for network metrics used in this study may be found in Fig. 2. We included sixteen patients, including eleven patients with epilepsy and five patients who underwent awake craniotomy for tumor resection. Participant demographics and clinical information are described in Supplementary Tables 1,2. Patients had a mean (± SD) of 77.2 ± 34.6 intracranial subdural electrodes after exclusion of noisy electrodes. Fifteen (93.8%) patients had frontal electrodes, thirteen (81.3%) had temporal electrodes, eleven (68.8%) had parietal electrodes, and two (12.5%) had occipital electrodes. Patients had a mean of 9.9 (±4.1) electrodes recording from areas that were labeled critical for speech or language using DES (critical nodes). When further subdivided into sites where stimulation caused language errors (LE nodes) vs. speech arrest (SA nodes), 6.2 (±4.1) were LE nodes, and 3.7 (±3.0) were SA nodes. There were, in total, 1234 electrodes, 150 critical nodes, 92 LE, and 52 SA nodes. Types of LEs and locations of LE and SA nodes are shown in Supplementary Table 3. SA nodes were predominantly located in ventral premotor regions, but also found in ventrolateral prefrontal and ventral temporal regions, whereas LE nodes were widely distributed across perisylvian regions (Fig. 3A). Figure 3 also illustrates three representative patient brain reconstructions (3B), network spring diagrams (3C), and network metrics (3D).
A DES was used either intraoperatively (depicted) or in the epilepsy monitoring unit to identify sites critical to language and speech. These were subdivided into cortical regions causing language errors (LE) or speech arrest (SA). B We recorded continuous ECoG while participants engaged in a word-reading task. C We generated one static network for each participant using pairwise high-gamma correlations. Color-coded adjacency matrix shown; the color in position (m,n) reflects to the high-gamma correlation between electrode m and n. r is the Fisher-transformed Pearson correlation. Community partitions were discovered using modularity maximization. Electrodes have been re-ordered so those belonging to the same community are adjacent (boundaries shown in black lines). D Spring-loaded network plot; nodes (circles) that are more strongly connected are drawn more closely together. The size of each node is proportional to its strength. Community membership is indicated by the fill color of each node. The nodes outlined in blue are LE nodes. E Network metrics were calculated—PC (participation coefficient), strength, CC (clustering coefficient), LE (local efficiency), and EC (eigenvector centrality). Metric values for every node are plotted; large colored points represent critical nodes and small gray points are all other nodes. Boxes demonstrate the median and interquartile range. We used these metrics to train machine learning classifiers to predict which nodes would be critical to language and speech. Example data (C–E) are provided from a single participant (n = 1) for each visualization. Source data are provided as a Source Data file.
PC participation coefficient, S strength, CC clustering coefficient, LEff local efficiency, EC eigenvector centrality. A Diagram illustrating coassignment. Two yellow-outlined coassigned nodes are found within the same community (dark blue fill); two blue-outlined nodes are found in two different communities (magenta and orange fill)—i.e., not coassigned. B Diagram demonstrating graph metrics. The large magenta node in the top panel has a high PC—it connects across all communities in this network. The same node has a low clustering coefficient (its neighbors are not themselves connected, denoted by dashed arrows) and low local efficiency (long path lengths between its neighbors). In the bottom panel, the large dark blue node has high strength, i.e., a high sum of connection weights. The large orange node has higher eigenvector centrality than the smaller orange node; both have the same number of connections, but the larger node’s connections themselves have more connections. C Intuition for three node types. Connector nodes connect across communities (high PC), while their neighbors do not connect as closely to each other (low CC, LEff). Global hubs connect to many nodes across the network (high PC, high S, likely high EC). Local hubs connect densely in their neighborhood (low PC, high CC/LEff).
PC participation coefficient, S strength, CC clustering coefficient, LEff local efficiency, EC eigenvector centrality. A Composite of all participants’ electrodes colocalized on a single template brain. Speech arrest nodes (yellow fill) were primarily located in ventral premotor regions, but also in ventrolateral prefrontal and ventral temporal regions. Language error nodes (blue fill) were widely distributed in perisylvian regions. B Three example participant brain reconstructions. Node color (filled) represents community assignment, and node size is proportional to its participation coefficient. The outline color indicates critical nodes (blue—LE node, yellow—SA node). C Corresponding three network diagrams. The electrode position is spring-weighted (stronger connections draw electrodes closer together). Fill color indicates community, and if present, outline color indicates critical node type (LE vs. SA) D Corresponding network metrics for the three example patients. Metrics for all nodes (electrodes) for each of the three participants (n = 1 per graph) are plotted. Here, colored circles represent critical nodes; gray circles represent other nodes. Boxes demonstrate median and interquartile range, and whiskers demonstrate non-outlier maxima/minima. Source data are provided as a Source Data file.
Community structure
We applied the Louvain algorithm to partition networks into communities (groups of nodes within the network whose interconnections maximally exceed what would be expected by chance). We discovered a median of four communities (range 2–6) in each network (Fig. 4A). The stability of these assignments was tested by varying the community resolution parameter (Supplementary Fig. 1). Communities contained a median of 18.5 nodes [IQR 11-27]. By randomly permuting the community assignments, we compared the percentage of critical, LE, and SA node pairs that belonged to the same community (Coassignment percentage, or CoA%) to chance. Critical nodes were not randomly distributed across different communities, but rather, concentrated within their own community (Figs. 3B, 4B). We found that critical node pairs were significantly more likely than chance to share a community (CoA% 55.7 vs. 39.7%, p < 0.001 permutation test). When examining SA and LE node pairs in more detail, we found that 78.7% of SA and 62.2% of LE node pairs shared a community, compared to 61.0% and 48.9% in the permuted data, respectively (p < 0.001 for both, permutation test). When we examined cross-assignment% – the percentage of node pairs consisting of an LE and an SA node that shared a community with each other— we found that this was not more likely than chance (35.2 vs. 30.4%, p > 0.05, permutation test; Fig. 4B). This implies that the significant CoA% of all critical nodes was actually driven by the even higher CoA% of SA nodes and LE nodes with nodes of their own subtype (i.e., LE with LE, and SA with SA).
PC participation coefficient, S strength, CC clustering coefficient, LEff local efficiency, EC eigenvector centrality. *p < 0.05. **p < 0.01. ***p < 0.001 (FDR-corrected). A Histogram of the number of communities per participant (n = 16). B Coassignment percentages vs. chance. Coassignment is calculated as the mean % of critical, LE, or SA node pairs per participant sharing a community. Empiric chance was calculated based on 1000 random shuffles of community assignment per participant, presented as mean coassignment% per participant with bars indicating standard error of mean (n = 16 for Critical, n = 15 for LE and SA). Critical nodes, language error nodes, and speech arrest nodes were significantly more likely to coassign in the same communities than chance (p < 0.001 for all, one-tailed estimate against empiric chance). Language error and speech arrest nodes were not more likely to be found in the same community as each other compared to chance (35.2 vs. 30.4%, p = 0.112, one-tailed estimate against empiric chance). C Network metrics for critical vs. all other nodes (150 critical nodes, 1084 non-critical nodes). Critical nodes have higher PC and lower CC, LEff, and EC than other nodes. D Network metrics for LE, SA, and other nodes (92 language error nodes, 52 speech arrest nodes, 1084 non-critical nodes). LE nodes have markedly higher PC than SA and other nodes. C, D Metrics were z-scored for each subject prior to pooling all nodes together. All nodes are plotted in light gray; mean values per participant in larger, bolder colors. Boxes indicate the median and IQR, and notch indicates the standard error of the median. Statistical testing is based on a two-sided two-sample t-test on z-scored metrics across all pooled nodes with FDR correction. For additional details, refer to Table 1. Source data are provided as a Source Data file.
Network signatures of critical nodes
We calculated several well-described node-based network metrics (Fig. 2) for critical, LE, and SA nodes and compared their means against non-critical, LE, and SA nodes. We z-scored the metrics per each participant and applied the two-sample t-test with independent variances with the Storey false discovery rate correction for multiple comparisons.
We calculated each node’s participation coefficient (pc)—a measure that ranges from 0 (node has connections only within its community) to 1 (node has connections distributed evenly among many communities). Critical nodes identified by DES exhibited significantly higher participation coefficients than did other nodes (0.24 vs. −0.03; Fig. 4C and Table 1). Interestingly, we found that the high pc was driven by a markedly high pc in LE, rather than SA nodes (Fig. 4D). LE nodes had a substantially and significantly higher pc than non-critical nodes (0.47 vs. −0.03, p < 0.001), whereas SA nodes did not. LE nodes had significantly higher pc than SA nodes as well (0.47 vs. −0.09, p = 0.002).
To further investigate these nodes’ candidacy as hubs, we calculated their clustering coefficient (CC) and local efficiency (LEff; Fig. 2B). Critical nodes were significantly lower in both measures than other nodes. This was also true for LE and SA nodes, though for SA nodes, only LEff, and not CC, met the criteria for significance, likely due to the smaller sample size. Node strength was not found to be different between critical LE, or SA nodes and other nodes. Interestingly, eigenvector centrality was significantly lower in critical, LE, and SA nodes than in other nodes (Fig. 4C, D). Table 1 summarizes these results.
Thus, critical nodes exhibited lower local connectivity (clustering coefficient and local efficiency, Fig. 4C, D) and lower eigenvector centrality, while not differing from other nodes in global connectivity (strength). Simultaneously, LE nodes demonstrated higher connectivity across different communities. Thus, critical nodes, and particularly language error nodes, were connectors between brain network modules, rather than local or global hubs.
Critical node prediction
We assessed whether network signatures alone could identify which nodes were predicted by DES to be critical for speech and language within each participant. Using ten-fold cross-validation, we trained support vector machines (SVM) and k-nearest neighbor (KNN) classifiers to separately predict whether nodes were critical, LE, or SA nodes in a binary fashion (i.e., critical vs. not-critical, LE vs. not-LE, and SA vs. not-SA). We compared classifier performance against chance by permuting the node labels.
Balanced accuracy and sensitivity for predicting critical nodes as well as LE nodes and SA nodes separately were both significantly better than chance (p < 0.001 for balanced accuracy and sensitivity for both SVM and KNN vs. chance, permutation test) For critical nodes, median balanced accuracy was 70.4% and 72.8% for SVM and KNN, respectively, compared to 60.0% and 58.9% for chance (detailed results in Fig. 5A and Tables 2, 3). The corresponding median sensitivity was 83.7% and 84.4%, compared to 66.7% and 54.5% for chance (Fig. 5B and Table 2). When predicting LE nodes and SA nodes (vs. non-LE and non-SA nodes), separately, both balanced accuracy and sensitivity remained substantially better than chance (p < 0.001, permutation test, Fig. 5A, B and Table 3). The mean area under the curve (AUC) of the receiver operating characteristic (ROC) over all participants for critical node prediction was 0.65 for SVM, and 0.72 for KNN. This, as well as the AUC of the ROC for predicting LE and SA nodes, exceeded that of the 99.9% confidence interval of the chance predictions (Table 3).
For within-participant classification, participants with at least four nodes of the relevant class were included; for critical nodes, LE nodes, and SA nodes, n = 15, 10, and 8, respectively. For across-participant classification, participants with at least one node of the relevant class were included—for critical nodes, LE nodes, and SA nodes, n = 16, 13, and 13, respectively. A–D Each dot represents average classification balanced accuracy or sensitivity for a single participant. Box plots show median and IQR across participants and are derived from a single value per participant. Whiskers indicate a non-outlier maximum range. True balanced accuracy and sensitivity were compared against empirical chance calculated by label-shuffling. The average chance classification accuracy per participant is represented by the chance box plots for SVN and KNN (one value per participant). Data for SVM, KNN, and chance for SVM and KNN are presented in different colors as indicated by the legend. E, F ROC curves presented for SVM (solid lines) and KNN (dashed lines) classifiers, when classifying SA (orange), LE (magenta), and critical (dark blue) nodes separately, as indicated by the legend. For further details, refer to Tables 2, 3. Source data are provided as a Source Data file.
We further investigated whether a classifier trained using these network features could predict critical nodes in an entirely new and separate participant, by applying the same methodology in a leave-one-patient-out cross-validation. For critical nodes, classification median balanced accuracy was 65.9% and 66.0% for SVM and KNN, respectively, which was also significantly better than chance (p < 0.001 for both, permutation test). The corresponding median sensitivity was 76.4% and 77.3 for SVM and KNN. The balanced accuracy and sensitivity (up to 90%) for both models for predicting LE, and SA nodes were statistically better than chance (Fig. 5D, E and Table 2). The mean AUC of the ROC ranged from 0.56 to 0.66 and remained higher than the 99.9% confidence interval for chance predictions in all cases (Fig. 5F and Table 3).
Discussion
We examined functional brain networks serving language by applying network neuroscience measures to ECoG high-gamma activity recorded during word reading. We found that cortical sites critical to speech and language differed from other sites with regard to multiple network measurements. Further, sites where stimulation caused language errors had different network properties than those where stimulation caused speech arrest. Both types of nodes exhibited low local clustering (as measured by clustering coefficient and local efficiency) and eigenvector centrality—i.e., they were neither local nor global hubs. Sites where DES caused language errors demonstrated high participation coefficients. This suggests that language error nodes acted as connector nodes among communities in the language network. In contrast, sites where DES caused speech arrests, did not resemble connector nodes in the measured networks.
These findings highlight and begin to bridge the gap in our understanding of how focal cortical stimulation interacts with complex networks in the human brain to elicit language deficits. Higher-order cognitive functions such as language involve actions of multiple subnetworks20,29,30. Our finding that language error nodes are connectors among these subnetworks implies that these nodes serve to help coordinate among subnetworks, and that this property makes them critical to function. This extends findings showing disruption of working memory with inhibitory transcranial magnetic stimulation of connector nodes27, suggesting that the criticality of connector nodes is a general property of cognitive networks. In contrast, for lower-order functions, such as speech articulation (the negation of which causes speech arrests), connectors appear to be less critical. The metrics we used only distinguished speech arrest nodes as non-hubs and non-connectors; it would be interesting to investigate if other metrics can further characterize their role in the network. Our recordings may also have under-sampled the frontal regions connected by SA nodes; participants typically had many dozens of electrodes spanning frontal and temporal regions but relatively few electrodes in face, oral, or hand motor areas. Since movements and speech articulation have homologous organization in the frontal cortices31, it seems plausible that DES-labeled critical nodes in motor networks may have similar properties or form important connections to SA nodes. In these participants, given the relatively small number of these electrodes, it is possible that SA nodes’ important role in interacting with articulator motor networks was not fully characterized and remains to be determined in future investigations.
Numerous studies of the causal mechanisms of cortical stimulation have uncovered complex relationships between DES and behavioral manifestations. Many areas that show activation during human behavior or experimental tasks fail to manifest behavioral or subjectively reported effects when stimulated. When examining the trial-averaged Hγ power, we found that while ~50–60% of critical, LE, and SA nodes modulated around speech onset, many did not, and a substantial minority of non-critical nodes exhibited modulation as well (Supplementary Fig. 3). Among other factors, this complex relationship has been suggested to relate to the uni- or trans-modality of the stimulated network as well as to interconnections of causal and non-causal brain areas32,33. Stimulation effects are often frequency-dependent34, and stimulation may activate locally dispersed tissue as well as remote areas18,35 Studies of stimulation alongside structural and functional connectivity suggest that stimulation-induced behaviors may relate to the recruitment of distributed cortical and cortico-thalamic networks36,37. Whether the effects elicited in our study result from dysfunction in language networks due to the inactivation of connector nodes, or due to the spread of stimulation via these connector nodes, remains to be determined.
In addition to possessing different network signatures, LE and SA nodes colocalized within different communities in the language network which, in combination with their role as connectors, has further implications for the functionality of LE nodes within language networks. For example, two schemes for language network organization have been proposed. In one, a control network consisting of more flexible connector nodes helps integrate information from more peripheral network modules38. In this scheme, LE nodes would likely serve as connector nodes within the control network, while SA nodes might fall within a smaller subnetwork important for speech articulation. In another scheme, the language network could contain a functionally specialized “core” with a more ___domain-general periphery that coactivates with the language core at times, but at other times with other specialized systems39. In this view, SA and LE nodes may fall within different subnetworks within a larger language core, but LE nodes might play a different role—bridging language submodules within the core, and/or connecting to peripheral modules that assist language function.
In dual-stream models of language1,40,41, SA nodes might be more related to the dorsal stream, which serves more sublexical, gestural, and motor functions, while LE nodes could play a more important role in the ventral stream, which processes semantic information, or in connecting the two streams. While a majority of SA nodes were localized more dorsally in our patients, some were located on the ventral temporal surface. Also, while a majority of LE nodes were in ventral locations, they were also found in dorsal locations (Fig. 3A). Our network calculations were independent of anatomic localization; therefore, the network signatures derived in our investigations provide new information that may complement pre-existing functional neuroanatomical associations when assessing the criticality of cortical sites to speech and language. Interestingly, we found that many critical nodes, and connector nodes, lay at the boundaries between communities within our language networks. This is similar to recent findings that DES effects were also more likely to be elicited closer to boundaries between resting-state transmodal networks33, again suggesting that connector nodes may play an important role in many types of functional networks.
By applying straightforward machine learning classifiers to this limited set of network-based features, we predicted critical nodes with balanced accuracy and sensitivity as high as 79.3 and 93.3%, respectively. Our results compare favorably with other studies attempting to use ECoG to predict critical language areas. This is true of both those using Hγ power or modulation in each electrode as a marker for spectral functional mapping42,43,44,45,46 and another study that used a combination of trial-averaged and stimulus- or articulation-aligned power and network features47. Unlike most prior studies, we also took the extra step of classifying across participants. We achieved a balanced classification accuracy as high as 70.8% with a sensitivity of over 80%. Although the accuracy of these predictions would require improvement, and comparative evaluation to other non-stimulus based functional mapping methodologies as well as traditional mapping techniques have not yet been performed, these results suggest that the network signatures we identified are reproducible both among different critical nodes within each individual and as a finding that generalizes across individuals with different disease states, electrode coverage, and sampling conditions. We found that false positive critical nodes and LE nodes were more likely to be nearest neighbors with true positive critical and LE nodes (Supplementary Fig. 5). This suggests similar network topology of adjacent brain tissue, and the clinical implications of lesioning this tissue is yet unknown.
Importantly, our methods resemble how ECoG mapping could potentially be used in clinical practice—by applying a decoder trained on prior patients to data from a new, previously unseen patient. In one prior report of critical node prediction48, the authors achieved a high cross-validation accuracy using multiple time- and frequency-___domain ECoG features and deep-learning methods. Their data contained a higher percentage of DES-defined positive nodes than in our study and far fewer total electrodes. Moreover, their study pooled electrodes across participants; in contrast, we held a participant completely out of the training data for use as the test set. Given differences in setting, electrode coverage, and inter-individual neurological and neuroanatomical differences, our method is both a more clinically relevant and a more challenging classification problem. Importantly, our technique takes into account network connectivity patterns without prior functional MRI, anatomic, or band-limited power modulation, thus providing additional, independent information that should help improve ECoG-based functional mapping. The combination of powerful network features (such as those we used in our study), used alongside strategies applying other non-network-based techniques and deep-learning approaches, might yield even higher prediction accuracies.
Functional connectivity derived from intracranial EEG may be assessed using a variety of methods, including power correlations, phase coherence or synchrony, mutual information, or regression-based techniques in different frequency bands. Our choice of technique is informed by previous efforts identifying intrinsic functional networks using Hγ power correlations49,50,51,52,53. Although in some cases, lower frequency-band activity from intracranial EEG has demonstrated correlations with fMRI52,54,55, Hγ power is the best-known intracranial correlate of the fMRI BOLD signal49,56,57, upon which most functional connectivity studies have been based. Other groups have utilized the low-pass filtered envelope of the Hγ band to demonstrate strong correlations with broad resting-state and memory-associated fMRI networks53,58, however, it is likely that the faster dynamics that occur during language processing are lost when low-pass filtering at 1 Hz. While we did apply some smoothing, the 150-ms moving average we used retains higher-bandwidth fluctuations in the signal than these prior studies. This window was chosen by visual inspection as one that reduced very rapid, small oscillations of the Hγ signal while preserving its overall structure on a sub-second scale. Hγ power reflects highly local information—with negligible volume condition, showing minimal correlations at distances greater than ~1 mm59,60,61, and has demonstrated high information content in numerous previous studies of human speech and language62. We expect that functional connectivity measured in this way will exhibit greater values for shorter interelectrode distances, due to the intrinsic structure of the brain. We examined the relationship between interelectrode distance and connectivity strength and found that while there was an inverse relationship, there was also substantial variability at each distance (Supplementary Fig. 2). This variability, combined with our key finding that language error nodes exhibited increased connections across—rather than within—communities, and critical nodes had lower local connectivity than other nodes, suggests that our findings are not mainly due to distance effects.
Prior work using different techniques has shown state-invariance in functional networks derived from phase coupling or slow fluctuations of the (low-pass filtered) high-gamma band, suggesting that these types of networks may be interrogated without structured task activity50,51,53,58. In clinical practice, language task-activated fMRI is frequently used to estimate language representations in the human cortex, and previous non-stimulation-based functional mapping efforts have also relied upon language tasks to engage cortical regions to modulate frequency-band activity. In light of this, we applied a language task and analysis paradigm that would be straightforward to implement in clinical scenarios.
During preprocessing, we applied global signal regression for noise reduction purposes, which has also been shown in previous work to enhance neuronal-hemodynamic correspondence49. This technique has been demonstrated to cause mandatory anticorrelations63. Our methodology for community partitioning maximized positive intracommunity connections; further, most of the graph metrics we used (participation coefficient, clustering coefficient, local efficiency) considered only the contribution from positive-strength edges. Thus, anticorrelations are unlikely to have contributed to our main findings.
Our findings provide insight into the different roles of language error and speech arrest nodes in language networks. However, our functional networks only sampled the portions of language networks colocalized under the electrode grids and strips placed for clinical purposes in these patients. We were unable to sample from the entirety of the brain or broader language network. The fact that our findings persisted despite a wide range of electrode coverage across different patients suggests that the network signature we identified was preserved on a regional scale. Further studies with fMRI and intracranial EEG studies with broad, bilateral sampling (including depth electrodes) may yield additional insight into this regard. Causal methods for interrogating effective network connectivity such as cortico-cortical evoked potentials may also yield important insight into the structural-functional connectivity of language-critical nodes.
Our approach to network generation was to create a static network encompassing several minutes of language task-activated ECoG. While this approach is attractive due to its simplicity and potential ease of clinical implementation for functional mapping, language is a dynamic process integrating activity from multiple areas and subnetworks. The vast majority of the study of these networks has been done through fMRI, with a minimum time resolution spanning at least several seconds64,65. It is unlikely that most nodes in language subnetworks revealed by fMRI remain persistently active overall for several seconds. Rather, they more likely reflect the summation of the rapid reconfiguration of networks serving multiple language subprocesses11,66. Language is likely subserved by, and may be better described by, dynamic networks, and DES may actually identify nodes that play important, yet dynamic and different, roles during language processing. These might be further elucidated experimentally with dynamic network analyses.
Despite these limitations, our findings identify a critical role for connector nodes in the function of language networks. Although the use of a static network and division of critical nodes into only two categories (i.e., language error vs. speech arrest) likely oversimplifies the complex contribution of different network states and critical cortical areas to language processing, we were able to use these techniques to classify critical language and speech nodes with remarkable accuracy, even across participants with different disease conditions, cortical sampling, and task conditions. The fact that the data were heterogeneous and yet still enabled accurate classification of DES-critical sites speaks to the robustness of our findings overall. Further investigations into the network connectivity of critical cortical regions, and the network states subserving speech and language, are ongoing. These findings also suggest that further investigation into the ECoG network representations underlying other processes besides language may yield new insights into human cognitive processing.
Methods
Participants
This study was conducted in patients with medically intractable epilepsy who required invasive ECoG monitoring for clinical treatment of their epilepsy (n = 11) and patients who required awake craniotomy and functional mapping for the resection of brain tumors (n = 5). All procedures were approved by the Institutional Review Boards of either Northwestern University or Johns Hopkins University, and written informed consent was obtained from all participants. We included patients who were found by DES to have cortical sites critical to speech or language. We excluded participants with tumor-related symptoms affecting speech production (as determined by neuropsychological assessment) and nonnative English speakers from the study.
As per the standard of care for awake craniotomies, patients with brain tumors were first anesthetized with low doses of propofol and remifentanil, which were then discontinued during the awake portion of the operation for direct cortical stimulation mapping. All experiments were performed after cortical stimulation, hence, during experiments, no general anesthesia had been administered for at least 45 min. After functional mapping, we placed 8×8 electrode grids with 4-mm or 5-mm interelectrode spacing over the posteroventral frontal cortices, and occasionally over the superior temporal/angular gyri. All tumors were located at least two gyri away from the recording electrodes. In participants with epilepsy, standard clinical ECoG grids and strips (1-cm interelectrode spacing) were placed according to clinical necessity. All patients in this study were left hemisphere-dominant and had left-sided temporal, frontal, and/or parietal electrode coverage.
Functional mapping and definition of critical nodes
Functional mapping was performed using DES according to the standard of care by the neurosurgery (for intraoperative mapping, using a bipolar Ojemann stimulator) or epilepsy (for extraoperative mapping in the epilepsy monitoring unit) teams. In the intraoperative setting, after patients were sufficiently awake, bipolar stimulation was delivered with an Ojemann stimulator using a manual silver ball bipolar probe with 5-mm spacing. Stimulation current began at 1 mA and was increased in 0.5 to 1 mA increments to elicit stimulation-induced speech and language deficits. In the extraoperative setting, stimulation mapping followed routine clinical procedures. Tasks included free speech, repetition, picture naming, and comprehension. Extraoperative mapping was performed in 2–3 h blocks over 1–2 days and relied upon both monopolar and bipolar stimulation delivered through the implanted subdural grids to elicit reproducible language deficits in the absence of after-discharges.
We defined regions of the cortex that mapped positive for language or speech function to be “critical nodes”; these were subdivided into “language error (LE)” and “speech arrest (SA)” nodes. Areas where stimulation resulted in reproducible cessation of all speech output during every task modality were defined as SA nodes, and all other critical nodes—i.e., those that caused patients to have aphasia, dysnomias, paraphasic errors, or comprehension errors, were designated as LE nodes. We also adjudicated nodes where stimulation resulted in the inability to speak during some, but not all tasks, to be LE nodes. This effect suggested stimulation-induced interference with a language processing ability (such as word recall, reading, or auditory comprehension) critical to completing certain tasks, but the continued ability to speak during other tasks (such as spontaneous speech) demonstrated the continued function of articulatory (and other) components of the speech network.
Word-reading task and data acquisition
An overview of the experimental design and analysis is shown in Fig. 1. For intraoperative participants, after DES mapping was completed, surface (subdural) electrode arrays were placed for data acquisition. We co-registered the nearest surface electrodes with the previously identified positive mapping locations using intraoperative photographs. For participants with epilepsy, both electrodes in each bipolar stimulation pair were considered to be “positive” when a language deficit was elicited during stimulation.
All participants performed a word-reading task in which they read single words from a screen while continuous ECoG was acquired. This task was performed separately from DES mapping. Each trial began with the display of a word on-screen for ~2 s (timing and word set differed slightly across institutions and participants). In some participants, the word was read upon presentation. In others, a variable-length instructed delay (1–2 s blank screen) preceded a “go” cue prompting vocalization. Words used were single-syllabic, largely consonant-vowel-consonant format. Several minutes of continuous task data from each participant were used for analysis, typically including forty to one hundred words.
Data preprocessing and power extraction
We acquired data at sampling rates from 500 to 2 kHz. We applied notch filters at 60, 90, and 120 Hz in a zero-phase manner and re-referenced data to the common mean. We extracted the Hγ power by applying eight finite impulse response band-pass filters with approximate pass-band widths of 10 Hz and linearly spaced band centers from 70 to 150 Hz, followed by a Hilbert transform to extract the analytic amplitude. After squaring the amplitude, the sub-band powers were averaged to obtain the Hγ power. At every step (i.e., after initial filtering, re-referencing, and after obtaining the Hγ power) of preprocessing, we excluded electrodes whose signals were contaminated with frequent interictal spiking activity, as well as those with substantial noise based on visual inspection. Afterward, the preprocessing pipeline was reiterated from the beginning without the excluded electrodes (thus preventing contamination in re-referencing) until no further noisy electrodes remained. For the remaining electrodes, we identified and removed any transient epochs of significant artifact (defined as simultaneous non-physiologic, high-amplitude activity across many electrodes) and concatenated the remaining data with a flat-top (trapezoidal) taper with linear transition zones of 100-ms. We z-scored the Hγ power on each electrode.
We then performed a global signal regression67, ensuring that the residual data used to construct our networks was orthogonal to the global average Hγ signal. We smoothed the resultant signal by applying a zero-lag 150-ms moving mean; this length was selected by visual inspection as one that reduced small rapid fluctuations in the Hγ power signal while maintaining its overall underlying characteristics.
For extraoperative patients, we localized electrodes in a semi-automated fashion by co-registering post-implantation CT scans with preoperative thin-cut T1 MRI sequences. Brain surface reconstructions were generated in FreeSurfer (http://surfer.nmr.mgh.harvard.edu/), and electrode contacts were colocalized in standardized space with the help of LeGUI68, a graphical user interface for the detection and localization of intracranial electrodes. For intraoperative patients, an expert neuroanatomical review of intraoperative photographs of the cortical surface before and after grid electrode placement was used to visually co-register electrode and positive mapping locations with visible cortical surface landmarks.
Network generation
We constructed one network (i.e., graph) for each participant, representing functional connectivity during the entire task duration. In these networks, each node represented the activity in the cortex underlying an electrode. We connected these nodes with edges based on the zero-lag, Fisher-transformed Pearson correlation of their Hγ power; edges were therefore weighted and signed and spanned the interval [−1 1]. The Hγ band was selected based on its representation of very local activity (thus eliminating potential confounds from volume conduction), its correlation with the fMRI BOLD signal49,53,56,57, and its established utility in prior studies of language function. Networks are described by their connectivity matrices, denoted by \(A\) where \({A}_{{ij}}\) represents the weight of the connection between electrodes i and j. We avoided thresholding edges whenever possible, leaving them as weighted positive and negative connections between nodes, as this reduced the potential parameterization bias in subsequent analyses. We tested the length of datasets and its association with classification accuracy and found that sufficient amounts of data were used (Supplementary Fig. 4).
Characterizing networks
Community detection
We used modularity maximization to detect communities, i.e., groups of nodes whose connections to one another maximally exceeds what would be expected by chance. This intuition is formalized by the modularity quality function, (1) \(Q={\sum }_{{ij}}({A}_{{ij}}-{P}_{{ij}})\delta ({z}_{i},{z}_{j})\), where \({A}_{{ij}}\) and \({P}_{{ij}}\) are the observed and expected weights of edge \(\left\{{ij}\right\}\), \({z}_{i}\) is the community assignment of node \(i\), and\(\,\delta \left(x,y\right)\) is the Kronecker delta function. Effectively, this summation is over within-community nodes. Intuitively, larger values of \(Q\) correspond to better partitions of the network into segregated communities. We used a uniform null model and set the elements of \({P}_{{ij}}=\langle {A}_{i\ne j}\rangle\), which has been shown to be an appropriate null model for correlation networks.
We optimized \(Q\) using the Louvain algorithm (100 repetitions) and resolved variability across these repetitions via consensus clustering. In this procedure, we first calculate a node-by-node allegiance matrix, whose elements are equal to the fraction of partitions in which nodes \(i\) and \(j\) were assigned to the same community. We then compare these elements to their expected values and cluster the allegiance matrix (100 repetitions). These two steps—construction and clustering of an allegiance matrix—are repeated until convergence, i.e., the detected communities are identical to one another. We tested the stability of our findings by exploring a range of values for \({P}_{{ij}}\), which did not substantially change results (Supplementary Materials).
Community membership of critical nodes
We examined whether critical nodes (LE and SA nodes taken together), LE nodes, or SA nodes colocalized in the same communities with other nodes of their own type. To accomplish this, we calculated the coassignment percentage (CoA%): for each participant, the percentage of all pairs of each node type that were assigned to the same community (Fig. 2A). To test whether the CoA% was different from chance, we randomly permuted the community assignments of all nodes 1000 times. We compared the true CoA% for each group to that of the surrogate distribution and estimated p values in a one-tailed manner. We also calculated the cross-assignment percentage (CrossA%): the fraction of node pairs consisting of one LE and one SA node that were assigned to the same community and compared it to chance in the same manner.
Network signatures
We hypothesized that a node with connections across multiple different communities plays a different role (and maybe more critical to network function) than one with strong connections only within its community. To quantify this, we calculated the participation coefficient (pc) of each node, defined as (2) \({p}_{i}=1-{\sum }_{s=1}^{C}{(\frac{{k}_{{is}}}{{k}_{i}})}^{2}\), where s ∈ {1,…, C} represents community assignment, \({k}_{i}\) is the node’s total strength (for weighted networks) and \({k}_{{is}}\) is the node’s sum weight of connections to community \(s\)69; pc is bounded between 0 (only makes connections to a single community) and 1 (connections are uniformly distributed across many different communities). We considered only the contribution of positive-strength edges to the participation coefficient.
We also investigated several other well-described graph metrics (Fig. 2B): node strength (normalized to the number of nodes in each network), eigenvector centrality, clustering coefficient, and local efficiency, using code derived from the Brain Connectivity Toolbox70. Node strength quantifies the sum of a node’s weighted connections. Eigenvector centrality simultaneously considers a node’s number of connections as well as their relative importance. The clustering coefficient of a node describes the likelihood that its neighbors are also connected to each other, and local efficiency is a related measure that quantifies the shortest path lengths in the local neighborhood of a node. Local efficiency was calculated based on positive edges only by converting connection strengths to path lengths via their inverse (\({L}_{{ij}}={{A}_{{ij}}}^{-1}\)); the remainder of the calculations were based on the weighted adjacency matrix. To standardize comparisons between participants, we z-scored all network metrics for each participant. Given the number of nodes in each group, we compared metrics between critical, LE, SA, and other nodes using the two-sample t-test, with Storey’s false discovery rate correction for multiple comparisons.
Prediction of critical nodes
We investigated whether the network signatures alone could be used to predict whether nodes would be found to be critical by DES. As there was substantial heterogeneity in the number of grids, electrodes, coverage, and clinical characteristics of the underlying patients, we trained and evaluated machine learning classifiers of critical vs. non-critical nodes within each participant using ten-fold cross-validation. This process roughly estimates the potential accuracy of these classifiers in predicting critical nodes when trained and tested on data closely resembling that of each individual patient. We used support vector machine (SVM) and k-nearest neighbor (KNN) classifiers due to their power, wide recognition, and straightforward implementation. Participants with less than four critical nodes were excluded due to class underrepresentation in training folds.
Input features to these models included node pc, strength, clustering coefficient, local efficiency, and eigenvector centrality—i.e., the full set of graph measures calculated above. We determined classifier hyperparameters (i.e., kernel type and size, cost-weighting of false negatives, etc.,) using training data alone by using Bayesian optimization to select hyperparameters that maximized the AUC (area under curve of the receiver operating characteristic). We did this using five-fold cross-validation within each training set (in the overall ten-fold cross-validation), which subdivided the training data into independent sub-training and sub-test sets, to avoid overfitting the hyperparameters. With the use of a completely independent test set (unused for hyperparameter optimization as well as classifier training), we avoided introducing bias into our accuracy estimations.
We then trained the SVM and KNN classifiers on the training set and applied them to the test set. By varying the threshold for positive class prediction through the range of classifier positive class prediction scores, we generated receiver operating characteristic (ROC) curves of the accuracy of predicting critical nodes. We defined optimal class prediction score thresholds for each participant’s ROC curve as those maximizing balanced accuracy.
Using these same methods and the same limited set of network features, we further investigated whether the network signatures of critical nodes generalized across patients, by testing whether a classifier trained on a set of patients could be used to predict critical nodes in an entirely separate patient. We trained classifiers in a leave-one-patient-out manner: data (consisting of the input features) from electrodes pooled from N-1 patients were used to train and optimize the classifier, after which its classification accuracy was determined on the electrodes from the remaining, previously unseen patient. This process, repeated N times, estimates the generalizable real-world classification accuracy of a pre-trained model using only these features. With pooled electrodes, class underrepresentation in the training fold was less of an issue, so we included for this analysis all participants who had at least one electrode of the positive class. For each participant, we again used critical node prediction scores to generate ROC curves, and we defined optimal thresholds (i.e., score cutoff for positive class prediction) to be those that maximized balanced accuracy.
We repeated the above process twenty times (as the hyperparameter learning process, and therefore classification accuracy, was non-deterministic) and averaged the results to generate a point estimate of balanced accuracy, sensitivity, specificity, and average ROC for each participant. To test the accuracy of these classifiers against chance, for each of the twenty trained classifiers, we randomly permuted the positive class labels 100 times (resulting in 2000 chance predictions) and used the same methodology as for the true data for each iteration to extract an estimate of the peak balanced accuracy, sensitivity, specificity, and AUC of the ROC that could be obtained by chance. We resampled this chance distribution with replacement 1000 times (each sample containing the same number of predictions as the true data) and compared the mean performance to that of the true data.
Statistics and reproducibility
Critical nodes were identified during clinical DES mapping sessions that were separate from the research paradigm and were not influenced by the research question. ECoG recordings, preprocessing, and network calculations were performed in an unbiased manner, and we tested the reliability of our results. For community assignments, we tested a range of parameter values to confirm the stability of our key results (Supplementary Materials and Supplementary Fig. 1). For network metric comparisons, all electrodes were pooled across subjects and compared directly using the two-sample t-test and FDR correction. For within-subject critical node prediction, we assessed prediction accuracy in a ten-fold cross-validated manner; the test dataset was not used for model training or for parameter optimization. For across-subject critical node prediction, we utilized a leave-one-subject-out scheme where again, the test data was not used for model training or for parameter optimization. In both instances, we performed classification multiple times as the hyperparameter optimization process was not deterministic, and we averaged the performance of each of these attempts. Statistical testing was performed using label-shuffling where appropriate, comparing the average performance of the classifiers on the true data against empiric chance.
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.
Data availability
Raw data were generated at Northwestern University and Johns Hopkins University. The raw data were available; access can be obtained by direct request to the corresponding author. A minimum dataset is available at the data archive for the brain initiative at https://doi.org/10.18120/9qat-kr87. Source data are provided with this paper.
Code availability
Code for these analyses are available under restricted access; access can be obtained for non-commercial use by direct request to the corresponding author.
References
Hickok, G. & Poeppel, D. The cortical organization of speech processing. Nat. Rev. Neurosci. 8, 393–402 (2007).
Price, C. J. The anatomy of language: a review of 100 fMRI studies published in 2009. Ann. N. Y. Acad. Sci. 1191, 62–88 (2010).
Towle, V. L. et al. ECoG gamma activity during a language task: differentiating expressive and receptive speech areas. Brain 131, 2013–2027 (2008).
Fox, M. D. et al. The human brain is intrinsically organized into dynamic, anticorrelated functional networks. Proc. Natl Acad. Sci. USA 102, 9673–9678 (2005).
Sonoda, M. et al. Six-dimensional dynamic tractography atlas of language connectivity in the developing brain. Brain 144, 3340–3354 (2021).
Chang, E. F. et al. Cortical spatio-temporal dynamics underlying phonological target detection in humans. J. Cogn. Neurosci. 23, 1437 (2011).
Nishida, M. et al. Brain network dynamics in the human articulatory loop. Clin. Neurophysiol. 128, 1473–1487 (2017).
Korzeniewska, A., Crainiceanu, C. M., Kuś, R., Franaszczuk, P. J. & Crone, N. E. Dynamics of event-related causality in brain electrical activity. Hum. Brain Mapp. 29, 1170–1192 (2008).
Müller, R. A. et al. Receptive and expressive language activations for sentences: a PET study. Neuroreport 8, 3767–3770 (1997).
Riès, S. K. et al. Spatiotemporal dynamics of word retrieval in speech production revealed by cortical high-frequency band activity. Proc. Natl Acad. Sci. USA 114, E4530–E4538 (2017).
Flinker, A. et al. Redefining the role of broca’s area in speech. Proc. Natl Acad. Sci. USA 112, 2871–2875 (2015).
Binder, J. R. et al. Human brain language areas identified by functional magnetic resonance imaging. J. Neurosci. 17, 353–362 (1997).
De Witt Hamer, P. C., Robles, S. G., Zwinderman, A. H., Duffau, H. & Berger, M. S. Impact of intraoperative stimulation brain mapping on glioma surgery outcome: a meta-analysis. J. Clin. Oncol. 30, 2559–2565 (2012).
Gil-Robles, S. & Duffau, H. Surgical management of World Health Organization grade II gliomas in eloquent areas: the necessity of preserving a margin around functional structures. Neurosurg. Focus 28, E8 (2010).
Sanai, N., Mirzadeh, Z. & Berger, M. S. Functional outcome after language mapping for glioma resection. N. Engl. J. Med. 358, 18–27 (2008).
Haglund, M. M., Berger, M. S., Shamseldin, M., Lettich, E. & Ojemann, G. A. Cortical localization of temporal lobe language sites in patients with gliomas. Neurosurgery 34, 567–576 (1994).
Chang, E. F. et al. Functional mapping-guided resection of low-grade gliomas in eloquent areas of the brain: improvement of long-term survival. Clinical article. J. Neurosurg. 114, 566–573 (2011).
Borchers, S., Himmelbach, M., Logothetis, N. & Karnath, H. O. Direct electrical stimulation of human cortex — the gold standard for mapping brain functions? Nat. Rev. Neurosci. 13, 63–70 (2011).
Bullmore, E. & Sporns, O. Complex brain networks: graph theoretical analysis of structural and functional systems. Nat. Rev. Neurosci. 10, 186–198 (2009).
Cohen, J. R. & D’esposito, M. The segregation and integration of distinct brain networks and their relationship to cognition. J.Neurosci. https://doi.org/10.1523/JNEUROSCI.2965-15.2016 (2016).
Bertolero, M. A., Thomas Yeo, B. T. & D’Esposito, M. The modular and integrative functional architecture of the human brain. Proc. Natl Acad. Sci. USA 112, E6798–E6807 (2015).
Gordon, E. M. et al. Three distinct sets of connector hubs integrate human brain function. Cell Rep. 24, 1687–1695.e4 (2018).
Cole, M. W. et al. Multi-task connectivity reveals flexible hubs for adaptive task control. Nat. Neurosci.16, 1348–1355 (2013).
Power, J. D., Schlaggar, B. L., Lessov-Schlaggar, C. N. & Petersen, S. E. Evidence for hubs in human functional brain networks. Neuron 79, 798–813 (2013).
Braun, U. et al. Dynamic reconfiguration of frontal brain networks during executive cognition in humans. Proc. Natl Acad. Sci. USA 112, 11678–11683 (2015).
Gratton, C., Nomura, E. M., Pérez, F. & D’Esposito, M. Focal brain lesions to critical locations cause widespread disruption of the modular organization of the brain. J. Cogn. Neurosci. 24, 1275–1285 (2012).
Lynch, C. J. et al. Precision inhibitory stimulation of individual-specific cortical hubs disrupts information processing in humans. Cereb. Cortex 29, 3912–3921 (2019).
Alstott, J., Breakspear, M., Hagmann, P., Cammoun, L. & Sporns, O. Modeling the impact of lesions in the human brain. PLoS Comput. Biol. 5, e1000408 (2009).
Zhang, W., Tang, F., Zhou, X. & Li, H. Dynamic reconfiguration of functional topology in human brain networks: from resting to task states. Neural Plast. 2020, 8837615 (2020).
Yin, S., Li, Y. & Chen, A. Functional coupling between frontoparietal control subnetworks bridges the default and dorsal attention networks. Brain Struct. Funct. 227, 2243–2260 (2022).
Mugler, E. M. et al. Differential representation of articulatory gestures and phonemes in precentral and inferior frontal gyri. J. Neurosci. 38, 9803–9813 (2018).
Foster, B. L. & Parvizi, J. Direct cortical stimulation of human posteromedial cortex. Neurology 88, 685–691 (2017).
Fox, K. C. R. et al. Intrinsic network architecture predicts the effects elicited by intracranial electrical stimulation of the human brain. Nat. Hum. Behav. 4, 1039–1052 (2020).
Mohan, U. R. et al. The effects of direct brain stimulation in humans depend on frequency, amplitude, and white-matter proximity. Brain Stimul. 13, 1183–1195 (2020).
Matsumoto, R. et al. Functional connectivity in the human language system: a cortico-cortical evoked potential study. Brain 127, 2316–2330 (2004).
Parvizi, J. et al. Altered sense of self during seizures in the posteromedial cortex. Proc. Natl Acad. Sci. USA 118, e2100522118 (2021).
Parvizi, J. et al. Complex negative emotions induced by electrical stimulation of the human hypothalamus. Brain Stimul. 15, 615–623 (2022).
Li, Q. et al. Core language brain network for fMRI language task used in clinical applications. Netw. Neurosci. 4, 134 (2020).
Fedorenko, E. & Thompson-Schill, S. L. Reworking the language network. Trends Cogn. Sci. 18, 120–126 (2014).
Saura, D. et al. Ventral and dorsal pathways for language. Proc. Natl Acad. Sci. USA 105, 18035–18040 (2008).
Duffau, H., Moritz-Gasser, S. & Mandonnet, E. A re-examination of neural basis of language processing: proposal of a dynamic hodotopical model from data provided by brain stimulation mapping during picture naming. Brain Lang. 131, 1–10 (2014).
Wang, Y. et al. Spatial-temporal functional mapping of language at the bedside with electrocorticography. Neurology 86, 1181–1189 (2016).
Arya, R. et al. Electrocorticographic language mapping in children by high-gamma synchronization during spontaneous conversation: comparison with conventional electrical cortical stimulation. Epilepsy Res. 110, 78–87 (2015).
Arya, R., Horn, P. S. & Crone, N. E. ECoG high-gamma modulation versus electrical stimulation for presurgical language mapping. Epilepsy Behav. 79, 26–33 (2018).
Tamura, Y. et al. Passive language mapping combining real-time oscillation analysis with cortico-cortical evoked potentials for awake craniotomy. J. Neurosurg. 125, 1580–1588 (2016).
Ogawa, H. et al. Clinical impact and implication of real-time oscillation analysis for language mapping. World Neurosurg. 97, 123–131 (2017).
Yellapantula, S., Forseth, K., Tandon, N., Aazhang, B. & NetDI Methodology elucidating the role of power and dynamical brain network features that underpin word production. eNeuro 8, 1–17 (2021).
RaviPrakash, H. et al. Deep learning provides exceptional accuracy to ECoG-based functional language mapping for epilepsy surgery. Front. Neurosci. 14, 409 (2020).
Keller, C. J. et al. Neurophysiological investigation of spontaneous correlated and anticorrelated fluctuations of the BOLD signal. J. Neurosci. 33, 6333–6342 (2013).
Nir, Y. et al. Interhemispheric correlations of slow spontaneous neuronal fluctuations revealed in human sensory cortex. Nat. Neurosci. 11, 1100–1108 (2008).
Foster, B. L., Rangarajan, V., Shirer, W. R. & Parvizi, J. Intrinsic and task-dependent coupling of neuronal population activity in human parietal cortex. Neuron 86, 578–590 (2015).
Hacker, C. D., Snyder, A. Z., Pahwa, M., Corbetta, M. & Leuthardt, E. C. Frequency-specific electrophysiologic correlates of resting state fMRI networks. Neuroimage 149, 446–457 (2017).
Kucyi, A. et al. Intracranial electrophysiology reveals reproducible intrinsic functional connectivity within human brain networks. J. Neurosci. 38, 4230–4242 (2018).
Haufe, S. et al. Elucidating relations between fMRI, ECoG, and EEG through a common natural stimulus. Neuroimage 179, 79–91 (2018).
Foster, B. L. et al. Spontaneous neural dynamics and multi-scale network organization. Front. Syst. Neurosci. 10, 7 (2016).
Conner, C. R., Ellmore, T. M., Pieters, T. A., DiSano, M. A. & Tandon, N. Variability of the relationship between electrophysiology and BOLD-fMRI across cortical regions in humans. J. Neurosci. 31, 12855–12865 (2011).
Logothetis, N. K., Pauls, J., Augath, M., Trinath, T. & Oeltermann, A. Neurophysiological investigation of the basis of the fMRI signal. Nature 412, 150–157 (2001).
Mostame, P. & Sadaghiani, S. Oscillation-based connectivity architecture is dominated by an intrinsic spatial organization, not cognitive state or frequency. J. Neurosci. 41, 179–192 (2021).
Flint, R. D., Lindberg, E. W., Jordan, L. R., Miller, L. E. & Slutzky, M. W. Accurate decoding of reaching movements from field potentials in the absence of spikes. J. Neural Eng. 9, 046006 (2012).
Muller, L., Hamilton, L. S., Edwards, E., Bouchard, K. E. & Chang, E. F. Spatial resolution dependence on spectral frequency in human speech cortex electrocorticography. J. Neural Eng. 13, 056013 (2016).
Trumpis, M. et al. Sufficient sampling for kriging prediction of cortical potential in rat, monkey, and human μECoG. J. Neural Eng. https://doi.org/10.1088/1741-2552/abd460 (2020).
Mugler, E. M. et al. Direct classification of all American English phonemes using signals from functional speech motor cortex. J. Neural Eng. 11, 035015 (2014).
Murphy, K., Birn, R. M., Handwerker, D. A., Jones, T. B. & Bandettini, P. A. The impact of global signal regression on resting state correlations: are anti-correlated networks introduced? Neuroimage 44, 893–905 (2009).
Gonzalez-Castillo, J. et al. Tracking ongoing cognition in individuals using brief, whole-brain functional connectivity patterns. Proc. Natl Acad. Sci. USA 112, 8762–8767 (2015).
Zalesky, A., Fornito, A., Cocchi, L., Gollo, L. L. & Breakspear, M. Time-resolved resting-state brain networks. Proc. Natl Acad. Sci. USA 111, 10341–10346 (2014).
Pei, X. et al. Spatiotemporal dynamics of electrocorticographic high gamma activity during overt and covert word repetition. Neuroimage 54, 2960–2972 (2011).
Macey, P. M., Macey, K. E., Kumar, R. & Harper, R. M. A method for removal of global effects from fMRI time series. Neuroimage 22, 360–366 (2004).
Davis, T. S. et al. LeGUI: a fast and accurate graphical user interface for automated detection and anatomical localization of intracranial electrodes. Front. Neurosci. 15, 769872 (2021).
Guimerà, R. & Amaral, L. A. N. Functional cartography of complex metabolic networks. Nature 433, 895–900 (2005).
Rubinov, M. & Sporns, O. Complex network measures of brain connectivity: uses and interpretations. Neuroimage 52, 1059–1069 (2010).
Acknowledgements
We thank our EEG technologists and the participants in this study, without whose help this work would not be possible. This study was supported in part by grants from NIH (R01NS094748, R01NS099210, R21NS084069, and RF1NS125026 (M.W.S.)), R01NS115929 (N.E.C.)), the Doris Duke Charitable Foundation (Clinician Scientist Development Award #2011039) (M.W.S.), the Northwestern Memorial Foundation Dixon Translational Research Grant (supported in part by NIH grant UL1RR025741) (M.W.S.), and the Northwestern Medicine Malnati Brain Tumor Institute of the Lurie Cancer Center (M.W.S.).
Author information
Authors and Affiliations
Contributions
J.K.H.: Conceptualization, methodology, software, formal analysis, investigation, and writing—original draft. R.D.F.: Methodology, software, investigation, and data curation. Z.F.: Methodology and visualization. E.M., P.R.P., J.M.R., J.W.T., and Y. W.: Investigation and data curation. N.E.C.: Conceptualization, investigation, data curation. M.C.T.: Conceptualization, investigation, and data curation. R.B.: Conceptualization, methodology, and software. M.W.S.: Conceptualization, methodology, supervision, funding acquisition, and project administration. All authors reviewed and edited the manuscript.
Corresponding author
Ethics declarations
Competing interests
J.K.H., M.C.T., R.F.B., and M.W.S. are inventors on patent application US20230123659A1 which has been submitted and is currently pre-reviewed, which is relevant to the critical node identification approaches used in this work. The remaining authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks Ajay Halai, Aaron Kucyi, Omri Raccah and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Source data
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Hsieh, J.K., Prakash, P.R., Flint, R.D. et al. Cortical sites critical to language function act as connectors between language subnetworks. Nat Commun 15, 7897 (2024). https://doi.org/10.1038/s41467-024-51839-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-024-51839-z