Introduction

Concerted proton and electron transfer reactions (proton-coupled electron transfer, PCET) are ubiquitous in Nature enabling processes ranging from photosynthesis, signaling and respiration to biosynthesis and nitrogen fixation. The exquisite control and efficiency of these processes inspires the development of, for example, artificial leaves, catalysts, or fuel cells1,2,3,4, and more recently, PCET based molecular electronics5,6 that aims to produce electronic devices with atomic-scale control over the mechanisms of charge transport bridging chemistry and quantum physics7,8,9. Nature exploits PCET reactions ranging from distinct yet coupled proton and electron transfer steps to concerted proton-electron transfer2,10,11, but molecular electronic devices operate in the solid state and usually under fixed conditions lacking a proton source and so only electron transport is considered. Here, we demonstrate the expansion in materials functionality and improvement in device performance obtainable in molecular junctions by PCET. Operating at room temperature, the devices exhibit giant hysteric negative differential resistance (NDR, a decrease in current with increasing voltage) with peak-to-valley ratio RPtV = 120 ± 6.6 and on/off ratio Ron/off = (2.4 ± 0.6) × 103, an order of magnitude improvement on prior work5. The molecules inside the junctions switch between on and off states via dynamic N-H bond formation due to sequential PCET resulting in a large change in the energy level alignment of the junctions and associated quantum mechanical tunneling rates.

Unlike our previous report of synapse-like plasticity in the 5,6,11,12,17,18-hexaazatrinaphthylene (HATNA) junctions, we show here that the observed dynamical behavior leads to an unprecedented control over the device properties depending both on device operation parameters, such as the bias voltage sweep rate, and environmental factors, such as relative humidity (RH) and pH of the junction. These tunable and dynamical features coupled to giant NDR and memory effects underpin the key advance of this work and demonstrate the potential applications for new forms of matrix or logic computing12, as well as neuromorphic computing13.

Inorganic NDR devices are used in high frequency oscillators and amplifiers, and are promising alternatives for logic and memory applications in semiconductor technologies12,13,14,15, but organic devices can provide the biocompatibility or flexibility needed for healthcare or wearables16. Although NDR has been observed in molecular devices before5,6,17, often the NDR feature visible in current density–voltage J(V) curves is noisy and the underlying mechanisms are unclear and may involve filament formation18, decomposition of the molecule19,20, or charge trapping at the interfaces21,22,23,24. Stable NDR features have been only rarely reported for molecular junctions and usually require ultra-high vacuum (UHV) conditions at cryogenic temperatures (see benchmark table in Section S1 and ref. 5). For example, Perrin et al.17 reported the molecular equivalent of a resonant tunnel diode with RPtV ratio of 3.0–7.1 at 6 K with symmetrical shapes, and Guisinger et al.20 found molecular NDR at room temperature, but with small RPtV ratios < 2 measured by ultrahigh vacuum scanning tunneling microscopy (STM). None of those examples show tunable NDR behavior with external environment or sweep rate and thus highlight the need to develop alternative molecular switches to realize stable electronic function such as NDR in molecular junctions in different atmospheres at room temperature25,26.

The mechanism of PCET depends on the physical and temporal separations of the electron and proton transfer, which in turns depends on the nuclear motions that couple them. For instance, successive initial proton (or electron) addition can accelerate the second step coupling the two processes by changing the free energy landscape of the overall reaction, or the two steps occur simultaneously (concerted PCET), where proton or electron transfer, or both, may involve nuclear tunneling2,27. Although PCET reactions are important in many areas of chemistry, their potential in molecular devices is only starting to be explored5,6. In this work, PCET stabilizes different redox states of 5,6,11,12,17,18-hexaazatrinaphthylene (Hn-HATNA where n indicates the redox state) inside a molecular tunnel resulting in large hysteric switching28. Hn-HATNA and derivatives have been widely studied and used for applications in energy storage, photovoltaics and thin film electronics29,30,31, but the mechanism of PCET in operation has not been experimentally verified. Here we report a detailed mechanistic study (by changing pH and RH and hydrogen–deuterium exchange) supported by modeling that enabled an improvement of device function of one order of magnitude highlighting the potential of PCET to advance molecular devices.

Results

Operating principle of the dynamic molecular switch

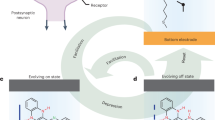
Figure 1 shows schematic illustrations of the junctions used in this study, consisting of self-assembled monolayers (SAMs) of Hn-HATNA supported by an Au bottom electrode and contacted by a Ga2O3/EGaIn top electrode5. The full characterization of the SAMs has been reported before5 from which we derived the molecular energy levels, and concluded that the SAMs are well-ordered and densely packed with all molecules in the upright position (see SI). In solution, the PCET mechanism of Hn-HATNA under electrochemical conditions has been reported before and involves ring-by-ring reduction of each pyrazine ring via six consecutive PCET steps by dynamical N-H bond formation28. Although Hn-HATNA has seven different oxidation states, Fig. 1a shows only one of the on-states (for n = 1–4) and two distinct off-states (for fully oxidized (n = 0) or reduced (n = 5–6 states), for the sake of simplicity, as characterized from previously reported cyclic voltammetry (CV) experiments and density functional theory (DFT) calculations5.

Fig. 1: Operating principle and giant NDR of the dynamic molecular switch.
figure 1

a Schematic illustration of the HATNA junctions that switches between a high conductive state (on-state) and a low conductive state (off-state). b Operating principle of the dynamic molecular switch in terms of energy (supplied by the applied bias voltage) diagram for the PCET process, the energy gap between the respective on and off states is indicated by χ. c Heatmap of log10 | J| vs. V of the Au-S-C10-HATNA//Ga2O3/EGaIn junctions at 24 °C, relative humidity = 80%, sweep rate of 2 mV/s. The black is the median average curve of <log10 | J | >m vs. V with on state, off state and reset regions. In all our experiments the voltage is applied to the top electrode and the bottom electrode is grounded. RPtV, the peak-to-valley ratio; VNDR, the voltage of the NDR peak; Ron/off, the on/off ratio.

Full size image

Figure 1b shows the operating principle of the dynamic molecular switch in terms of a simplified Gibbs free energy (ΔG) diagram and Extended Data Fig. 1 in SI shows the corresponding energy level diagrams to explain how changes in oxidation states of Hn-HATNA modulates the current flow across the junction. The positions of the Fermi level (EF) of the bottom and top electrodes and the molecular frontier orbitals (highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO)) are indicated in Extended Data Fig. 1 in SI. The applied voltage is the energy source (blue arrows in Fig. 1b) that drives changes in ΔG pushing the system continuously out of equilibrium leading to a flow of current across the molecules. Most of the electrons directly tunnel through the molecules, but occasionally an the interaction of an electron with Hn-HATNA triggers proton transfer and N-H formation changing the molecular structure of Hn-HATNA. This change in molecular structure, in turn, leads to a change in the electronic structure of the molecule and associated energy gap between the respective on and off states (indicated by χ in Fig. 1b) and associated changes in energy level alignment (Extended Data Fig. 1 in SI). Fully oxidized H0-HATNA has a large HOMO-LUMO gap and, therefore, the junction is in the off-state. For intermediate reduced states (n = 2, 3; Fig. 1b), Hn-HATNA turns on because a new molecular energy level appears. This midgap state changes the energy level alignment of the junction and increases the tunneling rate of the electrons (as shown in the Extended Data Fig. 1 in SI). In the fully reduced form (for n = 5, 6; Fig. 1b), the midgap state disappears again restoring the large HOMO-LUMO gap that turns the junctions off. In other words, Hn-HATNA turns on and off again in a single negative voltage sweep leading to the fully reduced form (arrow labeled Vred in Fig. 1b) leading to NDR. By applying a positive voltage to the junction (arrow labeled Vox in Fig. 1b), the Hn-HATNA moieties are oxidized back to the original state (n = 0) leading to hysteretic memory behavior. The hysteresis behavior occurs at a voltage sweep rate where the HATNA moieties can undergo reduction and oxidation. When the sweep rate is fast, the hysteresis diminishes due to partial redox switching (meaning that only one redox state remains populated). Thus, the molecular redox rate is crucial for modulating the performance of hysteretic NDR and memory. The charge transport mechanism in the dynamic molecular switch involves a complex interplay of resonant tunneling (on and off) and molecular redox state modulation of the Hn-HATNA molecules, which alters the energy level alignment and facilitates the observed on-off switching and giant NDR behavior in the junction.

Our experiments described below show that the protons involved with PCET are provided by water from the ambient environment and that protonation precedes electron transfer (ET). Therefore, ET and proton transfer (PT) occur at different time scales leading to time-dependent changes in the switching probability of Hn-HATNA between the on (Pon) and off (Poff) states (indicated by solid arrows in Fig. 1b). The result is a gradual, analog change in the on and off states (in sharp contrast to the digital on/off molecular switches widely reported to-date)5. For this reason, we introduce the term “dynamic molecular switch” to describe our junction.

Modeling of switching probabilities

We used the theory developed by Migliore and Nitzan32 to model the current–voltage I(V) curves (see Section S2 for details). This model quantifies how the switching probabilities change with time (scan rates) and we can extract the proton transfer rates as a function of relative humidity, acidity and kinetic isotope effect, as described in the following sections.

Although the electron flow is coherent in nature (straight blue arrow in Fig. 1a), PC is incoherent and protons must hop over an energy barrier (dashed double black arrows in Fig. 1b). The measured J of the on (Ion) and off (Ioff) states are described by the Landauer−Büttiker equation (modified to describe tunneling though SAMs33), where the tunneling barrier heights for the on and off states change by a value χ and the molecule–electrode coupling strength in the on and off state changes from \({\Gamma }_{{AB}}\) to \({{{\rm{\kappa }}}\Gamma }_{{AB}}\) (Extended Data Fig. 1 in SI). In other words, this model accounts for the lowering of the tunneling barrier by the midgap state and the associated increase in tunneling rate leading to a sharp increase in current through the multiplication factor \({{\rm{\kappa }}}\) and the value χ which was estimated from DFT5. The much slower proton hopping rates (\({R}_{{PC}}\)) are described by Marcus theory21 (which is often used to describe PC steps2,11,34) leading to a time-dependent switching probability (see Section S2 for full expressions). Thus, the current that flows across the junction depends on the probability P to be in the on and off states where \({P}^{{on}}(V){=1-P}^{\overline{{off}}}(V)\) and is given by

$$I\left(V\right)={P}^{{on}}\left(V\right){I}^{{on}}\left(V\right)+{P}^{\overline{{off}}}\left(V\right){I}^{\overline{{off}}}\left(V\right)$$
(1)

The switching probability depends on the \({R}_{+{PC}}\) and \({R}_{-{PC}}\) giving the junctions their time-dependent character as follows:

$$\frac{{{\rm{d}}}{P}^{{on}}}{{{\rm{d}}}t}=\left(1-{P}^{{on}}\right) < {R}_{+{PC}} > -{P}^{{on}} < {R}_{-{PC}} > $$
(2)

To simplify the calculations, our model assumes that ET proceeds via coherent tunneling and PT via incoherent tunneling. However, in principle, NDR simply requires that one process is much slower than the other (see for instance ref. 6). Future temperature dependent measurements may identify thermally activated components in the mechanism of ET or PT, which lies beyond the scope of the present work.

Operation mechanism of giant NDR

Figure 1c shows the measured heatmap of the J(V) response from the HATNA junctions (see “Methods” for details). The large hysteric NDR peak at negative bias is caused by the switching of the molecules from the off, to the on, and to the off state again (as visualized in Fig. 1a in the direction of Vred). In our experiments, the voltage was first increased from 0 V to +1.0 V to ensure n = 0. As the bias is then dialed back and into negative voltage, the current increases sharply at around −0.9 V because the midgap state enters the bias window5. Further increasing the voltage results in continuous reduction of HATNA which then turns off again for n = 5, 6 leading to a decrease of current despite an increase of voltage, i.e., NDR. The HATNA moieties remain in reduced form when the voltage changes from −2 V to 0 V resulting in large hysteretic behavior. The reduced Hn-HATNA moieties can oxidize back to HATNA (n = 0) only at positive bias.

The individual J(V) traces in Fig. 1c are smooth and the NDR peak is symmetrical and stable in our molecular devices. These features indicate that our switches avoid stochastic transitions characterized by excessive noise, or triangular peak shapes, as frequently observed21,22,32,35,36 which cannot be modeled with any tunneling model and strongly indicate filament formation37 (Section S1). Unlike resonant tunneling diodes17, our junctions show pronounced hysteresis which is a desirable feature for device applications, e.g., memory or artificial neurons38,39. Figure 1c defines the NDR peak position (VNDR), peak-to-valley ratio (RPtV), and current on/off ratio (Ron/off, current at forward bias divided by current at reverse bias at V = VNDR). The value of RPtV and Ron/off are 120 ± 6.6 and (2.4 ± 0.6) × 103 at a scan rate of 2 mV/s, and the value of RPtV is comparable to state-of-the-art molecular resonant tunnel diodes17. To our knowledge, giant hysteric NDR with such a large Ron/off has not been reported before (see benchmarks in Section S1 and ref. 5).

Environmental control over NDR

It is well-known that PCET is highly sensitive to water2,40,41,42. To investigate the mechanism of NDR in more detail and to further assess the importance of PCET in driving NDR, we conducted the J(V) measurements at 10 mV/s in a controlled atmosphere of Ar with a relative humidity RH ranging from 5% to 85% (water condensation hampered experiments at RH > 85%; Section S1.5.243). Figure 2a–c shows the heatmaps of all log10 | J| vs. V curves of the junctions measured at RH of 30%, 60% and 80%, respectively. In each heatmap, the black line represents the log-median average curve ( < log10|J | >m vs. V). Figure 2d (and see also Table S2) shows that NDR was absent at RH = 5%, and that the value of RPtV increases from 1.2 ± 0.1 at RH = 10% to 41.1 ± 6.7 at RH = 85% (error is the mean absolute deviation). Figure 2e shows the <log10 | J | >m vs. V curves as a function of RH along with a clear NDR peak shift at RH = 40–50% as indicated by the dashed line. These results demonstrate that ambient water is important in the mechanism of charge transport and that it is the proton source for PCET in our junctions.

Fig. 2: Electrical characteristics of the AuTS-SC10-HATNA//EGaIn junctions at different RH.
figure 2

a Log10 | J| vs. V heatmap of the AuTS-SC10-HATNA//EGaIn junctions at RH = 30%, (b) RH = 60%, and (c) RH = 80%. The black line is the mean <log10 | J | >m vs. V curve. d Distribution of RPtV as a function of RH for all measured junctions. The error bars represent the standard deviations of the mean value of RPtV. e Typical J-V curves of the junction with RH increasing from 5 to 85%. All measurements were conducted at 10 mV/s. The dashed line intersecting the NDR peak is a visual guide. The red curves are the modeling fits to the data. The error bars are standard deviations for relative humidity and mean absolute deviation for RPtV. The respective values are summarized in Table S2.

Full size image

It is well-known that water adsorption on surfaces (or interfacial water) can lead to changes in the energy level alignment of surfaces44,45. We note that there is a distinct, abrupt shift in the NDR peak position (VNDR defined in Fig. 1c) at RH = 40–50% of about 260 meV (as indicated by the vertical dashed lines, Fig. 2e). This shift suggests that water causes a small change in energy-level alignment of the junctions at around this humidity level. To investigate this effect in more detail, we conducted Kelvin probe force microscopy (KPFM) experiments at different RH levels (Section S1.6). These measurements reveal a small change in the work function of the gold substrate of around 40–50 meV at higher RH, supporting the hypothesis that the shift in VNDR is caused by water adsorption.

Figure 2e shows a direct comparison between experimental and theoretical J(V) curves (black and red lines) as a function of humidity. The model reproduces the experimental results in detail accounting for the gradual change in shape of the J(V) curves and the eventual disappearance of the NDR peak at low relative humidity values. While all parameters from the fits are given in Table S5, analysis of these fits determined that much of the variation in responses from low humidity to high humidity can be explained by just two parameters, \(\kappa\) and \(\lambda\), that govern the J(V) response. As mentioned above and described in further detail in the supplemental information, \(\kappa\) (≥\(1\)) is a multiplier describing the change in the coupling strength of the molecule to the electrodes between the on (\({\Gamma }_{{AB}}\)) and off (\({{{\rm{\kappa }}}\Gamma }_{{AB}}\)) states, with \(\kappa\) = \(1\) representing the case where no change in the coupling strength occurs. Extended Data Fig. 2a in SI shows how \(\kappa\) changes as a function of RH. At low RH\(,\,\kappa\) ~1 showing no noticeable change in the molecule–electrode coupling strength, but we find a large increase to \(\kappa\)~10 for high RH values, indicating a large increase in coupling strength when more water is present. The other governing parameter, \(\lambda\), represents the reorganization energy in the junction as PCET progresses. Extended Data Fig. 2b in SI shows a decrease in the value for \(\lambda\) as the RH is increased, clearly illustrating how the protonation process is facilitated at higher RH values.

Mechanism of proton-coupled electron transfer (PCET)

There are in principle three types of PCET reactions where the H+ and e- transfer simultaneously, or sequentially where either H+ or e- precedes the addition of the other charge carrier. Ohsaka et al.28 suggested that initial protonation of HATNA precedes PCET under wet electrochemical conditions in acidic electrolyte. To establish whether initial protonation is important in our junctions, we carried out the following experiments. By flowing Ar though 1 M aqueous HCl or 1.3 M aqueous NH4OH, we obtained an acidic or basic atmosphere with RH = 60%. Although it is not possible to measure the pH of molecular junctions directly, the effect of the acidity of the atmosphere on the junction characteristics was significant. Figure 3 shows the heatmaps of the J(V) curves along with the <log10 | J | >m vs. V curves recorded in acidic, basic or neutral Ar atmospheres with RH = 62–65%. Under neutral conditions, RPtV = 18.5 ± 2.8, but its value increases to 31.2 ± 3.2 under acidic conditions while NDR is suppressed under basic conditions and RPtV decreases to 7.9 ± 1.4. The values of Ron/off under acidic, basic and neutral conditions are 198 ± 23, 178 ± 95 and 104 ± 21, respectively. Figure 3e shows a direct comparison between experimental and theoretical I(V) curves (black and red lines) as a function of pH. The value of \(\kappa\) decreases sharply from acidic to basic conditions while \(\lambda\) is far less sensitive (Extended Data Fig. 2 in SI). We repeated the measurement under D2O atmosphere to determine the kinetic isotope effect (KIE). Figure 3c shows the heatmap of the junction recorded under D2O atmosphere with RH = 63%. The value of RPtV decreases to 11.4 ± 2.2 with respect to that recorded under H2O atmosphere resulting in a H/D ratio of 1.6. Fitting to theory shows that this change is mainly driven by a decrease of \(\kappa\) (Extended Data Fig. 2 in SI). These observations are consistent with stepwise PCET reaction where a proton first binds to HATNA, which may be favored by the basic nature of HATNA, followed by electron addition and N-H bond formation3,27. Figure 3d summarizes the distribution of the value of RPtV obtained from the junctions under different conditions with the corresponding <log10 | J | >m vs. V curves in Fig. 3e. We note that the NDR peak shapes vary depending on the experimental conditions which may be caused by a change in relative proton and electron (incoherent) tunneling rates. These results show that it is possible to control the NDR effect by changing the concentration of H+ to gate the tunneling channels in the on and off states.

Fig. 3: Electrical characteristics of the AuTS-SC10-HATNA//EGaIn junctions in acidic, basic, neutral and D2O atmospheres.
figure 3

a Log10 | J| vs. V heatmap of the AuTS-SC10-HATNA//EGaIn junctions under the condition of HCl, NH4OH (b) and D2O (c) at RH 60%, the black line is <log10 | J | >m vs. V curve. d The distribution of RPtV as a function of the determined conditions under basic (blue), acidic (green), D2O (gray) and neutral atmospheres (black), along with (e) the corresponding log-average J-V curves of the junction with red curves showing the modeling fits to the measured data. The error bars are standard deviations for relative humidity and mean absolute deviation for RPtV. The respective values are summarized in Table S2.

Full size image

Sweep rate dependent behavior

To demonstrate the dynamic behavior of the junctions, we recorded J(V) curves at scan rates ranging from 0 to 250 mV/s. Figure 4a and b show the data in the corresponding semi-log plots and linear scales. First, the RPtV ratio decreased from 18.8 at 10 mV/s to 1.17 at 250 mV/s while the NDR peak current increases from 142 μA at 10 mV/s to 254 μA at 36 mV/s and decreases to 72 μA at 250 mV/s (Extended Data Fig. 3 in SI). This dynamical behavior is also clearly reflected in the changes in the value of ΔINDR at forward Ifw and backward bias Ibwd direction (ΔI = Ifwd – Ibwd) which goes through a maximum at 36 mV/s (Fig. 4d). To establish the dynamical behavior of the junctions, we mapped the changes in switching probabilities of the molecules inside the junctions by fitting our data to the model by Nitzan32. The agreement between experiment and theory is excellent (see Section S2 for details of fitting) and the experimentally measured dynamical nature of the system is consistent with the behavior predicted by the Nitzan model.

Fig. 4: Sweep rate characterization of the junctions.
figure 4

a–b Scan rate dependent J(V) and I(V) measurements. c Calculated probability of the system being in the off state (\({P}^{\overline{{AB}}}\)) at the different scan rates given in panel b, with labels 1-4 marking bias voltage cycles 0 → + 1 V [1] → 0 V [2] → −2V [3] →0 V [4]. d ΔI values (ΔI = Ifwd - Ibwd) between the forward (Ifwd) and backward (Ibwd) sweeps at VNDR determined from (e) the I(V) fits (red) to the experimental I(V) data (black). Figures 4a–b and 4e are adapted from data first reported in [5], with the evolution of the probability investigated and fully modeled in the present work.

Full size image

Figure 4c shows the evolution of the probability of the junction to be in the off state (\({P}^{\overline{{AB}}}\)) as bias voltage cycles (0 →  + 1 V [1] → 0 V [2] → -2V [3] → 0 V [4]) are repeated with different scan rates. Starting in the on-state (1 and 2) with \({P}^{\overline{{AB}}}=0\) (blue line, ↻1), the system evolves towards the off state (3) and completely turns off (4) and then shifts back towards the on state at positive bias of the second bias voltage cycle (1 and 2 of the orange line, ↻2) at low scan rates. At increasingly high scan rates, the system only partially recovers to the on state at positive bias because the system does not have sufficient time to switch back. Hence, \({P}^{\overline{{AB}}}\) increases as the cycling evolves, with each initial probability at the start of the cycle progressively approaching \({P}^{\overline{{AB}}}\) = 1.

To provide more insight into this behavior, ΔI reaches a maximum around 25–36 mV/s (Fig. 4d, e) due to shifting of the transition to higher negative voltages as scan rate increases, which increases current. Therefore, ΔI is a trade-off between the initial probability and the scan rate, which together determine the observed non-linear behavior of the NDR.

Discussion

In summary, we report giant NDR of RPtV = 120 ± 6.6 enabled by PCET via optimization of pH, humidity and scan rate. The NDR feature in our junctions is stable and is not disadvantaged by the stochastic behavior found in NDR devices based on charge traps or filament formation19,22,23,24, because the different oxidation states of the HATNA active layer are stabilized by reversible covalent N-H bonds. The molecules switch depending on the bias polarity resulting in hysteresis with large values of current on/off ratios of (2.4 ± 0.6) × 103. Our giant NDR enables rapid and efficient switching with high resolution and sensitivity. This combined functionality of an on/off switch and NDR provides a pathway to develop new types of devices beyond resonant tunneling diodes, such as biosensors46. The NDR modulation by humidity, pH and sweep rate could be a useful new feature for next-generation sensors and artificial neural networks that respond to, and learn from their environment5,6,47,48,49. Our findings demonstrate that PCET is an advantageous mechanism of charge transport in molecular devices, enabling improved performance and generating new types of dynamical electronic function for molecular-scale electronics applications.

Methods

Molecule synthesis and self-assembled monolayer (SAM) formation

5,6,11,12,17,18-hexaazatrinaphthylene (HATNA) was synthesized and characterized in accordance with our previous report5 and the HATNA SAMs were prepared by employing a well-established method50. 1.0 mg HS-C10-HATNA was dissolved in 5 ml of freshly distilled tetrahydrofuran (THF) at a concentration of 0.35 M. The solution was then given a 15 min N2 flush to eliminate the oxygen. Subsequently, freshly prepared Au surfaces were immersed in the solution. After about 24 h, the Au substrates were removed from the solution, promptly washed with THF and ethanol, and gently dried in a flow of N2. For Kelvin probe force microscopy (KPFM) experiments HATNA-SAc SAMs were employed. 1.0 mg AcS-C10-HATNA was dissolved in 5 ml of freshly distilled tetrahydrofuran (THF) at a concentration of 0.33 M. This was following by addition of 20 μl ammonia (26–28%), and freshly prepared Au surfaces were immersed in the solution. After about 24 h, the Au substrates were removed from the solution and immediately washed with large volumes of THF and ethanol, and the substrates were then gently dried with N250.

Electrode preparation

The top electrode was prepared based on the well-known EGaIn technique. In this procedure, an EGaIn alloy was ultilized to shape a freshly conical tip, which was subsequently used for establishing contacts with the SAMs by serving as the top electrode51. The well-known template-stripping method was used to fabricate the bottom electrode with a root mean square surface roughness over an area of 1 × 1 μm2 of 2–3 Å. Barber et al. reported water condensation on EGaIn junctions for RH > 85%; for this reason, we limited our experiments to RH = 85%43,52. Initially, a 200 nm thick Au (99.999% Au granules, ACI Alloys) was thermally evaporated onto a silicon wafer (featuring a native SiO2 thin layer on the surface, Syst Integration Pte Ltd). Pre-cleaned glass slides were then glued on the Au surface using thermal glue (EPOTEK 353ND). The Au thin film was then heated at 80 °C for 3 h to cure the adhesive. The resulting Au electrode was stored in a dry box and template-stripped immediately prior to usage.

Surface characterization

The X-ray photoelectron spectroscopy (XPS), ultraviolet photoelectron spectroscopy (UPS), and near-edge X-ray absorption fine structure (NEXAFS) spectroscopy of the HATNA SAMs were conducted on template-stripped Au surfaces coated with S-C10-HATNA SAM, following established procedures5,53.

Junction fabrication and electrical measurements in air

The junctions were fabricated with a grounded Au bottom electrode, a HATNA monolayer, and a cone-shaped GaOx/EGaIn top electrode, where the bias was applied to the top EGaIn electrode, following the method given in ref. 51. Electrical measurements were conducted by employing a LabVIEW-controlled Keithley 6430 source meter. J(V) curves were recorded with a voltage sweep sequence from 0 V → +1 V → 0 V → -2 V → 0 V, at intervals of 20 mV.

Junction fabrication and electrical measurements in different RH and pH

Here, we report a modified setup of the EGaIn technique with atmospheric control of the junction to probe the electrical properties and explore the underlying mechanism of NDR effects in large area junctions. The detailed experimental setup and atmospheric control of humidity level and acid/base conditions can be found in the SI (Supplementary Section S1.3).

The Kelvin probe force microscopy (KPFM)

The experiments were conducted in a Bruker Icon atomic force microscopy (AFM) in a controlled temperature and humidity environment. The humidity is controlled by a home-built humidity controller which mixes N2 gas with H2O vapor54. The humidity is measured (with a TFA®Digital Professional Thermo-Hygrometer KLIMA BEE) both at the inlet and the outlet of the environmental chamber, to verify if the relative humidity remains constant throughout the process. The sample is heated using a platinum resistive-type heater in a ceramic body and a tungsten cap controlled by a thermal applications controller. Before the measurement, the sample is first heated to 90 °C in a N2 environment to remove any water present in the system. A heavily doped n-type Si-cantilever with a resonance frequency 75 kHz and a force constant of 2.8 N/m (SSS-FMR, Nanosensors). The FM-KPFM mode is used, where the electrostatic force gradient is detected by the frequency shift of the cantilever oscillation. The tip work function is determined to be 4.5 eV after calibration on a Au surface. The sample was grounded in the KPFM-measurement and therefore the contact potential difference (VCPD) is determined by:

$${V}_{{CPD}}=\frac{{\varphi }_{t}+{\varphi }_{s}}{\left|e\right|}$$
(3)

With e the elementary charge and φs and φt the work function of the sample and tip, respectively. When the work function of the tip is known, the work function of the sample can be determined.

Statistical analysis of J(V) characteristics

We performed the statistical analysis of J(V) data with the median averages of the current ( < log10| J | >m) and the median absolute deviations (σm) following a previously reported method55. This approach is applied for its independence from presumptions about the data distribution as detailed elucidated in ref. 5. The values of <log10 | J | >m and σm were calculated from the log10 | J| values measured at each bias step. To visualize the J(V) curves, heatmaps were generated using OriginPro 2019b software with 2D kernel density estimations. In these estimations, the density values were calculated based on a bi-dimensional Gaussian kernel, and the bandwidth was determined through a bivariate kernel density estimator with a grid size of 100.

Theoretical modeling of the transport dynamics

We analyzed the switching behavior of the junctions using a theoretical model developed by Migliore and Nitzan32. The currents passing through the junctions in the on and off conduction states were described by the standard Landauer single-level quantum model, adjusted to describe currents across large-area junctions33. The fitting results are given in Figs. 2–4. The detailed description of the modeling is provided in Supplementary Section S2.