Introduction

The concept of chiral (TRS breaking) charge order is a fascinating aspect of modern condensed matter physics, reflecting a state where electron arrangements break mirror symmetry, akin to left-handed and right-handed twists. This chiral charge ordering can lead to unconventional electronic properties1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28, and host exotic quasi-particles, potentially useful for quantum computing and novel electronic devices due to its influence on electronic band structures and interactions.

The AV3Sb5 kagome superconductors represent a unique and ideal platform known for hosting charge orders that possibly break TRS11,12,13,15,16,29,30,31,32,33,34. This phenomenon of high-temperature TRS breaking charge order is exceedingly rare. It offers a profound analogy to pivotal theoretical models in physics: the Haldane model35 for the honeycomb lattice and the Varma model36 for the square lattice. The evidence for TRS breaking in these materials primarily comes from zero-field and high-field muon spin rotation (μSR) measurements. μSR, recognized for its exceptional sensitivity to magnetic phenomena15,37,38,39,40, has provided indications of TRS breaking in the charge ordered state of all three variants of AV3Sb5; KV3Sb512, RbV3Sb513, and CsV3Sb516. This uniformity across different compositions suggests that the nature of this symmetry breaking is intrinsic to Kagome superconductors in general.

In addition to the increase of the internal magnetic fields in the TRS breaking state by μSR, other manifestations of unconventional charge order in these materials have been observed. Notably, these include the giant anomalous Hall effect24,25 detected through transport measurements. Furthermore, a field-tunable chirality switch effect11,41,42,43 and the ability to control chiral transport23 properties have been reported. These features point to the presence of chiral electronic states, which are sensitive to external magnetic fields. Kerr effect measurements regarding TRS breaking are contradictory; some indicate its presence30, while others do not44. Among these various techniques, μSR stands out as arguably the most magnetically sensitive, providing a critical tool for detecting and understanding the subtle magnetic quantum phenomena occurring in these Kagome superconductors. The combination of high-temperature TRS breaking charge order and the unique set of properties in AV3Sb5 superconductors therefore not only challenge existing theoretical frameworks but also open up potential avenues for novel electronic applications10.

Previous μSR experiments12,13,15,16,29 have primarily focused on exploring the TRS breaking response within the bulk of AV3Sb5 superconductors. However, there is a notable gap in our understanding regarding the magnetic characteristics near the surfaces of these materials. The lack of understanding in this area is particularly crucial given the research on thin films45, which show non-monotonic variations in charge ordering temperature as a function of thickness. Additionally, it is vital to comprehend the influence of the surface on the overall electronic and magnetic properties of the materials. Given this context, it becomes imperative to extend our investigations to probe the magnetism at the surface of AV3Sb5. Understanding surface magnetism is not only crucial for a comprehensive understanding of the material’s magnetic properties, but also for unraveling the interplay between charge order and TRS breaking. Thus, a focused effort to explore and characterize the magnetic fingerprints at the surface of AV3Sb5 is essential to advance our knowledge in this area.

In this study, we utilize the unique low-energy muon spin rotation method46,47, coupled with local field numerical analysis, to investigate the depth-dependent TRS breaking response in single crystals of RbV3Sb5 (which exhibits charge order) and Cs(V0.86Ta0.14)3Sb5 (which does not exhibit charge order). In RbV3Sb5, we detect a notable fourfold enhancement of the zero-field muon spin relaxation rate near the crystals surface compared to the bulk. Calculations indicate that the observed increase in the relaxation rate is attributable to magnetism, rather than being a consequence of muon-induced structural distortions or a secondary effect due to structural changes stemming from charge order48. In Cs(V0.86Ta0.14)3Sb5, which lacks charge order, there is no noticeable increase in the internal field width, both in the bulk and near the surface. These observations imply a strong connection between the TRS breaking response and the presence of charge order. This finding emphasizes the need for a microscopic understanding of why the surface offers more favorable conditions for the formation of novel magnetism.

Results and discussion

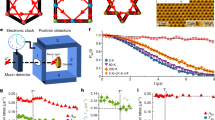
The AV3Sb5 structure comprises a Kagome lattice of V atoms interlaced with a hexagonal lattice of Sb atoms, crystallizing in the P6/mmm space group (Fig. 1a, b). Scanning tunneling microscopy (STM) atomic topographic images of the Sb surface for RbV3Sb5 and Cs(V0.86Ta0.14)3Sb5 single crystals are presented in Fig. 1c and d, respectively. The Fourier transform of the image for RbV3Sb5 (inset of Fig. 1c) reveals both 1 × 1 lattice Bragg peaks (blue circles) and 2 × 2 charge-order peaks (red circles). In contrast, the Fourier transform for Cs(V0.86Ta0.14)3Sb5 displays only the Bragg peaks, indicating the absence of 2 × 2 ordering and thus charge order in this compound. The critical temperature for superconductivity and the superfluid density are significantly higher in Cs(V0.86Ta0.14)3Sb5 compared to RbV3Sb5, as shown in the Supplementary Note 1 and the Supplementary Fig. 1. This enhancement is attributed to the complete suppression of charge order in the Ta-doped sample. Figure 1e illustrates a schematic of the zero-field (ZF) and transverse-field low-energy μSR setup. Various detectors placed around the sample track the incoming μ+ and the outgoing e+. We employed a muon beam with an adjustable energy range from E = 1 keV to 30 keV. Each E corresponds to a different muon implantation depth profile. This range of energies allows us to vary the implantation depths of the muons from a fraction of a nanometer up to 200 nm, therefore enabling us to conduct depth-dependent μSR studies (approximately \(\bar{z}\) = 10–200 nm in depth). Figure 1f shows the muon implantation profile in (Rb,Cs)V3Sb5 for various implantation energies, simulated using the Monte Carlo algorithm TrimSP46.

Fig. 1: Atomic topographic images of AV3Sb5 and experimental setup.
figure 1

a The crystallographic structure of prototype compound AV3Sb5 (A = Rb or Cs). The V atoms form a kagome lattice intertwined with a hexagonal lattice of Sb atoms. The (Rb,Cs) atoms occupy the interstitial sites between the two parallel kagome planes. In (b) the vanadium kagome net has been emphasized, with the interpenetrating antimony lattice included to highlight the unit cell (see dashed lines). c Scanning tunneling microscopy of the Sb surface for RbV3Sb5. The inset is the Fourier transform of this image, displaying 1 × 1 lattice Bragg peaks (blue circles) and 2 × 2 charge-order peaks (red circles). d Atomic topographic image of Sb surface in Ta-doped Cs(V0.86Ta0.14)3Sb5. The inset is the Fourier transform of this image, showing the absence of 2 × 2 ordering peaks, leaving only Bragg peaks. e Experimental LE-μSR setup with applied field vector Bext perpendicular to the sample surface (i.e., along the c-axis of RbV3Sb5), and arrays of positron detectors used to count muon decay events. f Muon implantation profile of (Rb,Cs)V3Sb5 simulated for several implantation energies.

Full size image

In Fig. 2a, we present high-statistics ZF-μSR spectra for RbV3Sb5, displayed as the polarization function PZF(t) = AZF(t)/AZF(0). These measurements were taken both above and below the charge ordering temperature TCO ≃ 110 K in the bulk of the material. A sizeable increase in the relaxation of the asymmetry observed at T = 5 K is accompanied by a gradual change from a Gaussian-like curve to a more exponential-like curve for P(t) at early times. The ZF-μSR spectrum is well described using the Gaussian Kubo-Toyabe (GKT) depolarization function49 multiplied by an exponential decay function, consistent with previous work12:

$${P}_{ZF}^{{{\rm{GKT}}}}(t)=\left(\frac{1}{3}+\frac{2}{3}(1-{\Delta }_{ZF}^{2}{t}^{2}) \exp \left[-\frac{{\Delta }_{ZF}^{2}{t}^{2}}{2}\right]\right) \exp (-{\Gamma }_{ZF}t)$$
(1)

where Δ/γμ represents the width of the local field distribution, arising from nuclear moments and γμ/2π = 135.5 MHz/T is the muon gyromagnetic ratio. ΓZF is attributed to muon spin relaxation originating from electronic sources12,15.

Fig. 2: Muon stopping site and ab initio prediction in RbV3Sb5.
figure 2

a Zero-field μSR time spectra in the bulk of RbV3Sb5 at two temperatures, above and below TCO. The light green curve represents the ab initio prediction in the absence of electronic moments. The dashed black line is obtained by displacing the muon from its equilibrium position by only 0.03 Å, which restores almost perfect agreement with the experimental results. b The muon site, indicated by the red ball located between the in-plane Sb1 and the Rb atom in RbV3Sb5, was obtained using the DFT+μ method. The figure also shows the displacement of the nearest neighbor Sb atom from the kagome plane formed by V atoms.

Full size image

To obtain a quantitative understanding of the zero-field muon spin relaxation in RbV3Sb5, we utilized first-principles calculations to compute the muon polarization function, using Density Functional Theory (DFT) simulations within the DFT+μ approach50. The first principles prediction of P(t) accounts for the interaction between the muon and the surrounding nuclear dipole moments. Additionally, the muon’s impact on both the lattice and the electric field gradient at various nuclear sites was assessed. This is crucial since all isotopes in RbV3Sb5 undergo quadrupolar interactions. A comprehensive explanation of our methodology is available in the Supplementary Note 3 and Supplementary Figs. 3–9. Our analysis reveals a single stable muon site in RbV3Sb5, depicted in Fig. 2b. The muon’s nearest neighbor is the in-plane Sb1 atom, followed by an Rb atom, with two hexagonal arrangements of out-of-plane Sb2 and V atoms from the kagome lattice as further neighbors. We then calculated the muon polarization function, P(t), using Celio’s approach51, as implemented in the UNDI code52. This estimate does not include the uncertainties related to the ab initio estimates of atomic positions and electric field gradients. The calculated polarization closely matches experimental observations, albeit with a slightly faster depolarization. A perfect alignment with experimental data is achieved by minutely adjusting the muon’s position, specifically a 0.03 Å shift from the nearest Sb atom. Notably, similar discrepancies have been observed in other DFT+μ studies50,53. At T~TCO, the experimental and theoretical results align well, indicating that nuclear moments are predominantly responsible for the muon spin relaxation. However, the relaxation rates increase in the charge-ordered state indicating a deviation from static nuclear dipole-induced relaxation. Persisting with a nuclear-focused explanation for P(t), the observed low-temperature variations imply significant shifts in the position or electronic environment of the muons two nearest neighbors, Sb1 and Rb, within the charge-ordered state. This is not mirrored for Sb in CsV3Sb5, as evidenced by nuclear quadrupole resonance studies54, nor for Rb in RbV3Sb555. This reinforces the conclusion12 that the observed increase in the relaxation rate at low temperatures is of electronic origin, and that the parameter ΓZF in Eq. (1) reflects mostly the temperature-dependent electronic contribution. Therefore, an increase in ΓZF signifies an increase of the local magnetic fields, i.e., the breaking of time-reversal symmetry.

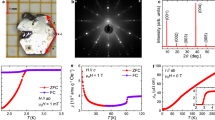
We then examine the depth dependence of the time-reversal symmetry (TRS) breaking signal in both RbV3Sb5 and Cs(V0.86Ta0.14)3Sb5 crystals. This is achieved through ZF and low transverse field μSR experiments. For RbV3Sb5, the ZF-μSR spectra measured at both the surface (E = 2 keV, corresponding to a mean implantation depth, \(\bar{z}\), of 10 nm) and in the bulk (E = 14 keV, \(\bar{z}\) = 90 nm) are shown in Fig. 3a. A noticeable difference in the shape of the field distribution was observed between these two depths. Specifically, the ZF-μSR spectrum in the bulk was analyzed using the Eq. 1. Conversely, the ZF-μSR spectrum at the surface is accurately described by only the exponential term. The zero-field relaxation, which is decoupled by applying a small external magnetic field longitudinally aligned with the muon spin polarization (BLF = 5 mT, where LF stands for “Longitudinal Field” (see Fig. 3a), suggests that the substantial relaxation observed at the surface is due to spontaneous fields that are static on the microsecond timescale56,57. The enhancement of the relaxation rate is also observed in weak transverse field (BTF = 5 mT) experiments (transverse-field μSR spectra are shown in the Supplementary Note 2 and the Supplementary Fig. 2). Figure 3b, c depict the temperature dependences of the zero-field and transverse-field relaxation rates, respectively. This is represented in terms of the differences: ΔΓZF = ΓZF(T) - ΓZF(T=300K) (see Fig. 3b) and ΔσTF = σTF(T) − σTF(300K) (see Fig. 3c). This approach is adopted to facilitate a clearer comparison between the two sets of data and to remove any potential systematic errors due to the different implantation energies used. The response observed at a depth of 90 nm from the surface is characterized by a two-step increase in the relaxation rate, commencing at the onset of the charge order temperature TCO ≃ 110 K. This finding aligns with previous results13 obtained using the GPS instrument58, which predominantly probes the bulk response. Previously13, it was also shown that the two-step behavior becomes more pronounced when a high magnetic field is applied along the c-axis. At a shallower depth of 10 nm, the increase in the relaxation is about four times larger than in the bulk and decreases monotonously with increasing temperature, lacking the two-step feature. Interestingly, this rate tends to plateau at a temperature about 60 K higher than TCO of the bulk. This observation suggests that not only does the magnitude of the magnetic response vary, but also the onset temperature shifts towards higher values at shallower depths. Specifically, the emergence of the TRS breaking signal near the surface occurs at \({T}_{{{\rm{TRSB}}}}^{{{\rm{Surf}}}}\simeq\) 175 K. The relaxation rate as a function of implantation energy or mean depth \(\bar{z}\), measured under a transverse field of 5 mT and at a temperature of 5 K, is depicted in Fig. 3d. The energy dependence was fitted to the function59,60:

$$\Delta {\sigma }_{TF}(E)={\int_{0}^{\infty }}P(z,E)\Delta \sigma (z)dz.$$
(2)

where P(z, E) is the probability of the muon beam implanted with energy E to stop at a depth z, shown in Fig. 1f. ΔσTF is assumed to have a step-like function with two regions. This analysis reveals a characteristic depth of \({\bar{z}}_{c}\simeq\) 33 nm, in which we observe a notable enhancement in the relaxation rate. This finding is significant as it establishes a characteristic depth where the materials properties begin to exhibit marked changes, distinguishing the near surface behavior from that of the bulk.

Fig. 3: Depth dependent magnetism in RbV3Sb5.
figure 3

a The ZF μSR time spectra for the single crystal sample of RbV3Sb5, obtained at T = 5 K at the surface (mean implantation depth of \(\bar{z}\) = 10 nm) and in the bulk (\(\bar{z}\) = 90 nm). The dashed curve represents a fit to Eq. (1). The solid line represents a fit using only the exponential function \(\exp (-\varGamma t)\). The μSR time spectrum, obtained at T = 5 K under the magnetic field of 5mT, applied parallel to the initial muon spin polarization is also shown. The error bars are the standard error of the mean (s.e.m.) in about 106 events. b Temperature dependence of the relaxation rate ΔΓZF = ΓZF(T) − ΓZF(T=300K), measured in zero-field, at the surface (\(\bar{z}\simeq\) 10 nm) and in the bulk (\(\bar{z}\simeq\) 90 nm) of the single crystal RbV3Sb5. The absolute value of zero-field relaxation rate at room temperature is as follows: ΓZF ≃ 0.153(5) μs−1. c Temperature dependence of the relaxation rate ΔσTF = σTF(T)-σTF(300K), measured in an applied field of 5 mT, at the surface (\(\bar{z}\simeq\) 10 nm) and in the bulk (\(\bar{z}\simeq\) 90 nm) of the single crystal RbV3Sb5. The error bars represent the standard deviation of the fit parameters. d The muon-spin relaxation rate in RbV3Sb5, measured at 5 K and in applied field of 5 mT, as a function of muon implantation energy, E. Top axis shows the average implantation depth, \(\bar{z}\). The dashed curve is the predicted behavior of the ΔσTF assuming a step-like depth dependence and considering the muon implantation profile59,60.

Full size image

We now turn our attention to the results for Cs(V0.86Ta0.14)3Sb5, which are summarized in Fig. 4. Contrary to RbV3Sb5, the variation in the field distribution shape between these two depths is much less pronounced. Figure 4a shows the ZF-μSR spectra measured at both the surface (corresponding to a mean implantation depth, \(\bar{z}\), of 10 nm) and in the bulk (\(\bar{z}\) = 90 nm), indicating a nearly perfect overlap of the field distribution between these two depths. Figure 4b displays the temperature dependence of the zero-field relaxation rate ΔΓZF, as measured in the bulk at a depth of 90 nm. The rate remains constant across the entire temperature range, with no discernible increase at lower temperatures. These results indicate that in Cs(V0.86Ta0.14)3Sb5, where charge order is fully suppressed, there is an absence of a TRS breaking response. Additionally, as depicted in Fig. 4c, there is no enhancement in the relaxation rate near the surface. This is evident when comparing the transverse field (TF) relaxation rates at depths of \(\bar{z}\) = 90 nm and \(\bar{z}\) = 10 nm. The initial asymmetry also exhibits no temperature dependence down to 5K (see Fig. 4d), further confirming the lack of any low-temperature anomalies in Cs(V0.86Ta0.14)3Sb5.

Fig. 4: Absence of magnetism in Cs(V0.86Ta0.14)3Sb5.
figure 4

a The ZF μSR time spectra for the single crystal sample of Cs(V0.86Ta0.14)3Sb5, obtained at T = 10 K at the surface (mean implantation depth of \(\bar{z}\) = 10 nm) and in the bulk (\(\bar{z}\) = 90 nm). The dashed curve represents a fit to Eq. (1). The error bars are the standard error of the mean (s.e.m.) in about 106 events. b Temperature dependence of the relaxation rate ΔΓZF = ΓZF(T) - ΓZF(T=300K), measured in the bulk (\(\bar{z}\simeq\) 90 nm) of the single crystal Cs(V0.86Ta0.14)3Sb5. c, d The temperature dependence of the low transverse field (5mT) muon spin relaxation rate ΔσTF = σTF(T)-σTF(200K) (c) and the initial asymmetry (d), measured at the surface (\(\bar{z}\simeq\) 10 nm) and in the bulk (\(\bar{z}\simeq\) 90 nm) of the single crystal Cs(V0.86Ta0.14)3Sb5. The error bars represent the standard deviation of the fit parameters.

Full size image

Previous μSR research12,13,16 uncovered weak internal magnetic fields of around 0.6 G in the charge ordered state of AV3Sb5, hinting at spontaneous time-reversal symmetry breaking. However, the faintness of internal fields has often prompted inquiries into their intrinsic nature. In this paper, we report four key findings: (1) Through muon stopping site calculations and local field numerical analysis, we have ruled out muon-induced effects or structural distortions as the cause for the increased zero-field muon spin relaxation rate, attributing it instead to intrinsic magnetism. The observation of TRS-breaking charge order in AV3Sb5 has been ascribed to orbital current order within the vanadium kagome layer18,20,31,32, potentially exerting a significant influence on the superconducting state. Theoretical models indicate an exceedingly small net flux, resulting in a correspondingly minor net magnetic moment within the unit cell of the orbital current order. The hypothesized orbital current is thought to be consistent throughout the lattice, but with an alternating flow direction, leading to non-uniform fields at the muon site. In this context, muons could interact with these closed current loops below the temperature \({T}_{{{\rm{TRSB}}}}^{{{\rm{Surf}}}}\), which would result in an enhanced internal field width as detected by the muon ensemble, in the charge ordered state. Similar effects of static magnetic fields appearing near the surface due to orbital loop currents were observed in Sr2RuO4 crystals39. The muon stopping site in RbV3Sb5 is notably distant ( ~ 3.5 Å) from the vanadium lattice, symmetrically situated around the hexagon of vanadium atoms. This symmetric arrangement, together with the negligible net flux resulting from the orbital currents, can account for the observed small TRS breaking signal in the charge-ordered state. (2) A pronounced enhancement, by a factor of four, of the zero/low-field muon spin relaxation rate is observed near the surface of RbV3Sb5 compared to the bulk. The characteristic depth scale at which the enhancement of relaxation occurs is \({\bar{d}}_{c}\simeq\) 33 nm. Near the surface, i.e., below 33 nm, the estimated field strength is Γ12/γμ ≃ 2.5 G, whereas in the bulk it is 0.6 G. This not only provides stronger evidence of TRS breaking in this material but also demonstrates the significant tunability of the TRS signal under zero-field conditions. (3) Near the surface, the onset of the TRS breaking response seems to occur at a temperature \({T}_{{{\rm{TRSB}}}}^{{{\rm{Surf}}}}\simeq\) 175 K. This indicates that in the bulk of RbV3Sb5, TRS breaking takes place within the charge ordered state, whereas near the surface, it emerges at a temperature notably higher than the onset of charge order TCO ≃ 110 K. Given that a range of surface and bulk-sensitive methods identify 110 K as the onset temperature for charge order in RbV3Sb5, it can be logically inferred that the temperature at which charge order occurs is consistent across both the surface and the bulk. Recent work on the sister compound CsV3Sb5 shows that reducing the crystal thickness below 27 nm increases the charge ordering temperature, with a maximum of \({T}_{{{\rm{CO}}}}^{{{\rm{Surf}}}}\simeq\) 120 K (see the Supplementary Note 4 and the Supplementary Fig. 10). However this is still significantly lower than the \({T}_{{{\rm{TRSB}}}}^{{{\rm{Surf}}}}\simeq\) 175 K we found near the surface. (4) Furthermore, in Cs(V0.86Ta0.14)3Sb5, which lacks charge order, no increase in relaxation rate is observed either at the surface or in the bulk down to 5 K. This strongly suggests a direct correlation between charge order and the TRS breaking signal in AV3Sb5 Kagome superconductors and rules out systematic effects as a source of the relaxation enhancement near the surface. These findings also show that while the TRS breaking response is closely related to the presence of charge order, TRS breaking can manifest at temperatures higher than those of charge order onset. In this regard, recent torque measurements61 have demonstrated a two-fold in-plane magnetic anisotropy above charge order, which breaks the rotational symmetry of the crystal. This finding aligns with our observations.

Our research identifies a kagome superconductor RbV3Sb5 as the system with the highest TRS breaking temperature, reaching ≃ 175 K. The observation that the TRS breaking signal at the surface of RbV3Sb5 occurs at a higher temperature than the onset of charge order presents an intriguing and novel aspect of the physics in these materials. This suggests that the mechanism driving the TRS breaking phenomenon might be different or more pronounced near the surface. This could mean that surface interactions or reconstructions play a significant role, possibly indicating an enhanced or modified electron correlation effect near the surface compared to the bulk. Typically, it is anticipated that surface effects occur extremely close to the surface. Present investigations suggest that the transition from bulk to surface occurs over a range of 33 nm in RbV3Sb5. This observation might open avenues for tuning the electronic properties of these materials through surface engineering, which could be relevant for potential applications in electronic devices where surface properties are crucial. The fact that TRS breaking occurs at a higher temperature than charge order in RbV3Sb5 mirrors the behavior observed in cuprate high-temperature superconductors62, where the pseudogap phase, thought to involve orbital currents36, also emerges at a higher temperature than charge order. This similarity draws intriguing parallels between these two distinct types of materials and points to potentially fundamental and universal behaviors in these complex material systems.

Methods

Muon-spin rotation

In a μSR (muon spin rotation) experiment, nearly 100% spin-polarized muons μ+ are implanted into the sample one at a time. These positively charged μ+ particles thermally stabilize at interstitial lattice sites, effectively serving as magnetic microprobes within the material. In the presence of a magnetic field, the muon spin undergoes precession at the local field Bμ at the muon site, with a Larmor frequency νμ given by γμ/(2π)Bμ, where γμ/(2π) = 135.5 MHz T−1 represents the muon gyromagnetic ratio.

Experimental details

Zero field (ZF) and weak transverse field (TF) μSR experiments were conducted on single crystalline samples of RbV3Sb5 and Cs(V0.86Ta0.14)3Sb5 using the low energy μSR instrument at the Swiss Muon Source (SμS), Paul Scherrer Institut, in Villigen, Switzerland46,47. For these measurements, large single crystal pieces were used. The crystals were carefully arranged in a mosaic layout on a nickel-coated plate and secured with silver epoxy, covering an area of 1.5 × 1.5 cm2. The samples were mounted on a cold finger cryostat, which accommodates temperatures ranging from 5–300 K. The crystals were aligned such that was done such that the c-axis was parallel to the muon beam and the applied magnetic field. Measurements were carried out with the muon spin polarization both parallel to the c-axis (in a longitudinal configuration) and perpendicular to the c-axis (in a transverse field configuration). We utilized a muon beam that could be adjusted within an energy range of 1 keV to 30 keV. The implantation energy, E, corresponds to a specific muon implantation depth profile, allowing us to vary the implantation depths from a few nanometers to several tens nanometers. This capability facilitated our depth-resolved μSR studies, with approximate depths ranging from \(\bar{z}\) = 1–200 nm. In Fig. 3d, we plot our results as a function E (which is the control parameter) and present the corresponding mean depth as a measure of the stopping depth to make the plot more meaningful for the general reader. We also note that the mean depth is almost proportional to E, hence the top axis is scaled accordingly. The muon implantation profiles in (Rb,Cs)V3Sb5 for various implantation energies, were simulated using the TrimSP Monte Carlo algorithm46.

Measurements of both normal and superconducting bulk state properties were conducted using the GPS and the high-field HAL-9500 instruments. HAL-9500 is equipped with a BlueFors vacuum-loaded, cryogen-free dilution refrigerator (DR) for probing the low ttemperature deep bulk properties. At the GPS instrument (πM3) beamline, we utilized a “spin rotator" to alter the muon’s spin orientation. Typically, a muons spin is naturally antiparallel to its momentum, but we rotated it by 45° relative to the c-axis of the crystal. This allowed the samples orientation to remain fixed while the muon spin was adjusted. The rotation angle of 44.5(3)° was precisely determined through measurements in a weak magnetic field, applied transversely to the muon spin polarization.

The μSR data, shown in Fig. 2a, were taken at the ISIS Pulsed Neutron and Muon Source at the Rutherford Appleton Laboratories (UK) using the EMU spectrometer. The powder sample was pressed into a disk of 30 mm in diameter and 1.9 mm in thickness. A 1.25 mm thick Kapton mask was mounted on top of the aluminum sample holder in order to eliminate the background signal originating from muons implanted in the sample holder. It is reasonable to assume that a 1% background is still present in the measurements but, for the sake of simplicity, it is not removed from the experimental asymmetry. Measurements were carried out at 120 K, above the charge ordering transition, and at 5 K, well below TCO. The total asymmetry is determined through transverse field calibration measurements at each temperature, and it is subsequently employed to assess the zero-field total asymmetry. Alternatively, this information can be extracted by fitting the asymmetry with a Kubo-Toyabe function in the interval 0.4 μs to 4μs. The two approaches yield very similar results differing by less than 1%. This procedure allows for the experimental determination of the muon’s spin polarization as a function of time.

ISIS is a pulsed muon source which allows for high data rates. This increases substantially the time window that can be explored and allows to carefully characterize the tail of the polarization function. At the same time, the muon beam spot size is much larger than at PSI thus precluding single crystal measurements for these materials.

Analysis of transverse field μSR data

Muon spin rotation data were processed utilizing the software Musrfit, which was developed at the Paul Scherrer Institute63. The TF-μSR data were analyzed by using the following functional form63:

$${A}_{TF}(t)={A}_{S}{e}^{\left[-\frac{{\sigma }_{TF}^{2}{t}^{2}}{2}\right]}\cos ({\gamma }_{\mu }{B}_{{{\rm{int}}}}t+\varphi ),$$
(3)

Here AS denotes the initial assymmetry, and φ is the initial phase of the muon-spin ensemble. Bint represents the internal magnetic field at the muon site, and the relaxation rate σTF characterize the damping of the μSR signal.

Computational details

The muon sites in RbV3Sb5 have been investigated with Density Functional Theory (DFT) using the so called DFT+μ50 approach. The tri-hexagonal lattice structure64,65 was used to perform all simulations unless otherwise specified. This structure has Fmmm symmetry with lattice parameters set to 10.943, 18.954 and 18.146 Å for a, b and c, respectively66. The simulations were carried out using the plane wave based code QuantumESPRESSO v7.167 The structural relaxation of all lattice structures was performed with GBRV ultrasoft pseudopotentials68 using 40 Ry cutoff for the planewave expansion of wavefunctions and 320 Ry cutoff for the charge density. The PBEsol69 functional was used to estimate the exchange and correlation term. The reciprocal space was sampled with the Gamma point. The optimization of atomic coordinates was carried out until forces and total energy differences were less than 0.5 mRy/Bohr and 0.09 mRy respectively. In order to find the stable muon sites we sampled the interstitial space of the host lattice using a grid with 1.2 Å spacing between the points and removed all symmetry equivalent positions as well as all points closer than 1.3 Å to the atoms of RbV3Sb5. This results in 71 starting interstitial positions. After structural relaxations, 34 symmetrically inequivalent positions are found using the clustering algorithm available in ref. 70. For the stable muon sites a refined equilibrium position and the Electric Field Gradients (EFG) at the nuclei of the lattice, obtained with the GIPAW code71, are estimated with a 2 × 1 × 1 supercell.