Carbon sequestration potential of tree planting in China

Yao, Ling; Liu, Tang; Qin, Jun; Jiang, Hou; Yang, Lin; Smith, Pete; Chen, Xi; Zhou, Chenghu; Piao, Shilong

doi:10.1038/s41467-024-52785-6

Download PDF

Article
Open access
Published: 27 September 2024

Carbon sequestration potential of tree planting in China

Nature Communications volume 15, Article number: 8398 (2024) Cite this article

15k Accesses
27 Citations
15 Altmetric
Metrics details

Subjects

Abstract

China’s large-scale tree planting programs are critical for achieving its carbon neutrality by 2060, but determining where and how to plant trees for maximum carbon sequestration has not been rigorously assessed. Here, we developed a comprehensive machine learning framework that integrates diverse environmental variables to quantify tree growth suitability and its relationship with tree numbers. Then, their correlations with biomass carbon stocks were robustly established. Carbon sink potentials were mapped in distinct tree-planting scenarios. Under one of them aligned with China’s ecosystem management policy, 44.7 billion trees could be planted, increasing forest stock by 9.6 ± 0.8 billion m³ and sequestering 5.9 ± 0.5 PgC equivalent to double China’s 2020 industrial CO₂ emissions. We found that tree densification within existing forests is an economically viable and effective strategy and so it should be a priority in future large-scale planting programs.

Maximizing carbon sequestration potential in Chinese forests through optimal management

Article Open access 11 April 2024

Estimation of changes in carbon sequestration and its economic value with various stand density and rotation age of Pinus massoniana plantations in China

Article Open access 22 July 2024

Maximum carbon uptake potential through progressive management of plantation forests in Guangdong Province, China

Article Open access 06 January 2025

Introduction

Tree planting is regarded as a cost-effective strategy and one of the most practical nature-based solutions for capturing carbon from the atmosphere and mitigating climate change^1,2,3. Since the early 1970s, China has launched a series of ambitious tree-planting programs, such as the Three-North Shelter Forest program, the Natural Forest Protection Program and the Yangtze River Shelter Forest project, whose main goals are to reduce soil erosion and sandstorms and improve local ecological environments^4,5,6. Reflecting the efforts of these programs, China has led the world in terms of planted tree area⁷, significantly increasing the country’s forest cover from less than 13% in 1978 to about 23% in 2019⁸, and substantially enhancing its terrestrial carbon sinks^9,10. However, the rate of forest expansion has slowed in recent years compared to earlier periods¹¹. To achieve the pledge of realizing carbon neutrality before 2060¹², China is stepping up the tree-planting campaign to sequester more carbon, with the aim of raising its overall forest coverage to 26% by 2035¹³ and 30% by 2050 s⁸.

However, the potential carbon sink provided by tree-planting projects is highly dependent upon where and how trees are planted. Lessons from previous unsuccessful tree-planting projects are that the lack of preliminary planning led to low survival and growth rates of trees^14,15,16. For example, the overall survival rate of trees in China’s afforestation projects from 1949 to 2005 was as low as 15% across the arid and semi-arid regions of northern China^17,18. Additionally, during this period, the cumulative area dedicated to afforestation in China was nearly triple the sum of areas currently forested and those that have been deforested, underscoring the vast scale of these initiatives^19,20. The fundamental reason is that trees were planted in unsuitable places. For example, in several afforestation projects in Ningxia, China, funded by the World Bank, almost no trees survived due to the relatively harsh natural conditions^14,21. Such cases of unsuccessful tree planting not only largely undermine potential carbon benefits^1,22, but also cause a series of adverse environmental effects such as aggravation of drought^23,24 and soil erosion¹⁴. In addition, planted forests in China are often short, sparse, and scattered^8,25, leading to these forests having a weak carbon sequestration capacity compared to natural forests^1,22,26.

More importantly, the remaining area of land for future tree plantation programs in China is rather limited in practice. On one hand, previous tree planting activities primarily happened in areas where climatic conditions are suboptimal for tree growth, and similar areas without tree cover have been scant²⁷. On the other hand, the areas suitable for tree growth are predominantly located in agricultural lands that were previously reclaimed from native forests, but these existing croplands are not suitable for reforestation due to the threat to food security²⁵. China’s forests as a whole are relatively sparse, with more than 26% of the forests having fewer than 500 trees per hectare⁸. For example, according to ultra-high spatial resolution satellite images, there are large quantities of Moderate-resolution Imaging Spectroradiometer (MODIS or Landsat) pixels with wide areas that are not covered by any trees (Fig. 1a), but are similar to forested areas in terms of environmental characteristics²⁸. These non-forested areas are most likely to be suitable for tree growth, and tree densification within these areas could have the potential to increase the stock volume and enhance their capacities to capture carbon. However, we still lack rigorous quantitative studies to directly evaluate where and how trees can be planted, and the associated economic costs and potential carbon benefits for future tree-planting projects in China.

**Fig. 1: The framework for tree planting and carbon sink potential assessment.**

Here we present a comprehensive methodological framework for assessing the potential of tree planting and carbon sequestration (see “Methods”). The core idea is to determine the tree planting potential of an area based on its historical tree cover. If an area was once extensively covered by forests, its climatic conditions are suitable for tree growth. Conversely, if an area has long been devoid of tree cover and has not been disturbed by human activities, it is likely unsuitable for tree growth. Areas that fall in between these two extremes will have tree growth-carrying capacities that are crucial for further enhancing forest carbon sequestration. First, we use environmental covariates related to tree growth (such as climate, soil, and topography) along with forest distribution time series data²⁹ to quantify tree growth suitability (TGS) scores in different areas. This score serves as a standard for measuring the environmental carrying capacity for a certain area (Fig. 1b). Based on this, we introduce tree density data³⁰ and analyze its relationship with the TGS score to estimate the potential of increasing tree density for different forest types (Fig. 1c). Considering the resolution of climatic environmental layers and existing tree density dataset, as well as the feasibility of large-scale intensive calculations, this study sets the grid size to 1 km. For grid cells without trees (i.e., tree density is 0), tree planting activities are considered as afforestation; for grid cells with existing trees, it is designated as densification (Fig. 1d). Furthermore, we have constructed a quantitative relationship between the number of trees and their aboveground/belowground forest biomass carbon stocks (AGFBC/BGFBC) to compute the amount of carbon that could be sequestrated, and the economic costs and carbon returns via tree planting (Fig. 1e).

Results

Potential of afforestation and densification

We firstly evaluated the feasibility of afforestation and densification using the estimated TGS scores. The spatial pattern of these scores matches well with the density of the existing trees, which declines from the southeast to the northwest (Fig. 2a). From their quantitative relationship, we can find that a larger score is generally associated with a higher tree density, but one score can correspond to various densities (Fig. 2c). This implies that the pixels with the same potential have the possibility of being afforested or densified. The pixels on one score can be assigned four forest types (deciduous broadleaf, deciduous needleleaf, evergreen broadleaf, and evergreen needleleaf). So, we divided the general relationship for all trees into four specific ones for each forest type, including deciduous broadleaf forest (D.B.), deciduous needleleaf forest (D.N.), evergreen broadleaf forest (E.B.), and evergreen needleleaf forest (E.N.) (Fig. 2d). The tree densities of the four types monotonically increase with the scores, but their shapes exhibit distinct characteristics and their tree density dispersions at the equal score are distinct.

**Fig. 2: Spatial distribution of the estimated tree growth suitability (TGS) scores and their quantitative relationship with the tree densities.**

Based on the above analysis, the pixels in each narrow score bin for every forest type can be covered by a different number of trees (Figs. 3a1–a4). We evaluated the empirical cumulative distribution function (CDF) for these tree quantities using bins at 0.01 intervals across a range from 0 to 1. All pixels in one score bin have the same potential for holding equal tree numbers (Figs. 3b1–b4). In accordance with this, we designed three scenarios for afforestation and densification, in which the number of trees is escalated to 25%, 50%, and 75% quantiles of the CDF for each score bin if the tree density of a certain pixel is less than these three quantiles. We mapped the potential of afforestation and densification for the four forest types by implementing the above operation to every pixel of all score bins. Additionally, the original state was maintained in residential and agricultural areas to ensure continued food production and habitation.

**Fig. 3: The increased tree densities and carbon sequestration due to afforestation and densification.**

Patterns of afforestation at the three quantile levels varied with spatial locations and forest types (Figs. 4a1–a3). The remaining areas available for future afforestation in China are principally located in the Hengduan Mountains, the middle and lower reaches of the Yangtze River Plain, and the Qinba Mountains under all the three ideal scenarios. If they were implemented, China could afforest about 58.2, 63.2, and 70.0 million hectares, respectively (Supplementary Table 4). But only if the latter two were implemented, could China’s goal of reaching the globally averaged forest cover (30%) by 2050 s be achieved. Additionally, densifying existing forests is another way to enhance forest stock and quality, which also offers substantial potential in terms of spatial patterns and increments (Figs. 4b1–b3). The potential areas for tree densification in China are mainly distributed in the south of the Qinling Mountains-Huaihe River line, especially in the Qinba Mountains and the Yunnan-Guizhou Plateau. Densification to the 25%, 50%, and 75% quantile levels could bring a total of 7.8, 21.1, and 37.5 billion trees to China, respectively, whereas afforestation could deliver 10.1, 17.2 and 25.2 billion trees, respectively (Table 1). Forest stock could increase by 1.3 ± 0.1, 3.7 ± 0.4 and 7.9 ± 0.7 billion m³ through densification, or by 1.7 ± 0.1, 3.1 ± 0.2 and 4.5 ± 0.3 billion m³ through afforestation (Supplementary Table 7). In the latter two ideal scenarios, densification provides more potential for tree-planting.

**Fig. 4: The spatial distributions of afforestation and densification potential in China.**

Table 1 Tree-planting potential for four forest types, the numbers in the table represent the potential number of trees that can be planted, expressed in billions

Full size table

Carbon sink potential of tree planting

Both afforestation and densification can have an impact on forest biomass carbon stocks. Therefore, we quantitatively estimated this carbon sink potential using the relationship between tree densities and forest biomass carbon in a similar manner to computing the potential of afforestation and densification. Statistical analysis of extensive pixel-scale data reveals that within similar TGS score ranges, both AGFBC and BGFBC in forests exhibit various forms of monotonic increase as tree density increases. However, this increase varies between AGFBC and BGFBC, and these differences are also evident across different forest types (Fig. 3c, d). This trend is also consistently reflected across different TGS score intervals (Supplementary Fig. 4 c and d, Supplementary Fig. 5c and d). When the tree plantation was raised up to the 25%, 50%, and 75% quantiles, the amounts of AGFBC and BGFBC increased accordingly.

The carbon sink potential for aboveground forest biomass is estimated to be 891.0 ± 58.4 (± is the uncertainty, calculations are in Methods), 1311.8±82.8, and 1866.9±110.1 TgC through afforestation (Figs. 5a1–a3) and 711.4 ± 55.7, 1782.7 ± 169.4, and 3604.6±286.4 TgC by densification (Figs. 5b1–b3) for the three quantiles, respectively (Table 2). The spatial patterns of carbon sink potential due to increasing belowground forest biomass, achieving 333.8 ± 101.6, 450.4 ± 112.7, and 576.8 ± 125.7 TgC by afforestation (Figs. 5c1–c3) and 314.1 ± 14.7, 631.8 ± 26.3, and 1029.8 ± 43.0 TgC by densification (Figs. 5d1–d3), respectively (Table 2). We found that an increase in the number of trees may lead to a decrease in carbon stocks on certain pixels, for which the AGFBC losses are significantly higher than the BGFBC (Supplementary Fig. 4c and d, Supplementary Figs. 5c and d). On one hand, this phenomenon may be due to the inherent imperfections of the pixel-based statistical method used. Besides tree density, the carbon sequestration capacity of trees is influenced by many other factors such as species diversity, photosynthetic capacity, and canopy architecture^31,32. Some overlooked factors may play a significant role at certain points, leading to a non-monotonic relationship between tree numbers and carbon stock. On the other hand, it could be related to the maturity of trees and more complex forest structure characteristics. These pixels are sporadically distributed in regions such as the Changbai Mountain, the Xiaoxinganling Mountains, the Qinba Mountains, and the Hengduan Mountains (Fig. 5). These areas have high potentials for tree carrying capacity (Fig. 2a). In reality, most of them have been long covered by natural forests. Due to complex stand structures and relatively older tree ages^11,33,34, their existing biomass carbon stocks are relatively high compared to other forests in China. For these forests, even with a lower density, it is not advisable to artificially enhance their density through intervention.

**Fig. 5: The spatial distributions of carbon sink potential of aboveground and belowground forest biomass carbon by afforestation and densification.**

Table 2 Carbon sink from aboveground and belowground forest biomass gains by afforestation and densification to 25%, 50%, and 75% quantiles

Full size table

Considering the potential impact of biomass carbon distribution datasets on carbon storage estimates, we also selected two datasets with similar resolutions for aboveground and belowground forest biomass carbon to assess the robustness of our method^35,36. The results indicate that the estimates based on different data sources exhibit broadly similar spatial trends (Supplementary Fig. 7), and the proportions of the estimates relative to their data sources are very close. For example, when densified to the 50% quantiles scenario, the increments in forest biomass carbon storage contributed by the three datasets account for 41.7%, 41.4%, and 40.9% of the total original dataset, respectively (Table 2, Supplementary Table 5, and Supplementary Table 6). They indicate that the method for estimating forest biomass carbon sequestration is both consistent and robust, providing reliable results across different datasets.

Realistic tree-planting scenario

The Chinese central government has formulated the national zoning program of ecological functions (NZPEF)³⁷ to guide the sustainable development. This policy should be taken into account when implementing tree planting initiatives. For example, the NZPEF mandates that tree planting is strictly prohibited in key water-conserving areas. At the same time, tree planting should not take place if tree planting in an area would result in a decrease in carbon stocks. So, we designed a realistic tree-planting scenario by imposing the above constraints on the three ideal scenarios. This includes prohibiting planting trees in some reserves under the NZPEF scheme, maximizing tree planting in areas primarily designated for forest rehabilitation (implementing the 75% scenario), and implementing moderate tree planting in other ecological planning zones based on habitat conditions (for instance, implementing the 25% scenario in water-scarce areas and the 50% scenario in water-rich areas, see Supplementary Table 8 for details)

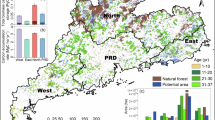
Under this realistic scenario, it is estimated that approximately 18.3 billion trees can be planted across 55.8 million hectares of forests, which would cover about 6% of China’s total land area (Fig. 6a). China’s forest stock can increase by a total of about 3.1 ± 0.4 billion m³ with reference to its current level (Supplementary Table 9). In the realistic scenario, the Hengduan Mountain has the highest afforestation potential, and can harbor about 14.84 million hectares of newly planted forests, accounting for 27.1% of the total afforested area in the realistic scenario. The potential afforestation locations are mainly (over 60%) distributed within the scope of the shelterbelt project for the upper and middle reaches of the Yangtze River implemented by the Chinese government since the 1990s. Other potential afforestation areas are mainly located in the Sichuan-Chongqing Area and the middle and lower reaches of the Yangtze River, where about 5.1 billion trees can be planted in the realistic scenario, accounting for about 28 % of the total afforested area. Due to the relatively favorable natural and socio-economic conditions in these two regions, they could be the priority areas to enhance China’s forest cover.

**Fig. 6: The spatial distributions of the realistic scenario of afforestation and densification in China.**

Through persistent efforts in recent decades, many planted forests, including Yulin Desert National Forest Park, Manzhoulin Mechanical Forestry, and Sehanba Mechanical Forestry Park, have been generated in the Loess Plateau, the Inner Mongolian Plateau, and the northern part of the North China Plain. Nevertheless, afforestation in these areas has already approached the local environmental capacities, and continued large-scale afforestation would then threaten local water resources and food security^15,23,24. Therefore, in the realistic scenario, we assumed a more conservative afforestation strategy. A total of about 1.5 billion trees could be planted in these regions, which accounts for about 8.2% of the total afforested area.

In the realistic scenario, the potential for densification is about planting 26.4 billion trees (Fig. 6b). With reference to the current China’s forest status, the total stock can rise by roughly 6.7 ± 0.6 billion m³ and the stock per hectare can increase by at least 44.7 ± 4.0 m³ (Supplementary Table 9). In the realistic scenario, both the Qinba Mountains and the Yunnan-Guizhou Plateau, which are located in the ecological subzones of forest, have a great potential for tree densification. This action can provide a total of 7.5 billion trees in nearly 37.2 million hectares of forest area, and this number is around 29% of the total number of densified trees in the realistic scenario. In the Hengduan Mountains, a total of 3.8 billion trees, which are distributed in the 17.8 million hectares forest area, can be planted, accounting for 14.7 % of the total number of densified trees. In Northern and Northeastern China, the forests that could be densified are mainly distributed in the Taihang Mountains, Xiaoxing’anling Mountains and Changbai Mountains, accounting for about 8.9 % of the densified trees.

It is worth noting that the ambiguity in terminology definitions can alter the scope of “densification” and “afforestation,” thereby potentially shifting the balance between these two strategies. Our work differentiates the two modes of tree planting based on whether the tree density value is zero or non-zero, whereas the tree cover is often used to determine the presence of a forest. To accommodate different forest types and management needs across countries, the United Nations Framework Convention on Climate Change (UNFCCC) provides a reference definition range of 10-30% tree cover for forest³⁸. At the current resolution of 1 km, whether based on a 10% or 30% threshold, the potential for densification exceeds that of afforestation (Fig. 6c). A 20% threshold shows a ratio similar to our previous definitions and aligns with the threshold range stipulated by the current Chinese forest policy³⁹. Increasing the threshold to above 30% (such as 60% by International Geosphere-Biosphere Program⁴⁰) results in more pixels being defined as “non-forest,” causing the proportion of afforestation to surpass densification.

In fact, the ratio of the number of trees planted for these two strategies does not affect the overall practical potential for tree planting, because a certain amount of space is necessary for each planted tree to grow (Supplementary Fig. 6). Our research highlights the planting potential of sparse “forest” areas that might be overlooked in aiming for more substantial and cost-effective carbon sequestration. Historically, tree planting projects in China have largely been carried out in provinces along the upper reaches of the Yellow River and Yangtze River, but the increase in forest cover has mainly occurred in southeastern and northeastern China. Our findings suggest that, due to favorable hydrothermal conditions, some “forest” areas in Southeast and Northeast China still have considerable potential for tree densification. In the future, resources should be further invested in these regions to enrich forest stock and enhance carbon sink.

Economic costs and carbon returns

In 2010, the aboveground forest biomass carbon stock in China’s forest ecosystems is about 7.6 PgC (1 PgC = 10³ TgC) and the belowground one is about 2.4 PgC⁴¹. In the realistic tree-planting scenario, the increment in the aboveground and belowground forest biomass carbon stock in China is 4.5 ± 0.3 PgC and 1.4 ± 0.1 PgC, respectively, if the status of the newly planted trees achieves the average one in 2010. The increment in the forest biomass carbon stock due to afforestation and densification is roughly 1.9 ± 0.2 and 4.0 ± 0.3 PgC, respectively (Supplementary Figs. 8a and b, Supplementary Table 9). The uncertainty in carbon sink potential for densification is much greater than that for afforestation (Supplementary Figs. 8c and d). The uncertainty can be attributed to factors such as the diversity of tree species and the inconsistency between the datasets used. Regionally, Southwest China, especially Guangxi and Sichuan, exhibits the largest carbon stocks. On the other hand, the contribution from Northeast China is insignificant. Our estimate based on the realistic scenario is higher than the previous estimate (3.3 PgC⁴², 4.0 PgC⁴³), because our densification scheme can provide the extra potential for carbon sink in the provinces of Sichuan, Guizhou, and Hunan. Tree planting would also alter soil organic carbon stocks. The latest research showed that the mean value of the sink ratio of forest soil organic carbon to forest biomass carbon from planting trees in China is about 0.14⁴⁴. According to this ratio, the incremental soil organic carbon stock is about 0.3 ± 0.01 PgC for afforestation and 0.5 ± 0.03 PgC for densification in our realistic tree-planting scenario. If the realistic tree-planting scenario is implemented by the year of 2025, then from 2025 to 2060, the annual average carbon sink rate of the newly planted trees is about 169.1 ± 11.7 TgC yr⁻¹. Here, the afforestation and densification would bring 55.5 ± 4.1 TgC yr⁻¹ and 113.5 ± 7.5 TgC yr⁻¹, respectively. Moreover, because of the sink saturation effect in maturing tress, the carbon sink of China’s forest ecosystems would decrease from 0.18 PgC yr⁻¹ in the 2020 s to 0.08 PgC yr⁻¹ in the 2060 s, given no changes in future climate or atmospheric CO₂⁴⁵. In 2019, China has approximately 115 million hectares of young and middle-aged forests⁸. If the task of planting trees under the realistic scenario was completed, China would have at least 135 million hectares of young and middle-aged forests in the 2060 s. These additional forests, still relatively young, would continue to offer substantial carbon sink benefits. Considering that the carbon accumulation rate of forests varies with the age, in the first decade of afforestation, the average annual carbon sink is about 0.08 PgC yr⁻¹. By the 2060 s, the carbon sink capacity of these newly planted trees can reach its peak, with a sink of approximately 0.2 PgC yr⁻¹ (Supplementary Table 11). Thus, the carbon sequestration capacity of China’s forests can be maintained at a level higher than their current capacity, thereby extending the service life of the forest carbon sink. This will provide more time and opportunities for industrial sectors to improve their abatement technologies or to offset the carbon that must be emitted, to achieve net carbon neutrality.

With reference to China’s investment in various tree-planting projects during 1998–2010, the average cost of sequestrating carbon in past ecological projects in China is about $21.18 per tonne of CO₂¹⁰. The main reason for this cost is that the Chinese government invested most of the afforestation funding in regions with poor natural conditions for ecological restoration, and the low survival rate of trees in these regions led to higher afforestation costs per unit area in China⁷. For example, the cost of tree planting in Northwestern China was about $4.37 per tree, based on the costs of the Three-North Shelter Forest program and the Sand Control project. In contrast, the cost in Southeastern China reduced to around $1.17 per tree, according to the costs of the Yangtze River Shelter Forest project and the Zhujiang River Shelter Forest project (Supplementary Table 12). According to the two different costs, and without considering inflation and rising labor costs, the realistic tree planting scenario needs a total investment of about $116.1 billion. The average cost of sequestering one tonne of CO₂ is about $4.77, much lower than the current average cost ($21.18). The cost of forest carbon sequestration in the Sichuan-Chongqing Area, the middle and lower reaches of the Yangtze River, the North China Plain and South China is about $1.65 per tonne of CO₂, and the cost of carbon sequestration in Northwestern China (the Loess Plateau, the Inner Mongolia Plateau, and the northwest Arid Region) is about $17.1 per tonne of CO₂ (Supplementary Table 13). For carbon sequestration, afforestation and densification in areas with favorable natural conditions (the Sichuan-Chongqing Area, the middle and lower reaches of the Yangtze River and South China) are recommended. If the intensity of tree planting was further increased (i.e., trees are planted to the 75% quantile in all potential pixels), the total carbon sink potential would reach 8.07 ± 0.45 PgC (Table 2), which is 1.26 PgC more than that in the realistic scenario, and roughly equal to the CO₂ emissions of China in 2020. Approximately $47.46 billion is required in order to procure such a sink increment, and the average cost is about $34.90 per tonne of CO₂ (Supplementary Table 14).

Discussion

We formulated a realistic tree planting scenario for future decades at a 1-km spatial resolution and analyzed its approximate economic cost and potential carbon benefits. Our findings suggest that densifying existing forests could potentially be more effective than afforestation in achieving the ambitious targets set by the Chinese central government, while preserving existing land uses such as croplands. Meanwhile, large-scale tree planting could continue to boost terrestrial carbon sinks and will play a prominent role in realizing carbon neutrality before 2060. We thus highlight the feasibility and necessity of adopting large-scale tree planting programs as a climate mitigation strategy in China. To understand the implications of these findings, it is important to consider the limitations of our analytical approach detailed below.

The spatial scale (1 kilometer) for the current analysis is a compromise between the availability of data and the effective depiction of climatic backgrounds. The inherent limitations of the analysis are twofold. The first is that this scale is insufficient to capture the spatial pattern of the originally existing trees in each grid box and thus accurately locate each tree to be planted⁴⁶. The second limitation is that the mean climate state is considered for each grid box, but its microclimate heterogeneity is not factored in. These two spatial variabilities could have a significant impact on the actual growth conditions of trees. Therefore, it remains crucial to adopt localized approaches that are tailored to specific environmental conditions when the tree-planting projects are practically implemented.

Apart from the analysis scale, it is also crucial to address the ecological effects and potential ecological risks associated with our strategies. Although we have constrained tree growth potential based on external environmental conditions, the competition and the self-thinning effect intrinsic to forest ecosystems may limit further increases in tree density. At the same time, increased tree density can intensify the vulnerability of forests to wildfires, diseases, and pests, potentially leading to significant losses in carbon storage and biodiversity⁴⁷. Especially in regions prone to wildfires, such as southern China and areas bordering North Korea^48,49, future research should comprehensively assess the pros and cons of this strategy. The key is to avoid unintentionally exacerbating forest disturbances and balance carbon sequestration with the health and stability of the forest ecosystem.

Additionally, our economic assessments also have certain limitations. We acknowledge that the costs of tree densification may differ from the expenses associated with the past afforestation projects due to potential differences in project implementation methods. Furthermore, dynamic economic factors such as inflation, changes in labor costs, fluctuations in material costs over time, and possible losses during the project implementation process have not been considered. However, despite these imperfections, we have made pioneering efforts to estimate the economic costs of tree densification and afforestation at a national scale, an aspect often overlooked in similar studies. From an economic perspective, densifying existing forests in regions with favorable water and thermal conditions may be a better choice.

Although the described limitations highlight the importance of scale and socioeconomic realism in determining potential outcomes, our assessment reveals the significant potential contribution of increasing the density of existing forests to carbon neutrality in China. Future research should aim to incorporate more detailed high-resolution data and dynamic modeling approaches to better capture the complexities of forest ecology and economics. Additionally, efforts should be made to integrate risk assessment models to predict the impacts of large-scale afforestation and forest densification more accurately and to improve the formulation of forest management policies and practices.

Methods

Calculation of tree growth suitability score

By leveraging a variety of environmental variables and historical tree cover data, we calculate tree growth suitability (TGS) scores for different regions using a neural network classification model. The cross-validation and third-party data validation are taken to ensure that the results were accurate and reliable.

Environmental factors include five climate variables (annual solar radiation⁵⁰, annual aridity index⁵¹, annual maximum land surface temperature⁵², annual minimum land surface temperature⁵², and annual snow cover index⁵³), nine soil variables⁵⁴ (bulk density, coarse fragments, organic carbon density, pH value, sand content, silt content, clay content, cation exchange capacity, and total nitrogen), and three topographic variables⁵⁵ (digital elevation model, roughness, and slope) (Supplementary Table 1). All these variables were resampled to 1-km resolution (Supplementary Fig. 1 a–o).

The Hansen Global Forest Change dataset with a spatial resolution of 30 m × 30 m is used to characterize the growth conditions of trees²⁹. So, there are approximately a total of 1111 30-m pixels within one 1 km grid. The grids, wherein no pixels have been covered by trees since the year 2000, are marked as 0, indicating complete unsuitability for tree growth. The grids, wherein more than 30% of pixels are covered by trees, are marked as 1, signifying suitability for tree growth. The other grids falling between these two categories are left unmarked and do not participate in the training of the classification model. Additionally, we excluded grids where the fraction of cropland and/or urban area is greater than 30% (Supplementary Fig. 1p). This exclusion was conducted using the Finer Resolution Observation and Monitoring of Global Land Cover (FROM-GLC 2017) product⁵⁶, which has a spatial resolution of 30 m. These excluded grids, similar to the unmarked grids, do not participate in the training of the classification model.

The artificial neural network model takes environmental variables as input to perform a binary classification of suitability for tree growth and unsuitability for tree growth. The confidence level for each pixel can be regarded as the probability of that pixel being suitable for tree growth (Fig. 2b). In econometrics, this probability is referred to as the propensity score, which is often used to match units to remove confounding effects. Units with the same propensity score can be regarded as receiving the same treatment. According to this conception, grids with equal scores have the potential of having the same tree numbers. The neural network used in this study includes two hidden layers, with 64 and 32 neurons respectively (Supplementary Fig. 2), and the model is trained using the stochastic gradient descent method.

To ensure the robustness and reliability of our model, we conducted a 5-fold cross-validation, achieving high average scores in training and validation: Accuracy of 0.98 and F1-score of 0.98. However, the test performance showed lower results, with an accuracy of 0.91 and an F1-score of 0.88, indicating the model’s variability when generalized to new data (Supplementary Table 2). By training the final model on all available data, we aim to improve the assessment accuracy for each pixel, enhancing the model’s reliability and applicability in realistic scenarios.

To validate the performance of the Tree Growth Suitability (TGS) evaluation model, we utilized a range of test sites, including data from 184 natural forest field survey plots, 586 field survey plots for plantation forests⁵⁷, and a catalog of 816 forest parks in China (Fig. 2a). These sites are all deemed suitable for tree growth. Overall, the model achieves a general classification accuracy of about 0.8, with natural forests showing higher suitability for tree growth (Fig. 2b and Supplementary Table 3). The classification accuracy for plantation forest points is notably lower, primarily due to the larger number of plantation sites located in the northwest region of China.

Tree-planting potential estimation

We divided the TGS scores (ranging from 0 to 1) with a resolution of 1 km into 100 intervals, each with an increment of 0.01. Then, we used the global tree density map³⁰ with the same resolution (Supplementary Fig. 3) to determine the number of trees in each pixel. We observed that tree densities vary among different forest types. Therefore, based on the plant functional types in the MODIS MCD12Q1 product²⁸ (Supplementary Fig. 1q)—including deciduous broadleaf trees, deciduous needleleaf trees, evergreen broadleaf trees, and evergreen needleleaf trees—we separated this general relationship into four specific ones for each forest type (Fig. 3a). According to the forest type distribution, we established a statistical relationship between these 100 score bins and the tree densities within each bin and generated cumulative distribution functions of tree numbers for the grids in each score bin. Examples for the bins are presented to illustrate this process: Fig. 3 corresponds to TGS 0.9-0.91, while Supplementary Fig. 4 and Supplementary Fig. 5 represent 0.5–0.51 and 0.2–0.21, respectively.

Since the grids in the same score bin have the potential of the same tree numbers existing, we could radically plant trees up to the maximum density that a certain grid in this bin has. However, we chose three relatively moderate pathways to plant trees to 25%, 50%, and 75% quantile levels, respectively, for any grid whose tree density is lower than these three quantiles. For one grid with a label of 0, this operation is named afforestation. Otherwise, it is called densification. For afforestation, the forest type, which should be planted, was designated as the type which the nearest grid with label 1 has. The grid by densification has its original forest type. We conducted the above operation for every 1 km grid and finally obtained the spatial distributions of afforestation and densification potential in China. The TGS obtained from the 5 models of 5-fold cross-validation and one final model trained using all data were used to establish statistical relationships between tree densities (Table 1).

Carbon sink potential estimation

The statistical relationships were constructed between the aboveground/belowground forest biomass carbon maps⁴¹ and the tree densities for evaluating the amount of carbon sink by afforestation and densification. The carbon maps originally have a spatial resolution of 300 m and were aggregated to 1 km by using the mean aggregation method. For each score bin, we divided its grids into 20 intervals based on tree density per hectare, with an increment of 35 trees. Each interval’s grids correspond to a specific range of aboveground and belowground forest biomass carbon values. Across multiple TGS score levels, a clear positive correlation between tree density and carbon storage is evident (Fig. 3 corresponds to TGS 0.9–0.91, while Supplementary Fig. 4 and Supplementary Fig. 5 represent 0.5–0.51 and 0.2–0.21, respectively).

The uncertainties in forest biomass carbon stocks for the tree intervals are used to define the upper (maximum value, 95% quantile) and lower (minimum value, 5% quantile) limits of carbon sequestration for the trees. The medians are taken as the representative carbon values (including aboveground and belowground forest biomass carbon) for the tree intervals. We also observed that both aboveground forest biomass carbon and belowground one almost monotonically rise with the tree densities increasing. Thus, the amount of carbon sink is completely determined by the increased tree number. For example, if we afforest one grid with no trees to the 50% quantile, the amount is simply equal to the forest biomass carbon which this quantile level corresponds to. If we densify one grid with trees to the 50% quantile, the amount is equal to the difference between the forest biomass carbon which this grid’s tree number corresponds to and the one which the 50% quantile does. The aforementioned algorithm was implemented to each 1 km grid in China. We obtained the spatial distributions of carbon sequestration of aboveground and belowground biomass by afforestation and densification. For each grid, the maximum value, the minimum, and the median are included, and the average standard deviation among these three layers serves as the uncertainty in the carbon estimation.

Given that our carbon potential estimates are made entirely through the statistical analysis of the gridded data, the quality of the data sources determines the accuracy of our estimates. Therefore, we collected forest biomass carbon data from two additional sources^35,36 to compare the robustness of our carbon potential prediction method. Overall, the estimates from all three data sources are broadly similar across various ideal scenarios. Especially, the ratios of the calculated results to the total carbon storage of each data source keep constant (Table 2, Supplementary Table 5 and Supplementary Table 6). Spatially, there are no significant differences among them (Supplementary Fig. 7). For the realistic scenario, the differences in the carbon sink potentials among the three data sources are mainly attributed to both the distinct aboveground biomass carbon stocks for densification (2481.9 ~ 3104.1 TgC) and the belowground biomass carbon stocks (367.4 ~ 536.1 TgC for afforestation and 759.9 ~ 879.7 TgC for densification). However, the aboveground carbon stock potentials for afforestation are fairly similar (1333.7 ~ 1412.7 TgC, Supplementary Table 10). This indicates that the reliability of our method in estimating forest biomass carbon potential depends on the stability of the existing datasets themselves, so subsequent analyzes will continue to primarily use one data source.

The realistic scenario designs

The national zoning program of ecological functions³⁷ divides China into three ecological zones and 48 ecological subzones according to the ecological and climatic characteristics. In the realistic scenario, we planted trees to 75% quantile for the ecological subzones of forest. For other subzones, trees were planted to 50% quantile in the monsoon zone of Eastern China and to 25% quantile in the arid zone of Northwestern China or the alpine zone of the Tibetan Plateau for reducing their ecological stress. In addition, this program stipulates that tree planting is strictly prohibited in the key areas of water-conserving ecological function. Therefore, their status of trees is maintained in the realistic scenario (Supplementary Table 8).

Forest stock estimation

In our research, we utilized a method to back-calculate the stand timber volume from estimated forest biomass carbon⁵⁸. This involved using the Biomass Expansion Factor (BEF), which is crucial for converting biomass back into timber volume. The formula used for BEF is:

$${BEF}=a+b/{V}_{{stock}}$$

(1)

where ${V}_{{stock}}$ represents the stand timber volume, $a$ and $b$ are constants derived based on direct field measurements⁵⁸ and tailored to specific forest types. So the ${V}_{{stock}}$ can be calculated as:

$${V}_{{stock}}=\frac{\left({\Delta C}_{{above}}+{\Delta C}_{{below}}\right)\times \delta -b}{a}$$

(2)

where ${\Delta C}_{{above}}$ and ${\Delta C}_{{below}}$ denote the increments of aboveground and belowground forest biomass carbon, respectively. $\delta$ is the constant representing the relationship between carbon and biomass, where $\delta=2$.

Soil organic carbon estimation

Hong et al. indicated that the ratio $\eta$ of soil organic carbon sinks to forest biomass carbon sinks from tree-planting in China is about 0.14⁴⁴. In this study, we calculated soil organic carbon increment $\Delta {SOC}$ as:

$$\Delta {{{\rm{SOC}}}}=\left(\Delta {{{{\rm{C}}}}}_{{{{\rm{above}}}}}+\Delta{{{{\rm{C}}}}}_{{{{\rm{below}}}}}\right)\times {{{\rm{\eta }}}}$$

(3)

where ${\Delta C}_{{above}}$ and ${\Delta C}_{{below}}$ denote the increments of aboveground and belowground forest biomass carbon, respectively.

The cost of carbon sequestration

The investments and the forest areas of a series of tree-planting projects in China during 1998–2010 are shown in Supplementary Table 12. The tree-planting cost per hectare ${\overline{{COST}}}_{{hectare}}$ for each project can be calculated as:

$${\overline{{COST}}}_{{tree}}=\frac{{{COST}}_{{total}}}{{{AREA}}_{{total}}}$$

(4)

where ${{COST}}_{{total}}$ and ${{AREA}}_{{total}}$ denote the total cost and the total area for a tree-planting project, respectively. The average cost of planting a single tree ${\overline{{COST}}}_{{tree}}$ was calculated as follows:

$${\overline{{COST}}}_{{tree}}=\frac{{\overline{{COST}}}_{{hectare}}}{{\bar{N}}_{{hectare}}}$$

(5)

where ${\bar{N}}_{{hectare}}$ denote the average number of trees per hectare for a project. So, the total investment for our tree-planting scenarios ${{INVEST}}_{{total}}$ was calculated as:

$${{INVEST}}_{{total}}={\overline{{COST}}}_{{tree}}\times \Delta {N}_{{trees}}$$

(6)

The average cost of sequestering one ton of CO2 ${{COST}}_{{{co}}_{2}}$ was calculated as:

$${{COST}}_{{{co}}_{2}}=\frac{{{INVEST}}_{{total}}}{(\Delta {C}_{{above}}+\Delta{C}_{{below}}+\Delta {SOC})\times {{{\rm{\lambda }}}}}$$

(7)

where $\lambda$ is the ratio of CO₂ to C molecules.

Data availability

All data used in the analysis are publicly accessible. The data generated in this study can be accessed at https://doi.org/10.6084/m9.figshare.25707414. Source data are provided with this paper. The land cover and land use change dataset is available at http://data.ess.tsinghua.edu.cn/fromglc2017v1.html (including urban and agricultural land data); The Hansen Global Forest Change 2000-2022 Data is available at https://glad.earthengine.app/view/global-forest-change; The global tree density map is available at http://elischolar.library.yale.edu/yale_fes_data/1/; The nine soil variables can be found at https://soilgrids.org/; The three topographic variables can be found at https://research.utwente.nl/en/publications/hole-filled-srtm-for-the-globe-version-4-data-grid; The annual solar radiation data can be found at https://doi.org/10.6084/m9.figshare.c.4891302, The aridity index data can be found at https://doi.org/10.5281/zenodo.10074189. Annual maximum land surface temperature and annual minimum land surface temperature are available at https://lpdaac.usgs.gov/products/mod11a1v006/. Annual snow cover index can be found at https://nsidc.org/data/mod10a2/versions/5, Forest types of classification dataset (MCD12Q1: Type5 Plant Functions Types) can be obtained at https://lpdaac.usgs.gov/products/mcd12q1v006/. The aboveground and belowground biomass carbon maps are from https://daac.ornl.gov/cgi-bin/dsviewer.pl?ds_id=1763. The catalog of 816 forest parks can be found at www.gisrs.cn. All plantation forest field survey plots are available at https://doi.org/10.11922/sciencedb.j00076.00091. Source data are provided with this paper.

Code availability

The computer code of key methods related to this work is available on GitHub at https://github.com/sddpltwanqiu/Tree_planting_potential. The software used to generate all thematic maps in this study is ArcGIS 10.8.

References

Lewis, S. L., Wheeler, C. E., Mitchard, E. T. A. & Koch, A. Restoring natural forests is the best way to remove atmospheric carbon. Nature 568, 25–28 (2019).
Article ADS CAS PubMed Google Scholar
Griscom, B. W. et al. Natural climate solutions. Proc. Natl Acad. Sci. Usa. 114, 11645–11650 (2017).
Article ADS CAS PubMed PubMed Central Google Scholar
Masson-Delmotte, V. et al. Global Warming of 1.5 °C. An IPCC Special Report on the impacts of global warming of 1.5 °C above pre-industrial levels and related global greenhouse gas emission pathways, in the context of strengthening the global response to the threat of climate change, sustainable development, and efforts to eradicate poverty, 93–174 (Cambridge University Press, 2018).
Bryan, B. A. et al. China’s response to a national land-system sustainability emergency. Nature 559, 193–204 (2018).
Article ADS CAS PubMed Google Scholar
Zhang, P. et al. China’s Forest Policy for the 21st Century. Science 288, 2135–2136 (2000).
Article CAS PubMed Google Scholar
Wang, F. et al. Vegetation restoration in Northern China: a contrasted picture. Land Degrad. Dev. 31, 669–676 (2020).
Article Google Scholar
FAO. Global Forest Resources Assessment 2020: Main Report. (FAO, 2020).
National Forestry and Grassland Administration. Forest Resource Report of China (2014–2018). (Forestry Publishing House, 2019).
Yue, X., Zhang, T. & Shao, C. Afforestation increases ecosystem productivity and carbon storage in China during the 2000s. Agr. For. Meteorol. 296, 108227 (2021).
Article Google Scholar
Lu, F. et al. Effects of national ecological restoration projects on carbon sequestration in China from 2001 to 2010. Proc. Natl Acad. Sci. USA. 115, 4039–4044 (2018).
Article ADS CAS PubMed PubMed Central Google Scholar
Abbasi, A. O. et al. Spatial database of planted forests in East Asia. Sci. Data 10, 480 (2023).
Article PubMed PubMed Central Google Scholar
The CPC Central Committee & The State Council. Opinions on the Complete and Accurate Implementation of the New Development Concept to Do a Good Job of Carbon Peaking and Carbon Neutrality. https://www.gov.cn/zhengce/2021-10/24/content_5644613.htm. (CPCCC&SC, 2022).
PRC National Development and Reform Commission (NDRC) & Ministry of Natural Resource. Master Plan for Major Projects for the Protection and Restoration of Important Ecosystems in China (2021-2035). https://www.gov.cn/zhengce/zhengceku/2020-06/12/content_5518982.htm. (NDRC&MNR, 2020).
Cao, S. et al. Excessive reliance on afforestation in China’s arid and semi-arid regions: Lessons in ecological restoration. Earth-Sci. Rev. 104, 240–245 (2011).
Article ADS Google Scholar
Cao, S. Impact of China’s large-scale ecological restoration program on the environment and society in arid and semiarid areas of china: achievements, problems, synthesis, and applications. Crit. Rev. Env. Sci. Tec. 41, 317–335 (2011).
Article CAS Google Scholar
Xu, J. China’s new forests aren’t as green as they seem. Nature 477, 371–371 (2011).
Article ADS CAS PubMed Google Scholar
Cao, S. Why large-scale afforestation efforts in china have failed to solve the desertification problem. Environ. Sci. Technol. 42, 1826–1831 (2008).
Article ADS CAS PubMed Google Scholar
Li, C. et al. Drivers and impacts of changes in China’s drylands. Nat. Rev. Earth Env 2, 858–873 (2021).
Article Google Scholar
National Forestry and Grassland Administration. China Forestry and Grassland Statistical Yearbook 2018. (China Forestry Publishing House Beijing, 2017).
Zhang, Y. & Song, C. Impacts of afforestation, deforestation, and reforestation on forest cover in China from 1949 to 2003. J. Forestry 104, 383–387 (2006).
Article Google Scholar
Cao, S., Xu, C., Chen, L. & Wang, X. Attitudes of farmers in China’s northern Shaanxi Province towards the land-use changes required under the Grain for Green Project, and implications for the project’s success. Land Use Policy 26, 1182–1194 (2009).
Article Google Scholar
Yu, Z. et al. Natural forests exhibit higher carbon sequestration and lower water consumption than planted forests in China. Glob. Change Biol. 25, 68–77 (2019).
Article ADS Google Scholar
Feng, X. et al. Revegetation in China’s Loess Plateau is approaching sustainable water resource limits. Nat. Clim. Change 6, 1019–1022 (2016).
Article ADS Google Scholar
Lu, C., Zhao, T., Shi, X. & Cao, S. Ecological restoration by afforestation may increase groundwater depth and create potentially large ecological and water opportunity costs in arid and semiarid China. J. Clean. Prod. 176, 1213–1222 (2018).
Article Google Scholar
Ahrends, A. et al. China’s fight to halt tree cover loss. P. Ro. l Soc. B-Biol. Sci. 284, 20162559 (2017).
Google Scholar
Crouzeilles, R. et al. Ecological restoration success is higher for natural regeneration than for active restoration in tropical forests. Sci. Adv. 3, e1701345 (2017).
Article ADS PubMed PubMed Central Google Scholar
Zhang, L., Sun, P., Huettmann, F. & Liu, S. Where should China practice forestry in a warming world? Glob. Change Biol. 28, 2461–2475 (2022).
Article CAS Google Scholar
Friedl, M. & Sulla-Menashe, D. MCD12Q1 MODIS/Terra+aqua land cover type yearly L3 global 500m SIN grid. NASA LP DAAC. https://doi.org/10.5067/MODIS/MCD12Q1.006 (NASA EOSDIS Land Processes Distributed Active Archive Center, 2018).
Hansen, M. C. et al. High-resolution global maps of 21st-century forest cover change. Science 342, 850–853 (2013).
Article ADS CAS PubMed Google Scholar
Crowther, T. W. et al. Mapping tree density at a global scale. Nature 525, 201–205 (2015).
Article ADS CAS PubMed Google Scholar
Pan, Y. et al. A large and persistent carbon sink in the world’s forests. Science 333, 988–993 (2011).
Article ADS CAS PubMed Google Scholar
Luyssaert, S. et al. Old-growth forests as global carbon sinks. Nature 455, 213–215 (2008).
Article ADS CAS PubMed Google Scholar
Shang, R. et al. China’s current forest age structure will lead to weakened carbon sinks in the near future. Innovation 4, 100515 (2023).
PubMed PubMed Central Google Scholar
Cheng, K. et al. A 2020 forest age map for China with 30m resolution. Earth Syst. Sci. Data 16, 803–819 (2024).
Article ADS Google Scholar
Chen, Y. et al. Maps with 1km resolution reveal increases in above- and belowground forest biomass carbon pools in China over the past 20 years. Earth Syst. Sci. Data 15, 897–910 (2023).
Article ADS Google Scholar
Soto-Navarro, C. et al. Mapping co-benefits for carbon storage and biodiversity to inform conservation policy and action. Philos. T R. Soc. B 375, 20190128 (2020).
Article CAS Google Scholar
Ministry of Environment Projection & Chinese Academy of Sciences. The National Zoning Program of Ecological Functions. https://www.mee.gov.cn/gkml/hbb/bgg/201511/t20151126_317777.htm (CAS, 2015).
Sexton, J. O. et al. Conservation policy and the measurement of forests. Nat. Clim. Change 6, 192–196 (2016).
Article ADS Google Scholar
People’s Republic of China, Forest Law of the People’s Republic of China. (People’s Republic of China, 2020).
National Center for Atmospheric Research Staff. The Climate Data Guide: CERES: IGBP Land Classification. https://climatedataguide.ucar.edu/climate-data/ceres-igbp-land-classification (NCAR, 2024).
Spawn, S. A., Sullivan, C. C., Lark, T. J. & Gibbs, H. K. Harmonized global maps of above and belowground biomass carbon density in the year 2010. Sci. Data 7, 112 (2020).
Article PubMed PubMed Central Google Scholar
Xu, B., Guo, Z., Piao, S. & Fang, J. Biomass carbon stocks in China’s forests between 2000 and 2050: a prediction based on forest biomass-age relationships. Sci. China Life Sci. 53, 776–783 (2010).
Article PubMed Google Scholar
Jiang, X., Ziegler, A. D., Liang, S., Wang, D. & Zeng, Z. Forest restoration potential in china: implications for carbon capture. J. Remote Sens. 2022, 0006 (2022).
Article Google Scholar
Hong, S. et al. Divergent responses of soil organic carbon to afforestation. Nat. Sustain 3, 694–700 (2020).
Article Google Scholar
Piao, S., Yue, C., Ding, J. & Guo, Z. Perspectives on the role of terrestrial ecosystems in the ‘carbon neutrality’ strategy. Sci. China Earth Sci. 65, 1178–1186 (2022).
Article Google Scholar
Brandt, M. et al. An unexpectedly large count of trees in the West African Sahara and Sahel. Nature 587, 78–82 (2020).
Article ADS PubMed Google Scholar
Leverkus, A. B., Thorn, S., Lindenmayer, D. B. & Pausas, J. G. Tree planting goals must account for wildfires. Science 376, 588–589 (2022).
Article ADS CAS PubMed Google Scholar
Wu, Z. et al. Current and future patterns of forest fire occurrence in China. Int. J. Wildland. Fire 29, 104–119 (2019).
Lan, Z. et al. Are climate factors driving the contemporary wildfire occurrence in China? Forests 12, 392 (2021).
Article Google Scholar
Jiang, H., Lu, N., Qin, J. & Yao, L. Hourly 5-km surface total and diffuse solar radiation in China, 2007–2018. Sci. Data 7, 311 (2020).
Article PubMed PubMed Central Google Scholar
Yao, L. et al. Satellite-derived aridity index reveals China’s drying in recent two decades. Iscience 26, 106185 (2023).
Article ADS PubMed PubMed Central Google Scholar
Wan, Z., Hook, S. & Hulley, G. MOD11C3 MODIS/Terra Land Surface Temperature/Emissivity Monthly L3 Global 0.05Deg CMG V006. https://doi.org/10.5067/MODIS/MOD11C3.006 (NASA EOSDIS Land Processes Distributed Active Archive Center, 2015).
Hall, D. K., Riggs, G. A. & Salomonson, V. V. MODIS/terra snow cover daily L3 global 500m grid, version 6. https://nsidc.org/data/mod10a1/versions/6 (NASA National Snow and Ice Data Center Distributed Active Archive Center, 2016).
Hengl, T. et al. SoilGrids250m: global gridded soil information based on machine learning. PLoS one 12, e0169748 (2017).
Article PubMed PubMed Central Google Scholar
Jarvis, A., Reuter, H. I., Nelson, A. & Guevara, E. Hole-filled SRTM for the globe Version 4. http://srtm.csi.cgiar.org/ (CGIAR Consortium for Spatial Information, 2008).
Li, C. et al. The first all-season sample set for mapping global land cover with Landsat-8 data. Sci. Bull. 62, 508–515 (2017).
Article MathSciNet Google Scholar
Wu, X. et al. CPSDv0: A forest stand structure database for plantation forests over China. SCIENCEDB. https://doi.org/10.11922/sciencedb.j00076.00091 (Science Data Bank, 2022).
Fang, J., Chen, A., Peng, C., Zhao, S. & Ci, L. Changes in forest biomass carbon storage in China between 1949 and 1998. Science 292, 2320–2322 (2001).
Article CAS PubMed Google Scholar

Download references

Acknowledgements

This study is supported by the Strategic Priority Research Program of the Chinese Academy of Sciences (Grant No. XDB 0740200, L. Yao, J. Q. and H. J.) and the National Natural Science Foundation of China (Grant No. 42471386, L. Yao).

Author information

These authors contributed equally: Ling Yao, Tang Liu.

Authors and Affiliations

State Key Laboratory of Resources and Environmental Information System, Institute of Geographic Sciences and Natural Resources Research, Chinese Academy of Sciences, Beijing, PR China
Ling Yao, Tang Liu, Jun Qin, Hou Jiang & Chenghu Zhou
Faculty of Geography, Yunnan Normal University, Kunming, PR China
Jun Qin
School of Geography and Ocean Science, Nanjing University, Nanjing, PR China
Lin Yang
Institute of Biological and Environmental Sciences, University of Aberdeen, Aberdeen, UK
Pete Smith
State Key Laboratory of Desert and Oasis Ecology, Xinjiang Institute of Ecology and Geography, Chinese Academy of Sciences, Urumqi, PR China
Xi Chen
Center for Ocean Remote Sensing of Southern Marine Science and Engineering Guangdong Laboratory (Guangzhou), Guangzhou Institute of Geography, Guangdong Academy of Sciences, Guangzhou, PR China
Chenghu Zhou
College of Urban and Environmental Sciences, Peking University, Beijing, PR China
Shilong Piao
Institute of Tibetan Plateau Research, Chinese Academy of Sciences, Beijing, PR China
Shilong Piao

Authors

Ling Yao
View author publications
Search author on:PubMed Google Scholar
Tang Liu
View author publications
Search author on:PubMed Google Scholar
Jun Qin
View author publications
Search author on:PubMed Google Scholar
Hou Jiang
View author publications
Search author on:PubMed Google Scholar
Lin Yang
View author publications
Search author on:PubMed Google Scholar
Pete Smith
View author publications
Search author on:PubMed Google Scholar
Xi Chen
View author publications
Search author on:PubMed Google Scholar
Chenghu Zhou
View author publications
Search author on:PubMed Google Scholar
Shilong Piao
View author publications
Search author on:PubMed Google Scholar

Contributions

L.Y. and T.L. wrote the manuscript. L.Y. performed the formal analysis, funding acquisition, and investigation. T.L. handled data curation, methodology, validation, and visualization. J.Q. supervised the study and conceptualized the project. H.J. contributed to data curation, software, and methodology. L.Y. worked on software, validation, and data curation. P.S. supervised the work and reviewed and edited the manuscript. X. C. provided resources and secured funding. C.Z. supervised the project, provided resources, and managed the project administration. S.P. conceptualized the study and supervised the work. All authors contributed to the manuscript.

Corresponding authors

Correspondence to Jun Qin, Xi Chen or Shilong Piao.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Communications thanks Javier Gamarra, and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. A peer review file is available.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Peer Review File

Source data

Source Data

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.

Reprints and permissions

About this article

Cite this article

Yao, L., Liu, T., Qin, J. et al. Carbon sequestration potential of tree planting in China. Nat Commun 15, 8398 (2024). https://doi.org/10.1038/s41467-024-52785-6

Download citation

Received: 15 March 2023
Accepted: 20 September 2024
Published: 27 September 2024
DOI: https://doi.org/10.1038/s41467-024-52785-6