Introduction

Today’s semiconductor industry faces ever-increasing demands for computing power and data storage due to emerging technology, such as artificial intelligence. The new platform for memory and/or logic device need to overcome challenges such as continuous downscaling, Joule heating, and low-power consumption in traditional Si-based device. Manipulation of collective state variables could provide progressive miniaturization, superior energy efficiency, and non-volatility1. Spin-based devices that exploit the collective state of ferromagnetism carrying a non-volatile nature have shown great potential and versatile opportunities. In particular, the control of magnetization through spin-transfer torque (STT) and/or spin-orbit torque (SOT) have brought major advances in the integration of chip architecture with improved device endurance, switching speed and reliability, and fabrication compatibility2,3,4,5,6. However, the reversal of magnetization via STT or SOT requires current flow over the threshold value, which involves significant energy dissipation. In order to alleviate such energy consumption, voltage-controlled magnetic anisotropy (VCMA) has been extensively explored as it reduces the barrier for magnetization reversal7,8. Yet, this approach still requires an external magnetic field or current-driven torque to switch magnetic polarity. The complete control of magnetization solely by an electric field will bring significant merits in improving power loss as well as heating issues in device operations. Employing multi-ferroic materials to control the magnetization with only an electric field has recently been proposed with a prospect of beyond CMOS technology1. It should be noted that the recent report of Vaz et al. showed the voltage control of magnetization using multi-ferroic materials and its electrical readout9.

Spin-orbit interaction could drive conversion between spin and charge flow as it couples spin and momentum of itinerant electrons. Thus, the generation of pure spin currents from the charge flow can be achieved without ferromagnets. Conversely, spin currents could be converted into electrical output without ferromagnets. In particular, Rashba-type spin-orbit interaction which occurs at the interfaces or surfaces due to broken inversion symmetry leads to intertwined spin texture at the Fermi surface10,11. Here, the conversion between spin and charge flow could also occur through the shift of spin-textured Fermi surface12,13,14. And such conversion could be magnified when the itinerant electrons are confined in two-dimensional (2D) systems15,16,17,18,19,20. More interestingly, Rashba-type spin-orbit interaction, which relies on the inversion asymmetry could be tuned by simply applying gate voltage10,11,21,22. Thus, the electrical output voltage from the conversion of spin flow, i.e. inverse Edelstein effect (IEE), could be modulated with gate voltage23. However, this gate effect is transient as it disappears when the gate voltage is turned off. Applying a ferroelectric channel may enable switching of the polarity of inversion asymmetry and allow non-volatile control of spin-charge conversion24. This approach lays out a new concept of memory devices with superior energy efficiency24. Demonstrations of non-volatile spin-charge conversion have recently been achieved in two distinct ferroelectric systems. One is SrTiO3-based conductive interface24 and the other is ferroelectric GeTe25. However, the ferroelectricity of SrTiO3 appears only under 40 K24. And ferroelectric property of GeTe is rather weak due to the presence of free carriers25. It is highly challenging to develop relevant systems that retain both ferroelectricity and decent conductivity to function as a tunable spin-charge conversion channel.

In this report, we introduce an alternative control of spin-charge conversion through the non-volatile tuning of Fermi level in graphene. We demonstrate that the sign change of spin-charge conversion can be also achieved by inverting energy-momentum dispersion of Rashba spin texture instead of reversing the polarity of Rashba spin-orbit interaction. Ferroelectric insulator polyvinylidene fluoride-co-trifluoroethylene (PVDF-TrFE) film was employed to tune the Fermi level in between above and below the charge neutral point (CNP) in graphene. The spin accumulation to the inverted electron dispersion with Rashba spin texture leads to opposite shift of momentum. The ferromagnetic resonance (FMR) and IEE results show non-volatile switching of output voltage at room temperature with robust endurance. In addition, tuning Fermi level by using adjacent ferroelectric insulator is electric-field-only process and thus ultralow-power device operation, whereas switching the polarity of ferroelectric conductor involves with large leackage currents. Our approach opens an alternative route for highly energy-efficient manipulation of spin signal with a promising prospect for the new class of spin-orbitronic devices.

Results

Concept of nonvolatile control of spin-charge conversion in graphene

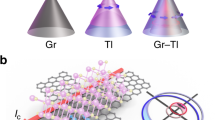
Figure 1a shows a schematic for non-volatile spin-charge conversion in PVDF-TrFE/graphene/YIG heterostructure. Graphene is a well-known 2D system with outstanding electrical properties and exhibits robust spin-charge conversion when the spin-orbit interaction is implemented through various methods26,27,28,29,30,31,32,33,34,35,36. It has also been shown that the proximity effect from the interfaces with a yttrium iron garnet (Y3Fe5O12, YIG) drives Rashba-type spin-orbit interaction as well as spin-charge conversion15,16,17,18. Here, ferromagnetic insulator YIG film can also function as a spin source with outstanding low magnetic damping37,38. The propagation of magnon in YIG excited by FMR transfers spin angular moments (Js, spin current) into graphene. Then, the injected spin current in graphene is altered into a transverse charge current by IEE. Here, the direction of the charge current can be inverted through the poling of the ferroelectric PVDF-TrFE without requiring an additional electric field or magnetic anisotropy. The electrical dipole moment of PVDF-TrFE could tune the Fermi level and thus switch the type of majority carriers between electron and hole in graphene as shown in Fig. 1b.

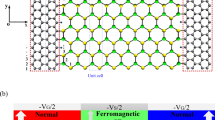
Fig. 1: Concept for the nonvolatile control of spin-charge conversion via ferroelectric charging.
figure 1

a Schematic illustration of the inversion of the spin-charge conversion in single-layer graphene. Vertical spin flow generated by the ferromagnetic resonance is converted into a transverse charge flow via IEE. Here, the direction of charge flow in graphene depends on the poling state of PVDF-TrFE. b Spin-split energy dispersion in graphene due to Rashba spin-orbit interaction induced by the proximity effect from YIG. Red and blue lines represent energy dispersion for spin-up and spin-down electrons, respectively. The ferroelectricity of PVDF-TrFE allows the adjustment of the Fermi level in graphene above the CNP (upper) and below the CNP (lower). Arrows indicate the change of electron distribution when electron spins with polarization of +y is accumulated. c Schematic illustration of IEE in graphene when the Fermi level is above the CNP (upper) or below the CNP (lower). When the spins of polarization y are injected into graphene, the shift of the Fermi contour occurs. This Fermi contour shift is toward the opposite direction for each upper and lower case, respectively. Finally, ± Δk in momentum space produces output voltage with a nonvolatile sign change depending on the ___location of the Fermi level controlled by the poling of ferroelectric PVDF-TrFE.

Full size image

To examine the impact of the carrier switching in spin-to-charge conversion, we diagonalized the graphene Hamiltonian with Rashba spin-orbit coupling expressed as \(H={{\hslash }}{v}_{F}(\tau {q}_{x}{\sigma }_{x}+{q}_{y}{\sigma }_{y})+{\lambda }_{{{{\rm{SO}}}}}\tau {\sigma }_{z}{s}_{z}+{\lambda }_{R}(\tau {\sigma }_{x}{s}_{y}-{\sigma }_{y}{s}_{x})\), where \({v}_{F}\) is the Fermi velocity (without spin-orbit coupling), \({{{\bf{q}}}}\) is the relative momentum with respect to the Dirac point, \({{{\boldsymbol{\sigma }}}}\) and \({{{\bf{s}}}}\) are the pseudo-spin and real-spin Pauli matrices, respectively, \(\tau=\pm 1\) for K and K’ valleys respectively, and \({\lambda }_{{{{\rm{SO}}}}}\) and \({\lambda }_{R}\) are the spin-orbit coupling and the Rashba parameters, respectively39,40. The resulting band structure and the spin texture are illustrated in Fig. 1b. Provided that the spin-orbit coupling and the Rashba parameters are positive, the spin texture is given by \(\left\langle {{{\bf{s}}}}\right\rangle \parallel \hat{{{{\bf{z}}}}}\times \hat{{{{\bf{q}}}}}\) for the higher electron and the lower hole bands and \(\left\langle {{{\bf{s}}}}\right\rangle \parallel -\hat{{{{\bf{z}}}}}\times \hat{{{{\bf{q}}}}}\) for the other. In other words, the spin textures at the Fermi level are equivalent for both above and below the CNP in graphene as long as the polarity of inversion asymmetry induced by the proximity effect from YIG remains unchanged. When the spin angular moment, polarized along the y direction, is accumulated in graphene by spin pumping, the shift of Fermi momentum so does the Fermi contour occurs in the opposite direction between electron doping and hole doping cases (Fig. 1b and c). This leads to net ±Δkx producing net charge current ± Jx. Thus, the output voltage of IEE changes sign depending on the carrier type of graphene, which can be tuned by the poling of PVDF-TrFE. An explicit demonstration of the carrier dependence of the Edelstein effect is also presented in Supplementary Note 1. In this way, we can control the non-volatile spin-charge conversion in graphene with an electric-field only without reversing inversion asymmetry.

Ferroelectric charging and switching of inverse Edelstein effect

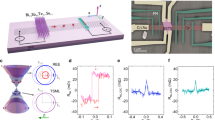
Figure 2a shows an illustration of the studied graphene-based heterostructures for field effect transistor (FET) and FMR-IEE measurement. CVD graphene was transferred on top of epitaxial YIG films. The graphene channel has dimensions of 1 mm width and 5 mm length (see Supplementary Note 2 and Fig. S1 for details). Then, PVDF-TrFE film was spin-coated on graphene. According to XRD results, the spin-coated PVDF-TrFE film is beta phase having a lamellar structure, which leads to out-of-plane ferroelectricity41,42 (see Supplementary Note 2 and Fig. S2 for details). MoO3 film was thermally deposited before the top Au gate electrode to protect the molecular PVDF-TrFE layer and prevent unwanted pinholes.

Fig. 2: FET characteristics and FMR-IEE in graphene-based heterostructure.
figure 2

a Configuration of the device structure for the study of FET and FMR-IEE characteristics. For FMR-IEE measurements, the sample is placed on top of a coplanar waveguide. b Resistivity of graphene as a function of electric field for ± 5.19 mV/nm sweeping ranges at 300 K. The blue line displays FET curve measured by sweeping electric field from +5.93 mV/nm to −5.93 mV/nm, and the red line represents FET curve for opposite electric field sweeping. c, d The measured VIEE upon sweeping the in-plane magnetic field at 6 GHz for opposite remanent poling state of PVDF-TrFE. Measurements were performed at room temperature. The positive poling state (c) is obtained by increasing electric field up to +5.93 mV/nm and then removing it to be 0 mV/nm, whereas the negative poling state (d) was prepared by the opposite electric field pulse. Each remanent poling state results in a Fermi level above the CNP (electron majority carriers) or below the CNP (hole majority carriers), respectively. The obtained VIEE spectra display sharp peaks with opposite signs for electron and hole doping cases indicating inversion of spin-charge conversion by the ferroelectric charging. e, f The PVDF-TrFE/Graphene heterostructures are calculated using the density functional theory method. From the projected density-of-state (PDOS) of graphene depicted by red lines, the CNP is shifted by ~2 eV depending on the direction of ferroelectric polarization.

Full size image

Figure 2b shows the Field-Effect Transistor (FET) characteristics of the graphene-based heterostructure. The typical characteristic of FET curve in graphene exhibits a sharp resistance peak at the CNP and rapid decrease of resistance along with doping either electrons or holes by electric field (Supplementary Note 2 and Fig. S3). Due to the ferroelectric poling state of adjacent PVDF-TrFE, FET curves display large shifts depending on the direction of electric field sweeping43,44,45. As increasing gate bias from –5.19 mV/nm to +5.19 mV/nm, the peak of FET curve appears at around +2.96 mV/nm, where the ferroelectric polarity reverses. The shift of FET curve occurs to the opposite side as reversing electric field sweeping and it becomes larger with increasing range of electric field sweeping (see Supplementary Fig. S4). Therefore, the positive (negative) electric field pulse, which induces positive (negative) remanent poling state of PVDF-TrFE, makes the graphene to be electron (hole) doping state.

The effect of ferroelectric charging on the spin-charge conversion in graphene can be probed via FMR-IEE experiments. Here, FMR in YIG induces propagation of magnon resulting in spin-pumping at the interface of YIG/graphene. Then, the transferred spin angular momentum in graphene can be converted into the transverse charge current through the IEE. As shown in Fig. 2c, d, the output voltage produced by FMR-IEE displays the non-volatile switching of the spin-charge conversion at room temperature. For a positive electric field pulse (+5.93 mV/nm to 0 mV/nm), which induces positive remanence poling state of PVDF-TrFE and electron doping in graphene, the measured VIEE signal exhibits a sharp negative peak at the resonance field. If the graphene is in a hole doping state by negative electric field pulse (–5.93 mV/nm to 0 mV/nm), VIEE exhibits a sharp positive peak. In other words, spin-charge conversion in graphene can be switched in a non-volatile manner by ferroelectric poling of adjacent PVDF-TrFE as it enables to tune the Fermi level and switch between electron and hole doping. Ab initio density functional theory calculations confirm the shift of CNP via ferroelectric control. As shown in the projected density-of-states plots of PVDF-TrFe/graphene heterostructure (Fig. 2e, f), the CNP of the graphene is shifted by ~2 eV through the ferroelectric reversal. Theoretical calculation also shows that the Rashba spin splitting induced by ferroelectric poling is nearly negligible (See Supplementary Fig. S5). Thus, the ferroelectric PVDF-TrFE layer allows to tune the carrier type through the Fermi level shift with negligible impact on the Rashba spin-orbit interaction induced by the YIG film. We note that the underlying YIG film could drive ferromagnetism in graphene through the proximity-induced exchange interaction as previously reported46. However, the proximity-induced ferromagnetism in graphene by the adjacent YIG film becomes nearly negligible at room temperature, and thus its impact on the observed FMR-IEE spectra at room temperature can be ignored (See Supplementary Note 3 and Fig. S6).

It is also possible that the inverse spin Hall effect (ISHE) may partially contribute to the observed spin-charge conversion. However, perpendicular injection of spin flow into a 2D system is not likely to generate extrinsic spin Hall effect as it is derived from a series of scattering for the spin-dependent deflection47,48. The intrinsic spin Hall effect would also provide a negligible contribution to spin-charge conversion because the momentum perpendicular to the plane is highly suppressed in 2D systems. The spin-charge conversion in graphene has been more extensively studied in lateral transport geometry30,31,32,33,34,35,36. In such case, symmetry given by the polarization direction of spin flow and its precession in response to the external field allows to distinguish between ISHE and IEE31,32,33. We note that ISHE observed in lateral transport geometry shows no sign change of output voltage regardless of the ___location of the Fermi level, instead, it displays rapid decay as the Fermi level moves away from the CNP33,49. Another possible origin for the observed FMR-induced voltage generation is thermoelectric effects. The resonance absorption of microwave could cause local heating and thus voltage across lateral direction due to the Seebeck effect. However, this thermally induced signal should not be associated with the magnetic polarity of YIG. The measured VIEE changes sign with the inversion of the magnetization of YIG, and thus obtained VIEE in our experiments is not associated with thermoelectric effects (See supplementary Note 4 and Fig. S7).

Nonvolatile tuning of spin-charge conversion and its stability

The electric field dependence of spin-charge conversion and its hysteric behavior due to ferroelectricity are displayed in Fig. 3a and b. The FMR-IEE measurements were performed by first increasing the poling electric field from –5.93 mV/nm to +5.93 mV/nm and then decreasing the poling electric field from +5.93 mV/nm to –5.93 mV/nm. Starting from –5.93 mV/nm, VIEE(H) displays a sharp positive peak and maintains until +3.70 mV/nm and then undergoes inversion when the poling electric field reaches +4.44 mV/nm. In a reverse variation of the poling electric field (+5.93 mV/nm to –5.93 mV/nm), VIEE exhibits complete inversion when the poling electric field reaches –4.44 mV/nm, in consistency with the hysteric behavior of the adjacent PVDF-TrFE layer. The efficiency of spin-charge conversion, represented by the inverse Edelstein length (\({\lambda }_{{{{\rm{IEE}}}}}\)), can be estimated once we get the spin mixing conductance at the YIG/graphene interface from the relation, \({G}_{{{{\rm{eff}}}}}^{\uparrow \downarrow }=\frac{4\pi {M}_{{{{\rm{s}}}}}{t}_{{{{\rm{FM}}}}}}{\hslash \omega }(\Delta {H}_{{{{\rm{YIG}}}}/{{{\rm{Gr}}}}}-\Delta {H}_{{{{\rm{YIG}}}}})\)18. Where \({t}_{{{{\rm{FM}}}}}\) is the FM thickness, \(\hslash\) is the reduced Planck constant, \(\omega\) is the microwave frequency, \(\Delta {H}_{{{{\rm{YIG}}}}}\) is the linewidth of the GGG/YIG, and \(\Delta {H}_{{{{\rm{YIG}}}}/{{{\rm{Gr}}}}}\) is the linewidth of the GGG/YIG/graphene/PVDF-TrFE. Finally, \({\lambda }_{{{{\rm{IEE}}}}}\) can be obtained from the relation, \({\lambda }_{{{{\rm{IEE}}}}}=\frac{4{V}_{{{{\rm{IEE}}}}}^{{{{\rm{peak}}}}}}{{R}_{{{{\rm{s}}}}}{wefp}{G}_{{{{\rm{eff}}}}}^{\uparrow \downarrow }({h}_{{{{\rm{rf}}}}}/\triangle H)}\)18. Where, \({R}_{{{{\rm{s}}}}}\) is the resistance of the graphene, \(w\) is the width of the graphene, \(p\) is the precession ellipticity, and \({h}_{{{{\rm{rf}}}}}\) is the amplitude of the RF magnetic field. The maximum value obtained for \({\lambda }_{{{{\rm{IEE}}}}}\) is ~0.0095 nm at –1.48 mV/nm (see also Supplementary Note 5 and Figs. S8–11), which is similar in magnitude compared to the previously reported \({\lambda }_{{{{\rm{IEE}}}}}\) in graphene-based heterostructures16,18. Figure 3c displays the stability of the remanent poling effect on the spin-charge conversion. The time-dependent FMR-IEE measurements were performed after poling PVDF-TrFE with either a positive (+5.93 mV/nm) or negative (–5.93 mV/nm) electric field pulse. Both of VIEE signals are maintained for over several hours, which demonstrates robust stability of the non-volatile spin-charge conversion within the measurement windows.

Fig. 3: Electric field-dependent spin-charge conversion.
figure 3

a FMR-IEE voltage (VIEE) as a function of the magnetic field measured at various poling electric fields. Numbers on the top left of each panel represent spectra measured at each electric field poling indicated in (b). All data were recorded with a microwave frequency of 6 GHz. b Maximum value of VIEE as a function of poling electric fields. The red symbols are results recorded with increasing poling electric field from –5.93 mV/nm to + 5.93 mV/nm, whereas blue symbols are for decreasing poling electric field from + 5.93 mV/nm to –5.93 mV/nm. Each measurement was performed after poling the PVDF-TrFE layer. c The time-dependent VIEE measured after poling PVDF-TrFE layer with maximum positive or negative electric field pulse (± 5.93 mV/nm). The magnitude of the VIEE signals was maintained over several hundred minutes. Data in (a, b, and c) are all recorded at room temperature.

Full size image

The observed non-volatile switching of spin-charge conversion could be attributed to the inversion of Rashba spin-orbit interaction induced by the ferroelectric poling. However, our DFT results showed negligible spin-splitting by the ferroelectric polarization. And the switching of spin-charge conversion in graphene due to the change of the type of majority carriers has been observed in various graphene-based heterostructures17,33,34,35,50. In order to confirm the origin of spin-charge conversion in our studied devices, we performed FMR-IEE study with a control device of YIG/graphene (see Supplementary Note 6 and Fig. S12). Instead of ferroelectric PVDF-TrFE, an insulating Parylene layer was used for the top gate. The control device exhibits CNP at around +1.11 mV/nm. When the electric fields were set to –0.59 mV/nm and +0.59 mV/nm, reversing the polarity of electric field while maintaining the graphene’s carrier type as hole carriers, we observed that the sign of VIEE signal remained unchanged. When the electric fields were set to +0.59 mV/nm and +1.56 mV/nm, maintaining the electric field polarity while changing the carrier type from holes to electrons, we observed a reversal of the VIEE signal. These results reflect that the observed inversion of spin-charge conversion via the ferroelectric poling originated from the change of the Fermi level rather than the change in the polarity of inversion asymmetry.

Discussion

In conclusion, we demonstrated non-volatile control of spin-to-charge current conversion at room temperature, which brings a promising potential to implement new memory and spin logic devices. Instead of manipulating the magnetization direction of ferromagnetic materials as in conventional STT- or SOT-MRAM devices, we focused on controlling the Rashba effect using ferroelectric materials, along with the associated spin-to-charge current conversion. This approach aimed to address the durability issues of soft magnetic-based devices and the thermal stability problems. Additionally, we aimed to realize voltage-based operation, non-volatility, and control over current direction in low-dimensional materials like graphene. Through experimental measurements using FMR at room temperature, we demonstrated that the direction of charge current converted by the graphene carrier type can be controlled by aligning the polarization direction of PVDF-TrFE. This ferroelectric-based control of output signal offers non-volatile characteristics, different from conventional gate-voltage control methods. The complete switching of spin-charge conversion in our system was achieved by applying a electric field pulse over ~4.44 mV/nm. Thus, it can evolve into an exceptionally energy-efficient writing process with further development of a relevant thin ferroelectric layer. We note that there have been tremendous efforts to realize non-volatile switching of spin-charge conversion through the inversion of Rashba spin-orbit interaction24,25. However, the ferroelectric channel that allows the inversion of Rashba spin-orbit interaction requires large energy consumption due to strong leakage currents, as evidenced by the electric field required for GeTe25 being two orders of magnitude larger than our system. In contrast. control of spin-charge conversion through Fermi level tuning with an adjacent insulating ferroelectric layer relies exclusively on electric-field manipulation, making it an outstanding energy-efficienct process. Moreover, this non-volatile control of spin-charge conversion by inverting energy-momentum dispersion could be extended to various semiconductors and/or semi-metallic systems other than graphene. Finally, we anticipate that incorporating such ferroelectric-controlled spin-charge conversion can lead to the implementation of new Process-In-Memory (PIM) devices, enabling low-power read/write operations, high integration density, and both memory and computational functionalities.

Methods

Materials preparation

GGG/YIG substrates were cut to dimensions of 8 mm by 8 mm by using the dicing saw and cleaned by using an ultra-sonicator. Then, CVD-graphene with dimensions of 1 mm by 5 mm was transferred on the substrate by using PMMA-based dry transfer method with the thermal release tape51,52. Thermally deposited Au were used for contact electrodes to detect VIEE. The ferroelectric PVDF-TrFE film was coated by using spin coater at 2500 rpm followed by a soft baking process at 110 °C for 20 minutes to remove the solvent. Then, a crystallization process was performed in a furnace at 130 °C for 6 hours. Molybdenum trioxide (MoO3) were thermally deposited over the molecular layer of PVDF-TrFE to prevent unwanted pinholes. Finally, aluminum (Al) were deposited by using thermal evaporation for the top gate.

FMR and FMR-IEE measurements

For the FMR measurements, we used the broadband FMR of the PPMS option with a coplanar waveguide (CPW) and a Rohde & Schwarz RF signal generator operated in the frequency range of 2–19 GHz. For the FMR-driven IEE measurements, we used CPW FMR with contact pads for the detection of IEE (RNDWARE Co. Ltd.). Devices used for FMR-IEE studies have a channel size of 1 mm width and 3 mm length with gold contact pads at both sides. Electric field to switch ferroelectric poling was applied using Keithley 2636 A source meter. Voltages generated by FMR-IEE were detected by using Keithley 2182 nanovoltmeter with remanent electric field after applied electric field. All FMR and FMR-IEE measurements were performed in the PPMS chamber at 300 K.

First-principles calculation

We performed the first-principles calculation using the DFT method within the local-density approximation as implemented in VASP53,54. We used an 800 eV plane wave cut-off energy and 10 × 20 × 1 k-points for all calculations and the projector augmented wave method. During the geometry optimizations, the in-plane lattice constant was fixed at the experimental value of graphene, and the tolerance on atomic forces was set to 0.02 Å−1. The electronic density of states was calculated using a fine mesh 20 × 40 × 1 k-points.