Introduction

The importance of the Jahn-Teller (JT) effect reaches across many areas of chemistry, physics, and applied sciences1. Examples range from localized systems like photo-excited methane cations2,3, ultra-fast transients in molecular complexes4, and vacancy diffusion in graphene5 towards more cooperative phenomena, including high-temperature superconductivity in cuprates6, colossal magneto-resistance in manganites7, metal-insulator transition in ruthenates8 and antiferroelectricity in lacunar spinels9. The cornerstone of the JT effect is the existence of an electronic state with orbital degeneracy, leading to an overall decrease in the energy once the degeneracy is lifted. Typically, this occurs through ligand (L) displacement, which consequently affects both the electronic and magnetic properties of materials. In strongly correlated systems, where ligands are shared between neighboring metal (M) sites, the distortions at one site are correlated with distortions on neighboring sites, leading to a cooperative JT effect10.

In the case of isolated, highly symmetric clusters, the system can choose among equivalent directions of distortion, resulting in a potential energy surface (PES) with multiple valleys and energy barriers between them. In the simplest case of an ML6 octahedron having a single electron or a hole in a doubly-degenerate orbital state (well-known cases are Mn3+ and Cu2+ ions), the distortion can freeze along principal axes x, y, and z, producing a static JT effect. If the barriers are small enough so that the wave function is distributed over all valleys equally, the vibronic symmetry is restored, resulting in a dynamic JT effect. Many aspects of solid-state physics have been theoretically investigated through the coupling to continuous symmetries in JT systems11,12,13, but the available materials are rather scarce. The inter-cluster interaction needs to be very small to avoid a cooperative JT effect, while other couplings, like exchange interactions, should remain appreciable. Examples of materials where a dynamic JT effect has been suggested to occur include an unconventional molecular superconductor Cs3C60, where, together with Mott localization, it drives the material across a metal-to-insulator transition14,15,16. It has also been argued that the observed permittivity17 in a paraelectric phase of BaTiO3 stems from the resonating state between minima of the PES, which, under the influence of an electric field, become nonequivalent and trap Ti ions along one direction18. Eventually, the dynamic JT effect is overcome by the interaction between the centers, leading to a ferroelectric phase transition.

These examples involve relatively light elements, including 3d transition metal cations, where the influence of spin-orbit coupling (SOC) is considered negligible. Recently, a growing interest has been devoted to strong SOC systems, encompassing topological insulators19, Dirac and Weyl semimetals20, and Kitaev spin liquids21. The JT effect, on the other hand, has seldom been investigated in the context of strong SOC, with several examples devoted to Ir4+ systems22,23. Some 4f systems have been investigated before, like PrO224, where the crystal field effect is much weaker compared to compounds based on d orbitals. More generally, a strong SOC qualitatively changes the ground-state wave functions and has been proposed to renormalize the associated distortion, or even completely remove it above a certain critical value25.

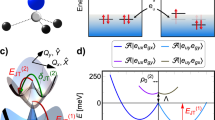
In this study, we present compelling evidence that Ba2MgReO6, a member of the 5d1 double-perovskite family, displays a distinctive set of properties that make it exceptionally well-suited for the exploration of the role of the dynamic JT effect on strongly correlated electrons in the presence of a strong SOC. This is promoted by a high-symmetry environment of Re6+ ions, covalently coupled to six oxygen ions, alternating with ionic Mg2+ ions and forming a three-dimensional array of nearly-independent, JT-active ReO6 octahedra, Fig. 1a. Strong SOC mixes the t2g levels into a jeff = 3/2 quartet and a jeff = 1/2 doublet, separated by ΔSO, as shown in Fig. 1b. The JT instability manifests itself as the splitting of the ground-state quartet into two doublets, with the gap ΔJT directly related to the amplitude of the distortion. The correlated nature of 5d electrons is reflected in the formation of a multipolar order26,27, encompassing a charge quadrupole state below TQ = 33 K and a magnetic dipole state below TM = 18 K (Fig. 1c, d).

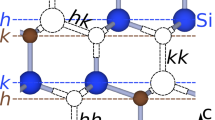
Fig. 1: The crystal environment of Ba2MgReO6 and the multipolar order.
figure 1

a The unit cell of Ba2MgReO6 with semi-transparent ReO6 octahedra and red circles representing oxygen ions. Mg and Ba ions are represented by orange and green circles, respectively. b Schematic representation of the splitting of Re 5d-levels under the influence of crystal field (ΔO), spin-orbit coupling (ΔSO), and a JT effect (ΔJT). Light gray lines represent orbitals, each allowing for two spin states. Dark blue lines represent SOC-entangled states. c T-dependence of dc magnetic susceptibility measured with B = 0.1 T after zero-field-cooled (blue circles) and field-cooled (green diamonds) protocols. The transition temperature into long-range magnetic order occurs at TM = 18 K and is marked by the splitting of two curves. d T-dependence of the inverse susceptibility with the temperature of the quadrupolar order TQ indicated as a change of the slope.

Full size image

Using spectroscopic and thermodynamic evidence, we show that the JT instability causes the doublet-doublet splitting in Ba2MgReO6 at temperatures T > > TM, TQ. We quantify the associated distortions through local cluster calculations and determine that the energy barriers between the local minima are smaller than the zero-point motion energy, establishing Ba2MgReO6 as a dynamic JT system. Additionally, through a careful analysis of specific heat results, we establish that the total entropy across both transitions reaches only \(R{{{\rm{\ln }}}}2\).

Results

Local d-d excitations

To probe the localized states of Re ions, we employ resonant inelastic x-ray scattering (RIXS). In Fig. 2a, we display the low temperature (T = 8 K) energy dependence of the scattering intensity obtained at the Re L3 edge, displaying multiple peaks of varying widths, which we assign as follows (see also the Supplementary Material). The peak around zero energy is an elastic line, where no energy transfer occurs during the virtual excitation of core-level electrons. Further peaks reflect virtual processes where core-level electrons are excited to unoccupied states while the recombination of the core-level hole occurs with electrons on occupied Re 5d states. We find that the observed scattering intensity profile can be fully described by assuming that each peak is represented by a simple Gaussian contribution. The positions of maxima correspond to crystal field levels of Re 5d-orbitals and can be readily assigned following the scheme presented in Fig. 1b. The first peak at ΔE > 0 represents the SOC-induced splitting between the ground state quartet and the higher-lying doublet state ΔSO ≅ 0.5 eV which allows the estimate of the SOC constant λ ~ 335 meV. Up to 4 eV, the line shape is featureless, with two additional peaks present around 4.5−5 eV. A notable tail coming from an even higher-lying peak can be observed, which can be assigned to virtual processes involving the recombination with electrons originating from lower-lying, predominantly oxygen p-orbitals, located  ~ 6.3 eV below the elastic line. A recent report28 focusing on the comparison between Ba2MgReO6, Sr2MgReO6, and Ca2MgReO6 found a slightly asymmetric line-shape around ΔSO, ascribing it to the influence of phonon modes on spin-orbit excitations. Nevertheless, their value for ΔSO in Ba2MgReO6, as well as the energies of higher-lying excitations, are in excellent agreement with our results.

Fig. 2: Resonant inelastic x-ray scattering on Ba2MgReO6.
figure 2

a RIXS spectra at the Re L3 edge. The full purple line represents a sum of Gaussian contributions (shaded areas with black lines) centered around the positions of localized 5d Re levels (gray lines between panels (a) and (b)). b RIXS spectra at the O K edge. The excitations below 1 eV correspond to localized d − d processes, while the broad features above 2.8 eV arise from fluorescence. The inset shows an expanded region below 1 eV with highlighted contributions from individual modes. The cascade of modes above ΔJT and ΔSO is indicated by shaded areas with broken lines. The RIXS scattering involves a virtual process of core-level electron excitation with a photon of energy Ein while the outgoing photon’s energy Eout is reduced by the energy difference ΔE, measuring the position of higher-lying d-levels. c Re RIXS spectra below and above TQ. d T-dependence of ΔSO. e T-dependence of ΔJT and Emode. The dashed line represents a hypothetic mean-field order parameter behavior \({\Delta }_{{{{\rm{JT}}}}} \sim \sqrt{1-T/{T}_{{{{\rm{JT}}}}}}\) with TJT = 1000 K. The error bars are given as one standard deviation obtained from the fit.

Full size image

The two peaks, situated at 4.7 eV and 4.9 eV, can be assigned to states belonging to eg orbitals, with four-fold degeneracy being split into two doublets, in accordance with the JT scenario. An equivalent split of the ground state quartet is expected but not directly observed due to an insufficient energy resolution (~ 100 meV) of the experimental setup at the Re L3 edge. On the other hand, the results obtained at the O K edge (Fig. 2b), with its  ~ 50 meV resolution, show an additional peak at low energies reflecting the doublet-doublet splitting ΔJT ≅ 88 meV. A similar finding has been reported very recently29 for the sister compound Ba2NaOsO6, with the corresponding excitation at 95 meV. It is interesting to note that both experiments at the O K edge resulted in a similarly asymmetric line shape around ΔJT and ΔSO, with possible faint features on the high-energy side. The description of those features has recently been attempted in terms of coupling of phonon modes with spin-orbit excitations28, although the asymmetry itself is still not fully understood. It is clear that several additional modes are necessary to describe such an asymmetric line shape, but if all the parameters are left independent, it quickly becomes unfeasible to perform the fitting procedure (see the Supplementary Material for more details). The approach we used is to model the high-energy tail of each d − d excitation through a set of n dependent modes, whose energies and amplitudes are determined by simple relations, \({E}_{n}^{\alpha }={E}_{\alpha }+n\cdot {E}_{mode}\) and \({A}_{n}^{\alpha }={A}_{0}^{\alpha }{e}^{-n\cdot B}\), with all the additional modes having the same width. Here α stands for a JT or SO d − d excitation (indicated by light colors in the inset of Fig. 2b), while additional modes are indicated by darker colors. Such an approach significantly reduces the number of independent parameters and leads to a very satisfactory description of the observed line shape within the relevant energy range up to 1 eV.

The central result of RIXS experiments comes from the temperature evolution of the acquired spectra. In Fig. 2c, we compare the Re L3 RIXS spectra above and below TM and TQ. Within the resolution, there is no visible variation between the two line profiles. Specifically, the asymmetric shape at 4.5−5 eV, associated with the splitting of eg orbitals, remains clearly unaffected. A more direct and profound evidence comes from ΔSO(T) and ΔJT(T), extracted from O K RIXS spectra and plotted in Panels 2d, e. Both are practically T-independent, with a small decrease of ΔJT below TQ.

It is not surprising that ΔSO shows very little temperature dependence. On the contrary, the persistence of ΔJT well above 200 K goes against the prevailing idea that the splitting of the ground-state quartet is linked with the appearance of the quadrupolar order at TQ30,31. Moreover, we can infer that ΔJT > 0 to much higher temperatures since any order-parameter-like decrease would be readily observed in our data, as indicated in Fig. 2e by a dashed line.

Potential energy surface and the Jahn-Teller effect

Now we turn our efforts to characterize the type of distortion that accompanies the observed splitting. The relevant modes of an ML6 octahedron are sketched in Fig. 3a–c. The magnitude of the isotropic mode mainly determines the octahedral splitting ΔO which for Ba2MgReO6 is large enough to disregard the t2g − eg mixing. Two other modes are JT-active, with Q3 representing a tetragonal distortion while Q2 describes the orthorhombic mode. For an isolated octahedron, with a linear coupling and in the limit of very small distortions, the PES is characterized by an infinite-degeneracy line, the so-called ‘Mexican hat’ potential (Fig. 3d). The octahedron remains dynamic, exploring all possible linear combinations in the Q2 − Q3 parameter space, with ΔJT = const. > 0. Increasing the amplitude of distortions leads to anharmonic effects and, together with the presence of surrounding charges, breaks the line degeneracy, resulting in a multi-valley PES. An opposing effect has been argued to arise from strong SOC25, driving the PES back towards a Mexican-hat potential but also suppressing the JT distortion, as well as reducing the energy gain due to the JT effect.

Fig. 3: Vibrational modes and potential energy surface for a ReO6 cluster.
figure 3

Definition of displacement modes: (a) isotropic mode Qiso = (1, 1, 1), (b) \({{{{\boldsymbol{Q}}}}}_{{{{\boldsymbol{3}}}}}=(-\frac{1}{2}, -\frac{1}{2},1)\) and (c) Q2 = (− 1, 1, 0). d A Mexican-hat potential with an infinite line degeneracy. e The PES was obtained using quantum chemistry calculations. Superimposed on top is the numerically calculated probability density ∣Ψ∣2 of the ground-state wave function Ψ(E = E0) with a cut-off at 20 % of the maximum value. f A cross-section of the PES for Q2 = 0. g A probability distribution of ΔJT calculated from P(ΔJT) = ∫ ΔJT(Qi)∣Ψ(Qi)∣2dQi.

Full size image

For a more quantitative insight, we perform embedding multi-reference quantum chemistry calculations taking into account SOC (see “Methods”). We start from the experimentally established structure at 40 K27 and calculate the PES of the ReO6 octahedron by parameterizing ligand displacements in terms of the above-described modes for a general distortion τ = αQiso + βQ3 + γQ2. In Fig. 3e, we show the calculated PES exhibiting three valleys, corresponding to tetragonal distortions along the three principal axes. One of the minima is given by α ≈ − 1%, β ≈ − 1.5%, and γ = 0, where β < 0 indicates that the degeneracy lifting of the ground-state quartet occurs through a contraction of the Re − Oapical distance. A similar result has been obtained for Ba2NaOsO629, while calculations performed for a 4d1 compound Ba2YMoO6 indicate the same sign and a similar magnitude of distortions32, thus establishing a clear tendency of d1 octahedral systems towards a contraction, regardless of the strength of SOC. Importantly, both the sign and the magnitude of the calculated JT distortion are in stark contrast with the reported shift of oxygen ions below TQ27. Detailed synchrotron x-ray diffraction analysis revealed27 the lowering of the global symmetry from a cubic \(Fm\overline{3}m\) above TQ to a tetragonal P42/mnm below TQ, with a tetragonal elongation amounting to  ~ 0.1% at low temperatures. This separation of scales undoubtedly disentangles the formation of the quadrupolar order at TQ from the dominant, JT-induced splitting of the presumed ground-state quartet30,33,34.

The validity of the performed calculations can be assessed by comparing the calculated energy levels with experimental data, as listed in Table 1. The calculations for the experimentally established structure at 40 K and the isotropically contracted one contain undistorted octahedra, resulting in ΔJT = 0 as well as four-fold degenerate eg states (see Fig. 1). The calculations for distortions characterizing the minimum of a valley lead to ΔJT = 78 meV and the splitting of eg states, a hallmark of the JT effect. All the calculated observables are found to be in the range of 10−20 % from the experimental values.

Table 1 Calculated energy levels for various structures
Full size table

The minimum of the PES does not directly reflect the amplitude of the distortion of an octahedron. We use the calculated PES to obtain the wave function Ψ of the quantum-mechanical oscillator and its ground-state energy E0. As shown in Fig. 3e, the wave function reflects the three-fold symmetry of the PES, extending towards each valley but still maintaining the absolute maximum at the center of the PES. More importantly, the energy E0 ≈ 56 meV is found well above the barrier between valleys EB ≈ 35 meV (Fig. 3f), implying that the zero-point motion prevents the freezing of vibronic degrees of freedom, which leaves each octahedron in a dynamic state. The characteristic time is typically expressed in the form \({({t}_{0})}^{-1}=({E}_{1}-{E}_{0})/h\), where E1 ≈ 102 meV is the first excited state35. With t0 ≈ 9 ⋅ 10−14 s, only the scattering processes of x-rays and neutrons are fast enough to observe an instantaneous state of the system, all other experimental techniques obtain a dynamically averaged response.

We can calculate the probability distribution of ΔJT using S(ΔJT) = ∫ ΔJT(Qi)∣Ψ(Qi)∣2dQi, where dQi designates an integration over the Q2 − Q3 space. The result presented in Fig. 3g reveals an asymmetric shape with a maximum occurring around 60 meV. We should emphasize that despite numerous approximations that underlie calculations, the results are directly comparable to experimentally obtained values. For comparison, the last column in Table 1 contains the results for a fictitious tetragonal I4/mmm structure, where a small 0.15 % tetragonal elongation is implemented to reflect the observed cubic-to-tetragonal transition at TQ27. The calculated ΔJT is two orders of magnitude too small, unambiguously assigning the observed doublet-doublet splitting to a JT instability.

These results can be naturally extended to other members of the double perovskite family, where bonding with ligands alternates regularly between an ionic and a covalent type. Many similarities exist with Ba2NaOsO6, which exhibits much smaller TM = 7.5 K and TQ = 9.5 K31,36,37. Another example is Cs2TaCl6, where a tetragonal contraction of  < 1 % has also been associated with the quadrupolar order38, although a later single crystal study indicated a different value for TQ39. Several d2 compounds seem to retain high local symmetry40, as well as a d3 Ba2YOsO6 system41, offering a variety of configurations where the interplay of a (dynamic) JT effect and strong SOC can be tested25.

Entropy and the ground state doublet

The JT-splitting of the ground-state quartet has profound consequences for the thermodynamic properties of 5d1 systems. Already, the first report on Ba2NaOsO6 indicated a ‘missing entropy’36, extracted from electronic specific heat (Cel) measurements Sel = ∫(Cel/T)dT reaches only \(\lesssim R{{{\rm{\ln }}}}2\), significantly smaller than the expected \(R{{{\rm{\ln }}}}4\). Namely, the total recovered entropy is expected to reflect the ground-state degeneracy at high temperatures, released across two successive transitions TM and TQ, each contributing one \(R{{{\rm{\ln }}}}2\)30,33,34. Experimentally, the main uncertainty comes from the determination of a proper phonon background, which leads to a wide array of recovered values of Sel26,37,42,43,44. We approach the problem of the phonon background determination by measuring specific heat CP in magnetic fields, which, by affecting the electronic levels, causes a redistribution of measured CP. Since the g-factor is strongly renormalized due to the partial cancellation of spin and orbital moments30, it is necessary to apply large magnetic fields to see those effects around TQ and above. In Fig. 4c, we plot the CP(T) of Ba2MgReO6 in magnetic fields up to 35 T. For B = 0, a sharp peak is seen at TM and a broad shoulder around TQ, in agreement with previously published results26,44. For B = 35 T, a broad feature is seen around TQ, with the tail merging with CP(B = 0 T) above  ~ 45 K. We take this as an estimate up to which temperature the electronic contribution is appreciable and consider only the phonon contribution above it. Instead of an analytical form, we aim to utilize the results of first-principle calculations, which were recently used as an approximate description of the phonon specific heat in Ba2MgReO644. We use a functional rescaling of the calculated results along both T − and CP − axes to match the experimental data in the range 60–100 K (see the Supplementary Material for more details). The result of this procedure is presented in Fig. 4a as a black line, with the relative discrepancy remaining below 0.5% across the relevant range (see Fig. 4b).

Fig. 4: Specific heat measurements of Ba2MgReO6.
figure 4

a T-dependence of the total specific heat of Ba2MgReO6. b The relative error of the electronic specific heat after the phonon background subtraction. c T-dependence of the electronic specific heat in various magnetic fields. d T-dependence of recovered entropy. The error bars in Panel (a) are obtained during the measurement as a result of the fitting procedure. The error bars in panels (c) and (d) are calculated based on errors in Panel (a).

Full size image

The electronic contribution Cel extracted in this manner is displayed in Fig. 4c. Both features at TM and TQ are more clearly seen, as well as the magnetic field dependence. Initially TM becomes rounded and shifts to higher temperatures, while there is very little effect on TQ. With B = 35 T, however, we see the two features practically merged, with a sharp high-temperature tail. Qualitatively similar behavior has been observed in CeB645,46 and assigned to field-induced octupolar moments on Ce ions47,48. Similarly, the NMR study31 revealed a shift to higher temperatures of the order-disorder boundary in Ba2NaOsO6.

The total electronic entropy Sel extracted from Fig. 4c is presented in Fig. 4d. Within an error, the recovered values for all magnetic fields saturate very close to \(R{{{\rm{\ln }}}}2\), with very little change above 40 K. This result is rather robust against small changes of the exact functional form of the phonon background and therefore, together with spectroscopic evidence obtained by RIXS and supported by quantum chemistry calculations, unequivocally establishes that the low energy physics in Ba2MgReO6 is dominated by a ground state doublet. A similar conclusion has been reached by a recent study on Ba2NaOsO6 where a somewhat larger doublet-doublet splitting has been found (95 meV) based on O K edge RIXS and x-ray magnetic circular dichroism29. We note that these two 5d1 systems exhibit qualitatively very similar behavior in terms of multi-polar ordering tendencies, with the advantage that Re6+ orders at sufficiently larger temperatures than Os7+ to allow a better insight into the peculiar interplay between magnetic dipole and charge quadrupole orders.

Discussion

The calculated ground-state energy suggests a dynamic type of distortion, where ReO6 octahedra fluctuate with  ~ 10 THz between elongations along three equivalent principal axes. The scattering of x-ray photons, which occurs at a time scale much faster than these oscillations, reflects a statistical average of all the distortions distributed across the sample at a given time and, therefore, cannot be used to distinguish it from a random distribution of frozen static distortion, which might still preserve the global cubic symmetry, despite the breaking of the local one. On the contrary, the static version of the JT effect can be reasonably argued against using several lines of reasoning (see Fig. 5 for details). First, there is a clear signature of order-parameter-like increase of intensity associated with charge quadrupolar order composed of two components, an antiferro \({{{{\mathcal{T}}}}}_{x}\) and a ferro \({{{{\mathcal{T}}}}}_{z}\)27,49. Concomitantly, it is observed that oxygen ions move away from their high-symmetry positions accordingly, reflecting a strong coupling between local distortions and \({{{{\mathcal{T}}}}}_{z}\) charge quadrupoles30,50. Those distortions are, however, 5 times smaller than calculated for the Jahn-Teller effect, and of an opposite sign. The frozen landscape of static JT distortions would inevitably lead to a glassy behavior of a charge quadrupolar and magnetic dipole orders since the direction of magnetic dipoles below TQ is determined by the local orientation of \({{{{\mathcal{T}}}}}_{z}\) quadrupolar moments50.

Fig. 5: Comparison of dynamic and static JT effect on equilibrium ion positions at time-scales longer than t0.
figure 5

At very high temperatures, the octahedra are not distorted, and the ground state is four-fold degenerate. In the dynamical JT scenario, the degeneracy is lowered by a contraction of Re - O distances (~ − 1.5 %) on time scales t < t0, but the equilibrium positions of ions at t > t0 do not change significantly, with the Re charge distribution remaining spherical (gray circle). At much lower temperatures (T < TQ), a quadrupolar order sets in, including the ferroic \({{{{\mathcal{T}}}}}_{z}\) (blue - increased charge density, yellow - decreased charge density), which is accompanied by a coherent shift of apical oxygen ions (red arrows), leading to a small c-axis elongation (~ + 0.15 %)27 (green arrows). In the static JT scenario, each octahedron is locally distorted, with an equal distribution of elongations along three principal axes. This implies a random distribution of \({{{{\mathcal{T}}}}}_{z}\) quadrupolar moments and a lack of coherent ordering at low temperatures. The local Ba cage is also distorted, leading to the accumulation of lattice strain.

Full size image

The second argument for the dynamic JT state is related to the local symmetry of Re ions. As has been demonstrated in 23Na NMR experiments on Ba2NaOsO6, a single resonance line at high temperatures splits into three lines below TQ, indicating a lowering of the local symmetry31. This has been associated with changes in local charge distribution around Na ions, which are surrounded by six OsO6 octahedra and, therefore, directly reflect shifts of oxygen equilibrium positions. Since the time scale of NMR experiments is much longer than t0, in the dynamic JT scenario, the local symmetry breaks only below TQ, while in the static scenario, the triplet line would have been observed at all temperatures, which is in clear contradiction with experimental results31. We note that the deformation due to the JT effect is significantly larger than what occurs below TQ, therefore the splitting of the NMR line would have been clearly seen.

Finally, an argument against the random distribution of locally deformed octahedra comes from the consideration of the effect on the local crystal environment. As revealed by high-resolution synchrotron experiments27, below TQ the equilibrium of apical oxygen ions shifts by  ~ + 0.36 %, accompanied by a unit cell tetragonal elongation of  ~ + 0.15 %. Within the static JT scenario, the random orientation of local distortions would lead to a significant local strain on the surrounding cage of eight Ba ions (almost 1 % of local compression) in order to maintain the observed high-symmetry, cubic unit cell environment above TQ. Since the quadrupolar moments are randomly frozen, and with such a high lattice strain, there is a clear lack of a feasible mechanism which would lead to the observed coherent distortions below TQ along the c-axis for both apical oxygen ions and the unit cell as a whole. In addition, if the local distortions are static, the system could remove the strain by lowering the unit cell symmetry from cubic to tetragonal, which is the scenario observed in a series of JT-active d9 double perovskites A2Cu\({B}^{{\prime} }\)O6 (A = Ba, Sr; \({B}^{{\prime} }=\) W, Te)51.

The dynamic JT effect ensures the local and global cubic symmetry above TQ, in accordance with experimental observations in both Ba2MgReO627 and Ba2NaOsO631, as well as with ab initio results reported for Ba2NaOsO652. Without the shared ligand between ReO6 octahedra, a feature characteristic for double perovskites, the dynamic distortions on one cluster are not correlated with its neighbors. Following the development of the charge quadrupolar order, where a coherent charge redistribution occurs on Re ions, the PES becomes slightly renormalized, which leads to a slight, but coherent shift of the equilibrium position of oxygen ions, giving rise to the signal observed in REXS experiments27,49. Crucially, the dynamic state of ReO6 octahedra continues to dominate the local Re environment even within the multi-polar ordered state. Even with a complete model of spin-orbit-vibronic coupling, the qualitative picture remains the same34.

The revelation that the ground-state doublet dominates the low-temperature physics in this class of materials establishes a new paradigm from the thermodynamic point of view. With two phase transitions and two order parameters, it is puzzling how to reconcile \(R{{{\rm{\ln }}}}2\) across both TM and TQ. Concurrently, specific heat at TQ does not exhibit a typical λ-type profile, and, as we have shown, no lifting of degeneracy accompanies the quadrupolar order. Some of the entropy (\(\sim 1/3R{{{\rm{\ln }}}}2\)) is released above TM, pointing to a reduction from a three-dimensional towards a two-dimensional phase space for fluctuating magnetic moments50. The plane of fluctuation below TQ is then dictated by the orientation of quadrupolar moments \({{{{\mathcal{T}}}}}_{x}\) and \({{{{\mathcal{T}}}}}_{z}\), being perpendicular to the \({{{{\mathcal{T}}}}}_{z}\)-induced elongation. At TM the directional locking within that plane leads to magnetic dipole order and removes the remaining entropy. We infer that the magnetic and quadrupolar order parameters are part of a single, entangled object that goes through a two-step transition53.

Spin-orbit entanglement plays another crucial role that relates to the dynamical state of ReO6 octahedra. In the weak SOC limit, the available states forming a Mexican hat potential are composed of purely orbital contributions, each state allowing for two spin projections. For the strong SOC case involving 5d orbitals, the entanglement entails a varying spin projection along the degeneracy line, resulting in a dynamically renormalized directional coupling between neighboring ReO6 octahedra. Similar to Kitaev physics21, and aided by the frustration on an FCC lattice, it could be envisaged that such a renormalization could lead to a spin-liquid state or other exotic quantum phases.

Methods

Sample preparation

Single crystals were grown by the flux method. A stoichiometric mixture of BaO, MgO, and ReO3 powders was mixed with a flux composed of 36 wt % BaCl2 and 64 wt % MgCl2 in an argon-filled glove box. The mixture was sealed in a platinum tube of 20 mm length and 6 mm diameter. The tube was heated at 1300 0C and then slowly cooled to 900 0C at a rate of 5 0C/h, followed by furnace cooling to room temperature. After the residual flux was washed away with distilled water, several crystals were obtained, The crystals exhibit octahedral morphology, forming flat triangles along [111] and equivalent directions. Specific heat measurements up to 14 T were performed on as-grown crystals (up to 1 mm in size), while the B = 35 T experiment was performed on a 0.3 mm polished crystal. For the Re L3 edge RIXS experiment the sample was glued on a copper sample holder with the [111] direction perpendicular to the surface. An in situ cleaving has been utilized for the O K edge RIXS experiment.

Resonant inelastic x-ray scattering

The experiments at the Re L3 edge were performed at BL11XU of SPring-8, Japan synchrotron facility. Incident x-rays were monochromatized by a Si(111) double-crystal monochromator and a two-bounce channel-cut monochromator Si(444), and π-polarized x-rays were irradiated on the samples. Horizontally scattered photons were energy-analyzed by a Ge(733) analyzer. The total energy resolution was 140 meV (full width at half maximum). The experiments at the O K edge were performed at the ADRESS beamline of the Swiss light source (SLS) at the Paul Scherrer Institute (PSI), Switzerland in both the normal and grazing configuration with 50° between incoming and outgoing beams54.

Embedding quantum chemistry calculations

Many-body wavefunction calculations on electrostatically embedded finite-size clusters were performed using the Molpro package55. The model involved a 21-atom cluster consisting of the ReO6 octahedron together with the nearest 6 Mg and 8 Ba atoms. Re atoms were represented with core potentials and triple-zeta plus two polarization f-functions basis functions56. All-electron triple-zeta basis functions were used for O atoms57. Both Mg and Ba atoms in the cluster were described by effective core potential and supplemented with a single s basis function58. The effect of the crystal lattice surrounding the cluster was treated at the level of Madelung ionic potential, as described in ref. 59. For the complete active space self-consistent field (CASSCF) calculations, an active space of 3 t2g + 2, eg orbitals, was used. The optimization was carried out for an average of 5 states, each of unit weight, of the scalar relativistic Hamiltonian. Multireference configuration interaction (MRCI) treatment was performed with single and double substitutions with respect to the CASSCF reference, as described in refs. 60,61. The spin-orbit coupling correction was added as described in ref. 62. The PES was mapped out with respect to isotropic mode Qiso = (x1 − x2 + y3 − y4 + z5 − z6), and eg-type distortions Q2 = (− x1 + x2 + y3 − y4) and Q3 = (− x1 + x2 − y3 + y4 + 2z5 − 2z6), with superscripts 1,2 referring to the x-axis O atoms, 3,4 to the y-axis O atoms and 5,6 to the z-axis O atoms.

In order to assess the PES, calculations were performed on a grid that varies isotropic distortions were varied from 0.5% to  − 1.5% with 0.5% steps, with amplitudes referring to non-normalized Qiso = [1, 1, 1] and the percentage being relative to the undistorted 1.926 Å Re − O interatomic distance. A 60∘ sector of the Q2 − Q3 plane was simulated, with the angle being varied with steps of 15∘ and radius being varied from 0 to 3.5%, with the step of 0.25%, with amplitudes referring to normalized \({{{{\boldsymbol{Q}}}}}_{{{{\boldsymbol{2}}}}}=\frac{1}{\sqrt{2}}[-1,1,0]\) and \({{{{\boldsymbol{Q}}}}}_{{{{\boldsymbol{3}}}}}=\frac{1}{\sqrt{6}}[1,1,-2]\). The stability of the minimum with respect to the t2g-type distortions Q4 = (y1 − y2 + x3 − x4) was confirmed. In addition, an attempt was made to find a minimum with a non-zero amplitude of the t2g-type distortions by alternating Qiso, Q2, Q3, and Q4 as energy optimization coordinates, starting at the cubic configuration. No such minimum was found, with all paths considered converging back to the minimum described in the article.

Specific heat

For magnetic fields up to 14 T we used a PPMS system (Quantum Design) that utilizes a relaxation method. The measurement at 35 T was performed at LNCMI, Grenoble, France using a Cernox thermometer as a platform and a semi-adiabatic method. In both cases the addenda has been measured separately and subtracted to obtain specific heat of the sample. Zero-field measurements have been used to normalize the results from two setups.