Introduction

Ruddlesden−Popper 2D layered metal halide perovskites, denoted as (LA)2(A)n−1BnX3n+1 where n is inorganic layer thickness, have garnered considerable research interests in past few years1,2,3,4,5,6,7,8,9,10. Segmenting metal halide inorganic layer by long-chain organic cations (LA+) not only establishes a robust barrier against water vapor erosion and ion migration, but provides tunable structures, compositions, and properties, in particular, strongly bound electron-hole pairs (excitons) arising from dielectric and quantum confinement. Compared to the conventional Pb counterparts which has been extensively investigated in past years, 2D tin halide perovskites with environmental hazard Pb substituted by biocompatible Sn has emerged very recently and exhibited remarkable optoelectronic properties and technological prospects including stable lasing5, high-mobility field-effect transistors11,12 and efficient light-emitting diodes with excellent external quantum efficiency1.

The exciton nature and dynamics at excited state, rather than ground state, lies at the heart of optoelectronic materials and devices. In 2D lead halide perovskites, a general consensus has been reached that photoexcited excitons are dressed by lattice polarization and distortion, forming exciton polarons with screened electron-hole interaction, due to the interaction between exciton and soft, polarizable lattice13,14,15,16,17,18,19. The formation of exciton polaron has strong impact on the intriguing properties in 2D lead halide perovskites, including the rich exciton spectral structure, anomalous exciton spin relaxation, exciton dissociation and asymmetric light emission17,18,19,20,21,22. Compared to the Pb counterparts, the excited state exciton nature and dynamics in the emerging 2D tin halide perovskites have been much less investigated, except for a few recent photophysical comparison studies of 2D (n = 1) lead and tin halide perovskite polycrystalline films23,24. Recent studies on 2D (n = 1) and 3D tin halide perovskites by steady-state spectroscopy measurements suggest a lower exciton binding energy in tin halide perovskites than that in their Pb counterparts7,24,25,26,27,28, which potentially would favor exciton dissociation into free carriers and thus light-to-electricity conversion, rather than the reverse light emission process. However, this seems to contradict a very recent report of highly efficient light-emitting diodes based on 2D tin halide perovskites1. The ultimate question lies in the exact nature and fate of exciton at excited state, especially how it is regulated by exciton-lattice coupling in this family of materials, which remains a puzzle and hinders the design of 2D tin halide perovskites and devices.

Here, we perform a comparison photophysical study between n = 2 (PEA)2(MA)Sn2I7 (PEA and MA stand for C6H5CH2CH2NH3+ and CH3NH3+, respectively) and its Pb counterpart (PEA)2(MA)Pb2I7 by combining state-of-the-art time-resolved spectroscopy and theoretical simulation to reveal the excited state exciton properties in high quality 2D tin halide perovskite single crystals. Although (PEA)2MASn2I7 and the Pb counterpart exhibit a same large exciton binding energy \({{E}_{{{\rm{b}}}}}^{0}\) ~ 0.2 eV from steady-state exciton Rydberg series measurement, spin-resolved transient absorption (TA) measurements indicate (PEA)2(MA)Sn2I7 retain the strong bound excitons at excited state with an excited state exciton binding energy \({{E}_{{{\rm{b}}}}}^{*}\,\)~ 0.18 eV, in striking contrast to the strongly screened excitons with \({{E}_{{{\rm{b}}}}}^{*}\) ~ 0.10 eV in Pb counterpart. An in-depth spectroscopy analysis reveals significantly weaker long- and short-range exciton-phonon interactions in (PEA)2(MA)Sn2I7, resulting in alleviated excited state polaronic screening effect and robust exciton in 2D tin halide perovskites, which is further confirmed with atomic level excited state stimulations. The robust excited state excitons in 2D tin halide perovskites manifest excitation-power-independent, high-efficiency and high color-purity emission, lending them to light emission and lasing applications.

Results

Sample preparation and characterizations

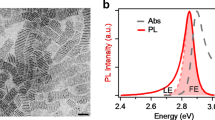
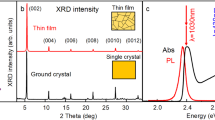
The high-quality (PEA)2(MA)Sn2I7 single crystals (Fig. 1a) were synthesized under N2 environment by our recently developed method5. We mechanically exfoliated optically thin (PEA)2(MA)Sn2I7 flakes which were further sandwiched by thin-layer h-BN (Fig. 1a) through van der Waals stacking to protect the 2D perovskite samples from degradation and obtain reliable results29. As a reference, we also prepared (PEA)2(MA)Pb2I7 sample with only different B site cation using similar method for comparison. The thickness of exfoliated 2D perovskite flakes were characterized by atomical force microscopy which indicates 20–30 layers and thus bulk-like 2D perovskite samples (Supplementary Fig. 1). As shown in Fig. 1b, the absorption spectra of (PEA)2(MA)Sn2I7 and (PEA)2(MA)Pb2I7 exhibit a strong and sharp peak at 1.831 eV and 2.195 eV, respectively, corresponding to their lowest energy exciton resonance. The photoluminescence (PL) spectra show a corresponding sharp peak with a slight Stokes shift (~0.04 eV). The temperature-dependent PL spectra (Supplementary Fig. 2) and optical characterizations at 80 K (Supplementary Fig. 3) indicate negligible emission from other n or extrinsic edge states even at cryogenic temperature and the absence of phase transition in 80–300 K6,30,31, confirming high phase purity and high crystal quality.

Fig. 1: Optical characterizations.
figure 1

a Schematic of (PEA)2(MA)Sn2I7 and optical image of BN-encapsulated (PEA)2(MA)Sn2I7 thin flake (~20 layers). Scale bar: 10 μm. Inset: optical image of (PEA)2(MA)Sn2I7 single crystal. b The absorption and photoluminescence (PL) spectra of (PEA)2(MA)Sn2I7 and (PEA)2(MA)Pb2I7 flakes at room temperature. c The 1st derivative spectra of the reflectance contrast of (PEA)2(MA)Sn2I7 and (PEA)2(MA)Pb2I7 at 4 K. The 1s and 2s exciton states are denoted.

Full size image

We first determined the exciton binding energy \({{E}_{{{\rm{b}}}}}^{0}\) by conventional steady-state exciton Rydberg series measurement, following previous success on 2D transition metal dichalcogenides and 2D lead halide perovskites32,33. We measured the reflectance contrast spectra δ\(R\) of (PEA)2(MA)Sn2I7 and its Pb counterpart at 4 K and the reflectance contrast derivative \( (d\left({{\rm{\delta }}}{{\rm{\it R}}}\right)/{dE})\) spectra exhibit clearly resolvable 1s and 2s excitonic peaks with similar energy spacing (\({\Delta }_{12}\) ~ 0.16 eV) (Fig. 1c). Thus, the exciton binding energy \({{E}_{{{\rm{b}}}}}^{0}\) can be estimated from \({\Delta }_{12}\) by \({{{E}_{{{\rm{b}}}}}^{0}\approx 1.35\Delta }_{12}\)33. We determined a near identical \({{E}_{{{\rm{b}}}}}^{0}\) for (PEA)2(MA)Pb2I7 and (PEA)2(MA)Sn2I7, \(0.22\pm 0.02\) eV and \(0.21\pm 0.02\) eV, respectively. The obtained \({{E}_{{{\rm{b}}}}}^{0}\) for (PEA)2(MA)Pb2I7 falls into the range of the exciton binding energy in similar materials reported previously (see Supplementary Table 1). We also note the exact value of \({{E}_{{{\rm{b}}}}}^{0}\) in 2D perovskites are currently still largely dispersed and requires further experimental and theoretical study, which is beyond the scope of this study focusing on the excited state properties. In the absence of phase transition, \({{E}_{{{\rm{b}}}}}^{0}\) can be regarded as a constant from 4 K to room temperature and is about ten times of thermal energy \({k}_{{{\rm{B}}}}T\) (\({k}_{{{\rm{B}}}}\) is Boltzmann constant and \(T\) is temperature) at room temperature7,8. According to Saha-Langmuir equation34,35, at room temperature, more than 95% photoexcitation remain as excitons in both (PEA)2(MA)Pb2I7 and (PEA)2(MA)Sn2I7 at excitation density of ~1011 cm−2 (see details in Supplementary Note 1).

The result from steady-state optical measurements does not necessarily reflect the excited state properties because of possible electronic and structural relaxation at excited state. We first resort to PL measurements to get a sense of the excited state behavior in these two 2D metal halide perovskites. The PL quantum yields (QYs) of (PEA)2(MA)Sn2I7 and (PEA)2(MA)Pb2I7 were measured as a function of excitation power (see details in Supplementary Note 2) and shown in Fig. 2a. Interestingly, PLQY of (PEA)2(MA)Sn2I7 remains a near constant of ~60% over three orders of magnitude of excitation power, while that of the Pb counterpart increases continuously from ~1% to ~20% at same range. This result suggests pure exciton recombination with monomolecular-like recombination behavior in (PEA)2(MA)Sn2I7 where PLQY does not depends on photoexcitation density but the presence of free carrier recombination in the Pb counterpart with bimolecular-like recombination behavior where higher photoexcitation power increases encounter probability of electron and hole carriers thus PLQY (Fig. 2b and Supplementary Note 3)32,36. The excited state recombination dynamics can be directly obtained from time-resolved (TR) measurements. Importantly, TR-PL and TA exhibit near-identical kinetics for (PEA)2(MA)Sn2I7 but large deviation for (PEA)2(MA)Pb2I7 (Fig. 2c and Supplementary Fig. 5), which again suggests dominant excitonic recombination process in (PEA)2(MA)Sn2I7 but substantial fraction of dissociated electron and hole recombination process in (PEA)2(MA)Pb2I719.

Fig. 2: Photoluminescence (PL) properties of 2D (PEA)2(MA)Sn2I7 and (PEA)2(MA)Pb2I7.
figure 2

a Photoluminescence quantum yield (PLQY) as a function of excitation power. b Schematic of recombination for excitons and free carriers with monomolecular- and bimolecular-like behavior, respectively. c PL (black circles) and transient absorption (TA, red squares) kinetics of (PEA)2(MA)Sn2I7 thin flake. d TRPL0 as a function of laser power density for (PEA)2(MA)Sn2I7 and (PEA)2(MA)Pb2I7 at 300 K and 80 K, which are extracted from TRPL results in Supplementary Fig. 4. The corresponding power law fitting are shown with a power factor \(\beta\) value listed. The values of \({{{\rm{TRPL}}}}_{0}\) have been vertically shifted for clarity.

Full size image

Key information about the excited state species is from examining the initial TR-PL intensity at \(t=0\) (denoted as \({{{\rm{TRPL}}}}_{0}\)), which is proportional to the radiative recombination rate of the initial (~6 ps) photogenerated excited state species since TA kinetics shows no decay in the first 20 ps. Depending on the nature of emitting species, the radiative recombination rate or \({{{\rm{TRPL}}}}_{0}\) is proportional to photoexcitation densities (\(\propto {n}_{0}\)) for exciton recombination with monomolecular-like behavior or \({{\propto n}_{0}}^{2}\) for dissociated electron and hole recombination with bimolecular-like behavior (Fig. 2b)36. \({{{\rm{TRPL}}}}_{0}\) at 80 and 300 K for both materials are plotted as a function of \({n}_{0}\) in Fig. 2d. A power law fitting (\({{{\rm{TRPL}}}}_{0}\propto {n}_{0}^{\beta }\)) of experimental results shows (PEA)2(MA)Sn2I7 increases linearly with a power factor \(\beta\) of 1.06 and 1.04 at 300 and 80 K, respectively, indicating a robust exciton emission with negligible dissociation at 300 K. In contrast, the Pb counterpart exhibits a similar linear behavior at 80 K (\(\beta\) = 1.06) but a super-linear relationship (\(\beta\) = 1.31) at 300 K, confirming high concentration of free electron/hole carriers by exciton thermal dissociation at room-temperature. Similar β values were obtained under near-resonant excitation conditions (Supplementary Fig. 6), demonstrating that the independence of β on excess energy under our experimental conditions.

Exciton spin relaxation

Robust excitonic recombination in (PEA)2(MA)Sn2I7 and substantial free carrier recombination in its Pb counterpart indicates their different electron-hole Coulomb interaction strength at excited state, which strongly contradict with their similar \({{E}_{{{\rm{b}}}}}^{0}\) of ~0.2 eV extracted from steady state measurements, but suggest different polaronic screening effect at excited state considering their polar and dynamic lattice nature16,17,18,35. As demonstrated by our previous study on 2D CsPbBr3, the excited state polaronic effect and the resulting screened exciton binding energy at excited state (denoted as \({{E}_{{{\rm{b}}}}}^{*}\)) can be inferred from exciton spin relaxation dynamics35. In excitonic systems, the exciton spin relaxation is governed by excited state electron-hole exchange interaction (\(J\)) through Maialle-Silva-Sham (MSS) mechanism35,37,38,39,40. Since \(J\) is proportional to \({{E}_{{{\rm{b}}}}}^{*}\), exciton spin relaxation rate \({k}_{{{\rm{s}}}}\) provides a facial way to quantify \({{E}_{{{\rm{b}}}}}^{*}\) by

$${k}_{{{\rm{s}}}} \approx \left\langle {{\varOmega }_{{{\rm{K}}}}}^{2}\right\rangle {\tau }_{{{\rm{p}}}}\propto {J}^{2}T{\tau }_{{{\rm{p}}}}\propto ({{{E}_{{{\rm{b}}}}}^{*}})^{2}T/\varGamma$$
(1)

where \({\varOmega }_{{{\rm{K}}}}\) is momentum-dependent Larmor frequency under an effective magnetic field, T denotes temperature and \({\tau }_{{{\rm{p}}}}\) is momentum scattering time which is inversely proportional to PL linewidth \(\varGamma\) (see details in Supplementary Note 4)38,39. The MSS model has described the T-dependent exciton spin relaxation in 2D transition metal dichalcogenides and quantum wells in a quantitative manner38,39,40,41.

We performed spin-resolved femtosecond TA spectroscopy measurements on the exciton spin relaxation dynamics in (PEA)2(MA)Sn2I7 at 80–300 K. As shown in Fig. 3a, spin-polarized excitons |+1> (|−1>) can be selectively excited by right (left) circularly polarized pump pulse \({{{\rm{\sigma }}}}^{+}\) (\({{{\rm{\sigma }}}}^{-}\)) and probed by another circular polarized probe pulse with either same (SCP) or opposite (OCP) circular polarization conditions (see Methods for details)35,42,43,44,45,46. Spin-resolved TA results of (PEA)2(MA)Sn2I7 at 1.93 eV near-resonant excitation under SCP and OCP conditions are shown in Fig. 3b, with a few representative spectra at indicated delay times (0.4, 4, and 20 ps) in Fig. 3c for better view. The pump fluence was kept low of 3–8 μJ cm−2 to ensure TA signal in linear regime.

Fig. 3: Spin-resolved transient absorption spectroscopy of (PEA)2(MA)Sn2I7 thin flake at room temperature.
figure 3

a Scheme of spin-resolved TA measurements where spin-polarized excitons are photoexcited by circularly polarized pump pulse and probed by same (SCP) or opposite (OCP) circular polarization. b 2D color plot of TA spectra under SCP and OCP conditions at 8 μJ cm−2 pump fluence. c Spectral evolution for SCP and OCP conditions at representative time delay (0.4, 4, and 20 ps). d TA kinetics of SCP and OCP and spin polarization kinetics with single exponential fitting (green line).

Full size image

Generally speaking, TA signal in 2D semiconductors stems from combined band filling effect and Coulombic effect including band renormalization, biexciton effect, and exciton screening35,42,43. While band filling and biexciton effect are sensitive to photoexcited exciton occupation in a specific spin state, other effects would apply to both spin states, leading to TA spectral difference. At early time (0.4 ps) after photoexcitation, SCP spectra of (PEA)2(MA)Sn2I7 show a dominant photoinduced bleach (PB) feature at exciton resonance due to band filling and band renormalization effect, and a photoinduced absorption (PA2) at higher energy side due to biexciton repulsion effect (interaction between pump-generated preexisted exciton and probe-induced excitonic transition) from excitons with same spin. On the other hand, OCP spectra show a derivative line shape with PA1 feature around exciton resonance which can be ascribed to spin-independent band renormalization effect35,42. Therefore, the difference on TA spectra between SCP and OCP (i.e. \({{\rm{\delta }}}{{\mbox{T}}}_{{\mbox{SCP}}}-{{\rm{\delta }}}{{\mbox{T}}}_{{\mbox{OCP}}}\)) indicates the imbalance of exciton population in +1 and −1 spin states and the creation of spin polarization, which vanishes in ~20 ps (Fig. 3c). To extract the exciton spin relaxation dynamics, we spectrally integrated SCP and OCP spectra at low energy side, where the difference between them is mainly ascribed to the band filling of spin-polarized excitons. The degree of exciton spin polarization (Pol) is calculated by \({\mbox{Pol}}=({{\rm{\delta }}}{{\mbox{T}}}_{{\mbox{SCP}}}-{{\rm{\delta }}}{{\mbox{T}}}_{{\mbox{OCP}}})/({{\rm{\delta }}}{{\mbox{T}}}_{{\mbox{SCP}}}+{{\rm{\delta }}}{{\mbox{T}}}_{{\mbox{OCP}}})\). As shown in Fig. 3d, the spin polarization shows a fast relaxation with a lifetime of \(2.79\pm 0.06\) ps in (PEA)2(MA)Sn2I7. This lifetime is two orders of magnitude shorter than exciton population lifetime, indicating a pure spin relaxation process. This exciton spin relaxation rate is 1–2 orders of magnitude faster that than in 3D bulk Sn-based materials, confirming the dominant electron-hole exchange interaction (MSS) mechanism in 2D perovskites47. The spin relaxation rates are also found to depend on pump fluences linearly in (PEA)2(MA)Sn2I7 (Supplementary Fig. 7), which further proves the dominant MSS spin relaxation mechanism rather than the Bir−Aronov−Pikus (BAP) or the D’yakonov-Perel (DP) mechanism35,40,48. In addition, we performed the same spin relaxation measurement with larger (0.15 eV) or smaller (0.05 eV) excess energies (relative to bandgap) and found that the excess energy mostly affects the initial spin polarization degree and has little effect on the spin relaxation dynamics (Supplementary Fig. 8), which is consistent with previous studies35,49.

According to Eq. (1), information about excited state electron-hole interaction comes from examining T-dependent exciton spin relaxation kinetics. As shown in Fig. 4a, b, interestingly, by increasing temperature from 80 K to 300 K, exciton spin relaxation is accelerated in (PEA)2(MA)Sn2I7 but decelerated in the Pb counterpart. The ks by single exponential fitting on exciton spin relaxation kinetics are plotted (symbols) in Fig. 4c, d for (PEA)2(MA)Sn2I7 and (PEA)2(MA)Pb2I7, respectively, showing interestingly opposite T-dependence.

Fig. 4: Temperature dependence of spin relaxation process.
figure 4

Exciton spin relaxation kinetics at different temperatures from 80 to 300 K and their single exponential fitting of (a) (PEA)2(MA)Sn2I7 and (b) (PEA)2(MA)Pb2I7 under near-resonant excitation at 3 μJ cm−2 pump fluence. Temperature dependent exciton spin relaxation rate for (c) (PEA)2(MA)Sn2I7 and (d) (PEA)2(MA)Pb2I7, showing opposite trend. The error bars represent fitting errors. The lines are modeled temperature dependent exciton spin relaxation rate according to Maialle-Silva-Sham (MSS) mechanism (Eq. (1)) with constant exciton binding energy Eb. The modeled curve has been scaled to match experiment results at 80 K where polaronic effect is negligible.

Full size image

The T-dependent ks in excitonic system can be described by Eq. (1) and the modeled results assuming a T-independent constant \({{E}_{{{\rm{b}}}}}^{*}\) are plotted in Fig. 4c, d (line) for (PEA)2(MA)Sn2I7 and the Pb counterpart, respectively. The modeled curve has been scaled to match experimental value at 80 K where lattice is mostly frozen and excited state polaronic screening effect can be approximated to be negligible (i.e. \({{E}_{{{\rm{b}}}}}^{*}\) = \({{E}_{{{\rm{b}}}}}^{0}\))50. Interestingly, the measured ks for (PEA)2(MA)Sn2I7 shows similar trend as the modeled curve but diverges slightly at high temperature while the measured and modeled ks for (PEA)2(MA)Pb2I7 show completely opposite trend. The negative deviation of experimental ks compared to modeled value assuming constant \({{E}_{{{\rm{b}}}}}^{*}\) = \({{E}_{{{\rm{b}}}}}^{0}\) indicates that \({{E}_{{{\rm{b}}}}}^{*}\) is temperature dependent and significantly screened at elevated temperature. The extent of deviation between experimental and model values allows a quantitative calculation of \({{E}_{{{\rm{b}}}}}^{*}\) since \({k}_{{{\rm{s}}}}\propto {({{E}_{{{\rm{b}}}}}^{*})}^{2}\)18,35. For example, at room temperature, modeled \({k}_{{{\rm{s}}}}\) of (PEA)2(MA)Pb2I7 is 4.54 times the measured value which yields an excited state exciton binding energy \({{E}_{{{\rm{b}}}}}^{*}\) of ~ 0.10 \(\pm\) 0.01 eV. A similar analysis on (PEA)2(MA)Sn2I7 provides a \({{E}_{{{\rm{b}}}}}^{*}\) of ~ 0.18 \(\pm\) 0.02 eV, almost twice of that in Pb counterpart.

Exciton-phonon interaction

The screened \({{E}_{{{\rm{b}}}}}^{*}\) well explains different light emission behaviors in (PEA)2(MA)Sn2I7 and the Pb counterpart where robust excitonic behavior in the former but partial free carrier behavior in latter have been observed, despite of near identical \({{E}_{{{\rm{b}}}}}^{0}\). Because of their polar and dynamic lattice, photoexcited excitons in 2D metal halide perovskites can polarize lattice through exciton-phonon interaction, forming exciton polarons16,18,19,35. Depending on the nature and range of exciton-lattice interaction, the excited state polaronic effect can arise from both long-range electrostatic polarization response (Fröhlich interaction) and short-range deformation potential (Holstein interaction)17,18,20. The long-range Fröhlich coupling strength is proportional to the lattice polarization response and can be captured by T-dependent PL linewidth20,51, while the short-range Holstein interaction manifests itself as a Urbach tail on absorption/PL spectra52,53,54,55.

The PL spectra of (PEA)2(MA)Sn2I7 and its Pb counterpart at different temperatures (80–300 K) are shown in Fig. 5a, b, respectively, which are broader and more asymmetrical with a prominent low energy tail (Urbach tail) at higher temperature. The full-width-at-half-maximum (FWHM) of PL spectra at different temperatures can be described by a phenomenological equation31,50,51

$${{\rm{FWHM}}}={\varGamma }_{0}+\frac{{\gamma }_{{{\rm{LO}}}}}{\left[\exp \left({E}_{{{\rm{LO}}}}/{k}_{{{\rm{B}}}}T-1\right)\right]}$$
(2)

where the first term \({\varGamma }_{0}\) is T-independent and the second term is contributed by longitudinal optical (LO) phonon scattering with an effective phonon energy \({E}_{{{\rm{LO}}}}\) and a coupling strength \({\gamma }_{{{\rm{LO}}}}\). By extracting and fitting the FWHM of PL spectra with Eq. (2) (Fig. 5c), we obtain a coupling strength \({\gamma }_{{{\rm{LO}}}}\) of 0.072 ± 0.004 eV for (PEA)2(MA)Sn2I7, which is smaller than \({\gamma }_{{{\rm{LO}}}}\) of 0.095 ± 0.008 eV for its Pb counterpart.

Fig. 5: Analysis of temperature dependent PL spectra.
figure 5

PL spectra of (a) (PEA)2(MA)Sn2I7 and (b) (PEA)2(MA)Pb2I7 in a semi-log scale at different temperatures between 80 and 300 K. The black dashed lines represent the fit of Urbach tail by Eq. (4). c PL full-width-at-half-maximum (FWHM) as a function of temperature for (PEA)2(MA)Sn2I7 (square) and its Pb counterpart (triangle) and the fit (dashed line) by Eq. (2). d Steepness factor \(\sigma \left(T\right)\) as a function of temperature and the fit (dashed line) of the low temperature region by Eq. (5). The error bars represent fitting errors.

Full size image

We also analyzed the Urbach tail of PL to quantify the short-range Holstein exciton-phonon coupling strength. The absorption coefficient \(\alpha \left(E,T\right)\) of Urbach tail below optical band gap can be described by refs. 52,53,54

$$\alpha \left(E,T\right)={\alpha }_{0}\exp \left(\frac{\sigma \left(T\right)\left(E-{E}_{0}\right)}{{k}_{{{\rm{B}}}}T}\right)$$
(3)

where \({\alpha }_{0}\) and \({E}_{0}\) are constants, \(\sigma \left(T\right)\) is a T-dependent steepness parameter which contains exciton-phonon coupling information. With van Roosbroeck-Schockley relation, the Urbach tail of PL can be described by refs. 53,54

$${I}_{{{\rm{PL}}}}\left(E,T\right)\propto {E}^{2}\exp \left(\frac{\sigma \left(T\right)-1}{{k}_{{{\rm{B}}}}T}\left(E-{E}_{0}\right)\right)$$
(4)

Generally, \(\sigma \left(T\right)\) increases with T and approaches a limit of steepness constant \({\sigma }_{0}\) at high temperature (e.g., 300 K) by

$$\frac{\sigma \left(T\right)}{{k}_{{{\rm{B}}}}T}=\frac{2{\sigma }_{0}}{{{\hslash }}{\omega }_{{{\rm{ph}}}}}\tanh \left(\frac{{{\hslash }}{\omega }_{{{\rm{ph}}}}}{2{k}_{{{\rm{B}}}}T}\right)$$
(5)

where \(\hslash {\omega }_{{{\rm{ph}}}}\) is the average energy of interaction phonon modes. Importantly, the steepness constant \({\sigma }_{0}\) is an inherent property for a certain material and inversely proportional to the Holstein exciton-phonon coupling strength, i.e., smaller \({\sigma }_{0}\) indicates a stronger short-range exciton-phonon coupling. In high-quality semiconductors with weak electron-phonon coupling strength, \({\sigma }_{0}\) from PL measurement (corresponding to excited-state configuration, denoted as \({{\sigma }_{0}}^{*}\)) and that from absorption measurement (corresponding to ground-state configuration, \({{\sigma }_{0}}^{0}\)) have near same value54,55.

We determined the steepness parameters \(\sigma \left(T\right)\) for (PEA)2(MA)Sn2I7 and its Pb counterpart by fitting PL tails with Eq. (4) (Fig. 5a, b) and the obtained \(\sigma \left(T\right)\) are plotted in Fig. 5d as a function of temperature. For (PEA)2(MA)Sn2I7, \(\sigma \left(T\right)\) increases with temperature and approaches a limit of \(1.58\pm 0.01\) (\({{\sigma }_{0}}^{*}\)). This value is smaller than that (2.28) in its 3D counterpart54, which can be ascribed to the increased exciton-phonon coupling at reduced dimensionality. As a comparison, \(\sigma \left(T\right)\) of (PEA)2(MA)Pb2I7 initially increases with temperature at cryogenic region (80–120 K) and then decreases monotonically to a plateau of \({{\sigma }_{0}}^{*} \sim 1.46\pm 0.01\) at 300 K, which is much smaller than that of (PEA)2(MA)Sn2I7. \(\sigma \left(T\right)\) of (PEA)2(MA)Pb2I7 at low temperature (<120 K) where lattice is frozen and polaronic effect is negligible50 can be well fitted by Eq. (5) (dashed line in Fig. 5d) and the deviation at high temperature indicates the excited state electronic and structural relaxation due to exciton-lattice coupling. As shown in Fig. 5d, the measured \(\sigma \left(T\right)\) of (PEA)2(MA)Sn2I7 exhibits slight deviation from the fitted curve at high temperature, indicating the presence but rather weak excited state polaronic effect in (PEA)2(MA)Sn2I7. In contrast, the measured \(\sigma \left(T\right)\) deviates significantly from the fitted curve at high temperatures for (PEA)2(MA)Pb2I7, revealing prominent T-dependent excited state polaronic effect. To further confirm the fitted curve from low temperature \({{\sigma }_{0}}^{*}\) in (PEA)2(MA)Pb2I7, we also determined \({{\sigma }_{0}}^{0}\) from absorption tail by PL excitation (PLE) measurement at 300 K (see details in Supplementary Note 5) and the obtained \({{\sigma }_{0}}^{0} \sim 1.58\pm\)0.02 (blue circle) falls on the fitted curve.

Discussion

The determined photophysical parameters for (PEA)2(MA)Sn2I7 and its Pb counterpart are summarized in Table 1. We also extracted the high-frequency dielectric constant \({\varepsilon }_{\infty }\) along c axis and exciton effective mass from first-principles calculation for discussions (see Supplementary Note 6). (PEA)2(MA)Sn2I7 and its Pb counterpart have same crystal structure with only different B site cations, which results in near identical \({\varepsilon }_{\infty }\) and justifies similar \({{E}_{{{\rm{b}}}}}^{0}\) of ~0.21 eV for (PEA)2(MA)Sn2I7 and 0.22 eV for (PEA)2(MA)Pb2I7 by steady-state optical measurement56. However, in-depth PL analysis reveals very different long- and short-range exciton-lattice coupling strength, as evidenced by \({\gamma }_{{{\rm{LO}}}}\) and \({{\sigma }_{0}}^{*}\). \({\gamma }_{{{\rm{LO}}}}\), which is proportional to the long-range polarization response20,31,51, is much smaller in (PEA)2(MA)Sn2I7 than the Pb counterpart. Smaller \({\gamma }_{{{\rm{LO}}}}\) suggests less excited state structural relaxation in (PEA)2(MA)Sn2I7, i.e., less displacement of excited-state potential energy surface (PES) relative to ground-state PES21,57. Meanwhile, \({{\sigma }_{0}}^{*}\), inversely proportional to short-range deformation potential, is much larger in (PEA)2(MA)Sn2I7 (1.58 ± 0.01) than its Pb counterpart (1.46 ± 0.01), which also suggests much less excited state structural deformation in the former.

Table 1 Comparison of the physical parameters of (PEA)2(MA)Sn2I7 and its Pb counterpart
Full size table

A more intuitive way to understand \({{\sigma }_{0}}^{*}\) is to compare it with the critical value \({\sigma }_{{{\rm{c}}}}\) of 1.42 for 2D materials, which determines the relative energy position and thus stability between band edge delocalized exciton and deformed Urbach exciton (UE)17,52,58. As \({\sigma }_{{{\rm{c}}}}\) is much smaller than \({{\sigma }_{0}}^{*}\) of (PEA)2(MA)Sn2I7 but similar to that of the Pb counterpart, UE state lies much higher than the band edge state in (PEA)2(MA)Sn2I7 but close to that in (PEA)2(MA)Pb2I7 (Fig. 6a, b)17,52. Therefore, compared to Pb counterpart with dynamic interconversion between band edge state and UE state, (PEA)2(MA)Sn2I7 retains its band edge exciton with much weaker excited state polaronic effect (Fig. 6a). In the context of exciton polaron, electrons and holes with oppososing lattice deformation are mutually separated in real space. Specifically, the hole induces a compression of bonds, while the electron causes an elongation of bonds in metal halides17,18,21. Hence, weaker excited state polaronic effect in (PEA)2(MA)Sn2I7 results in less polaronic screening effect and larger binding energy \({{E}_{{{\rm{b}}}}}^{*}\), and vice versa for (PEA)2(MA)Pb2I7. With \({{E}_{{{\rm{b}}}}}^{*}\) of 0.18 eV for (PEA)2(MA)Sn2I7, Saha-Langmuir equation (Supplementary Note 1) yields little exciton dissociation (7% at \({n}_{0}\) = 1011 cm-2) at room temperature, which well explains the exciton recombination behavior. On the other hand, a \({{E}_{{{\rm{b}}}}}^{*}\) of 0.10 eV for (PEA)2(MA)Pb2I7 implies 35% exciton dissociation at \({n}_{0}\) = 1011 cm-2 and a power factor \(\beta\) of 1.35 (Supplementary Note 1), which also agrees well with experimental value (1.31) from TRPL0 results. This result aligns with earlier observations of elevated free-carrier densities in 2D lead halide perovskites. The measured densities surpass the values predicted by the Saha-Langmuir equation when using the exciton binding energy from the ground state34,59,60. This discrepancy highlights the significant polaronic effect in the excited states of these materials. Meanwhile, Moser et al. have demonstrated exciton-exciton Auger heating contributes to the formation of long-lived free carriers59, which might be the primary reason for the observation of non-negligible free carrier THz signals even at 4 K34.

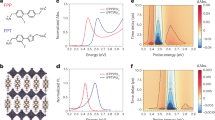
Fig. 6: Calculation of exciton polaron in 2D metal halide perovskites.
figure 6

Scheme of potential energy surface labeled with ground state (GS), excited state (ES) and Urbach exciton (UE) states of (a) (PEA)2(MA)Sn2I7 and (b) its Pb counterpart. c Illustrations of inter-octahedron distortion and the corresponding distortion descriptors including length displacement (\({L}_{{{\rm{d}}}}\)) and angle deviation (\({\theta }_{{{\rm{d}}}}\)) in octahedral layers along a-b direction. The arrows denote the movement direction of the iodine atoms. The calculated (d) \({L}_{{{\rm{d}}}}\) and (e) \({\theta }_{{{\rm{d}}}}\) of (PEA)2(MA)Sn2I7 and (PEA)2(MA)Pb2I7 (labeled as Sn and Pb) in GS and ES configurations. DOS of ground-state and excited-state configurations in (f) (PEA)2(MA)Sn2I7 and (g) its Pb counterpart. h Summed electron (hole) densities in a-b plane (\({\rho }_{i}\left(z\right)\)) as a function of z coordinate. i Effective distance between electron and hole along z coordinate in ground-state and excited-state configurations of (PEA)2(MA)Sn2I7 and its Pb counterpart.

Full size image

To substantiate the excited state polaronic effect and the screening of electron-hole interactions at atomic level, we conducted theoretical atomistic simulations employing density functional theory (DFT) and time-dependent density functional theory (TDDFT). These approaches allowed for the directly visualization of photo-induced structural and electronic relaxation at excited state61. The details of computational methods are provided in Supplementary Note 6. Briefly speaking, the primitive cell of (PEA)2(MA)Sn2I7 or its Pb counterpart with experimental lattice parameters (Supplementary Table 2) was used to generate a 2 × 2 × 1 supercell. With Perdew-Burke-Ernzerhof functional, the ground-state configurations were optimized by the DFT approach, followed by relaxation of the lowest-energy excited-state geometries through TDDFT approach. Given that the dielectric screening is weak along c axis, the density of states (DOS) and photogenerated electron-hole distributions were calculated by DFT and TDDFT, respectively, with optimally tuned and range-separated hybrid functional62.

From the calculation, the iodine atoms in PbI2 layers displace at excited state, with the concave and protruding iodine atoms moving towards straightening the Pb-I-Pb bonds (Fig. 6c). As a result, the distances between the concave (protruding) iodine atoms and the end -NH3 of organic ligands, which are highlighted by red (green) lines in Fig. 6c, are increased (decreased). As distances guided by the red lines are 0.1–0.2 Å smaller than those guided by the green lines, the hydrogen bonds are overall weakened under photoexcitation. This agrees with the partial DOS where the valence and conduction band are predominantly contributed by the 5p orbital of iodine and the 5p (6p) orbital of Sn (Pb) cation (see details in Supplementary Note 6), respectively. Thereby, a fraction of electron densities transfers from iodine atoms to B site atoms under photoexcitation, attenuating hydrogen bonding.

We quantify the overall light-induced structural changes in (PEA)2(MA)Sn2I7 and its Pb counterpart by a set of inter-octahedron geometry descriptors including length displacement \({L}_{{{\rm{d}}}}\) and angle deviation \({\theta }_{{{\rm{d}}}}\)63

$${L}_{{{\rm{d}}}}=\sum _{i=1}^{N}\left|{L}_{i}-L\right|$$
(6)
$${\theta }_{{{\rm{d}}}}=\sum _{i=1}^{N}\left|90-{\theta }_{i}\right|$$
(7)

where \({L}_{i}\) is the distance between two adjacent B site atom (B-B), \({\theta }_{i}\) is the right angle of B-B-B and L denotes the average value of all \({L}_{i}\) at a-b plane (Fig. 6c). The \({L}_{{{\rm{d}}}}\) and \({\theta }_{{{\rm{d}}}}\) for (PEA)2(MA)Sn2I7 and the Pb counterpart at both ground-state and relaxed excited-state configurations are calculated and plotted in Fig. 6d, e, respectively. Interestingly, both materials exhibit reductions of \({L}_{{{\rm{d}}}}\) and \({\theta }_{{{\rm{d}}}}\) at excited-state relative to ground state, which is consistent with very recent experimental results showing photoexcitation-induced lattice straightening in lead halide perovskites64. Importantly, (PEA)2(MA)Sn2I7 shows less change of \({L}_{{{\rm{d}}}}\) and \({\theta }_{{{\rm{d}}}}\) at excited state compared to the Pb counterpart. On the other hand, the electronic structure change can be captured by the change of DOS in Fig. 6f, g. The conduction band edge at excited-state shifts down compared to ground-state in both materials and the shift is less in (PEA)2(MA)Sn2I7 than the Pb counterpart. These calculations on ground state and excited state nuclear and electronic structures confirm less excited state relaxation in (PEA)2(MA)Sn2I7.

The excited state polaronic effect on the screening of electron-hole interaction can be scrutinized by calculating the distance between electron and hole, \(\left|d\left(e\right)-d\left(h\right)\right|\). The effective positions of electron and hole along c direction can be defined as

$$d=\frac{{\sum }_{i}z{\rho }_{i}\left(z\right)}{{\sum }_{i}{\rho }_{i}\left(z\right)}$$
(8)

where z denotes the coordinate along c direction and the \({\rho }_{i}\left(z\right)\) represents the summed electron (hole) densities in a-b plane at z coordinate (Fig. 6h). As shown in Fig. 6i where we compare electron-hole separation at ground and excited state configurations, the distance between electron and hole are increased at excited state in both 2D tin- and lead-halide perovskites and the separation is significantly smaller in (PEA)2(MA)Sn2I7. This electron-hole separation at excited state, together with geometric and electronic structure above, directly confirms excited state polaronic effect screens electron-hole interaction in both materials, forming exciton polaron and the polaronic screening effect is much weaker in (PEA)2(MA)Sn2I7 than in the Pb counterpart.

To unveil the ultimate structural origin for different excited state polaronic effect in (PEA)2(MA)Sn2I7 and the Pb counterpart, we calculated the orientation-dependent Young’s modulus in a-b plane, which reflects the material stiffness (see Supplementary Note 6 for details)65. Notably, Young’s modulus along a and b axis in (PEA)2(MA)Sn2I7 is ~90% and ~65% larger than that in Pb counterpart. The much larger Young’s modulus in (PEA)2(MA)Sn2I7 indicates a more stiffened and less deformable lattice, which can be attributed to the shorter Sn-I bond. Furthermore, the exciton effective mass of (PEA)2(MA)Sn2I7 is about half of that in the Pb counterpart. A larger effective mass implies a narrower electronic structural bandwidth and stronger exciton-phonon coupling strength, which tends to drive polaron formation17,21,57.

To preclude external factors, we have performed additional TRPL0 (Supplementary Fig. 9) and temperature dependent spin relaxation (Supplementary Fig. 10) measurements and analysis on different sets of (PEA)2(MA)Sn2I7 flakes and its Pb counterparts and observed similar excited state recombination and spin relaxation behaviors as observed above. We have also compared 2D tin- and lead- halide perovskites with different n (n = 1 and 3, Supplementary Figs. 11, 12, 13) and different long-chain ligands (BA+: butylammonium, 2T+: bithiophenylethylammonium and 3T+: 2-([2,2′:5′,2″-terthiophen]-5-yl)ethan-1-aminium, n = 2) (Supplementary Fig. 14). For n = 2 and n = 3 perovskites, we have observed consistently excitonic behavior in tin halide perovskites but partial free carrier behavior due to much weakened electron-hole interaction in Pb counterparts, indicating a fairly robust exciton in 2D tin halide perovskites rather than their Pb counterparts. Interestingly, we note both n = 1 tin- and lead- halide perovskites exhibit a linear TRPL0 dependence on photoexcitation density at room temperature, indicating persistently bound electron-hole pair and strong excitonic effect in both n = 1 perovskites at room temperature. This is reasonable since the n = 1 inorganic layer is too thin to screen electron-hole binding energy sufficiently to be comparable to kBT at room temperature. As a contrast, previous studies on 2D and 3D tin halide perovskites have suggested a lower \({E}_{{{\rm{b}}}}\) than their Pb counterparts7,24,25,26,27,28. In 3D tin halide perovskites, the more stiffened Sn-I lattice and lighter Sn element should lead to higher optical phonon frequencies \({\upsilon }_{{{\rm{Sn}}}-{{\rm{I}}}}\) which can reach the exciton characteristic frequency \({\upsilon }_{{{\rm{b}}}}={E}_{{{\rm{b}}}}/{{\hslash }}\) and thus excitons in 3D tin halide perovskites experience more effective screening by the ionic metal-halide lattice26,27,28. Although \({\upsilon }_{{{\rm{b}}}}\) increases dramatically and gets out of optical phonon frequencies from 3D to 2D, the smaller exciton effective mass and band gap still imply a smaller exciton binding energy in 2D tin halide perovskites than the Pb counterparts7,24,25. These results highlight excited state polaronic screening effect, rather than ground state properties, govern the photogenerated exciton nature and dynamics. In contrast to Pb counterpart with free carrier characteristics, the robust exciton with weak exciton-phonon coupling defines 2D tin halide perovskites as genuine excitonic semiconductors, which greatly benefits their optoelectronic applications, especially for light emission purposes. The robust excitonic effect facilitates the encounter and radiative recombination of photo- or electric- injected electron and hole carriers and inhibits the reverse exciton thermal dissociation. This, together with higher carrier mobility11,12 and color purity due to weak exciton-phonon coupling, is ideal for light emission and lasing applications.

In conclusion, we have performed a combined spectroscopy and theoretical study on the excited state exciton nature and dynamics in high-quality 2D tin halide perovskites by comparing to the Pb counterpart. Despite both exhibiting a same large \({{E}_{{{\rm{b}}}}}^{0}\) ~ 0.2 eV from steady state exciton Rydberg series measurement, we reveal a much weaker long- and short-range exciton-phonon coupling in 2D tin halide perovskites than the Pb counterpart, resulting in weak excited state polaronic screening effect and the persistence of robust excitons in 2D tin halide perovskites. The excited state exciton binding energy in n = 2 2D tin halide perovskites has been determined to be ~0.18 eV, about twice of that in the Pb counterpart with same structure. This finding challenges the conventional view of exciton behavior and highlights the critical role of excited state polaronic effect on exciton nature and dynamics in these materials. The robust excitons at excited state in 2D tin halide perovskites exhibits excitation power-insensitive, high-efficiency and high color-purity light emission, rendering them superior for light-emitting diodes and lasers than their Pb counterparts.

Methods

Preparation of perovskite single crystals

All single crystals were grown using the slow cooling method5. For (PEA)2(MA)Sn2I7, 0.17 mmol phenethylammonium iodide (PEAI, Greatcell Solar Ltd.), 0.4 mmol methylammonium iodide (MAI, Greatcell Solar Ltd.) and 0.4 mmol SnI2 (Shanghai Macklin Biochemical Co., Ltd.) were added into 1 mL hydriodic acid (HI, 57wt.%, TCI) and 0.1 mL hypophosphorous acid (H3PO2, J&K Scientific). For (PEA)2(MA)2Sn3I10, 0.17 mmol PEAI, 0.67 mmol MAI and 0.4 mmol SnI2 were added into 1 mL HI and 0.1 mL H3PO2. For (PEA)2(MA)Pb2I7, 0.43 mmol PEAI, 0.60 mmol MAI and 0.59 mmol PbI2 (TCI (Shanghai) Development Co., Ltd.) were added into 0.9 mL HI and 0.1 mL H3PO2. For (PEA)2(MA)2Pb3I10, 0.15 mmol PEAI, 0.53 mmol MAI and 0.59 mmol PbI2 were added into 0.8 mL HI and 0.1 mL H3PO2. As for (BA)2(MA)Sn2I7, (2T)2(MA)Sn2I7 and (3T)2(MA)Sn2I7 single crystals, they were synthesized using the previously reported recipes5. After heating and complete dissolution, they were put into a muffle furnace for cooling down from 383 K to 293 K at a cooling rate of 1 °C/h, and finally high purity halide perovskite single crystals were obtained. It is worth noting that all the processes, starting from the weighing of precursors and ending with the drying of single crystals, are conducted within N2 glove box. The CCDC numbers for (PEA)2(MA)Sn2I7 and (PEA)2(MA)Pb2I7 are 2240837 and 2299252, respectively. 2D perovskites and h-BN (Onway Technology) thin flakes were mechanically exfoliated onto gel films (Gel-Pak PF-X4) from bulk single crystals. Under an optical microscope, we fabricated BN/perovskites/BN heterostructures to preserve 2D perovskites from the damage caused by water, oxygen and vacuum by transferring the exfoliated thin flakes from gel film to SiO2 substrate in sequence29. The whole processes are operated in N2 glovebox.

Steady state optical measurements

We used a home-built microscope setup integrated with liquid-nitrogen-cooled cryostat (custom-made STC-W30, LANHAI Science Instrument) for optical characterizations and the samples are consistently in controlled environment of vacuum or N2. The TeslatronPT VTI cryostat (Oxford Instruments Inc., temperature range from 4 to 300 K) was utilized for reflection spectra at Ultra-low temperature (4 K) with a home-made optical probe inserts with a 50X objective lens (MPlan 50X, Olympus, NA = 0.75) seated on the probe for the optical excitation and collection. A broadband halogen lamp (OSLR, Thorlabs, Inc.) is used as the light source. In steady-state absorption measurement, the fundamental 1030 nm femtosecond-pulsed laser (CARBIDE, Light Conversion Ltd) was focused onto a YAG (Yttrium Aluminum Garnet) crystal for generating a continuum white light. The steady-state transmission and reflection differential spectra were obtained by normalizing the transmitted (\({{\rm{\delta }}}T=({T}_{{{\rm{sample}}}}-{T}_{{{\rm{sub}}}})/{T}_{{{\rm{sub}}}}\)) and reflected (\({{\rm{\delta }}}R=({R}_{{{\rm{sample}}}}-{R}_{{{\rm{sub}}}})/{R}_{{{\rm{sub}}}}\)) light from the sample on transparent SiO2 substrate to that from the bare substrate, respectively. And The collection and analysis of transmitted and reflected light were conducted by liquid nitrogen cooled detectors (PyLon 100B, Princeton Instruments). The absorption coefficient of sample was calculated by \(A=1-({T}_{{{\rm{sample}}}}+{R}_{{{\rm{sample}}}})/({T}_{{{\rm{sub}}}}+{R}_{{{\rm{sub}}}})\). In PL measurement, PL spectra were obtained with a 532 nm continuous-wave (CW) laser excitation. A supercontinuum laser (SC-OEM, YSL Photonics) coupled with a monochromator was used as excitation light source for PL excitation measurements.

Time-resolved photoluminescence measurements

The fundamental 1030 nm femtosecond-pulsed laser (pulse width ~200 fs and frequency of 100–1000 KHz, YactoFiber-FL-20, Yacto-Tech) was focused onto a barium metaborate (BBO) crystal to generate a 515 nm excitation light for TRPL measurements. The TRPL decay kinetics were collected using a TCSPC module (SPC-130INX) and ultrafast detector (Hybrid PMT, HPM-100-07) with an instrument response function ~30 ps.

Spin-resolved transient absorption spectroscopy

For TA measurements, two 1030 nm femtosecond-pulsed lasers (~150 fs pulse duration, supplied by CARBIDE, Light Conversion Ltd) were focused onto YAG (Yttrium Aluminum Garnet) crystals, producing a continuum white light. One served as the probe light, and the other was filtered to selected central wavelength with narrow FWHM (i.e., 640–660 nm) and served as the pump light. To accurately regulate the time delay between the pump and probe beams, a high-precision motorized delay stage from Newport was employed. Both beams were converged and focused by a microscope equipped with a 50X transmissive lens, resulting in spot size smaller than 2 μm. The transmitted probe light, with the pump beam efficiently filtered out, was detected by liquid nitrogen cooled detectors (PyLon 100B, Princeton Instrument). The TA signal (\(\Delta T/T\)) was derived by normalizing the spectral intensity from the pumped to the unpumped state, yielding \({{\rm{\delta }}}T=\Delta T/T=({T}_{{{\rm{pump}}}\; {{\rm{on}}}}-{T}_{{{\rm{pump}}}\; {{\rm{off}}}})/{T}_{{{\rm{pump}}}\; {{\rm{off}}}}\). For the spin-resolved transient absorption measurement, circularly polarized lights were generated by passing the linear polarized pump and probe beams through a quarter wave plate (1/4λ). By manipulating the pump beam’s polarization direction using a half wave plate, either same (SCP) or opposite (OCP) circular polarization conditions could be achieved relative to the probe beam. Throughout all optical measurements, the laser beam was focused to a spot size of less than 2 μm.