Introduction

A milestone development of density functional theory (DFT) is the invention of hybrid functionals1, developed first as an ad hoc correction to local density or generalized gradient approximations (LDA/GGA)2, and later formulated more rigorously in the generalized Kohn–Sham framework3. Superior to conventional density functionals, hybrid functionals provide a viable route to solve the critical “band-gap problem” of DFT4,5, thus indispensable for reliable material prediction and particularly useful for computational studies in (opto-)electronics, spintronics, topological electronics, etc. The practical use of hybrid functionals, however, is limited for large-scale materials simulations, because their computational cost is considerably higher than local and semi-local DFT methods. Great efforts have been devoted to improving the numerical algorithms6,7,8,9,10,11,12,13,14. This helps reduce the computational overhead and facilitates linear-scaling hybrid-functional calculations, but cannot fundamentally change the landscape of ab initio computation.

Deep learning methods shed light on revolutionizing ab initio materials simulation15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40. For instance, the use of artificial neural networks to represent DFT Hamiltonian enables efficient electronic-structure calculations with ab initio accuracy, whose computational cost is as low as that of empirical tight-binding calculations26,27,28,29,30. The so-called deep-learning DFT Hamiltonian (DeepH) approach has been demonstrated powerful in large-scale materials simulation for both non-magnetic and magnetic systems26,27,28,29,30. However, the method was originally designed within the Kohn–Sham (KS) framework. Therein the deep-learning problem is simplified by the local nature of the exchange-correlation potential. In contrast, hybrid functionals are usually done within the generalized Kohn–Sham (gKS) scheme3, giving rise to non-local exchange potentials. Considering that the deep-learning approach relies critically on the locality property41,42,43, whether the same strategy is applicable to the gKS scheme or not is an important open question.

In this work, we find that the gKS-DFT Hamiltonian of hybrid functionals \({H}_{{{{\rm{DFT}}}}}^{{{{\rm{hyb}}}}}\) can be represented by neural networks similar to conventional DFT, benefiting from the preservation of the nearsightedness principle on a localized basis. We apply deep E(3)-equivariant neural networks to model \({H}_{{{{\rm{DFT}}}}}^{{{{\rm{hyb}}}}}\) as a function of material structure (Fig. 1a), from which the electronic structure and physical properties of materials can be predicted without invoking ab initio codes. The method is tested to show good performance by systematic numerical experiments and further applied to study Moiré-twisted superstructures, such as magic-angle twisted bilayer graphene, demonstrating the capability for large-scale electronic-structure calculations with hybrid-functional accuracy. Our work paves the way for accurate, efficient materials simulation, and also opens a door for developing deep-learning electronic structure methods beyond DFT.

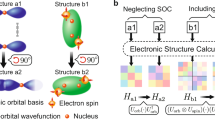
Fig. 1: Schematic workflow and illustration of non-local nature in hybrid functionals.
figure 1

a Schematic workflow of the DeepH-hybrid method. Neural networks are used to learn the relationship between hybrid-functional Hamiltonian and material structure. The method applies ab initio calculations of small-size systems for training and makes inferences on large-size systems for predicting electronic structure and physical properties. b Non-local nature of the exact-exchange potential. Two non-overlapping atomic orbitals ϕi and ϕj with a finite cutoff radius RC can contribute non-zero hybrid-functional Hamiltonian matrix elements due to the presence of non-local potential \(v({{{\bf{r}}}},{{{{\bf{r}}}}}^{{\prime} })\). Other atomic orbitals ϕk and ϕl are involved in the non-local coupling.

Full size image

Results

Consideration of nearsightedness principle

In the KS-DFT44, the challenging interacting-electron problem is mapped to an auxiliary non-interacting problem whereby the complicated many-body effects are incorporated in an exchange-correlation function. Within the conventional approximations of KS-DFT, the exchange-correlation energy is expressed as an explicit functional of density and a local form of exchange-correlation potential Vxc(r) is assumed. Such approximations greatly simplify the problem and are widely used in ab initio calculations. Unfortunately, the delocalization error45 is prevalent in such density-based functionals, which could result in systematic failures of DFT, including the band gap problem4,46. In fact, the fundamental band gap will be underestimated within the KS-DFT framework if the functional derivative discontinuity is not taken into account47,48,49. This critical issue needs to be addressed to make reliable property predictions on electronic materials.

The gKS scheme allows the use of orbital-dependent exchange-correlation potential, which helps relieve the band-gap problem. As a typical example, hybrid-functional methods replace a portion of semi-local exchange with the (screened) Hartree-Fock exact exchange, by which the band gap problem could be largely resolved. However, a non-local, exact-exchange potential \({V}_{{{{\rm{Ex}}}}}({{{\bf{r}}}},{{{{\bf{r}}}}}^{{\prime} })\) will be introduced into the effective Hamiltonian, which significantly complicates the calculation. Let us illustrate this with the localized orbital basis functions \({\phi }_{{{{\bf{i}}}}}({{{\bf{r}}}})={R}_{ipl}(r){Y}_{lm}(\hat{r})\), where Ripl is the radial function centered at the ith atom labeled by the multiplicity p and angular momentum quantum number l, Ylm is the real spherical harmonics of degree l and order m, and i ≡ (iplm) is used for simplicity. In the localized basis, the nth KS eigenstate is ψn(r) = ∑icniϕi(r), and the (screened) exact-exchange potential is written as

$${V}_{{{{\bf{ij}}}}}^{{{{\rm{Ex}}}}} =- {\sum}_{n}^{{{{\rm{occ}}}}} {\sum}_{{{{\bf{k,l}}}}}{c}_{n{{{\bf{k}}}}}{c}_{n{{{\bf{l}}}}}^{ * }({{{\bf{ik}}}}| {{{\bf{lj}}}}),\\ ({{{\bf{ik}}}}| {{{\bf{lj}}}}) =\iint\,{\rm {d}}{{{\bf{r}}}}{\rm {d}}{{{{\bf{r}}}}}^{{\prime} }{\phi }_{{{{\bf{i}}}}}^{ * }({{{\bf{r}}}}){\phi }_{{{{\bf{k}}}}}({{{\bf{r}}}})v({{{\bf{r}}}}-{{{{\bf{r}}}}}^{{\prime} }){\phi }_{{{{\bf{l}}}}}^{ * }({{{{\bf{r}}}}}^{{\prime} }){\phi }_{{{{\bf{j}}}}}({{{{\bf{r}}}}}^{{\prime} }),$$
(1)

where \(v({{{\bf{r}}}}-{{{{\bf{r}}}}}^{{\prime} })\) denotes the Coulomb potential \(1/| {{{\bf{r}}}}-{{{{\bf{r}}}}}^{{\prime} }|\) or its screened version. Note that the two-electron Coulomb repulsion integral (ik∣lj) involves a four-center integration over six spatial coordinates (Fig. 1b), and the number of integrals to be calculated is enormous, growing quickly with the system size. Hence the computation becomes much more expensive than local or semi-local DFT. The situation is alleviated with significant algorithm improvements (e.g., resolution of identity and linear-scaling techniques)13,14,50, but the significant increase of the computational cost from semi-local to hybrid DFT methods is not fundamentally changed. This is the major drawback of hybrid functionals, which restricts broad applications of the methods.

The exchange-correlation potentials of hybrid functionals share the form \({V}_{{{{\rm{xc}}}}}^{{{{\rm{hyb}}}}}({{{\bf{r}}}},{{{{\bf{r}}}}}^{{\prime} })={V}_{{{{\rm{xc}}}}}^{{\prime} }({{{\bf{r}}}})\delta ({{{\bf{r}}}}-{{{{\bf{r}}}}}^{{\prime} })+\alpha {V}_{{{{\rm{Ex}}}}}({{{\bf{r}}}},{{{{\bf{r}}}}}^{{\prime} })\), where a fraction α of the semi-local exchange potential is replaced by VEx and the remaining part \({V}_{{{{\rm{xc}}}}}^{{\prime} }\) is the same as that of the semi-local DFT. For example, the Heyd–Scuseria–Ernzerhof (HSE) hybrid functional uses an error-function-screened Coulomb potential in VEx with α = 25%51. According to the Hohenberg–Kohn theorem52, the auxiliary non-interacting Hamiltonian is uniquely determined by the external potential Vext that is defined by the material structure \(\{{{{\mathcal{R}}}}\}\). Thus \({H}_{{{{\rm{DFT}}}}}^{{{{\rm{hyb}}}}}\) and VEx can be expressed as a function of \(\{{{{\mathcal{R}}}}\}\). It has been established that the KS-DFT Hamiltonian \({H}_{{{{\rm{DFT}}}}}^{{{{\rm{KS}}}}}(\{{{{\mathcal{R}}}}\})\) can be well represented by deep neural networks26,27,28. We will attempt to use neural networks to model \({H}_{{{{\rm{DFT}}}}}^{{{{\rm{hyb}}}}}(\{{{{\mathcal{R}}}}\})\) to generalize the deep-learning approach to achieve hybrid-functional accuracy (Fig. 1a). Compared with the KS case, a special non-local component \({V}_{{{{\rm{Ex}}}}}(\{{{{\mathcal{R}}}}\})\) is introduced here, whose neural-network representation has not been considered before.

Satisfying the nearsightedness principle is essential to simplify the deep-learning Hamiltonian problem, as learned from the study of KS-DFT. Multiple existing studies have investigated the nearsightedness of various quantities, such as total energy53,54, yet discussions regarding the nearsightedness of gKS-DFT Hamiltonians remain exclusive to date. On a localized basis, the KS-DFT Hamiltonian can be viewed as an ab initio tight-binding Hamiltonian. The hopping between atoms i and j, namely the Hamiltonian matrix block Hij, is nonzero only when the atomic distance rij is smaller than a cutoff radius RC. Moreover, Hij is predominately determined by the neighboring environment, whose value is insensitive to distant variations of atomic structure. Thus Hij can be simplified to be a function of \({\{{{{\mathcal{R}}}}\}}_{{{{\rm{N}}}}}\), which includes structural information of neighboring atoms {k} with rik, rjk < RN, where RN denotes a nearsightedness length26.

For hybrid functionals, whether the non-local exact exchange is compatible with the nearsightedness principle or not should be checked. In Eq. (1), the KS eigenvector cnk or cnl can be influenced by distant changes in boundary conditions, which breaks the nearsightedness principle. The two-electron Coulomb repulsion integral (ik∣lj) displays long-distance (short-distance) decay between atoms i and j when the bare (screened) Coulomb potential is considered. Thus the product \({c}_{n{{{\bf{k}}}}}{c}_{n{{{\bf{l}}}}}^{*}({{{\bf{ik}}}}| {{{\bf{lj}}}})\) is a non-local quantity, whose dependence on material structure is expected to be complicated. However, the summation over occupied states \({\sum }_{n}^{{{{\rm{occ}}}}}{c}_{n{{{\bf{k}}}}}{c}_{n{{{\bf{l}}}}}^{*}\) yields the density matrix element ρk,l that is a local quantity55,56. Moreover, the Coulomb integral (ik∣lj) is nonzero only when both atom pairs i–k and l–j have finite orbital overlaps (Fig. 1b). Hence the local property gets preserved for \({V}_{{{{\bf{ij}}}}}^{{{{\rm{Ex}}}}}\). This is the reminiscent of W. Kohn’s principle, which states that the nearsightedness of electronic matter is originated from wave-mechanical destructive interference in many-particle systems55,56. Benefiting from the nearsightedness property, \({V}_{{{{\bf{ij}}}}}^{{{{\rm{Ex}}}}}\) can be determined by local structural information of neighborhood, similar to local exchange-correlation potentials. The merit enables us to treat the conventional and generalized KS-DFT within a unified deep-learning framework. The inclusion of exact exchange, however, could significantly weaken the sparseness and nearsightedness properties of the DFT Hamiltonian. This will be accounted for by changing the important length scales RC and RN in the design of deep neural networks.

The DFT Hamiltonian matrix of local or semi-local functionals is sparse, whose elements are nonzero only when the distance between atom pairs i and j is smaller than a cutoff length RC = Ri + Rj, where Ri and Rj denote the basis cutoff radii of atoms i and j, respectively. In contrast, the Hamiltonian matrix of hybrid functionals is denser. To describe this feature, we set a larger cutoff length \({R}_{{{{\rm{C}}}}}^{{{{\rm{hyb}}}}}=\gamma {R}_{{{{\rm{C}}}}}\), with γ being an adjustable parameter. Choosing a larger γ generally results in a more accurate DeepH-hybrid model capable of capturing more non-local features, at the expense of increased time and memory costs. Numerical tests on this parameter are presented in Supplementary Section 5, indicating that a γ value of 2.0 is appropriate. This value is used for studies presented in the main text. This selection is a compromise between accuracy and efficiency, which reflects the non-local nature of hybrid functionals.

Equivariance neural networks

In our work, we use the method of E(3)-equivariant deep learning DFT Hamiltonian (DeepH-E3)28 to model the mapping from the material structure {\({{{\mathcal{R}}}}\)} to the corresponding hybrid-functional DFT Hamiltonian \({H}_{{{{\rm{DFT}}}}}^{{{{\rm{hyb}}}}}\) under numerical atomic orbital (NAO) basis. A graph is associated with each material structure, with each vertex representing an atom, and edges are connected between atoms within a certain cutoff. The feature vectors associated with vertices and edges are iteratively updated with neural networks, and the final edge features are used to construct the output hopping matrices. Updating a vertex or edge only uses information within its neighborhood, and so the nearsightedness property is utilized for the prediction of Hamiltonians. Moreover, since the Hamiltonian transforms covariantly between coordinate frames, it is most natural and advantageous to construct neural networks that explicitly handle the covariant property of the Hamiltonian. To achieve this, all the input, output and internal vectors of the neural networks transfer according to irreducible representations of the O(3) group under coordinate rotations and inversion. The incorporation of the requirements of locality and symmetry as a priori knowledge has greatly enhanced the performance of DeepH-E3 and has led to its sub-meV level accuracy and excellent generalization ability28.

Utilizing the equivariant neural network (ENN)57,58, the mapping \(\{{{{\mathcal{R}}}}\}\to {\hat{H}}_{{{{\rm{DFT}}}}}\) in the DeepH-E3 approach is equivariant with respect to the Euclidean group in three-dimensional space, the E(3) group, which is composed of translations, rotations and spatial inversion in three-dimensional space, thus preserving the fundamental symmetries. To realize equivariance in neural networks, DeepH-E3 labels each network feature with angular quantum number l. Upon spatial rotation R to the input structure, all features will transform as \({{{{\bf{x}}}}}_{m}^{l}{\longrightarrow }^{{{{\bf{R}}}}}{\sum }_{{m}^{{\prime} }}{D}_{m{m}^{{\prime} }}^{l}({{{\bf{R}}}}){{{{\bf{x}}}}}_{{m}^{{\prime} }}^{l}\), in which \({D}_{m{m}^{{\prime} }}^{l}({{{\bf{R}}}})\) is the Wigner-D matrix. DFT Hamiltonians block Hij can be divided into sub-blocks \({{{\bf{h}}}}\equiv {[{H}_{ij}]}^{{p}_{1}{p}_{2}}\) by grouping orbitals with the same p together. The resulting sub-blocks are equivariant tensor whose elements transform as \({{{{\bf{h}}}}}_{{m}_{1}{m}_{2}}^{{l}_{1}{l}_{2}}\to {\sum }_{{m}_{1}^{{\prime} },{m}_{2}^{{\prime} }}{D}_{{m}_{1}{m}_{1}^{{\prime} }}^{{l}_{1}}({{{\bf{R}}}}){D}_{{m}_{2}{m}_{2}^{{\prime} }}^{{l}_{2}}({{{\bf{R}}}}){{{{\bf{h}}}}}_{{m}_{1}^{{\prime} }{m}_{2}^{{\prime} }}^{{l}_{1}{l}_{2}}\) upon rotation R. Equivariant tensors and equivariant vectors can be associated by Wigner–Eckart theorem l1 ⊗ l2 = ∣l1−l2∣⊕ ⋯ ⊕(l1 + l2). Hamiltonian sub-blocks are regarded as equivariant tensors with representation l1 ⊗ l2 and constructed accordingly. DeepH-E3 starts with l = 0 (scalar) features by embedding atomic numbers (Zi) and distance between atom pairs (∣rij∣). Relative direction of atom pairs are also taken as input features with l = 1, 2, ⋯   by enforcing spherical harmonics on \({\hat{{{{\bf{r}}}}}}_{ij}\). Regarding equivariance with respect to spatial inversion, feature vectors are additionally labeled by their parity upon spatial inversion, either even (e) or odd (o). All intermediate ENN operations are designed to preserve features’ parity characteristics. In all training, our neural networks are composed of three message-passing blocks, with 64 × 0e + 32 × 1o + 16 × 2e + 8 × 3o + 8 × 4e equivariant layer for each intermediate layer. Here, 64 × 0e stands for 64 even-parity equivariant vectors with l = 0.32 × 1o stands for 32 odd-parity equivariant vectors with l = 1. Atomic configuration information is embedded into 64-dimensional equivariant vectors as initial vertex and edge features. Mean squared error of Hamiltonian matrix elements is selected as the loss function for training neural network models. Datasets are randomly split into training, validation, and test sets with a ratio of 6:2:2.

Case studies

To demonstrate the capability of DeepH-hybrid, we carry out example studies on various material systems, including monolayers and bilayers of graphene and MoS2. Figure 2 shows the performance of DeepH-hybrid on studying monolayer graphene and related systems. Neural network models are trained by a dataset containing randomly perturbed structures of graphene supercells, which will be generalized to investigate new structures of graphene supercells as well as carbon nanotubes (CNTs). The mean absolute errors (MAEs) of gKS-DFT Hamiltonian matrix elements are 0.207, 0.208, and 0.208 meV for training, validation, and test sets, respectively. The MAEs are even smaller than that for the DeepH study using the Perdew–Burke–Ernzerhof (PBE) exchange-correlation functional (MAE = 0.40 meV)28. The test set consisting of 100 perturbed graphene supercells is sorted in terms of MAE. The band structures corresponding to the best, median and worst MAEs are shown in Fig. 2a. All of them agree well with the benchmark calculations, demonstrating the good accuracy of DeepH-hybrid. In addition, we use the trained neural network model to study CNTs that have a curved geometry unseen in the training set for testing the generalization ability of the method (Fig. 2b). As shown in Fig. 2c for (49, 0) CNT, a good agreement between DeepH-hybrid and DFT-hybrid (i.e., benchmark calculations using the HSE hybrid functional) is achieved for the study of band structure. One major improvement of hybrid function over LDA/GGA is the improved description of the band gap, which is closely related to optical properties. We further calculate the electric susceptibility by the method developed in ref. 59 using the gKS-DFT Hamiltonians obtained from DFT-hybrid and DeepH-hybrid, respectively. The real and imaginary parts of electric susceptibility as a function of light frequency ω are presented in Fig. 2d. The calculated results of DeepH-hybrid are in good consistency with the DFT-hybrid benchmark data. All of these prove the reliability of our neural network method.

Fig. 2: Example studies on monolayer graphene and carbon nanotube (CNT).
figure 2

a Band structures of supercells of monolayer graphene computed by hybrid density functional theory (DFT-hybrid) and DeepH-hybrid. Representative test structures with the smallest, median and largest mean absolute error (MAE) in the prediction of hybrid-functional Hamiltonian are displayed. b Schematic workflow of the DeepH-hybrid method, which learns from training datasets of nearly flat structures and then generalizes to study curved nanotube structures. c Band structures and d real and imaginary parts of electric susceptibility χzz as a function of frequency ω of (49, 0) CNT computed by DFT-hybrid and DeepH-hybrid. The periodic direction of the nanotube is defined as the z-axis. Source data are provided as a Source Data file.

Full size image

Next, we apply the developed method to study material systems of twisted bilayer graphene (TBG), which belongs to a general class of Moiré-twisted materials, gaining increasing interest in recent years60. Various kinds of intriguing correlated phases, such as correlated insulators, ferromagnetism, and superconductivity, have been discovered in the TBG system61,62,63. In particular, the TBG with twist angle θ ≈ 1.08° is theoretically proposed to have ultra flat bands near the Fermi energy, which is thus named magic-angle TBG. The flat band structure of magic-angle TBG has been reproduced by DFT calculations using the PBE exchange-correlation functional in GGA. The DFT-PBE study is inherently challenging, considering that the magic-angle TBG contains 11,164 atoms per Moiré cell. In principle, the more advanced hybrid functional methods might improve the description of electronic structure but are much more expensive than DFT-PBE. Whether the flat-band feature is preserved or not in the description of hybrid functionals is a fundamentally important problem, but has not been investigated before due to the computational challenge.

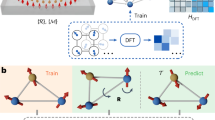
DeepH-hybrid is able to overcome the computational challenge. The strategy is as follows (Fig. 3a)26,28: Use datasets containing small-size supercells of non-twisted bilayer graphene to train neural networks, and then apply the trained neural network models to study TBGs with varying twist angles, including those with large-supercell Moiré structures. Training on bilayer graphene datasets creates a neural network model of DeepH-hybrid, whose MAEs of gKS-DFT Hamiltonian matrix elements are 0.146, 0.147, and 0.147 meV for training, validation, and test sets, respectively. Such low MAEs ensure accurate prediction of band structures, which is confirmed by studying representative test structures as summarized in Supplementary Fig. 1. We further check the reliability of DeepH-hybrid on calculating TBGs with varying twist angles, focusing on systems with small Moiré cells for facilitating benchmark calculations. Figure 3b–d displays comparisons of the band structure of (2, 1) TBG (twist angle θ ≈ 21.79°, 28 atoms/cell), (3, 2) TBG (θ ≈ 13.17°, 76 atoms/cell), and (17, 16) TBG (θ ≈ 2.00°, 3,268 atoms/cell). Note that we applied low-scaling algorithms at large computational cost by DFT-hybrid to compute the benchmark data for the final TBG system. Notably, the MAE of DeepH-hybrid and low-scaling DFT-hybrid Hamiltonian is 0.179 meV for (17, 16) TBG, which is comparable to the training loss, thus exemplifying DeepH-hybrid’s ability to generalize to exascale systems. For all the case studies, band structures predicted by DeepH-hybrid can precisely match the benchmark results obtained by DFT-hybrid calculations.

Fig. 3: Example studies on twisted bilayer graphene (TBG).
figure 3

a Schematic workflow of the DeepH-hybrid method, which applies deep neural networks to learn from training datasets of non-twisted bilayer graphene and then generalizes to study TBG systems with varying twist angle θ. b–d Band structures of b (2, 1) TBG (θ ≈ 21.79°, 28 atoms/cell), c (3, 2) TBG (θ ≈ 13.17°, 76 atoms/cell), and d (17, 16) TBG (θ ≈ 2.00°, 3,268 atoms/cell) computed by hybrid density functional theory (DFT-hybrid) and DeepH-hybrid. e Computation time for predicting hybrid-functional Hamiltonians of TBGs by DFT-hybrid using linear-scaling algorithms versus by DeepH-hybrid using neural-network inference. The dashed black line represents the time cost trend as a function of system size for an algorithm with O(N) scaling. f Top-view atomic structure of magic-angle TBG (θ ≈ 1.08°, 11,164 atoms/cell). The Moiré supercell is highlighted by a red dashed frame. g,h Band structures of magic-angle TBG computed by g DeepH-PBE and h DeepH-hybrid. DeepH-PBE denotes the deep-learning DFT Hamiltonian of the PBE functional. The relaxed atomic structure of magic-angle TBG adapted from ref. 63 is used. The results of DeepH-PBE are adapted from ref. 28. Source data are provided as a Source Data file.

Full size image

The CPU times of calculating Hamiltonians by DFT-hybrid and DeepH-hybrid as a function of system size (i.e. number of atoms per supercell) are compared in Fig. 3e. Here linear-scaling algorithms as implemented in the ABACUS package14,64,65 are applied in the DFT-hybrid calculations. In contrast, DeepH-hybrid can still reduce the computational cost by orders of magnitude, and its computational time roughly grows linearly with the system size, which demonstrates the superior efficiency of the neural network method. A more comprehensive analysis of DeepH-hybrid’s time cost, taking dataset preparation and neural network optimization time into consideration, is presented in Supplementary Section 6.

Benefitting from the good accuracy and high efficiency of DeepH-hybrid, the hybrid-functional electronic structure of magic-angle TBG (Fig. 3f) can be predicted. Figure 3g,h demonstrates our results of PBE and HSE band structures of magic-angle TBG with structure relaxed by ref. 63. Both PBE and HSE Hamiltonians bear four flat bands near the Fermi surface. Compared with the PBE band structure, the bandwidth of the flat bands of the HSE band structure is increased to 41.1 meV from 4.1 meV. In addition, perturbation theory is applied to calculate the Fermi velocity of HSE and PBE Hamiltonians, yielding vF = 36.2 and 0.9 m s−1, respectively. From our calculation, introduction of exact exchange dramatically weakens the flatness of magic-angle TBG’s flat bands, and thus could have a qualitative impact on the flat band physics of magic-angle TBG.

Regarding hybrid functionals’ capability to solve the “band-gap problem”, we carried out further example studies on monolayer and bilayer H-MoS2 (Fig. 4a, b). H-MoS2 is a representative material of transition metal dichalcogenides, a family of materials gathering interest for its emerging new physics66,67. HSE calculations are anticipated to yield a heightened level of accuracy in the electronic band gap. Consequently, these calculations are poised to establish a more robust foundation for predicting optical properties, as well as other quasiparticle calculations. Analogous to graphene, two datasets containing monolayer and bilayer H-MoS2 are constructed and used to train DeepH-hybrid models. For monolayer MoS2, the final MAEs of the predicted hybrid-functional Hamiltonian are 0.259, 0.259, and 0.258 meV for training, validation, and test sets, respectively. Band structures of representative test data predicted by DeepH-hybrid are summarized in Supplementary Fig. 2, showing good matching with DFT-hybrid band structures. For bilayer MoS2, the MAEs of the predicted hybrid-functional Hamiltonian are 0.266, 0.266, and 0.265 meV for training, validation, and test sets, respectively. Band structures of representative test data predicted by DeepH-hybrid are summarized in Supplementary Fig. 3. Comparisons of band gap of test structures between DFT-hybrid and DeepH-hybrid are summarized in Supplementary Fig. 4. Figure 4 demonstrates DeepH-hybrid’s robustness in case studies of MoS2. Mean average error of the band gap on test sets of the two models is 15.1 and 16.0 meV, which are the order of magnitude smaller than the gap difference between PBE and HSE functionals. Figure 4c–f examines the capability of generalization from untwisted bilayer MoS2 to twisted structures. Band structures as well as electric susceptibility of (2, 1) and (3, 2) twisted bilayer MoS2 predicted by DeepH-hybrid, match well with the results of DFT-hybrid. DeepH-hybrid’s efficiency makes it applicable to Moiré-twisted MoS2 superstructures. Figure 4g shows the band gap of a series of (n, n − 1) twisted bilayer MoS2. The band gap shifts for up to 70 meV in the tested twist angles. Flat bands can be observed in twisted MoS2 with large Moiré cells. The band width of the topmost occupied band and its effective mass at the Γ point are summarized in Fig. 4h. Band structures of these materials predicted by DeepH-hybrid are presented in Supplementary Fig. 5. A representative band structure with a flat valence band is shown in Fig. 4i.

Fig. 4: Example studies on twisted bilayer MoS2.
figure 4

a Top-view atomic structure of monolayer MoS2. b Schematic workflow of the DeepH-hybrid method, which learns from training datasets of non-twisted bilayer MoS2 and then generalizes to study twisted bilayer MoS2 with varying twist angle θ. c, e Band structures and d, f real and imaginary parts of electric susceptibility χxx as a function of frequency ω for c, d (2,1) twisted bilayer MoS2 (θ ≈ 21.79°, 42 atoms/cell) and e, f (8,7) twisted bilayer MoS2 (θ ≈ 13.17°, 114 atoms/cell) computed by hybrid density functional theory (DFT-hybrid) and DeepH-hybrid. The x-axis is defined in (a). g Band gap, h bandwidth and effective mass of the top valence band as a function of system size for Moiré-twisted bilayer MoS2 predicted by DeepH-hybrid. i Band structure of (8,7) twisted bilayer MoS2 (θ ≈ 4.41°, 1,014 atoms/cell), which displays a flat valence band (highlighted in red). Source data are provided as a Source Data file.

Full size image

Discussions

In conclusion, we demonstrate that the conventional and generalized KS DFT can be treated within a unified deep-learning framework. Owing to the preservation of the nearsightedness principle, DeepH-hybrid’s capability is proved in predicting the hybrid-functional Hamiltonian as a function of the material structure by multiple case studies. While an increased cutoff radius compared with semi-local DFT Hamiltonians is essential for handling the non-local exact exchange in DeepH-hybrid, the Hamiltonians in conventional and generalized KS frameworks share similar physical priors. This enables the deep-learning modeling of the gKS Hamiltonians with high accuracy without requiring extensive modifications to the neural network architecture, thus facilitating the simultaneous development of the neural network frameworks for both tasks in the future. Regarding the improved accuracy of band gaps with hybrid functionals, our work enables efficient study of optical properties, non-adiabatic molecular dynamics, etc., in which unoccupied conduction bands play an important role. By bypassing the time-consuming self-consistent field iterations and four-center Coulomb repulsion integrals, DeepH-hybrid has the potential to study electronic properties of superstructures at the hybrid functional level, which was previously bottlenecked due to the timely cost. Owing to the increased time cost in hybrid functionals, the relative time-saving of DeepH-hybrid will be even more significant than that in (semi)local density functionals. Test study on magic-angle TBG reveals DeepH-hybrid’s ability to apply hybrid-level functionals to Moiré-twisted superstructures with over 104 atoms. Application of DeepH-hybrid to magic-angle TBG shows a dramatic change of flat band properties when the HSE functional is applied, implying that the exact exchange could have a qualitative impact on the flat band physics of magic-angle TBG. DeepH-hybrid’s success on the HSE functional can be a starting point for the generalization of DeepH to Hamiltonians from higher-level electronic structure theory, and this methodology may overcome the accuracy-efficiency dilemma of ab initio methods in general.

While the DeepH-hybrid method applies successfully to the HSE functional with a screened exact exchange, its applicability to other hybrid functionals, particularly those with unscreened exchange, is also a significant concern. There is no fundamental barrier for DeepH-hybrid being applied to unscreened hybrid functionals, since the “nearsightedness principle” is not violated. This is demonstrated by a numerical experiment on the graphene dataset using the PBE0 functional, a well-known unscreened hybrid functional68. A test-set mean absolute error (MAE) of 0.458 meV is achieved, indicating that DeepH-hybrid can also predict on PBE0 datasets with sub-meV level accuracy. Supplementary Fig. 6 shows a comparison of DFT-calculated and DeepH-predicted band structures for the test-set structure with the largest MAE, displaying a reasonable match.

Regarding the deep-learning modeling of higher-level electronic structure theories beyond hybrid DFT, the GW approximation may be of great concern, as the GW approximation offers significantly improved description in quasiparticle excitations69. Previous research has proposed several pathways to machine learning GW, including modeling GW self-energy at imaginary frequencies70, quasiparticle spectra from the GW approximation71, etc. As a common practice, quantities in the GW approximation are projected under localized bases for machine learning, allowing them to fit within the DeepH-hybrid framework. Nevertheless, previous methods either predominantly focus on molecular systems or have relatively limited accuracy, arguably due to the non-local nature of the GW approximation. More careful design will be beneficial for deep-learning GW using DeepH-based frameworks in the future.

Methods

Datasets

We use the ABACUS package14,64,65 to carry out hybrid functional calculations with norm-conserving pseudopotentials72 using the NAO basis. The HSE06 functional with Hartree–Fock mixing constant a = 0.25 and screening parameter ω = 0.11 Bohr−1 is applied in all calculations51,73. While full-range hybrid functionals yield problematic results in metals due to the long-range part of the Hartree–Fock exchange74, the HSE functional screens out such contributions, facilitating its use in general solid systems. The energy cutoff for real-space grid is 400 Ry. C6.0-2s2p1d, Mo8.0-3s2p2d and S7.0-2s2p1d NAOs are applied for carbon, molybdenum, and sulfur atoms, respectively, including 13 basis functions with a cutoff radius of 6.0 Bohr for carbon, 19 basis functions with a cutoff radius of 8.0 Bohr for molybdenum and 13 basis functions with a cutoff radius of 7.0 Bohr for sulfur. For monolayer graphene and CNT, dataset is composed of 500 random structures with 5 × 5 graphene supercell. Random structures are generated by introducing random offsets up to 0.1 Å, on each atom about the equilibrium configuration. For bilayer graphene, dataset is composed of 1000 random structures with 4 × 4 supercell of bilayer graphene. In addition to random offsets on each atom, an overall in-plane shift is randomly assigned to each structure of bilayer graphene, and the interlayer distance is randomly sampled with normal distribution with mean 3.408 Å, and standard deviation 0.047 Å, A 9 × 9 × 1 Monkhorst–Pack k-mesh75 is applied for supercells of monolayer and bilayer graphene. The dataset for monolayer MoS2 consists of 500 randomly generated structures, while the dataset for bilayer MoS2 comprises 1000 randomly generated structures. Both datasets include random structures with random offsets up to 0.1 Å on each atom in the 4 × 4 supercell. A random overall interlayer shift is introduced to bilayer MoS2 structures, analogous to the dataset of bilayer graphene. The interlayer distance of bilayer MoS2 is fixed at 2.931 Å. A 5 × 5 × 1 Monkhorst–Pack k-mesh is employed for supercells of monolayer and bilayer MoS2. For the (17, 16) TBG including 3268 atoms/cell studied in Fig. 3d, a Gamma-only calculation is performed by using low-scaling techniques of resolution of identity and prescreening14. The tolerance for constructing auxiliary basis functions was set at 10−4. Screening tolerances for expansion coefficients, Coulomb matrix, and density matrix were set to be 10−4, 1.0, and 10−3, respectively.

Calculation of electric susceptibility

To demonstrate the ability of DeepH-hybrid in computing physical properties, electric susceptibility is computed by using the DFT-hybrid or DeepH-hybrid Hamiltonian together with the HopTB package59 via the formula:

$${\chi }^{ab}=\frac{{e}^{2}}{{\epsilon }_{0}\hslash }\int\frac{{d}^{3}{{{\bf{k}}}}}{{(2\pi )}^{3}} \mathop{\sum}_{n,m}{f}_{nm}\frac{{r}_{nm}^{a}{r}_{mn}^{b}}{{\omega }_{mn}({{{\bf{k}}}})-\omega -i\eta },$$
(2)

where a, b, and c are Cartesian directions, while ϵ0, ℏ, and e represent the vacuum permittivity, the reduced Planck’s constant, and the charge of the electron, respectively. \({\omega }_{mn}({{{\bf{k}}}})=\frac{{E}_{m{{{\bf{k}}}}}-{E}_{n{{{\bf{k}}}}}}{\hslash }\) and fnm = fn(k)−fm(k) are abbreviations for the difference of band energy and Fermi–Dirac occupations of bands n and m at wave vector k, respectively. \({r}_{nm}^{a}\) is the Berry connection, which is defined to be zero when n = m. To ensure the integration over the Brillouin zone remains invariant with respect to the vacuum layer in low-dimensional systems, the displayed χ are multiplied by the cross-sectional area A for quasi-one-dimensional systems or the thickness d of the supercell along the non-periodic direction for quasi-two-dimensional systems. For the CNT studied in Fig. 2d, the periodic direction is defined as the z-axis. A 1 × 1 × 40 k-grid was employed for the Brillouin zone integration. For the twisted bilayer MoS2 studied in Fig. 4, the out-of-plane direction is defined as the z-axis. A 20 × 20 × 1 k-grid is employed for the Brillouin zone integration.