Introduction

The makeup and origins of Earth’s deep and inaccessible interior have long been mysterious. Ever since the detection by seismic tomography of the two antipodal large low shear-wave velocity provinces (LLSVPs)—regions in the lowermost mantle in which the shear-wave velocity is lower than that of the ambient mantle1—their origin has been extensively debated. Although a purely thermal origin of LLSVPs cannot be excluded2, multiple sources of geophysical data indicate that the LLSVPs are thermally hot and should also be chemically distinct3,4,5,6. Whether the LLSVPs derive most or part of their density from a primordial layer of dense materials (such as from the crystallization of magma ocean7 or moon-forming giant impact8) and/or a layer of subducted oceanic crust growing over time, the antiquity of their current morphology into two piles most likely developed at some later point in Earth’s history1. Yet despite great advances in recent decades, many features of the LLSVPs remain enigmatic. There is a great debate about the stability and antiquity of the LLSVPs. In general, there are two end-member interpretations where the LLSVPs are fixed, ancient structures9,10 or dynamic, young structures11,12,13.

Various types of geological data appear to suggest the African LLSVP has been essentially fixed since 200–300 million years ago (Ma) (i.e., supercontinent Pangaea age), including large igneous provinces (LIPs)10, palaeogeography14, and net-characteristics of plate motions15. Some studies have even argued for LLSVP stability back to > 500 Ma10 or even since early in Earth’s history9,16. Alternatively, recent work has challenged LLSVP stability as far back as ca. 200–300 Ma Pangaea age. Numerical modeling of basal mantle structures (BMSs; referring to LLSVPs created in models) parameterized by plate kinematics and thus the mobility of subduction zones at the surface and slabs sinking into the mantle suggest that the lower mantle is more dynamic than previously considered12. Although BMSs are suggested to be very actively dynamic in recent studies, this conclusion is based on imposed plate reconstructions whose accuracy decreases back in time12. Therefore, a fully dynamic approach provides a viable alternative approach.

In this study, we conduct numerical modeling of BMSs to assess their mobility under self-consistent mantle convection with plate-like lithospheric behavior as the top boundary condition. We explore the parameter space that does or does not permit the creation of two antipodal BMSs akin to the areal extent of the LLSVPs. Those results that successfully satisfy such criteria are able to constrain the relative velocity of the BMSs and the ambient mantle, thereby testing the validity of LLSVP stability on 100 million years (Myr) and 1 billion years (Gyr) time scales as both have been proposed by competing models.

Results

Role of plate tectonics in the topology of basal mantle structures

Three-dimensional thermochemical mantle convection models in spherical geometry on the Yin-Yang grid17,18 were conducted with plastic yielding to generate plate boundaries at the top19,20 and an initially even basal layer of dense materials in an attempt to generate BMSs over an evolutionary period of 4.56 Gyrs (comparable to the history of the Earth; “Methods”). As our goal is to investigate the stability time scale of LLSVPs, we first investigate the reaction of the topology of BMSs to plate tectonics by varying the strength of the oceanic lithosphere. We then analyze the mobility of BMSs in an Earth-like model where a Pacific-like subduction girdle and antipodal degree-2 BMSs form.

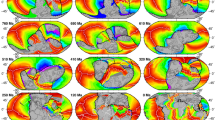
In our models, slabs penetrate into the lower mantle21 and push aside the BMSs. When plastic yielding is taken into account, two antipodal BMSs are split by a great subduction girdle (Fig. 1d), which is consistent with the present-day Earth where the two LLSVPs are separated by the Pacific “ring of fire” of subduction at the surface as well as with previous 3D models12,22. In 2D convection models with plastic yielding, two antipodal slabs could cut the layered BMSs and then push them into two piles22. In our work, we achieve a 3-D Earth-like model with quasi-stationary BMSs that maintain degree-2 structure for about 630 Myrs when yield stress is set to 100 MPa (Fig. 1d).

Fig. 1: Viscosity, basal mantle structures, plumes, and slabs in models with different yield stresses at t = 4.56 Gyr.
figure 1

Viscosity at the surface (columns 1 and 4), basal mantle structures (isosurface of the composition with contour level \(C=0.5\), columns 2 and 5), plumes (isosurface of non-dimensional temperature with contour level \({f}_{{{\rm{p}}}}=0.5\), columns 3 and 6, orange), and slabs (isosurface of non-dimensional temperature with contour level \({f}_{{{\rm{s}}}}=0.1\), columns 3 and 6, blue). Columns 4–6 show the opposite hemisphere of columns 1–3. From row a to row e, the values of yield stress are 30, 50, 70, 100, and 200 MPa with the same buoyancy ratio of 0.26 and chemical viscosity contrast of 10.

Full size image

To evaluate the influence of plate tectonics on BMSs, we vary the yield stress, hence the strength of the oceanic lithosphere from 10–200 MPa, which controls the plate tectonics configuration20. Figure 1 shows snapshots of the surface viscosity, BMSs, plumes, and subduction. In our series of models, the observed planforms can be divided into four groups. (i) Ultra-low yield stress (30 MPa) yields four subduction systems that stir BMSs, and no piles are observed on the CMB. (ii) Low yield stress (50 MPa) yields a triple-junction-like subduction zone that is concentrated in a semi-sphere and cannot migrate because of the hindering of intense upwelling from the margin or interior of the one-pile BMS with high topography. (iii) Intermediate yield stress (70–100 MPa) yields more than one subduction girdle that cuts the BMSs and pushes them into two piles, where the distance between them increases with increasing yield stress. (iv) High yield stress (200 MPa) yields one circular pile that is pushed against by the downwelling. We further find that successful Earth-like models with two antipodal piles covering the CMB with areas of ~ 25% similar to LLSVPs occur in our study within a narrow range of moderate yield stress (90–100 MPa) (Fig. 2).

Fig. 2: CMB area covered by basal mantle structures and the number of basal mantle structures as a function of yield stress at t = 4.56 Gyr.
figure 2

Note that the antipodal two-pile basal mantle structures similar to the LLVSPs occur within a narrow range of medium yield stress (90–100 MPa), and our preferred model (100 MPa) is marked with a star.

Full size image

More sluggish thermochemical LLSVPs than thermal LLSVPs

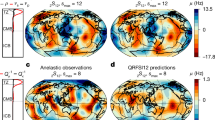
To quantify the mobility of LLSVPs, we calculate the horizontal velocities of BMSs and the ambient mantle in our simulations (Fig. 3). The horizontal velocities of the BMSs are ~ 4 times slower than that of the ambient mantle at the same depth in the lowermost mantle. These sluggish BMSs could be maintained for several hundreds of millions of years (Supplementary Fig. 1). For comparison, we formulate an isochemical convection case to investigate the mobility of purely thermal LLSVPs2. A great subduction girdle akin to the Pacific ring of fire subduction girdle and plume bundles can be obtained with the same yield stress as the thermochemical convection models (Fig. 4a). We define plumes (purely thermal LLSVPs) as the areas of temperature higher than Tp(z) (see “methods”), and find the horizontal velocity of plumes is similar to that of the bulk mantle in the lower mantle (Fig. 4b). Thus, comparing Figs. 4, 3, the mobility of purely thermal LLSVPs is higher than thermochemical LLSVPs.

Fig. 3: 1-D profiles of horizontal velocities of basal mantle structures and the ambient mantles for models with different yield stresses at t = 4.56 Gyr.
figure 3

The averaged mantle horizontal velocity profiles of the basal mantle structures (solid lines), and the ambient mantles (dotted lines) with different yield stress: 30 (orange), 90 ~ 100 (purple), and 200 MPa (green). Gray shadow marks the standard deviation for statistics of 90, 95, and 100 MPa cases. Note that the global average velocity of modern plates is ~ 5 cm yr−1 (ref. 49).

Full size image
Fig. 4: Thermal convection model with yield stress of 100 MPa at t = 4.56 Gyr.
figure 4

a Viscosity at the surface (top row), plumes, and slabs (bottom row). The right column shows the opposite hemisphere of the left column. The plumes and slabs are defined by setting \({f}_{{{\rm{p}}}}\) = 0.5 and \({f}_{{{\rm{s}}}}\) = 0.1, respectively. b Horizontal velocities of plumes and bulk mantle (only the horizontal velocity of thermal plumes in the lower mantle is plotted).

Full size image

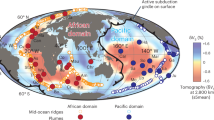
To further clarify such mobility contrast, we calculate the vote maps (Methods) of BMSs and plumes for the preferred thermal and thermochemical models over the last 630 Myrs (Fig. 5). The main parts of the BMSs at the bottom of the mantle remain stable during this period of time, while the margins of BMSs are deformed and migrate depending on the push from the sinking slabs (column 1 of Fig. 5a, b), which is consistent with the temporal evolution of the BMSs (Supplementary Fig. 2). In contrast, plumes in the deep mantle of the thermal model are so mobile that almost none of them can be maintained for such a period of time compared to the BMSs in the thermochemical model (Column 3 of Fig. 5a, b). Our vote maps, therefore, indicate that the thermochemical LLSVPs in the lower mantle are more sluggish in their lateral motion than thermal LLSVPs (Fig. 5a, b). These differences between the thermal and thermochemical models in the deep mantle may also affect the temporal and spatial distributions of plumes in the shallow mantle. Since the roots of these plumes are generally associated with the hot basal mantle structures, the plumes in the shallow mantle are temporally less intermittent and spatially more stationary in the thermochemical model than those in the thermal model (columns 2 and 4 of Fig. 5a, b).

Fig. 5: Vote maps of BMSs and plumes for the thermo-chemical model and plumes for the thermal model with yield stress of 100 MPa in the last 630 Myrs.
figure 5

a Vote maps of BMSs at 2800 km depth and plumes at 300 km depth for the thermo-chemical convection model with a yield stress of 100 MPa in the last 630 Myrs (columns 1 and 2) and vote maps of plumes at 2800 km depth and 300 km depth for the thermal convection model with a yield stress of 100 MPa in the last 630 Myrs (columns 3 and 4). Row 2 shows the views of the opposite hemisphere of Row 1. b The distribution histograms of vote maps of BMSs and plumes for the thermochemical model and plumes for the thermal model.

Full size image

Influence of physical properties of basal mantle structures on model space

The topology of BMSs in our models (i.e., 1, 2, or no piles) is affected by the distribution of the subduction girdle (Fig. 1). However, in turn, the pattern of BMSs may also affect the plate tectonic configuration. We thus adjust the buoyancy ratio, which previous work has shown to be the first-order factor dominating the configuration of BMSs12,18,23 regardless of the vigor of mantle convection to change the pattern of BMSs. We vary the buoyancy ratio (B) from 0.18–0.30, corresponding to the chemical density contrast from 74–124 kg/m3 (Supplementary Fig. 3), which is consistent with the estimate of density anomalies in the lower mantle4, and keep yield stress and chemical viscosity contrast constant (100 MPa and 10, respectively). We find the BMSs are fully entrained by ambient mantle materials, and subduction forms a great-circle girdle in small buoyancy ratio cases (B = 0.18 and 0.20). In large buoyancy ratio cases (B = 0.22, 0.26, and 0.30), subduction also forms a great-circle girdle, but BMSs form in 2 piles with different topographies and shapes. Thus, the adjustment of the buoyancy ratio in large buoyancy ratio cases has effects on the topography of BMSs but limited effects on the position of subduction zones, hence the plate tectonic configuration, and the stability of BMSs (Supplementary Figs. 3, 4).

Tomography study indicates that LLSVPs contain more bridgmanite than the ambient mantle4. MgSiO3 bridgmanite is more viscous than MgO periclase by up to 1000 times24,25. A chemical viscosity contrast of 10 for BMSs in our preferred model can decrease the viscosity difference between BMSs and the ambient mantle because the BMSs are hot and thermally less viscous26. We vary the chemical viscosity contrasts between the BMSs and the ambient mantle from 1–100 to test the influence of chemical viscosity on the pattern of BMSs (Supplementary Fig. 5). With increasing chemical viscosity contrast, the topography of BMSs rises, and the area of BMSs decreases, due to the decreasing efficiency of mantle convection and hence decreasing heat loss efficiency26. When the chemical viscosity contrast is > 30, BMSs form three piles, and the position of subduction changes considerably. BMSs form two piles when the chemical viscosity contrast is < 30. Note that the horizontal velocity of BMSs in these cases remains notably slower than that of the bulk mantle, indicating these BMSs are relatively sluggish (Supplementary Fig. 6).

Discussion

Our modeling exhibiting degree-2 BMSs formed by mantle convection with plate-like lithospheric behavior demonstrates that the mobility of dense BMSs is more than an order of magnitude slower than surface plate motions and also much slower (~ 1/4) than the ambient mantle at the same depth (Fig. 3). The strength of the oceanic lithosphere on Earth ranges from dozens to hundreds of MPa. The maximum yield stress of oceanic lithosphere derived from surface flexures is > 100–200 MPa27. However, the strength of the oceanic lithosphere at plate boundaries can be 15–30 MPa (ref. 28). The area and distribution of plates in previous numerical models with a yield stress of 150 MPa match Earth’s plate layout reasonably well29. The yield stress values used in our models are in this range (between 10 and 200 MPa). Continental lithosphere, whose strength is lower than oceanic lithosphere30, is not included in our models. Given the heterogeneity in the strength of the lithosphere, the reality of Earth’s lithospheric evolution is more complex than our models. Considering the bulk yield stress of continental and oceanic plates, our model should be regarded as an intermediate-strength end-member in Earth’s history.

Such sluggish BMSs provide theoretical reinforcement for the empirical geological data as old as 200–300 Ma that have been linked to the assumed stability of the LLSVPs over this time scale. Our Earth-like model indicates that the velocity of BMSs is ~ 4 times slower than the ambient mantle at the same depth in the lowermost mantle. When the subduction girdle forms and the BMSs are cut by the subduction girdle, the main BMS bodies move very slowly, and mostly only their margins are pushed aside by sinking slabs. The formation process for the degree-2 BMSs is protracted for two reasons. A relatively young subduction girdle formed ~ 1 Gyr ago (Supplementary Fig. 2) and pushed the BMSs to form two piles around their current locations within the following 200 ~ 300 Myrs. Then, the subduction girdle and degree-2 BMSs could be very stable for about 630 Myrs in our model. Geological data suggest that subduction zone locations after 250 Ma can be precisely fitted by a girdle adding an “arm” (Tethyan), and subduction zone locations between 540 and 250 Ma can be fitted by a girdle without an arm31. If we consider the subduction girdle is persistent for 540 Myrs or even longer, the African LLSVP may have formed at least by 380 Ma because a slab takes about 160 Myrs to penetrate the CMB assuming free sinking rates of 3 cm yr−1 in the upper mantle and 2 cm yr−1 in the more viscous lower mantle32. Long-lived stable or sluggish BMSs are also favored by core dynamics studies33,34,35,36,37,38 that suggest the localized mushy zones found at the inner core boundary are related to the long-term stable pattern of mantle convection, especially the degree-2 pattern for hundreds of millions of years.

If the LLSVPs are likely as old as the late Paleozoic–Mesozoic supercontinent Pangaea, the next question is how long they might have existed. Considering the resistance to motion of our sluggish BMSs model, it is easier for slabs to move a slab graveyard (the high-velocity anomaly in tomography) and to deform and shift the margins of BMSs than to push BMSs away (Fig. 5a). The presently elongated African LLSVP might have been reshaped by the circum-Pangaea subduction girdle. The circum-Pangaea subduction girdle was close to approximating a great circle during the Pangaea tenure14 and has since slightly contracted to a present-day small circle ring of fire as the Pacific Ocean shrunk after the Pangaea breakup. We do not observe a degree 1-2-1 planform alternation cycle as has been suggested11,39 (Supplementary Fig. 7). Considering the lesser mobility of thermochemical LLSVPs than purely thermal LLSVPs, the numbers of LLSVPs will increase when the newborn subduction girdle cuts the LLSVPs, and the present antipodal LLSVPs should have been cut by a subduction girdle one time from the age of their formation more easily than thereafter. In this scenario, the LLSVPs could already have formed their degree-2 structure when a circum-supercontinent girdle formed, then deformed and shifted the two BMSs from one supercontinent cycle to the next13. Lastly, an unresolved question is whether a new subduction girdle forms with every supercontinent assembly and whether the newborn subduction girdle cuts the BMSs entirely or not since the thermochemical BMSs are more sluggish in the lower mantle compared to the ambient mantle and may even be preserved in the lower mantle from the early history of the Earth7.

Methods

Thermochemical mantle convection models

We assume an anelastic and compressible fluid with an infinite Prandtl number, and we solve the non-dimensional equations of mass, momentum, heat, and chemical conservation in a 3D spherical shell on the Yin-Yang grid40 using the finite difference/volume code StagYY17. The main model setup used here is similar to that published previously18, and we further take plastic yielding into account to generate plate boundaries19,20. The reference Rayleigh number \({{{\rm{Ra}}}}_{{{\rm{s}}}}\) is expressed as:

$${{{\rm{Ra}}}}_{{{\rm{s}}}}=\frac{{\rho }_{{{\rm{s}}}}g{\alpha }_{{{\rm{s}}}}{\varDelta T}_{{{\rm{s}}}}{D}^{3}}{{\eta }_{0}{\kappa }_{{{\rm{s}}}}},$$
(1)

where \({\rho }_{{{\rm{s}}}}\) the surface density, \(g\) the gravitational acceleration, \({\alpha }_{{{\rm{s}}}}\) the thermal expansivity, \({\varDelta T}_{{{\rm{s}}}}\) the superadiabatic temperature jump, \(D\) the mantle thickness, \({\eta }_{0}\) the surface viscosity and \({\kappa }_{{{\rm{s}}}}\) the surface thermal diffusivity. In this study, \({{{\rm{Ra}}}}_{{{\rm{s}}}}\) is fixed to 1 × 108.

Temperature-, depth-, and composition-dependent viscosity coupled with plastic yielding is used. Meanwhile, we imposed a viscosity jump of 30 at 660 km depth. The viscosity is described fully by

$${\eta }_{{{\rm{eff}}}}=\frac{1}{\frac{1}{\eta \left(T,d,C\right)}+\frac{1}{{\eta }_{{{\rm{Y}}}}}},$$
(2)

with

$$\eta \left(T,d,C\right)={\eta }_{0}\left[1+29{{\rm{H}}}\left(d-660\right)\right]\exp \left[{V}_{{{\rm{a}}}}\frac{d}{D}\right]\exp \left[{E}_{{{\rm{a}}}}\frac{{\varDelta T}_{{{\rm{s}}}}}{T+{T}_{{{\rm{off}}}}}+{K}_{{{\rm{a}}}}C\right],$$
(3)

and

$${\eta }_{{{\rm{Y}}}}=\frac{{\sigma }_{0}+{\dot{\sigma }}_{z}d}{2{\dot{\varepsilon }}_{\Pi }},$$
(4)

where \({\eta }_{{{\rm{Y}}}}\) is the yield viscosity, \({\sigma }_{0}\) the surface yield stress, \({\dot{\sigma }}_{z}\) the yield stress gradient, which is set to 0 to introduce transform faults as suggested by previous study41, and \({\dot{\varepsilon }}_{\Pi }\) the second invariant of the strain rate tensor. H is the Heaviside step function, Va the non-dimensional activation volume, \({E}_{{{\rm{a}}}}\) the non-dimensional activation energy, Toff the offset temperature, which is fixed to \(0.88{\Delta T}_{{{\rm{s}}}}\) to reduce the temperature-induced viscosity variation at the surface, C the composition field, and Ka the parameter controlling the chemical viscosity contrast \({\Delta \eta }_{{{\rm{C}}}}=\exp \left({K}_{{{\rm{a}}}}\right)\). No prescribed plate boundaries are imposed and the yield stress helps to generate plate-like behavior at the top of the ___domain. To avoid numerical problems, the viscosity is truncated between 10−3 and 105 of the reference viscosity.

Initial condition and model setup

To introduce basal mantle structures (BMSs), we initially set up an even dense layer above CMB whose thickness is 0.06 (173 km in dimensional unit)42,43. The grid resolution is 64 × 192 × 64 × 2 with grid refinement at both the surface, the bottom, and at 660 km depth (the ringwoodite phase change to bridgmanite). The boundary conditions of the bottom and the top are free-slip, and the temperature of the top is set to 0.12 (300 K), and the bottom is 1.5 (3750 K) (Supplementary Fig. 8a). The model includes both internal and basal heating. The internal heating rate is 7.08 × 10−12 W/kg, as suggested in ref. 44. Given the LLSVPs possibly enriched in heat-producing elements, we assume the heating rate of the BMSs is ~ 7 times that of the ambient mantle materials26,45. The superadiabatic thermal boundary layers are located at the surface and the bottom, the thickness of which is ~ 87 km. Random temperature perturbation is implemented at both boundaries. The curvature of the shell f defined as the ratio between the radius of the core and the total radius is set to 0.55 corresponding to the Earth’s value. We use a tracer ratio method to track the compositional field46. Two types of tracers are used to represent the compositional field, where 0 corresponds to the ambient mantle, and 1 corresponds to BMS material. The number of total tracers of all models is 24 million, corresponding to about 15 tracers per cell, which is sufficient for simulating material entrainment46. The composition field is calculated from the ratio between BMS tracers and total tracers. The initial thickness of the BMS material is 0.06 (corresponding to 173 km), and the initial volume of the BMS material is ~ 3% of the mantle42,43. The density contrast between BMSs and the ambient mantle is controlled by the buoyancy ratio:

$$B=\frac{{\Delta \rho }_{{{\rm{c}}}}}{{\alpha }_{{{\rm{s}}}}{\rho }_{{{\rm{s}}}}{\Delta T}_{{{\rm{s}}}}},$$
(5)

where \({\Delta \rho }_{{{\rm{c}}}}\) is the density contrast between BMSs and the ambient mantle.

Detection of plumes and slabs

To determine plumes and subduction zones in our models, we calculate threshold temperatures of plumes and slabs following those of ref. 47, which assumes that a point is located within a plume (subduction zone) if the temperature at this point is higher (lower) than:

$${T}_{{{\rm{p}}}}\left(d\right)={T}_{{{\rm{avg}}}}\left(d\right)+{f}_{{{\rm{p}}}}\left({T}_{\max }\left(d\right)-{T}_{{{\rm{avg}}}}\left(d\right)\right),$$
(6)
$${T}_{{{\rm{s}}}}\left(d\right)={T}_{{{\rm{avg}}}}\left(d\right)+{f}_{{{\rm{s}}}}\left({T}_{\min }\left(d\right)-{T}_{{{\rm{avg}}}}\left(d\right)\right),$$
(7)

where \({T}_{{{\rm{avg}}}}\left(d\right)\),\(\,{T}_{\max }\left(d\right)\) and \({T}_{\min }\left(d\right)\) are the horizontally averaged, maximum, and minimum temperature at depth d, and \({f}_{{{\rm{p}}}}\) and \({f}_{{{\rm{s}}}}\) are fixed to 0.5 and 0.1, respectively, in this study.

Horizontal velocities of BMSs and plumes

The horizontal velocities of BMSs and plumes are defined as the root-mean-square averaged velocity within the BMSs and plumes at each depth by

$${V}_{{{{\rm{H}}}}_{{{\rm{BMSs}}}}}\left(d\right)=\sqrt{\frac{{\int }_{C > 0.5}{{{{\bf{V}}}}_{{{\rm{H}}}}(d,\theta,\varphi )}^{2}{dA}}{{\int }_{C > 0.5}{dA}}},$$
(8)
$${V}_{{{{\rm{H}}}}_{{{\rm{Plumes}}}}}\left(d\right)=\sqrt{\frac{{\int }_{T > {T}_{{{\rm{p}}}}(d)}{{{{\bf{V}}}}_{{{\rm{H}}}}(d,\theta,\varphi )}^{2}{dA}}{{\int }_{T > {T}_{{{\rm{p}}}}(d)}{dA}}},$$
(9)

where \({{{\bf{V}}}}_{{{\rm{H}}}}=({V}_{\theta },{V}_{\varphi })\) is the horizontal velocity at the point of \((d,\theta,\varphi )\), \(\theta\) colatitude, \(\varphi\) longitude, dA infinitesimal area. The temporal variation of the horizontal velocity of BMSs is calculated at each time step by

$${V}_{{{{\rm{H}}}}_{{{\rm{BMSs}}}}}=\sqrt{\frac{{\int }_{C > 0.5}{{{{\bf{V}}}}_{{{\rm{H}}}}(d,\theta,\varphi )}^{2}{dV}}{{\int }_{C > 0.5}{dV}}},$$
(10)

where dV is infinitesimal volume.

Vote maps of BMSs and plumes

To quantify the stability of BMSs, we calculate vote maps of BMSs following a similar strategy of ref. 48. For a given depth of the composition field, a binary threshold of 0 (no BMSs) or 1 (BMSs) is applied to every latitude-longitude pixel in each time slice within the period of time we selected, followed by a pixel-wise summation of all N time slices within the period selected. The pixels of the vote map hence take values between 0 and N. We then divided the value of each pixel on the vote map by N to get a normalized vote map on which all pixels take values between 0 and 1. A value of 0 on a vote map indicates no BMSs have existed in this pixel during the whole selected period of time, while a value of 1 indicates that BMSs have existed in this pixel at some point during the whole selected period of time, and a value between 0 and 1 indicates the normalized time length that BMSs have existed in this pixel compared to the selected period of time. Vote maps of plumes are calculated by using the same method in the temperature field.