Factors governing $${\rm H}_{3}^{+}$$ formation from methyl halogens and pseudohalogens

Stamm, Jacob; Priyadarsini, Swati S.; Sandhu, Shawn; Chakraborty, Arnab; Shen, Jun; Kwon, Sung; Sandhu, Jesse; Wicka, Clayton; Mehmood, Arshad; Levine, Benjamin G.; Piecuch, Piotr; Dantus, Marcos

doi:10.1038/s41467-024-55065-5

Download PDF

Article
Open access
Published: 06 January 2025

Factors governing ${\rm H}_{3}^{+}$ formation from methyl halogens and pseudohalogens

Nature Communications volume 16, Article number: 410 (2025) Cite this article

4428 Accesses
1 Citations
112 Altmetric
Metrics details

Subjects

Abstract

The formation of ${\rm H}_{3}^{+}$ following the double ionization of small organic compounds via a roaming mechanism, which involves the generation of H₂ and subsequent proton abstraction, has recently garnered significant attention. Nonetheless, a cohesive model explaining trends in the yield of ${\rm H}_{3}^{+}$ characterizing these unimolecular reactions is yet to be established. We report yield and femtosecond time-resolved measurements following the strong-field double ionization of CH₃X molecules, where X = OD, Cl, NCS, CN, SCN, and I. These measurements, combined with double-ionization-potential equation-of-motion coupled-cluster ab initio calculations used to determine the geometries and energetics of CH₃X²⁺ dications, are employed to identify the key factors governing the formation of ${\rm H}_{3}^{+}$ in certain doubly ionized CH₃X species and its absence in others. We also carry out ab initio molecular dynamics simulations to obtain detailed microscopic insights into the mechanism, yields, and timescales of ${\rm H}_{3}^{+}$ production. We find that the excess relaxation energy released after double ionization of CH₃X molecules combined with substantial geometrical distortion that favors H₂ formation prior to proton abstraction boost the generation of ${\rm H}_{3}^{+}$. Our study provides useful guidelines for examining alternative sources of ${\rm H}_{3}^{+}$ in the universe.

Direct tracking of H₂ roaming reaction in real time

Article Open access 06 August 2024

Formation of H₃⁺ from ethane dication induced by electron impact

Article Open access 09 November 2020

Exclusive roaming mechanism for the Cl + C₂H₂→C₂H + HCl bimolecular reaction

Article Open access 19 March 2025

Introduction

The role of the trihydrogen cation (${\rm H}^{+}_{3}$) as a catalytic protonator of atoms and molecules, along with its capacity for radiative cooling, renders it one of the most important species in interstellar chemistry^1,2,3. The formation of ${{\mbox{H}}}_{3}^{+}$ ions within the interstellar medium proceeds via the Hogness and Lunn mechanism⁴, ${\,{\rm{H}}}_{2}^{+}+{{{\rm{H}}}}_{2}\to {{\mbox{H}}}_{3}^{+}+{{\rm{H}}}$, where ${\rm H}_{2}^{+}$ is generated through the ionization of molecular hydrogen by cosmic rays. The resulting ${{\mbox{H}}}_{3}^{+}$ species are highly acidic and exhibit enhanced reactivity by acting as universal proton donors to other species (M) through the proton-hop reaction ${{\rm{M}}}+{{\rm{H}}}_{3}^{+}\to {{{\rm{H}}}}_{2}+{{{\rm{MH}}}}^{+}$¹. Furthermore, reactions involving ${\rm H}_{3}^{+}$ display very high rate constants² that can be attributed to its ability to polarize and attract neutral molecules, even at large distances⁵. The abundance of ${\rm H}_{3}^{+}$ in the interstellar medium and its key role as the initiator of ion-molecule reactions highlight the importance of understanding the mechanisms, timescales, and yields of ${\rm H}_{3}^{+}$ production.

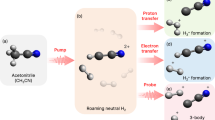
In recent years, various small molecules, including CH₃X, where X is a halogen or pseudohalogen, have been identified as potential sources of ${\rm H}_{3}^{+}$ in interstellar and star-forming environments⁶. Upon double ionization, the three C–H bonds in CH₃X may be cleaved and three new bonds between the detached H atoms may form, leading to the formation of ${\rm H}_{3}^{+}$. Given that equal numbers of bonds are broken and formed, this unimolecular reaction was initially thought to proceed via a concerted pathway in which the three H atoms in CH₃X²⁺ coalesce and ${\rm H}_{3}^{+}$ is ejected by Coulombic repulsion^7,8. However, it was observed that in methanol, the mechanism of ${\rm H}_{3}^{+}$ formation involves a three-step process, where the double ionization of CH₃OH generates a neutral H₂ which then roams the CHOH²⁺ dication before abstracting a proton from it⁹. In this case, femtosecond time-resolved strong-field ionization and photoion-photoion coincidence measurements on CH₃OH and its isotopologues, accompanied by ab initio molecular dynamics (AIMD) simulations, revealed two distinct routes for the production of ${\rm H}_{3}^{+}$ depending on which proton is abstracted from CHOH²⁺ by H₂, including a faster ∼ 100 fs process, in which the H atom attached to carbon is attacked, and a slower ∼ 250 fs one, when the abstracted proton originates from the hydroxyl group⁹ (for the follow-up studies of ${\rm H}_{3}^{+}$ formation from CH₃OH and other alcohols, see refs. ^10,11,12). It was also demonstrated that the faster pathway, corresponding to the deprotonation of carbon by the roaming H₂, as shown in the lower half of Fig. 1, is the dominant process in CH₃OH. In this study, we argue that a similar process applies to the ${\rm H}_{3}^{+}$-producing doubly ionized CH₃X molecules in which X lacks hydrogen atoms. It should also be noted that this way of generating ${\rm H}_{3}^{+}$ from CH₃X molecules closely resembles the Hogness and Lunn mechanism, as both involve the abstraction of a proton by a neutral H₂ molecule. In support of this observation, a recent experiment applying a two-color femtosecond laser field to D₂—D₂ dimers confirmed a 139 fs timescale for ${{\rm{{D}}}}_{3}^{+}$ production¹³, which matches the timeframe of ${\rm H}_{3}^{+}$ formation from the doubly ionized methanol via the pathway shown in Fig. 1, suggesting the possibility of a similar roaming mechanism in the interstellar space.

**Fig. 1: The roaming model for the production of ${\rm H}_{3}^{+}$ following the strong-field double ionization of methanol.**

Another CH₃X species that has been identified as a source of ${\rm H}_{3}^{+}$ in the interstellar clouds is methyl chloride¹⁴. Previous experiments on the strong-field ionization of CH₃Cl^7,15 have focused on the kinetic energy release and anisotropy of various fragmentation channels of the CH₃Cl²⁺ dication, but insights into the timescale and mechanism of ${\rm H}_{3}^{+}$ formation from methyl chloride remain largely unexplored. Computational studies have predicted a variety of pathways for producing the trihydrogen cation from CH₃Cl, including the mechanism in which ${\rm H}_{3}^{+}$ emerges from ionization of the Rydberg state of CH₃Cl⁺ based on the lower appearance energy of the CCl⁺/${\rm H}_{3}^{+}$ pair compared to the double ionization of methyl chloride¹⁶ or the concerted process without involving the roaming of H₂⁸, but the most recent calculations combining high-level quantum chemistry and molecular dynamics¹⁷ suggest the roaming mechanism similar to Fig. 1. Thus, there is a growing need to understand the intimate details of the molecular picture behind ${\rm H}_{3}^{+}$ formation following the double ionization of CH₃Cl and other methyl halides and pseudohalides. A number of other observations are worth exploring as well. For example, complementary cross-section measurements at 70 eV electron ionization of the CH₃X molecules with X = F, Br, and I have shown that similarly to CH₃Cl, ${\rm H}_{3}^{+}$ forms readily from CH₃Br, but only trace amounts of the trihydrogen cation have been found in the case of the doubly ionized CH₃F and CH₃I species¹⁸. This pattern, which remains consistent across different experimental studies, including two-color laser field ionization¹⁹, suggests that one has to look for factors other than electronegativities of the halogen atoms to explain ${\rm H}_{3}^{+}$ formation from methyl halogens. The behavior of methyl pseudohalides upon double ionization is not well understood either. For instance, as shown in the early photoionization and electron impact mass spectrometry measurements involving several small organic molecules²⁰, the doubly ionized methyl cyanide produces negligible amounts of ${\rm H}_{3}^{+}$ despite the high electronegativity of the CN group. A comprehensive explanation of the varied yields of ${\rm H}_{3}^{+}$ from methyl halogens and pseudohalogens remains elusive to this date.

In this article, we report femtosecond time-resolved measurements following the strong-field double ionization of several CH₃X molecules, where X is a halogen (Cl and I) or a pseudohalogen (OH, represented by OD, NCS, CN, and SCN). In the ultrafast experiments carried out in this work, the double ionization is triggered by electron rescattering²¹, as opposed to being induced by radiation or collision with high-energy light nuclei and electrons, which are the dominant processes in the interstellar medium. In electron rescattering, a departing electron, after tunnel-ionization of the molecule by the electric field of the laser, accelerates back toward the molecule when the field reverses its direction. The returning electron can gain tens of eV of kinetic energy, sufficient to remove the second electron from the molecule within the optical cycle of the laser pulse (∼ 2.66 fs). In principle, the returning electron can populate several electronic states of the resulting CH₃X²⁺ dications, but the previous studies on the doubly ionized methanol, reported in refs. ¹¹, ²², suggest that the excited manifolds of the CH₃X²⁺ species, including singlet as well as triplet states, do not significantly impact the ${\rm H}_{3}^{+}$ formation dynamics investigated in this work. The results reported in the present article point to the same conclusion. While we chose tunnel-ionization and electron rescattering to generate CH₃X²⁺ dications in our experiments, which are illustrated in the upper half of Fig. 1 using methanol as an example, the dynamics of ${\rm H}_{3}^{+}$ formation following the double ionization of CH₃X species via a roaming mechanism examined in the present study are not influenced by the electric field of the laser pulse once H₂ is formed. This also means that they do not depend on the specific method by which the CH₃X²⁺ dications are created. To gain further insights into the yields and timescales of ${\rm H}_{3}^{+}$ formation from the various methyl halides and pseudohalides under investigation and to obtain information about the low-lying electronic states of the CH₃X²⁺ dications involved, we augment the ultrafast time-resolved measurements reported in this study with the high-level double-ionization-potential (DIP) equation-of-motion (EOM) coupled-cluster (CC) ab initio computations with up to 3-hole–1-particle (3h-1p)^{23,24,25,26,27,28,29} and 4-hole–2-particle (4h-2p)^28,29 correlations on top of the CC treatment^30,31,32 with singles and doubles (CCSD)^33,34 of the parent CH₃X species, abbreviated as DIP-EOMCC(3h-1p) and DIP-EOMCC(4h-2p), respectively, and the AIMD simulations employing the complete-active-space self-consistent-field (CASSCF) approach³⁵ calibrated to the DIP-EOMCC data. While our experimental measurements and theoretical models, despite their state-of-the-art nature, have inherent limitations, their complementary blend provides a detailed understanding of the microscopic factors that explain the formation of ${\rm H}_{3}^{+}$ by some doubly ionized CH₃X species and its absence in the others, alongside the underlying molecular mechanisms, timescales, and yields, which may offer guidelines for examining small organic compounds as alternative sources of the trihydrogen cation in the interstellar medium.

Results

Experimental

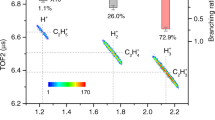
The ${\rm H}_{3}^{+}$ regions of the time-of-flight (TOF) mass spectra of all CH₃X compounds with X = OD, Cl, NCS, CN, SCN, and I are shown in Fig. 2. For the CH₃OD, CH₃Cl, and CH₃NCS molecules, which after double ionization produce the trihydrogen cation, the ${\rm H}_{3}^{+}$ signal in the mass spectrum appears as a doublet due to the forward and backward trajectories of the ${\rm H}_{3}^{+}$ ion resulting from the Coulomb repulsion of the ${{{\rm{CH}}}}_{3}{{{\rm{X}}}}^{2+}\to {{{\rm{CX}}}}^{+}+{{{\rm{H}}}}_{3}^{+}$ reaction products. This is because out of a set of randomly oriented CH₃X molecules interacting with a laser, those with the dipole moments aligned parallel to the electric field of the laser are preferentially ionized, resulting in ${\rm H}_{3}^{+}$ ions that move toward or away from the detector. The ${\rm H}_{3}^{+}$ ions moving directly toward the detector arrive earlier, whereas those moving away arrive with a delay, after being turned around by the static electric field of the mass spectrometer. The forward and backward ${\rm H}_{3}^{+}$ peaks seen in Fig. 2 are sharp because the ${{{\rm{CH}}}}_{3}{{{\rm{X}}}}^{2+}\to {{{\rm{CX}}}}^{+}+{{{\rm{H}}}}_{3}^{+}$ dissociation processes that produce them are faster than rotations of the CH₃X²⁺ dications (see Results: Timescales of ${\rm H}_{3}^{+}$ formation for further details). The presence of separate peaks due to the forward and backward trajectories of ${\rm H}_{3}^{+}$ ions resulting from the Coulomb repulsion of the positively charged CX⁺ and ${\rm H}_{3}^{+}$ species in our TOF mass spectra for the CH₃OD, CH₃Cl, and CH₃NCS compounds implies that ${\rm H}_{3}^{+}$ formation in our strong-field ionization experiments originates from the dication states of the parent CH₃X molecules rather than from their singly ionized counterparts. We used the deuterated form of methanol, CH₃OD, where the ¹H atom in the OH group is replaced by its ²H isotope, to ensure that the trihydrogen cation produced in our double ionization experiments originated from the three hydrogens of the methyl group. This gives rise to the HD⁺ signal from singly ionized methanol, which appears at m/z = 3 in Fig. 2 between the ${{{\rm{H}}}}_{3}^{+}$ forward and backward peaks. As shown in refs. ^{9, 36}, the contribution of HD⁺ to the forward and backward peaks for CH₃OD is expected to be small. We confirmed this by performing separate measurements on CD₃OH which demonstrated that the contribution of HD⁺ to the forward and backward peaks, determined by forming a ratio of the HD⁺ yield normalized to all dication channels in CD₃OH to the ${\rm H}_{3}^{+}$ yield normalized to all dication channels in CH₃OD, is ∼ 9%.

**Fig. 2: The m/z = 3 regions of the mass spectra obtained in this work.**

To determine the ${\rm H}_{3}^{+}$ yield for each of the three CH₃X compounds that produce it, shown in Table 1, we first normalized the corresponding mass spectrum to the integral of all ion signals attributed to dication channels. We then fit each of the two peaks in the ${\rm H}_{3}^{+}$ doublet to a Gaussian, integrated the outer halves of both peaks (the shaded regions in Fig. 2), and doubled the outcome. We only integrated the outer halves of each doublet to avoid contamination of the measured ${\rm H}_{3}^{+}$ yields by low kinetic energy features. We normalized the yields to all ion signals attributed to dication channels to correct for slight changes in pressure and/or intensity that may occur when going from one molecule to another, although these variables were carefully controlled in our experiments. In presenting the ${\rm H}_{3}^{+}$ yields resulting from the above procedure, we normalized them to the maximum one obtained for CH₃OD, which was set to 1.0. This provided us with the relative ${\rm H}_{3}^{+}$ yields used in our later theoretical analysis. Furthermore, by normalizing the ${\rm H}_{3}^{+}$ yields relative to all dication channels to CH₃OD, we counterbalanced the impact of the less controllable factors, such as the relative population levels of the singlet and triplet manifolds of the CH₃X²⁺ species produced in our double ionization experiments or the competing fragmentation channels, on the ${\rm H}_{3}^{+}$ yields reported in Table 1, making them and, most importantly, the trends they follow less sensitive to all such factors. To illustrate the effect of the number of ion channels on yield determination, we also show in Table 1 the relative yields of ${\rm H}_{3}^{+}$ normalized to all positive ion channels. We only included cations in normalizing the ${\rm H}_{3}^{+}$ yields since our TOF system is configured for the detection of positively charged species. Our relative ${\rm H}_{3}^{+}$ yields match the results of the previous measurements using 70 eV electron impact ionization¹⁸.

Table 1 Normalized ${\rm H}_{3}^{+}$ yields from the CH₃X compounds with X = OD, Cl, and NCS, which after double ionization produce the trihydrogen cation

Full size table

Ab initio electronic structure calculations

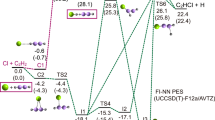
To provide insights into the molecular mechanisms leading to the observed trends in ${\rm H}_{3}^{+}$ yields and the geometrical and energetic factors that affect them, we performed high-level ab initio quantum chemistry calculations for the low-lying electronic states of the neutral and doubly ionized CH₃X species examined in this work, details of which are provided in Methods: Electronic structure calculations. We did not consider higher-lying states since, as shown in ref. ¹¹ using methanol as an example, the probability of ${\rm H}_{3}^{+}$ formation is the highest when a given dicationic species is in its lowest singlet state. The selected bond lengths, which are crucial for our analysis, characterizing the equilibrium geometries of the CH₃X molecules with X = OH, Cl, NCS, CN, SCN, and I in their ground electronic states and the minima on the lowest singlet potential energy surfaces of the corresponding CH₃X²⁺ dications resulting from our most accurate CC and DIP-EOMCC computations, are shown in Table 2. The complete information about the geometries of the CH₃X molecules included in our experiments and the CH₃F species, which was only considered in computations, and the low-lying states of the corresponding CH₃X²⁺ dications obtained in all of our CC and DIP-EOMCC calculations, along with the associated electronic energies, can be found in Supplementary Information (see Supplementary Data). For the three H atoms bonded to the carbon in the CH₃X and CH₃X²⁺ species, H(2) and H(3) designate hydrogens that may coalesce in the CH₃X²⁺ dication and subsequently approach the remaining H atom on carbon, labeled as H(1), to form ${\rm H}_{3}^{+}$ (see Fig. 1). The vertical and adiabatic double ionization energies associated with the low-lying states of the CH₃X²⁺ dications relevant to our discussion, obtained in our most accurate DIP-EOMCC calculations, are provided in Fig. 3. Our CC and DIP-EOMCC geometries of the CH₃Cl, CH₃Cl²⁺, CH₃F, and CH₃F²⁺ species and double ionization energies corresponding to the lowest singlet states of CH₃Cl²⁺ and CH₃F²⁺ are in very good agreement with the CASSCF-based second-order multireference perturbation theory calculations reported in ref. ¹⁷.

Table 2 Comparison of the key internuclear distances, in Å, characterizing the doubly ionized CH₃X molecules with X = OH, Cl, NCS, CN, SCN, and I in their lowest singlet states, which influence ${\rm H}_{3}^{+}$ formation, with their counterparts in the neutral CH₃X species obtained in the most accurate CC and DIP-EOMCC computations carried out in this study (see Methods: Electronic structure calculations for the details)

Full size table

**Fig. 3: Energy level diagrams and molecular geometries associated with the double ionization of CH₃X species.**

As shown in Fig. 3, the neutral CH₃OH, CH₃NCS, and CH₃SCN molecules in their ground electronic states are characterized by the C_s, C₁, and C_s symmetries, respectively, while the remaining CH₃Cl, CH₃CN, and CH₃I species are all C_3v-symmetric. Our computations demonstrate that the doubly ionized CH₃OH, CH₃NCS, and CH₃SCN molecules in their lowest-energy singlet states relax to the respective adiabatic minima, adopting a C_s symmetry. As can be seen in Table 2, in the case of CH₃OH²⁺ and CH₃NCS²⁺, the resulting geometrical reorganization elongates the C–H(2) and C–H(3) bonds while bringing the H(2) and H(3) atoms close together, so that the distances between them are almost as small as in the isolated H₂ molecule (0.741 Å³⁷). This should be contrasted with the behavior of CH₃SCN, where the H(2)–H(3), C–H(2), and C–H(3) distances do not change much when the geometries of the ground-state CH₃SCN molecule and the CH₃SCN²⁺ dication in its lowest singlet state are compared with each other.

The situation with the CH₃Cl, CH₃CN, and CH₃I molecules is more complex. These three species, in their neutral forms, possess C_3v-symmetric ground electronic states in which all C–H bonds have the same length. Following vertical double ionization, prior to any geometric relaxation, the three lowest electronic states of each of the resulting dications include a spatially nondegenerate triplet of the A₂(C_3v) symmetry and a doubly degenerate singlet that belongs to the E irreducible representation of C_3v (see Fig. 3). The two components of the doubly degenerate singlet consist of a multi-configurational state mixing two closed-shell determinants, in which one of the two highest-occupied molecular orbitals (HOMOs) of the neutral species remains occupied by two electrons and the other one is empty, and the open-shell singlet state where each of the two degenerate HOMOs of the neutral system is singly occupied. The two degenerate HOMOs are also singly occupied in the lowest triplet state. Upon the geometric relaxation after double ionization, the lowest-energy triplet states of CH₃Cl²⁺, CH₃CN²⁺, and CH₃I²⁺ remain C_3v-symmetric, having structures similar to their neutral counterparts. In particular, the C–H bond lengths do not change much and the hydrogen atoms remain separated by rather large distances (see Supplementary Data, especially Supplementary Table 1). However, the lowest doubly degenerate singlets of these dications undergo Jahn–Teller (JT) distortion that removes the degeneracy and lowers their symmetry to C_s, splitting the ¹E(C_3v) singlets into the ${}^{1}{{{\rm{A}}}}^{{\prime} }({{{\rm{C}}}}_{{{\rm{s}}}})$ and ${}^{1}{{{\rm{A}}}}^{{\prime\prime} }({{{\rm{C}}}}_{{{\rm{s}}}})$ states. While the geometrical distortions and the JT splitting in CH₃I²⁺ are minimal, so that the ${}^{1}{{{\rm{A}}}}^{{\prime} }({{{\rm{C}}}}_{{{\rm{s}}}})$ and ${}^{1}{{{\rm{A}}}}^{{\prime\prime} }({{{\rm{C}}}}_{{{\rm{s}}}})$ states, having three practically equidistant C–H bonds and large H–H separations, remain nearly degenerate and the A₂(C_3v)-symmetric triplet remains the ground state, the analogous changes in the CH₃Cl²⁺ and CH₃CN²⁺ species are massive. Indeed, as shown in Fig. 3, the ${}^{1}{{{\rm{A}}}}^{{\prime} }({{{\rm{C}}}}_{{{\rm{s}}}})$ states of the CH₃Cl²⁺ and CH₃CN²⁺ dications lower their energies so much, compared to the multi-configurational closed-shell components of the respective E(C_3v)-symmetric singlets from which they originate, that they become the nondegenerate, predominantly single-reference, ground states. The ${}^{1}{{{\rm{A}}}}^{{\prime\prime} }({{{\rm{C}}}}_{{{\rm{s}}}})$ states resulting from the JT splitting of the E(C_3v)-symmetric singlets of CH₃Cl²⁺ and CH₃CN²⁺, which retain the open-shell singlet character upon geometrical relaxation, lower their energies too, but not enough to go below the A₂(C_3v)-symmetric triplet states. Similarly to the triplet states, they do not undergo significant structural changes compared to the neutral CH₃Cl and CH₃CN molecules either (see Supplementary Data and Supplementary Table 1). As a result, the ordering of the adiabatic minima on the lowest potential energy surfaces of the CH₃Cl²⁺ and CH₃CN²⁺ dications becomes ${}^{1}{{{\rm{A}}}}^{{\prime} }({{{\rm{C}}}}_{{{\rm{s}}}}){ < \,}^{3}{{{\rm{A}}}}_{2}({{{\rm{C}}}}_{3{{\rm{v}}}}){ < \,}^{1}{{{\rm{A}}}}^{{\prime\prime} }({{{\rm{C}}}}_{{{\rm{s}}}})$. The stabilization of the C_s-symmetric structures of CH₃Cl²⁺ and CH₃CN²⁺ in their ground electronic states and the distortion in nuclear geometries compared to their neutral parents are so significant that the main features of the ground-state geometries of these two dications relevant to ${\rm H}_{3}^{+}$ production are similar to those characterizing the lowest singlet states of CH₃OH²⁺ and CH₃NCS²⁺. Indeed, as shown in Table 2, and in analogy to the lowest singlet states of CH₃OH²⁺ and CH₃NCS²⁺, the H(2)–H(3) distances in the ground-state CH₃Cl²⁺ and CH₃CN²⁺ structures are close to that in the isolated H₂ molecule and the C–H(2) and C–H(3) bonds are considerably elongated compared to the neutral CH₃Cl and CH₃CN species. This should be contrasted with CH₃I²⁺, where the H–H distances in the lowest singlet and triplet states are similar to those in neutral CH₃I, preventing two of the three hydrogen atoms from coalescing and disabling the roaming mechanism of ${\rm H}_{3}^{+}$ production examined in this study.

One might think that the CH₃X systems that undergo significant structural changes upon double ionization, which bring the H(2) and H(3) atoms bonded to the carbon close together while elongating the C–H(2) and C–H(3) bonds, favor ${\rm H}_{3}^{+}$ generation via the roaming mechanism shown in Fig. 1, but these structural changes are not the only factors influencing the yield of ${\rm H}_{3}^{+}$. For example, as shown in Table 2, the H(2)–H(3) distance in the lowest singlet state of CH₃CN²⁺ is quite close to that in the isolated H₂ (and much shorter than in neutral CH₃CN) and the C–H(2) and C–H(3) bonds substantially elongate upon the double ionization of CH₃CN, and yet we do not see an appreciable ${\rm H}_{3}^{+}$ signal in our experiments involving CH₃CN (cf. Fig. 2 and Table 1). As noted in the Introduction, only trace amounts of the trihydrogen cation were found in the double ionization experiments involving CH₃F¹⁸ despite the fact that CH₃F²⁺ has a lot in common with its CH₃Cl²⁺ analog, which readily forms ${\rm H}_{3}^{+}$ (as pointed out in Discussion, our AIMD simulations show no evidence for ${\rm H}_{3}^{+}$ production from the CH₃F²⁺ species either). Indeed, the effects of JT distortion in the CH₃F²⁺ and CH₃Cl²⁺ species are similar, resulting in the ${}^{1}{{{\rm{A}}}}^{{\prime} }({{{\rm{C}}}}_{{{\rm{s}}}})$-symmetric ground states and short, nearly identical, H(2)–H(3) distances (see the geometry of the CH₃F²⁺ dication in its lowest-energy ${}^{1}{{{\rm{A}}}}^{{\prime} }({{{\rm{C}}}}_{{{\rm{s}}}})$ state and the electronic state ordering in CH₃F²⁺ in Supplementary Data, especially Supplementary Fig. 1 and Supplementary Tables 1 and 2), but unlike in CH₃Cl²⁺, no ${\rm H}_{3}^{+}$ is produced from CH₃F²⁺. For all these reasons, in addition to examining the relationship between the geometrical changes in the CH₃X systems upon double ionization and the observed yield of ${\rm H}_{3}^{+}$, we also considered other factors that might affect the production of trihydrogen cation from the CH₃X²⁺ species. Thus, as further elaborated on in Methods: Electronic structure calculations, we computed the adiabatic relaxation energies

$$\Delta {E}_{{{\rm{rlx}}}}=\Delta {E}_{{{\rm{vert}}}}-\Delta {E}_{{{\rm{adiab}}}},$$

(1)

where ΔE_vert and ΔE_adiab are the vertical and adiabatic double ionization energies corresponding to the lowest singlet states of the CH₃X²⁺ dications, and the dissociation energies associated with the H₂ formation from the doubly ionized CH₃X molecules, defined as

$$\Delta {E}_{{{\rm{diss}}}}=E({{{\rm{CHX}}}}^{2+})\,+\,E({{{\rm{H}}}}_{2})\,-\,E({{{\rm{CH}}}}_{3}{{{\rm{X}}}}^{2+}),$$

(2)

where E(CHX²⁺) and E(CH₃X²⁺) are the energies of the CHX²⁺ and CH₃X²⁺ species in their lowest singlet states, respectively, and E(H₂) is the ground-state energy of a neutral H₂. ΔE_rlx provides a measure of the excess energy available to the CH₃X²⁺ dications at their adiabatic minima, which may drive the separation of a neutral H₂ from the CHX²⁺ moiety and facilitate ${\rm H}_{3}^{+}$ generation via a roaming mechanism shown in Fig. 1. ΔE_diss estimates the energy required to liberate H₂ from the parent CH₃X²⁺ ion. We also computed potential energy profiles for the ${{{\rm{CH}}}}_{3}{{{\rm{X}}}}^{2+}\to {{{\rm{CX}}}}^{+}+{{{\rm{H}}}}_{3}^{+}$ reactions initiated by double ionization of the CH₃X species with X = OH, Cl, and NCS that produce ${\rm H}_{3}^{+}$ in our experiments, finding out that the adiabatic relaxation energies ΔE_rlx characterizing the CH₃OH²⁺, CH₃Cl²⁺, and CH₃NCS²⁺ dications are sufficiently large to overcome the barriers associated with the transition states on their lowest singlet potentials and release neutral H₂ molecules that can subsequently roam their CHX²⁺ companions, abstracting protons from them to form ${\rm H}_{3}^{+}$ (see Supplementary Discussion and Supplementary Fig. 4). As shown in Discussion, the H(2)–H(3) distances combined with the ΔE_rlx and ΔE_diss values characterizing the doubly ionized CH₃X species and information about the ${{{\rm{CH}}}}_{3}{{{\rm{X}}}}^{2+}\to {{{\rm{CX}}}}^{+}+{{{\rm{H}}}}_{3}^{+}$ reaction profiles, including barrier heights associated with the final ${{{\rm{CHX}}}}^{2+}+{{{\rm{H}}}}_{2}\to {{{\rm{CX}}}}^{+}+{{{\rm{H}}}}_{3}^{+}$ proton abstraction steps, can be used to explain why some CH₃X species form ${\rm H}_{3}^{+}$ while others do not and rationalize the observed ${\rm H}_{3}^{+}$ ion yields.

Timescales of ${\rm H}_{3}^{+}$ formation

For each compound, we also studied the ${\rm H}_{3}^{+}$ formation time using a technique called disruptive probing, as outlined in Methods: Experimental details³⁸. In short, we split the laser pulse into a strong pump (5 × 10¹⁴ W/cm²) and a weak probe (9.5 × 10¹³ W/cm²). By changing the delay between these two pulses with a variable delay stage, the weak probe can disrupt the formation of some ions in the mass spectra, leading to an exponential decay and recovery in the ion yields as a function of pump-probe delay. The timescale of formation of each ion seen in the mass spectrum, including ${\rm H}_{3}^{+}$, can be determined by fitting the corresponding pump-probe delay-dependent ion yield to the function

$$P(t,{\tau }_{1},{\tau }_{2})=A{e}^{-{t}^{2}/{s}^{2}}+{P}_{1}(t,{\tau }_{1})+{P}_{2}(t,{\tau }_{2}),$$

(3)

where

$${P}_{i}(t,{\tau }_{i})={A}_{i}{e}^{-t/{\tau }_{i}}\left[1+{{\rm{erf}}}\left(\frac{t}{s}-\frac{s}{2{\tau }_{i}}\right)\right],\,\,i=1,2,$$

(4)

and t is a pump-probe time delay. The first term on the right-hand side of Eq. (3) describes the dependence of the ion yield on the Gaussian pump pulse, whereas the second and third terms are solutions of the differential rate equation described in ref. ³⁸ that accounts for changes in the populations of ion states by Gaussian pump pulses. In the case of the pump-probe experiments reported in the present study, we need two types of such solutions, P₁(t, τ₁) characterized by time constant τ₁ for a decay (τ_decay) of the ion signal and P₂(t, τ₂) using time constant τ₂ for the signal’s rise (τ_rise). The parameters A in Eq. (3) and A₁ and A₂ in Eq. (4) are the respective amplitude factors and s is related to the full width at half maximum pulse duration τ_FWHM through the expression ${\tau }_{{{\rm{FWHM}}}}=2s\sqrt{\ln 2}$.

To obtain information about the time-resolved dynamics of ${\rm H}_{3}^{+}$ formation for each of the three CH₃X compounds that produce the trihydrogen cation in measurable amounts, i.e., CH₃OD, CH₃Cl, and CH₃NCS, the peak area of the doublet assigned to ${\rm H}_{3}^{+}$ in the corresponding mass spectrum was integrated as a function of pump-probe delay. The resulting time-resolved yields of ${\rm H}_{3}^{+}$ from CH₃OD, CH₃Cl, and CH₃NCS, shown in Fig. 4, were normalized such that the ion yield at negative pump-probe delays is 1.0 and the minimum is 0.0. We could not perform the analogous analysis for the remaining CH₃X species examined in this study since they do not generate enough ${\rm H}_{3}^{+}$ to obtain time-resolved data with sufficient signal-to-noise ratio (cf. Fig. 2 and Table 1).

**Fig. 4: Pump-probe delay dependent ${\rm H}_{3}^{+}$ yields.**

From the time-resolved ${\rm H}_{3}^{+}$ yields in Fig. 4, we see a large spike at the pump-probe delay t = 0. The presence of this spike is a consequence of the intensities of the pump and probe pulses combining to give an increased ionization efficiency within the focal volume. Shortly after the double ionization of the CH₃X compounds by the pump pulse, the resulting CH₃X²⁺ dications are far from equilibrium and can easily be disrupted by the probe pulse. This leads to a depletion of the ${\rm H}_{3}^{+}$ ion yield at short positive pump-probe delay times t because, as explained in ref. ³⁸, the probe pulse can promote the transient CH₃X²⁺ system to some other electronic state that results in a reduced ${\rm H}_{3}^{+}$ yield or does not produce ${\rm H}_{3}^{+}$ at all. For example, the probe may suppress the return of the roaming H₂ to the CHX²⁺ moiety, preventing ${\rm H}_{3}^{+}$ formation. For each CH₃X²⁺ molecule, a resonant single or multiphoton transition induced by the probe has a complicated relationship with the reaction coordinate as the H₂ moiety changes orientation and distance from the CHX²⁺ species during the roaming process. Averaging over the ensemble of CH₃X²⁺ dications excited by the pump pulse washes out these specific details, leaving only a measure of the fraction of the ensemble that has yet to form ${\rm H}_{3}^{+}$. As the pump-probe delay becomes larger and the fraction of the roaming ensemble that has undergone the ${{{\rm{CHX}}}}^{2+}+{{{\rm{H}}}}_{2}\to {{{\rm{CX}}}}^{+}+{{{\rm{H}}}}_{3}^{+}$ reaction increases, the yield of ${\rm H}_{3}^{+}$ ions begins to grow, eventually leveling off because the ${\rm H}_{3}^{+}$ ions that have already been formed are not appreciably disturbed by the probe pulse. Averaging over the ensemble’s stochastic roaming dynamics results in an exponential signal dependence proportional to the reaction time, as observed here and in other direct measurements of roaming reactions^9,10,39,40. Interestingly, the doubly ionized CH₃OD generates the most ${\rm H}_{3}^{+}$ (Table 1), while having the shortest time for ${\rm H}_{3}^{+}$ formation when compared to CH₃Cl and CH₃NCS (Fig. 4).

Ab initio molecular dynamics simulations

To further investigate the timescale and mechanism of ${\rm H}_{3}^{+}$ formation, AIMD simulations were conducted for a few representative CH₃X²⁺ species in their lowest singlet states using the CASSCF approach to generate electronic energies and energy gradients (see Methods: Ab initio molecular dynamics simulations for the details). Exploring single-state dynamics on the lowest-energy singlet potentials of the CH₃X²⁺ species is sufficient to provide useful insights that help us understand the outcomes of our experiments since, as already alluded to above (cf. the beginning of Results: Ab initio electronic structure calculations), the probability of ${\rm H}_{3}^{+}$ formation from the doubly ionized methanol is the highest in its lowest singlet state, rapidly dropping down when higher excited states are considered¹¹. At the same time, states belonging to triplet manifolds of the CH₃X²⁺ dications are not conducive to the release of a neutral H₂ that could subsequently roam and abstract a proton from the CHX²⁺ moiety to form ${\rm H}_{3}^{+}$ ²². Of all the molecules that we examined with AIMD, ${\rm H}_{3}^{+}$ only forms from the doubly ionized CH₃OH and CH₃Cl, and, to a much lesser extent, CH₃CN. Consistent with the experiment, from the trajectories obtained in our AIMD calculations, the doubly ionized CH₃OH produced the most ${\rm H}_{3}^{+}$ (9% of the trajectories, counting only those where all three hydrogens in ${\rm H}_{3}^{+}$ originate from the methyl group), followed by CH₃Cl (6% of the trajectories). In the case of CH₃CN²⁺, the calculated ${\rm H}_{3}^{+}$ yield was much smaller than those obtained for CH₃OH²⁺ and CH₃Cl²⁺ (only 1% of the trajectories). This matches our experimental findings too, as the doubly ionized CH₃CN molecule does not produce an appreciable ${\rm H}_{3}^{+}$ signal in the mass spectrum under the conditions of our ionization experiments (cf. Fig. 2). Furthermore, formation of the H₂ precursor, which in the roaming mechanism explored in this work leads to ${\rm H}_{3}^{+}$, rarely occurred in CH₃CN²⁺ trajectories. In agreement with our experiments, none of the trajectories obtained for CH₃SCN²⁺ produced ${\rm H}_{3}^{+}$. Consistent with the earlier experimental¹⁸ and computational¹⁷ studies, no trajectories obtained for the doubly ionized CH₃F molecule resulted in the formation of ${\rm H}_{3}^{+}$ either.

To understand the different timescales of ${\rm H}_{3}^{+}$ formation, trajectories that resulted in ${\rm H}_{3}^{+}$ were further analyzed. On average, ${\rm H}_{3}^{+}$ formed faster from CH₃OH²⁺ (∼ 208 fs) than from CH₃Cl²⁺ (∼ 343 fs), which agrees with previous AIMD simulations^9,11,17 and our experimental observations. Interestingly, in a majority of the trajectories that led to ${\rm H}_{3}^{+}$, the neutral H₂ fragment formed very fast (in ∼ 30 fs) and then roamed the CHX²⁺ moiety for most of the remaining time prior to proton abstraction. Snapshots of one of the AIMD trajectories resulting in the formation of ${\rm H}_{3}^{+}$ from the doubly ionized CH₃Cl are shown in Fig. 5. Supplementary Movies 1 and 2 show representative trajectories leading to ${\rm H}_{3}^{+}$ formation from CH₃Cl²⁺ and CH₃OH²⁺. Supplementary Movie 3 shows an example of a trajectory obtained for CH₃F²⁺, where the liberated H₂ fragment becomes positively charged and subsequently dissociates, so that the final products are the CH₂F⁺ moiety and a proton.

**Fig. 5: Snapshots of an AIMD trajectory of the doubly ionized CH₃Cl resulting in ${\rm H}_{3}^{+}$ formation.**

Discussion

In our ultrafast time-resolved double ionization experiments on a series of methyl halides and pseudohalides, we observed a progressive decrease in the yield of ${\rm H}_{3}^{+}$ from CH₃OD to CH₃Cl to CH₃NCS, while no appreciable amount of this ion was detected in CH₃CN, CH₃SCN, and CH₃I (see Table 1 and Fig. 2). Moreover, as shown in Fig. 4, the process of forming ${\rm H}_{3}^{+}$ from the doubly ionized CH₃X species was the fastest for CH₃OD, followed by CH₃NCS and CH₃Cl, with the time of ${\rm H}_{3}^{+}$ formation from CH₃Cl being the longest. Based on our experiments and computations, the following three conditions must be simultaneously met in order for the doubly ionized CH₃X species to have the potential of generating ${\rm H}_{3}^{+}$ via a roaming mechanism illustrated in Figs. 1 and 5:

(i)
Geometrical distortion following double ionization should result in two substantially elongated C–H bonds compared to the neutral CH₃X molecule.
(ii)
The H(2)–H(3) internuclear distance characterizing the equilibrium geometry of a given CH₃X²⁺ dication in its lowest singlet electronic state should be close to the H–H bond length in an isolated H₂ molecule.
(iii)
The adiabatic relaxation energy ΔE_rlx characterizing the CH₃X²⁺ dication, as defined by Eq. (1), should exceed the dissociation energy ΔE_diss, Eq. (2), associated with the fragmentation of the doubly ionized CH₃X species into CHX²⁺ and H₂, and be large enough to overcome the barrier(s) along the ${{{\rm{CH}}}}_{3}{{{\rm{X}}}}^{2+}\to {{{\rm{CX}}}}^{+}+{{{\rm{H}}}}_{3}^{+}$ potential energy profile, including that corresponding to the ${{{\rm{CHX}}}}^{2+}+{{{\rm{H}}}}_{2}\to {{{\rm{CX}}}}^{+}+{{{\rm{H}}}}_{3}^{+}$ proton abstraction by the roaming H₂, but it cannot be so large that other reactive mechanisms and other ways of decomposing CH₃X²⁺ become dominant.

The C–H bond lengths characterizing the neutral and doubly ionized CH₃X molecules in their lowest singlet states, summarized in Table 2, and the H(2)–H(3) distances and the ΔE_rlx and ΔE_diss values characterizing the CH₃X²⁺ dications, reported in Fig. 6, along with the ${{{\rm{CH}}}}_{3}{{{\rm{X}}}}^{2+}\to {{{\rm{CX}}}}^{+}+{{{\rm{H}}}}_{3}^{+}$ (X = OH, Cl, and NCS) reaction profiles shown in Supplementary Fig. 4, demonstrate that of all CH₃X compounds considered in our experiments, only CH₃OH, CH₃Cl, and CH₃NCS satisfy all three conditions listed above in their entirety. This is in perfect agreement with our observations, where CH₃OD, CH₃Cl, and CH₃NCS are the only three molecules of the six CH₃X species considered in our double ionization experiments that produce ${\rm H}_{3}^{+}$ (the experimental ${\rm H}_{3}^{+}$ yields normalized to CH₃OH²⁺, taken from Table 1, are included in Fig. 6 as well). In fact, as shown in Fig. 6, the sequence of the experimental ${\rm H}_{3}^{+}$ yields CH₃OH > CH₃Cl > CH₃NCS closely mirrors the difference between the adiabatic relaxation and dissociation energies, ΔE_rlx and ΔE_diss, respectively. This difference is the largest for CH₃OH, which produces the highest amount of ${\rm H}_{3}^{+}$, smaller for CH₃Cl, resulting in a correspondingly lower yield, and the smallest for CH₃NCS, characterized by the least production of ${\rm H}_{3}^{+}$.

**Fig. 6: Comparison of the parameters that are most relevant to explaining the trends in ${\rm H}_{3}^{+}$ yields.**

None of the remaining CH₃X compounds included in our experiments satisfy all three conditions (i)–(iii), which means that they should not generate ${\rm H}_{3}^{+}$ upon double ionization, and, as shown in Fig. 2, they do not. The CH₃SCN and CH₃I systems violate each of the three conditions. CH₃CN, which meets conditions (i) and (ii), violates condition (iii), which states that ΔE_rlx must be greater than ΔE_diss. Clearly, the energy released by the geometrical relaxation of the CH₃X²⁺ dication, measured by the difference of the vertical and adiabatic double ionization energies defining ΔE_rlx, must be large enough to liberate a neutral H₂, without which the roaming and proton abstraction mechanism of ${\rm H}_{3}^{+}$ production shown in Figs. 1 and 5 cannot be initiated, and CH₃CN²⁺ does not satisfy this requirement. This demonstrates that the elongation of two of the three C–H bonds and two of the three hydrogens bonded to the carbon in CH₃X²⁺ coming close, while important, do not suffice; one also has to meet the condition ΔE_rlx > ΔE_diss. Interestingly, despite satisfying conditions (i) and (ii) and the ΔE_rlx > ΔE_diss requirement, which is part of condition (iii) (see Supplementary Tables 1 and 2 for the C–H and H(2)–H(3) distances characterizing the neutral and doubly ionized CH₃F molecule and the ΔE_rlx and ΔE_diss values obtained in our best DIP-EOMCC calculations for CH₃F²⁺), the CH₃F species that we studied only computationally does not form ${\rm H}_{3}^{+}$ upon double ionization. As mentioned in Results: Ab initio molecular dynamics simulations, and in agreement with the older experimental¹⁸ and more recent computational¹⁷ studies, none of the trajectories obtained in our AIMD simulations for CH₃F²⁺ produced ${\rm H}_{3}^{+}$. In this case, as shown in Supplementary Fig. 3, the adiabatic relaxation energy ΔE_rlx, i.e., the energy released by the geometrical relaxation of CH₃F²⁺ after double ionization of CH₃F, is much higher than in the remaining CH₃X²⁺ species included in our experiments and, as a result, redistributed very differently than in the CH₃OH²⁺, CH₃Cl²⁺, and CH₃NCS²⁺ dications that form ${\rm H}_{3}^{+}$. This is illustrated by Supplementary Movie 3, which shows a typical trajectory obtained in our AIMD simulations for CH₃F²⁺, where the liberated, positively charged, H₂ fragment dissociates and the final products are CH₂F⁺ and a proton. It may be worth noticing that the adiabatic relaxation energy ΔE_rlx resulting from our most accurate DIP-EOMCC computations for the CH₃F²⁺ dication, reported in Supplementary Table 2 and Supplementary Fig. 3, is large enough to dissociate both H₂ and ${{{\rm{H}}}}_{2}^{+}$, and we plan to study the significance of this finding further in the future work, but we can already observe that CH₃F²⁺ is the only CH₃X²⁺ species considered in the present study which has this property. In a small number of trajectories, the liberated H₂ fragment, having sufficiently large energy available to it, escaped the system, preventing ${\rm H}_{3}^{+}$ formation as well. Once again, this is consistent with condition (iii), which allows such a scenario if the adiabatic relaxation energy ΔE_rlx is high enough, which is the case when CH₃F²⁺ is examined.

As explained in Results and Methods, the mechanism of ${\rm H}_{3}^{+}$ formation from the doubly ionized CH₃X species that emerges from the above conditions (i)–(iii), in which the neutral H₂ fragment resulting from a geometrical distortion of the CH₃X²⁺ dication roams CHX²⁺, abstracting a proton from it, was confirmed and further examined using AIMD simulations. AIMD simulations have limitations, which in our case are the relatively small number and limited duration of the computed trajectories and the limited quality of the CASSCF potential surfaces on which we had to rely (see Methods: Ab initio molecular dynamics simulations). It is also very difficult to precisely model the stochastic nature of the roaming dynamics examined in our experiments, discussed in Results: Timescales of ${\rm H}_{3}^{+}$ formation. Nevertheless, our calculated yields and timescales of ${\rm H}_{3}^{+}$ formation are in qualitative agreement with the experimental observations. The analysis of the AIMD trajectories shows that the timescale of ${\rm H}_{3}^{+}$ formation is related to the ability of the roaming H₂ to appropriately align itself relative to the CHX²⁺ fragment. From the trajectories resulting from our AIMD simulations, such as that shown in Fig. 5 or those visualized by Supplementary Movies 1 and 2, for a substantial portion of time prior to the formation of ${\rm H}_{3}^{+}$, a neutral H₂ roams the CHX²⁺ moiety before orienting itself in a suitable edge-on configuration facing the hydrogen of CHX²⁺, which facilitates the completion of the ${{{\rm{CHX}}}}^{2+}+{{{\rm{H}}}}_{2}\to {{{\rm{CX}}}}^{+}+{{{\rm{H}}}}_{3}^{+}$ proton abstraction step (molecular structures corresponding to these edge-on configurations can also be seen in the ${{{\rm{CH}}}}_{3}{{{\rm{X}}}}^{2+}\to {{{\rm{CX}}}}^{+}+{{{\rm{H}}}}_{3}^{+}$ reaction profiles shown in Supplementary Fig. 4). The easier it is for the H₂ and CHX²⁺ fragments to find this configuration, the faster the timescale of ${\rm H}_{3}^{+}$ formation becomes. This is reflected in our AIMD computations which demonstrate that the neutral H₂ roaming the CHCl²⁺ fragment in the doubly ionized CH₃Cl species explores a much larger portion of the phase space, when searching for a suitable alignment with CHCl²⁺, than the H₂ roaming CHOH²⁺ in CH₃OH²⁺. As a result, the average timescale of ${\rm H}_{3}^{+}$ formation from the doubly ionized CH₃Cl species seen in our experiments and AIMD simulations is longer than in the CH₃OH case (see Fig. 4, Results: Ab initio molecular dynamics simulations, and Supplementary Movies 1 and 2). Based on the above observation that the H₂ and CHX²⁺ fragments have to align in a very specific configuration to enable ${\rm H}_{3}^{+}$ formation, one might speculate that larger adiabatic relaxation energy of a given doubly ionized CH₃X molecule should lead to a faster exploration of the phase space and, thus, a shorter time needed to produce ${\rm H}_{3}^{+}$, but the results in Figs. 4 and 6 show that there is no direct correlation between the ΔE_rlx values characterizing the CH₃X²⁺ dications and the timescales of ${\rm H}_{3}^{+}$ formation from these ions. This agrees with the recent computational study of the CH₃X systems with X = F, Cl, and Br¹⁷.

Finally, an interesting pattern emerges when we compare the molecular orbitals obtained in the restricted Hartree–Fock (RHF) calculations for the CH₃X molecules and the corresponding CH₃X²⁺ dications that produce ${\rm H}_{3}^{+}$. This is illustrated in Fig. 7 using the neutral CH₃OH and CH₃Cl species and the corresponding dications at the respective equilibrium geometries as examples. In the neutral CH₃Cl molecule, the two degenerate HOMOs exhibit bonding and antibonding characteristics with respect to the H(2) and H(3) atoms involved in H₂ formation. The same is true when the nondegenerate HOMO − 1 and HOMO of the neutral CH₃OH are examined. According to our DIP-EOMCC computations, the dominant process defining the double ionization of the CH₃OH and CH₃Cl species is the removal of two electrons from the highest-energy occupied orbital that has the antibonding H₂ character. This makes the orbital that binds the two hydrogens of H₂ the HOMO of the respective dication, bringing the H(2) and H(3) atoms close together, almost as in the isolated H₂ molecule, facilitating its liberation and initiating the roaming mechanism shown in Figs. 1 and 5.

**Fig. 7: Highest-energy occupied orbitals of methyl chloride, methanol, and their dications.**

In conclusion, we reported highly accurate yield and femtosecond time-resolved measurements following the strong-field double ionization of the CH₃X molecules with X = OD, Cl, NCS, CN, SCN, and I, along with the ab initio quantum chemistry and AIMD computations. The goal was to obtain a detailed understanding of the microscopic factors that govern the production of ${\rm H}_{3}^{+}$ via a roaming mechanism in which a neutral H₂ liberated from the CH₃X²⁺ dication abstracts a proton from the CHX²⁺ moiety. By combining state-of-the-art experiments and computations, we provided deep insights into the molecular mechanism of ${\rm H}_{3}^{+}$ formation from the doubly ionized CH₃X species, which allowed us to explain the observed yields and timescales and determine geometric and energetic conditions that must be met in order for ${\rm H}_{3}^{+}$ to form. The results reported in this work may be used to predict the behavior of methyl halides and pseudohalides upon strong-field double ionization and help future studies of alternative sources of ${\rm H}_{3}^{+}$ in the universe. They also lead to interesting new questions. One such question is the generality of the geometrical and energetic conditions (i)–(iii) laid down in Discussion, i.e., to what extent these three conditions apply to other organic compounds of astrophysical significance, such as hydrocarbons^41,42,43,44 and longer-chain alcohols^10,45, which may produce ${\rm H}_{3}^{+}$ as well. Our preliminary examination of the doubly ionized ethane and ethene using the same CC and DIP-EOMCC methodologies as those employed in our calculations for the CH₃X systems, which are analyzed in greater detail in the Supplementary Discussion section of Supplementary Information, and our earlier studies of ethanol^10,45 suggest that our conditions (i)–(iii) may apply to organic compounds outside the CH₃X family, although additional factors may have to be considered as well. We will investigate to what extent these three conditions developed in the context of examining ${\rm H}_{3}^{+}$ formation from the doubly ionized methyl halides and pseudohalides apply to other organic compounds in future work.

Methods

Experimental details

We employed the disruptive probing technique for the synchronous monitoring of the ultrafast time-resolved product yields induced by strong-field ionization³⁸. Our experimental setup features a regeneratively amplified Ti:sapphire laser system as the ionization source, which produces 35 fs pulses at a central wavelength of ∼ 800 nm and operates at a repetition rate of 1 kHz. The pulses were compressed using a Multiphoton Intrapulse Interference Phase Scan (MIIPS)⁴⁶, which measures all orders of spectral phase distortions and compensates them using a pulse shaper (MIIPS-HD) with a spatial light modulator (640 × 800, Hamamatsu). Following compression, the pulses were split into a strong pump and a weak probe, with intensities of 5 × 10¹⁴ W/cm² and 9.5 × 10¹³ W/cm², respectively, using a beam splitter. The pump pulses used in this work are sufficiently intense to doubly ionize the CH₃X molecules, and they are somewhat more intense than those employed in ref. ³⁸, potentially populating several electronic states of the CH₃X²⁺ dications, but this does not have a significant effect on the outcome of our experiments. The ${\rm H}_{3}^{+}$ formation dynamics via a roaming mechanism considered in the present study proceeds mainly on the lowest singlet states of the CH₃X²⁺ species¹¹, which means that any pump pulse providing enough energy to doubly ionize the molecules of interest suffices. For yield measurements, the probe pulse was blocked, allowing only the pump pulse to interact with the sample. The time delay between the pump and probe pulses was controlled using an optical delay line equipped with a programmable translation stage capable of nanometer-level precision control. The laser pulses were focused inside a Wiley-McLaren TOF mass spectrometer by a gold-coated concave focusing mirror with f = 300 mm. At the focus, the pump and probe pulses reached their peak intensities, which were calibrated by measuring the Ar²⁺/Ar⁺ ion yield ratios⁴⁷.

The ionization potentials of the compounds under investigation span a range of approximately 9–12 eV, which corresponds to an average Keldysh parameter γ of 0.4 under our laser conditions⁴⁸. It is well-known that γ < 1 suggests tunnel ionization as the dominant process, where the timescale of classical ionization is faster than the optical cycle. On the other hand, γ > 1 signifies that the ionization spans multiple optical cycles, indicative of multiphoton ionization. The average γ value of 0.4 in our experiments points to the tunneling regime, implying that the electric field is strong enough to ionize the molecules within a single optical cycle.

The CH₃OD, CH₃Cl, CH₃NCS, CH₃CN, CH₃SCN, and CH₃I samples, used without further purification, were degassed and loaded into the TOF chamber as a room-temperature effusive beam through a needle valve. The static pressure inside the vacuum chamber was maintained below 1 × 10⁻⁵ Torr during data acquisition. Upon closing the needle valve, the vacuum pressure quickly dropped to the baseline pressure of 5 × 10⁻⁸ Torr, which ensures fast sample refresh. The positively charged ions formed in the interaction volume were sent to a Chevron dual microchannel plate detector (RM Jordan) by a + 2168 V repeller plate and a + 1080 V extractor plate separated by 10 mm. Ion signals generated at the microchannel plate detector were digitized using an oscilloscope (LeCroy WaveRunner 610Zi, 1 GHz) and transferred to a computer for further processing and analysis.

Electronic structure calculations

To enhance our understanding of the experimental findings, we performed a series of high-level ab initio quantum chemistry calculations which shed light on the geometrical, energetic, and other factors that influence the mechanisms and yields of ${\rm H}_{3}^{+}$ formation following the strong-field double ionization of the methyl halides and pseudohalides examined in this work. As is normally done, all of our electronic structure calculations, including those for methanol, which in our experiments was represented by its deuterated CH₃OD form, were performed using masses of atomic nuclei that correspond to the most abundant isotopes since isotopic substitution has no effect on electronic properties. We started by optimizing the ground-state equilibrium geometries of the closed-shell neutral CH₃X (X = OH, Cl, NCS, CN, SCN, I, and F) molecules using the CCSD approach^33,34. Then, in order to obtain the desired information about the electronic states of the CH₃X²⁺ dications involved in our strong-field double ionization experiments and, to enrich our discussion of the behavior of the CH₃X systems upon double ionization, of CH₃F²⁺, we computed vertical double ionization energies of all studied CH₃X species at their respective CCSD-optimized geometries using high-level methods belonging to the DIP-EOMCC hierarchy^{23,24,25,26,27,28,29}. For the CH₃X systems with the smaller X = OH, Cl, and F groups, we used both the state-of-the-art DIP-EOMCC(4h-2p) approach^28,29 and its more economical DIP-EOMCC(3h-1p) counterpart^{23,24,25,26,28,29}. In the case of the remaining CH₃X molecules with the larger X = NCS, CN, SCN, and I fragments, we utilized DIP-EOMCC(3h-1p). The same DIP-EOMCC methods were applied to determine the minima on the ground and low-lying excited-state potential energy surfaces of the CH₃X²⁺ species, which allowed us to obtain information about the adiabatic double ionization energies associated with the respective dicationic states and, more importantly, the energies released upon geometrical relaxation of the doubly ionized CH₃X molecules to their respective equilibrium structures. We chose the particle-nonconserving DIP-EOMCC methodology in our computations since it is particularly well suited for an accurate description of the many-electron systems that are formally obtained by removing two electrons from their closed-shell parents (which themselves were treated by a highly correlated CCSD level) while relaxing the remaining electrons after double ionization. Furthermore, the DIP-EOMCC methods, including the DIP-EOMCC(3h-1p) and DIP-EOMCC(4h-2p) approaches used in our calculations, offer several advantages over the conventional particle-conserving CC^30,31,32 and EOMCC^49,50,51,52 treatments of open-shell species employing unrestricted or restricted open-shell reference determinants, such as rigorous spin and symmetry adaptation of the calculated electronic states and the ability to describe singlet and triplet manifolds of the doubly ionized species in a well-balanced manner.

The DIP-EOMCC computations for the CH₃X²⁺, CHX²⁺, and CX⁺ ions and the preceding CCSD calculations for their closed-shell CH₃X, CHX, and CX⁻ parents, needed to set up the respective DIP-EOMCC eigenvalue problems, in addition to the aforementioned geometry optimizations for the CH₃X molecules, were performed using the routines described in refs. ^{28,29,53, 54}, which are part of the GAMESS software package^55,56,57. In constructing the relevant wave functions, all CCSD and DIP-EOMCC computations relied on the RHF molecular orbitals of the CH₃X, CHX, and CX⁻ species and the correlation-consistent basis sets, including the cc-pVDZ and cc-pVTZ bases for H, C, N, F, O, S, and Cl atoms^58,59, as implemented in GAMESS, with the additional tight d functions for S and Cl taken from ref. ⁶⁰, and cc-pVTZ-PP^61,62, taken from the EMSL Basis Set Exchange⁶³, for iodine. In all post-RHF calculations, the core orbitals correlating with the 1s shells of the C, N, F, and O atoms and the 1s, 2s, and 2p shells of the S and Cl atoms were kept frozen. For the heavier I atom, the 28 inner-shell electrons ([Ar]3d¹⁰) were replaced by the relativistic effective core potential of Peterson et al.^61,62 and the remaining 25 valence electrons were described by the cc-pVTZ-PP basis set. All of our geometry optimizations were initially carried out without imposing any symmetry constraints, but, once the minima on the relevant potential energy surfaces were found and a given species had symmetry higher than C₁, which was the case for all systems examined in this work other than CH₃NCS, we reoptimized the resulting structures using the appropriately chosen symmetrized Cartesian coordinates adapted to the point group symmetries of the molecules of interest. To confirm that all of our optimized geometries are minima on the respective potential energy surfaces, we determined the corresponding harmonic vibrational frequencies, which were real in each studied case.

The Cartesian coordinates defining all geometries of the CH₃X and CH₃X²⁺ species optimized in our CCSD (all CH₃X molecules), DIP-EOMCC(3h-1p) (all CH₃X²⁺ dications), and DIP-EOMCC(4h-2p) (CH₃OH²⁺, CH₃Cl²⁺, and CH₃F²⁺) calculations, along with the corresponding total electronic energies, can be found in Supplementary Data. In presenting the selected bond lengths in Table 2, which are important for the material included in Results and the follow-up analysis in Discussion, characterizing the optimized geometries of the CH₃X molecules with X = OH, Cl, NCS, CN, SCN, and I in their ground electronic states and the minima on the lowest singlet potential energy surfaces of the corresponding CH₃X²⁺ dications, we use the data obtained in the most accurate CCSD (neutral CH₃X molecules), DIP-EOMCC(4h-2p) (CH₃OH²⁺ and CH₃Cl²⁺), and DIP-EOMCC(3h-1p) (CH₃NCS²⁺, CH₃CN²⁺, CH₃SCN²⁺, and CH₃I²⁺) calculations performed in this work in which we utilized the cc-pVTZ basis set for H, C, N, O, S, and Cl (with additional tight d functions on S and Cl) and the cc-pVTZ-PP basis for iodine. The same applies to the vertical and adiabatic double ionization energies of the CH₃OH, CH₃Cl, CH₃NCS, CH₃CN, CH₃SCN, and CH₃I molecules reported in Fig. 3 and the geometries of the lowest singlet and triplet states of the CH₃X²⁺ species with X = F, Cl, CN, and I and their ground-state CH₃X parents shown in Supplementary Table 1 (the computational methodologies applied to CH₃F and CH₃F²⁺ were exactly the same as those used for the neutral and doubly ionized CH₃OH and CH₃Cl molecules).

Among the quantities that are useful in our theoretical analyses (other than the geometries and energies of the neutral and doubly ionized CH₃X molecules) are the adiabatic relaxation energies ΔE_rlx characterizing the CH₃X²⁺ dications, shown in Figs. 3 and 6, Supplementary Figs. 1–4, and (for X = F only) Supplementary Table 2 and defined by Eq. (1), and the dissociation energies ΔE_diss associated with the fragmentation of the doubly ionized CH₃X species into CHX²⁺ and H₂ prior to ${\rm H}_{3}^{+}$ formation, Eq. (2), reported in Fig. 6, Supplementary Fig. 3, and Supplementary Table 2. In our most accurate calculations presented in Figs. 3 and 6, Supplementary Fig. 3, and Supplementary Table 2, the vertical and adiabatic double ionization energies entering the definition of ΔE_rlx were calculated at the DIP-EOMCC(4h-2p)/cc-pVTZ level of theory for X = OH, Cl, and F and the DIP-EOMCC(3h-1p)/cc-pVTZ approach (using cc-pVTZ-PP for I atom) for the remaining CH₃X²⁺ dications. The energies of the CHX²⁺ and CH₃X²⁺ species in their lowest singlet states entering the definition of ΔE_diss were determined using the DIP-EOMCC(3h-1p)/cc-pVDZ theory level for all CH₃X²⁺ and CHX²⁺ dications except CH₃I²⁺ and CHI²⁺, which were treated with DIP-EOMCC(3h-1p)/cc-pVTZ (cc-pVTZ-PP for I atom). To be consistent in our calculations of the energies that appear on the right-hand side of Eq. (2), the energy of the H₂ molecule entering the definition of ΔE_diss was computed using the CCSD/cc-pVDZ approach when the X = OH, Cl, NCS, CN, SCN, and F systems were considered and CCSD/cc-pVTZ in the X = I case (determining the equilibrium H–H distance in H₂ at the respective CCSD/cc-pVDZ or CCSD/cc-pVTZ level using GAMESS). We note that the CCSD calculation for H₂, which has only two electrons, is equivalent to an exact, full configuration interaction, computation.

In addition to the above characteristics of the CH₃X²⁺ ions, we calculated potential energy profiles for the ${{{\rm{CH}}}}_{3}{{{\rm{X}}}}^{2+}\to {{{\rm{CX}}}}^{+}+{{{\rm{H}}}}_{3}^{+}$ reactions following double ionization of the CH₃X molecules with X = OH, Cl, and NCS, along with the corresponding ${{{\rm{CH}}}}_{3}{{{\rm{X}}}}^{2+}\to {{{\rm{CHX}}}}^{ 2 +}+{{{\rm{H}}}}_{2}$ dissociation asymptotes relevant to the roaming mechanism examined in the present study (see Supplementary Fig. 4). In the case of the CH₃X²⁺, CHX²⁺, and CX⁺ ions, we used the DIP-EOMCC(3h-1p)/cc-pVDZ approach, whereas the CH₃X, H₂, and ${\rm H}_{3}^{+}$ molecules were handled with CCSD/cc-pVDZ (again using additional tight d functions for S and Cl atoms). These calculations allowed us to demonstrate that the doubly ionized CH₃OH, CH₃Cl, and CH₃NCS species have enough energy to liberate molecular hydrogen, which is a key step in the roaming mechanism considered in this work, and to overcome the barriers for ${\rm H}_{3}^{+}$ formation.

The details of our preliminary CC and DIP-EOMCC computations for the doubly ionized ethane and ethene species, which resulted in Supplementary Figs. 5–7 and Supplementary Tables 3 and 4 analyzed in Supplementary Discussion, can be found in Supplementary Information.

Ab initio molecular dynamics simulations

To gain further insights into the yields and timescales of ${\rm H}_{3}^{+}$ formation, we performed AIMD simulations for the CH₃X²⁺ ions with X = OH, Cl, CN, SCN, and F by utilizing the GPU-accelerated CASSCF code implemented in the TeraChem software^64,65,66,67. For each CH₃X²⁺ species, the potential energy surface corresponding to its lowest singlet electronic state and its gradients were computed on-the-fly by using the CASSCF method with 4 electrons in 4 orbitals as an active space, abbreviated as CAS(4,4)SCF, in conjunction with the cc-pVDZ basis set. The orbital active spaces were carefully tailored to closely reproduce the adiabatic relaxation energies ΔE_rlx, Eq. (1), and the geometries of the CH₃X²⁺ dications in their lowest singlet states obtained using the DIP-EOMCC(4h-2p)/cc-pVDZ approach for CH₃OH²⁺, CH₃Cl²⁺ and CH₃F²⁺ and DIP-EOMCC(3h-1p)/cc-pVDZ for the remaining species (see Supplementary Fig. 2). To provide a reasonable representation of the molecular dynamics following double ionization, a total of 200 trajectories were computed for each CH₃X²⁺ system. All trajectories were initiated and subsequently propagated on the lowest singlet states of the CH₃X²⁺ dication species reached after vertical double ionization of their CH₃X parents. The initial conditions (positions and momenta of atomic nuclei) were sampled from the Wigner distributions obtained for the neutral CH₃X molecules using the B3LYP/cc-pVDZ approach^68,69. All trajectories were integrated for 700 fs with a time step of 0.5 fs by using the velocity Verlet algorithm. Of the six CH₃X systems included in our experiments, three, namely, CH₃OH, CH₃Cl, and CH₃NCS, produce ${\rm H}_{3}^{+}$ after double ionization, so we wanted to perform AIMD simulations for CH₃NCS²⁺ as well. However, the low yield of ${\rm H}_{3}^{+}$ resulting from the double ionization of CH₃NCS would necessitate the determination of a much larger number of trajectories than in the CH₃OH²⁺ and CH₃Cl²⁺ cases to obtain sufficiently good statistics for describing the dynamics of the ${{{\rm{CH}}}}_{3}{{{\rm{NCS}}}}^{2+}\to {{{\rm{CNCS}}}}^{+}+{{{\rm{H}}}}_{3}^{+}$ process, which turned out to be prohibitively expensive for us.

Data availability

All data needed to evaluate the conclusions of this study are included in the article and Supplementary Information. Source data are provided in the Source Data folder. Any additional information related to this study may be requested from the authors.

Code availability

All ab initio DIP-EOMCC computations for the CH₃X²⁺, CHX²⁺, and CX⁺ cations and the preceding CCSD calculations for the CH₃X, CHX, and CX⁻ parent molecules, as well as the additional computations for the neutral and doubly ionized ethane and ethene, were performed using the routines described in refs. ^{28, 29, 53}, ⁵⁴, which are part of the GAMESS software package^55,56,57 that can be obtained from https://www.msg.chem.iastate.edu/gamess/download.html. The AIMD simulations for the selected CH₃X²⁺ species, using CASSCF information calibrated to the DIP-EOMCC data, were carried out using the development version of TeraChem software^64,65,66,67 provided by B.G.L.

References

Oka, T. Interstellar ${{{\rm{H}}}}_{3}^{+}$. Chem. Rev. 113, 8738–8761 (2013).
Article CAS PubMed Google Scholar
Herbst, E. & Klemperer, W. The formation and depletion of molecules in dense interstellar clouds. ApJ 185, 505–534 (1973).
Article ADS CAS MATH Google Scholar
Kannan, G., Chien, J. R., Benjamin, A. J., Bhatia, N. & Saykally, R. J. Rydberg states of H₃ and HeH as potential coolants for primordial star formation. J. Phys. Chem. A 125, 4267–4275 (2021).
Article CAS PubMed Google Scholar
Hogness, T. & Lunn, E. The ionization potentials of hydrogen as interpreted by positive ray analysis. Proc. Natl. Acad. Sci. USA 10, 398–405 (1924).
Article ADS CAS PubMed PubMed Central MATH Google Scholar
Tennyson, J. Spectroscopy of ${{{\rm{H}}}}_{3}^{+}$ : planets, chaos and the universe. Rep. Prog. Phys. 58, 421–476 (1995).
Article ADS CAS MATH Google Scholar
Pilling, S. et al. Production of ${{{\rm{H}}}}_{3}^{+}$ via photodissociation of organic molecules in interstellar clouds. Mon. Not. R. Astron. Soc. 375, 1488–1494 (2007).
Article ADS CAS MATH Google Scholar
Sun, S. et al. Ejection of triatomic molecular ion ${{{\rm{H}}}}_{3}^{+}$ from methyl chloride in an intense femtosecond laser field. Chem. Phys. Lett. 581, 16–20 (2013).
Article ADS CAS Google Scholar
Palaudoux, J. & Hochlaf, M. Formation of ${{{\rm{H}}}}_{3}^{+}$ through chloromethane dication fragmentation. ACS Earth Space Chem. 3, 980–985 (2019).
Article ADS CAS Google Scholar
Ekanayake, N. et al. Mechanisms and time-resolved dynamics for trihydrogen cation (${{{\rm{H}}}}_{3}^{+}$) formation from organic molecules in strong laser fields. Sci. Rep. 7, 4703 (2017).
Article ADS PubMed PubMed Central MATH Google Scholar
Ekanayake, N. et al. H₂ roaming chemistry and the formation of ${{{\rm{H}}}}_{3}^{+}$ from organic molecules in strong laser fields. Nat. Commun. 9, 5186 (2018).
Article ADS PubMed PubMed Central MATH Google Scholar
Livshits, E., Luzon, I., Gope, K., Baer, R. & Strasser, D. Time-resolving the ultrafast H₂ roaming chemistry and ${{{\rm{H}}}}_{3}^{+}$ formation using extreme-ultraviolet pulses. Commun. Chem. 3, 49 (2020).
Article CAS PubMed PubMed Central Google Scholar
Wang, E. et al. Ultrafast proton transfer dynamics on the repulsive potential of the ethanol dication: Roaming-mediated isomerization versus coulomb explosion. J. Phys. Chem. A 124, 2785–2791 (2020).
Article ADS CAS PubMed PubMed Central MATH Google Scholar
Zhou, L. et al. Ultrafast formation dynamics of ${{{\rm{D}}}}_{3}^{+}$ from the light-driven bimolecular reaction of the D₂–D₂ dimer. Nat. Chem. 15, 1229–1235 (2023).
Article CAS PubMed MATH Google Scholar
Fayolle, E. C. et al. Protostellar and cometary detections of organohalogens. Nat. Astron. 1, 703–708 (2017).
Article ADS MATH Google Scholar
Ma, P. et al. Ultrafast proton migration and coulomb explosion of methyl chloride in intense laser fields. J. Chem. Phys. 146, 244305 (2017).
Article ADS PubMed Google Scholar
Duflot, D., Robbe, J.-M. & Flament, J.-P. Ab initio study of the chloromethane dication fragmentation. Int. J. Mass Spectrom. Ion Proc. 171, 215–230 (1997).
Article ADS CAS MATH Google Scholar
Matsubara, T. Dynamic effects on the ionization-induced reactions of methyl halides: Quantum mechanical and molecular dynamics studies. J. Phys. Chem. A 127, 4801–4814 (2023).
Article CAS PubMed MATH Google Scholar
Newton, A. S., Sciamanna, A. & Thomas, G. The occurrence of the ${{{\rm{H}}}}_{3}^{+}$ ion in the mass spectra of organic compounds. Int. J. Mass Spectrom. Ion Phys. 5, 465–482 (1970).
Article ADS CAS Google Scholar
Walt, S. G. et al. Role of multi-electron effects in the asymmetry of strong-field ionization and fragmentation of polar molecules: The methyl halide series. J. Phys. Chem. A 119, 11772–11782 (2015).
Article ADS CAS PubMed MATH Google Scholar
Eland, J. The origin of primary ${{{\rm{H}}}}_{3}^{+}$ ions in mass spectra. Rapid Commun. Mass Spectrom. 10, 1560–1562 (1996).
Article ADS CAS MATH Google Scholar
Corkum, P. Plasma perspective on strong multiphoton ionization. Phys. Rev. Lett. 71, 1994–1997 (1993).
Article ADS CAS PubMed MATH Google Scholar
Gope, K., Livshits, E., Bittner, D. M., Baer, R. & Strasser, D. Absence of triplets in single-photon double ionization of methanol. J. Phys. Chem. Lett. 11, 8108–8113 (2020).
Article CAS PubMed PubMed Central Google Scholar
Nooijen, M. & Bartlett, R. J. A new method for excited states: Similarity transformed equation-of-motion coupled-cluster theory. J. Chem. Phys. 106, 6441–6448 (1997).
Article ADS CAS MATH Google Scholar
Wladyslawski, M. & Nooijen, M. The photoelectron spectrum of the NO₃ radical revisited: A theoretical investigation of potential energy surfaces and conical intersections. In Low-lying potential energy surfaces. ACS Symposium Series (eds. Hoffmann, M. R. & Dyall, K. G.), vol. 828, pp. 65–92 (American Chemical Society, Washington, D.C., 2002).
Nooijen, M. State selective equation of motion coupled cluster theory: Some preliminary results. Int. J. Mol. Sci. 3, 656–675 (2002).
Article CAS MATH Google Scholar
Sattelmeyer, K. W., Schaefer III, H. F. & Stanton, J. F. Use of 2h and 3h-p-like coupled-cluster Tamm–Dancoff approaches for the equilibrium properties of ozone. Chem. Phys. Lett. 378, 42–46 (2003).
Article ADS CAS Google Scholar
Kuś, T. & Krylov, A. I. Using the charge-stabilization technique in the double ionization potential equation-of-motion calculations with dianion references. J. Chem. Phys. 135, 084109 (2011).
Article ADS PubMed MATH Google Scholar
Shen, J. & Piecuch, P. Doubly electron-attached and doubly ionized equation-of-motion coupled-cluster methods with 4-particle-2-hole and 4-hole-2-particle excitations and their active-space extensions. J. Chem. Phys. 138, 194102 (2013).
Article ADS PubMed Google Scholar
Shen, J. & Piecuch, P. Doubly electron-attached and doubly ionised equation-of-motion coupled-cluster methods with full and active-space treatments of 4-particle-2-hole and 4-hole-2-particle excitations: The role of orbital choices. Mol. Phys. 112, 868–885 (2014).
Article ADS CAS MATH Google Scholar
Čížek, J. On the correlation problem in atomic and molecular systems. Calculation of wavefunction components in Ursell-type expansion using quantum-field theoretical methods. J. Chem. Phys. 45, 4256–4266 (1966).
Article ADS MATH Google Scholar
Čížek, J. On the use of the cluster expansion and the technique of diagrams in calculations of correlation effects in atoms and molecules. Adv. Chem. Phys. 14, 35–89 (1969).
MATH Google Scholar
Paldus, J., Čížek, J. & Shavitt, I. Correlation problems in atomic and molecular systems. IV. Extended coupled-pair many-electron theory and its application to the BH₃ molecule. Phys. Rev. A 5, 50–67 (1972).
Article ADS MATH Google Scholar
Purvis III, G. D. & Bartlett, R. J. A full coupled-cluster singles and doubles model: The inclusion of disconnected triples. J. Chem. Phys. 76, 1910–1918 (1982).
Article ADS MATH Google Scholar
Cullen, J. M. & Zerner, M. C. The linked singles and doubles model: An approximate theory of electron correlation based on the coupled-cluster ansatz. J. Chem. Phys. 77, 4088–4109 (1982).
Article ADS CAS MATH Google Scholar
Roos, B. O., Taylor, P. R. & Siegbahn, P. E. M. A complete active space SCF method (CASSCF) using a density matrix formulated super-CI approach. Chem. Phys. 48, 157–173 (1980).
Article MathSciNet CAS MATH Google Scholar
Eland, J. H. D. & Treves-Brown, B. J. The fragmentation of doubly charged methanol. Int. J. Mass Spectrom. Ion Processes 113, 167–176 (1992).
Article ADS CAS Google Scholar
Huber, K. P. & Herzberg, G. Molecular spectra and molecular structure: IV. Constants of diatomic molecules (Van Nostrand Reinhold, New York, 1979).
Jochim, B., DeJesus, L. & Dantus, M. Ultrafast disruptive probing: Simultaneously keeping track of tens of reaction pathways. Rev. Sci. Instrum. 93, 033003 (2022).
Article ADS CAS PubMed Google Scholar
Ekanayake, N. et al. Substituent effects on ${{{\rm{H}}}}_{3}^{+}$ formation via H₂ roaming mechanisms from organic molecules under strong-field photodissociation. J. Chem. Phys. 149, 244310 (2018).
Article ADS PubMed Google Scholar
Word, M. D. et al. Ultrafast dynamics of nitro-nitrite rearrangement and dissociation in nitromethane cation. J. Phys. Chem. A 126, 879–888 (2022).
Article CAS PubMed Google Scholar
Zhang, Y. et al. Formation of ${{{\rm{H}}}}_{3}^{+}$ from ethane dication induced by electron impact. Commun. Chem. 3, 160 (2020).
Article CAS PubMed PubMed Central MATH Google Scholar
Hoshina, K., Kawamura, H., Tsuge, M., Tamiya, M. & Ishiguro, M. Metastable decomposition and hydrogen migration of ethane dication produced in an intense femtosecond near-infrared laser field. J. Chem. Phys. 134, 064324 (2011).
Article ADS PubMed Google Scholar
Hoshina, K., Furukawa, Y., Okino, T. & Yamanouchi, K. Efficient ejection of ${{{\rm{H}}}}_{3}^{+}$ from hydrocarbon molecules induced by ultrashort intense laser fields. J. Chem. Phys. 129, 104302 (2008).
Article ADS PubMed Google Scholar
Zhang, Y. et al. Formation of ${{{\rm{H}}}}_{3}^{+}$ from hydrocarbon dications induced by collisions with charged particles. Phys. Rev. A 100, 052706 (2019).
Article ADS CAS Google Scholar
Severt, T. et al. Initial-site characterization of hydrogen migration following strong-field double-ionization of ethanol. Nat. Commun. 15, 74 (2024).
Article ADS CAS PubMed PubMed Central Google Scholar
Xu, B., Gunn, J. M., Dela Cruz, J. M., Lozovoy, V. V. & Dantus, M. Quantitative investigation of the multiphoton intrapulse interference phase scan method for simultaneous phase measurement and compensation of femtosecond laser pulses. J. Opt. Soc. Am. B 23, 750–759 (2006).
Guo, C., Li, M., Nibarger, J. P. & Gibson, G. N. Single and double ionization of diatomic molecules in strong laser fields. Phys. Rev. A 58, 4271–4274 (1998).
Article ADS MATH Google Scholar
Keldysh, L. V. Ionization in the field of a strong electromagnetic wave. Soviet Phys. JETP 20, 1307–1314 (1965).
MATH Google Scholar
Emrich, K. An extension of the coupled cluster formalism to excited states (I). Nucl. Phys. A 351, 379–396 (1981).
Article ADS MATH Google Scholar
Geertsen, J., Rittby, M. & Bartlett, R. J. The equation-of-motion coupled-cluster method: Excitation energies of Be and CO. Chem. Phys. Lett. 164, 57–62 (1989).
Article ADS CAS MATH Google Scholar
Stanton, J. F. & Bartlett, R. J. The equation of motion coupled-cluster method. A systematic biorthogonal approach to molecular excitation energies, transition probabilities, and excited state properties. J. Chem. Phys. 98, 7029–7039 (1993).
Article ADS CAS MATH Google Scholar
Piecuch, P. & Bartlett, R. J. EOMXCC: A new coupled-cluster method for electronic excited states. Adv. Quantum Chem. 34, 295–380 (1999).
Article ADS CAS MATH Google Scholar
Piecuch, P., Kucharski, S. A., Kowalski, K. & Musiał, M. Efficient computer implementation of the renormalized coupled-cluster methods: The R-CCSD[T], R-CCSD(T), CR-CCSD[T], and CR-CCSD(T) approaches. Comp. Phys. Commun. 149, 71–96 (2002).
Article ADS CAS Google Scholar
Shen, J. & Piecuch, P. Double electron-attachment equation-of-motion coupled-cluster methods with up to 4-particle–2-hole excitations: Improved implementation and application to singlet–triplet gaps in ortho-, meta-, and para-benzyne isomers. Mol. Phys. 119, e1966534 (2021).
Article ADS Google Scholar
Schmidt, M. W. et al. General atomic and molecular electronic structure system. J. Comput. Chem. 14, 1347–1363 (1993).
Article CAS MATH Google Scholar
Barca, G. M. J. et al. Recent developments in the general atomic and molecular electronic structure system. J. Chem. Phys. 152, 154102 (2020).
Article ADS CAS PubMed MATH Google Scholar
Zahariev, F. et al. The general atomic and molecular electronic structure system (GAMESS): Novel methods on novel architectures. J. Chem. Theory Comput. 19, 7031–7055 (2023).
Article CAS PubMed MATH Google Scholar
Dunning Jr, T. H. Gaussian basis functions for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 90, 1007–1023 (1989).
Article ADS MATH Google Scholar
Woon, D. E. & Dunning Jr, T. H. Gaussian basis functions for use in correlated molecular calculations. III. The atoms aluminum through argon. J. Chem. Phys. 103, 1358–1371 (1993).
Article ADS MATH Google Scholar
Dunning, J., Thom, H., Peterson, K. A. & Wilson, A. K. Gaussian basis sets for use in correlated molecular calculations. X. The atoms aluminum through argon revisited. J. Chem. Phys. 114, 9244–9253 (2001).
Article ADS CAS MATH Google Scholar
Peterson, K. A., Figgen, D., Goll, E., Stoll, H. & Dolg, M. Systematically convergent basis sets with relativistic pseudopotentials. II. Small-core pseudopotentials and correlation consistent basis sets for the post-d group 16-18 elements. J. Chem. Phys. 119, 11113–11123 (2003).
Article ADS CAS Google Scholar
Peterson, K. A., Shepler, B. C., Figgen, D. & Stoll, H. On the spectroscopic and thermochemical properties of ClO, BrO, IO, and their anions. J. Phys. Chem. A 110, 13877–13883 (2006).
Article CAS PubMed Google Scholar
Pritchard, B. P., Altarawy, D., Didier, B., Gibson, T. D. & Windus, T. L. New basis set exchange: An open, up-to-date resource for the molecular sciences community. J. Chem. Inf. Model. 59, 4814–4820 (2019).
Article CAS PubMed Google Scholar
Ufimtsev, I. S. & Martínez, T. J. Quantum chemistry on graphical processing units. 3. Analytical energy gradients, geometry optimization, and first principles molecular dynamics. J. Chem. Theory Comput. 5, 2619–2628 (2009).
Article CAS PubMed MATH Google Scholar
Fales, B. S. & Levine, B. G. Nanoscale multireference quantum chemistry: Full configuration interaction on graphical processing units. J. Chem. Theory Comput. 11, 4708–4716 (2015).
Article CAS PubMed MATH Google Scholar
Hohenstein, E. G., Luehr, N., Ufimtsev, I. S. & Martínez, T. J. An atomic orbital-based formulation of the complete active space self-consistent field method on graphical processing units. J. Chem. Phys. 142, 224103 (2015).
Article ADS PubMed Google Scholar
Seritan, S. et al. TeraChem: A graphical processing unit-accelerated electronic structure package for large-scale ab initio molecular dynamics. WIREs Comput. Mol. Sci. 11, e1494 (2021).
Article MATH Google Scholar
Becke, A. D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 98, 5648–5652 (1993).
Article ADS CAS MATH Google Scholar
Lee, C., Yang, W. & Parr, R. G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 37, 785–789 (1988).
Article ADS CAS MATH Google Scholar

Download references

Acknowledgements

S.K. was supported by the Air Force Office of Scientific Research under award number FA9550-21-1-0428 to M.D. The experimental work was funded by the Department of Energy, Office of Basic Energy Sciences, Atomic, Molecular, and Optical Sciences Program under award number SISGR (DE-SC0002325) to M.D. The theoretical and computational work using the CC and DIP-EOMCC methodologies was supported by the Chemical Sciences, Geosciences, and Biosciences Division, Office of Basic Energy Sciences, Office of Science, U.S. Department of Energy (Grant No. DE-FG02-01ER15228 to P.P.). The AIMD simulations were performed using the Expanse GPU system at the San Diego Supercomputer Center through allocation CHE230046 from the Advanced Cyberinfrastructure Coordination Ecosystem: Services & Support (ACCESS) program, which is supported by National Science Foundation grants #2138259, #2138286, #2138307, #2137603, and #2138296. A.M. and B.G.L. gratefully acknowledge support from the National Science Foundation under award number CHE-1954519 and from the Institute for Advanced Computational Science. S.S. thanks Moaid Shaik, for his help with analyzing preliminary AIMD trajectories.

Author information

Authors and Affiliations

Department of Chemistry, Michigan State University, East Lansing, Michigan, USA
Jacob Stamm, Swati S. Priyadarsini, Shawn Sandhu, Arnab Chakraborty, Jun Shen, Sung Kwon, Jesse Sandhu, Clayton Wicka, Piotr Piecuch & Marcos Dantus
Department of Chemistry, Stony Brook University, Stony Brook, New York, USA
Arshad Mehmood & Benjamin G. Levine
Institute for Advanced Computational Science, Stony Brook University, Stony Brook, New York, USA
Arshad Mehmood & Benjamin G. Levine
Department of Physics and Astronomy, Michigan State University, East Lansing, Michigan, USA
Piotr Piecuch & Marcos Dantus

Authors

Jacob Stamm
View author publications
Search author on:PubMed Google Scholar
Swati S. Priyadarsini
View author publications
Search author on:PubMed Google Scholar
Shawn Sandhu
View author publications
Search author on:PubMed Google Scholar
Arnab Chakraborty
View author publications
Search author on:PubMed Google Scholar
Jun Shen
View author publications
Search author on:PubMed Google Scholar
Sung Kwon
View author publications
Search author on:PubMed Google Scholar
Jesse Sandhu
View author publications
Search author on:PubMed Google Scholar
Clayton Wicka
View author publications
Search author on:PubMed Google Scholar
Arshad Mehmood
View author publications
Search author on:PubMed Google Scholar
Benjamin G. Levine
View author publications
Search author on:PubMed Google Scholar
Piotr Piecuch
View author publications
Search author on:PubMed Google Scholar
Marcos Dantus
View author publications
Search author on:PubMed Google Scholar

Contributions

M.D. conceived the project and oversaw the execution of all experiments. J. Stamm, S.K., and C.W. carried out the experiments under M.D.’s supervision, and J. Sandhu helped with the analysis of experimental data. P.P. and B.G.L. conceived the computational parts of the project. A.C., S.S.P., and J. Shen performed all ab initio electronic structure calculations using the CC and DIP-EOMCC methodologies under P.P.’s supervision. S.S. performed all AIMD simulations, consulting A.M., B.G.L., and P.P. All authors contributed to the interpretation of the results and J. Stamm, S.S.P., S.S., A.C., P.P., and M.D. led the manuscript writing, with the remaining authors offering comments and helping with respective tables and/or figures.

Corresponding authors

Correspondence to Benjamin G. Levine, Piotr Piecuch or Marcos Dantus.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Communications thanks the anonymous reviewer(s) for their contribution to the peer review of this work. A peer review file is available.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Description of Additional Supplementary Files

Supplementary Movie 1

Supplementary Movie 2

Supplementary Movie 3

Transparent Peer Review file

Source data

Source Data

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.

Reprints and permissions

About this article

Cite this article

Stamm, J., Priyadarsini, S.S., Sandhu, S. et al. Factors governing ${\rm H}_{3}^{+}$ formation from methyl halogens and pseudohalogens. Nat Commun 16, 410 (2025). https://doi.org/10.1038/s41467-024-55065-5

Download citation

Received: 20 February 2024
Accepted: 28 November 2024
Published: 06 January 2025
DOI: https://doi.org/10.1038/s41467-024-55065-5

Subjects

Abstract

Similar content being viewed by others

Introduction

Results

Experimental

Ab initio electronic structure calculations

Timescales of \({\rm H}_{3}^{+}\) formation

Ab initio molecular dynamics simulations

Discussion

Methods

Experimental details

Electronic structure calculations

Ab initio molecular dynamics simulations

Data availability

Code availability

References

Acknowledgements

Author information

Authors and Affiliations

Contributions

Corresponding authors

Ethics declarations

Competing interests

Peer review

Peer review information

Additional information

Supplementary information

Source data

Rights and permissions

About this article

Cite this article

Share this article

Search

Quick links