Multivariate stochastic modeling for transcriptional dynamics with cell-specific latent time using SDEvelo

Liao, Xu; Kang, Lican; Peng, Yihao; Chai, Xiaoran; Xie, Peng; Lin, Chengqi; Ji, Hongkai; Jiao, Yuling; Liu, Jin

doi:10.1038/s41467-024-55146-5

Download PDF

Article
Open access
Published: 30 December 2024

Multivariate stochastic modeling for transcriptional dynamics with cell-specific latent time using SDEvelo

Nature Communications volume 15, Article number: 10849 (2024) Cite this article

5954 Accesses
1 Citations
6 Altmetric
Metrics details

Subjects

Abstract

Recently, RNA velocity has driven a paradigmatic change in single-cell RNA sequencing (scRNA-seq) studies, allowing the reconstruction and prediction of directed trajectories in cell differentiation and state transitions. Most existing methods of dynamic modeling use ordinary differential equations (ODE) for individual genes without applying multivariate approaches. However, this modeling strategy inadequately captures the intrinsically stochastic nature of transcriptional dynamics governed by a cell-specific latent time across multiple genes, potentially leading to erroneous results. Here, we present SDEvelo, a generative approach to inferring RNA velocity by modeling the dynamics of unspliced and spliced RNAs via multivariate stochastic differential equations (SDE). Uniquely, SDEvelo explicitly models inherent uncertainty in transcriptional dynamics while estimating a cell-specific latent time across genes. Using both simulated and four scRNA-seq and spatial transcriptomics datasets, we show that SDEvelo can model the random dynamic patterns of mature-state cells while accurately detecting carcinogenesis. Additionally, the estimated gene-shared latent time can facilitate many downstream analyses for biological discovery. We demonstrate that SDEvelo is computationally scalable and applicable to both scRNA-seq and sequencing-based spatial transcriptomics data.

Generalizing RNA velocity to transient cell states through dynamical modeling

Article 03 August 2020

UniTVelo: temporally unified RNA velocity reinforces single-cell trajectory inference

Article Open access 03 November 2022

Temporal modelling using single-cell transcriptomics

Article 31 January 2022

Introduction

The advent of single-cell RNA sequencing (scRNA-seq) has revolutionized our understanding of molecular and cellular processes. It offers unprecedented opportunities to explore gene expression profiles at the single-cell resolution, identify rare cell (sub)types, track cell lineages, etc., which were not achievable with bulk RNA-seq^1,2. Using scRNA-seq data for a population of cells at different stages of a developmental process, trajectory inference methods aim to reconstruct the developmental paths of individual cells over time^3,4,5,6. Recently, spatial transcriptomics technologies have emerged that preserve information on physical spatial locations^7,8. For instance, in situ sequencing-based spatial transcriptomics analyzes the transcripts within discrete “spots” on histological tissue sections⁹. A major challenge in trajectory inference is the destructive nature of these technologies, which captures only a static snapshot of the transcriptome related to cellular states at the moment of measurement. Therefore, conventional trajectory inference methods require enough cells to be profiled from all intermediate states to enable the reconstruction of continuous trajectories¹⁰, and prior knowledge is needed to specify the progenitor cells and determine the inferred direction^3,11,12,13, which largely limits the applicability of these methods when datasets do not contain cells from all states and/or the cell fates are unknown.

Transitioning from trajectory models of the descriptive states of cells to predictive models of cell dynamics, RNA velocity recovers dynamic information by modeling the cellular transcription process between unspliced pre-mRNAs and spliced mRNAs^14,15. Using the kinetics of the transcription of pre-mRNAs, their conversion into spliced mRNAs, and eventual degradation, RNA velocity can be inferred. A positive velocity indicates a gene being up-regulated in spliced transcripts whilst a negative velocity indicates down-regulation. Assuming that the transcriptional phases of the induction and repression of gene expression last sufficiently long enough to reach an equilibrium between transcription and steady state, La Manno et al.¹⁴ first used physics-informed ordinary differential equations (ODE) to model the biological/causal mechanisms in the transcription of molecules. Since then, the field of RNA velocity has rapidly evolved with various variants and applications emerging^{15,16,17,18,19,20,21,22,23,24,25,26}. However, non-negligible limitations and potential pitfalls still underly the core of these methods^27,28.

An ideal RNA velocity method should be capable of tackling the following three tasks: (1) establish a collaborative system across multiple genes with a cell-specific latent time for each cell/spot; (2) characterize the stochastic nature of dynamic transcriptional kinetics by utilizing stochastic differential equations (SDE), especially in the context of biochemical processes such as transcription where randomness and uncertainty are intrinsic^29,30; and (3) show robustness to transcriptomics data from different sequencing technologies. Most existing RNA velocity methods only consider the univariate model for each single gene, neglecting the shared information between multiple genes in the same cell/spot, which potentially leads to false fate direction identification in steady-state cells^14,18,27. Moreover, most methods have been developed based on deterministic ODE models, with incorporating extrinsic noise for measurement errors but without considering the intrinsic stochastic noise and uncertainty that occur during the transcription process^{14,15,16,17,19,21}. Recent approaches have made progress in incorporating stochasticity, notably scVelo¹⁵, which computes higher-order moments to capture local stochasticity among neighboring cells, and VelvetSDE³¹, which utilizes a neural SDE framework for a more accurate approximation of the underlying stochastic process dynamics. However, these models do not explicitly estimate the SDE parameters (transcription, splicing, and degradation rates) necessary for biophysical interpretability. More recently, PhyloVelo was proposed as a way to characterize stochastic variation during cell division via the diffusion process, but it requires dedicated experiments to delineate the phylogenetic tree in the data, which is largely inapplicable to human samples²⁴. Finally, because of the complex structure and low sequencing depth of spatial transcriptomics data, it is challenging to apply existing RNA velocity methods³².

To address the challenges presented by RNA velocity and facilitate downstream analyses by integrating inferred latent time and velocity, we propose the use of SDE-informed RNA velocity, SDEvelo, which collaboratively estimates multivariate RNA velocity across multiple genes governed by a cell-specific latent time, accounts for the inherent stochastic nature of kinetics during the transcription process, and infers a cell-specific latent time across genes, accurately revealing the progression of cell differentiation. In SDEvelo, we propose a computational framework that uses a generative model with adversarial learning. As a result, SDEvelo can uniquely obtain the multivariate RNA velocity governed by a cell-specific latent time in cells/spots, while capturing underlying stochastic process dynamics through an SDE framework; achieve excellent visualizations, such as velocity streamline plots and latent-time heatmaps; be applicable to both scRNA-seq and in situ sequencing-based spatial transcriptomics data; and facilitate downstream analyses by leveraging the estimated velocity and latent time for biological discoveries.

Results

An overview of SDEvelo

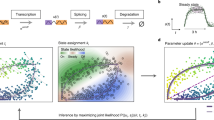
Conventional RNA velocity methods primarily use coupled differential equations to delineate the gene transcription/splicing/degradation kinetics with a physics-informed mechanism (Fig. 1a, left panel). Instead of sequentially applying ODE to individual genes, SDEvelo uniquely applies multivariate SDE in combination with a nonlinear and differentiable sigmoid function for the transcription rate underlying each cell-specific latent time to characterize both the intrinsic and extrinsic noises attributed to the transcription process and measurement errors, respectively (see “Methods”; Fig. 1a, right panel; b),

$$\begin{array}{rcl}d{\boldsymbol{U}}(t)&=&\!\!\!\!\!\!\!\!\!\!\!({\boldsymbol{\alpha }}(t)-{\boldsymbol{\beta }}\odot {\boldsymbol{U}}(t))dt+{{\boldsymbol{\sigma }}}_{1}d{\boldsymbol{B}}(t),\\ d{\boldsymbol{S}}(t)&=&({\boldsymbol{\beta }}\odot {\boldsymbol{U}}(t)-{\boldsymbol{\gamma }}\odot {\boldsymbol{S}}(t))dt+{{\boldsymbol{\sigma }}}_{2}d{\boldsymbol{B}}(t),\end{array}$$

(1)

where U(t) and S(t) are normalized vectors for unspliced and spliced mRNA reads across p genes, respectively, with the transcriptional dynamics modulated by vectors of transcription rate α(t), splicing rate β, and degradation rate γ, and accounting for randomness using a Wiener process B(t) over a common latent time t for all p genes, with σ₁ and σ₂ used for noise levels.

The innovations provided by the generative model SDEvelo come from the following perspectives (Fig. 1c). First, unlike the deterministic cell trajectories generated by ODE-based methods, SDEvelo estimates the transcriptional dynamics associated with a cell-specific latent time with a stochastic component via adversarial learning (Fig. 1b), providing a more robust and realistic framework of transcriptional dynamics and effectively avoiding erroneous directions in terminal cell states. Moreover, the use of sigmoid functions for the transcription rate α(t) (see “Methods”) allows SDEvelo to identify gradual and smooth expression changes to better model the biological processes of gene expression regulation that involve multiple interactions between transcription factors, enhancers, and silencers^33,34. Strikingly, SDEvelo leverages data on multiple genes simultaneously to infer the transcriptional dynamics with a cell-specific latent time that is shared across genes for a single cell/spot, which is achieved by a multivariate SDE framework with explicitly interpretable parameters. This consideration can potentially capture candidate genes involved in co-interactions and co-regulation, which is crucial in understanding complex biological processes^35,36. Furthermore, by incorporating intrinsic noise through a multivariate SDE, SDEvelo achieves superior accuracy in velocity and latent time estimation, as demonstrated in our simulated experiments section. Notably, this modeling enables SDEvelo to effectively distinguish between actively transitioning cells and mature populations, which avoids reports of false transitions in mature cells where RNA velocity vector flows should be random on visualization.

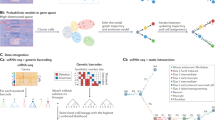
We illustrated the benefits of SDEvelo’s ability to correctly identify cell lineage/transcription dynamics using both scRNA-seq and sequencing-based spatial transcriptomics data, especially its ability to resolve the erroneous fate direction detected in datasets of most mature-state cells using existing methods. Moreover, with the inferred latent time and velocity, SDEvelo can facilitate many downstream tasks, as depicted in Fig. 1d. First, users can visualize streamline plots with inferred RNA velocity, latent time heatmaps, etc. Second, by correlating gene expression with the estimated latent time from SDEvelo, we can identify cancer driver genes, allowing us to examine the dynamics of carcinogenesis, delineate the boundaries between tumor and non-tumor regions, and construct protein interaction networks. Third, by combining the inferred velocity and latent time from SDEvelo with gene expression data, we can detect cell states and delineate a global map of cell fates.

Validation using simulated data

We performed comprehensive simulations to evaluate the performance of SDEvelo and compare it with that of several other methods. To achieve this, we considered the following eight RNA velocity methods: Velocyto¹⁴, scVelo (stc)¹⁵, scVelo (dyn)¹⁵, UniTVelo¹⁹, DeepVelo²⁶, VeloVI²¹, Dynamo³⁷ and VeloVAE¹⁷. The simulation details are provided in the “Methods” section. Briefly, we performed simulations for unspliced and spliced mRNAs with both deterministic²⁷ (Supplementary Fig. S1a, left panel) and stochastic (Eqn. (1); Supplementary Fig. S1a, right panel) settings using ODE and SDE, respectively (see “Methods”). Note that in the ODE setting, extrinsic noise was added. In both settings, SDEvelo accurately inferred the velocity of streamline plots and correctly estimated latent time that aligned well with the underlying truth (Fig. 1e; Supplementary Fig. S1b), while scVelo failed to provide consistent directions or accurate latent times (Fig. 1e; Supplementary Fig. S1c).

The estimation of the steady-state ratio between unspliced and spliced mRNAs determines the accuracy of a model in calculating the RNA velocity^14,15. To quantify the performance of the models in estimating this ratio, we calculated the absolute relative errors between the estimated ratios and the underlying truths. In both the ODE and SDE settings, SDEvelo achieved the best performance in all methods, had the smallest ratio errors, and presented robustness to various numbers of genes (Fig. 1f, upper panel). Using a constant value for the steady-state ratio in the ODE setting, we compared the distributions of estimated errors in all methods (Supplementary Fig. S2a), and the distribution of estimated errors using SDEvelo aligned well with the underlying truth. However, those of other methods exhibited biased estimations, and those of Velocyto and scVelo (stc), particularly, showed bimodal distributions. We further investigated the models’ ability to estimating the switch time points that separate the induction and repression phases. Compared to scVelo (dyn), SDEvelo accurately estimated the marginal distribution of the underlying switch time points (Supplementary Fig. S2b).

Unlike other methods, SDEvelo models velocities for multiple genes with a cell-specific latent time. We thus evaluated the performance of SDEvelo’s latent time estimation. We first estimated the latent time with all methods and calculated the Pearson’s correlation between the estimated latent time and the underlying truth. SDEvelo notably outperformed all other methods, providing the highest Pearson’s correlation across different numbers of genes (Fig. 1f, lower panel). Using joint kernel density estimation (KDE) plots, the latent time inferred using SDEvelo aligned well with the underlying truth, while those from other methods exhibited substantial deviations from the true values (Fig. 1e, left panel; Supplementary Fig. S2c).

Furthermore, we exhibit SDEvelo’s ability to identify branching trajectories in another simulated dataset (see “Methods”). SDEvelo accurately identified the correct velocities in the streamline plots, even with as few as 100 genes, while scVelo showed some inconsistencies (Supplementary Fig. S3a). In the latent time estimation, SDEvelo, along with Dynamo and UniTVelo, closely aligned with the true latent times, outperforming the other methods which displayed notable inconsistencies (Supplementary Fig. S3b). Among a range of gene numbers (100 to 1000), SDEvelo consistently demonstrated superior performance in both steady-state ratio estimation and latent time prediction (Supplementary Fig. S3c). These results underscore SDEvelo’s robust performance in identifying complex branching trajectories, even in scenarios with limited gene numbers, highlighting its potential for accurate velocity estimation and trajectory inference in diverse biological contexts.

Negative controls of transcriptional dynamics in mature-state cell populations

We applied SDEvelo and other methods to the analysis of four datasets obtained from scRNA-seq or spatial transriptomics (see “Methods”). By obtaining both the inferred velocity and latent time from SDEvelo, we could perform various downstream analyses. Here, to better understand the differentiation process, we showcase the CellRank analysis used to detect cell fate decisions and prioritize genes related to the terminal fates^38,39, the gene enrichment analysis used for latent-time-associated genes, and the cell-cell communication analysis used for genes related to latent time^40,41.

We first applied SDEvelo and other methods to analyze a dataset for peripheral blood mononuclear cells (PBMCs) in the mature state consisting of 65, 877 cells and 33, 939 genes generated using the 10x platform. After quality control (QC), we applied RNA velocity analysis to the remaining 601 genes (see “Methods”). Ideally, cells sampled from steady-state/mature-state populations should lack dynamic information, as the mRNA levels of these cells have already equilibrated (Fig. 2a). By collaborative modeling across multiple genes while taking into account the noise levels in SDE, SDEvelo detected random directions between most cell types (Fig. 2b). Whereas scVelo and other methods detected strong but arbitrary directional patterns, a phenomenon pointed out by other authors^27,28 (Fig. 2b; Supplementary Fig. S4a, upper panel). Using simulated datasets²⁷, we further demonstrated that SDEvelo could successfully detect the random directions of cells in nondynamic states, while scVelo and the other methods estimated strong but erroneous directions (Fig. 2c; Supplementary Fig. S4b). The heatmap of the inferred latent time from SDEvelo shows that most cells were close to the end of their differentiation, consistent with the terminal cell types seen among PBMCs (Fig. 2d, left panel). However, those generated using scVelo and DeepVelo erroneously show that most cells were at an early stage (Fig. 2d, right panel; Supplementary Fig. S4a, lower panel).

**Fig. 2: Negative controls of transcriptional dynamics in mature-state cell populations (n = 65,877 cells).**

To test if SDEvelo can reduce the number of false-positives for genes that drive transcription dynamics, we focused on driver genes identified by scVelo (dyn), including MYL6, APOBEC3G, and HLA-DRB1. As most PBMC cells are in steady or mature states, induction and repression phases are not expected. The projected spliced and unspliced abundance of these genes showed no clear patterns (Supplementary Fig. S4c), further suggesting there were no strong direction dynamics in these genes. ScVelo (dyn), however, identified strong dynamic kinetics with clear trajectories generated from its ODE model between these genes (Fig. 2e, upper panel), while the generated trajectories along latent time by SDEvelo displayed randomness (Fig. 2e, lower panel). We also observed a strong clustered cell-type pattern in the abundance of spliced mRNAs along the latent time estimation from scVelo (Fig. 2f, upper panel), but this was randomly distributed along the estimated latent time by SDEvelo (Fig. 2f, lower panel), effectively preventing the detection of erroneous trajectories in mature-state cell populations.

Although SDEvelo identified no transitions between most cell types, a notable within-group trajectory was observed for CD8+ cytotoxic T and CD56+ NK cells, potentially driven by cell-cycle mechanisms. To investigate this hypothesis, we analyzed the expression of cell-cycle genes. The heatmap revealed consistent areas of high expression in these cell types (Supplementary Fig. S5a), corresponding to velocity trajectories. A one-tailed t-test further confirmed the significantly higher expression of most cell-cycle genes in CD8+ cytotoxic T and CD56+ NK cells compared to other cell types (Supplementary Fig. S5b). When we divided the cell-cycle genes into subsets and obtained a heatmap of expression along the inferred latent time (Supplementary Fig. S5c), we observed a clear pattern of expressional changes along the latent time estimated by SDEvelo, supporting the presence of a cell-cycle-driven trajectory within these populations.

SDEvelo correctly infers the dynamics of carcinogenesis in hepatocellular carcinoma spatial transcriptomcis

We further studied the carcinogenesis dynamics of hepatocellular carcinoma (HCC) using SDEvelo. The dataset contained two sections from tumor tissues (HCC1-2) and two from tumor-adjacent tissues (HCC3-4) generated using the 10x Visium platform, with 2982, 1334, 2732, and 2764 spots, respectively. We applied SDEvelo and other methods to each of the four sections. The histology images with manual annotations for tumor/normal epithelium (TNE) and stroma provided by a pathologist can be seen in Fig. 3a on the first and third rows. In all sections, the latent time estimated by SDEvelo presented a pattern similar to the manual annotations, with early stages identified in the stroma but late stages in the TNE (Fig. 3a, second & fourth rows). However, the latent time estimated by scVelo and the other methods presented either no clear patterns or provided reverse latent time data for TNE and stromal regions (Fig. 3a, second & fourth rows; Supplementary Fig. S6a). Interestingly, using PRECAST group labels⁴², SDEvelo correctly detected all carcinogenic transitions from stromal to TNE clusters in four HCC sections (Fig. 3b). In contrast, scVelo and the other methods incorrectly detected reverse transitions from the TNE regions to stromal regions, except UniTVelo for HCC1 and VeloVAE for HCC2 (Supplementary Figs. S7, S8). To quantitatively evaluate the correctness of the inferred transitions, we employed cross-boundary direction correctness (CBDir) for velocity assessment, and the area under the receiver operating characteristic curve (AUC) and the area under the precision-recall curve (AUPR) ratio for transition probability evaluation (see “Methods”). SDEvelo achieved the highest values across all metrics (CBDir, AUC, and AUPR ratio), as shown in Fig. 3c and Supplementary Fig. S9a, b. For the latent time evaluation, we used rank correlation, for which SDEvelo demonstrated superior performance across all four HCC sections (Fig. 3d; Supplementary Fig. S9a).

**Fig. 3: Analysis of HCC data with spatial transcriptomics (n = 9, 812 spots).**

To detect cancer-driver genes, we further correlated the estimated latent time with gene expression. In total, we detected 562 genes with adjusted p-values of less than 0.05 (Benjamini-Hochberg procedure), many of which were apolipoprotein (APO) genes (Supplementary Data 1). Many APO genes ranked top in positive correlations with latent time (Supplementary Fig. S10a). After visualizing the expression levels of the top correlated APO genes, we observed sharp transitions in the tumor-adjacent tissues (HCC3-4), but smooth expression changes in the tumor tissues (HCC1-2) (Supplementary Fig. S10b), suggesting these genes have essential roles in carcinogenesis dynamics. Using an empirical cut-off value of 0.3 for HCC3-4 (Supplementary Fig. S10b), we observed a substantial number of spots with estimated latent time between 0.275 and 0.325 that were located within the boundaries of the annotated stromal and TNE regions (Fig. 3e), suggesting these detected driver genes potentially play important roles in carcinogenesis.

Using PINA v3.0, we further constructed a protein-protein interaction (PPI) network for the detected cancer driver genes⁴³ (Fig. 3f). A heatmap of the correlation coefficients between all pairs of interacting proteins across all cancer types in the Cancer Genome Atlas (TCGA) dataset⁴⁴ suggested the strong enrichment of these genes in two cancers (Supplementary Fig. S10c), liver hepatocellular carcinoma (LIHC) and cholangiocarcinoma (CHOL), the latter of which occurs along the biliary tree and is sometimes classified as a type of liver cancer⁴⁵. This provides evidence for co-regulation and interactomics between genes detected in liver-related cancers.

SDEvelo predicts cell fates in mouse embryonic reprogramming data

To investigate the reprogramming process involved in mouse embryonic fibroblast (MEF) trajectory toward induced endoderm progenitors (iEPs), we applied SDEvelo and other methods to analyze a mouse reprogramming dataset, consisting of 85, 010 cells and 22, 630 genes, obtained using the 10x Genomics and the Drop-seq platform⁴⁶. After QC, we analyzed a total of 2000 highly variable genes. The original study provided information on cell annotations that allowed us to quantitatively evaluate the latent time estimation. We visualized the days of reprogramming in the cells using two components of PCA for expression counts (Fig. 4a). The heatmap of the estimated latent time from SDEvelo closely matched the reprogramming days recorded in the experiment (Fig. 4b), while those from other methods showed several velocity transitions or latent time directions that were reversed compared to the reprogramming days (Fig. 4a, right panel; Supplementary Fig. S11a, b). To quantitatively evaluate the performance of latent time estimation, we calculated Pearson’s correlation coefficients between the estimated latent time by SDEvelo and other methods with the reprogramming day using five-fold cross-validation. As shown in Fig. 4c, SDEvelo outperformed the other methods in evaluating the correctness of the inferred transitions, achieving the highest Pearson’s correlation coefficients with the smallest variations (upper panel) and the highest AUC metrics (lower panel). We also estimated the pseudotime using Monocle^3,5 and compared it with the reprogramming days. The aligned heatmap of pseudo-time, latent time, and reprogramming days shows that SDEvelo exhibited better performance than Monocle and scVelo, and had the highest Pearson’s correlation coefficient for the recorded reprogramming days compared with estimated latent time (Fig. 4d).

**Fig. 4: Analysis of mouse embryonic reprogramming data (n = 85, 010 cells).**

With annotations from t-SNE clusters, Biddy et al.⁴⁷ revealed two distinct trajectories, with one leading to successfully reprogrammed cells (Clusters 2 → 6 → 1) and the other leading to a dead-end state (Clusters 8 → 4 → 3). SDEvelo correctly detected these two distinct trajectories (Fig. 4e, Supplementary Fig. S12a), in which the expression of MEF and iEP marker genes Col1a2 and Apoa1 aligned well with the streamline plots for the subsets in the dead-end and successfully reprogrammed trajectories, respectively (Fig. 4e, left top and bottom panels). By combining gene expression data with inferred velocity and latent time, we detected the cell macrostates and created a global map of estimated fate potentials for each cell using CellRank^38,39 (Supplementary Fig. S12b). The six detected macrostates included two terminal states (Cluster 1 for successfully reprogrammed cells and Cluster 3 for a dead-end state; Fig. 4e, right middle panel). A violin plot of latent time showed the temporal order of the terminal macrostates (Supplementary Fig. S12c). Using CellRank, we also detected driver genes that regulate fate decision in the differentiation of from MEFs to iEPs and accurately predicted both dead-end and successfully reprogrammed lineages (Fig. 4e, right top/bottom panel; Supplementary Fig. S12d, e). These genes included the MEF marker Col1a2 (Supplementary Fig. S12d) and the iEP marker Apoa1 (Fig. 4e, right bottom panel).

SDEvelo accurately recognized known transitions between cell subtypes in mouse erythroid data

We analyzed a mouse gastrulation erythroid dataset generated using the 10x Genomics platform⁴⁸ consisting of 9815 cells and 53,801 genes. Using UMAP, Pijuan-Sala et al.⁴⁸ identified sub-clusters of blood progenitors 1 and 2 (BP1 and BP2) and erythroids 1-3 (Ery1-Ery3) and revealed the transitions between these cell subtypes, allowing us to evaluate the performance of the detected directionality by taking the annotated transitions as ground truth. We first drew up the stratified histograms of the unspliced and spliced transcripts for each cell type for the selected genes after QC (Supplementary Fig. S13a), and observed correlated patterns between the transcript abundances and cell types throughout erythroid differentiation. For each method, we summarized the velocity-based streamlines and latent time heatmaps along erythroid differentiation and visualized them on embeddings from UMAP (Fig. 5a, b; Supplementary Figs. S13b; S14a). The resulting SDEvelo streamlines showed the differentiation of blood progenitors into terminal erythroid states and were smoother and more coherent across these cell subtypes than the streamlines of other methods (Fig. 5a; Supplementary Fig. S13b). Strikingly, using the estimated latent time, SDEvelo recovered accurate transitional patterns using a smooth sigmoid function for the transcription rate (Fig. 5b). In contrast, scVelo identified erroneous directions in the transcriptional dynamics because of its inability to account for the expression boost problem possibly induced by a change in transcription rate^27,49.

**Fig. 5: Analysis of mouse gastrulation erythroid data (n = 9, 815 cells).**

As a generative model that uses sigmoid functions for the transcription rates and a cell-specific latent time, SDEvelo is capable of generating flexible and generalizable trajectories for a specific gene. As shown in Fig. 5c, SDEvelo generated trajectories when transcriptional boost or a reversed direction was present along the estimated latent time for the differentiation progression. Heatmaps of expression levels showed that Redrum and Svbp were highly expressed in Ery1-Ery3 (Fig. 5d), while Prtg and Runx1 were highly expressed in BP1 and BP2 (Fig. 5d), consistent with the abundance results generated by SDEvelo.

To reveal the progress of erythroid differentiation, we further applied SDEvelo to prioritize genes related to the estimated latent time. The expression levels of the top genes correlated to the SDEvelo-solved dynamics showed clear transitional patterns along the estimated latent time (Fig. 5e). Among these genes were Ezh2, which regulates cell proliferation and differentiation via histone methylation⁵⁰; the transcription factor Tead2, which plays a pivotal role in cell differentiation, proliferation, and development⁵¹; and Hells, which is involved in chromatin remodeling, a process essential for the transcriptional regulation of genes during differentiation⁵². Further analysis showed that these genes were significantly enriched in many pathways related to erythroid differentiation (Fig. 5f; Supplementary Fig. S14b), such as the positive regulation of cell population proliferation and erythrocyte differentiation.

We also performed a cell-cell communication (CCC) analysis^40,41 of these prioritized genes and detected important ligand-receptor interaction pairs. Specifically, we identified BP1-2 cells as the senders and Ery1-3 cells as the receivers in the following key ligand-receptor interactions: Tgfb1-Itgb1, Mdk-Sdc1/Ncl, and Lgals1-Itgb1 (Fig. 5g; Supplementary Fig. S15a). Among these were Tgfb1-Itgb1, which plays a role in modulating cell adhesion and migration^53,54, and the growth factor Mdk, which interacts with Sdc1 and Ncl, indicating their involvement in cell growth and migration processes⁵⁵. Visualizing the expression levels of the pairs of interacting ligand-receptors, we observed synchronous variation within the pairs along the estimated latent time (Supplementary Fig. S15b). Summarizing the overall interaction intensity indicated the directed of the interactions was from BP1-2 to Ery1-3 (Fig. 5h; Supplementary Fig. S14c), providing insights into the interactions relevant to erythroid maturation.

Discussion

As a result of our work, we propose the use of SDEvelo for quantifying RNA velocity for multiple genes simultaneously in a manner governed by cell-specific latent times. Unlike methods that model the RNA velocity of each gene with gene-specific latent time using univariate ODE, SDEvelo explicitly models the RNA velocity of multiple genes governed by the cell-specific latent time while considering the inherent stochastic nature of the dynamics that account for the randomness of biological processes during transcription using SDE. Moreover, SDEvelo uses nonlinear but differentiable sigmoid functions for the transcription rate to gradually and smoothly model expression changes, instead of using indicator functions that show instant changes. All these considerations mean SDEvelo provides reliable and robust velocity and latent time estimations.

Conventionally, solving SDE requires temporal information for each data point, which is largely missing from sequencing data. Taking advantage of the successes of both deep generative models and adversarial learning, SDEvelo infers all parameters via a strategy that minimizes the divergence between the real input data and the data generated by the SDE model. In the data-generation steps, the Euler-Maruyama method is used to discretize the continuous SDE process and generate trajectories based on the current model.

With a PBMC dataset and simulations, we demonstrated that SDEvelo can mitigate the long-standing problem of the erroneous directions inferred by existing methods for mature-state cells. In cells sampled from populations in mature states, we expect to observe a noisy velocity field without a clear direction. Among the PBMC and simulated datasets, only SDEvelo estimated a noisy, directionless velocity field, while the others erroneously inferred particular directions within the t-SNE representation. Additionally, SDEvelo is applicable to datasets generated using various sequencing-based technologies, including sequencing-based spatial transcriptomics data of low depth. From a dataset of four HCC sections generated using 10x Visium, SDEvelo correctly estimated the velocity directions and latent times in both tumor and tumor-adjacent tissues, facilitating the detection of cancer driver genes in HCC, as well as constructing a PPI network. Further analysis of pairwise correlations between these genes suggested their strong enrichment in liver-related cancers.

SDEvelo provides a systematic solution for the rapidly developing area of RNA velocity. First, although SDEvelo can be applied to spatial transcriptomics data, it does not model spatial information explicitly. The desired velocity method should account for both spatial locations and various spatial resolutions. Secondly, it would be interesting to apply the computational framework of SDEvelo to the integration of other modality data within single-cell genomics with a time-dependent transcription rate. Thirdly, a robust computational framework for RNA velocity that accounts for batch effects is needed, particularly when analyzing a vast number of cells originating from multiple heterogeneous batches.

Methods

Modeling Stochastic Kinetics with SDEvelo

As in conventional RNA velocity analyses, the transcriptional kinetics for each gene were modeled by a deterministic and gene-gene-independent ODE system,

$$\frac{du(t)}{dt}=\alpha (t)-\beta u(t),\quad \frac{ds(t)}{dt}=\beta u(t)-\gamma s(t).$$

(2)

The ODE system delineates the dynamics of unspliced transcripts, u(t), and spliced transcripts, s(t), over time. The transcription rate, denoted by α(t), is commonly approximated by a step-wise indicator function^14,15. β and γ represent the scalar parameters for the rates of splicing and degradation, respectively. However, this ODE-based model has three limitations: (1) It delineates a deterministic process that cannot capture the intrinsic randomness of transcriptional dynamics; (2) The step-wise transcription function is non-differentiable and suggests an intermediate transition between induction and repression phases; and (3) The univariate system of ODE equations models the transcriptional dynamics for each gene independently, without consideration of the interactive regulatory pathways acting across multiple genes.

Here, we present a model overview of SDEvelo, and further details are available in the Supplementary Notes. Consider the multivariate state variables U(t) and S(t) in all p genes, which represent the dynamics for unspliced and spliced transcripts, respectively, over a cell-specific latent time t. With p genes, we assume the corresponding p-dimensional vectors for transcription rates, splicing rates, and degradation rates ${\boldsymbol{\alpha }}(t)={(\alpha {(t)}_{1},\ldots,\alpha {(t)}_{p})}^{\top }$, ${\boldsymbol{\beta }}={({\beta }_{1},\ldots,{\beta }_{p})}^{\top }$, and ${\boldsymbol{\gamma }}={({\gamma }_{1},\ldots,{\gamma }_{p})}^{\top }$. SDEvelo employs a multivariate SDE model across multiple genes collectively, with this modeling governed by a unified cell-specific latent time. Without loss of generality, we assume t ∈ [0, 1] describes a finite period, and SDEvelo models the unspliced and spliced transcripts, U(t) and S(t), respectively, as in Eq. (1), with a Wiener process that accounts for both the intrinsic and extrinsic noises of unspliced and spliced transcripts. Within the SDE framework, SDEvelo is a stochastic model that incorporates intrinsic noise into the velocity estimation. In contrast, other methods use deterministic ODE without accounting for this intrinsic noise. From a mathematical perspective, the key difference lies in the velocity calculation, where other methods use deterministic ODE, SDEvelo employs SDEs with an additional stochastic term to account for the random nature of transcriptional dynamics.

For transcription function α(t), we consider differentiable sigmoid functions to avoid describing intermediate transitional states between two phases,

$$\alpha {(t)}_{i}=\frac{{c}_{i}}{1+\exp \{b(t-{a}_{i})\}},\quad i=1,\ldots,p,$$

(3)

where ${\boldsymbol{a}}={({a}_{1},\ldots,{a}_{p})}^{\top }$ is a vector of the switch time points, ${\boldsymbol{c}}={({c}_{1},\ldots,{c}_{p})}^{\top }$ is a vector of the transcription rates of all p genes, and b is the hyperparameter used to tune the shape of the sigmoid function.

Adversarial learning parameters

In practice, resolving multivariate ODE/SDE remains challenging. Most univariate ODE-based methods utilize the EM algorithm to infer model parameters, for which the explicit solutions of ODE are essentially required during iterations^15,17,22. However, for nonlinearly coupled multivariate SDE, it is difficult to obtain explicit solutions. SDEvelo estimates the model parameters by adversarially comparing real and generated data from the SDE, and the Euler-Maruyama method^56,57 is used to discretize the continuous SDE process and generate trajectories from the current iteration. The parameters are updated by stochastic gradient descent, minimizing divergence loss with the incorporation of the transcription/splicing/degradation rate, as well as the noise levels that characterize both the extrinsic and intrinsic stochasticity.

The flowchart for estimating the parameters in SDEvelo is displayed in Fig. 1b. SDEvelo adversarially estimates the parameters for the combination of stochastic gradient descent and generative modeling by minimizing the divergence between the distributions obtained from real data and those from SDE-generated data using the maximum mean discrepancy (MMD)^58,59, for which the core functions of SDEvelo are in line with the generative adversarial networks of deep learning⁶⁰.

To generate trajectories from SDE, we used the Euler-Maruyama method^56,57 to obtain the discretized observations from the continuous diffusion process as

$$\begin{array}{rcl}{\boldsymbol{U}}(t+\Delta t)&=&{\boldsymbol{U}}(t)+\left(\frac{{\boldsymbol{c}}}{1+\exp ({\boldsymbol{b}}\odot (t-{\boldsymbol{a}}))}-{\boldsymbol{\beta }}\odot {\boldsymbol{U}}(t)\right)\Delta t+{{\boldsymbol{\sigma }}}_{1}\sqrt{\Delta t}{{\boldsymbol{Z}}}_{1},\\ {\boldsymbol{S}}(t+\Delta t)&=&\!\!\!\!\!\!\!\!\!\!\!\!\!\!{\boldsymbol{S}}(t)+({\boldsymbol{\beta }}\odot {\boldsymbol{U}}(t)-{\boldsymbol{\gamma }}\odot {\boldsymbol{S}}(t))\Delta t+{{\boldsymbol{\sigma }}}_{2}\sqrt{\Delta t}{{\boldsymbol{Z}}}_{2},\end{array}$$

(4)

where ${{\boldsymbol{Z}}}_{1},{{\boldsymbol{Z}}}_{2} \sim {\mathcal{N}}(0,1)$. We denoted the set of unknown parameters as $\Theta=\left\{{\boldsymbol{a}},{\boldsymbol{c}},{\boldsymbol{\beta }},{\boldsymbol{\gamma }},{{\boldsymbol{\sigma }}}_{1},{{\boldsymbol{\sigma }}}_{2}\right\}$, which dominates the generated trajectories of the transaction process. We estimated Θ by minimizing the empirical MMD objective with the kernel trick^58,59,

$${{\mathcal{L}}}_{{{\rm{MMD}}}^{2}}(\Theta )=\frac{1}{{{N}_{g}}^{2}}\mathop{\sum }\limits_{i=1}^{{N}_{g}}\mathop{\sum }\limits_{{i}^{{\prime} }=1}^{{N}_{g}}k\left({g}_{i}(\Theta ),{g}_{{i}^{{\prime} }}(\Theta )\right)-\frac{2}{{N}_{g}{N}_{r}}\mathop{\sum }\limits_{i=1}^{{N}_{g}}\mathop{\sum }\limits_{j=1}^{{N}_{r}}k\left({g}_{i}(\Theta ),{r}_{j}\right)+\frac{1}{{{N}_{r}}^{2}}\mathop{\sum }\limits_{j=1}^{{N}_{r}}\mathop{\sum }\limits_{{j}^{{\prime} }=1}^{{N}_{r}}k\left({r}_{j},{r}_{{j}^{{\prime} }}\right).$$

(5)

The divergence measures the discrepancy between two datasets: the first consists of N_g cell samples, ${\boldsymbol{G}}(\Theta )={\{{g}_{i}(\Theta )\}}_{i=1}^{{N}_{g}}$, generated from SDE trajectories; the second comprises N_r real cell samples, ${\boldsymbol{R}}={\{{r}_{j}\}}_{j=1}^{{N}_{r}}$, where each ${g}_{i}\in {{\mathbb{R}}}^{2p}$ is a concatenated vector of unspliced and spliced data for p genes in cell i, and each ${r}_{j}\in {{\mathbb{R}}}^{2p}$ represents the real data for the corresponding cell. In the kernel trick, we chose the Gaussian kernel $k\left(x,{x}^{{\prime} }\right)=\mathop{\sum }\nolimits_{q=1}^{K}\exp \left(-\frac{1}{2{w}_{q}}{\left\vert x-{x}^{{\prime} }\right\vert }^{2}\right)$, combining different bandwidth parameters w_q. Since the MMD loss (5) is differentiable, we applied stochastic gradient descent to minimize the loss of function (5) and estimate parameters Θ^61,62. Thus, the computational framework is scalable and applicable to both CPU and GPU platforms.

With the proposed optimization strategy, the overall computational framework of SDEvelo is illustrated in Fig. 1b, consisting of four main steps. The process begins with the input of unspliced and spliced gene profiles, which serve as the real data during the training process. In the generation step, the nonlinear multivariate SDE model produces simulated data by numerically integrating the SDE using the Euler-Maruyama method with the current parameter estimates Θ. During the training process, the SDE model parameters Θ are updated by minimizing the distributional divergence between the real and generated data. Specifically, we compute the MMD objective function (5) to quantify the distributional discrepancy between the two data sources. Finally, with the trained parameters, SDEvelo outputs the estimated velocities and the cell-specific latent time. Through this iterative procedure, SDEvelo can accurately capture the underlying transcriptional dynamics by continuously updating its parameters to match the observed data. Further details on the implementation are provided in the Supplementary Notes.

Estimation of latent time

To infer latent time in SDEvelo, we used the estimated SDE with these generated points. In detail, we first generated trajectories from the SDE with the inferred parameters. Then, using the idea of optimal transport^63,64, we matched the generated trajectories with the real observed data.

We used G(Θ) to denote the trajectories generated from SDEvelo using the inferred parameters Θ, with R for the observed data. Assuming that each point g_i(Θ) ∈ G(Θ) is governed by a time t_i in SDEvelo, we aimed to identify a bijection ϕ: G(Θ) → R that minimizes the total cost of transportation. Formally, this can be defined as follows:

$${{\boldsymbol{\phi }}}^{*}=\mathop{{\arg }\,{\min}}\limits_{{\boldsymbol{\phi }}:{\boldsymbol{G}}({\Theta })\to {\boldsymbol{R}}} \sum_{{i }={1}}^{{N}_{g}}{\vert {g}_{i}({\Theta })-{\boldsymbol{\phi }}({g}_{i}({\Theta }))\vert}_{2},$$

(6)

where ${\left\vert \cdot \right\vert }_{2}$ denotes a squared Euclidean distance. After obtaining the optimal bijection ϕ^* with Sinkhorn-Knopp matrix scaling algorithm^65,66, each observed point r_i = ϕ(g_i(Θ)) was assigned a latent time t_i from its corresponding generated point g_i(Θ). By estimating the cell-specific latent time across multiple genes, SDEvelo can reveal the temporal progression of cell differentiation processes.

Downstream analyses

GO enrichment analysis

We conducted GO enrichment analysis of each gene set selected by SDEvelo using the GOATOOLS library in Python⁶⁷. This enrichment analysis, based on Fisher’s exact test complemented by the Benjamini-Hochberg method for multiple test correction, aimed to identify significant GO terms within the gene set, with the significance threshold set at 0.05. The ontology analysis was implemented within the context of biological process (BP), cellular component (CC), and molecular function (MF), providing insights into the functional characteristics of the input gene set.

CellRank analysis

We utilized CellRank implemented in the Python package cellrank to combine the estimated RNA velocity and latent time from SDEvelo with RNA expression in high-dimensional space^38,39. To be specific, this multi-faceted information was integrated into the kernel-induced cell-cell transition matrix with equal weighting. CellRank coarse-grained the cell-level information to the macrostate level using the generalized perron cluster cluster analysis (GPCCA) algorithm with function cr.estimators.GPCCA(). We further used predict_terminal_states() to identify the terminal states. With simulated random walks, the fate probabilities on the Markov chain were computed with function compute_fate_probabilities() to predict the cellular fates. Finally, we prioritized driver genes by correlating the calculated fate probabilities with gene profiles with function compute_lineage_drivers().

Cell-cell communication analysis

After prioritizing the genes associated with inferred latent time from SDEvelo, we performed cell-cell communication analyses with LIANA using the Python liana package to infer the ligand-receptor interactions⁴¹. Specifically, we utilized CellPhoneDB method⁴⁰ to calculate the ligand-receptor scores with cellphonedb() and resource_name='mouseconsensus' functional settings. The permutation-based p-values were used to ascertain the interaction specificity, with a significance threshold of 0.05.

Protein-protein interaction analysis

We further investigated the protein-protein interactions within the putative driver genes on the protein interaction network analysis (PINA) platform^43,68,69 of https://omics.bjcancer.org/pina/. We used the network construction function to explore known interactions. Then, we conducted network analysis to calculate the Spearman correlation coefficients for expression between proteins pairs across cancer types from TCGA dataset⁴⁴.

Comparisons of methods

We performed extensive comparisons between the performance of SDEvelo and existing methods in both simulated and real data analyses.

To evaluate the performance of SDEvelo, we used the following RNA velocity methods as benchmarks: (1) Velocyto¹⁴ implemented in the Python package scvelo¹⁵ utilizing the scvelo.tl.velocity() function with the mode='deterministic' on default settings; (2) scVelo (stc)¹⁵ implemented in the Python package scvelo and applying the scvelo.tl.velocity() function with mode=‘stochastic’ on default settings; (3) scVelo (dyn)¹⁵ implemented in the Python package scvelo (0.2.5) utilizing the scvelo.tl.velocity() function with the mode=‘dynamical’ and the scvelo.tl.recover_dynamics() on default settings from https://scvelo.readthedocs.io/en/stable/index.html; (4) VeloAE¹⁶ implemented in the Python module veloproj, employing the function main_AE() on default settings from https://github.com/qiaochen/VeloAE/tree/main; (5) UniTVelo¹⁹ implemented in the Python package unitvelo (0.2.5.2) and applying the function utv.run_model() with the default configuration file from https://github.com/StatBiomed/UniTVelo; (6) DeepVelo²⁶ implemented in the Python package deepvelo, employing the function deepvelo.train() on default settings from https://github.com/bowang-lab/DeepVelo; (7) VeloVI²¹ implemented in the Python package velovi (0.2.0) and applying the function vae.train() with default settings from https://github.com/YosefLab/velovi; (8) Dynamo³⁷ implemented in the Python package dynamo and applying the function dynamo.tl.dynamics() with default settings from https://dynamo-release.readthedocs.io/en/latest/index.html; (9) VeloVAE¹⁷ implemented in the Python module velovae and employing the function velovae.vae.train() with default settings from https://github.com/welch-lab/VeloVAE.

Evaluation metrics

We evaluated the performance of the methods’ ability to infer the RNA velocity in both the simulated and the real datasets. For the simulations, we directly compared the estimated parameters with the underlying true ones via either ratio errors or their Pearson’s correlation coefficients. In the real dataset, we quantified the resemblance of the predicted flow directions with relevant celltype lineage established in biological studies using cross-boundary direction score, correct directions, and in-cluster coherence.

Ratio errors For a given gene i, the steady-state ratio, defined as the ratio of the degradation rate (γ_i) to the splicing rate (β_i), can be used to infer the velocity^14,15,18. In simulations, the true values of the degradation rate (γ) and the splicing rate (β) were known. To quantify differences between the estimated steady-state ratios and the underlying true ones, we used the metric of ratio errors by evaluating the average absolute difference between them, as follows:

$$\,\text{Ratio errors}\,=\frac{1}{p}\mathop{\sum }\limits_{i=1}^{p}{\left| \left| \frac{{\hat{\gamma }}_{i}}{{\hat{\beta }}_{i}}-\frac{{\gamma }_{i}}{{\beta }_{i}}\right| \right| }_{1},$$

where ∥ ⋅ ∥₁ is the L1-norm, p is the number of genes, γ_i and β_i are the true degradation and splicing rates, and ${\hat{\gamma }}_{i}$ and ${\hat{\beta }}_{i}$ are their corresponding estimates from the RNA velocity method. A lower value of ratio errors suggests a better estimation of the steady-state ratios with improved accuracy in RNA velocity.

Pearson’s correlation coefficients in latent time SDEvelo considers and estimates a cell-specific latent time across multiple genes for a single cell/spot. We denoted ${t}_{j}^{*}\in [0,1]$ as the estimated latent time for cell j and ${{\boldsymbol{t}}}^{*}={({t}_{1}^{*},\ldots,{t}_{n}^{*})}^{\top }$ as the estimated latent time vector for all n cells/spots. In the simulations, we computed Pearson’s correlation coefficients for the relationship between the estimated latent time and the true ones. A larger value of Pearson’s correlation coefficient suggested a better estimation of latent time.

Cross-boundary direction correctness score For real data, it is not possible to compare the estimated parameters and latent time with the ground truth. By taking the known transitions and established flow directions among cell (sub)types as ground truth, we gauged the accuracy of the inferred velocity via CBDir^16,19. We denoted the set of K known transitions between cell types as ${\mathcal{T}}=\{({A}_{1},{B}_{1}),\ldots,({A}_{K},{B}_{K})\}$, where A_k and B_k represent a source and target cell cluster, respectively, for the known transition k, and K as the total number of known transitions. The CBDir metric assesses the directional correctness of the known cell-type transitions, as follows:

$${\rm{CBDir}}=\frac{1}{K}\mathop{\sum }\limits_{k=1}^{K}\frac{1}{| {A}_{k}| }\sum _{j\in {A}_{k}}\frac{1}{| {B}_{k}\cap {\mathcal{N}}(j)| }\sum _{{j}^{{\prime} }\in {B}_{k}\cap {\mathcal{N}}(j)}\frac{{{\boldsymbol{\nu }}}_{j}\cdot {{\boldsymbol{d}}}_{j,{j}^{{\prime} }}}{\left\Vert {{\boldsymbol{\nu }}}_{j}\right\Vert \cdot \left\Vert {{\boldsymbol{d}}}_{j,{j}^{{\prime} }}\right\Vert },$$

(7)

where ν_j is the velocity vector of cell j, ${{\boldsymbol{d}}}_{j,{j}^{{\prime} }}$ represents the low-manifold difference in position vectors between cell j and its neighbor ${j}^{{\prime} }$, and ${\mathcal{N}}(j)$ denotes the neighborhood of cell j. The higher the CBDir measured, the better the performance in inferring an RNA velocity that aligns with the given directions.

Simulation settings

Simulated data from ODE model In this scenario, we adopted the ODE-based simulation settings from²⁷. The simulation was carried out using the scvelo.datasets.simulation function in the Python module scvelo¹⁵. Specifically, the datasets were simulated with 500 cells, each containing 100, 500, and 1000 genes, and Gaussian noise was added to mimic external variability. The parameters included constant rates for transcription (α = 5), splicing (β = 0.3), and degradation (γ = 0.5). The population of unspliced mRNA molecules at time τ (denoted u(τ)) is described by the following differential equation:

$$u(\tau )={u}_{0}{e}^{-\beta \tau }+\frac{\alpha }{\beta }\left(1-{e}^{-\beta \tau }\right).$$

(8)

Here, u₀ denotes the initial abundance of unspliced mRNA. The population of spliced mRNA molecules at time τ (denoted s(τ)) is modeled by:

$$s(\tau )={s}_{0}{e}^{-\gamma \tau }+\frac{\alpha }{\gamma }\left(1-{e}^{-\gamma \tau }\right)+c\left({e}^{-\gamma \tau }-{e}^{-\beta \tau }\right),$$

(9)

where s₀ is the initial abundance of spliced mRNA, and $c=\frac{\alpha -{u}_{0}\beta }{\gamma -\beta }$. The time events are from a Poisson process, and switching time points are obtained as fractions [0.1, 0.4, 0.7, 1] of the maximum time.

Simulated data from SDE model Gene-expression dynamics within single cells are subject to intrinsic stochastic fluctuations and inter-cellular heterogeneity. Therefore, we used SDE-based model to simulate the temporal variations of gene profiles across multiple stochastic trajectories.

The state of expression of each gene i in trajectory k at time t is characterized by the levels of unspliced mRNA, U_i,k(t), and spliced mRNA, S_i,k(t). Given a time step Δt, the discretized versions of the equations for U_i,k(t) and S_i,k(t) at the m-th time step, t_m, are:

$${{\boldsymbol{U}}}_{i,k}({t}_{m+1})={{\boldsymbol{U}}}_{i,k}({t}_{m})+\left(\frac{{c}_{i}}{1+\exp (-b({t}_{m}-{a}_{i}))}-{\beta }_{i}{{\boldsymbol{U}}}_{i,k}({t}_{m})\right)\Delta t+{\sigma }_{1,i}\sqrt{\Delta t}\,{\xi }_{1,i,k}(m),$$

(10)

$${{\boldsymbol{S}}}_{i,k}({t}_{m+1})={S}_{i,k}({t}_{m})+\left({\beta }_{i}{{\boldsymbol{U}}}_{i,k}({t}_{m})-{\gamma }_{i}{S}_{i,k}({t}_{m})\right)\Delta t+{\sigma }_{2,i}\sqrt{\Delta t}\,{\xi }_{2,i,k}(m),$$

(11)

where a_i and c_i represents the switch point and transcription rate, respectively; β_i and γ_i are the gene-specific rates of splicing and degradation, respectively; ξ_1,i,k(m) and ξ_2,i,k(m) are independent samples drawn from a standard normal distribution and represent the contribution of discretized noise contributions to the unspliced and spliced mRNA dynamics, respectively, at the m-th time step; and Δt is the discrete time step size used for the numerical integration by the Euler-Maruyama method^56,57. All parameters were sampled from uniform distributions. More detailed information regarding SDE and branching settings can be found in the Supplementary Notes.

Datasets and preprocessing

We applied SDEvelo to four publicly available scRNA-seq and spatial transcriptomics datasets, as detailed in the ‘Data availability’ section. These datasets included human HCC Visium data⁴², human PBMCs^15,27, mouse embryonic reprogramming³⁸, and mouse erythroid data¹⁵ collected using 10x technology. For each dataset, we adhered to the default gene and cell filtering steps¹⁵, employing scv.pp.filter_and_normalize(adata, min_shared_counts=20, n_top_genes=2000) followed by scv.pp.moments(adata, n_neighbors=30, n_pcs=30) for preprocessing from https://scvelo.readthedocs.io/en/stable/index.html. Our SDEvelo software package sdevelo then builds upon this preprocessed data for subsequent RNA velocity analysis.

Spatial transcriptomics datasets We used HCC datasets originating from four tissue sections of an HCC patient. BAM files generated by CellRanger using raw sequence reads were processed with the velocyto run command to obtain spliced and unspliced read counts¹⁴. Gene expression profiles, featuring 2, 000 highly variable genes along with cluster annotations from⁴², were refined through filtering, resulting in datasets with 2, 982, 1, 334, 2, 732, 2, 764 spots, and 1, 985 genes, as input for all analytical methods. Visualizations included streamline plots in PCA space and latent time heatmaps for physical locations. Additionally, a pathologist manually annotated TNE and stromal regions using Visium’s companion hematoxylin and eosin H&E images for this dataset.

Single-cell transcriptomics datasets For the PBMC dataset, publicly available unspliced and spliced counts of 65, 877 cells and 33, 939 genes, respectively, were filtered, resulting in 601 highly variable genes being selected for analysis. We visualized the data using a streamline plot on t-SNE. For the reprogramming dataset, we selected cells with available ‘reprogramming_day’ information, resulting in a subset of 22, 630 genes across 85, 010 cells. After preprocessing, we extracted 2, 000 highly variable genes for analysis. The data were visualized in PCA space. For the mouse erythroid dataset, publicly available unspliced and spliced counts of 9, 815 and 53, 801 were reduced to 9, 815 and 2, 000, respectively, after the filtering procedure. We visualized these data using a streamline plot on UMAP.

Statistics & reproducibility

No statistical method was used to predetermine sample size. No data were excluded from the analyses. The experiments were not randomized. The Investigators were not blinded to allocation during experiments and outcome assessment.

To reproduce the results presented in this paper, the demo code with default parameters is available at our GitHub repository: https://github.com/Liao-Xu/SDEvelo.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.

Data availability

All datasets utilized in this study are publicly accessible. The processed PBMCs dataset^15,27 is available through scv.datasets.pbmc68k(). The processed mouse embryonic reprogramming dataset³⁸ can be retrieved from cr.datasets.reprogramming_morris(). Access to the processed mouse erythroid data¹⁵ is provided by scv.datasets.gastrulation_erythroid(). The raw FASTQ data for the human HCC Visium datasets⁴² can be found at https://www.ncbi.nlm.nih.gov/sra?linkname=bioproject_sra_all&from_uid=858545, while the H&E images are accessible at https://doi.org/10.6084/m9.figshare.21280569.v1 and https://doi.org/10.6084/m9.figshare.21061990.v1. Source data are provided with this paper.

Code availability

SDEvelo⁷⁰ is freely available as a Python package accessible at https://github.com/Liao-Xu/SDEvelo(https://doi.org/10.5281/zenodo.14038380) with detailed tutorials and documentation at https://sdevelo.readthedocs.io/en/latest/. To facilitate replication of the figures and results presented in this paper, detailed workflows are provided as Jupyter notebooks within the GitHub repository and documentation. Additionally, the latest version of SDEvelo is now available on PyPI at https://pypi.org/project/sdevelo/.

References

Mereu, E. et al. Benchmarking single-cell rna-sequencing protocols for cell atlas projects. Nat. Biotechnol. 38, 747–755 (2020).
Article CAS PubMed MATH Google Scholar
Jovic, D. et al. Single-cell rna sequencing technologies and applications: A brief overview. Clin. Transl. Med. 12, e694 (2022).
Article CAS PubMed PubMed Central MATH Google Scholar
Trapnell, C. et al. The dynamics and regulators of cell fate decisions are revealed by pseudotemporal ordering of single cells. Nat. Biotechnol. 32, 381–386 (2014).
Article CAS PubMed PubMed Central Google Scholar
Ji, Z. & Ji, H. Tscan: Pseudo-time reconstruction and evaluation in single-cell rna-seq analysis. Nucleic Acids Res. 44, e117–e117 (2016).
Article PubMed PubMed Central MATH Google Scholar
Qiu, X. et al. Reversed graph embedding resolves complex single-cell trajectories. Nat. Methods 14, 979–982 (2017).
Article CAS PubMed PubMed Central MATH Google Scholar
Setty, M. et al. Characterization of cell fate probabilities in single-cell data with palantir. Nat. Biotechnol. 37, 451–460 (2019).
Article CAS PubMed PubMed Central MATH Google Scholar
Rao, A., Barkley, D., França, G. S. & Yanai, I. Exploring tissue architecture using spatial transcriptomics. Nature 596, 211–220 (2021).
Article ADS CAS PubMed PubMed Central Google Scholar
Moses, L. & Pachter, L. Museum of spatial transcriptomics. Nat. Methods 19, 534–546 (2022).
Article CAS PubMed MATH Google Scholar
Ståhl, P. L. et al. Visualization and analysis of gene expression in tissue sections by spatial transcriptomics. Science 353, 78–82 (2016).
Article ADS PubMed MATH Google Scholar
Ding, J., Sharon, N. & Bar-Joseph, Z. Temporal modelling using single-cell transcriptomics. Nat. Rev. Genet. 23, 355–368 (2022).
Article CAS PubMed PubMed Central Google Scholar
Herman, J. S., Sagar, n. & Gruen, D. Fateid infers cell fate bias in multipotent progenitors from single-cell rna-seq data. Nat. Methods 15, 379–386 (2018).
Article CAS PubMed Google Scholar
Chen, J., Schlitzer, A., Chakarov, S., Ginhoux, F. & Poidinger, M. Mpath maps multi-branching single-cell trajectories revealing progenitor cell progression during development. Nat. Commun. 7, 11988 (2016).
Article ADS CAS PubMed PubMed Central Google Scholar
Wolf, F. A. et al. Paga: graph abstraction reconciles clustering with trajectory inference through a topology preserving map of single cells. Genome Biol. 20, 1–9 (2019).
Article MATH Google Scholar
La Manno, G. et al. Rna velocity of single cells. Nature 560, 494–498 (2018).
Article ADS PubMed PubMed Central MATH Google Scholar
Bergen, V., Lange, M., Peidli, S., Wolf, F. A. & Theis, F. J. Generalizing rna velocity to transient cell states through dynamical modeling. Nat. Biotechnol. 38, 1408–1414 (2020).
Article CAS PubMed MATH Google Scholar
Qiao, C. & Huang, Y. Representation learning of rna velocity reveals robust cell transitions. Proc. Natl. Acad. Sci. 118, e2105859118 (2021).
Article CAS PubMed PubMed Central MATH Google Scholar
Gu, Y., Blaauw, D. T. & Welch, J. Variational mixtures of odes for inferring cellular gene expression dynamics. In International Conference on Machine Learning, 7887–7901 (PMLR, 2022).
Gorin, G., Fang, M., Chari, T. & Pachter, L. Rna velocity unraveled. PLOS Comput. Biol. 18, e1010492 (2022).
Article ADS CAS PubMed PubMed Central MATH Google Scholar
Gao, M., Qiao, C. & Huang, Y. Unitvelo: temporally unified rna velocity reinforces single-cell trajectory inference. Nat. Commun. 13, 6586 (2022).
Article ADS CAS PubMed PubMed Central Google Scholar
Chen, Z., King, W. C., Hwang, A., Gerstein, M. & Zhang, J. Deepvelo: Single-cell transcriptomic deep velocity field learning with neural ordinary differential equations. Sci. Adv. 8, eabq3745 (2022).
Article ADS CAS PubMed PubMed Central Google Scholar
Gayoso, A. et al. Deep generative modeling of transcriptional dynamics for rna velocity analysis in single cells. Nat. Methods 21, 50–59 (2024).
Farrell, S., Mani, M. & Goyal, S. Inferring single-cell transcriptomic dynamics with structured dynamical representations of rna velocity. Bull. Am. Phys. Soc. 2023, N10-002 (2023).
Li, S. et al. A relay velocity model infers cell-dependent rna velocity. Nat. Biotechnol. 42, 99–108 (2024).
Wang, K. et al. Phylovelo enhances transcriptomic velocity field mapping using monotonically expressed genes. Nat. Biotechnol. 42, 778–789 (2024).
Li, C., Virgilio, M. C., Collins, K. L. & Welch, J. D. Multi-omic single-cell velocity models epigenome–transcriptome interactions and improves cell fate prediction. Nat. Biotechnol. 41, 387–398 (2023).
Article CAS PubMed MATH Google Scholar
Cui, H. et al. Deepvelo: deep learning extends rna velocity to multi-lineage systems with cell-specific kinetics. Genome Biol. 25, 27 (2024).
Article CAS PubMed PubMed Central MATH Google Scholar
Bergen, V., Soldatov, R. A., Kharchenko, P. V. & Theis, F. J. Rna velocity—current challenges and future perspectives. Mol. Syst. Biol. 17, e10282 (2021).
Article CAS PubMed PubMed Central Google Scholar
Zheng, S. C., Stein-O’Brien, G., Boukas, L., Goff, L. A. & Hansen, K. D. Pumping the brakes on rna velocity by understanding and interpreting rna velocity estimates. Genome Biol. 24, 246 (2023).
Article CAS PubMed PubMed Central Google Scholar
Swain, P. S., Elowitz, M. B. & Siggia, E. D. Intrinsic and extrinsic contributions to stochasticity in gene expression. Proc. Natl Acad. Sci. 99, 12795–12800 (2002).
Article ADS CAS PubMed PubMed Central MATH Google Scholar
Li, T., Shi, J., Wu, Y. & Zhou, P. On the mathematics of rna velocity i: Theoretical analysis. CSIAM Trans. Appl. Math. 2, 1–55 (2021).
Maizels, R. J., Snell, D. M. & Briscoe, J. Reconstructing developmental trajectories using latent dynamical systems and time-resolved transcriptomics. Cell Syst. 15, 411–424 (2024).
Article CAS PubMed Google Scholar
Saul, D. & Kosinsky, R. L. Spatial transcriptomics herald a new era of transcriptome research. Clin. Transl. Med. 13, e1264 (2023).
Segert, J. A., Gisselbrecht, S. S. & Bulyk, M. L. Transcriptional silencers: Driving gene expression with the brakes on. Trends Genet. 37, 514–527 (2021).
Article CAS PubMed PubMed Central Google Scholar
Pang, B., van Weerd, J. H., Hamoen, F. L. & Snyder, M. P. Identification of non-coding silencer elements and their regulation of gene expression. Nat. Rev. Mol. Cell Biol. 24, 383–395 (2023).
Article CAS PubMed MATH Google Scholar
Davidson, E. H. Emerging properties of animal gene regulatory networks. Nature 468, 911–920 (2010).
Article ADS CAS PubMed PubMed Central MATH Google Scholar
Zufferey, M., Liu, Y., Tavernari, D., Mina, M. & Ciriello, G. Systematic assessment of gene co-regulation within chromatin domains determines differentially active domains across human cancers. Genome Biol. 22, 1–24 (2021).
Article Google Scholar
Qiu, X. et al. Mapping transcriptomic vector fields of single cells. Cell 185, 690–711 (2022).
Article CAS PubMed PubMed Central MATH Google Scholar
Lange, M. et al. Cellrank for directed single-cell fate mapping. Nat. methods 19, 159–170 (2022).
Article CAS PubMed PubMed Central MATH Google Scholar
Weiler, P., Lange, M., Klein, M., Pe’er, D. & Theis, F. CellRank 2: unified fate mapping in multiview single-cell data. Nat. Methods. 21, 1196–1205 (2024).
Efremova, M., Vento-Tormo, M., Teichmann, S. A. & Vento-Tormo, R. Cellphonedb: inferring cell–cell communication from combined expression of multi-subunit ligand–receptor complexes. Nat. Protoc. 15, 1484–1506 (2020).
Article CAS PubMed Google Scholar
Dimitrov, D. et al. LIANA+ provides an all-in-one framework for cell-cell communication inference. Nat. Cell Biol. 26, 1613–1622 (2024).
Liu, W. et al. Probabilistic embedding, clustering, and alignment for integrating spatial transcriptomics data with precast. Nat. Commun. 14, 296 (2023).
Article ADS CAS PubMed PubMed Central MATH Google Scholar
Du, Y. et al. Pina 3.0: Mining cancer interactome. Nucleic Acids Res. 49, D1351–D1357 (2021).
Article CAS PubMed Google Scholar
Weinstein, J. N. et al. The cancer genome atlas pan-cancer analysis project. Nat. Genet. 45, 1113–1120 (2013).
Article PubMed PubMed Central MATH Google Scholar
Brindley, P. J. et al. Cholangiocarcinoma. Nat. Rev. Dis. Prim. 7, 65 (2021).
Article PubMed Google Scholar
Macosko, E. Z. et al. Highly parallel genome-wide expression profiling of individual cells using nanoliter droplets. Cell 161, 1202–1214 (2015).
Article CAS PubMed PubMed Central MATH Google Scholar
Biddy, B. A. et al. Single-cell mapping of lineage and identity in direct reprogramming. Nature 564, 219–224 (2018).
Article ADS CAS PubMed PubMed Central Google Scholar
Pijuan-Sala, B. et al. A single-cell molecular map of mouse gastrulation and early organogenesis. Nature 566, 490–495 (2019).
Article ADS CAS PubMed PubMed Central Google Scholar
Barile, M. et al. Coordinated changes in gene expression kinetics underlie both mouse and human erythroid maturation. Genome Biol. 22, 1–22 (2021).
Article MATH Google Scholar
Mu, W., Starmer, J., Yee, D. & Magnuson, T. Ezh2 variants differentially regulate polycomb repressive complex 2 in histone methylation and cell differentiation. Epigenetics chromatin 11, 1–14 (2018).
Article Google Scholar
Zhao, B. et al. Tead mediates yap-dependent gene induction and growth control. Genes Dev. 22, 1962–1971 (2008).
Article CAS PubMed PubMed Central MATH Google Scholar
Han, Y. et al. Lsh/hells regulates self-renewal/proliferation of neural stem/progenitor cells. Sci. Rep. 7, 1136 (2017).
Article ADS PubMed PubMed Central MATH Google Scholar
Pang, X. et al. Targeting integrin pathways: mechanisms and advances in therapy. Signal Transduct. Target. Ther. 8, 1 (2023).
Article CAS PubMed PubMed Central MATH Google Scholar
Yoon, H. et al. Tgf-β1-mediated transition of resident fibroblasts to cancer-associated fibroblasts promotes cancer metastasis in gastrointestinal stromal tumor. Oncogenesis 10, 13 (2021).
Article CAS PubMed PubMed Central Google Scholar
Filippou, P. S., Karagiannis, G. S. & Constantinidou, A. Midkine (mdk) growth factor: a key player in cancer progression and a promising therapeutic target. Oncogene 39, 2040–2054 (2020).
Article CAS PubMed Google Scholar
Platen, E. An introduction to numerical methods for stochastic differential equations. Acta Numerica 8, 197–246 (1999).
Article ADS MathSciNet MATH Google Scholar
Halidias, N. & Kloeden, P. E. A note on the euler–maruyama scheme for stochastic differential equations with a discontinuous monotone drift coefficient. BIT Numer. Math. 48, 51–59 (2008).
Article MathSciNet MATH Google Scholar
Gretton, A., Borgwardt, K., Rasch, M., Schölkopf, B. & Smola, A. A kernel method for the two-sample-problem. Advances in neural information processing systems 19 (2006).
Gretton, A., Borgwardt, K. M., Rasch, M. J., Schölkopf, B. & Smola, A. A kernel two-sample test. J. Mach. Learn. Res. 13, 723–773 (2012).
MathSciNet MATH Google Scholar
Goodfellow, I. et al. Generative adversarial networks. Commun. ACM 63, 139–144 (2020).
Article MATH Google Scholar
Rumelhart, D. E., Hinton, G. E. & Williams, R. J. Learning representations by back-propagating errors. nature 323, 533–536 (1986).
Article ADS MATH Google Scholar
LeCun, Y., Bengio, Y. & Hinton, G. Deep learning. nature 521, 436–444 (2015).
Article ADS CAS PubMed MATH Google Scholar
Santambrogio, F. Optimal transport for applied mathematicians. BirkäUse., NY 55, 94 (2015).
MATH Google Scholar
Peyré, G. et al. Computational optimal transport: With applications to data science. Found. Trends® Mach. Learn. 11, 355–607 (2019).
Article MATH Google Scholar
Cuturi, M. Sinkhorn distances: Lightspeed computation of optimal transport. Advances in neural information processing systems 26 (2013).
Flamary, R. et al. Pot: Python optimal transport. J. Mach. Learn. Res. 22, 1–8 (2021).
MATH Google Scholar
Klopfenstein, D. et al. Goatools: A python library for gene ontology analyses. Sci. Rep. 8, 10872 (2018).
Article ADS CAS PubMed PubMed Central MATH Google Scholar
Cowley, M. J. et al. Pina v2. 0: Mining interactome modules. Nucleic Acids Res. 40, D862–D865 (2012).
Article CAS PubMed Google Scholar
Wu, J. et al. Integrated network analysis platform for protein-protein interactions. Nat. Methods 6, 75–77 (2009).
Article CAS PubMed MATH Google Scholar
Liao, X. et al. Multivariate stochastic modeling for transcriptional dynamics with cell-specific latent time using SDEvelo https://github.com/Liao-Xu/SDEvelo (2024).

Download references

Acknowledgements

This work was partially supported by the National Natural Science Foundation of China (grant No. 12371283 to J.L.; No. 12371441 and U24A2002 to Y.J.), the University Development Fund from the Chinese University of Hong Kong, Shenzhen (grant No. UDF01003033), the Guangdong Provincial Key Laboratory of Mathematical Foundations for Artificial Intelligence (grant No. 2023B1212010001), Shenzhen Key Laboratory of Cross-Modal Cognitive Computing (grant No. ZDSYS20230626091302006), and the Fundamental Research Funds for the Central Universities. We express our sincere gratitude to the editorial board for their guidance and to the three reviewers for their valuable feedback. Their insights and constructive comments have significantly improved our manuscript and enhanced the quality of our work.

Author information

These authors contributed equally: Xu Liao, Lican Kang.

Authors and Affiliations

School of Data Science, The Chinese University of Hong Kong-Shenzhen, Shenzhen, China
Xu Liao, Yihao Peng & Jin Liu
Centre for Quantitative Medicine, Duke-NUS Medical School, Singapore, Singapore
Xu Liao
Institute for Math and AI, Wuhan University, Wuhan, China
Lican Kang
School of Mathematics and Statistics, Wuhan University, Wuhan, China
Lican Kang
Cancer and Stem Cell Biology Program, Duke-NUS Medical School, Singapore, Singapore
Xiaoran Chai
School of Biological Science & Medical Engineering, Southeast University, Nanjing, China
Peng Xie
Key Laboratory of Developmental Genes and Human Disease, School of Life Science and Technology, Southeast University, Nanjing, China
Chengqi Lin
Department of Biostatistics, Johns Hopkins Bloomberg School of Public Health, Baltimore, Maryland, USA
Hongkai Ji
School of Artificial Intelligence, Wuhan University, Wuhan, China
Yuling Jiao
Hubei Key Laboratory of Computational Science, Wuhan University, Wuhan, China
Yuling Jiao

Authors

Xu Liao
View author publications
Search author on:PubMed Google Scholar
Lican Kang
View author publications
Search author on:PubMed Google Scholar
Yihao Peng
View author publications
Search author on:PubMed Google Scholar
Xiaoran Chai
View author publications
Search author on:PubMed Google Scholar
Peng Xie
View author publications
Search author on:PubMed Google Scholar
Chengqi Lin
View author publications
Search author on:PubMed Google Scholar
Hongkai Ji
View author publications
Search author on:PubMed Google Scholar
Yuling Jiao
View author publications
Search author on:PubMed Google Scholar
Jin Liu
View author publications
Search author on:PubMed Google Scholar

Contributions

J.L. initiated and designed the study, X.L. revised and implemented the model and developed the pipeline with assistance from L.K., X.C., and Y.J.; X.L., Y.P., and X.C. performed the benchmark evaluations and the downstream analyses; J.L. and X.L. wrote the manuscript, and X.L., L.K., X.C., P.X., C.L., H.J., Y.J., and J.L. edited and revised the manuscript.

Corresponding authors

Correspondence to Yuling Jiao or Jin Liu.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Communications thanks Anthony Baptista, Sijie Chen and Dario Righelli for their contribution to the peer review of this work. A peer review file is available.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Description of Additional Supplementary Files

Supplementary Dataset 1

Reporting Summary

Transparent Peer Review file

Source data

Source Data

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.

Reprints and permissions

About this article

Cite this article

Liao, X., Kang, L., Peng, Y. et al. Multivariate stochastic modeling for transcriptional dynamics with cell-specific latent time using SDEvelo. Nat Commun 15, 10849 (2024). https://doi.org/10.1038/s41467-024-55146-5

Download citation

Received: 02 May 2024
Accepted: 28 November 2024
Published: 30 December 2024
DOI: https://doi.org/10.1038/s41467-024-55146-5

This article is cited by

Multivariate stochastic modeling for transcriptional dynamics with cell-specific latent time using SDEvelo
- Xu Liao
- Lican Kang
- Jin Liu
Nature Communications (2024)