A dexterous and compliant aerial continuum manipulator for cluttered and constrained environments

In the past decade, unmanned aerial vehicles (UAVs) gain significant interest from both robotics researchers and industry. UAV applications are rapidly expanding, including infrastructure monitoring, agriculture, and disaster response¹. To increase UAV capabilities, they have to evolve from passive flight platforms to active manipulators capable of grasping, maintenance, and installation tasks. Helicopters or multi-rotors equipped with robotic systems, like grippers and arms, enable aerial manipulators (AMs) to perform tasks such as transporting, positioning, and assembly^2,3,4. This mobility allows AMs to assist in hazardous or inaccessible environments, like post-disaster sites, construction zones, and high structures^5,6.

Despite the advantages of AMs, designing efficient manipulation systems remains a technical challenge, particularly for grasping in constrained environments^7,8,9,10. While aerial grippers are developed for basic pick-and-place tasks^11,12, their manipulation abilities are limited. Rigid-link robotic manipulators, offering more degrees of freedom (DOFs), are becoming mainstream^{13,14,15,16,17,18}, enabling complex operations in confined spaces. However, this also makes control more challenging when dealing with obstacles^{19,20,21,22,23}. A key challenge with rigid-link manipulators is that the arm’s weight reduces the UAV’s payload capacity, creating a trade-off between the DOFs and payload limits. Higher DOFs add weight, so small UAVs typically carry robotic arms with up to 3 DOFs^{24,25,26,27,28}, while larger UAVs like octo-rotors or helicopters are needed for arms with more DOFs^29,30. These larger UAVs allow more complex tasks (e.g., perching, force exertion)^{31,32,33,34,35,36,37,38}, but are restricted to open areas. Additionally, the inclusion of additional joints and motors increases arm inertia, necessitating greater energy and time for controlling movements, thereby affecting overall efficiency.

The trade-off between DOFs and weight limits the dexterity of rigid-link manipulators, but a recent concept, aerial continuum manipulators (ACMs) offers a solution^39,40. ACMs are designed with lightweight, flexible continuum arms that can bend compliantly, making them suitable for accessing confined spaces and performing complex manipulation tasks. Unlike conventional robotic arms with discrete joints, continuum arms^{41,42,43,44,45,46,47,48,49,50,51,52} have a continuous, flexible backbone, providing near-infinite DOFs due to omnidirectional bending, making them highly dexterous and ideal for varied aerial tasks⁵³. Despite their dexterity, continuum manipulators face significant design challenges. Existing actuation systems are often large and complex, as they require multiple sections for high dexterity and larger workspaces, which in turn demand more actuators. To minimize arm inertia, actuators should ideally be placed outside the continuum arm, but as sections increase, so does the distance to actuators, complicating the system further^54,55,56. Such bulky designs are impractical for low-payload UAVs like quadrotors, making them unsuitable for aerial manipulation.

According to the actuation mechanism, continuum arms are roughly categorized into tendon-driven, pneumatic, and material-driven types, among which tendon-driven ones have the largest payload bearing capacity. However, the challenge of controlling tendon-driven continuum arms is tendon slacking^57,58,59,60 during bending motions. Tendon slacking occurs frequently when the tension of the tendon changes significantly. As such, a tendon-slacking prevention mechanism is usually required. It further increases the weight and complexity of the actuation system. Otherwise, it is unreasonable for UAVs that have limited payload capacity to carry such a heavy system. Thus, current ACMs in the literature have made many compromises. State-of-the-art designs on aerial continuum arm either only have one section⁶¹ or simply install the actuation system on the ground⁶². Other studies only deploy a virtual model of an ACM in simulation to conduct theoretical analysis without a real hardware design⁶³. Apart from these issues, the control of continuum arms also remains challenging. Due to significant nonlinearities introduced by the bending motion, modeling of continuum arms is difficult. Furthermore, tendon slacking also brings uncertainties to the controller design. Therefore, it is straightforward that combining UAVs with tendon-driven continuum arms makes ACMs even more difficult to realize.

To avoid the rigid-link mechanism, and facilitate the feasibility of continuum arms, we propose Aerial Elephant Trunk (AET), a lightweight yet highly dexterous aerial continuum manipulator in this work. The arm of AET is highly dexterous and resembles the elephant trunk. A comparison with existing AMs in terms of weight and DOF is given in Supplementary Note 1. In contrast to conventional rigid-link AMs that house motors within the arm’s body, AET strategically locates all motors externally to the arm’s structure. This significantly reduces the inertia of the arm as motors are the main source of weight. A low-inertia arm is beneficial as it is easier to actuate the motion of the arm and saves energy. It is important to note that we design the arm’s actuation system to be as compact as possible, ensuring that the continuum arm system can be efficiently accommodated by a small-scale quadrotor. Another comparison with existing continuum manipulators in terms of design and motion capabilities is present in Supplementary Note 2. Another advantage is that it can adapt to the environments and the objects. AET is compliant as it can bend and deform to various shapes to operate in complicated environments. This is useful for aerial manipulation as the environments in which UAVs work are usually complex, unstructured, and filled with obstacles. AET can also use its arm to interact with objects with irregular shapes and sizes in aerial flights as the elephant trunk does, which is a special capability not owned by conventional rigid-link AMs.

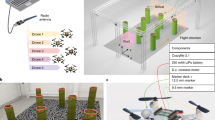
In our experiments, we validate the fundamental attributes of the continuum arm using the robust hardware system, assessing parameters such as maximum bending ranges, bending velocity, and the upper limit of tip loading. We then analyze the dexterity distribution within the arm’s effective workspace to inform motion planning strategies. Moreover, we evaluate the precision of the geometrical configuration solver, which is derived from actuated tendon lengths, and the efficacy of the close-loop tip’s pose control, grounded in the inverse kinematic (IK) model. Leveraging these comprehensive evaluations, we conduct experiments on obstacle avoidance and object winding, guided by our findings. Additionally, the assessment of AET’s flight control system confirms its proficiency in aerial manipulation. As a result, we convincingly demonstrate AET’s dexterity and compliance through the execution of aerial manipulation tasks. AET showcases remarkable proficiency in winding objects of various irregular shapes and sizes by leveraging the full extent of its arm. It also exhibits the capability to navigate through semi-closed constrained environments. Then, we demonstrate AET’s ability to perform aerial grasping in complex, unstructured, cluttered environments fraught with obstacles. Finally, we demonstrate the capability of automatic whole-body planning through aerial locomotion experiments, utilizing a comprehensive combined kinematic model. These findings highlight the potential of our AET to undertake more intricate aerial manipulation tasks across a spectrum of scenarios, as vividly depicted in Fig. 1a, b, c, d.

a Grassland. b Blue sky. c Factory. d Chemical scenario.

Full size image

AET system overview

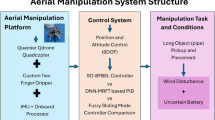
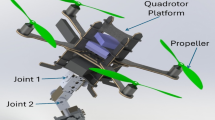
AET comprises a lightweight UAV and a three-section tendon-driven continuum arm, featuring a highly compact actuation system, as depicted in Fig. 2a. The total weight of AET stands at 1.8 kg, with over half of this weight attributed to the onboard computer, LIDAR, MCU board, and battery. The mechatronics architecture is detailed in Fig. 2b, highlighting the integration of the flight controller and the arm’s controller into a single MCU board.

a Appearance diagram of AET with the mechanical design of the manipulator’s torso which is divided into three sections. A simple bending motion which is actuated by inside tendons, is shown beside AET. b Components description of computing devices and electronics modules. c Detailed mechanical description of the mid disks and end disks with the arm’s IMUs. d Mechanical design of the manipulator’s actuation system, whose base contains six tendon motors with shafts and winding reels. Each tendon motor drives a pair of diagonal tendons, which are marked with green, blue, and red colors pointing to different sections.

Full size image

The lightweight UAV platform is a quadrotor constructed from aluminum metal, boasting an edge length of 318 mm. This UAV serves as a stable floating platform in three-dimensional space for the three-section continuum arm, which measures 630 mm in total length and 25 mm in cross-sectional radius, as shown in Fig. 2c. The manipulator’s torso, weighing just 155 g, significantly contributes to its overall lightweight design, with further details provided in Supplementary Table 3. Also, we simulate the force effects on a single section using Finite Element Analysis (FEA), as detailed in Supplementary Note 3. Additionally, Supplementary Movie 1 provides a visual demonstration of the outdoor aerial flights, showcasing the dynamic shape deformation of the continuum arm.

Compact continuum arm actuation system

To create a compact actuation system suitable for a small quadrotor to transport, we have implemented three key strategies: (1) reducing the number of motors, (2) designing a compact structural layout for the actuation system, and (3) employing a controller-based approach to prevent tendon slackening. The structural overview of this actuation system is visually represented in Fig. 2d. Traditionally, continuum arms have utilized four independent motors to drive the four tendons in each section⁶⁴. More recent advancements have seen a reduction in the number of tendons to three, forming an equilateral triangle⁶⁵. However, further reduction in the number of tendons appears impractical due to the requirement for omnidirectional rotation capabilities. In our design, we maintain the use of four tendons for each continuum section. Each tendon motor is configured to drive a pair of diagonal tendons, thereby enabling the actuation of one continuum section with just two motors. One tendon is wound clockwise onto the reel, while its diagonal counterpart is wound counterclockwise. As the section bends towards a specific tendon, it is pulled by the corresponding motor, with the length of the tendon pulled being equally released to its diagonal counterpart during the bending motion. This innovative motor reduction effectively mitigates the common issue of tendon slackening in multi-section continuum arms. Additionally, we have arranged all six motors horizontally within a single plane to minimize the height of the actuation system. We utilize various iron rings to manage the path each tendon takes, ensuring they do not intersect with others. This compact structural design allows for integration with a lightweight quadrotor, enhancing portability and functionality.

Kinematic configuration and software architecture

Figure 3a presents AET airborne, alongside its synchronized model within the simulation environment. The figure correlates the generalized coordinate frames and states, and details the continuum arm’s configuration, which is resolved through the actuated lengths. The bending angles and direction angles are also illustrated in the analysis diagram of the continuum arm. In Fig. 3b, the systematic software architecture of AET is depicted. The LiDAR-IMU odometry (200 Hz) contributes to position estimation through point cloud and IMU measurements⁶⁶. The onboard IMU captures accelerations and angular velocities, which are fed into an EKF (1000 Hz) to yield attitude estimation. The manipulator configuration solver (500 Hz), responsible for determining the manipulator’s shape, is derived from the actuated lengths of all the tendons. Subsequently, we develop a real-time state visualization simulator (30 Hz) to depict the comprehensive state of AET, encompassing position, attitude, and manipulator configuration.

a Generalized frames and configuration of AET system with state illustration on actual AET in air and its synchronized virtual model. b Essential software systems developed for AET, including state estimation, kinematics solver, flight controller, and manipulator controller.

Full size image

In alignment with aerial manipulation missions and environments, the flight controller integrates a position and velocity controller (100 Hz), an attitude controller (200 Hz), and an angular velocity controller (500 Hz). For manipulator control, a three-tier control structure is employed: the geometric controller (100 Hz) generates desired tendon tensions for the tendon tension controller (200 Hz), which in turn derives desired tendon speeds for the linear speed controller (500 Hz). Both the flight controller and the manipulator controller are constructed upon feedback from the entire state, as illustrated in Fig. 3b.

Arm fundamental motion verification

Each arm segment is driven by two orthogonal tendon sets, each controlled by a separate motor. To test 3D movement, we send speed commands to all six motors and record sensory data, as shown in Fig. 4a. During the verification motion, the ith and i + 1th tendon motors (i ∈ {1, 3, 5}) output actuated length (ΔL_i, ΔL_i+1) and tendon tension (t_i, t_i+1). IMUs on the end disks provide real-time attitude and angular data (\({\theta }_{j}^{m},{\phi }_{j}^{m}\), \({\dot{\theta }}_{j}^{m},{\dot{\phi }}_{j}^{m}\), j ∈ {1, 2, 3}), showing that these changes are influenced by actuated lengths and tensions, as depicted in Fig. 4a. Additionally, the bending angle α^j, which is calculated based on the corresponding actuated lengths, undergoes simultaneous alterations. For general motions, the speed command of one tendon motor is limited within [−5, 5] mm ⋅ s⁻¹. The tendon’s change of length and tension are limited within [−20, 20] mm and [−1, 1] kg ⋅ cm, respectively. The end disk’s attitude and angular speed are limited within [−100, 100] degrees and [−2, 2] rad ⋅ s⁻¹, respectively. Extensive real-motion testing has validated our continuum arm’s effectiveness in overcoming common challenges like tendon slackening and structural fragility without overshoots or noise.

“CMD” means commands, “EST” means estimates, and “MEA” means measurements. θ^u and ϕ^u denote UAV's attitude. a The actuation mechanism of the continuum arm with essential measurable signals during individual bending motion. b, c, d Limitation evaluation of the bending range, the bending velocity, and the arm tip loading capacity. e Attitude control verification of AET. f Workspace and dexterity maps derivation of the continuum arm.

Full size image

The bending angles of each section are limited by the actuation tendon tension’s upper threshold. By testing each section individually with other end disks kept horizontal, we measure the attitude angle until tendon tension limits are reached, determining maximum bending ranges: 105 degrees for the first section, 120 degrees for the second, and 132 degrees for the third, as depicted in Fig. 4b. The bending velocity of each section affects the arm’s motion response and task efficiency. We test each section individually, recording the maximum angular velocity of each end disk as tendon tension nears its limit, as shown in Fig. 4c. The results are: 1.6 rad ⋅ s⁻¹ for the first end disk, 1.5 rad ⋅ s⁻¹ for the second, and 1.7 rad ⋅ s⁻¹ for the third, respectively. We determine the continuum arm’s payload capacity by placing it under closed-loop control to maintain a straight line, then increasing the tip weight and monitoring shape deformation. We record tendon tensions and end disk attitudes, as shown in Fig. 4d. Below 0.75 kg, tensions are within [−0.1, 0.1] kg ⋅ cm and attitudes within [−2, 2] degrees, indicating minimal shape change. Above 0.8 kg, significant deformation occurs.

After verifying the continuum arm’s basics, we assess AET’s aerial flight using a closed-loop attitude control system based on quadrotor state estimation, as shown in Fig. 4e. During flight, rotor thrusts are kept at 50% Given the total weight of AET, which stands at 1.8 kg, it is prudent to limit the external payload to less than 0.8 kg to ensure the safety of aerial activities. The desired pitch θ^u and roll ϕ^u angles are prescribed within the range of [−20, 20] degrees. we observe that the attitude tracking remains nimble, with the tracking errors for the pitch angle θ^u and the roll angle ϕ^u confined to [−0.8, 0.8] degrees and [−0.4, 1] degrees, respectively.

Workspace and dexterity analysis of the continuum arm

Leveraging the tested bending ranges of the three sections, we discretely sample each section’s bending range and calculate the 6 DOF pose of the arm’s tip through forward kinematics. Subsequently, we extract the translation components from all the resolved tip poses, representing numerous locations relative to the arm’s base frame. These locations collectively define the effective 3D workspace of the continuum arm. Given the omnidirectional nature of the continuum sections, we present the XOZ plane of the 3D workspace in Fig. 4f, designating the XOZ plane as a workspace map for subsequent analysis. Broadly, the 3D workspace is confined within the bounds: X, Y ∈ [−55, 55] cm and Z ∈ [−63, 20] cm with respect to the base frame. Within the workspace map, we randomly select three distinct ___location points, for each of which we visualize one or several virtual AET configuration shapes, ensuring each shape’s tip aligns with its corresponding ___location point.

As depicted in Fig. 4f, each ___location point within the workspace map is associated with multiple configuration shapes, each featuring different rotation vectors at the tips. These vectors, termed effective rotation vectors, are derived from the orientation components of the tips’ 6 DOF poses. Additionally, we delineate circles around these tips’ locations, defining these circles as the tip’s rotation range. Within each circle, all the effective rotation vectors of the arm’s shapes can form a circular sector. The ratio of the circular sector’s area to the entire circle’s area is then defined as the dexterity rate of the selected ___location point⁶⁷. For example, we calculate all the effective rotation vectors for the aforementioned ___location points in the workspace map and illustrate the relationship between these rotation vectors and the locations’ rotation ranges in Fig. 4f. We calculate the dexterity rates for these three locations, yielding 37.8%, 64.3%, and 85.4%, respectively. A higher dexterity rate at a ___location indicates a greater variety of configuration shapes the arm can adopt around that same ___location. In this manner, we calculate the dexterity rate for every individual ___location within the workspace map and present all the dexterity rates as a color map in Fig. 4f. This color map, also known as the dexterity map, facilitates the planning of more successful motions in regions with high dexterity rates (≥50%), as the arm’s tip enjoys more options for shape deformation in these areas.

Shape estimation of the continuum arm

Actuated lengths are critical for the continuum arm’s configuration in closed-loop control. We perform repeatable swinging motions to collect data on configuration changes with actuated lengths. Using forward kinematics, we calculate each end disk’s 3 DOF orientation and convert it to Euler angles. Each end disk has an IMU for precise attitude measurements. Comparing our estimated Euler angles with IMU data evaluates our configuration estimation accuracy. We perform individual swinging motions for each section, recording data as shown in Fig. 5a. The actual and virtual arms are displayed, with each section’s motion lasting 40 s within a 120 s experiment. We compare estimated attitudes with IMU measurements, finding attitude errors within [−10, 10] degrees, with average errors near zero. This indicates our shape estimation method is feasible, providing precise configurations based on actuated lengths, with each section’s estimation independent of others.

“EST” denotes estimates and “COM” denotes center of mass. “deg” means degrees. τ_arm denotes arm’s shifting moment. a Single section’s shape estimation. b Multiple sections' shape estimation. c Illustration of arm’s COM in simulation. d Evaluation of arm’s COM in actual motions.

Full size image

We assess multi-section configuration estimation during complex arm motions, as shown in Fig. 5b, where the arm undergoes random actuated length changes over 100 s. We display nine pairs of shapes: estimated “Estimate” and actual “Real”. Although the estimated shapes closely match the actual ones, we consolidate them into series “M1” to “M9” for systematic evaluation. We calculate similarity values by averaging section curvatures, finding a range from 81.7% to 97.2% in a histogram, with variance due to the partial arm’s weight affecting the constant curvature assumption. Despite this, our method provides accurate real-time configuration results, showcasing its robustness and utility. We record experimental data including actuated lengths, bending angles, estimated end disk attitudes, and IMU measurements, as shown in Fig. 5b. Estimated attitudes match IMU data in three graphs, with average attitude errors of 2.2 degrees for the first end disk, 5.6 degrees for the second, and 1.6 degrees for the third. Compared to single-section estimation in Fig. 5a, multi-section estimation shows a 3.1 degrees average error increase, which is acceptable for the arm’s overall motion.

Estimation of the continuum arm’s COM

We estimate each section’s center of mass (COM) relative to the base frame after establishing the continuum arm’s configuration space. We simulate AET’s virtual model in the simulation environment with a sequence of bending angles, showing four COM locations in Fig. 5c. We record bending angles and corresponding COM moments, summing them to find the total COM moment for the arm. This moment disturbs the quadrotor system, prompting the flight controller to adjust thrusts for stability, enabling AET to maintain stable flight during arm movements.

After showing the arm’s estimated COM, we assess COM estimation precision by attaching a rotation torque sensor to the base frame for accurate moment measurements. The arm performs random movements within its resolved configuration space. We calculate the real-time COM moment and compare it with sensor measurements in the curve graph, as shown in Fig. 5d, displaying five arm shape states with the rotation torque sensor. Moreover, the average moment error consistently hovers around zero, and the real-time moment error fluctuates within a narrow range of [−0.1, 0.1] kg ⋅ cm. This observation underscores that, irrespective of the arm’s motion, the error associated with its disruptive moment is consistently kept at a minimal level. The comprehensive evaluation of the COM’s moment serves to further corroborate the dependability of the shape estimation method.

Arm’s inverse kinematic model evaluation

The IK model determines the desired configuration space for the tip’s 6 DOF pose. A human-controlled 6 DOF pose interactor provides real-time desired poses for the IK model, which calculates the optimal configuration space, allowing the AET model’s tip to track desired poses in the simulation environment, as shown in Fig. 6a. Over 240 s, we demonstrate eight shapes tracking the interactor across various poses. The configuration controller guides the continuum arm to converge its current estimated configuration towards the desired configuration, enabling both estimated and actual shapes to track desired shapes in real-time, as seen in Fig. 6a and Supplementary Movie 2. We compare desired poses with current poses resolved by the forward kinematic model, finding nimble responses in tracking commands. Position errors are within [0.005, 0.03] m, and orientation errors are within [0.01, 0.07]. Larger errors mostly occur during pose tracking, but static interactor states yield zero pose error, as shown in Fig. 6a. The current configuration effectively tracks the desired configuration, with tracking results clearly displayed in Fig. 6a, showcasing the system’s performance.

“CMD” means commands and “EST” means estimates. \([{p}_{x}^{e},{p}_{y}^{e},{p}_{z}^{e}]\) and \([{q}_{x}^{e},{q}_{y}^{e},{q}_{z}^{e},{q}_{w}^{e}]\) denote arm tip’s position and orientation. [α, β] denotes arm’s configuration space. S_obj and m_obj denote object’s grasped area and weight. a Inverse kinematic model evaluation. b Obstacle avoidance c Vertical object winding. d Horizontal object winding. e Evaluation of the object winding range.

Full size image

Object interaction by IK within the arm’s workspace

Using the validated IK model, the continuum arm’s tip tracks a trajectory of desired poses. In Fig. 6b, the tip navigates around an obstacle to reach the target pose, with the distance to the target reducing from 0.15 m to  m in 35 s. Leveraging the IK model, we explore more compliant functionalities, such as winding objects, inspired by elephants. In Fig. 6c, we guide the arm’s tip to envelop a white cylinder using desired tip poses, successfully winding a 556 g object vertically. In Fig. 6d, we repeat the experiment with a different trajectory, wrapping around a vertical bottle. The arm effectively grasps the 141 g bottle, demonstrating its compliance and robust strength. These experiments validate the IK model’s efficacy in Cartesian space motion and confirm the arm’s object-winding proficiency.

We rigorously test the continuum arm’s object winding proficiency using six varied objects with different weights, sizes, and materials. We use the IK model to create custom winding trajectories for each object. The arm successfully winds objects including tools (weighing 360 g), a robot arm (weighing 727 g), a bag (weighing 521 g), a pillow (weighing 350 g), a hand drill (weighing 1136 g), and a drone (weighing 1188 g). Concurrently, each object undergoes five trials, and the success rates are as follows: white cylinder (100%), bottle (80%), tools (60%), robot arm (100%), bag (100%), pillow (100%), hand drill (60%), and drone (40%). Our tests show the continuum arm can wind objects under 1200 g with contact areas between 50 cm² and 400 cm², as shown in Fig. 6e. The payload capacity is quantified by a ratio of 7.74 (maximum object-winding weight 1200 g to arm weight 155 g).

AET control evaluation in aerial flights

Following a series of comprehensive evaluation experiments on the continuum arm, we proceed to test the integrated motion capability of the AET by conducting shape transition motions during aerial flights. The UAV system is tasked with maintaining stable hovering flights at a predetermined setpoint, while the continuum arm is dynamically controlled to alter its shapes through a sequence of consecutive desired configuration angles. As illustrated in Fig. 7a, we present ten sets of the desired configurations alongside the actual configurations of the continuum arm. Concurrently, we meticulously document the experimental data and visually represent them in curve graphs. The analysis reveals that the estimated bending angles adeptly track the desired angles with remarkably low errors. This combined motion serves to further validate the system’s feasibility of the AET during aerial flights.

“CMD” means control commands and “GT” means ground truth. \([{p}_{x}^{u},{p}_{y}^{u},{p}_{z}^{u}]\) and [ϕ^u, θ^u, ψ^u] denote UAV's position and orientation. a Evaluation on the continuum arm’s shape control during aerial flights. b UAV's level circle-trajectory tracking. c UAV's level rectangle-trajectory tracking. d UAV's vertical heart-trajectory tracking. e UAV's vertical eight-trajectory tracking.

Full size image

Then, we validate the tracking performance of the entire aerial continuum manipulator. We have meticulously designed four distinct trajectories for the UAV to track within the 3D space: the level circle trajectory (as depicted in Fig. 7b), the level rectangle trajectory (shown in Fig. 7c), the vertical heart-trajectory (illustrated in Fig. 7d), and the vertical eight-trajectory (exhibited in Fig. 7e). In each trajectory-tracking experiment, AET can successfully track the UAV’s desired positions even though the arm conducts repetitive swing motions. Additionally, the fluctuations in attitude are effectively contained within the range [−5, 5] degrees for the majority of the time. This performance underscores that the flight controller is capable of ensuring stable flights for the UAV platform during aerial manipulation tasks, as vividly demonstrated in the supplementary Supplementary Movie 3.

Aerial object winding

The AET exhibits the remarkable ability to adapt to objects of varying shapes, sizes, and poses, a capability we will showcase through a series of challenging scenarios that are often intractable for conventional grippers. We focus on three specific cases: a horizontally placed pillar, a vertically placed pillar, and a bench with an irregular shape. The difficulty in winding these objects using grippers primarily stems from their dimensions; their substantial radii pose significant challenges, even for large grippers, which can easily lose balance if not grasped near the center of gravity.

To tackle these challenges, we leverage AET’s unique whole-body manipulation ability, a feature not commonly found in traditional AMs. The winding process is orchestrated into four sequential steps: approaching, winding, transporting, and dropping. In Fig. 8a, AET initiates the approach to the horizontal pillar with a front-top bending shape at t = 19 s. By t = 23 s, AET employs its entire body to form an O shape, effectively winding the pillar without the need for a gripper. The successful completion of the task is marked at t = 41 s. This intricate motion is the result of synchronized trajectory control of the aerial platform and configuration control of the continuum manipulator, with both the desired UAV trajectory and arm configuration being dynamically provided by a remote operator in real time. For the vertical pillar scenario, AET’s approach diverges from the previous O-shaped winding. Recognizing the potential for the pillar to slide during transportation, AET adopts a spiral shape to wind the pillar multiple times, ensuring a secure grasp and preventing any slippage, as demonstrated in Fig. 8b. The final demonstration involves winding a bench with an irregular shape, a task fraught with challenges and risks when attempted with a gripper. However, AET’s versatility shines through as it approaches the bench, employing the closed-loop configuration control of its continuum arm to wind the corner, as seen in Fig. 8c. Following the winding, AET proceeds to transport and drop the bench at the designated destination.

The AET showcases its versatility by adeptly winding a diverse array of objects, leveraging its unique whole-body manipulation capability. Furthermore, AET exhibits adaptability by adjusting the states of its arm to conform to the contours of a tube, thereby enabling it to seamlessly navigate through the tube’s confines. a A level pillar winding. b A vertical pillar winding. c A bench winding. d AET navigates through the L-shaped tube. e AET navigates through the C-shaped tube. f AET navigates through the S-shaped tube.

Full size image

These experiments unequivocally highlight AET’s unique object-winding capabilities, showcasing its ability to adapt to a diverse array of objects through shape deformation, as demonstrated in Supplementary Movie 4. By morphing into various shapes, AET not only winds objects but also secures them to prevent any falls, positioning it as an exceptional platform for aerial transportation.

Aerial object adaptation

The operational environments for AMs are typically far more complex than those encountered by ground mobile manipulators. These versatile devices are employed in a variety of settings, including construction sites, post-earthquake zones, bridges, forests, and power lines. Such environments are often characterized by their complexity, constraints, and unstructured nature, making them one of the most formidable challenges in the realm of grasping technology. The capacity to operate effectively within these intricate environments holds the potential to significantly expand the practical applications of AMs.

In recognition of this, we showcase the ability of the AET to function within constrained or semi-closed environments. To simulate such a challenging setting, we employ a pipeline featuring bends in the shapes of L, C, and S, which presents a slender (with a radius of 6 cm), semi-closed, and uniquely shaped passage that poses significant difficulties for conventional rigid-link AMs. Drawing upon the specific shapes of the pipelines, we pre-define the arm’s configuration and execute the desired tracking motions during actual experiments under the guidance of human teleoperation. As shown in Fig. 8d, e, f and Supplementary Movie 5, AET demonstrates its proficiency by successfully navigating through the pipeline, which is intricately bent into these specific shapes. The key to this success lies in AET’s inherent continuous motion capability. The ability to bend continuously allows it to adapt seamlessly to the convoluted and narrow confines of the pipeline.

Aerial grasping within complex cluttered environments

Under the guidance of human teleoperation and predefined tracking motions, we aim to validate the manipulation capabilities of the AET in navigating through complex cluttered environments replete with obstacles. In Fig. 9a, we meticulously arrange several stacked boxes, creating a vertical gap and positioning an object to be grasped beneath one of the boxes. The crux of the challenge lies in the long, narrow gap between the two boxes. To successfully traverse this gap and grasp the object, the robotic arm must exhibit exceptional flexibility; otherwise, the UAV risks colliding with the boxes as the robotic arm extends to reach the magnetic object. To this end, we equip the arm’s tip with a magnet. The entire process is systematically divided into four distinct steps: entering the environment, navigating within the environment or avoiding obstacles, interacting with the object, and retreating. Fig. 9a chronicles the sequences of AET executing each step, culminating in the successful completion of the grasping process.

We set up three different challenging scenarios: a an L crevice (12 cm × 12 cm  × 40 cm). b Single hole and box (5 cm + 8 cm × 15 cm). AET has to pass through a hole and avoid an obstacle to reach the object. c Double holes (5 cm × 5 cm). AET has to pass through two holes and then bend to reach the object.

Full size image

In the second experiment (Fig. 9b), we escalate the complexity of the aerial manipulation task. Here, the object is placed within a semi-closed box featuring circular holes. The AM must navigate through these holes to access the box and subsequently evade an obstacle to ultimately reach the object. Given the small size of the holes (with a radius of 5 cm), conventional AMs, hindered by their rigid links, would find it challenging to penetrate the box, let alone maneuver around obstacles to grasp the object. However, as depicted in Fig. 9b, AET adeptly enters the box through the hole, sidesteps the obstacle, and successfully grasps the object, thereby showcasing its proficiency in operating within highly intricate environments. Lastly, in Fig. 9c, the environment presents an even greater level of complexity. It is assumed that the object can only be accessed via the circular hole of the transparent box. To clearly demonstrate the manipulator’s motion, we ensure the front and back sides of the object are unobstructed. This task poses a significant challenge, as the AM must pass through two holes on the top and right side (highlighted by orange circles) of the transparent box and then bend its arm to reach the object. Owing to its dexterity and compliance, AET triumphantly accomplishes these tasks, as evidenced in Supplementary Movie 6.

Whole-body motion planning for aerial manipulation

Based on the developed whole-body motion planning, we perform automatic aerial locomotion tasks using our AET. Two aerial locomotion tasks are designed: aerial writing and aerial traversal. In both tasks, only waypoints are pre-defined. All the motion planning and control is computed onboard in real time without any human intervention.

In Fig. 10a, we establish a series of waypoints to create a sequence of alphabets: ARCLAB on the horizontal plane, maintaining the same height as the initial tip height, and instruct AET’s end-effector to track this consistent trajectory. The trajectory is dynamically planned online, based on the initial pose of the tip within the world frame. Throughout the tracking motion, we progressively display the desired end trajectory and the estimated end trajectory derived from forward kinematics, synchronized with the time frame, to assess the tracking performance. Concurrently, we record experimental data pertaining to the end position, the UAV position, and the bending angles of the three continuum sections for comparison against their respective commands. The results vividly illustrate the tracking response and errors, conducted under a trajectory velocity of 0.1 m ⋅ s⁻¹.

“CMD” means control commands, “GT” means ground truth, and “EST” means estimated results. \([{p}_{x}^{e},{p}_{y}^{e},{p}_{z}^{e}]\) denotes arm tip’s position. \([{p}_{x}^{u},{p}_{y}^{u},{p}_{z}^{u}]\) denotes UAV's position. α denotes the arm section’s bending angle. a ARCLAB trajectory tracking. b Ring crossing for end-effector trajectory tracking.

Full size image

In Fig. 10b, we introduce a static ring with a diameter of 0.24 m as a confined space. We set a few waypoints to guide AET to traverse the ring and reach the final goal position. Through the developed motion planning and tracking controller, AET can generate a smooth trajectory online and follow the trajectory to traverse the ring and reach the final goal successfully without any human intervention. The seamless transition motion is executed successfully within a span of 25 s, whereas manual performance would incur a duration exceeding 60 s. These experiments (Supplementary Movie 7) fully demonstrate the capability of AET for aerial manipulation tasks.

In this research, we have innovated AET, a remarkably compliant and dexterous AM, extensively featured in Supplementary Movie 8. AET employs a triple-section continuum arm for efficient manipulation tasks. We have engineered a compact actuation system with all motors aligned on a single plane, optimizing motor usage without extra pretension hardware, resulting in just six motors powering three arm sections. This design allows a lightweight quadrotor to support the dexterous continuum arm.

For this innovative AM, we have developed critical estimation and control technologies, including UAV state estimation, continuum arm kinematic modeling, a multi-layer flight controller, and a continuum arm configuration controller, enabling comprehensive aerial manipulation capabilities. We have assessed the continuum arm’s core attributes and confirmed the viability of its forward and IK modeling. These evaluations have validated its adaptability to various grasped objects and operational environments. Utilizing our developed estimation and control technologies, AET can effectively manage configuration control and dynamically alter its form.

Extensive aerial trials have shown AET’s ability to adapt to objects of diverse irregular shapes and sizes, employing its entire arm to intricately wrap around objects using various shaped bends. Notably, AET has showcased exceptional manipulation skills in semi-closed constrained environments like pipelines of varying shapes. Moreover, its prowess was vividly demonstrated in complex, cluttered, unstructured environments with obstacles, where AET navigated through box holes, evaded obstacles, secured objects, and returned to its original position. Also, the whole-body planning technique enhances its efficiency in autonomous aerial manipulation.

AET significantly advances the practical utility of aerial manipulation, addressing the inherent trade-off between payload capacity and dexterity faced by current AMs. The rigid joints and links of existing arms severely limit their operational environments, lacking the necessary compliance for unstructured settings. AET, thanks to its compact design and reduced motor count, boasts high compliance and dexterity while maintaining payload capacity, making it suitable for a broad range of industrial applications such as powerline inspection, bridge maintenance, construction site monitoring, post-earthquake area assessments, and search and rescue operations. These applications demand high compliance and obstacle-avoidance capabilities from AMs.

In summary, with its superior compliance and dexterity, AET is versatile for various aerial manipulation scenarios. Looking ahead, our future research will concentrate on enhancing AET’s perception for fully autonomous aerial manipulation. By constructing environmental maps and developing obstacle avoidance techniques, we aim to boost AET’s autonomous navigation. Additionally, we plan to integrate object detection and recognition to further enhance its autonomous manipulation capabilities.

This section details AET’s core system modules, both hardware and software, developed by the authors. The hardware includes electronic devices and the continuum arm’s mechanical structures. A key feature is integrating all sensory data, flight control, and manipulator control into a single MCU board, simplifying AET’s architecture and centralizing software development. Another highlight is the comprehensive software architecture built for stable aerial maneuvers in various environments, leveraging our custom hardware design. All the symbols are defined in Supplementary Table 4.

Mechatronics design and manufacturing process

In Fig. 2b, AET’s electronic devices are labeled with model types and locations. We use a single DJI RoboMaster-A board with STM32F427IIH6 MCU for computing, managing UAV and manipulator control, communication, and sensor signals. For perception, a Livox Mid-360 LiDAR with a 360^o FoV and an embedded IMU captures real-time poses. An onboard MPU9250 IMU on the IC board measures 3-axis acceleration and angular velocity for UAV attitude. BUS motors (Feetech STS3032) drive the manipulator, with three WT JY301S IMUs on the torso’s end disks for pose initialization. The torso, made of Nitinol, has sections with six mid disks and one end disk, reinforced with ribs to resist tendon forces.

To enable AET’s end effector for aerial manipulation, accurate pose estimation and control are crucial. We define coordinate frames for the aerial platform and arm’s end disks, deriving transformations from CAD drawings or configuration spaces. The UAV’s state is estimated by the onboard IMU, and each section’s configuration by tendon lengths, forming a forward kinematic chain for end effector pose estimation. Given a target pose, we solve the IK model for the desired arm configuration and UAV pose, using a multi-layer controller for tracking. This completes the software and mechatronics system setup.

AET system kinematics model

Based on the overview of AET, we introduce general reference frames that describe the configuration of the proposed system. The inertial frame is denoted as \({{{\mathcal{I}}}}\), AET’s UAV body frame is denoted as \({{{\mathcal{V}}}}\), and the base frame of the continuum manipulator is denoted as \({{{\mathcal{B}}}}\). For the continuum manipulator, we define its three end disk frames as \({{{{\mathcal{S}}}}}_{1}\), \({{{{\mathcal{S}}}}}_{2}\), and \({{{{\mathcal{S}}}}}_{3}\) and define its end-effector frame as \({{{\mathcal{E}}}}\).

The system forward kinematics model is established to describe spatial motion relationships between key coordinate frames (\({{{\mathcal{I}}}},{{{\mathcal{V}}}},{{{\mathcal{B}}}},{{{\mathcal{E}}}}\)). These frames are shown in Fig. 3a. With the model, it is convenient to compute all the frames’ poses with respect to the inertial frame. However, we are more interested in obtaining the real-time pose of the end-effector, which is crucial to versatile manipulation tasks. To achieve this, a fundamental kinematics chain is built for the system: \({{{{\boldsymbol{T}}}}}_{{{{\mathcal{I}}}}}^{{{{\mathcal{E}}}}}={{{{\boldsymbol{T}}}}}_{{{{\mathcal{I}}}}}^{{{{\mathcal{V}}}}}\cdot {{{{\boldsymbol{T}}}}}_{{{{\mathcal{V}}}}}^{{{{\mathcal{B}}}}}\cdot {{{{\boldsymbol{T}}}}}_{{{{\mathcal{B}}}}}^{{{{\mathcal{E}}}}}\), where \({{{{\boldsymbol{T}}}}}_{{{{\mathcal{I}}}}}^{{{{\mathcal{E}}}}}\) is a transformation matrix that can be used to compute the pose of the end-effector in the inertial frame. \({{{{\boldsymbol{T}}}}}_{{{{\mathcal{I}}}}}^{{{{\mathcal{V}}}}}\) describes the transformation from \({{{\mathcal{I}}}}\) to \({{{\mathcal{V}}}}\), and its value can be obtained from the LiDAR-IMU odometry. Similarly, \({{{{\boldsymbol{T}}}}}_{{{{\mathcal{V}}}}}^{{{{\mathcal{B}}}}}\) determined by the mechanical design from the CAD drawing, describes the transformation \({{{\mathcal{V}}}}\) from to \({{{\mathcal{B}}}}\). \({{{{\boldsymbol{T}}}}}_{{{{\mathcal{B}}}}}^{{{{\mathcal{E}}}}}\) is associated with the specific continuum manipulator’s kinematics model. \({{{{\boldsymbol{T}}}}}_{{{{\mathcal{I}}}}}^{{{{\mathcal{V}}}}}\), \({{{{\boldsymbol{T}}}}}_{{{{\mathcal{V}}}}}^{{{{\mathcal{B}}}}}\) and \({{{{\boldsymbol{T}}}}}_{{{{\mathcal{B}}}}}^{{{{\mathcal{E}}}}}\) are formed by \({{{{\boldsymbol{T}}}}}_{{{{\mathcal{I}}}}}^{{{{\mathcal{V}}}}}=\left[\begin{array}{cc}{{{{\boldsymbol{R}}}}}_{{{{\mathcal{I}}}}}^{{{{\mathcal{V}}}}}&{{{{\boldsymbol{T}}}}}_{{{{\mathcal{I}}}}}^{{{{\mathcal{V}}}}}\\ 0&1\end{array}\right]\), \({{{{\boldsymbol{T}}}}}_{{{{\mathcal{V}}}}}^{{{{\mathcal{B}}}}}=\left[\begin{array}{cc}{{{{\boldsymbol{R}}}}}_{{{{\mathcal{V}}}}}^{{{{\mathcal{B}}}}}&{{{{\boldsymbol{T}}}}}_{{{{\mathcal{V}}}}}^{{{{\mathcal{B}}}}}\\ 0&1\end{array}\right]\), \({{{{\boldsymbol{T}}}}}_{{{{\mathcal{B}}}}}^{{{{\mathcal{E}}}}}=\left[\begin{array}{cc}{{{{\boldsymbol{R}}}}}_{{{{\mathcal{B}}}}}^{{{{\mathcal{E}}}}}&{{{{\boldsymbol{T}}}}}_{{{{\mathcal{B}}}}}^{{{{\mathcal{E}}}}}\\ 0&1\end{array}\right]\), where \({{{{\boldsymbol{R}}}}}_{{{{\mathcal{I}}}}}^{{{{\mathcal{V}}}}}\) and \({{{{\boldsymbol{T}}}}}_{{{{\mathcal{I}}}}}^{{{{\mathcal{V}}}}}\) are both obtained from the LiDAR-IMU odometry in this article. According to the CAD drawing, \({{{{\boldsymbol{R}}}}}_{{{{\mathcal{V}}}}}^{{{{\mathcal{B}}}}}\) is an identity matrix and \({{{{\boldsymbol{T}}}}}_{{{{\mathcal{V}}}}}^{{{{\mathcal{B}}}}}={[0,0,-{d}_{{{{\mathcal{V}}}}}^{{{{\mathcal{B}}}}}]}^{T}\) indicates that only vertical translation \({d}_{{{{\mathcal{V}}}}}^{{{{\mathcal{B}}}}}\) occurs between \({{{\mathcal{B}}}}\) and \({{{\mathcal{V}}}}\).

The continuum kinemactics model is built by the transformation matrix \({{{{\boldsymbol{T}}}}}_{{{{\mathcal{B}}}}}^{{{{{\mathcal{S}}}}}_{1}}\) between \({{{{\mathcal{S}}}}}_{1}\) and the base frame \({{{\mathcal{B}}}}\), the transformation matrix \({{{{\boldsymbol{T}}}}}_{{{{{\mathcal{S}}}}}_{1}}^{{{{{\mathcal{S}}}}}_{2}}\) between \({{{{\mathcal{S}}}}}_{2}\) and \({{{{\mathcal{S}}}}}_{1}\), and the transformation matrix \({{{{\boldsymbol{T}}}}}_{{{{{\mathcal{S}}}}}_{2}}^{{{{{\mathcal{S}}}}}_{3}}\) between \({{{{\mathcal{S}}}}}_{3}\) (\({{{\mathcal{E}}}}\)) and \({{{{\mathcal{S}}}}}_{2}\). Thus, \({{{{\boldsymbol{T}}}}}_{{{{\mathcal{B}}}}}^{{{{\mathcal{E}}}}}\) is given by: \({{{{\boldsymbol{T}}}}}_{{{{\mathcal{B}}}}}^{{{{\mathcal{E}}}}}={{{{\boldsymbol{T}}}}}_{{{{\mathcal{B}}}}}^{{{{{\mathcal{S}}}}}_{1}}\cdot {{{{\boldsymbol{T}}}}}_{{{{{\mathcal{S}}}}}_{1}}^{{{{{\mathcal{S}}}}}_{2}}\cdot {{{{\boldsymbol{T}}}}}_{{{{{\mathcal{S}}}}}_{2}}^{{{{{\mathcal{S}}}}}_{3}}\).

AET system state estimation

UAV attitude estimation

We use the onboard IMU measurements from the UAV to estimate its attitude. To avoid singularity, we use quaternion q^u to represent its attitude with superscript u denoting the UAV. The acceleration measurements are denoted by a^u while the angular velocity measurements are denoted by ω^u. The onboard 6-axis IMU measuring 3-axis acceleration and 3-axis angular velocity, is employed to provide the real-time attitude of the UAV.

UAV linear velocity estimation

We define the linear velocity of the UAV in the inertial frame \({{{\mathcal{I}}}}\) as v^u. Without any external velocity estimator, we estimate AET’s linear velocity by \({{{{\boldsymbol{v}}}}}^{u}={\int}^{{{{\mathcal{I}}}}}{{{{\boldsymbol{a}}}}}^{u}\), where \({}^{{{{\mathcal{I}}}}}{{{{\boldsymbol{a}}}}}^{u}\) is the acceleration of the UAV body frame \({{{\mathcal{V}}}}\) in the inertial frame. Due to the acceleration measurements from the onboard IMU, the acceleration measurement a^u in the UAV body frame is known. With the attitude estimation \({{{{\boldsymbol{R}}}}}_{{{{\mathcal{I}}}}}^{{{{\mathcal{V}}}}}\), we obtain the \({}^{{{{\mathcal{I}}}}}{{{{\boldsymbol{a}}}}}^{u}\) by coordinate transformation: \({}^{{{{\mathcal{I}}}}}{{{{\boldsymbol{a}}}}}^{u}={({{{{\boldsymbol{R}}}}}_{{{{\mathcal{I}}}}}^{{{{\mathcal{V}}}}})}^{-1}\cdot {{{{\boldsymbol{a}}}}}^{u}\). Then, we obtain the velocity estimation by integrating the acceleration in the inertial frame with the time interval Δt = 0.001s. However, the integration directly causes massive velocity drifts in the actual flights. Here, we introduce the differential values of the position estimation p^u from the LiDAR-IMU odometry, as the observation of the linear velocity: \({{{{\boldsymbol{v}}}}}^{u}={\dot{{{{\boldsymbol{p}}}}}}^{u}\). Consequently, we fuse the velocity from acceleration and the velocity from position estimation by a linear Kalman Filter, and obtain the updated UAV linear velocity \({\hat{{{{\boldsymbol{v}}}}}}^{u}\).

Manipulator IMUs attitude estimation

Torso IMUs are installed in the end-disk planes \({{{{\mathcal{S}}}}}_{1}\), \({{{{\mathcal{S}}}}}_{2}\), and \({{{{\mathcal{S}}}}}_{3}\) to provide measurements of acceleration and angular velocity, denoted by \({{{{\boldsymbol{a}}}}}_{i}^{m}\) and \({{{{\boldsymbol{\omega }}}}}_{i}^{m}\) with i denoting the ith end disk, respectively. We use a complementary filter⁶⁸ to fuse the acceleration and angular velocity measurements of the IMUs, to estimate the attitude of the ith end-disk frame \({{{{\mathcal{S}}}}}_{i}\), denoted by \({[{\phi }_{i}^{m},{\theta }_{i}^{m}]}^{T}\). The heading angle is neglected because the manipulator’s torso cannot conduct twisting motion. The superscript m denotes the continuum manipulator.

UAV flight controller

The flight controller is responsible for implementing position control, velocity control, attitude control, and angular velocity control with the feedback of the state estimation. The most critical task of the flight controller is to make AET track the desired position command in 3D space with high accuracy and agility. Here, the UAV state is denoted by \({{{{\boldsymbol{X}}}}}_{u}^{*}=\{{{{{\boldsymbol{p}}}}}^{u},{{{{\boldsymbol{q}}}}}^{u},{{{{\boldsymbol{v}}}}}^{u},{{{{\mathbf{\Omega }}}}}^{u}\}\), including the UAV position \({{{{\boldsymbol{p}}}}}^{u}\in {{\mathbb{R}}}^{3}\), its attitude \({{{{\boldsymbol{q}}}}}^{u}={[{q}_{w}^{u},{q}_{x}^{u},{q}_{y}^{u},{q}_{z}^{u}]}^{T}\) in the form of quaternion, the linear velocity \({{{{\boldsymbol{v}}}}}^{u}\in {{\mathbb{R}}}^{3}\), and the angular velocity \({{{{\mathbf{\Omega }}}}}^{u}\in {{\mathbb{R}}}^{3}\). The state is depicted in the virtual model of AET, as shown in Fig. 3a.

The position and velocity controller of AET takes the desired UAV position command \({{{{\boldsymbol{p}}}}}_{d}^{u}\), p^u, and v^u of AET as the inputs. It generates the total thrust T^u and the desired attitude \({{{{\boldsymbol{q}}}}}_{d}^{u}\). The desired velocity of AET, denoted by \({{{{\boldsymbol{v}}}}}_{d}^{u}={[{v}_{x,d}^{u},{v}_{y,d}^{u},{v}_{z,d}^{u}]}^{T}\), can be obtained by: \(\begin{array}{r}{{{{\boldsymbol{v}}}}}_{d}^{u}={{{{\boldsymbol{K}}}}}_{p}^{u}({{{{\boldsymbol{p}}}}}_{d}^{u}-{{{{\boldsymbol{p}}}}}^{u})\end{array}\) where \({{{{\boldsymbol{K}}}}}_{p}^{u}\in {{\mathbb{R}}}^{3\times 3}\) is a positive definite diagonal matrix. To control the velocity, we can design a control law as follows:

where \({{{{\boldsymbol{R}}}}}_{{{{\mathcal{I}}}},d}^{{{{\mathcal{V}}}}}\) is the desired rotational matrix, e₃ = [0, 0, 1]^T, \({T}_{d}^{u}\) is the desired total thrust, g = [0, 0, g]^T, ν_v is designed by a linear controller based on the velocity and its command⁶⁹. By combining with the desired yaw command \({\psi }_{d}^{u}\), we could obtain the desired \({{{{\boldsymbol{R}}}}}_{{{{\mathcal{I}}}},d}^{{{{\mathcal{V}}}}}\) and \({T}_{d}^{u}\). Then, we convert \({{{{\boldsymbol{R}}}}}_{{{{\mathcal{I}}}},d}^{{{{\mathcal{V}}}}}\) to obtain the desired quaternion \({{{{\boldsymbol{q}}}}}_{d}^{u}\). Let \({{{{\boldsymbol{q}}}}}_{e}^{u}={({{{{\boldsymbol{q}}}}}^{u})}^{-1}{{{{\boldsymbol{q}}}}}_{d}^{u}\) denote the error of attitude, we can compute the desired angular rates by \(\begin{array}{r}{{{{\mathbf{\Omega }}}}}_{d}^{u}={K}_{{{{\boldsymbol{q}}}}}^{u}sgn({{{{\boldsymbol{q}}}}}_{e,0}^{u}){{{{\boldsymbol{q}}}}}_{e,1:3}^{u}\end{array}\), where \({K}_{{{{\boldsymbol{q}}}}}^{u} > 0\) is a constant parameter.

By denoting the tracking error of the angular velocity as \({{{{\boldsymbol{e}}}}}_{{{{\mathbf{\Omega }}}}}^{u}={{{{\mathbf{\Omega }}}}}_{d}^{u}-{{{{\mathbf{\Omega }}}}}^{u}\), we can design the control law for the angular velocity as follows:

where \({{{{\boldsymbol{\tau }}}}}_{d}^{u}\) denotes the desired torque, J denotes the inertia matrix, ν_Ω can be designed by a linear control based on \({{{{\boldsymbol{e}}}}}_{{{{\mathbf{\Omega }}}}}^{u}\). Finally, through \({T}_{d}^{u}\) and \({{{{\boldsymbol{\tau }}}}}_{d}^{u}\), we can compute the command for four motors of the quadrotor.

Manipulator shape estimation

We define \({[{\alpha }^{i},{\beta }^{i}]}^{T}\) as the configuration state of the ith section. The configuration states of all the sections describe the bending shape of the manipulator’s torso. αⁱ denotes the bending angle and βⁱ denotes direction angle of the ith section. To solve the configuration states, the manipulator shape estimation is derived from the geometric relation between actuated tendon lengths that form the shape displacement. The geometric lengths of the entire continuum torso are defined as L* = {l¹, l², l³}. For one section, \({{{{\boldsymbol{l}}}}}^{i}={[{l}_{1}^{i},{l}_{3}^{i},{l}_{2}^{i},{l}_{4}^{i}]}^{T}\) is used to derive its configuration state. Here, the length pair \({[{l}_{1}^{i},{l}_{3}^{i}]}^{T}\) and the length pair \({[{l}_{2}^{i},{l}_{4}^{i}]}^{T}\) decide the rotational movement of the roll plane and the pitch plane, respectively. These variables are depicted in the configuration diagram of the manipulator, as shown in Fig. 3a.

Since the geometric lengths are driven by six tendon motors located in the manipulator’s base, with one motor simultaneously driving two tendons, the actuated lengths are denoted as \({{{\boldsymbol{D}}}}={[\Delta {l}_{r}^{1},\Delta {l}_{p}^{1},\Delta {l}_{r}^{2},\Delta {l}_{p}^{2},\Delta {l}_{r}^{3},\Delta {l}_{p}^{3}]}^{T}\), which can be directly obtained by the encoder sensors of tendon motors. The subscript r and p means that \(\Delta {l}_{r}^{i}\) and \(\Delta {l}_{p}^{i}\) are corresponding to \({[{l}_{1}^{i},{l}_{3}^{i}]}^{T}\) and \({[{l}_{2}^{i},{l}_{4}^{i}]}^{T}\), respectively. Based on the constant curvature assumption, the geometric relation between L* and D is given as:

where \(\Delta {l}_{r}^{i},\Delta {l}_{p}^{i}\) (i ∈ {1, 2, 3}) could be positive or negative, due to the clockwise or counterclockwise rotation of the motors. With the interval radian being π/2, the spatial relation is numerically built as:

where h ∈ {1, 2, 3, 4} and the tendon spacer radius is defined as r. Then, the ith section’s configuration state \({[{\alpha }^{i},{\beta }^{i}]}^{T}\) can be computed as follows:

By Equation (5), the configuration state of each individual section is obtained. Furthermore, the shape estimation of the manipulator is derived.

Manipulator forward kinematic chain

As we obtain the estimated configuration state \({[{\alpha }^{i},{\beta }^{i}]}^{T}\) of the ith section, the transformation matrix \({{{{\boldsymbol{T}}}}}_{{{{{\mathcal{S}}}}}_{i-1}}^{{{{{\mathcal{S}}}}}_{i}}=\left[\begin{array}{cc}{{{{\boldsymbol{R}}}}}_{{{{{\mathcal{S}}}}}_{i-1}}^{{{{{\mathcal{S}}}}}_{i}}&{{{{\boldsymbol{T}}}}}_{{{{{\mathcal{S}}}}}_{i-1}}^{{{{{\mathcal{S}}}}}_{i}}\\ 0&1\\ \end{array}\right]\) between the proximal end frame and the distal end frame of the section is given as⁵¹:

where i > 1, sαⁱ denotes \(\sin ({\alpha }^{i})\) and cαⁱ denotes \(\cos ({\alpha }^{i})\). sβⁱ denotes \(\sin ({\beta }^{i})\) and cβⁱ denotes \(\cos ({\beta }^{i})\). Thus, we obtain the transformation matrix \({{{{\boldsymbol{T}}}}}_{{{{\mathcal{B}}}}}^{{{{{\mathcal{S}}}}}_{i}}\) from the manipulator base frame \({{{\mathcal{B}}}}\) to the ith end disk frame \({{{{\mathcal{S}}}}}_{i}\) by the forward kinematic chain: \({{{{\boldsymbol{T}}}}}_{{{{\mathcal{B}}}}}^{{{{\mathcal{E}}}}}={{{{\boldsymbol{T}}}}}_{{{{\mathcal{B}}}}}^{{{{{\mathcal{S}}}}}_{1}}\cdot {{{{\boldsymbol{T}}}}}_{{{{{\mathcal{S}}}}}_{1}}^{{{{{\mathcal{S}}}}}_{2}}\cdot {{{{\boldsymbol{T}}}}}_{{{{{\mathcal{S}}}}}_{2}}^{{{{{\mathcal{S}}}}}_{3}}\), and equally obtain the pose of each end disk within the manipulator’s workspace. Furthermore, we assume the COM of each section is located at the center point of its proximal pose and distal pose, as shown in Fig. 5c. Then, the COM of the entire manipulator is estimated by the sum of the three sections’ individual COM. Consequently, the moment applied on the UAV frame can be computed by the manipulator’s COM and the distance between the COM and the UAV’s centerline. The validation is shown in Fig. 5d.

Manipulator inverse kinematic solver

The IKs aims to solve accurate configuration space as soon as possible to make the current manipulator’s tip reach the desired tip pose \({{{{\boldsymbol{T}}}}}_{{{{\mathcal{B}}}},d}^{{{{\mathcal{E}}}}}=\left[\begin{array}{cc}{{{{\boldsymbol{R}}}}}_{{{{\mathcal{B}}}},d}^{{{{\mathcal{E}}}}}&{{{{\boldsymbol{T}}}}}_{{{{\mathcal{B}}}},d}^{{{{\mathcal{E}}}}}\\ 0&1\end{array}\right]\). Here, we define the full configuration space as \({{{\boldsymbol{\xi }}}}={[{\alpha }^{1},{\beta }^{1},{\alpha }^{2},{\beta }^{2},{\alpha }^{3},{\beta }^{3}]}^{T}\) and we build a cost function:

where ξ_d is the desired configuration space that we manage to solve. To minimize the T(ξ), we implement a numerical optimization-based strategy⁷⁰ and conduct iterative computation. Given a desired tip pose, each iteration process will be terminated until T(ξ) is less than 10⁻⁵. At the termination point, the solved configuration space is considered as the ξ_d.

Manipulator controller

We design two closed-loop control modes: the configuration space controller (core) that controls the manipulator’s configuration to implement shape manipulation and the end disk attitude controller (assistive) that controls the three end disks’ attitudes to initialize vertically.

Configuration space controller

With the configuration space obtained from actuated tendon lengths, the real-time configuration is fed back to the manipulator configuration space controller.

Given by Equation (5), the configuration state \({[{\alpha }^{i},{\beta }^{i}]}^{T}\) of the ith continuum section is known. We define its desired configuration state as \({[{\alpha }_{d}^{i},{\beta }_{d}^{i}]}^{T}\). According to the spatial relation between tendon lengths and the configuration state given by Equation (4), the desired tendon lengths can be computed as follows:

Thus, the configuration space can be transformed into the actuation space. Then, we define the jth tendon-length control error within the ith section as \({e}_{j}^{i}={l}_{j,d}^{i}-{l}_{j}^{i}\). Moreover, we formulate the length control error vector for the ith section as \({{{{\boldsymbol{E}}}}}_{l}^{i}={[{e}_{1}^{i},{e}_{2}^{i},{e}_{3}^{i},{e}_{4}^{i}]}^{T}\). To reduce tendon slacking, we also design a tension controller. The tension feedback of the ith section’s tendons is denoted as \({{{{\boldsymbol{T}}}}}_{t}^{i}={[{t}_{1}^{i},{t}_{2}^{i},{t}_{3}^{i},{t}_{4}^{i}]}^{T}\). Consequently, the following control law can be designed to eliminate the length control errors:

where \({{{{\boldsymbol{E}}}}}_{t}^{i}\) denotes the tension error vector. \({K}_{p,l}^{i}\) denotes the proportional gain in the tendon length control. \({K}_{p,t}^{i}\) and \({K}_{i,t}^{i}\) denote the proportional gain and the integral gain in the tension control of ith section, respectively. \({{{{\boldsymbol{v}}}}}_{d}^{i}={[{v}_{1,d}^{i},{v}_{2,d}^{i},{v}_{3,d}^{i},{v}_{4,d}^{i}]}^{T}\) denotes the rotation velocity commands for the corresponding tendon motors within the section. Then, the embedded velocity controller drives the motors to track these commands, so that current tendon lengths can track desired tendon lengths as accurately as possible. Consequently, we have established the configuration controller for all the sections.

Attitude controller

If one only wants to control the attitude of each disk, the above control law can also be used. Let \({{{{\mathbf{\Phi }}}}}_{i,d}^{m}={[{\phi }_{i,d}^{m},{\theta }_{i,d}^{m}]}^{T}\) denote the desired attitude angles of the ith end disk, we can compute the attitude tracking error as \({{{{\boldsymbol{e}}}}}_{i}^{m}={{{{\mathbf{\Phi }}}}}_{i,d}^{m}-{{{{\mathbf{\Phi }}}}}_{i}^{m}\) where \({{{{\mathbf{\Phi }}}}}_{i}^{m}\) denotes the estimated attitude. Then, by replacing \({{{{\boldsymbol{E}}}}}_{l}^{i}\) with \({{{{\boldsymbol{e}}}}}_{i}^{m}\) in Equation (9) will achieve the end disks’ attitude controller design.

Whole-body motion planning

The whole-body motion planning is designed to determine a desired sequence of UAV positions \(\{{p}_{d}^{u}\}\) and the manipulator’s configuration space {ξ_d}, given a series of waypoints in three-dimensional space. To plan the motion, we need to generate a smooth trajectory \(\{{{{{\boldsymbol{T}}}}}_{{{{\mathcal{I}}}},d}^{{{{\mathcal{E}}}}}\}\) in the inertial frame \({{{\mathcal{I}}}}\) for AET to follow. The minimum jerk¹² is used to generate such a smooth trajectory.

To obtain the targeted 6 DOF trajectory \(\{{{{{\boldsymbol{T}}}}}_{{{{\mathcal{I}}}},d}^{{{{\mathcal{E}}}}}\}\), we plan the motion of the end-effector in SE(3) space. Firstly, we define the position of the end effector in the inertial frame as \({{{{\boldsymbol{p}}}}}_{{{{\mathcal{I}}}}}\), and the rotation as \({{{{\boldsymbol{e}}}}}_{{{{\mathcal{I}}}}}\). Then, the motion of the end effector can be precisely formulated as two 3 DOF minimum-jerk trajectories \({{{{\boldsymbol{p}}}}}_{{{{\mathcal{I}}}}}(t)\) and \({{{{\boldsymbol{e}}}}}_{{{{\mathcal{I}}}}}(t)\), each delineated with respect to time. For simplification, here we only take the position trajectory of \({{{{\boldsymbol{p}}}}}_{{{{\mathcal{I}}}}}(t)\) as an example. A piece-wise 3-dimension and 5-degree polynomials \({{{{\boldsymbol{p}}}}}_{{{{\mathcal{I}}}}}(t)\) with M pieces, and the lth piece can be expressed as:

where \({{{{\boldsymbol{c}}}}}_{l}\in {{\mathbb{R}}}^{6\times 3}\) is the coefficient matrix of the piece and \(\lambda (t)={[1,t,...,{t}^{5}]}^{T}\) is natural basis vector. T_l is the duration of the piece. The optimization problem of each piece is formulated as follows:

where \({d}_{0}^{j}\) and \({d}_{{T}_{l}}^{j}\) denote the initial and terminal boundary constraints, j ∈ [0, 3]. The trajectory generation of \({{{{\boldsymbol{e}}}}}_{{{{\mathcal{I}}}}}(t)\) is similar and these two trajectories share the same piece time vector \(T={[{T}_{1},...,{T}_{M}]}^{T}\in {{\mathbb{R}}}^{M}\). Consequently, \(\{{{{{\boldsymbol{T}}}}}_{{{{\mathcal{I}}}},d}^{{{{\mathcal{E}}}}}\}\) is the planned result of the combination of two minimum-jerk trajectories.

Finally, the desired base position and configuration space of the arm can be obtained using the following optimization problem:

where \({{{{\boldsymbol{p}}}}}_{d}^{u}\) and ξ_d represent the desired values that we successfully derive using the gradient descent algorithm, and \({{{{\boldsymbol{T}}}}}_{{{{\mathcal{I}}}}}^{{{{\mathcal{E}}}}}\) is given by \({{{{\boldsymbol{T}}}}}_{{{{\mathcal{I}}}}}^{{{{\mathcal{E}}}}}={{{{\boldsymbol{T}}}}}_{{{{\mathcal{I}}}}}^{{{{\mathcal{V}}}}}({{{{\boldsymbol{p}}}}}_{d}^{u})\cdot {{{{\boldsymbol{T}}}}}_{{{{\mathcal{V}}}}}^{{{{\mathcal{B}}}}}\cdot {{{{\boldsymbol{T}}}}}_{{{{\mathcal{B}}}}}^{{{{\mathcal{E}}}}}({{{{\boldsymbol{\xi }}}}}_{d})\). Subsequently, these solutions are utilized as control commands for both the UAV flight controller and the manipulator controller, enabling them to execute automatic aerial operations in a synchronized manner.