Introduction

Quantum entanglement can reveal the fundamental organizing principles of quantum matter, ranging from non-Fermi liquids in high-temperature superconductors to black holes1,2. However, extracting the entanglement structure in realistic many-body systems remains a significant challenge. A key step toward understanding these systems is reconstructing the quantum state of microscopic subregions, namely those that contain a small number of sites. By focusing on smaller subregions, we can fully reconstruct the reduced density matrix (RDM), potentially giving us access to complete entanglement information. The entanglement microscopy protocol thus involves first obtaining the RDM numerically, and then calculating multipartite entanglement within these subregions, providing deeper insights into quantum critical systems. This approach complements existing methods that focus on extended ensembles2,3,4,5,6,7,8,9,10,11,12, which handle larger subregions but are often limited in the choice of entanglement measures. It also differs from global measures like Quantum Fisher Information (QFI) and Quantum Variance (QV) which capture coarser quantum correlations in the entire system13,14.

In the simplest case of bipartite entanglement, having the full RDM allows us to compute the (logarithmic) negativity15,16,17,18, an entanglement monotone not polluted by classical correlations. However, negativity is challenging to compute in many-body systems for subregions with many degrees of freedom (including quantum field theories) where one can only obtain related quantities via the replica trick19,20. These Rényi analogs are not entanglement monotones and thus cannot be used to obtain the entanglement structure. This limitation becomes especially clear in boson/spin systems poised near a quantum critical point (QCP), where the logarithmic negativity (LN) decays faster than any power, as shown for CFTs in 1d20 and higher d 21, while the Rényi moments decay algebraically. These are special cases of a general phenomenon regarding the “fate of entanglement22” where any multi-partite form of entanglement (including but more general than bipartite) entirely disappears as a system heats up, evolves in time during certain protocols, or as its parts grow separated.

In the first step of our protocol, one compute the reduced density matrix (RDM) for microscopic or “skeletal” subregions of many-body systems23. This can be achieved through various computational approaches such as Exact Diagonalization (ED), Quantum Monte Carlo (QMC), or tensor network approaches such as the Density Matrix Renormalization Group (DMRG).

In this work, we focus on numerically constructing the RDM using ED and QMC24. To be more specific, we scrutinize systems near generic 2d quantum phase transitions, including (1) the celebrated QCP in the transverse field Ising model (TFIM) on the square lattice and (2) a Gross-Neveu-Yukawa (GNY) QCP of interacting Dirac fermions. Regarding bipartite entanglement, our microscopy yields the LN in the entire phase diagram including at finite temperature with the main findings: (i) the Ising model exhibits short-range entanglement with finite sudden death as a function of space and temperature; (ii) the fermionic variant of the LN, which takes into account the parity superselection rule, shows power-law decay at the GNY QCP for large separations with exponents consistent with the conformal field theory (CFT) prediction21. (iii) Going beyond bipartite entanglement, we do not detect any genuine 3-party entanglement in a large window near the 2d Ising QCP, but find its presence in the 1d model both in QMC and with the exact solution via fermionization. Overall, the 2d Ising model shows less bipartite and tripartite entanglement compared to 1d25,26,27,28.

Results

Entanglement microscopy

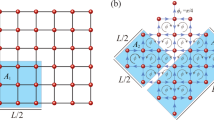
To extract the entanglement information in microscopic subregions for spin models, we use the algorithm introduced in ref. 24, schematically shown in Fig. 1. In general, the matrix elements of the RDM for spins in subregion A, \(\langle \alpha | {\rho }_{A}| \tilde{\alpha }\rangle\) is expressed as

$$\langle \alpha | {\rho }_{A}| \tilde{\alpha }\rangle=\frac{1}{Z}\left\langle \alpha \right\vert {{{{\rm{Tr}}}}}_{B}{e}^{-\beta H}\left\vert \tilde{\alpha }\right\rangle \\=\frac{1}{Z}\sum\limits_{\xi}\left\langle \alpha,\xi \right\vert {e}^{-\beta H}\left\vert \tilde{\alpha },\xi \right\rangle,$$
(1)

where \(\{\left\vert \xi \right\rangle \}\) forms a complete basis for the environment region B and β is the inverse temperature. Eq. (1) can be viewed as a modified partition function with imaginary-time periodicity only in the region B24, which can be easily simulated in path-integral QMC as shown in Fig. 1. Please refer to the latter section for a detailed description.

Fig. 1: Sampling the reduced density matrix in path-integral QMC.
figure 1

Panel (a) shows the partition function in the space (r) - time (τ) manifold appearing in usual QMC simulations, with the periodic structure of imaginary time. Panel (b) shows how the RDM is sampled in such QMC simulations, where one imposes open boundary conditions in time for the skeletal sites in subregion A. From the QMC histogram of configurations of these sites, in this case, there will be 4   4 configurations for the 2 spins in A, and the corresponding matrix elements in the RDM are recorded. The lower panel in (b) demonstrates the spatial partition of A and B in such a setting.

Full size image

For interacting fermions, one employs the determinant quantum Monte Carlo (DQMC) scheme29,30,31. In DQMC, the sampling of the RDM is attributed to the fact that fermions are considered free in each auxiliary field configuration. Thus the interacting RDM is the weighted average of free RDMs5. Recent advances in DQMC have enabled the reconstruction of the RDM for small subregions in many-body quantum systems, such as a four-site plaquette in the two-dimensional fermion Hubbard model32. However, in that work, genuine entanglement between sites within the plaquette has not been studied. Similarly, studies using dynamical mean-field theory (DMFT) on the Kagome Hubbard model have focused on subregions and examined only some diagonal elements of the RDM33, without exploring genuine entanglement. For the case that we focus on, where region A contains two sites, the interacting RDM in the occupation-number basis can be constructed with the density correlation function and fermion Green’s function34. We also note that the DQMC calculation of Rényi negativity with bipartition at finite temperature of interacting fermions, via the replica trick, has recently been worked out35. However, since the RDM therein is not explicitly computed, only integer moments of LN can be obtained.

Bipartite entanglement

Bipartite entanglement quantifies the quantum correlations between two subsystems, which cannot be reduced to classical correlations. Widely used bipartite entanglement measures include entanglement entropy, concurrence, and logarithmic negativity, the latter valued for its simplicity and applicability to both pure and mixed states, making it a robust tool for studying entanglement in systems near quantum critical points36. Consider a region A, which is divided into two parts, A1 and A2. The logarithmic negativity is defined as a function of the partial transpose on the RDM ρA in region A115,16,17

$${{{{\mathcal{E}}}}}^{b/f}=\ln | | {\rho }_{A}^{{T}_{1}^{b/f}}| {| }_{1}$$
(2)

where the ∣∣ ⋅ ∣∣1 is the matrix 1-norm which sums the absolute values of the eigenvalues of the partially transposed matrix \({\rho }_{A}^{{T}_{1}^{b/f}}\). The bosonic partial transpose of the RDM ρA operates as \(\left\langle {\alpha }_{1}{\alpha }_{2}\right\vert {\rho }_{A}^{{T}_{1}^{b}}\left\vert {\bar{\alpha }}_{1}{\bar{\alpha }}_{2}\right\rangle=\left\langle {\bar{\alpha }}_{1}{\alpha }_{2}\right\vert {\rho }_{A}\left\vert {\alpha }_{1}{\bar{\alpha }}_{2}\right\rangle\); the subscript denotes the subregions, A1 or A2, supporting the states. The superscript b in \({\rho }_{A}^{{T}_{1}^{b}}\) refers to the fact that, in doing partial transpose, one simply exchanges two states without any extra factor. For fermionic systems, one can also define the parity-respecting quantity \({{{{\mathcal{E}}}}}^{f}\) that takes the phase factor coming from the non-local commutation relation into account, thus recovering the basic properties of the fermionic entanglement measure21,35,37,38,39,40.

Tripartite entanglement

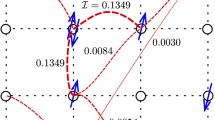
In the above, we have discussed bipartite entanglement between two subregions. Entanglement microscopy can also delve into the much richer realm of multi-party entanglement. We illustrate this by studying tripartite entanglement between 3 sites in the 2d quantum Ising model. In particular, we shall search for genuine tripartite entanglement (GTE), which cannot be described in terms of 2-party entanglement between any two subgroups of spins. A state with GTE cannot be written as a mixture of bi-separable physical density matrices, \(\rho \, \ne \, {\sum }_{k}{p}_{k}{\rho }_{A}^{k}{\rho }_{BC}^{k}+{q}_{k}{\rho }_{AB}^{k}{\rho }_{C}^{k}+{r}_{k}{\rho }_{AC}^{k}{\rho }_{B}^{k}\), where pk, qk, rk are non-negative. A simple example of GTE is given by a pure cat state (also known as GHZ state) of 3 spins, \(a\left\vert 000\right\rangle+b\left\vert 111\right\rangle\), with non-zero a, b. Criteria to detect GTE are more involved than those of the simple bipartite measures such as the LN. However, some criteria exist that can detect GTE by establishing that a state is not bi-separable.

Here, we shall focus on two such separability criteria, which we call W1 and W241. Let us describe W1 (W2 is analogously defined, see Supplemental Material (In this supplementary material, we will provide some additional data on 1d and 2d TFIM in Sec. 1, and 2d fermion t − V model in Sec. 2.).

$${W}_{1}\,=\,{\max }_{{{{\rm{LU}}}}}\left(\left\vert {\rho }_{1,8}\right\vert -\sqrt{{\rho }_{2,2}{\rho }_{7,7}}-\sqrt{{\rho }_{3,3}{\rho }_{6,6}}-\sqrt{{\rho }_{4,4}{\rho }_{5,5}}\right)$$
(3)

where ρi,j are the matrix element of the 3-site RDM. In order to get a meaningful answer, one has to remove the basis dependence by maximizing among all local unitary (LU) transformations acting on the RDM, ρ → UρU† with U = U1 ⊗ U2 ⊗ U3. Being local, such transformations leave the GTE structure invariant. If Wi > 0, there is GTE, while no conclusion can be reached if Wi ≤ 0. Although not sensitive to all forms of GTE, the Wi criteria do tend to perform well in a variety of states, especially when used together41.

Models

We perform entanglement microscopy on the 1d and 2d square lattice TFIM, as well as the spinless π-flux fermion t − V model on a square lattice. The Hamiltonian of the TFIM reads

$$H=-J{\sum}_{\langle i,j\rangle }{\sigma }_{i}^{z}{\sigma }_{j}^{z}-h{\sum}_{i}{\sigma }_{i}^{x},$$
(4)

where we shall set the ferromagnetic exchange coupling to J = 1; the QCP is at h = 1 for 1d, and h = 3.044 for 2d42. The T-h phase diagram is shown in panel (a) of Fig. 2. As will be shown below, besides the QMC simulation for RDMs, we have also performed exact diagonalization (ED) in 2d for small clusters, to obtain both bipartite and tripartite entanglement measures.

Fig. 2: Logarithmic negativity for adjacent sites.
figure 2

Color code plots of (a) \({{{{\mathcal{E}}}}}^{b}\) in 2d TFIM simulated in a 40 × 40 square lattice with β up to 40, and (b) \({{{{\mathcal{E}}}}}^{f}\) in 2d fermion t − V model simulated in a 6 × 6 square lattice with β up to 15. In both panels, the red curves represent the finite-temperature phase boundaries, which end at a zero temperature QCP located at hc = 3.044 in 2d TFIM42 and Vc = 1.27 in t − V model. The purple dashed lines show the maxima of \({{{{\mathcal{E}}}}}^{b/f}\) for each temperature. In both models, the maxima have converged with system size, as is shown in the SM. The bottom panel illustrates the schematic phase diagrams.

Full size image

For the spinless fermion t − V model, the Hamiltonian reads,

$$H=-t{\sum}_{\langle i,j\rangle }\left({e}^{i{\theta }_{i,j}}{c}_{i}^{{{\dagger}} }{c}_{j}+{{{\rm{h.c.}}}}\right)+V{\sum}_{\langle i,j\rangle }\left({n}_{i}-\frac{1}{2}\right)\left({n}_{j}-\frac{1}{2}\right),$$
(5)

it consists of the nearest neighbor hopping term with π-flux and nearest neighbor repulsion. We set t = 1 as the energy unit. The π-flux hopping term on the square lattice (\({\theta }_{i,j}=\frac{\pi }{2}\) on every other column of vertical bonds and 0 otherwise) leads to a dispersion with two Dirac cones at the \({{{\bf{X}}}}=(\pi,\pm \frac{\pi }{2})\) points in the Brillouin zone (BZ) taking two sites horizontally as a unit cell. At half-filling, a positive V drives the system from a Dirac semi-metal (DSM) to a \({{\mathbb{Z}}}_{2}\)-symmetry spontaneously broken charge density wave (CDW) state, where one sublattice acquires a higher density than the other. The QCP is described by the “chiral Ising” Gross-Nevey-Yukawa (GNY) theory with global symmetry \(O{({N}_{f})}^{2}\times {{\mathbb{Z}}}_{2}\) and, in our case Nf = 2 two-component Dirac fermions. The position of the QCP, the critical exponents of the Gross-Neveu transition, have been systematically worked out using QMC, field-theoretical expansions, and conformal bootstrap, for both Nf = 243,44,45,46,47,48 and other values of Nf44,45,46,47,48,49,50. The schematic T − V phase diagram is shown in the lower part of the panel (b) in Fig. 2.

By simulating this model with DQMC, we can probe entanglement near the chiral GNY-Ising QCP at Vc = 1.27, which we located via finite-size scaling and using the critical exponents from conformal bootstrap44. The detailed QMC finite-size data analysis and collapse are shown in the SM.

Logarithmic negativity

We present the results for \({{{{\mathcal{E}}}}}^{b}\) of the TFIM and \({{{{\mathcal{E}}}}}^{f}\) of the t − V model.

Ising model

Figure 2a shows the nearest neighbor \({{{{\mathcal{E}}}}}^{b}\) at finite temperature for the square lattice TFIM of linear system size L = 40 with inverse temperature β up to 40. The \({{{{\mathcal{E}}}}}^{b}\) maxima, marked by the purple dashed line, shifts from h > hc at high temperature to h ≈ hc = 3.044 at T = 1/40. These numerical values align with prior studies that compute negativity as a function of h rather than temperature or separation51. Going beyond the numerical results, we provide an argument for the absence of sudden death at small or large h based on the evolution of the RDM in space of states22. At h = ∞, the GS becomes the pure product state where all spins point up. The RDM of two adjacent spins is then also a pure product state, which lies at the boundary of all separable (un-entangled) RDMs. The entanglement at finite h is only lost at h = ∞. In the opposite limit h → 0, the GS becomes the cat or GHZ state \((\left\vert \,\uparrow \cdots \uparrow \right\rangle+\left\vert \,\downarrow \cdots \downarrow \right\rangle )/\sqrt{2}\), leading to a rank-deficient RDM with two eigenvalues being 1/2, and the two others zero. A non-full rank separable state lies at the boundary of all separable states (see ref. 52 and references therein) so that the RDM becomes separable only when h exactly vanishes.

At all h values, \({{{{\mathcal{E}}}}}^{b}\) has a sudden-death temperature, beyond which \({{{{\mathcal{E}}}}}^{b}\) is identically zero corresponding to the dark blue region in the phase diagram; it is also shown in panel (c) of Fig. 3. The existence of a thermal sudden death follows from the general fact that the infinite temperature state lies well within the continent of separable states, and so entanglement must disappear at a finite temperature corresponding to the point at which the system enters the continent22.

Fig. 3: Spatial and temporal dependence of the logarithmic negativity.
figure 3

a The decay of the two-site \({{{{\mathcal{E}}}}}^{b}\) and \({{{{\mathcal{E}}}}}_{3}^{b}\) as a function of separation r at the QCP hc = 3.04. The simulation is done with L = β = 40. \({{{{\mathcal{E}}}}}^{b}\) exhibits a sudden death beyond one lattice constant and the \({{{{\mathcal{E}}}}}_{3}^{b}\) exhibits a power-law decay with the fit shown as a purple dashed line; the exponent 3.9(2) is consistent with the expected Ising CFT value 4Δσ + 2 ≈ 4.07321,55. b The decay of \({{{{\mathcal{E}}}}}^{f}\) versus separation r in the t − V model with various system sizes, at the QCP Vc = 1.27. The simulation is done with L = β going from 8 to 16. The blue dashed line shows the algebraic scaling with the power predicted by CFT analysis21,44, with the expected GNY scaling dimension 4Δψ ≈ 4.174. Panel (c, d) demonstrate the temperature dependence of \({{{{\mathcal{E}}}}}^{b}\) for the L = 40 TFIM and \({{{{\mathcal{E}}}}}^{f}\) for the L = 6 t − V model at various values of h and V. In (c) the \({{{{\mathcal{E}}}}}^{b}\) always exhibit a finite sudden death temperature, and in (d) \({{{{\mathcal{E}}}}}^{f}\) decays as 1/T2 for adjacent sites r = 1, while 1/T6 for sites separated by r = 3 bonds. Each error bar shows the corresponding one sigma statistical uncertainty, computed by the standard deviation between independent bins.

Full size image

Let us now examine the fate of entanglement as the 2 sites become progressively more separated. Figure 3a shows the \({{{{\mathcal{E}}}}}^{b}\) between two sites separated with bond-distance r = ∣i − j∣. \({{{{\mathcal{E}}}}}^{b}\) drops to 0, within machine precision, even for the next-nearest neighbor separation, \(r=\sqrt{2}\). Strikingly, the 2d TFIM possesses the shortest possible range of entanglement for two spins, as it only exists for nearest neighbor, even shorter than the 1d case where the sudden-death distance was found to be rsd = 325,26,28. Such a sudden death separation again follows since the state at large separations lies within the separable continent22. Early 1d TFIM studies26 similarly show rapid concurrence decay with temperature and distance, consistent with our results in Fig. 3a, c. In addition, Roscilde et al.53 used quantum Monte Carlo simulations on another Ising model, confirming that concurrence remains short-ranged at a quantum phase transition.

We also computed the third-order moment \({{{{\mathcal{E}}}}}_{3}^{b}\) at the Ising QCP. The moments of the LN are defined19,20 as \({{{{\mathcal{E}}}}}_{n}^{b}=\ln \frac{{{{\rm{Tr}}}}{\rho }_{A}^{n}}{{{{\rm{Tr}}}}[{({\rho }_{A}^{{T}_{1}})}^{n}]},\) which can be easily computed from the full RDM, or one can sample \({{{{\mathcal{E}}}}}_{n}^{b}\) by using standard QMC and exploiting the replica trick54. The orange line in the inset of Fig. 3a shows the power-law decay of \({{{{\mathcal{E}}}}}_{3}^{b}\) with fitted power 3.9(2), which agrees with the CFT prediction 4Δσ + 2 ≈ 4.07321,55. The power-law decay of \({{{{\mathcal{E}}}}}_{3}^{b}\) is in sharp contrast with the rapid sudden death of \({{{{\mathcal{E}}}}}^{b}\), and arises since the former is not a proper entanglement measure and is thus polluted by non-entangling correlations.

Fermion t − V model

Figure 2b shows the analogous results for \({{{{\mathcal{E}}}}}^{f}\) of two adjacent sites for the square lattice t − V model of linear system size L = 6 with β up to 15. As denoted by the purple dashed line, the maxima start in the ordered CDW phase at high temperature and converge to V ≈ 1 at low temperature, which is near the QCP but in the DSM phase. It roughly follows the finite-temperature phase boundary, obtained from finite-size scaling and indicated by the red line, but clearly differs from it at most temperatures. We observe that the nearest-neighbor fermionic LN is less sensitive to the QCP compared to the bosonic LN in the square lattice Ising model. A key difference is that the DSM phase has gapless Dirac fermions, and these lead to a large \({{{{\mathcal{E}}}}}^{f}\). The QCP, being driven by the fluctuations of the bosonic order parameter, thus leaves a weaker imprint on \({{{{\mathcal{E}}}}}^{f}\).

As temperature increases, the nearest neighbor \({{{{\mathcal{E}}}}}^{f}\) does not suffer a sudden death. Instead, it decays algebraically as shown in Figs. 2b, 3d. We can actually obtain the scaling analytically in the large T limit for general models and separations. In order to determine \({{{{\mathcal{E}}}}}^{f}\) in a thermal state \(\rho=\exp (-\beta H)/{{{\mathcal{Z}}}}\), we need to find how the fermion Green’s function \({g}_{ij}={{{\rm{Tr}}}}({c}_{i}^{{{\dagger}} }{c}_{j}\rho )\) decays to zero. We will then have \({{{{\mathcal{E}}}}}^{f}=\alpha | {g}_{ij}{| }^{2}+\cdots \,\), where the coefficient α depends on the filling, and the ellipsis denotes subleading terms. By expanding, \(\exp (-\beta H)={\sum }_{n}{(\beta H)}^{n}/n!\) we see that the first non-zero contribution to the Green’s function will come from \({{{\rm{Tr}}}}({H}^{{n}_{r}}{c}_{i}^{{{\dagger}} }{c}_{j})\) such that the hopping term of \({H}^{{n}_{r}}\) connects sites i and j. The Green’s function thus decays as \(1/{T}^{{n}_{r}}\), and we have

$${{{{\mathcal{E}}}}}^{f}=A\,{T}^{-2{n}_{r}}+\cdots$$
(6)

To illustrate the result, let us consider a general Hamiltonian that includes nearest neighbor hopping terms, an example being our t − V model. If the sites are adjacent, nr = 1 and we get 1/T2. This scaling is in agreement with the result for adjacent regions in general Gaussian (free) fermionic states38, but we emphasize that it holds in interacting systems. If the sites are not adjacent, we will get \(1/{T}^{2{n}_{r}}\) scaling with nr ≥ 1. For instance, in the t − V model for third nearest neighbor sites, nr = 3, leading to 1/T6 scaling, as shown in Fig. 3d. Further information about the fits is given in the SM. Finally, the analysis above can be generalized to subregions with more sites: by using the locality of the large-temperature state, we infer that the exponent is the minimal one for all combinations of sites i ∈ A1 and j ∈ A2. This will yield 1/T2 decay for \({{{{\mathcal{E}}}}}^{f}\) of adjacent regions in generic interacting models. Interestingly, a smaller exponent n = 3/2 was observed in topological integer quantum Hall states for adjacent regions56, which does not contradict our general analysis since quantum Hall states live in the continuum.

Finally, Fig. 3b shows the scaling of \({{{{\mathcal{E}}}}}^{f}\) as we increase the separation between the two sites at the GNY QCP. In contrast to \({{{{\mathcal{E}}}}}^{b}\) for the Ising QCP, the fermionic LN shows long-range entanglement, manifested by its power-law decay with r. The dashed line shows the CFT prediction21 with power 4Δψ ≈ 4.174, where the fermion scaling dimension was obtained via conformal bootstrap44. The algebraic tail of the fermionic LN follows from the general structure of the space of separable states in fermion systems owing to the fermion parity superselection rule22.

Genuine tripartite entanglement

In 1d, the GTE of three consecutive spins was studied in the 1d anisotropic XY model, which includes the Ising case as a special limit27, using a quantum k-separability criterion57. GTE has also been studied in a cluster-Ising model that gives rise to RDMs with special fine-tuned properties58, while multi-partite entanglement of the entire system, not subregions as considered here, was studied for small system sizes in the TFIM in dimensions 1 to 359. GTE beyond 1d has not been previously computed. Figure 4 shows the GTE criterion W1 for the three closest sites as a function of the transverse field h for both the 1d and 2d TFIMs. The 1d data, obtained from the exact RDM via a Jordan-Wigner transformation60, shows that GTE exists for all finite values h, and becomes maximal in the paramagnetic phase near the QCP. The absence of sudden death with h, can be explained similarly to the LN case above. The asymptotic state at h = ∞ is a pure product state, and so is the RDM of 3 spins. This state actually lies at the boundary of all biseparable states since we can perturb with an arbitrarily small ϵ: \(\sqrt{1-\epsilon }\left\vert \uparrow \uparrow \uparrow \right\rangle+\sqrt{\epsilon }\left\vert \downarrow \downarrow \downarrow \right\rangle\) to generate a cat / GHZ state (with unequal amplitudes), which possesses GTE as detected by W1. At small h, we have a rank 2 RDM (since the full GS is the ferromagnetic cat state), which is rank deficient. In the zero-rank subspace, we can perturb with a W-state: \((1-\epsilon )\rho+\epsilon \left\vert W\right\rangle \left\langle W\right\vert\) where \(\left\vert W\right\rangle=(\left\vert \downarrow \uparrow \uparrow \right\rangle+\left\vert \uparrow \downarrow \uparrow \right\rangle+\left\vert \uparrow \uparrow \downarrow \right\rangle )/\sqrt{3}\). The W2 criterion detects GTE when ϵ > 0. This shows that the asymptotic state is on the boundary of biseparable states, and so the entanglement is only lost at h = ∞.

Fig. 4: Searching for genuine tripartite entanglement in the 1d/2d quantum Ising models.
figure 4

a In 1d, the criterion W1 ≥ 0 detects GTE for 3 consecutive spins at all the values of h. In 2d for 3 spins in a square plaquette, W1 ≤ 0, both in the small size exact diagonalization (ED) and large-scale QMC results, signifying no detection of GTE in a large region near the QCP. Similar behavior for W2 is shown in the SM. All QMC calculations are done with β = L. Panel (b) shows the logarithmic divergence of the derivative \(\frac{d{W}_{1}}{dh}\) near QCP for the 1d L  =  ∞ data: \(\frac{d{W}_{1}}{dh}{| }_{h}=\frac{{W}_{1}(h+\Delta h)-{W}_{1}(h-\Delta h)}{2\Delta h}\), with step size Δh = 10−4.

Full size image

In sharp contrast, in the 2d case, the large-scale QMC data has W1 ≤ 0 for all values h, indicating that no GTE is detected. We have also evaluated another complementary criterion W2, and reached the same conclusion in the range 0 < h/hc < 2 (see SM), although more powerful criteria are needed to make a definitive conclusion. Furthermore, we have checked that in both 1d and 2d no GTE is detected if the sites are non-adjacent. Extrapolating to higher dimensions, we expect that GTE decreases with increasing d partly due to the monogamy of entanglement. One could test this in the 3d TFIM on the cubic lattice.

Interestingly, in 2d, using ED on clusters up to 25 sites, we found that a small W2 ~ 2 × 10−4 appears at large values of the transverse field h ≳ 8, and our finite-size scaling analysis suggests that it will survive in the thermodynamic limit (see SM).

Scaling of multipartite entanglement near criticality

Let us now look more closely at the scaling of entanglement measures near the transition. We shall first present an analysis that establishes the singular scaling of W1 in a large class of quantum critical points that includes the Ising CFT in d ≥ 1, and then give a general argument for other multipartite entanglement measures (which includes bipartite as a special case). Let h be the non-thermal parameter that tunes the system to a QCP. Let Uc be the optimal LU transformation that yields W1 at hc, and \(\check{\rho }={U}_{c}\rho {U}_{c}^{{{\dagger}} }\) the transformed RDM. As h is varied away from hc, by the Envelope Theorem61, the only contribution comes from the direct variation of the RDM, with Uc unchanged, see Supplemental Material for a derivation. The density matrix elements are linear combinations of n-point functions of Pauli operators with n ≤ 3. The Pauli strings with non-zero expectation value need to preserve the symmetries of the finite-size Hamiltonian, which we take to have a unique ground state. These operators will generically have an overlap with the relevant low energy scalar of the quantum critical theory, which we call ε, with (spatial) scaling dimension Δε = d + z − 1/ν, where z is the dynamical critical exponent, and ν is the correlation length exponent. As such, the dominant variation of the expectation value at small ∣h − hc∣ will be proportional to \(| h-{h}_{c}{| }^{{\Delta }_{\varepsilon }\nu }\). In turn, this will lead to a singular variation \({W}_{1}={W}_{1}({h}_{c})+a| h-{h}_{c}{| }^{{\Delta }_{\varepsilon }\nu }+\cdots \,\).

A more basic argument can be made to explain the singularity of a generic entanglement measure or criterion, which we call \({{{\mathcal{M}}}}\), irrespective of the number of spins / parties considered. \({{{\mathcal{M}}}}\) depends on the expectation values within the subregion, and in a symmetric ground state the relevant scalar will typically dominate those, yielding the singular derivative:

$${\frac{d{{{\mathcal{M}}}}}{dh}\bigg| }_{h\to {h}_{c}}=\alpha \,| h-{h}_{c}{| }^{{\Delta }_{\varepsilon }\nu -1}$$
(7)

It may happen that α vanishes so that the singular behavior appears in higher-order derivatives, as is the case for the next-nearest neighbor concurrence in the 1d TFIM25, but that situation is not generic.

In the case of the 1d TFIM, described by the 1d Ising CFT, we have Δε = ν = z = 1, and a logarithmic divergence appears instead:

$${\frac{d{W}_{1}}{dh}\bigg| }_{h\to {h}_{c}}=-\!\alpha \ln | h-{h}_{c}|$$
(8)

where α ≈ 0.097, as can be seen in Fig. 4b. The GS correlation functions have indeed a logarithmic \(\ln | h-{h}_{c}|\), as can be verified from the exact solution62. The general result (7) also explains the logarithmic divergence numerically seen in various genuine 3-spin and 4-spin entanglement metrics in the 1d TFIM27,63. In the 2d Ising CFT, Δεν = 0.890, such that the exponent in (7) is  − 0.11. Such a divergence is difficult to reveal using our finite-size data, but the derivative becomes maximal in close proximity to the QCP, see Supplementary Fig. S5 in Supplemental Materials.

It is worth noting that in cases of symmetry breaking, which can occur, for instance in the magnetic phase of the quantum Ising model in the thermodynamic limit, the critical exponent in the ordered phase will generically differ from that in the symmetric phase. In the symmetry-broken phase, ε should then be replaced by the lowest operator that acquires an expectation value. In the Ising case, this will be the order parameter ϕ, so (7) will depend on Δϕ instead of Δε when h < hc.

Discussion

In this work, we performed entanglement microscopy to access the true entanglement hidden in quantum many-body systems, by scrutinizing the full RDMs of microscopic subregions obtained by ED and QMC24. We have studied the phase diagram of two representative QCPs in 1 and 2 spatial dimensions: the transverse field Ising model, both in 1d and 2d, and the 2d GNY chiral-Ising transition of Dirac fermions. We found (i) the Ising QCP exhibits short-range entanglement with a finite sudden death as a function of separation and temperature; (ii) the fermionic QCP exhibits power-law decay of the fermionic LN at large separations between the subregions; (iii) there is no detectable 3-party entanglement with our witnesses in a large window near the 2d Ising QCP, while it is present in the 1d counterpart. Finally, we present general non-perturbative results regarding the scaling of multipartite entanglement measures near quantum critical points. Our results demonstrate that precise entanglement microscopy is possible on large-scale quantum many-body systems beyond 1d. A new window into quantum many-body entanglement is opening, with countless systems waiting to be explored.

In the future, it will be interesting to explore the multipartite entanglement at various exotic QCPs, including transitions into a non-Fermi-liquid64,65, deconfined QCPs for both fermion and spin models9,10,66,67,68,69,70, and symmetric mass generation transitions71.

Methods

Stochastic series expansion

In the SSE simulation72, the partition function Z is Taylor-expanded as a power series of Hamiltonian operators, and each term is sampled stochastically. As mentioned in the previous section, the RDM matrix element resembles a partition function but with imaginary time boundary conditions open in region A, which is expressed as

$$\langle \alpha | {\rho }_{A}| \tilde{\alpha }\rangle= \frac{1}{Z}\sum\limits_{\xi}\left\langle \alpha,\xi \right\vert {e}^{-\beta H}\left\vert \tilde{\alpha },\xi \right\rangle \\= \frac{1}{Z}\sum\limits_{\xi }\sum\limits_{n}\frac{{\beta }^{n}}{n!}\left\langle \alpha,\xi \right\vert {H}^{n}\left\vert \tilde{\alpha },\xi \right\rangle$$
(9)

after series expansion of e−βH. Therefore, the sampling is almost identical to the standard SSE, but now we simply break the imaginary-time periodicity for loops that pass through sites in region A when doing loop updates. The frequency of any configuration pair \((\alpha,\tilde{\alpha })\) is proportional to the magnitude of the corresponding element in the RDM, i.e., \(\left\langle \alpha \right\vert {\rho }_{A}\left\vert \tilde{\alpha }\right\rangle\), according to the detailed balance condition. That is,

$$\frac{\left\langle \alpha \right\vert {\rho }_{A}\left\vert \tilde{\alpha }\right\rangle }{\left\langle \alpha ^{\prime} \right\vert {\rho }_{A}\left\vert \tilde{\alpha }^{\prime} \right\rangle }=\frac{P(\alpha,\tilde{\alpha })}{P(\alpha ^{\prime},\tilde{\alpha }^{\prime} )},$$
(10)

with P denotes the probability of a pair of states \((\alpha,\tilde{\alpha })\) to appear. Interested readers are welcome to read ref. 24 for more details.

Determinant quantum Monte Carlo

For the t − V model, we employ the determinant quantum Monte Carlo (DQMC) scheme29,30,31, where the fermion interaction is decoupled into fermion bilinear coupled to the auxiliary field. In each configuration, the free fermionic Green’s function can be calculated, and higher-order correlation functions are evaluated using Wick’s theorem.