A data-driven group retrosynthesis planning model inspired by neurosymbolic programming

Zhang, Xuefeng; Lin, Haowei; Zhang, Muhan; Zhou, Yuan; Ma, Jianzhu

doi:10.1038/s41467-024-55374-9

Download PDF

Article
Open access
Published: 02 January 2025

A data-driven group retrosynthesis planning model inspired by neurosymbolic programming

Nature Communications volume 16, Article number: 192 (2025) Cite this article

3783 Accesses
1 Citations
5 Altmetric
Metrics details

Subjects

Abstract

Deep generative models have garnered significant attention for their efficiency in drug discovery, yet the synthesis of proposed molecules remains a challenge. Retrosynthetic planning, a part of computer-assisted synthesis planning, addresses this challenge by recursively decomposing molecules using symbolic rules and machine-trained scoring functions. However, current methods often treat each molecule independently, missing the opportunity to utilize shared synthesis patterns and repeat pathways, which may contribute from known synthesis routes to newly emerging, similar molecules, a notable challenge with AI-generated small molecules. Our investigation reveals reusable synthesis patterns that augment the reaction template library, resulting in progressively decreasing marginal inference time as the algorithm processes more molecules. Nevertheless, expanding the library enlarges the search space, necessitating investigation into methods for effectively prediction of reactions in retrosynthesis search. Inspired by human learning, our algorithm, akin to neurosymbolic programming, builds upon commonly used multi-step concepts such as cascade and complementary reactions and can evolve from practical experiences, enhancing the prediction model for fundamental and compositional reaction templates. The evolutionary process involves wake, abstraction, and dreaming phases, alternatively extending the reaction template library and refining models for more efficient retrosynthesis. Our algorithm outperforms existing methods, discovers chemistry patterns, and significantly reduces inference time in retrosynthetic planning for a group of similar molecules, showcasing its potential in validating results from generative models.

Retrosynthesis prediction with an iterative string editing model

Article Open access 30 July 2024

Retrosynthesis prediction with an interpretable deep-learning framework based on molecular assembly tasks

Article Open access 03 October 2023

Retrosynthesis prediction using an end-to-end graph generative architecture for molecular graph editing

Article Open access 25 May 2023

Introduction

Deep generative models have recently gained great attention for their efficient and promising performance in the central task of designing molecules with desired properties in drug discovery^1,2,3,4,5. However, molecules proposed by generative models may be challenging or infeasible to synthesize^1,6. To address this synthesizability problem, retrosynthetic planning, one of the computer-assisted synthesis planning (CASP) methodologies, has been extensively explored^7,8. Retrosynthetic planning could be described as a process that recursively analyzes molecules and transforms them into simpler precursors until a set of commercially available molecules is obtained.

Recent advancements in retrosynthetic planning have been propelled by the development of modern machine learning-based search algorithms. Segler et al.⁹ introduced an integration of symbolic rules and deep neural networks to perform synthesis planning, laying the foundation for the widespread adoption of the neurosymbolic framework. Building on this approach, Kishimoto et al.¹⁰ introduced the AND-OR structure to enhance the illustration of the relationship between reactions and molecules. Chen et al.¹¹ further contributed by introducing a method to perform A* search under the guidance of a neural model estimating the cost of reactions and molecules. Subsequent research efforts have explored various aspects of retrosynthetic planning. Some have focused on improving the representation of molecular structures and the prediction of reactants for a target product in single-step transformations^12,13,14, while others have concentrated on refining models to select the most promising synthesis routes within the planning process^15,16,17,18.

Existing methods primarily concentrate on synthesizing individual molecules. There is no mechanism in literature to explicitly abstract common patterns arising from known molecular synthesis routes and reuse them for the inference of new and similar molecules. This challenge becomes particularly notable in the context of AI-generated small molecules since a large number of similar molecules are generated from a distribution learned from data. Intuitively, molecules with similar structures may have common intermediate molecules in their synthesis routes. For instance, both amiloride and cephalosporin-class antibiotics contain amide groups, and the synthesis of amides is a recurring step in the production of these two types of compounds. Incorporating the amide synthesis process from the first molecule’s synthesis route into the reaction template library, we can significantly expedite the search for the synthesis route of the second molecule. In addition to shared intermediate molecules, there are cases where similar molecules follow similar synthesis routes but do not have identical steps in common. For instance, Acetylsalicylic acid, also known as Aspirin, is a widely used medication. It can be synthesized by acetic anhydride and salicylic acid, which can be further synthesized from phenol. As the isomer of acetylsalicylic acid, 3-acetylsalicylic acid can be synthesized by acetic anhydride and 3-hydroxybenzoic acid, which is the isomer of salicylic acid. This isomer can also be further synthesized using phenol. These isomers typically adhere to common synthesis rules, specifically a series of reactions without regard to their reactants or products. Such a sequence of reactions can be directly applied to another isomer to expedite the retrosynthesis process. Based on these observations, we propose that extracting and incorporating these reusable patterns into the reaction template library could significantly improve the efficiency of retrosynthetic planning. In contrast, existing techniques in the literature mostly focus on effectively predicting a single reaction in a retrosynthetic process.

Our proposal calls for the development of new machine learning methodologies for abstracting common and useful multi-step reaction processes, as well as mastering and leveraging this growing library to enhance retrosynthetic efficiency and discover new reaction patterns. This parallels human learning, where knowledge is communicated and expanded with documentation, and internalization of knowledge leads to the development of new concepts that facilitate better and faster learning in the next step. To create machines that emulate human learning and evolve knowledge, Ellis et al.¹⁹ formulate learning as program induction and introduce DreamCoder, a neuro-symbolic framework that builds expertize by alternately extending the language for expressing ___domain concepts and training the neural network to guide the search for programs within these languages, taking a step closer to human learning abilities — to efficiently discover interpretable, reusable, and generalizable knowledge across a broad range of domains.

Motivated by the success of DreamCoder, our exploration delves into the potential of incorporating neurosymbolic programming into retrosynthetic planning. Just as quickly migrating and accomplishing functions can be achieved through encapsulating multiple program statements into functions, some challenging fragments in molecules that are the cumulative result of multi-step reactions of different types can be seen as products of abstract reactions. Being aware of these frequently used multi-step reaction processes is valuable for experts when they are working on retrosynthesizing complex molecules. This strategic integration aims not only to expedite retrosynthetic planning but also to unravel the constraints and repeat routes inherent in the synthesis of similar molecules.

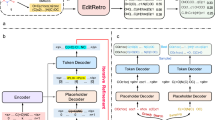
Here, we have drawn upon two common and significant concepts in multi-step reaction processes, applying them to the retrosynthesis search process: (1) cascade reactions, which are sequences of chemical transformations that happen consecutively, and (2) complementary reactions, which means that there is a complementarity between these reactions, where one reaction may serve as a precursor to another or interact with the product of another reaction. This informs the design of a retrosynthetic system that learns and evolves from practical experiences, aiming to enhance the utilization of fundamental reaction templates. Through the analysis of successes and failures, we derive strategies for more efficient retrosynthesis, facilitating the discovery of optimal synthesis routes. The entire evolutionary process is divided into three continuously alternating phases as shown in Fig. 1: (1) the wake phase, where attempts are made to solve retrosynthetic planning tasks, and the process is recorded for subsequent abstraction and dreaming phases; (2) the abstraction phase, an effort is made to extract strategies suitable for solving retrosynthesis problems, involving the previously mentioned cascade reactions and complementary reactions; (3) the dreaming phase, where numerous fantasies are generated based on replay of the wake phase, upon which built-in neural models practices with the strategies introduced in the abstraction phase and learns how to better apply them in the subsequent process.

To evaluate the performance of our algorithm, we conduct a comparative analysis by benchmarking our model against other state-of-the-art approaches. We evaluate success rates, search efficiency, and various commonly used metrics for single-target retrosynthetic planning following previous works^11,16. As part of our validation process, we examine the utility of patterns automatically extracted by the system during the abstraction phase, along with the corresponding refinement operations applied to the models during the dreaming phase. Most importantly, to evaluate the performance of our algorithm in retrosynthetic planning for a group of similar small molecules, we introduce an experimental setting designed to demonstrate the comparative advantages of different methods in this context. Comprehensive validation tests and analyses consistently demonstrate that our algorithm outperforms existing methods, reaffirming its effectiveness. Furthermore, our algorithm also demonstrates the capability to identify commonly used chemical patterns. Remarkably, in the experiment of retrosynthetic planning for groups of similar molecules, our algorithm substantially cuts down the inference time, showcasing the algorithm’s potential to address the issue of validating proposed results generated by generative models.

Results

Overview of our system

Our system can be divided into three phases that alternate continuously. In the wake phase (Fig. 1a), an AND-OR search graph is constructed in the process of retrosynthetic planning. Starting from the target molecule, two neural network models are adopted to guide the planning process to approach the purchasable molecule set more rapidly; one model helps choose where to expand the graph, and the other model guides how to expand the graph at a specified point. When the search terminates, we gather successfully solved synthesis routes and failed molecules for which no synthesis route was found for later use in the other two phases. The abstraction phase (Fig. 1b) mainly focuses on how to expand a node, and the goal is to go beyond existing fundamental rules and discover compositional strategies that are more suitable for retrosynthesis in the future. Here, we introduce two types of structures in the search graph that represent multi-step reaction processes: “cascade chains” for cascade reactions and “complementary chains” for complementary reactions. The most useful strategies are filtered out, defined as abstract reaction templates, and then added to the library. Apparently, a diverse set of strategies can enhance the performance to address various retrosynthesis problems effectively. However, the increase in the library also brings about more branches, thereby complicating the selection difficulty during expansion. Therefore, the dreaming phase (Fig. 1c) mainly focuses on how to refine the neural models. In this phase, we generate a substantial amount of retrosynthetic data, called fantasies, by simulating retrosynthesis experiences from both bottom-up and top-down approaches, to address the data-hungry problem of the machine learning model. We then refine the two models mentioned before using both replayed experiences and fantasies to improve their performance in the subsequent wake phase.

Performance of retrosynthetic planning for single molecule

To evaluate the planning efficiency of the proposed method, we compare the success rate under the same limit of planning cycles. A planning cycle involves evaluating candidate reactions suggested by the Neural Network, expanding the search space, and updating the search status. It is precisely defined as an iteration of the while loop at line 3 of Algorithm 1. We also refer to such a planning cycle as an iteration.

We first compare our method with the baselines on the Retro*-190 dataset (Fig. 2a–f). Under the iteration limit of 500, our method demonstrates superior performance over all the other approaches with respect to both the success rate and the time used to find the first synthesis route on the Retro*-190 dataset, as evidenced by the average results from 10 independent experiments. (Fig. 2a, c). In particular, our method achieves an average 98.42% success rate by on average solving three more retrosynthetic tasks than EG-MCTS and 2.9 more tasks than PDVN (Fig. 2a). This dataset is small and easy, so the performances of our model, EG-MCTS, and PDVN are comparable. However, it can be observed that we have a substantial advantage in terms of search efficiency, with an average of 21.95 fewer iterations than EG-MCTS and 18.31 fewer iterations than PDVN, which saves almost half of the running time (Fig. 2c). Another observation is that the maximum search time of our method is significantly shorter than EG-MCTS and PDVN (Fig. 2c). We also note that increasing the iteration limit from 500 to 1000 does not much improve the success rate for our method and the most competitive baselines (Fig. 2b). In addition, while PDVN can achieve an average success rate comparable to our method when the iteration limit exceeds 700, its performance exhibits higher variation across multiple experiments (Fig. 2b). The efficiency of the search is often reflected in the number of nodes on the tree or graph after the search is finished. Fewer expansion steps usually lead to shorter search times. In this regard, we count the number of molecular nodes and reaction nodes after finding synthetic routes using several methods, as shown in Fig. 2d, e. Our method demonstrates a significant advantage in terms of the number of expanded nodes, reducing the number of expansions by approximately half compared to EG-MCTS and PDVN. This corresponds to roughly a 50% reduction in search time as well. Typically, molecules with longer synthesis paths require longer search times. However, by extracting common chain reactions during the abstraction phase, our method effectively shortens the search graph’s synthesis paths, thereby accelerating the search process for such molecules. In addition, the length of the synthesis route is also a critical factor to consider. This is because chemical reactions typically have certain reaction efficiencies, and the length of the synthesis route directly affects the amount of starting materials required. If the synthesis route is too long, it necessitates the preparation of a larger quantity of initial raw materials, which can lead to increased costs and added complexity in the synthesis process. Therefore, apart from assessing the feasibility of finding a synthesis route and the efficiency of the search, we also evaluate the length of the discovered synthesis routes. In Fig. 2f, we present the comparison of the average number of the shortest synthesis routes found by our method and three competitive baselines. While our algorithm outperforms EG-MCTS by finding an average of 7 shorter paths, it does not outperform PDVN. This may be attributed to the multi-step reaction patterns extracted during our abstraction phase. On one hand, these patterns are applied as a single reaction in the search process, helping to enhance the search efficiency. On the other hand, this strategy may focus less on the number of reaction steps, leading to longer routes in many cases.

**Fig. 2: Performance of retrosynthetic planning of a single molecule.**

We then compare our method and the two most competitive baselines, EG-MCTS and PDVN, on the larger and more challenging dataset consisting of 20,000 molecules. Our approach consistently outperforms EG-MCTS and PDVN under different search iteration limits (Fig. 2g). Our method also uses significantly less time to complete the search compared to EG-MCTS and PDVN under higher iteration limits (Fig. 2h).

Performance of group retrosynthetic planning

Previous results prove that our methodology is more effective than using a search tree for the retrosynthetic planning of a single molecule. Then a reasonable assumption is that our method will have greater advantages when synthesizing multiple molecules simultaneously. There can be intermediate molecules that occur in the planning process which are the same, leading to redundancy in the tree. In addition, when doing multi-target planning, there may also be many repeat sub-paths. Naturally, one might hypothesize that molecules with higher similarity are prone to having more redundancy. To test this hypothesis, we first identify a group of molecules in the Retro-190 dataset with the highest similarity and can be successfully solved using several methods. Here, we use the Tanimoto distance over the embeddings of two molecules to define the pairwise molecular similarity. This process yields a group of 20 molecules, allowing us to compare the number of iterations required by these methods during the planning. We use two different settings of our method to compare with other baselines: (1) separately searching each molecule using an individual search graph and (2) collectively searching all molecules using a shared search graph. Remarkably, when individual graph searches for each molecule reduce the number of iterations by approximately 44.15% compared to EG-MCTS, the utilization of a shared graph search further amplifies this reduction by 20.85%, bringing greater search efficiency advantages (Fig. 3a). In order to better investigate the impact of similarity on the efficiency of group retrosynthetic planning, we conduct experiments using multiple sets of molecules with varying levels of similarity and we compare the benefits of reducing the number of nodes when planning on separated graphs and the shared search graph. From the results shown in Fig. 3b, we have the following findings: (1) For the single-target retrosynthetic planning, utilizing the search graph can effectively eliminate redundancy and reduce the number of added nodes in the search process by about 45%. The reduction ratio can also serve as an indicator of the amount of redundancy present in the search tree. (2) With the shared search graph, the higher the similarity of the group, the higher the reduction ratio we can achieve, and the shared search graph always performs better than the separated search graphs. Thus the shared graph is well-suited for retrosynthetic planning of a group of similar molecules. In addition, it is intuitive to assume that a larger group size should reduce the differences between samples. This could prove advantageous in minimizing redundancy when incorporating new molecules. Consequently, we carried out comparative studies involving different group sizes. As shown in Fig. 3c, with the increase in group size, the reduction ratio indeed grows until saturated. However, there is a noteworthy point that a large gap exists between the similarity of 85% and 80%. As shown from the pattern of molecules with different similarity (Fig. 3d), we can see that the slight decrease in similarity is usually reflected in changes to some peripheral functional groups, but molecules with 75% similarity have undergone alterations in the ring structures, which leads to a significant change in the synthesis route. In Fig. 3e, we provide an example of group planning on a shared search graph. These three similar target products share a common intermediate molecule after one or two retrosynthetic steps, which exemplifies the validity and correctness of our underlying motivation.

**Fig. 3: Analyses of using the search graph to perform retrosynthetic planning of a group of molecules.**

Analyzing the evolution of the wake-abstraction-dreaming cycle

We evaluate the performance of each functional module of our system in every wake-abstraction-dream cycle. One of the most important modules is to predict the best template in the library based on the currently given molecules. As shown in Fig. 4a, our single-step retrosynthesis prediction model achieves a better performance than other baseline approaches. To validate the effectiveness of our wake-abstraction-dreaming framework, we conduct a comprehensive investigation into how the system’s library evolves and its performance changes in both single-step and multi-step retrosynthesis tasks as the number of cycles increases. Firstly, we aim to understand the frequency and variety of patterns automatically extracted by the system during the abstraction phase. Our algorithm extracts patterns occurring more frequently than ζ = 1/20, 000, where the thresholding parameter ζ is chosen to achieve a good balance between search efficiency (average number of iterations) and the success rate, as observed on both datasets (Fig. 4g, h). Figure 4b displays the number of patterns extracted in each cycle, along with the distribution of patterns across different frequency ranges, shedding light on their prevalence. While the number of extracted patterns may seem relatively modest, it is crucial to note that these patterns represent commonly observed motifs. In comparison, a single cycle yields approximately 20, 000 patterns in total, with each pattern occurring at an average frequency of around 1/40, 000. As the library size grows, the complexity of the search space increases. This is consistent with our ablation study where performance degradation is observed when adding only the abstraction phase to the wake module (Fig. 4e, f). However, our dreaming module is able to refine the neural model via repeated fantasies, taking advantage of the expanded library to enhance the performance of the single-step model (Fig. 4c). This is the underlying reason for the significant improvement of our complete algorithm when adding both the abstraction and the dreaming modules (Fig. 4e, f). With the generated data and refinement during the dreaming phase, we observe continuous improvement in the accuracy of the single-step model in each cycle ultimately achieving a high level of performance. Notably, the top 1 accuracy, reflecting the model’s ability to correctly identify the most suitable template as its first choice, significantly increases. This suggests our augmented data enhances the model’s precision in mapping molecules to optimal templates. We expect improvements in the single-step model’s performance should, in principle, result in an overall increase in the retrosynthesis success rate. Figure 4d confirms our expectations, showing a continuous enhancement in the system’s retrosynthetic success rate with an increasing number of cycles. Moreover, when examining the distribution of step numbers in successfully solved synthesis routes, we notice that the initial improvement primarily addresses challenges related to longer routes. The continuous selection or prediction of multiple steps often makes many methods less effective in the final stages. However, our extracted patterns, tailored for multi-step reactions, allow us to indirectly shorten synthesis routes and impose constraints on certain routes, reducing the occurrence of such issues. Subsequent improvements mainly focus on resolving molecules with relatively shorter but crucial synthesis routes. In these routes, a wrong step can lead to failure, and this improvement is attributed to the enhanced accuracy of the single-step model.

**Fig. 4: Analyses of the evolution of wake-abstraction-dreaming cycles.**

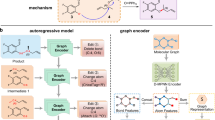
Next, we illustrate how the two strategies, “complementary chain” and “cascade chain”, are extracted and utilized. As shown in Fig. 5a, the “complementary chain” resides within the middlebox. We can observe that the first and last reactions involve the addition and elimination of t-Butyloxy carbonyl (BOC), respectively, making them complementary operations. In the abstraction phase, our system extracts the complementary chain from the synthesis route presented in the box above; then, our system uses it later in a new retrosynthetic task, as shown in the bottom box. In Fig. 5b, we show a “cascade chain” found in the abstraction phase, which is a very common synthesis route involving Amidation. Amidation and Amination often appear together in a common synthesis route. Our abstraction method combines these two steps into a composite reaction (in the black box on the right). We provide the route where our system identifies the cascade chain in the left black box and showcases two instances of its application in the wake phase, denoted by the red and blue arrows. In Fig. 5c, the upper route is selected from the dataset, while the lower one is generated by our approach. Remarkably, the upper route comprises a combination of the complementary chain displayed in Fig. 5a and another cascade chain, which is similar to the one displayed in Fig. 5b, enclosed within the red dashed box. These steps are further distilled into a new reaction template (more specifically, a new cascade chain), which is applied as indicated by the green arrow, effectively shortening the length of the synthesis route and thereby enhancing planning efficiency. To demonstrate our method’s ability to find high-quality routes, we illustrate two solution routes in Fig. 5d, where the top route is given by the dataset and the bottom route is found by our proposed method. These two routes share the same first reaction. Our approach then leaves out an extra step, selecting the better decomposition template in the second step with a better and more accurate template selection. More illustrations about how the two strategies are used in practice can be found in More illustration of retrosynthetic routes, Supplementary Figs. 5, 6.

**Fig. 5: Strategies and solution examples given by our system.**

Discussion

In this work, we perform group retrosynthetic planning as neurosymbolic programming for efficiently finding high-quality routes and learning to master synthesis strategies as experts. Our system leverages expertise from practical experiences and continues to improve through alternative three phases: wake, abstraction, and dreaming phases. The wake phase involves a search process on the AND-OR search graph guided by a template selection model and the most promising molecule selection model, while the abstraction phase extracts strategies for retrosynthesis mainly focusing on the two types of reactions: cascade reactions and complementary reactions. Besides, for better use of reaction templates and these extracted strategies, we propose two data augmentation approaches in the dreaming phase to generate representative fantasies based on a replay of experience. Our algorithm outperforms existing methods in planning efficiency on a real-world benchmark dataset and shows great performance in the experiment of retrosynthesis of a group of similar molecules generated by a generative model, which demonstrates the potential to address challenges in synthesizing molecules designed during the actual molecular design process, thus validating them.

Through analyzing experimental results, we find that summarizing synthesis routes enables the extraction of common patterns, significantly enhancing the efficiency of solving retrosynthesis problems. These patterns provide valuable guidance for searching multi-step synthetic reactions, incorporating constraints and priors from reactions along the routes, leading to an improved success rate in retrosynthetic problem-solving. However, relying solely on these insights is inadequate. The expansive search space demands the development of enhanced representations for molecules, chemical reactions, and more sophisticated filtering networks. Thus, the data augmentation strategies we devised, grounded in considerations of synthetic routes, are deemed indispensable. During the experimental process, analyzing multiple synthesis routes and unsuccessful cases uncovered recurring challenges, such as template extraction and representation for reactions of the same family. For example, both chlorination and bromination reactions can be categorized as halogenation reactions. This prompts consideration of whether incorrect in choosing between these reactions should be disregarded. Besides, for reactions present in the dataset, can we infer that reactions involving similar atomic families will follow the same reaction rules, thereby significantly expanding our repository of known reaction rules? Therefore, we aim to delve deeper into reaction representation, employing robust summarization methodologies to derive more general reaction rules in the future, simulating the human ability to draw analogies and connections.

Methods

We now describe the specifics of our system, beginning with the definition and preliminaries of the retrosynthetic planning problem, and then turning to the molecule encoder that we utilized to assist in the application of neural models, finally introducing the details of its three phases.

Preliminaries of retrosynthetic planning

Let ${{{\mathcal{M}}}}$ denote the space of all molecules, and let ${{{\mathcal{I}}}}$ denote the collections of available molecules, ${{{\mathcal{I}}}}\subseteq {{{\mathcal{M}}}}$. We have a target product to be synthesized, which is denoted as $t\in {{{\mathcal{M}}}}$. The goal is to synthesize t with the ingredients in ${{{\mathcal{I}}}}$. Instead of finding a forward route that starts from ${{{\mathcal{I}}}}$ to t, the most common method is to perform backward searching by decomposing the target molecule to its reactants recursively using one-step retrosynthesis prediction until all the reactants required are from ${{{\mathcal{I}}}}$. Such a method is called retrosynthetic planning in chemistry.

Following is the definition of the retrosynthetic planning process. Given any molecule $m\in {{{\mathcal{M}}}}$, we might have n ways to synthesize it:

$$R(m)=\{{R}_{1}(m),{R}_{2}(m),...,{R}_{n}(m)\},$$

(1)

where each R_i(⋅) is a reaction template, and R_i(m) is a reaction instantiated by the template to produce the molecule m, denoted by the triplet $(m,{{{{\mathcal{R}}}}}_{i}(m),{c}_{i}(m))$. Here, ${{{{\mathcal{R}}}}}_{i}(m)\subseteq {{{\mathcal{M}}}}$ denotes the reactants set of R_i(m) and ${c}_{i}(m)\in {{\mathbb{R}}}^{+}$ is the cost of the reaction. If ∃ R_i(m) ∈ R(m) satisfies that $\forall {m}^{{\prime} }\in {{{{\mathcal{R}}}}}_{i}(m),{m}^{{\prime} }\in {{{\mathcal{I}}}}$, then we find a successful route to synthesize m. If not, we need to choose a reaction R_i(m) and further synthesize all the reactants ${m}^{{\prime}{\prime}}\in {{{{\mathcal{R}}}}}_{i}(m)\backslash {{{\mathcal{I}}}}$. If the elements in ${{{{\mathcal{R}}}}}_{i}(m)\backslash {{{\mathcal{I}}}}$ can be synthesized using molecules in ${{{\mathcal{I}}}}$ through one or multiple steps, we can find a successful synthesis route as well.

In practical retrosynthetic planning, it’s time-consuming to gather all possible synthetic reactions for a molecule as the search space is vast. Instead of using brute force enumeration, a commonly used method is to utilize a neural model to map from molecules to the top-K potential reactions and do a beam search; thereby, the complexity can be limited. we define this model as B with parameters θ_b,

$$B(\cdot ;{\theta }_{b}):m \, \mapsto \, {\{{R}_{i}(m)=(m,{{{{\mathcal{R}}}}}_{i}(m),{c}_{i}(m))\}}_{i=1}^{K},$$

(2)

which generates at most K reactions for a given molecule m. B can be learned from a dataset of chemical reactions ${D}_{{{{\rm{train}}}}}=\{(m,{{{\mathcal{R}}}}(m))\}$. Here, since most datasets do not provide the actual price of a reaction R_i(m), most works simply use the negative log-likelihood of the reaction under model B as the cost c_i(m). Given the above definitions, there are two critical components that significantly limit the performance of retrosynthesis: mapping m to ${\{{R}_{i}(m)\}}_{i=1}^{K}$ and selecting the most promising R_i(m). These are the aspects that most work typically focuses on.

Molecule encoder

To enable machine learning algorithms to understand and utilize molecules, molecule representation learning (MRL) proposes to convert molecules into dense vectors and map them to a low-dimensional real space. A simplified molecular-input line-entry system (SMILES) is a line notation used to represent the structure of chemical species in computers using short ASCII strings. There are many SMILES-based methods that take SMILES strings as input and utilize natural language models such as BERT²⁰ or Transformers²¹ to get the embeddings of molecules^22,23. However, SMILES representation assumes a sequential order between the atoms in a molecule, which cannot effectively reflect the complex relationships between atoms in a molecule. As a result, these SMILES-based approaches fail to capture the rich chemical contexts and their interplays of molecules, resulting in unsatisfactory predictive performance²⁴. Here, we choose graph neural network (GNN)²⁵ as our base model instead for its high performance in capturing structural information and graph representation capability, which utilizes molecule structure and atom features to learn a representation vector for each atom and the entire molecule.

More specifically, we represent a molecule by a graph defined as G = (V, E), where V = {a₁, a₂, …} is the set of non-hydrogen atoms and E = {b₁, b₂, …} is the set of bonds. We use a feature vector x_i to encode the properties of the atom a_i. Here, the following types of atom properties are used: element type, total degree, formal charge, the number of hydrogen atoms, hybridization type, and whether the atom is an aromatic ring. Each type of atom c is represented as a one-hot vector. Besides, we use a multi-hot vector to represent whether c is included in a certain size of ring or not because we think ring structures are important for reactions. All feature vectors are concatenated into a single vector as the initial feature of c. Typical GNNs follow a neighborhood aggregation strategy, which iteratively updates the representation of an atom by aggregating representations of its neighbors and itself. Formally, the n-th layer of a GNN is:

$${h}_{i}^{n}={{{\rm{AGGREGATE}}}}({\{{h}_{j}^{n-1}\}}_{j\in {{{\mathcal{N}}}}(1)\cup \{i\}}),n=1,\ldots,N,$$

(3)

where ${h}_{i}^{n}$ is atom a_i’s representation vector at the n-th layer (${h}_{i}^{0}$ is initialized as the initial feature x_i), ${{{\mathcal{N}}}}(1)$ is the set of atoms directly connected to a_i, and N is the number of GNN layers. Finally, a readout function is used to aggregate all node representations output by the last GNN layer to obtain the entire molecule’s representation h_G:

$${h}_{G}={{{\rm{READOUT}}}}({\{{h}_{i}^{N}\}}_{{a}_{i}\in V}).$$

(4)

In a chemical reaction, the system is usually closed, and various physical quantities of the system, such as mass, energy, and charge, remain constant before and after the reaction. This creates an equivalence between the reactants and products in the chemical reaction space that we want to maintain in the molecule embedding space:

$${\sum}_{r\in {{{\mathcal{R}}}}}{h}_{r}={\sum}_{p\in {{{\mathcal{P}}}}}{h}_{p},$$

(5)

where ${{{\mathcal{R}}}}$ is reactant set, ${{{\mathcal{P}}}}$ is product set. As a result, a straightforward loss function for the proposed method is $\ell=\frac{1}{| D| }{\sum }_{({{{{\mathcal{R}}}}}_{i},{{{{\mathcal{P}}}}}_{i})\in D}\parallel {\sum }_{r\in {{{{\mathcal{R}}}}}_{i}}{h}_{r}-{\sum }_{p\in {{{{\mathcal{P}}}}}_{i}}{h}_{p}{\parallel }_{2}$, where $({{{{\mathcal{R}}}}}_{i},{{{{\mathcal{P}}}}}_{i})$ represents the i-th chemical reaction in a batch of training data D. However, simply minimizing the above loss does not work, since the model will degenerate by outputting all-zero embeddings for all molecules. Here, we follow the method used in Wang et al.²⁶ and use a minibatch-based contrastive learning framework similar to Radford et al.²⁷; we first use the GNN encoder to process all reactants ${{{{\mathcal{R}}}}}_{i}$ and products ${{{{\mathcal{P}}}}}_{i}$ in this batch and get their embeddings. The matched reactant-product pairs $({{{{\mathcal{R}}}}}_{i},{{{{\mathcal{P}}}}}_{i})$ are treated as positive pairs, whose embedding discrepancy will be minimized, while the unmatched reactant-product pairs $({{{{\mathcal{R}}}}}_{i},{{{{\mathcal{P}}}}}_{j})(i\ne j)$ are treated as negative pairs, whose embedding discrepancy will be maximized. The final loss function is

$$\ell= \frac{1}{| D| }{\sum}_{({{{{\mathcal{R}}}}}_{i},{{{{\mathcal{P}}}}}_{i})\in D} \left| \left| l {\sum}_{r\in {{{{\mathcal{R}}}}}_{i}}{h}_{r}-{\sum}_{p\in {{{{\mathcal{P}}}}}_{i}}{h}_{p} \right| \right|_{2}\\ +\frac{1}{| D| (| D| -1)}{\sum}_{i\ne j}\max (\gamma - \left| \left| l {\sum}_{r\in {{{{\mathcal{R}}}}}_{i}}{h}_{r}-{\sum}_{p\in {{{{\mathcal{P}}}}}_{j}}{h}_{p} \right| \right|_{2},0),$$

(6)

where γ > 0 is a margin hyper-parameter.

Wake phase (Neuro guided retrosynthetic planning)

The goal of the wake phase is to search for a synthesis route that leads from available molecules set to the target product. More specifically, we devise a retrosynthetic planning algorithm that works on the so-called AND-OR search graph. Below, we first introduce the definition of the AND-OR search graph and then dive into the details of the planning procedure.

AND-OR search graph

We define the AND-OR search graph as follows. A search graph $G=({{{\mathcal{V}}}},{{{\mathcal{E}}}})$, consists of a finite set ${{{\mathcal{V}}}}$ of vertices, a set ${{{\mathcal{E}}}}\subseteq {{{\mathcal{V}}}}\times {{{\mathcal{V}}}}$ of edges. G is a directed graph because there is a strict order between reactants and products in the synthesis process. As for the retrosynthetic search graph, the direction always goes from products to reactants and there are two types of nodes on the graph G: molecule and reaction. Let ${{{{\mathcal{V}}}}}_{m}$ and ${{{{\mathcal{V}}}}}_{r}$ denote the collections of molecule nodes and reaction nodes. It can be guaranteed that ${{{{\mathcal{V}}}}}_{m}\uplus {{{{\mathcal{V}}}}}_{r}={{{\mathcal{V}}}}$. Besides, molecule nodes only connect to reaction nodes, and vice versa. For a reaction ${R}_{i}(m)=(m,{{{{\mathcal{R}}}}}_{i}(m),{c}_{i}(m))$ mentioned before, it can be represented in the graph: (1) m, a molecule node, is the predecessor of the reaction node R_i; (2) molecule nodes in ${{{{\mathcal{R}}}}}_{i}(m)$ are the successors of R_i and belong to ${{{{\mathcal{V}}}}}_{m}$. Here, we define molecule nodes as the ‘OR’ nodes and reaction nodes as the ‘AND’ nodes because a molecule m can be synthesized using any one of its successor reactions (or relation), and each reaction can work only when all of its successor reactants to be ready (and-relation). Mathematically, we define the Boolean function avail(v) ↦ {true, false} that evaluates the success state of each node v, more specifically, whether the molecule can be synthesized or the reaction is ready to be executed. We further define ${{{\rm{pr}}}}(v)\mapsto {{{\mathcal{V}}}}$ to get the predecessor of node v. Then we have,

$${{{\rm{avail}}}}(v)=\left\{\begin{array}{lc}{\bigwedge }_{{{{\rm{pr}}}}({v}_{i})=v}\{{{{\rm{avail}}}}({v}_{i})\} \hfill &v\in {{{{\mathcal{V}}}}}_{r}\\ {\bigvee }_{{{{\rm{pr}}}}({v}_{i})=v}\{{{{\rm{avail}}}}({v}_{i})\}\vee \{v\in {{{\mathcal{I}}}}\}&v\in {{{{\mathcal{V}}}}}_{m}\end{array}\right.,$$

(7)

where ∨ , ∧ denote logical AND, OR operations, respectively. Specifically, (1) a reaction node is in true status if all its successors are in true status; (2) a molecule node v is in true status if one of the following two constraints is satisfied: (a) the molecule v is in the set ${{{\mathcal{I}}}}$; (b) it has at least one successor whose status is true.

An example of the search graph is shown in Fig. 6, where the prefix M or R indicates molecule nodes or reaction nodes, respectively. M1 is the target product and the building blocks $M5,M7\in {{{\mathcal{I}}}}$. M1 can be synthesized using reaction R1 or R2, so avail(M1) = avail(R1) ∨ avail(R2). It is apparent that R1 is a uni-molecular reaction because it has only one reactant, M2 and R2 is a bi-molecular reaction because it connects to M3 and M4. As a result, avail(R1) = avail(M2), and avail(R2) = avail(M3) ∧ avail(M4).

**Fig. 6: The search procedure based on the AND-OR search graph.**

Compared with the AND-OR search tree used in Retro*¹¹, the search graph merges the search nodes for identical intermediate molecules to reduce redundancy. Specifically, there are two types of redundancy in AND-OR trees. First, in typical single-target synthesis scenarios, the search tree for a target molecule might feature multiple identical sub-trees due to similar reactions yielding the same intermediate molecules (e.g., the node M6 in Fig. 6). Second, in multi-target synthesis tasks, different targets are often treated independently, overlooking the potential sharing of common intermediate molecules post-several reactions–a common phenomenon in synthetic chemistry (an example is illustrated in Fig. 3e). In both scenarios, search graphs would naturally merge these common intermediate molecules to avoid redundant search nodes, reducing the total number of search nodes and enhancing efficiency. Furthermore, if multiple molecules share a search graph, we refer to the search graph as a shared search graph.

AND-OR graph-based planning

Our planning algorithm is a best-first search algorithm that continuously explores and expands on the AND-OR search graph. In the search process, the ${{{{\mathcal{V}}}}}_{m}$ is split into two subsets: the open molecule nodes ${{{{\mathcal{V}}}}}_{{m}_{o}}$ and closed molecule nodes ${{{{\mathcal{V}}}}}_{{m}_{c}}$. A molecule node $v\in {{{{\mathcal{V}}}}}_{{m}_{c}}$, only if the molecule is in an available set ${{{\mathcal{I}}}}$ or it has been visited; otherwise, the node belongs to ${{{{\mathcal{V}}}}}_{{m}_{o}}$. For example, in Fig. 6, $M4,M6\in {{{{\mathcal{V}}}}}_{{m}_{o}}$ and other molecules are closed. Initially, the graph G contains only one molecule node, that is, the target product t. Then we do planning on G. Each planning step can be divided into three steps,

1.
Select: We select one open molecule node m which has never been visited before, and m is the most promising molecule proposed by the value model of molecules as shown in line 4 of Algorithm 1. A proper design of the value of molecules would improve search efficiency, and meet some user-defined requirements, such as the length of the route, the cost of ingredients, and so on. We will introduce the details of the cost function in the Value model.
2.
Expand: After selecting the node m with minimum cost estimation, we will expand the search graph with K proposals from single-step retrosynthesis model B(m; θ_b). Specifically, we first extract the molecule features and then feed them into the target template proposing model and get K proposals. For each proposed retrosynthesis reaction $(m,{{{{\mathcal{R}}}}}_{i}(m),{c}_{i}(m))$, we create a reaction node R = R_i under node m, and for each molecule ${m}^{{\prime} }\in {{{{\mathcal{R}}}}}_{i}(m)$, we create a molecule node under the reaction node R. If ${m}^{{\prime} }$ has already appeared in the graph, the node will be automatically merged, and the value of that node will be updated. This step is shown in lines 5–9 of Algorithm 1. The details of model B(m; θ_b) and how to get K proposals are shown in Single-step retrosynthesis prediction.
3.
Update: After expanding, we need to update the status (e.g., success state, historical cost) of all nodes as lines 12 to 17 of Algorithm 1. Here we use a bottom-up strategy and only update the affected nodes to save search time.

We repeat these three steps until the termination condition is satisfied: finding a route for the target, using up the iteration budget (L, given as input), or having no nodes to expand. It is clear that the algorithm guarantees to terminate. If the hyper-parameter K is large enough so that all possible expansions can be made, our algorithm guarantees to find a synthesis route as long as there exists one (since all possible synthesis paths will be examined until a solution is found). For a smaller K, successful planning of our algorithm relies on the accuracy of the K reactions proposed by the model B(⋅ ; θ_b).

If a synthetic route is found, we can apply a depth-first search (DFS) strategy to extract the synthetic route as a tree from the search graph as the “best route” shown in Fig. 6. Molecule nodes and reaction nodes occur alternatively on the tree; the molecule node is the parent of the best synthesis reaction, and all reactants are the children of the reaction node. The tree-like synthesis route is easily understood by humans.

Algorithm 1

Retrosynthetic planning on AND-OR search graph(t, L)

input :target molecule t, iteration limit L

output :if find the synthesis route of t, a synthesis graph G / ∗ topo_dist(m₁, m₂) = n if m₁ is the nth-level predecessor molecule node of m₂

1 Initialize $G=({{{\mathcal{V}}}},{{{\mathcal{E}}}})$ with ${{{\mathcal{V}}}}\leftarrow \{t\},{{{\mathcal{E}}}}\leftarrow {{\emptyset}}$;

2 n ← 0;

3 while avail(t) is not true and n ≤ L and ${{{{\mathcal{V}}}}}_{{m}_{o}}\,{{{\rm{is}}}}\,{{{\rm{not}}}}\,{{{\rm{empty}}}}$ do

4 ${m}_{{{{\rm{next}}}}}\leftarrow \arg {\min }_{m\in {{{{\mathcal{V}}}}}_{{m}_{o}}}{{{\rm{cost}}}}(m)$;

5 ${\{{R}_{i}=\{{m}_{{{{\rm{next}}}}},{{{{\mathcal{R}}}}}_{i},{c}_{i}\}\}}_{i=1}^{K}\leftarrow B({m}_{{{{\rm{next}}}}})$;

6 for i ← 1 to K do

7 Add a reaction node R_i to G under the molecule node m_next;

8 for j ← 1 to $| {{{{\mathcal{R}}}}}_{i}|$ do

9 Add ${{{{{\mathcal{R}}}}}_{i}}_{j}$ to G under R_i with an initial value ${{{\rm{Value}}}}({{{{{\mathcal{R}}}}}_{i}}_{j})$;

10 ${{{\rm{cost}}}}({R}_{i})\leftarrow {c}_{i}\times {\sum }_{m\in {{{{\mathcal{R}}}}}_{i}}{{{\rm{cost}}}}(m)$;

11 ${{{\rm{avail}}}}({R}_{i}){\leftarrow \bigwedge }_{m\in {{{{\mathcal{R}}}}}_{i}}\{{{{\rm{avail}}}}(m)\}$;

12 ${{{\rm{avail}}}}({m}_{{{{\rm{next}}}}}){\leftarrow \bigvee }_{R\in {\{{R}_{i}\}}_{i=1}^{K}}\{{{{\rm{avail}}}}(R)\}$;

13 ${{{\mathcal{M}}}}\,\leftarrow$ all predecessor molecule nodes of m_next;

14 sort ${{{\mathcal{M}}}}$ based on topo_dist(; , m_next);

15 for i ← 1 to $| {{{\mathcal{M}}}}|$ do

16 Update the cost of ${{{{\mathcal{M}}}}}_{i}$;

17 Update the success state of ${{{{\mathcal{M}}}}}_{i}$;

18 n ← n + 1;

19 return avail(t), G;

Value model

To parameterize the cost of synthesizing any molecule m which is used to guide the selection of the next node to expand in the select step of AND-OR graph-based planning, we first compute its embedding by the molecule graph encoder mentioned before, then feed it into a single-layer fully connected neural network of hidden dimension 128, which then outputs a scalar representing V_m.

Specifically, we construct retrosynthesis routes for feasible molecules in D_train, where the available set of molecule M is also given beforehand. The resulting dataset will be ${{{{\rm{rt}}}}}_{{{{\rm{train}}}}}=\{{{{{\rm{rt}}}}}_{i}=\left({m}_{i},{{{{\mathcal{R}}}}}_{i},{C}_{i},{\{R\}}^{K}\right.\}$, where each tuple rt_i contains the target molecule m_i, the total cost of the best route C_i, the single-step retrosynthesis candidates {R}^K, which also contains the true single-step retrosynthesis reaction R_i used in the planning solution. The learning of V_m consists of two parts, namely the value fitting which is a regression loss ${\ell }_{{{{\rm{regression}}}}}({{{{\rm{rt}}}}}_{i})={({V}_{{m}_{i}}-{C}_{i})}^{2}$ and the consistency learning which maintains the partial order relationship between the best single-step solution R_i and other solutions ${R}_{j}=({m}_{i},{{{{\mathcal{R}}}}}_{j},{c}_{j})\in {\{R\}}^{K}$, here we use the N-pair loss proposed by Sohn et al.²⁸:

$${\ell }_{{{{\rm{consistency}}}}}({{{{\rm{rt}}}}}_{i},{\{{R}_{j}\}}_{j=1}^{K-1})=\log (1+{\sum}_{j=1}^{K-1}\exp ({C}_{i}+\epsilon -{c}_{j}-{\sum}_{{m}^{{\prime} }\in {{{{\mathcal{R}}}}}_{j}}{V}_{{m}^{{\prime} }})),$$

(8)

where ϵ is a positive constant margin to ensure R_i has higher priority for expansion than its alternatives even if the value estimates have tolerable noise.

Single-step retrosynthesis prediction

The single-step retrosynthesis prediction model is used in the expansion step of AND-OR graph-based planning to generate K proposals. Here, we use a template-based model to predict the target reaction template and corresponding reactants. Our single-step prediction method consists of two steps: (1) predict the target reaction template, and (2) apply the template to the product and get corresponding reactants.

To begin with, we employ the molecule graph encoder to generate template fingerprints as y_fp. In addition, drawing inspiration from how reactions are defined and classified in chemistry, we construct a table comprising commonly utilized functional groups and identify all functional groups present in the templates, utilizing the open-source RDKit package. We then leverage the presence of all predefined functional groups to categorize the templates using adaptive clustering techniques and calculate the one-hot encoding y_class. As a result, the concatenation of y_fp and y_class is used as the embedding of templates, and we store them in the cache as set ${{{\mathcal{T}}}}$.

Subsequently, a Multi-Layer Perceptron (MLP) is employed to predict the target template class and its corresponding template embedding as z. Here, we use a loss function consisting of two components:

1.
To minimize the difference between the predicted embeddings and the target embeddings, we use the cosine similarity loss ${\ell }_{{{{\rm{similar}}}}}(z,y)=1-\frac{z\cdot y}{\parallel z\parallel \parallel y\parallel }$, where z is the predicted embedding and y is the target embedding.
2.
To optimize the class prediction performance, we use the InfoNCE loss²⁹,
$$\ell (z,{{{\mathcal{T}}}})=-\log \frac{\exp (z\cdot {x}_{+}/\tau )}{{\sum }_{x\in {{{\mathcal{T}}}}}\exp (z\cdot x/\tau )},$$
(9)
where x₊ is a positive embedding of the same class as z in ${{{\mathcal{T}}}}$, and τ is a hyper-parameter ("temperature”) that controls how concentrated the features are in the embedding space. Lower temperature means the faraway points would not affect the loss as much.

Once the target template class is determined, we employ Facebook AI Similarity Search (FAISS) to quickly search for K-nearest neighbors (K-NN) within such a cluster. The K-NN search is based on the cosine similarity between the query vector and the embeddings stored in ${{{\mathcal{T}}}}$. Consequently, we obtain the top-K template proposals. Then we use RDKit to apply these templates to get corresponding reactants.

Abstraction phase (Extract cascade reactions and complementary reactions as experts)

During the abstraction phase, the system grows its library of reaction templates with the goal of discovering specialized abstractions that allow it to express solutions to the retrosynthesis tasks easily. Intuitively, given a collection of synthesis trees extracted from the search graphs during the wake phase (as explained in AND-OR graph-based planning), we can identify and compress common sub-tree fragments as abstractions to reduce their depth. Therefore, we introduce two strategic types of abstractions to enhance the library: cascade chains and complementary chains. Specifically, motivated by the cascade reaction, we “compress out” the most frequently occurring sub-trees and add them to the library, and we call them “cascade chains” — sequences of consecutive chemical transformations. In addition, we focus on another crucial chemistry pattern: complementary reactions. We define these as “complementary chains” — pairs of reactions that are complementary and follow tree-like partial order. Unlike cascade chains, these do not occur consecutively but consistently perform complementary functions on certain groups. Below, we first introduce the reaction template tree to facilitate the analysis of synthesis trees and then detail how to define, extract, and apply these two abstraction strategies; additionally, in More illustration of the abstraction phase and Supplementary Fig. 1, we provide further illustration of these two types of abstraction strategies.

Preliminaries: reaction template tree

We focus on the abstraction of commonly used and generalizable reaction templates instead of the exact retrosynthetic routes. Therefore, we define and will be working on the reaction template trees. Given a synthesis route tree that contains both molecule and reaction nodes (e.g., the “best route” in Fig. 6), we define the corresponding reaction template tree which consists of only the reaction nodes of the synthesis route tree, where the parent of each node in the reaction template tree is naturally set to be its grandparent in the synthesis route tree (or the node becomes the root if its grandparent does not exist, as illustrated at the bottom left of Fig. 6).

A reaction template tree also naturally defines a reaction template R(⋅): given a target molecule m, we may instantiate each reaction template in a reaction node of the tree from the root to the leaves, feeding the reactants needed by the parent node (or m, if there is no parent node) to the reaction template of the node being processed. Finally, we define the instantiated reaction $R(m):=(m,{{{\mathcal{R}}}}(m),c(m))$ where the reactant set ${{{\mathcal{R}}}}(m)$ is the union of all reactions needed by the leaf nodes, and the cost c(m) is the total reaction costs instantiated in the tree.

Cascade chain

A cascade chain is a sequence of consecutive reaction templates that commonly appears in successful retrosynthesis routes, which can be abstracted to form a new reaction template.

Definition A cascade chain is formally described as a reaction template tree that frequently occurs as an induced sub-tree of the reaction template trees defined based on the successful retrosynthesis routes collected in our dataset. More specifically, let ${{{\mathcal{C}}}}$ be the collection of the successful reaction template trees, we extract the set ${{{\mathcal{P}}}}$ of cascade chains as

$$ {{{\mathcal{P}}}}:=\\ \left\{P \, {{{\rm{is}}}}\,{{{\rm{a}}}}\,{{{\rm{reaction}}}}\,{{{\rm{template}}}}\,{{{\rm{tree}}}}\, \Big| \,{{{{\rm{freq}}}}}^{({{{\rm{ind}}}})}(P,{{{\mathcal{C}}}}):=\frac{{\sum }_{T\in {{{\mathcal{C}}}}}{\mathbb{1}}(P{\preccurlyeq }^{({{{\rm{ind}}}})}T)}{| {{{\mathcal{C}}}}| }\ge \zeta \right\},$$

(10)

where ζ is the minimum frequency threshold, ${\mathbb{1}}(\cdot )$ is the indicator variable, and P ≼ ^(ind)T denotes that P is an induced sub-tree of T.

Fast extraction algorithm The number of the induced sub-trees increases exponentially as its size increases. Therefore, we employ the following algorithm to avoid enumerating too many induced sub-trees so as to run fast in practice. To describe our algorithm, we first define

$${{{{\mathcal{P}}}}}_{k}:\!\!\!=\{P\in {{{\mathcal{P}}}}\,| \,P \, {{{\rm{has}}}}\,k\,{{{\rm{nodes}}}}\}$$

(11)

as the set of k-node cascade chains, and the following 1-node extension operation on the set ${{{{\mathcal{P}}}}}_{k}$:

$${{{\rm{Ext}}}}({{{{\mathcal{P}}}}}_{k}):\!\!=\{P\, {{\mbox{is}}} \, {{\mbox{a}}} \, {{\mbox{reaction}}} \, {{\mbox{template}}} \, {{\mbox{tree}}} \, {{\mbox{of}}}\,\,k+1\,\,{ {\mbox{nodes}}}\,\,| \,\exists {P}^{{\prime} }\in {{{{\mathcal{P}}}}}_{k},{P}^{{\prime} }{\preccurlyeq }^{({{{\rm{ind}}}})}P\}.$$

(12)

The key of our fast algorithm is to observe that if a tree P is an induced sub-tree of ${P}^{{\prime} }$, then

$${{{{\rm{freq}}}}}^{({{{\rm{ind}}}})}({P}^{{\prime} },{{{\mathcal{C}}}})\le {{{{\rm{freq}}}}}^{({{{\rm{ind}}}})}(P,{{{\mathcal{C}}}}),$$

(13)

which implies that for any integer k ≥ 1, it holds that

$${{{{\mathcal{P}}}}}_{k+1}\subseteq {{{\rm{Ext}}}}({{{{\mathcal{P}}}}}_{k}).$$

(14)

Based on Eq. (14), our algorithm first constructs ${{{{\mathcal{P}}}}}_{1}$ by definition: enumerate all single-node reaction templates that appear in ${{{\mathcal{C}}}}$, calculate their frequency, and keep the ones above the threshold ζ. Then, the algorithm constructs the sets ${{{{\mathcal{P}}}}}_{k+1}$ for k = 1, 2, 3, … using Eq. (14): obtain the extension set ${{{\rm{Ext}}}}({{{{\mathcal{P}}}}}_{k})$ by enumerating all additions of a reaction template node to each tree in ${{{{\mathcal{P}}}}}_{k}$, and keep the ones in the extension set with frequency above ζ. This iteration terminates when ${{{{\mathcal{P}}}}}_{k}={{\emptyset}}$. Finally, the algorithm returns ${{{\mathcal{P}}}}={\cup }_{k}{{{{\mathcal{P}}}}}_{k}$. The computational cost of this algorithm is proportional to $| {{{\mathcal{P}}}}|$. Thus, it runs fast in practice since there are not excessively many useful cascade chains.

Using cascade chains during planning A cascade chain directly defines a reaction template by its reaction template tree (as described in Preliminaries: reaction template tree). Thus it can be used in the same way as existing reaction templates during planning (the wake phase).

Complementary chain

Complementary chains involve pairs of reaction templates performing complementary operations on the same functional groups. It is inspired by the common complementary reactions in synthetic chemistry: addition and elimination of a protective group, where the former temporarily masks a functional group due to its interference with another desired reaction, and the latter removes this mask after the completion of the desired reaction.

Definition To define the complementary chains, we first define the complementary reaction templates (CR templates): a pair of reaction templates R₊ and R₋ is called a pair of CR templates if the following two conditions hold: (1) the reaction centers (where the chemical transformation occurs) are the same in both reaction templates, (2) a product (or a reactant respectively) of R₊ and a reactant (or a product respectively) of R₋ share the same functional group that is adjacent to the common reaction center. In practice, we use RDChiral³⁰ to identify the reaction centers and the functional groups of the participating reactants and products. We then define a complementary reaction template tree (CR template tree) is a reaction template tree where the nodes can be partitioned into pairs of CR templates and the following two conditions hold: (1) each pair of CR nodes is an ancestor and an off-spring of each other, (2) no two pairs of CR nodes interleave with each other, i.e., there do not exists CR node pairs (R₊, R₋) and $({R}_{+}^{{\prime} },{R}_{-}^{{\prime} })$ with the following relationship (where a ≺ b denotes that a is an ancestor of b) : ${R}_{+}\prec {R}_{+}^{{\prime} }\prec {R}_{-}\prec {R}_{-}^{{\prime} }$.

We now formally define a complementary chain as a CR template tree that frequently occurs as an embedded sub-tree of the reaction template trees collected in our dataset. (In contrast an induced sub-tree, for Q to be an embedded sub-tree of T does not require Q to keep all edges in T; it is only required that every pair of parent and child in Q remains a pair of ancestor and off-spring in T ). More specifically, let ${{{\mathcal{C}}}}$ be the collection of the successful reaction template trees (as defined in Cascade chain), we define the set ${{{\mathcal{Q}}}}$ of complementary chains as

$$ {{{\mathcal{Q}}}}:=\\ \left\{Q\, {{\mbox{is}}} \, {{\mbox{a}}} \, {{\mbox{CR}}} \, {{\mbox{template}}} \, {{\mbox{tree}}}\,\, \Big| \,{{{{\rm{freq}}}}}^{({{{\rm{emb}}}})}(Q,{{{\mathcal{C}}}}):=\frac{{\sum }_{T\in {{{\mathcal{C}}}}}{\mathbb{1}}(Q{\preccurlyeq }^{({{{\rm{emb}}}})}T)}{| {{{\mathcal{C}}}}| }\ge \zeta \right\},$$

(15)

where ζ is the minimum frequency threshold (the same as the Cascade chain), and Q ≼ ^(emb)T denotes that Q is an embedded sub-tree of T.

Fast extraction algorithm We extend our fast extraction algorithm for cascade chains in Cascade chain to complementary chains. For each integer k ≥ 1, define

$${{{{\mathcal{Q}}}}}_{k}:\!\!=\{Q\in {{{\mathcal{Q}}}}\,| \,Q\, {{\mbox{consists}}} {{\mbox{of}}}\,\,k\, {{\mbox{pairs}}} \, {{\mbox{of}}} \, {{\mbox{CR}}} \, {{\mbox{nodes}}}\,\}.$$

(16)

We similarly define the 1-pair extension operation on the set ${{{{\mathcal{Q}}}}}_{k}$:

$$ {{{\rm{ExtPair}}}}({{{{\mathcal{Q}}}}}_{k}):=\\ \{Q\, {{\mbox{is}}} \, {{\mbox{a}}} \, {{\mbox{CR}}} \, {{\mbox{template}}} \, {{\mbox{tree}}} \, {{\mbox{of}}}\,(k+1)\, {{\mbox{pairs}}} \, {{\mbox{of}}} \, {{\mbox{CR}}} \, {{\mbox{nodes}}}\,\,| \,\exists {Q}^{{\prime} }\in {{{{\mathcal{Q}}}}}_{k},{Q}^{{\prime} }{\preccurlyeq }^{({{{\rm{emb}}}})}Q\}.$$

(17)

Using that $Q{\preccurlyeq }^{({{{\rm{emb}}}})}{Q}^{{\prime} }\Rightarrow {{{{\rm{freq}}}}}^{({{{\rm{emb}}}})}({Q}^{{\prime} },{{{\mathcal{C}}}})\le {{{{\rm{freq}}}}}^{({{{\rm{emb}}}})}(Q,{{{\mathcal{C}}}})$, we are able to establish for each k ≥ 1,

$${{{{\mathcal{Q}}}}}_{k+1}\subseteq {{{\rm{ExtPair}}}}({{{{\mathcal{Q}}}}}_{k}).$$

(18)

Our algorithm for extracting complementary chain is based on Eq. (18), similar to the one for cascade chains: first construct ${{{{\mathcal{Q}}}}}_{1}$ by enumerating all single-pair CR templates that appear in ${{{\mathcal{C}}}}$ and keep the ones with frequency above the threshold ζ; then for each k = 1, 2, 3, …, as long as ${{{{\mathcal{Q}}}}}_{k}\ne {{\emptyset}}$, construct ${{{\rm{ExtPair}}}}({{{{\mathcal{Q}}}}}_{k})$ by enumerating all possible insertions of a CR pair in ${{{{\mathcal{Q}}}}}_{1}$ to the CR template trees in ${{{{\mathcal{Q}}}}}_{k}$, and select the ones in this extension set with frequency above the threshold and form ${{{{\mathcal{Q}}}}}_{k+1}$. Finally, the algorithm returns ${{{\mathcal{Q}}}}={\cup }_{k}{{{{\mathcal{Q}}}}}_{k}$. The computational cost of this algorithm is proportional to $| {{{\mathcal{Q}}}}|$.

Integrating complementary chains into planning In contrast to cascade chains, a complementary chain does not directly define a reaction template, this is because the CR template tree of the chain may only be an embedded sub-tree of the desired reaction route, and much planning remains to further replace the internal edges of the CR template tree with synthesis sub-trees. Therefore, different from the cascade chains, we need a new method to integrate complementary chains into planning. We achieve this by introducing a complementary incentive score when proposing reaction nodes to expand (Line 5 of Algorithm 1). More specifically, when a complementary chain is adopted during the planning algorithm, the root node of the chain is first added to the search graph, and the planning algorithm keeps running as usual. Whenever proposing reaction nodes to expand the molecule m_next (Line 5 of Algorithm 1), we align the current search graph with the complementary chain and locate the edge $(R,{R}^{{\prime} })$ of the CR template tree to which m_next is aligned. Suppose R is the parent, then the reaction template ${R}^{{\prime} }$ is given a favorable score, which is incorporated into the proposing model B(⋅), to boost its priority in planning. This incentive score helps to guide the planning algorithm to follow and complete the complementary chain.

Dreaming phase (Learn to plan better through reflection and more practice with the growing reaction library)

During the dreaming phase, the system recalls past experiences and dreams and then refines its two neural models (introduced in the Value model and Single-step retrosynthesis prediction) used to guide graph expansion, which later speeds up retrosynthetic planning during the wake phase. We train such two networks on pairs drawn from two sources of data: replays of search graph expanded during waking, and fantasies. Replays ensure that these models are trained on the specific tasks they need to solve and prevent the models from forgetting how to solve them over time. On the other hand, generating diverse and extensive datasets through fantasies is crucial for data efficiency and enables models to learn from a wider range of scenarios. To fantasy about new reaction routes, we employ two strategies, the top-down strategy and the bottom-up strategy, which are detailed below. These routes are combined with the replays on a 50%/50% mix to train the two neural models. The refined models will be used in the subsequent wake phase.

Top-down strategy

In the wake phase, some products cannot be retrosynthesized. Inspired by that the synthesis route of similar molecules can help experts as hints, we generate some similar and synthesizable molecules to help our system solve the failure tasks. We refer to this approach as the top-down strategy as we modify the target product at the top of the search graph directly. As illustrated at the top of the fantasies panel in the dreaming module of Fig. 1c, in case a molecule M1 cannot be synthesized by the present system, we generate a similar molecule $M{1}^{{\prime} }$ at the top of the search graph and obtain a successful reaction route for $M{1}^{{\prime} }$ that may serve as a hint for the retrosynthesis of M1. In addition, a real example of the top-down fantasy is provided in the Top-down strategy and Supplementary Fig. 2.

Here, we use a generative model to sample some similar molecules first, then try to solve them using the same route search process as in waking, and we save the successful results to the dataset. The generative model we used is HierVAE³¹. In HierVAE, a hierarchical representation of molecules with three layers is proposed, and the generation process is implemented based on an encoder-decoder framework (Supplementary Fig. 4a, b). Given the generative model, we can easily perform similarity filtering in the embedding space of molecules by using the encoder, and the pairwise molecular similarity threshold we used is defined as the Tanimoto distance over the embeddings of two molecules. Besides, this motif-based hierarchical framework captures occurring substructures well, and molecules generated by it, therefore, have good chemical validity.

Hierarchical representation of molecules A molecule can be represented as a graph $G=({{{\mathcal{V}}}},{{{\mathcal{E}}}})$, with atoms ${{{\mathcal{V}}}}$ as nodes and bonds ${{{\mathcal{E}}}}$ as edges. Then, the motif can be defined as a sub-graph of G, denoted as ${{{{\mathcal{M}}}}}_{i}=({{{{\mathcal{V}}}}}_{i},{{{{\mathcal{E}}}}}_{i})$. We can extract a set of motifs $\{{{{{\mathcal{M}}}}}_{1},{{{{\mathcal{M}}}}}_{2},\ldots \,\}$ from G such that their union covers the entire molecular graph: ${{{\mathcal{V}}}}={\bigcup }_{i}{{{{\mathcal{V}}}}}_{i}$ and ${{{\mathcal{E}}}}={\bigcup }_{i}{{{{\mathcal{E}}}}}_{i}$. With the definition of motifs, the three hierarchical layers in HierVAE are structured as follows:

Motif layer: This layer outlines the high-level structure of the graph by capturing how motifs are coarsely interconnected. It consists of n nodes ${{{{\mathcal{M}}}}}_{1},\ldots,{{{{\mathcal{M}}}}}_{n}$, each representing a motif, and m edges $\{({{{{\mathcal{M}}}}}_{i},{{{{\mathcal{M}}}}}_{j})| {{{{\mathcal{M}}}}}_{i}\cap {{{{\mathcal{M}}}}}_{j} \, \ne \, {{\emptyset}}\}$, which indicate shared elements between motifs ${{{{\mathcal{M}}}}}_{i}$ and ${{{{\mathcal{M}}}}}_{j}$.
Attachment layer: This layer focuses on the finer-grained connectivity between motifs. Each node ${{{{\mathcal{A}}}}}_{i}=({{{{\mathcal{M}}}}}_{i},{v}_{j})$ represents a specific attachment configuration of motif ${{{{\mathcal{M}}}}}_{i}$, where v_j is the set of atoms shared between ${{{{\mathcal{M}}}}}_{i}$ and one of its neighboring motifs, ${{{{\mathcal{M}}}}}_{j}$.
Atom layer: At the most detailed level, this layer represents the atomic structure of the molecule. Each atom is represented by a node v labeled with a_v, denoting its atom type and charge. Edges (u, v) are labeled with b_uv, specifying the bond type between atoms u and v.

Together, these three layers form a hierarchical graph representation of the molecule, denoted as ${{{{\mathcal{H}}}}}_{G}$. This hierarchical approach enables the model to capture both coarse structural information and fine-grained atomic details, providing a comprehensive view of the molecular graph.

Moreover, to construct the motif vocabulary, we follow the procedure introduced in HierVAE³¹ and begin by breaking down all molecules in the training set into isolated fragments. The most frequently occurring fragments are then selected as motifs. For a given molecule G, we identify all bridge bonds $(u,v)\in {{{\mathcal{E}}}}$. These bonds are defined as those where both u and v have degrees δ_u, δ_v≥ 2, and at least one of them is part of a ring. By removing these bridge bonds along with their associated edges, the molecular graph G is divided into a collection of disconnected subgraphs {G₁, . . . , G_n}. A fragment G_i qualifies as a motif only if it appears in the training set more than Δ = 100 times.

Hierarchical graph encoder Based on the three hierarchical layers in the hierarchical graph ${{{{\mathcal{H}}}}}_{G}$, HierVAE uses an encoder containing three message-passing networks (MPNs) that encode each layer. Next, we introduce the details of the three MPNs. For simplicity, we denote the MPN encoding process as MPN_ψ(.) with parameter ψ.

Atom layer MPN: This MPN takes as input the embedding vectors e(a_u) and e(b_uv), which represent all atoms and bonds in the molecular graph G. The network propagates messages across atoms over N iterations, resulting in the atom representations h_v for each atom v. This process can be expressed as:
$$\{{h}_{v}\}={{{{\rm{MPN}}}}}_{{\psi }_{1}}({{{{\mathcal{H}}}}}_{G}^{a},\{e({a}_{u})\},\{e({b}_{uv})\}),$$
(19)
where ${{{{\mathcal{H}}}}}_{G}^{a}$ is the atom layer of ${{{{\mathcal{H}}}}}_{G}$.
Attachment layer MPN: In the attachment layer ${{{{\mathcal{H}}}}}_{G}^{{{{\mathcal{A}}}}}$, for each node ${{{{\mathcal{A}}}}}_{i}$, the input feature is constructed by concatenating the embedding with the sum of the atom vectors as follows:
$${f}_{{{{{\mathcal{A}}}}}_{i}}={{{\rm{MLP}}}}\left(e({{{{\mathcal{A}}}}}_{i}),{\sum}_{v\in {{{{\mathcal{M}}}}}_{i}}{h}_{v}\right).$$
(20)
For each edge $({{{{\mathcal{A}}}}}_{i},{{{{\mathcal{A}}}}}_{j})$, the input feature is represented by the embedding vector e(d_ij), which captures the relative relationship between nodes ${{{{\mathcal{A}}}}}_{i}$ and ${{{{\mathcal{A}}}}}_{j}$ during the decoding. Here, d_ij= k if ${{{{\mathcal{A}}}}}_{i}$ is the k-th child of ${{{{\mathcal{A}}}}}_{j}$ and d_ij = 0 if ${{{{\mathcal{A}}}}}_{i}$ is the parent node. The network then performs N iterations of message passing over ${{{{\mathcal{H}}}}}_{G}^{{{{\mathcal{A}}}}}$ to compute the attachment representations:
$$\{{h}_{{{{{\mathcal{A}}}}}_{i}}\}={{{{\rm{MPN}}}}}_{{\psi }_{2}}({{{{\mathcal{H}}}}}_{G}^{{{{\mathcal{A}}}}},\{{f}_{{{{{\mathcal{A}}}}}_{i}}\},\{e({d}_{ij})\}).$$
(21)
Motif layer MPN: At the motif layer, the input feature for each node ${{{{\mathcal{M}}}}}_{i}$ is computed by concatenating its embedding with the node vector obtained from the attachment layer.
$${f}_{{{{{\mathcal{M}}}}}_{i}}={{{\rm{MLP}}}}(e({{{{\mathcal{M}}}}}_{i}),{h}_{{{{{\mathcal{A}}}}}_{i}}).$$
(22)
Subsequently, N iterations of message passing are performed over the motif layer ${{{{\mathcal{H}}}}}_{G}^{{{{\mathcal{M}}}}}$ to generate the motif representations:
$$\{{h}_{{{{{\mathcal{M}}}}}_{i}}\}={{{{\rm{MPN}}}}}_{{\psi }_{3}}({{{{\mathcal{H}}}}}_{G}^{{{{\mathcal{M}}}}},\{{f}_{{{{{\mathcal{M}}}}}_{i}}\},\{e({d}_{ij})\}).$$
(23)

Finally, the molecule G is represented by a latent vector z_G, which is sampled using the reparameterization trick based on the mean $\mu ({h}_{{{{{\mathcal{M}}}}}_{1}})$ and the log variance $\sum ({h}_{{{{{\mathcal{M}}}}}_{1}})$. This process is given as:

$${z}_{G}=\mu ({h}_{{{{{\mathcal{M}}}}}_{1}})+\exp \left(\sum ({h}_{{{{{\mathcal{M}}}}}_{1}})\right)\cdot \upepsilon,\upepsilon \sim (0,1),$$

(24)

where ${{{{\mathcal{M}}}}}_{1}$ is the root motif, representing the first motif reconstructed during decoding.

Hierarchical graph decoder HierVAE generates a molecule by incrementally expanding its hierarchical graph using the graph decoder. At each generation step, the same hierarchical MPN architecture is used to encode all the motifs and atoms in ${{{{\mathcal{H}}}}}_{G}^{(t)}$, which refers to the (partial) hierarchical graph generated up to step t. This gives us motif vectors ${h}_{{{{{\mathcal{M}}}}}_{i}}$ and atom vectors ${h}_{{v}_{j}}$ for the existing motifs and atoms. During the decoding process, the model keeps track of a set of frontier nodes ${{{\mathcal{F}}}}$, where each motif ${{{{\mathcal{M}}}}}_{i}\in {{{\mathcal{F}}}}$ corresponds to a node that still has ungenerated neighbors. The frontier set ${{{\mathcal{F}}}}$ is organized as a stack, as motifs are generated in a depth-first manner. At step t, if ${{{{\mathcal{M}}}}}_{i}$ is the motif currently at the top of the stack ${{{\mathcal{F}}}}$, the model makes the following three predictions conditioned on the latent representation z_G:

1.
The model first predicts the next motif ${{{{\mathcal{M}}}}}_{t}$ that will be attached to the current motif ${{{{\mathcal{M}}}}}_{i}$. This is formulated as a classification problem over the motif vocabulary ${V}_{{{{\mathcal{M}}}}}$. The probability distribution for ${{{{\mathcal{M}}}}}_{t}$ is computed as follows:
$${p}_{{{{{\mathcal{M}}}}}_{t}}={{{\rm{softmax}}}}({{{\rm{MLP}}}}({h}_{{{{{\mathcal{M}}}}}_{i}},{z}_{G})).$$
(25)
2.
Once the next motif ${{{{\mathcal{M}}}}}_{t}$ is determined, the model predicts its attachment configuration ${{{{\mathcal{A}}}}}_{t}$. This involves identifying the specific atoms ${v}_{j}\in {{{{\mathcal{M}}}}}_{t}$ that will form the intersection with its neighboring motifs. The task is again treated as a classification problem, with the probability distribution computed as:
$${p}_{{{{{\mathcal{A}}}}}_{t}}={{{\rm{softmax}}}}({{{\rm{MLP}}}}({h}_{{{{{\mathcal{M}}}}}_{t}},{z}_{G})).$$
(26)
3.
In the final step, the model determines how ${{{{\mathcal{M}}}}}_{t}$ should be connected to ${{{{\mathcal{M}}}}}_{i}$. The attachment is defined by a set of atom pairs ${{{{\mathcal{P}}}}}_{ti}=\{({u}_{j},{v}_{j})| {u}_{j}\in {{{{\mathcal{A}}}}}_{i},{v}_{j}\in {{{{\mathcal{A}}}}}_{t}\}$ where atoms u_j and v_j represent the atoms that will be linked. The probability of a specific attachment configuration ${{{\mathcal{P}}}}$ is calculated based on the atom representations ${h}_{{u}_{j}}$ and ${h}_{{v}_{j}}$:
$${p}_{{{{\mathcal{P}}}}}={{{\rm{softmax}}}}({h}_{{{{\mathcal{P}}}}}\cdot {z}_{G}),$$
(27)
$${h}_{{{{\mathcal{P}}}}}={\sum}_{j=0}^{| {{{{\mathcal{P}}}}}_{ti}| }{{{\rm{MLP}}}}({h}_{{u}_{j}},{h}_{{v}_{j}}).$$
(28)

The three predictions above allow the model to decompose the probability distribution of the next motif and its attachment into sequential steps, enabling an autoregressive approach to molecule generation. Each decoding step depends on the results of the previous step, and the predicted attachments directly influence the subsequent motif predictions.

Training details We train the model using the following negative ELBO as the loss:

$${\ell }_{{{{\rm{n-ELBO}}}}}=-{{\mathbb{E}}}_{{z}_{G} \sim Q}[\log P(G| {z}_{G})]+{D}_{{{{\rm{KL}}}}}[Q({z}_{G}| G)\parallel P({z}_{G})],$$

(29)

where G is the graph of molecules, D_KL is the Kullback-Leibler divergence. We set the hidden layer dimension to 270 and the embedding layer dimension to 200. Furthermore, we set the latent vector dimension ∥z_G∥ = 8 and run N = 20 iterations of message passing in each layer of the encoder. We use the Adam optimizer with a learning rate of 0.001 to train the model for 30 epochs, where each epoch contains 56,000 batches with a batch size of 64. The training loss curve is shown in Supplementary Fig. 4c.

Bottom-up strategy

Our second approach to fantasy about successful synthesis routes is called the bottom-up strategy. This strategy aims to generate routes and quickly accumulate experience about the new reaction templates extracted in the abstraction phase. Given a synthesis route tree $T=({{{\mathcal{V}}}},{{{\mathcal{E}}}})$ where ${{{\mathcal{V}}}}$ is the set of nodes for molecules and reactions, we repeatedly replace the nodes starting from the leaves and toward the root and correspondingly update the entire synthesis route T to obtain a new one. More specifically, our bottom-up strategy includes the following three steps:

1.
We randomly choose a leaf node v in the synthesis route T, which is an available molecule in the available set ${{{\mathcal{I}}}}$.
2.
We substitute node v with another molecule $u\in {{{\mathcal{I}}}}$ that can be applied to the reaction template R in the parent node. Since the candidate set ${{{\mathcal{I}}}}$ is very large, we design the following method to accelerate the selection process for u: First, we characterize the reaction template R by its two key components: the reaction center and the surrounding fragments, where the reaction center refers to the part of the molecule where the chemical transformation occurs and the surrounding fragments are the portions of the molecule immediately adjacent to the reaction center that influences or participate in the reaction. Then we construct the set ${{{\mathcal{U}}}}\subseteq {{{\mathcal{I}}}}$ consisting of each $u\in {{{\mathcal{I}}}}$ containing the surrounding fragments of R that also appear in v. Usually we have $| {{{\mathcal{U}}}}| \ll | {{{\mathcal{I}}}}|$; thus the search space is significantly reduced. Finally, we use FAISS to find the top-κ similar elements to v in ${{{\mathcal{U}}}}$ (where similarity is defined according to the Tanimoto distance between the embeddings of two molecules), and each of them is trialed to replace v in the synthesis route T.
3.
After replacing v with a candidate molecule u, we iteratively apply each reaction template in the ancestor nodes of v from the bottom up till the root node is updated.

An illustrative example of the bottom-up strategy is shown at the bottom of the fantasies panel in the dreaming module (Fig. 1c). Suppose we have a molecule M1 that can be synthesized using an abstracted reaction template ${R}^{{\prime} }$ which uses reactants M4, M5, and M3. We find a building block $M{3}^{{\prime} }$ that also fits ${R}^{{\prime} }$ and replace v = M3 with $u=M{3}^{{\prime} }$. We finally update the reaction route and obtain $M{1}^{{\prime} }$. We also provide a real example of the bottom-up strategy in the Bottom-up strategy and Supplementary Fig. 3. Compared to the top-down strategy, the bottom-up strategy makes minimal changes to the entire synthesis route, making it more suitable for accumulating common empirical knowledge for newly discovered reaction templates.

Experimental setup

Datasets

To obtain a library of valid reaction templates, we use the publicly available reaction dataset extracted from the United States Patent Office (USPTO). Following the instructions in ref. ¹¹, we remove wrong labeling reactions and duplications, and adopt RDChiral³⁰ to construct the library of reaction templates with atom mapping. The processed library consists of about 1.3M reactions and is split randomly into train/val/test sets with 80%/10%/10% proportions.

To evaluate the performance of different retrosynthetic planning approaches, we use the building block set ${{{\mathcal{I}}}}$ comes from eMolecules, which consists of 231M commercially available molecules, and the route dataset used in Retro*¹¹ and Retro* +¹⁵, called Retro*-190. Retro*-190 comprises 299202 training routes, 65274 validation routes, and 190 test routes. Note that the target molecules of these 190 test routes cannot be efficiently synthesized by a simple heuristic-based BFS planning algorithm within a limited search time, making this dataset more challenging than the one conventionally used in previous works^9,10.

In addition, considering the small size of the Retro*-190 dataset, we create a new test route dataset based on the methodology described in ref. ³² and follow the same rules used in ref. ¹¹ to make sure that there is no overlap between the new test set and train/val sets. Next, we filter out the simpler molecules using Retro* ¹¹ by discarding the molecules that can be synthesized within fixed iterations. This process results in a dataset of 20,000 molecules.

Baselines

In this work, we compare our single-step model against existing single-step retrosynthesis models, which can be classified into three categories: template-based, template-free, and semi-template-based, as follows:

Template-based: Retrosim³³, Neuralsym³⁴, and GLN³⁵;
Template-free: Transformer³⁶ and Megan³⁷;
Semi-template-based: G2Gs³⁸ and GraphRetro³⁹.

Moreover, we compare our method against existing multi-step retrosynthetic planning methods: greedy Depth First Search (denoted as Greedy DFS), DFPN-E¹⁰, MCTS-rollout⁹, Retro* ¹¹, Retro* +¹⁵, EG-MCTS¹⁶ and PDVN⁴⁰ on the Retro*-190 dataset.

Metrics

Following previous works³⁹, we evaluate the performance of single-step models using exact match accuracy, which is calculated by comparing the set of reactants represented in canonical SMILES with the ground truth reactants in the dataset. We assess the top-N proposals provided by all models, where N = 1, 3, 5, 10, and check if any of the proposals match the dataset exactly. We also use the success rate and the time used to find the first route under the same 500 iteration limit to evaluate the efficiency of the planning algorithms. Specifically, we conduct experiments using 10 different random seeds, and then report the average of the results. While success rate and time efficiency are crucial, the quality of routes discovered by algorithms must not be overlooked. To evaluate the quality of routes found by algorithms, we calculate how many routes found by algorithms are equal to or shorter than the dataset.

Implementation details

Searching synthesis routes for a group of molecules generated by generative models is more demanded in practical application scenarios. To demonstrate the effectiveness of our method in addressing this challenge, we use a generative model proposed by Jin et al.³¹. We generate a group of similar molecules with varying similarity thresholds and perform retrosynthetic planning for each molecule separately on search graphs as well as on a shared search graph. Here, We generate 200 groups, with each group containing 20 synthesizable molecules. We then compare the performance of the search graph and the shared search graph to the search tree. We calculate the reduction in the number of nodes added during the entire planning process. The reduction ratio is defined as ${{{\rm{reduction\,ratio}}}}({{{\rm{method}}}})=\frac{\#\,of\,{{{{\rm{nodes}}}}}_{{{{\rm{tree}}}}}-\#\,of\,{{{{\rm{nodes}}}}}_{{{{\rm{method}}}}}}{\#\,of\,{{{{\rm{nodes}}}}}_{{{{\rm{tree}}}}}},{{{\rm{method}}}}\in \{{{{\rm{graph}}}},{{{\rm{shared\,graph}}}}\}$. We design an experiment to explore the impact of group size on the reduction ratio, and we choose the group size = 10, 20, 30, 40.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.

Data availability

The publicly available eMolecules dataset can be downloaded from https://downloads.emolecules.com/free/. In the experiments, we used the dataset after processing and the test set Retro*-190, which is provided by Chen et al. and available at https://github.com/binghong-ml/retro_star. The generated data used in the experiments is available at https://github.com/osu-zxf/DreamRetroerand also available at Zenodo repository⁴¹ through https://doi.org/10.5281/zenodo.14032989. In addition, source data of all figures are provided in this paper. Source data are provided in this paper.

Code availability

The source code of our method is available on our Github page https://github.com/osu-zxf/DreamRetroer. In addition, the source code is also available at Zenodo repository⁴² through https://doi.org/10.5281/zenodo.14011051.

References

Zhavoronkov, A. et al. Deep learning enables rapid identification of potent DDR1 kinase inhibitors. Nat. Biotechnol. 37, 1038–1040 (2019).
Article CAS PubMed MATH Google Scholar
Zimmerman, J. B., Anastas, P. T., Erythropel, H. C. & Leitner, W. Designing for a green chemistry future. Science 367, 397–400 (2020).
Article ADS CAS PubMed MATH Google Scholar
Jin, W., Barzilay, R. & Jaakkola, T. Junction tree variational autoencoder for molecular graph generation. In Proceedings of the 35th International Conference on Machine Learning (eds. Dy, J. & Krause, A.) 2323–2332 (PMLR, 2018).
Hoogeboom, E., Satorras, V. G., Vignac, C. & Welling, M. Equivariant diffusion for molecule generation in 3D. In Proceedings of the 39th International Conference on Machine Learning, 8867–8887 (PMLR, 2022).
Paul, S. M. et al. How to improve R&D productivity: the pharmaceutical industry’s grand challenge. Nat. Rev. Drug Discov. 9, 203–214 (2010).
Article CAS PubMed MATH Google Scholar
Gao, W. & Coley, C. W. The synthesizability of molecules proposed by generative models. J. Chem. Inf. Model. 60, 5714–5723 (2020).
Article CAS PubMed MATH Google Scholar
Feng, F., Lai, L. & Pei, J. Computational chemical synthesis analysis and pathway design. Front. Chem. 6, 199 (2018).
Article PubMed PubMed Central MATH Google Scholar
Coley, C. W. et al. A robotic platform for flow synthesis of organic compounds informed by AI planning. Science 365, eaax1566 (2019).
Article CAS PubMed MATH Google Scholar
Segler, M. H., Preuss, M. & Waller, M. P. Planning chemical syntheses with deep neural networks and symbolic ai. Nature 555, 604–610 (2018).
Article ADS CAS PubMed Google Scholar
Kishimoto, A., Buesser, B., Chen, B. & Botea, A. Depth-first proof-number search with heuristic edge cost and application to chemical synthesis planning. Advances in Neural Information Processing Systems 32 (2019).
Chen, B., Li, C., Dai, H. & Song, L. Retro*: Learning retrosynthetic planning with neural guided a* search. In International Conference on Machine Learning, 1608–1616 (PMLR, 2020).
Lin, M. H., Tu, Z. & Coley, C. W. Improving the performance of models for one-step retrosynthesis through re-ranking. J. Cheminf. 14, 1–13 (2022).
Article MATH Google Scholar
Zhong, W., Yang, Z. & Chen, C. Y.-C. Retrosynthesis prediction using an end-to-end graph generative architecture for molecular graph editing. Nat. Commun. 14, 3009 (2023).
Article ADS CAS PubMed PubMed Central MATH Google Scholar
Chen, S. & Jung, Y. Deep retrosynthetic reaction prediction using local reactivity and global attention. JACS Au 1, 1612–1620 (2021).
Article CAS PubMed PubMed Central MATH Google Scholar
Kim, J., Ahn, S., Lee, H. & Shin, J. Self-improved retrosynthetic planning. In International Conference on Machine Learning, 5486–5495 (PMLR, 2021).
Hong, S., Zhuo, H. H., Jin, K., Shao, G. & Zhou, Z. Retrosynthetic planning with experience-guided monte carlo tree search. Commun. Chem. 6, 120 (2023).
Article PubMed PubMed Central Google Scholar
Xie, S. et al. Retrograph: Retrosynthetic planning with graph search. In Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, 2120–2129 (2022).
Ishida, S., Terayama, K., Kojima, R., Takasu, K. & Okuno, Y. Ai-driven synthetic route design incorporated with retrosynthesis knowledge. J. Chem. Inform. Model. 62, 1357–1367 (2022).
Article CAS Google Scholar
Ellis, K. et al. DreamCoder: growing generalizable, interpretable knowledge with wake–sleep bayesian program learning. Philos.Trans. R. Soc. A 381, 20220050 (2023).
Article ADS Google Scholar
Devlin, J., Chang, M.-W., Lee, K. & Toutanova, K. BERT: Pre-training of deep bidirectional transformers for language understanding. North American Chapter of the Association for Computational Linguistics (2019).
Vaswani, A. et al. Attention is all you need. Advances in Neural Information Processing Systems 30 (2017).
Wang, S., Guo, Y., Wang, Y., Sun, H. & Huang, J. SMILES-BERT: Large scale unsupervised pre-training for molecular property prediction. In Proceedings of the 10th ACM International Conference on Bioinformatics, Computational Biology and Health Informatics, 429–436 (2019).
Shin, B., Park, S., Kang, K. & Ho, J. C. Self-attention based molecule representation for predicting drug-target interaction. In Proceedings of the 4th Machine Learning for Healthcare Conference, 230–248 (PMLR, 2019).
Hu, W. et al. Deep learning methods for small molecule drug discovery: A survey. IEEE Trans. Artif. Intell. 5, 459–479 (2023).
Kipf, T. & Welling, M. Semi-supervised classification with graph convolutional networks. In the 5th International Conference on Learning Representations (2017).
Wang, H. et al. Chemical-reaction-aware molecule representation learning. In the 10th International Conference on Learning Representations (2022).
Radford, A. et al. Learning transferable visual models from natural language supervision. In Proceedings of the 38th International Conference on Machine Learning, (eds. Meila, M. & Zhang, T.) 8748–8763 (PMLR, 2021).
Sohn, K. Improved deep metric learning with multi-class n-pair loss objective. Advances in Neural Information Processing Systems 29 (2016).
Oord, A. v. d., Li, Y. & Vinyals, O. Representation learning with contrastive predictive coding. Preprint at https://doi.org/10.48550/arXiv.1807.03748 (2018).
Coley, C. W., Green, W. H. & Jensen, K. F. Rdchiral: An rdkit wrapper for handling stereochemistry in retrosynthetic template extraction and application. J. Chem. Inf. Model. 59, 2529–2537 (2019).
Article CAS PubMed Google Scholar
Jin, W., Barzilay, D. & Jaakkola, T. Hierarchical generation of molecular graphs using structural motifs. In Proceedings of the 37th International Conference on Machine Learning, 4839–4848 (PMLR, 2020).
Gao, W., Mercado, R. & Coley, C. W. Amortized tree generation for bottom-up synthesis planning and synthesizable molecular design. In International Conference on Learning Representations (2022).
Coley, C. W., Rogers, L., Green, W. H. & Jensen, K. F. Computer-assisted retrosynthesis based on molecular similarity. ACS Cent. Sci. 3, 1237–1245 (2017).
Article CAS PubMed PubMed Central Google Scholar
Segler, M. H. & Waller, M. P. Neural-symbolic machine learning for retrosynthesis and reaction prediction. Chem A Eur. J. 23, 5966–5971 (2017).
Article CAS MATH Google Scholar
Dai, H., Li, C., Coley, C., Dai, B. & Song, L. Retrosynthesis prediction with conditional graph logic network. Advances in Neural Information Processing Systems, 32 (2019).
Karpov, P., Godin, G. & Tetko, I. V. A transformer model for retrosynthesis. In International Conference on Artificial Neural Networks, 817–830 (Springer, 2019).
Sacha, M. et al. Molecule edit graph attention network: modeling chemical reactions as sequences of graph edits. J. Chem. Inf. Model. 61, 3273–3284 (2021).
Article CAS PubMed MATH Google Scholar
Shi, C., Xu, M., Guo, H., Zhang, M. & Tang, J. A graph to graphs framework for retrosynthesis prediction. In International Conference on Machine Learning, 8818–8827 (PMLR, 2020).
Somnath, V. R., Bunne, C., Coley, C., Krause, A. & Barzilay, R. Learning graph models for retrosynthesis prediction. Adv. Neural Inf. Process. Syst. 34, 9405–9415 (2021).
Google Scholar
Liu, G. et al. Retrosynthetic planning with dual value networks. In International Conference on Machine Learning, 22266–22276 (PMLR, 2023).
Zhang, X., Lin, H., Zhang, M., Zhou, Y. & Ma, J. A data-driven group retrosynthesis planning model inspired by neurosymbolic programming. dreamretroerdata, https://doi.org/10.5281/zenodo.14032989 (2024).
Zhang, X., Lin, H., Zhang, M., Zhou, Y. & Ma, J. A data-driven group retrosynthesis planning model inspired by neurosymbolic programming. dreamretroer, https://doi.org/10.5281/zenodo.14011051 (2024).

Download references

Acknowledgements

This work is supported in part by the National Natural Science Foundation of China No. 62377030.

Author information

Authors and Affiliations

Institute for Artificial Intelligence, Peking University, Beijing, China
Xuefeng Zhang, Haowei Lin & Muhan Zhang
Yau Mathematical Sciences Center, Tsinghua University, Beijing, China
Yuan Zhou
Beijing Institute of Mathematical Sciences and Applications, Beijing, China
Yuan Zhou
Department of Mathematical Sciences, Tsinghua University, Beijing, China
Yuan Zhou
Department of Electronic Engineering, Tsinghua University, Beijing, China
Jianzhu Ma
Institute for AI Industry Research, Tsinghua University, Beijing, China
Jianzhu Ma

Authors

Xuefeng Zhang
View author publications
Search author on:PubMed Google Scholar
Haowei Lin
View author publications
Search author on:PubMed Google Scholar
Muhan Zhang
View author publications
Search author on:PubMed Google Scholar
Yuan Zhou
View author publications
Search author on:PubMed Google Scholar
Jianzhu Ma
View author publications
Search author on:PubMed Google Scholar

Contributions

J.M. devised the project. J.M., X.Z., M.Z., and Y.Z. conceived the presented idea and designed the model details. X.Z. implemented the code and carried out the experiment with assistance from H.L. All authors discussed the results and contributed to the final manuscript.

Corresponding authors

Correspondence to Yuan Zhou or Jianzhu Ma.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Communications thanks Adel Memariani, Hankz Hankui Zhuo, Shoichi Ishida, and the other anonymous reviewer(s) for their contribution to the peer review of this work. A peer review file is available.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information File

Peer Review File

Reporting Summary

Source data

Source Data

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.

Reprints and permissions

About this article

Cite this article

Zhang, X., Lin, H., Zhang, M. et al. A data-driven group retrosynthesis planning model inspired by neurosymbolic programming. Nat Commun 16, 192 (2025). https://doi.org/10.1038/s41467-024-55374-9

Download citation

Received: 27 February 2024
Accepted: 10 December 2024
Published: 02 January 2025
DOI: https://doi.org/10.1038/s41467-024-55374-9