Introduction

Multilayer ceramic capacitors (MLCCs), currently one of the most widely used and fastest-growing chip components globally, are extensively employed in diverse industries such as information technology, consumer electronics, communications, aerospace and industrial control on account of their large power density, stable mechanical properties and exceptional temperature stability1,2. Compared with traditional single-chip ceramic capacitors, MLCCs typically exhibit a larger energy storage density. This is attributed to the fact that the tape-casting and lamination process used in preparing MLCCs lowers the porosity of the ceramic dielectric layer, and the breakdown strength (Eb) enhances exponentially with the significantly decreased dielectric layer thickness3.

Theoretically, when the thickness of the dielectric layer and the number of stacked layers of MLCCs are defined, the attributes of the dielectric materials (such as chemical composition, grain size, or orientation structure, etc.) typically determine the crucial energy storage parameters of MLCCs. For example, Li et al.4 achieved a moderate Wrec of 9.5 J·cm−3 and a high η of 92% in the MLCCs with a composition of 0.55Bi0.5Na0.5TiO3-0.45Sr0.7Bi0.2TiO3. To further increase the energy storage density, they employed the template method to control the grain orientation and prepared the high-quality <111 > -textured MLCCs with the same chemical composition. The results indicate that the breakdown strength of the textured MLCCs could attain an astonishing 1030 kV·cm−1, and Wrec thereby achieved a significant breakthrough of 21.5 J·cm−3, along with an energy efficiency of approximately 80%5. However, this optimization scheme is challenging to be mass-produced in the industry due to the strictness and complexity of the grain texture process. By contrast, although the BiFeO3-BaTiO3-based MLCCs doped with Nd(Zn0.5Zr0.5)O3, which can fulfill the requirements of mass production, can obtain a large Wrec of 10.5 J·cm−3 and a high η of 87% at room temperature, the η is merely approximately 70% at 150 °C6. The high heating caused by this low energy efficiency will accelerate the failure of the MLCCs. Therefore, in addition to the pursuit of high energy storage parameters, considering that the ambient environment will gradually increase with heat dissipation during operation, attaining low loss at elevated temperatures is also a crucial technical indicator7.

There is a consensus that the energy storage performance of capacitors is determined by the polarization–electric field (P–E) loop of dielectric materials, and the realization of high Wrec and η must simultaneously meet the large maximum polarization (Pmax), small remanent polarization (Pr) and high Eb. Over the past decade, a significant amount of effort has been exerted to optimize these parameters for enhancing the energy storage performance. For instance, strategies such as the template-induced texture approach5, core-shell structure8, multilayer structure9, and improvements in the molding10 and sintering processes11 are employed to boost the Eb. Or the high-entropy approach12, regulation in specific temperature regions13, ___domain engineering14, chemical composition design15, and the construction of other polar structures16 can be utilized to suppress the polarization hysteresis and lower the energy loss. Through the judicious combination of the aforesaid strategies, the BT-based high-entropy MLCC, as disclosed in Science in 2024, attains the optimal comprehensive energy storage performance, specifically, a large Wrec of 20.8 J·cm−3 accompanied by a high η of 97.5%17. However, it should be noted that the Wrec value of this MLCC at a high temperature of 100 °C is sharply decreased to approximately 10.6 J·cm−3, and the corresponding η is also reduced to around 85%, which hinders its broad applicability. Moreover, the chemical composition of this high-entropy MLCC is overly complex and delicate, and minor errors in industrial production can lead to significant differences in performance parameters.

An effective method to optimize the energy storage properties of dielectric materials is to regulate the structure of their domains or polar nano-regions (PNRs). A considerable number of studies have demonstrated that it is efficacious to construct R (rhombohedral) + O (orthorhombic) + T (tetragonal) + C (cubic), R + T + C, O + T and other polarization configurations in ferroelectrics through the utilization of specific dielectric temperature regions regulation13,18, nano-scale polarization mismatch and reconstruction19, and crossover region design20. For instance, in the design of the energy storage thin film dielectrics, Pan et al.21 constructed an intriguing structure of R + T phase polymorphic nanodomains co-embedded within the C-phase matrix in the BiFeO3-BaTiO3-SrTiO3 thin film. The results indicated that the minimum polarization hysteresis was obtained while maintaining large Pmax, and eventually, a high Wrec of 112 J·cm−3 was accomplished. The η is approximately 80%. In addition, Chen et al.22 also realized local polymorphic (R + O + T + C) distortion and random oxygen octahedral tilt in K0.5Na0.5NbO3-based high-entropy ceramics. The polarization anisotropy and energy barrier were significantly weakened, resulting in a smoother ___domain-switching path and a delayed polarization saturation, attaining a Wrec of 10.06 J·cm−3 along with a high η of ~90.8%. Combine this with the following fact: although binary systems (such as BNT-ST, BNT-NN, and NN-ST) constituted by Bi0.5Na0.5TiO3 (BNT, R phase), NaNbO3 (NN, O phase), and SrTiO3 (ST, C phase), which are regarded as the most promising lead-free energy storage systems, have been extensively investigated23,24,25, the ___domain structure, polarization configuration and energy storage characteristics of BNT-NN-ST ternary system have not been deeply explored. Based on the above considerations, we propose that BNT, whose polarization characteristics are much higher than those of other lead-free ferroelectrics due to the hybridization between Bi 6 s and O 2p orbitals26,27, be taken as the main component, combines with NN with a broad-band gap to construct an R + O + T + C coexistence polarization configuration. and then introduces ST to further break the long-range ferroelectric order to establish local polymorphic polarization configuration of ultra-small size. To improve the energy storage capacity of ceramic capacitors and promote their application in more environments and a wider range, ceramic powders with such local polymorphic polarization configuration were selected to prepare MLCC prototype devices by tape-casting process and screen-printing technique.

Results and discussion

We first simulated the P–E loops of the designed BNT-NN-ST system throughout the entire composition range (Fig. 1a), all the loops are plotted in the same scale, as represented in Fig. 1b. Additionally, we derived and plotted the Wrec and η distribution maps in Fig. 1c, d. The compositions with more ST content exhibit higher η, which is attributed to the reduction in ___domain size and polarization hysteresis21. However, the highest Wrec is located inside the triangle (Fig. 1d), which implies that the energy storage potential of the one-component or binary system is lower than that of the BNT-NN-ST ternary solid solution. This also proves that it is feasible to optimize the Wrec by adjusting the chemical composition of BNT-NN-ST system. Based on these simulation results, we can identify the optimal compromise combination that could achieve both large Wrec and high η by overlapping the red regions of the two figures, namely (1-x)BNT-0.20NN-xST (x = 0.15, 0.20, 0.25 and 0.30) bulk ceramics. Details of samples preparation are given in the supplementary information. As verified by X-ray diffraction (XRD), all ceramics possess high-quality crystallinity and display a single perovskite structure (Fig. 2a). An amplified (200) peak shifting to a lower angle indicates an increment in the unit cell volume (Fig. 2b)28. With the rise of ST content, the average grain sizes (AGS) of the ceramics decreased significantly from 1.32 μm to 0.65 μm (SEM images, Fig. 2c, d and Supplementary Fig. 1), which was attributed to the increasing degree of lattice distortion that weakened the driving force of grain growth29. And the grain size distribution of all samples was uniform and normal from the fitting curve in the histogram (Fig. 2e). Grain refinement can enhance the Eb and reduce the leakage current (Supplementary Fig. 2), which is conducive to energy storage. Furthermore, the atomic-scale microstructures of the typical 55-20-25 ceramics were explored via atomic-resolution high-angle annular dark-field scanning transmission electron microscopy (HAADF-STEM) along both [100]c and [110]c directions, as shown in Fig. 2f–k. The ___domain structure was determined based on the projected displacement of the B-site cations (Nb/Ti, presenting a relatively weak intensity contrast) relative to the lattice centers of their closest four A-site cations (Bi/Na/ Sr, showing a relatively strong intensity contrast). The polarization vectors of the B-site cations were indicated by yellow arrows using 2D Gaussian peak fitting. STEM polarization vector maps along the [100]c direction show that the local structure of the sample includes <001 > T-phase domains (Fig. 2g) and the R- or O-phase domains in the <011> direction. The regions with extremely weak polarization should be associated with the C phase (Fig. 2h). To further distinguish between R and O phases, STEM polarization vector maps along the [110]c direction are also provided (Fig. 2i). Evidently, both <1-10 > O-phase domains (Fig. 2j) and <1-11 > R-phase domains (Fig. 2k) can be observed, which can confirm the designed local polymorphic polarization configuration of the R-O-T phase PNRs coexisting in the C-phase paraelectric matrix. The PNRs within this structure possess a fine size (regions with the same polarization direction form PNRs with a size of approximately 1–3 nm), high dynamics, and high sensitivity to external electric fields, thereby minimizing the polarization hysteresis and leading to the optimization of energy storage performance30. Our experimental results are in good agreement with our design expectations and the ___domain structures of 55-20-25 ceramics simulated by phase field, see Supplementary Fig. 3.

Fig. 1: Reasonable composition design of BNT-NN-ST ternary solid solutions via phase field simulation.
figure 1

a Phase-field simulated bipolar P–E loops of (100-x-y)BNT-xNN-yST solid solutions. Only P–E loops with x and y being multiples of 10 are shown for clarity. b An enlarged P–E loop with a 50-0-50 composition as an example. Contour plots of the simulated (c) η and (d) Wrec of BNT-NN-ST solid solutions.

Full size image
Fig. 2: Phase and ___domain structures of (1-x)BNT-0.20NN-xST ceramics.
figure 2

a XRD patterns of (1-x)BNT-0.20NN-xST ceramics. b The enlarged (200) peaks. SEM images of (c) 65-20-15 ceramics and (d) 55-20-25 ceramics. e Grain size distribution of ceramics. Atomic-resolution HAADF STEM polarization vector images of 55-20-25 ceramics along (f) [100]c and (i) [110]c. (g, h, j, k) Enlarged images corresponding to the marked area.

Full size image

The emergence of the small-size PNRs is frequently accompanied by an enhanced relaxor behavior31. The diffuseness degree (γ) calculated from the temperature spectrum data (Fig. 3a and Supplementary Fig. 4) slightly increases from 1.61 for x = 0.15 to 1.63 for x = 0.30 (Supplementary Fig. 5). In addition, Tm also gradually decreases towards room temperature with ST incorporation (Supplementary Table 1). Since ceramics present an ergodic relaxor phase near Tm, the presence of small-size PNRs rather than microscale domains in the ergodic relaxor region is consistent with the results observed in STEM. Unipolar P–E loops of all BNT-NN-ST bulk ceramics under an electric field of 300 kV·cm−1 were tested (Fig. 3b) and the results indicate that with the introduction of ST, the curve gradually becomes thinner, and the smallest Pr value (0.6 μC·cm−2) is obtained in 55-20-25 ceramics. To assess energy storage capacity, unipolar P–E loops were tested for all ceramic samples under their respective critical electric fields (Fig. 3c), and Wrec and η were calculated in Fig. 3d. The 55-20-25 ceramics exhibit the optimal energy storage capacity, with a Wrec of 5.4 J·cm−3 and a high η of 93.1%, owing to the reduction of the ___domain-switching barrier (resulting from the design of the local polymorphic polarization configuration) and the increase in Eb (induced by the decrease in the AGS).

Fig. 3: Dielectric performances, energy storage properties, breakdown characteristics, and evolution of polar structures for BNT-NN-ST ceramics.
figure 3

a Dielectric constant and dielectric loss as a function of temperature for 55-20-25 ceramics. P–E loops measured at (b) 300 kV·cm−1 and (c) their respective Eb for (1-x)BNT-0.20NN-xST ceramics. d Wrec and η, e Weibull plots of Eb, f AGS and Eb for (1-x)BNT-0.20NN-xST ceramics. g The Landau energy profiles, h Random field distribution, and i, simulated ___domain structures of 55-20-25-Mn ceramics. Different phases and various polar directions in the same phase are denoted by different colors.

Full size image

Weibull distribution results show that the large β value suggests the high reliability and small variances of the ceramics (Fig. 3e). At the same time, the Eb values of the ceramics monotonically improve from 420 kV·cm−1 to 468 kV·cm−1 with the increase of ST content (Fig. 3f), which may be due to the increase in grain boundary density caused by the decrease of grain size, thus impeding the expansion of the breakdown path32. In addition, the enhanced relaxor characteristics and thin P–E loops confirm that the energy loss released in the form of thermal energy is reduced, which greatly reduces the possibility of thermal breakdown33. Finally, the underdamped and overdamped discharge curves of 55-20-25 ceramics at different electric fields were tested in Supplementary Fig. 6. The corresponding Pd, Wdis and t0.9 values were calculated (Supplementary Fig. 7). Under an electric field of 320 kV·cm−1, 55-20-25 ceramics can simultaneously attain a high Pd of 286.9 MW·cm−3, a transient t0.9 of 224 ns, and a large Wdis of 2.8 J·cm−3, demonstrating excellent discharge characteristics.

To enhance the densification degree in the sintering process and the shrinkage matching between the dielectric and the electrode during the preparation of MLCC, 1.0% mol MnO2 is added to the 55-20-25 ceramic as a sintering aid (abbreviated as 55-20-25-Mn), and the sintering temperature is optimized at 1090 °C. The specific preparation process is presented in the Supplementary Information. The XRD results indicate that the introduction of MnO2 does not alter the crystallographic structure of the ceramic, only the diffraction peaks of the MnO2-doped ceramic shift to a lower angle (Supplementary Fig. 8), similar results have been verified in previous studies34. Although the AGS of the MnO2-doped ceramics has increased from 0.73 μm to 1.0 μm (Supplementary Fig. 9), the porosity has decreased markedly. This is because the addition of MnO2 can result in the formation of a liquid phase and enhance the sintering quality35. Furthermore, the homogeneous distribution of elements eliminates the possible local chemical property differences in the ceramics (Supplementary Fig. 10) and is one of the reasons why the differences between the samples can be negligible. Then, the impact of the addition of MnO2 on the dielectric properties was also investigated. It was found that the two ceramic samples presented a similar single dielectric anomaly peak. For the MnO2-doped ceramics, both the maximum dielectric constant and dielectric loss decreased gradually, and its Tm got closer to room temperature (Supplementary Fig. 11, reducing from 74.8 °C to 57.0 °C). The energy storage properties of the 55-20-25-Mn ceramic are evaluated by testing the P–E loops (Supplementary Fig. 12a). The Pr value is insensitive to the electric field and is only 0.41 μC·cm−2 at 500 kV·cm−1. The 55-20-25-Mn ceramic achieves a high η of 96.6% and a large Wrec of 6.5 J·cm−3 under the electric field of 500 kV·cm−1 (Supplementary Fig. 12b). In comparison with the 55-20-25 ceramic, its Eb is enhanced by 11.1%, Wrec is increased by 20.4%, and the η value also rises from 93.1% to 96.6%. This is ascribed to the introduction of MnO2, which strengthens the grain boundary effect, boosts the resistivity, and causes the enhancement of Eb and the reduction of dielectric loss. The mesoscale simulation approach is employed to investigate the polar structure evolution of the material. The schematics of the Landau free-energy landscape (Supplementary Fig. 13a, d) and the local polar order-disorder characteristic (Supplementary Fig. 13b, e) are presented to comprehend the relationship between the microstructures and the phase transition behavior. The reduction of the anisotropic field indicates the weakening of the B-O displacement, which flattens the free-energy profile and explains the enhancement of the relaxor behavior36. The built-in random field induced by the spatially distributed defect represents the evolution of the high-angle ___domain wall density. The increased volume fraction of the polar disordered region implies the intensification of the dielectric relaxor phenomenon. That is, the driving force for the large-sized domains induced by the electric field to recover to the polymorphic ___domain increases (Supplementary Fig. 14), resulting in the recoverable electric field-induced relaxor ferroelectric state37. In conclusion, the competition of local polar order-disorder among different states and the directional randomness are the crucial structural characteristics of high relaxation. The polar ___domain structures (Supplementary Fig. 13c, f) are acquired through solving the time-dependent Ginzburg–Landau equation38. On the one hand, the multiphase coexistence is consistent with the results recorded by STEM (Fig. 2f–k). On the other hand, in the designed ternary solid solution of BNT-NN-ST, the increment of the ST content forms a more dispersed ___domain structure (with a decreased ___domain size). Based on the simulation results of the same model, it is found that for the 55-20-25 components, the addition of an extremely small amount of MnO2 does not exert a significant impact on the Landau free-energy landscape, the local polar order-disorder characteristic and polymorphic ___domain structures (Fig. 3g–i).

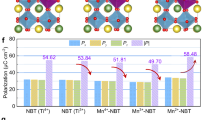
The MLCCs with four effective dielectric layers are produced using the 55-20-25-Mn ceramic powder, and the cross-sectional microstructures of the MLCCs are characterized to analyze the layered structure and the interfacial element diffusion (Fig. 4a and Supplementary Fig. 15). After sintering, the MLCC samples did not present dry cracking, warping, or bulging. The electrodes are dense and continuous, and the dielectric layer has relatively few unavoidable pores. The clear electrode-dielectric interface without obvious elements of diffusion proves that the average thickness of the 55-25-20-Mn dielectric layer is around 20 μm. A series of thin P–E loops were acquired in this MLCC device (Fig. 4b), manifesting the characteristics of a large Pmax and a small Pr (Pmax increased to 49.2 μC cm−2 at the breakdown electric field, while Pr remained below 0.6 μC cm−2). As the electric field improves, Wrec increases monotonically and η remains at above 85%. Eventually, a large Wrec of 20.0 J·cm−3 and a high η of 86.5% were obtained under a high electric field of 1200 kV·cm−1 (Supplementary Fig. 16), being significantly superior to most of the present advanced lead-free MLCCs (Fig. 4c)1,2,3,4,5,6,17,39,40,41,42,43,44,45. Considering the practical application of MLCC, we measured the temperature stability of the energy storage properties within the range of 25 °C to 150 °C (Supplementary Fig. 17a). The MLCC presented stable performance parameters at 900 kV·cm−1, with Wrec and η varying by less than ±5.2% over the entire temperature range (Supplementary Fig. 17b). The excellent temperature insensitivity is ascribed to the high stability of the designed local polymorphic polarization configuration over a wide temperature range (Supplementary Fig. 18). Although the energy storage parameters of our MLCCs at room temperature are slightly lower than those of the state-of-the-art work published in Science (Fig. 4c), it presents more remarkable high-temperature performance at 150 °C (Fig. 4d)1,2,4,6,17,39,41,42,43,44,45, suggesting its suitability for broad-high temperature dielectric capacitor applications. Additionally, cyclic reliability tests at an electric field of 900 kV cm−1 revealed that the Wrec and η of the MLCCs remained essentially unaltered over 104 cycles (Fig. 4e and Supplementary Fig. 19). The reduction in macroscopic ___domain walls and the high dynamic characteristics of the polymorphic polarization configuration can inhibit the “pinning effect” of ___domain walls17,46, thereby resulting in the high cyclic reliability of the MLCCs. Subsequently, the P–E loops under an electric field of 900 kV cm−1 within the frequency range of 1–100 Hz were examined to assess the frequency stability (Supplementary Fig. 20a). The results demonstrated that the energy storage characteristics were also insensitive to the frequency. Specifically, the Wrec and η values fluctuated around 14.4 J·cm−3 and 88.9% respectively, and the variation rate was less than ±3.5% (Supplementary Fig. 20b). Ultimately, the overdamped discharge curves of the MLCCs were measured (Supplementary Fig. 21). The excellent charge-discharge characteristics are characterized by a high discharge energy density (Wdis) of 14.8 J·cm−3 and a fast discharge rate of ~2.0 μs (t0.9), as shown in Fig. 4f. We believe that this excellent temperature, frequency and cycle reliability, as well as excellent discharge performance, contribute to the extensive application of MLCC devices.

Fig. 4: Energy storage properties of the 55-20-25-Mn MLCC devices.
figure 4

a Digital images of the MLCCs and SEM images of the cross-section area with corresponding element distribution. b P–E loops of 55-20-25-Mn MLCC under various electric fields. Comparison of the energy storage properties for 55-20-25-Mn MLCC and state-of-the-art other MLCCs at (c) room temperature and (d) 100–150 °C. e cycle number-dependent Wrec and η under 900 kV·cm−1. f Calculated Wdis and t0.9.

Full size image

In conclusion, through the experimental and theoretical analysis, we successfully established the composition-structure-performance correlation in the BNT-NN-ST system, our data set confirms that the construction of local polymorphic polarization configuration can greatly reduce the polarization hysteresis and improve the breakdown strength. The excellent energy storage properties of the 55-20-25-Mn MLCCs, characterized by a large Wrec of 20.0 J·cm−3 and a high η of 86.5%, obtained in this work are derived from the guidance of mesoscale phase-field simulation and the fabrication of prototype devices, demonstrating the great application potential of ceramic dielectric capacitors. The proposal of this strategy, which combines the design of local polymorphic polarization configurations and the fabrication of MLCC prototype devices, will benefit the optimal design of most energy storage capacitors and can trigger design considerations for other multifunctional materials.

Methods

Ceramics fabrication

Titanium dioxide (TiO2, 99.9%), niobium pentoxide (Nb2O5, 99.99%), bismuth trioxide (Bi2O3, 99%), sodium carbonate (Na2CO3, 99.9%), strontium carbonate (SrCO3, 99.8%) and manganese dioxide (MnO2, 99.95%) were adopted as raw materials. These powders were weighed according to the following compositions: 0.65BNT-0.20NN-0.15ST (65-20-15), 0.60BNT-0.20NN-0.20ST (60-20-20), 0.55BNT-0.20NN-0.25ST (55-20-25), 0.50BNT-0.20NN-0.30ST (50-20-30) and 0.99(0.55BNT-0.20NN-0.25ST)-0.01MnO2 (55-20-25-Mn), and mixed in ethanol. The mixed powder was dried and then calcined at 850 °C for 4 h. The calcined powder was mixed with alcohol again, and then the second ball-milling, drying and sieving were carried out in sequence. The obtained powder was pressed into pellets with a diameter of 10 mm by the cold isostatic pressing method, and the pellets were sintered at 1110-1230 °C for 4 h to obtain ceramic samples.

MLCCs fabrication

Butanone (MEK), butyl benzyl phthalate (BBP), QPAC, and glycerol trioleate are respectively selected as the organic solvent, the plasticizer, the binder, and the dispersant. These substances are blended with the 55-20-25-Mn ceramic powder in an appropriate ratio, and a high-speed mixer is utilized to prepare a slurry that is uniformly dispersed and bubble-free. The smooth and continuous ceramic tapes is then produced by a tape-casting machine. Then, the obtained ceramic tapes are cut sequentially, platinum paste is screen-printed onto them as an internal electrode, and they are stacked in a staggered manner. Subsequently, a thermocompression is employed to mold them at 75 °C and a pressure lower than 10 MPa for 30 min. The obtained intermediates are cut into individual MLCCs, and then warm water isostatic pressing is performed (the temperature is maintained at 75 °C, and the pressure is maintained for 25 min at 30 MPa) to obtain individual MLCC green bodies. To ensure the integrity of MLCC, the binder removal process is requisite to prevent the delamination and cracking of MLCC resulting from the rapid volatilization of organic compounds at high temperatures. The compact bodies were obtained through cold isostatic pressing (maintaining pressure at 200 MPa for 3 min) to reduce the pores left by volatilization of organic matter. Finally, the MLCC samples were obtained by sintering at 1000 °C for 4 h. The overlapping area of two adjacent platinum electrodes in the sintered MLCC is measured to be 2.1 mm × 1.6 mm, and the average thickness is approximately 20 μm, as depicted in Supplementary Fig. 22. Polish both sides until the internal electrodes are exposed, then coat the Ag paste as the external electrodes and encapsulate both ends for electrical testing.

Phase and microstructures

The microstructure of the designed ceramics and MLCCs was observed by using field-emission scanning electron microscopy (FESEM, Quanta 250 F, Japan) in combination with energy dispersive spectroscopy (EDS). The crystal structure was investigated by using X-ray diffraction (D8 Advance, Bruker, Germany).

Dielectric measurements

A precision impedance analyzer (E4980A, Aglient) was used to measure the dielectric properties of parallel plate capacitors composed of ceramic dielectrics.

Ferroelectric measurements

Polarization–electric field (P–E) loops were tested using a ferroelectric analyzer (TF-2000, Aix ACCT, Aachen, Germany).

Charge-discharge measurements

A charge-discharge test system (CFD-003, Tongguo Technology) was adopted to perform the charge-discharge experiments of ceramics.

Scanning transmission electron microscopy (STEM) experiments

The HAADF-STEM images of the samples were recorded via a Titan Themis G2 microscope equipped with a spherical-aberration corrector, and the two-dimensional Gaussian fitting was performed.

Phase-field simulations

For phase transistion analysis in ferroelectric materials, we typically choose polarization Pi(r, t) as order paramter. According to the principle of energy minimization, the evolution of the order parameter Pi(r, t) was usually solved by the time (t)-dependent Ginzburg–Landau equation47,48:

$$\frac{\partial {P}_{i}\left(r,t\right)}{\partial t}=-L\frac{\delta F}{\delta {P}_{i}\left(r,t\right)},\left(i=1,2,3\right)$$
(1)

where L denotes the kinetic coefficient components relating to the interface mobility, and F represents the total free energy of the system, which can be defined as:

$$F=\int \left({f}_{{bulk}}+{f}_{{grad}}+{f}_{{ela}}+{f}_{{elec}}\right){dV}$$
(2)

where \({f}_{{{{\rm{bulk}}}}}\), \({f}_{{{{\rm{grad}}}}}\), \({f}_{{{{\rm{ela}}}}}\) and \({f}_{{elec}}\) are the contributions from bulk free energy, gradient energy, elastic strain energy, and electric energy, respectively. And the bulk free energy is given as,

$${f}_{bulk}= {{\alpha }_{1}}({{P}_{1}^{2}}+{{P}_{2}^{2}}+{{P}_{3}^{2}})+{{a}_{11}}({{{P}_{1}}^{4}}+{{{P}_{2}}^{4}}+{{{P}_{3}}^{4}})\hfill \\ +{{\alpha }_{12}}({{P}_{1}^{2}}{{P}_{2}^{2}}+{{P}_{2}^{2}}{{P}_{3}^{2}}+{{P}_{1}^{2}}{{P}_{3}^{2}})+{{a}_{112}} [\left(\right.{{{P}_{1}}^{4}}({{{P}_{2}}^{2}}+{{{P}_{3}}^{2}} ) \hfill\\ +\left(\right.{{{P}_{2}}^{4}}({{{P}_{1}}^{2}}+{{{P}_{3}}^{2}})+\left(\right.{{{P}_{3}}^{4}}({{{P}_{1}}^{2}}+{{{P}_{2}}^{2}})]+{{{{\rm{a}}}}_{123}}{{{P}_{1}}^{2}}{{{P}_{2}}^{2}}{{{P}_{3}}^{2}}\hfill\\ +{{a}_{111}}({{{P}_{1}}^{6}}+{{{P}_{2}}^{6}}+{{{P}_{3}}^{6}})\hfill$$
(3)

where P1, P2, and P3 are polarization components. And α1, α11, α12, α111, α112, and α123 are the Landau coefficient.

The gradient energy is associated with the contribution of ___domain walls to the total free energy, which can be expressed by the inhomogeneous distribution of polarization as follows:

$${f}_{{grad}}=\frac{1}{2}{G}_{{ijkl}}{P}_{i,j}{P}_{k,l}$$
(4)

where \({P}_{i,j}=\partial {P}_{i}/\partial {x}_{j}\), and Gijkl is the gradient energy coefficient.

The elastic strain energy is based on elasticity theory, which can be described as

$${f}_{{elas}}=\frac{1}{2}{C}_{{ijkl}}\left({\varepsilon }_{{ij}}-{\varepsilon }_{{ij}}^{0}\right)\left({\varepsilon }_{{kl}}-{\varepsilon }_{{kl}}^{0}\right)$$
(5)

where Cijkl is the elastic stiffness tensor, ε and ε0 are the total local strain, and the eigenstrain, respectively. Eigenstrain contains local strain fluctuations εrand, modeled by Gaussian distribution. The gradient energy density can be expressed as,

$${f}_{{elec}}=-{P}_{i}(r){E}_{i}^{{ex}}(r)-{\frac{1}{2}}P_{i}(r){E}_{i}^{{in}}(r)$$
(6)

where Eex represents the external electric field, Ein represents the local electric field caused by the random point defects and interaction field generated by the dipole moment. In our model, randomly distributed points accounting for 5% to 20% of the total are considered as defect dipole.

The equation was solved by a semi-implicit Fourier spectral method and the simulation size is 64 Δx × 64 Δy × 64 Δz. (Δx is the number of grid points and equals 1 nm in this work). We use Landau coefficients of the BNT, NN, and ST system modified for the calculation21,49,50.