Introduction

Interfaces can significantly impede heat transport, especially if the properties of the neighboring materials differ strongly. In solids, the existence of an interfacial thermal resistance (ITR) mediated by different phonon modes and electron conductivities is well established1. First discussed by Fourier in 18222, ITR has been observed for solid-solid3, solid-gas4, and solid-liquid5 interfaces with numerous applications in microelectronics, batteries, and quantum computing, where the management of heat dissipation in small devices has led to a rich body of scientific discourse6,7,8. While there have been theoretical investigations for liquid-liquid interfaces9, the consideration of ITR has been notably absent in the realm of high-energy-density matter, where the abundance of conduction electrons will dominate the heat conduction over the boundary.

One area in high-energy-density sciences where ITR may have a strong influence is the performance of inertial confinement fusion experiments. Currently, the most successful designs use indirectly laser-driven spherical targets with a low-Z ablator shell containing a solid layer of deuterium-tritium (DT) fuel and a central region filled with DT gas10,11,12. Moreover, the ablator has a layer with a low concentration of a mid-Z element near the ablator-fuel interface, serving as an X-ray pre-heat shield. This design features multiple interfaces between dense, ionized materials with very different electronic properties. The presence of ITR in such a setup can significantly impede the heat flow across interfaces. This affects the density and temperature profiles near material boundaries, thereby influencing the growth of instabilities and ultimately determining the performance of capsule implosions13.

Despite its potential significance, there has been no direct observation of ITR at the boundary between two high-energy-density systems. This fact is likely tied to the general scarcity of thermal conductivity measurements in this regime14, which presents formidable challenges owing to the inherently short lifetimes and limited spatial scales15. First experiments using fluorescence16, streaked optical pyrometry17,18, and X-ray radiography19 have yielded significant progress in thermal conductivity measurement in high-energy-density matter, but no indications of a thermal barrier at the interface have been reported.

In our experiment, we designed a setup with a high potential to induce ITR by differentially heating a tungsten wire encased in a plastic layer. The hot tungsten will be highly conductive with abundant free electrons, while the plastic, which stays relatively cold, maintains a low degree of ionization. Thus, we create an interface with highly different temperatures and conductivities on either side. The temperature evolution of this system will answer the question: Can the ITR exist in high-energy-density (HED) matter despite the abundance of conducting electrons?

Results

Experimental platform

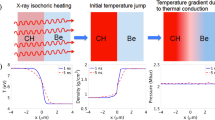
Our experiments were performed at the OMEGA 60 laser at the Laboratory for Laser Energetics20, using a setup similar to refs. 21,22,23. We create an HED interface by isochorically heating a plastic-coated (C8H4F4) tungsten wire with 8.3 keV copper He-α X-rays, as shown in Fig. 1a. The tungsten wire is heated to 18 eV within a nanosecond, triggering a rapid expansion until it reaches pressure equilibrium with the surrounding plastic. The resulting hydrodynamically stable interface exhibits a large thermal discontinuity, ideal for studying ITR. As heat flows across this interface, the material flows in response to thermally induced pressure gradients, resulting in a complex and discontinuous density profile.

Fig. 1: Interfacial thermal resistance platform.
figure 1

a A 4 μm diameter tungsten wire coated with plastic (C8H4F4) to an outer diameter of 125 μm is isochorically heated with copper He-α emission to high-energy-density conditions and imaged with Fresnel diffractive radiography using vanadium He-α emission through a narrow slit. b The delay of the backlighter beams, shown in red, is varied from shot to shot to image the target evolution after the heater beams, shown in blue. The X-ray framing camera integration time (dashed red line) starts 0.7 ns into the backlighter pulse when the probe X-ray emission is highest. c Due to its higher opacity, the tungsten will absorb significantly more energy, reaching an approximately 40 times higher temperature than the plastic. The tungsten expands rapidly until constrained by pressure equilibration with the surrounding plastic. The tungsten remains much hotter than the plastic, setting up a hydrodynamically stable interface that primarily evolves due to heat diffusion. d The imaged targets have sharp fringe features resulting from interference effects. For unheated conditions, the vacuum, plastic, and tungsten are all clearly differentiable with visible interfaces. After heating, multiple fringe features appear from the thermally induced pressure gradients at the interface and the shockwave driven by the tungsten expansion.

Full size image

We employ Fresnel diffractive radiography to observe the evolution of this density profile. The target is imaged using a 5.2 keV vanadium He-α X-ray source that is passed through a 1 μm-wide slit and recorded on an X-ray framing camera positioned 1 m away. The small source size and large propagation distance generate diffraction-enhanced images of the interface, where interference effects appear as vertical striations in the image, as seen in Fig. 1d. In particular, diffraction at the interface results in an intricate fringe pattern that can be used to reconstruct sub-micron changes in the density profile22,23,24. Using successive experiments, we imaged targets at unheated conditions and for delays of 2.3, 4.0, and 6.0 ns after the start of the heater beams. Matching the diffraction patterns yields a time sequence of density profiles that are converted to temperature profiles considering pressure equilibrium. The resulting temperature profiles encode the thermal conduction of both materials and, crucially, heat flow across the interface.

Density extraction

We use a forward-fitting method to determine the density profile from the recorded interference patterns. Using the Fresnel-Kirchoff integrals22,23,25, we propagate X-rays through parameterized radial density profiles to create synthetic diffraction patterns, which are compared to the experimental data. The analysis of the unheated wire is discussed in ref. 22, using step profiles for both materials. The driven shots require a more sophisticated density profile to account for thermal conduction, shock wave formation and propagation, and rarefaction at the vacuum-plastic boundary (see “Methods”).

Given the symmetry in the data, we are able to mirror and average the data to reduce noise. As shown in Fig. 2a, the best-fit simulated diffraction profiles closely match all features we see in the experimental data, with a particularly accurate representation of the fringe features near the material interface. The outgoing shock wave at 17 μm for the 2.3 ns data and 25 μm at 4.0 ns exhibits sharper features in the simulated profile than in the experimental data due to motion blurring of the shock, which is traveling at ~ 5.35 km/s at 2.3 ns. Additional data collected at 6.0 ns was clipped by the edge of the detector, leaving the center missing and rendering it unsuitable for full analysis. However, by aligning the shock fringe with the expected position based on the shock velocity, we observe that the interface ___location remains approximately consistent with earlier measurements, indicating that the interface does not continue to expand.

Fig. 2: Diffraction patterns and extracted density profiles.
figure 2

a Time sequence of the diffraction patterns, vertically offset for clarity. The unheated target (blue) has a strong absorption feature from the tungsten wire and significant refraction fringes at the plastic-vacuum boundary at ~65 μm. After heating (2.3 ns in red, 4.0 ns in yellow, 6.0 ns in green), the diffraction pattern is more complex, with strong fringe features resulting from the radial shockwave launched by the expanding tungsten, the evolution of the interface, and the rarefaction at the plastic-vacuum boundary. Data collected at 6.0 ns was clipped by the edge of the detector, making it unsuitable for full analysis. However, by aligning the signal with the estimated shock position, we can infer that the interface remains stationary at later times. b–d Density profiles corresponding to the simulated diffraction patterns (black dashed lines) in panel (a), which are fit to the experimental data. The shock velocity, estimated to be 5.35 km/s, is responsible for additional motion blurring of the refraction fringe resulting from the shock front.

Full size image

The density near the interface develops a complex profile as the expanded tungsten cools and densifies and the plastic heats and expands13. This density profile is responsible for the notable fringe structure in the driven samples. To determine the uncertainty in our density measurement near the interface, we employ a Bayesian inference model using Markov-Chain Monte Carlo (MCMC)26 (see “Methods”). The method utilized the hard boundary likelihood function and uniform prior distributions to retrieve the parameterized density profile from the experimental data, with the range of accepted density profiles shown by the shaded regions in Fig. 3. Notably, we are able to identify the ___location of the interface to within half a micron.

Fig. 3: Temperature extraction and evolution.
figure 3

a Density profile near the interface for the isochorically heated target at two times. The solid lines show the same best-fit density profiles from Fig. 2 for 2.3 ns (red) and 4.0 ns (blue). A Bayesian sampling process was used to determine the range of profiles that accurately recreate the diffraction patterns of Fig. 2, shown here as the shaded regions. A second Bayesian process is used to evolve the 2.3 ns best-fit data to 4.0 ns, resulting in a subset of density profiles given by the dark-shaded band. b Temperature profiles inferred from the density profiles (same color scheme). The temperature profiles show a steep discontinuity at the interface, providing evidence of interfacial thermal resistance. c–e Probability density functions of the main parameters in our Bayesian analysis of the propagation of the system from 2.3 ns to 4.0 ns: thermal conductivity coefficients for (c) tungsten and (d) plastic, and (e) the thermal resistance across the interface.

Full size image

Inferring temperature profiles

Thermally induced pressure gradients prompt the material to flow toward a state with equilibrated pressures, resulting in uniform pressure in the material behind the outgoing shock wave. The pressure in the tungsten is computed via an equation of state from the input energy density, i.e., the absorbed X-ray flux, which is readily obtained from opacity tables. The pressure in the plastic is calculated similarly, with an additional jump of 0.18 Mbar obtained from the Rankine-Hugoniot relationship, using the estimated shock velocity of 5.35 km/s at 2.3 ns. Using cold opacity tables and the Frankfurt Equation Of State (FEOS)27 (see “Methods”), we find an incident X-ray flux of 1590 J/cm2 gives rise to equal pressures on either side of the interface, corresponding to a laser-to-X-ray conversion efficiency of 0.6%, consistent with previous studies28,29. The resulting pressure is 0.39 Mbar at 2.3 ns.

Combining the FEOS tables with the density profiles at 2.3 ns and the obtained pressure allows us to extract the temperature profile across the interface at this time, as illustrated in Fig. 3b. We find that the tungsten reaches temperatures of 18 eV in the center, while the plastic remains comparatively cool at 0.3 eV away from the interface. The data show evidence for the expected heat conduction across the interface from the tungsten to the plastic. Moreover, we observe a temperature discontinuity at the interface of approximately 6 eV. This temperature jump demonstrates that the flow of heat is restricted, providing compelling evidence of substantial ITR.

Thermal transport coefficients

Quantitative values of the thermal conductivity in each material and ITR can be obtained by evolving the density and temperature profiles using the data at 2.3 ns and 4.0 ns as boundary conditions. In our simulations, the heat flow is calculated using Fourier’s Law, and updated temperature and density profiles are calculated from the FEOS tables. The material is allowed to respond instantly to thermally induced pressure gradients to ensure pressure equilibration in the region around the interface. Constant coefficients characterize the heat flow in the three distinctive regions: the tungsten, the plastic, and across the interface. We simulate the heat and mass transport using a Bayesian process, varying each of the three coefficients and the final pressure, which is assumed to decrease linearly between the two times. The resulting profiles are compared to those measured, and only solutions that fall within the experimental error bars at 4 ns are accepted.

The range of accepted solutions is shown by the dark-shaded bands in Fig. 3a and b, and the corresponding histograms of each of the coefficients are shown in Fig. 3c–e. It is important to note that the quantitative measurement of ITR cannot be disentangled from the measurement of the thermal conductivity coefficients; the behavior of the system is complex, and all parameters are interconnected. From the analysis, we extract optimal values for the thermal conductivity of the tungsten, κW = 590 ± 100 W/m/K, the plastic, κCHF = 910  ± 260 W/m/K, and the interfacial thermal resistance, RInt = 3.7 × 10−9 ± 8 × 10−10 m2K/W. The pressure at 4.0 ns was determined to be 0.27 ± 0.01 Mbar.

There are few published values of thermal conductivity in the WDM regime. For a comparable density (~ 0.6 g/cm3), the thermal conductivity of tungsten was previously found to be over an order of magnitude higher, albeit at temperatures that were also an order of magnitude higher16. No data could be found for parylene (C8H4F4) at conditions similar to our experiment. Recent measurements for C8H819 found a thermal conductivity of 400  ± 200 W/m/K at a temperature of 8 eV. Here, we find a significantly higher thermal conductivity, even at a lower temperature. One possible explanation for this variance is that the presence of fluorine in our samples leads to the formation of negative ions30, effectively removing most free electrons and leaving behind neutral hydrogen. These neutral atoms can move freely, efficiently transporting energy throughout the plastic component.

Our experiments confirm the presence of a heat barrier, demonstrating that ITR exists in HED matter. Despite the abundance of conducting electrons, we find an ITR coefficient comparable to those found across metal-ceramic interfaces31,32. This fact demonstrates that ITR is a critical but often overlooked factor in HED science, where interfaces are either constructed33 or develop34 in a myriad of experiments. A prominent example is inhibited thermal diffusion across interfaces in dynamic compression experiments, which could lead to a systematic and significant misinterpretation of temperature measured by optical pyrometry35.

We anticipate a particularly high significance of ITR in the context of inertial confinement fusion, where the fuel-containing capsules exhibit multiple materials interfaces10,12,36. During the acceleration phase of the implosion high energy x-rays flow through the shell and, thus, temperature discontinuities develop at these interfaces. The resulting pressure gradients lead to clear modifications of the radial density profiles13, which in turn can impact hydrodynamic instability growth. The latter has been identified as one of the main degradation mechanisms of fusion performance37. Thus, understanding temperature jumps and heat flow across these interfaces is crucial for achieving high hot spot temperatures required for ignition and burn. Incorporating ITR into the design of fusion targets will improve predictive capabilities and lead to innovative solutions that could ultimately pave the way to developing successful inertial fusion energy concepts.

Methods

Experimental setup

Our experiments were performed at the OMEGA 60 laser at the Laboratory for Laser Energetics20. The physics package consists of a coated tungsten wire surrounded by components for isochoric heating via X-rays. The tungsten wires have a radius of 2 ± 0.2 μm and are coated with C8H4F4 (ρ = 1.60 g/cm3 38) to an outer diameter of  ~ 125 μm. The tungsten is isochorically heated by 8.3 keV copper He-α X-rays generated by heating two 10 μm thick copper foils positioned 450 μm on either side of the wire. The foils are each driven by 8 laser beams (λ = 351 nm,  ~450 J/beam, SG5-650 phase plates) with a 1 ns square pulse. The diameter of the tungsten wire was carefully chosen to minimize initial temperature gradients by matching it to the tungsten attenuation length (~3.4 μm at 8.3 keV).

We utilize a foil-backlighter imaging setup to radiograph our targets. A 1 ns square pulse from 10 beams illuminates a vanadium foil and creates a broadband spectrum that is dominated by the vanadium He-α emission at 5.2 keV, which we isolate with a titanium-vanadium Ross Pair39 in front of an X-ray framing camera. The X-ray probe maximizes the contrast between the opaque tungsten and the more transparent plastic. Before the target, the source is apertured using a 1 μm  × 30 μm slit milled into a 30 μm thick tantalum plate for slit projection imaging with high magnification (M = 77). This creates a high-spatial-resolution, partially coherent X-ray source capable of resolving micron-scale features in the appropriate geometry40.

The imaging geometry, coupled with the very narrow slit, enables sensitivity to both refractive and diffractive interference effects. We have termed this imaging capability Fresnel diffractive radiography22,23. Evidence of thermal conductivity manifests in the evolution of diffraction features, which primarily arise from sharp density features. Assuming pressure equilibration, these discontinuities partly stem from tungsten cooling near the interface, leading to increased density, while the reverse process occurs in the plastic material. Thus, the diffraction pattern correlates with the density discontinuity, facilitating measurements of density profiles and corresponding scale lengths in both materials. By acquiring multiple shots, we track the evolution of density profiles over time, enabling inference of temperature profiles and extraction of the thermal conduction rate.

The time delay given in the main manuscript is between the X-ray framing camera acquisition time and the start of the heater beams. An example timing diagram is shown in Fig. 1b. The acquisition was typically timed 0.7 ns into the backlighter beam pulse when the backlighter flux is the highest.

X-ray Interference analysis

The diffraction patterns present in the raw data are matched using a forward-fitting methodology, where synthetic radial density profiles are used to create simulated diffraction patterns by propagating X-rays from the slit through the target according to the Fresnel-Kirchoff diffraction integrals22,23,24,25. We vary the parameters of the radial density profile until the best match between the simulated and the measured diffraction profiles is achieved.

The profile in the plastic between the vacuum and the shock front is dominated by refraction and thus can be determined using Abel inversion which provides a close match to the data. The density of the plastic ahead of the shock is assumed to be nominal solid density (~1.6 g/cm3). The shock front is then modeled as a density jump that decreases to a post-shock density, as determined by matching the signal level behind the shock.

The interface region, consisting of the entirety of the target between the two shocks, is a parameterized profile that accounts for the expansion of the tungsten and the shape of the interface near the discontinuity. The profile near the interface takes the form of two exponential functions. In the tungsten, the profile is given by

$${\rho }_{{{{{\rm{W}}}}}}(r)=\left({\rho }_{{{{{\rm{W}}}}}}^{{{{{\rm{peak}}}}}}-{\rho }_{{{{{\rm{W}}}}}}^{{{{{\rm{center}}}}}}\right)\exp \left(\frac{r-{r}_{{{{{\rm{int}}}}}}}{{\lambda }_{{{{{\rm{W}}}}}}}\right)+{\rho }_{{{{{\rm{W}}}}}}^{{{{{\rm{center}}}}}},$$
(1)

where the parameters for the tungsten peak density \({\rho }_{{{{{\rm{W}}}}}}^{{{{{\rm{peak}}}}}}\) and scale length λW define the shape and rint is the ___location of the tungsten-plastic interface. The nominal center tungsten density, \({\rho }_{{{{{\rm{W}}}}}}^{{{{{\rm{center}}}}}}\), is determined by calculating the areal densities of both the cold and expanded wires and solving for the central density in the expanded wire, such that the total mass of the tungsten stays constant.

The plastic profile is more complicated near the interface and is reminiscent of a Fermi function. We parameterize the plastic density profile as

$${\rho }_{{{{{\rm{CHF}}}}}}=\frac{{\rho }_{{{{{\rm{CHF}}}}}}^{{{{{\rm{shocked}}}}}}-{\rho }_{{{{{\rm{CHF}}}}}}^{{{{{\rm{trough}}}}}}}{\exp \left(\frac{-r+{r}_{{{{{\rm{int}}}}}}+{x}_{{{{{\rm{CHF}}}}}}}{{\lambda }_{{{{{\rm{CHF}}}}}}}\right)+1}+{\rho }_{{{{{\rm{CHF}}}}}}^{{{{{\rm{trough}}}}}},$$
(2)

where the parameters \({\rho }_{{{{{\rm{CHF}}}}}}^{{{{{\rm{trough}}}}}}\) and λCHF characterize the shape of the plastic profile in analogous and opposite ways to \({\rho }_{{{{{\rm{W}}}}}}^{{{{{\rm{peak}}}}}}\) and λW, xCHF shifts the profile horizontally from the interface to control the inflection in the profile and \({\rho }_{{{{{\rm{CHF}}}}}}^{{{{{\rm{shocked}}}}}}\) is the density value behind the shock. This profile is combined with the rarefaction profile to generate the full plastic density profile from the material to the vacuum interface.

To fit the second fringe seen in the 2.3 and 4.0 ns data at approximately 12–15 μm, we needed to include an additional density bump at the same radial distance, which we model with a Gaussian profile,

$${\rho }_{{{{{\rm{fringe}}}}}}(r)={\rho }_{{{{{\rm{G}}}}}}\exp \left(\frac{-{\left(r-{r}_{{{{{\rm{G}}}}}}\right)}^{2}}{2\,{\sigma }_{{{{{\rm{G}}}}}}^{2}}\right).$$
(3)

The physical implication of this density buildup is thought to be the result of hot plastic being pushed out by the expanding tungsten and constrained by the still-cold outer ring of plastic. The data reinforce this interpretation, as the Gaussian peak is much narrower and sharper at 4.0 ns than at 2.3 ns, suggesting that it has been further compressed.

A total of 13 parameters are used to fit the interface region, including the source size. While the best fit is obtained using a minimization, we use Bayesian inference to determine a range of acceptable combinations that would yield diffraction patterns within the noise of the data26. We allow the parameters to randomly vary as broad uniform prior distribution, with appropriate bounds placed to maintain meaningful physical parameters (e.g., positive densities) or to account for metrological tolerances (e.g., initial diameter of the tungsten wires), and then generate a simulated radiograph for each set of parameters. For the likelihood function, we use the hard boundary distribution, where a simulated radiograph is considered a match to the data if the maximum difference between the lineouts is within the experimental noise. Focusing on the region around the interface, we utilize a Metropolis-Hastings algorithm Markov-Chain Monte Carlo as our inference method, performing the typical burn-in of 1000 runs41 before recording comparisons. The span of accepted density profiles for the 2.3 and 4.0 ns data are shown in Fig. 3a as the shaded orange (2.3 ns) and blue (4.0 ns) regions.

Propagation code analysis

With the density profiles determined, the pressure of the system can be found by assuming pressure equilibration on either side of the interface. Using the FEOS tables, we calculate the pressure in both the tungsten and the plastic on either side of the interface as a function of internal energy. The latter is a function of X-ray flux and cold opacities. Moreover, the plastic experiences an additional jump in pressure due to the passage of the shock, which is found from the Hugoniot relation42

$$\Delta P={u}_{s}^{2}\left({\rho }_{1}-\frac{{\rho }_{1}^{2}}{{\rho }_{2}}\right),$$
(4)

where us is the shock speed and ρ1 and ρ2 are the densities of the plastic ahead and behind the shock, respectively. The shock velocity is estimated from the shock position at 2.3 and 4.0 ns, where we assume the shock velocity to decay somewhere between a linear (r ~ t) and cylindrical Sedov-like (r ~ t1/2) rate, with previous wire explosions finding r ~ t0.8 43. This yields a shock velocity of  ~ 5.35 km/s at 2.3 ns and a pressure jump of ΔP = 0.18 Mbar.

We consider a conversion efficiency of laser energy into copper He-α on the order of 0.5–1.0%28,29, providing a range of reasonable X-ray fluxes based on the geometry and laser energy. We determine the equilibrium pressure by taking the intersection of the two curves, as shown in Supplementary Fig. 1. We find an X-ray flux of 1590 J/cm2 gives rise to equal pressures of 0.39 Mbar on either side of the interface. We are then able to determine the temperature profile of the system near the interface using the density profile, pressure, and FEOS tables.

The timescales for achieving thermal and hydrodynamic equilibrium in our system are well-separated from the experimental timescales under consideration. The kinetic timescale for temperature relaxation is approximately 10 ps, which is orders of magnitude shorter than the experimental timescale of several nanoseconds. Pressure equilibration is governed by the sound speed of the material and a characteristic length scale. For our materials, the sound speed is estimated to be approximately 5900 m/s. Using a characteristic length scale of 3 μm, the approximate extent of thermal diffusion in the experiment, we estimate a pressure equilibration time of  ~0.5 ns. These timescales indicate that the system achieves both thermal and hydrodynamic equilibrium.

We estimate the uncertainty in our assumption of pressure equilibration throughout the sample from the small displacement (Δr) of the interface between the 2.3 ns and 4 ns data points. Assuming linear deceleration of the material during this period, we derive a pressure gradient of dP/dr ~ 2ρΔr/t2, which for the conditions near the interface (ρ ~ 1 g/cm3, t = 1.7 ns, Δr ~ 1 μm) yields 0.01 Mbar/μm. The corresponding uncertainty in the temperature profiles depicted in Fig. 3b is calculated to be dT/dr ~ 0.36 eV/μm in the tungsten and 0.045 eV/μm in the plastic, giving a relative uncertainly of 4.4 %/μm and 1.5 %/μm respectively. We emphasize that this uncertainty alone cannot explain the significant temperature discontinuity observed in the data.

The magnitude of the observed ITR also depends on the accuracy of the equation of state used to obtain the temperature. Although FEOS is a wide-range approach made for quick use, it compares well with a higher-fidelity equation of state data for the conditions encountered in our experiments. For tungsten, FEOS reproduces density functional simulations for densities in the range of 1–20 g/cm3 within 15%44,45,46. The plastic coating of the wire tends toward the Dulong-Petit law, as expected and in good agreement with PROPACEOS47. Discrediting the ITR at all would, on the other hand, require the FEOS data to be incorrect by at least a factor of three. Thus, the existence of the ITR in HED matter is a robust result with respect to errors in the FEOS tables.

To determine the thermal transport from tungsten to plastic, we evolve the system from 2.3 to 4 ns, in the lab reference frame. We use a Lagrangian approach, such as used in hydrodynamics, where computational cells move with the material, and the temperature is tied to the moving material. The heat flux is evaluated within this moving frame, ensuring consistency between the temperature distribution and the evolving material boundaries. We solve Fourier’s Law within each material region to determine the heat flux q(r, T):

$$q(r,T)=-\kappa \nabla T,$$
(5)

where κ is the thermal conductivity of the material. We also calculate the heat transfer across the interface as

$$q(r,T)=\frac{\Delta T}{{R}_{{{{{\rm{Int}}}}}}},$$
(6)

where RInt is the interfacial thermal resistance.

In addition to heat flux, we evaluated the impact of PdV work associated with the expansion of the tungsten wire between 2.3 and 4 ns. During this expansion, the pressure decreases from 0.39 Mbar to 0.27 Mbar, resulting in  ~ 5.5–6.5 MJ/kg of PdV work that is not accounted for in Fourier’s Law alone. However, as the wire decelerates, its kinetic energy is converted to  ~ 6–8 MJ/kg of internal energy, accounting for variations in the velocity distribution. This effectively balances the PdV work, indicating that PdV effects have minimal impact on the thermal transport in our system and that we can determine the thermal conductivities and interfacial thermal resistance from Eqns. (5) and (6).

We vary five parameters to fit the propagation of the density profile at 2.3 ns to that at 4.0 ns. In this case, the thermal conductivities of the tungsten, κW, the plastic, κCHF, and the interfacial thermal resistance, RInt, serve as the primary parameters. The pressure of the system at 4.0 ns is also allowed to vary to match the density and temperature profiles, while a small radial shift is used to account for small differences in the radius of the initial wire targets. As before, we use a Bayesian inference method to determine the statistical uncertainties, performing a Metropolis-Hastings MCMC search through a uniform prior distribution of the propagation parameters. Here, we modify the hard boundary likelihood function such that we accept any density profile at 4.0 ns that falls within the span of profiles found via the diffraction pattern fitting, shown by the blue-shaded region in Fig. 3a. The subset of accepted solutions is shown by the black-shaded region in Fig. 3a and b and corresponds to the parameters shown in Fig. 3c–e. We note that the additional radial shift was found to be  − 0.2 ± 0.1 μm.